Ðлгоритм Ð¿Ð¾Ð»ÑƒÑ‡ÐµÐ½Ð¸Ñ Ð´Ð²ÑƒÑˆÐµÐº Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдков n=4k+2
Message boards :
Science :
Ðлгоритм Ð¿Ð¾Ð»ÑƒÑ‡ÐµÐ½Ð¸Ñ Ð´Ð²ÑƒÑˆÐµÐº Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдков n=4k+2
Message board moderation
Previous · 1 · 2 · 3 · 4 · 5 · 6 . . . 11 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
Отлично Ñработал метод Пелегрино-ЛанÑелотти Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 54 на базе 96-ки 18-го порÑдка! Ð’Ñе ортогональные пары поÑтроилиÑÑŒ. 96-ка, конечно, не получилаÑÑŒ. ИнтереÑно: 96-ка раÑпалаÑÑŒ на шеÑтёрку, 24-ку и 66-ку. И таких групп 8 Order? 54 Enter the name of the squares file: INP1 Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file INP1-orthCounts.txt ..output file INP1-orthNos.txt squares 792 total orthogonal pairs 768 Maximum pairs for square 3: 66 There are 7 other squares with this maximum number of pairs. ..output file INP1-3orths.txt Pairs for square 3: 66 Вот фрагменты из Ñчётчика ортогональных пар orthogonal
square pairs
------ ----------
1 6
2 24
3 66
4 1
5 1
6 1
7 1
8 1
9 1
10 1
. . . . .
161 1
162 1
163 1
164 1
165 1
166 66
167 6
168 24
169 1
170 1
. . . . . .
191 1
192 1
193 24
194 6
195 66
196 24
197 66
198 6
199 1
200 1
. . . . . .
491 1
492 1
493 24
494 66
495 6
496 1
497 1
498 1
499 1
500 1
. . . . . . .
541 1
542 1
543 1
544 6
545 66
546 24
547 1
548 1
549 1
550 1
. . . . . . .
691 6
692 66
693 24
694 1
695 1
696 1
697 1
698 1
699 1
700 1
. . . . . . .
781 1
782 1
783 1
784 1
785 1
786 1
787 1
788 1
789 1
790 24
791 6
792 66Имеем 8 шеÑтёрок, 8 24-ок и 8 66-ок. Показываю оÑновной ДЛК одной из 66-ок и пару ортогоналек DLK 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 5 27 1 2 53 9 11 13 6 14 3 17 10 8 15 16 7 4 23 30 19 20 18 43 29 31 24 32 21 35 28 26 33 34 25 0 41 48 37 38 36 45 47 49 42 50 39 22 46 44 51 52 12 40 4 11 32 1 2 12 14 10 5 8 53 3 6 15 16 13 9 7 0 29 35 19 20 30 49 28 23 26 18 21 24 33 34 31 27 25 40 47 22 37 38 48 50 46 41 44 36 39 42 51 52 17 45 43 8 9 4 26 1 2 17 3 11 6 12 5 15 16 10 14 13 53 46 27 0 25 19 20 35 21 29 24 30 23 33 34 28 32 31 18 44 45 40 43 37 38 22 39 47 42 48 41 51 52 7 50 49 36 7 6 14 9 24 1 2 53 4 5 17 15 16 3 8 10 12 11 25 39 32 27 31 19 20 18 0 23 35 33 34 21 26 28 30 29 43 42 50 45 49 37 38 36 40 41 22 51 52 13 44 46 48 47 2 13 5 8 14 23 1 12 9 11 7 16 53 6 3 17 4 15 20 31 36 26 32 28 19 30 27 29 25 34 18 24 21 35 0 33 38 49 41 44 50 46 37 48 45 47 43 52 10 42 39 22 40 51 1 2 10 11 6 8 29 17 14 4 13 12 5 53 7 9 15 16 19 20 28 48 24 26 21 35 32 0 31 30 23 18 25 27 33 34 37 38 46 47 42 44 39 22 50 40 49 3 41 36 43 45 51 52 12 17 7 13 10 3 53 34 16 2 15 8 14 9 4 11 5 6 30 35 25 31 28 21 18 19 51 20 33 26 32 27 0 29 23 24 48 22 43 49 46 39 36 37 52 38 1 44 50 45 40 47 41 42 9 14 8 6 5 11 4 2 20 1 16 13 7 17 12 53 3 10 27 32 26 24 23 29 0 37 33 19 34 31 25 35 30 18 21 28 45 50 44 42 41 47 40 38 51 15 52 49 43 22 48 36 39 46 10 3 53 12 17 7 13 15 2 19 1 9 4 11 5 6 8 14 28 21 18 30 35 25 31 33 20 34 38 27 0 29 23 24 26 32 46 39 36 48 22 43 49 51 16 52 37 45 40 47 41 42 44 50 17 7 13 10 3 53 12 16 1 15 33 14 9 4 11 5 6 8 35 25 31 28 21 18 30 34 19 52 20 32 27 0 29 23 24 26 22 43 49 46 39 36 48 2 37 51 38 50 45 40 47 41 42 44 3 16 15 53 11 6 8 14 10 17 5 25 13 12 9 7 2 1 21 34 33 18 29 24 26 32 28 35 23 0 31 30 27 44 20 19 39 52 51 36 47 42 4 50 46 22 41 40 49 48 45 43 38 37 16 15 3 5 8 14 10 9 13 12 6 1 35 7 53 4 17 2 34 33 21 23 26 32 28 27 31 30 24 19 29 25 18 0 50 20 52 51 39 41 44 11 46 45 49 48 42 37 47 43 36 40 22 38 15 10 6 14 9 13 16 4 7 53 8 2 1 30 17 3 11 12 33 28 24 32 27 31 34 0 25 18 26 20 19 23 35 21 29 45 51 46 42 50 5 49 52 40 43 36 44 38 37 41 22 39 47 48 13 8 9 4 7 16 15 11 17 3 14 53 2 1 18 12 10 5 31 26 27 0 25 34 33 29 35 21 32 40 20 19 24 30 28 23 49 44 45 6 43 52 51 47 22 39 50 36 38 37 42 48 46 41 14 4 11 17 16 15 7 5 12 10 9 6 3 2 1 21 53 13 32 0 29 35 34 33 25 23 30 28 27 24 47 20 19 26 18 31 50 40 8 22 52 51 43 41 48 46 45 42 39 38 37 44 36 49 11 5 12 16 15 17 9 6 53 13 4 7 8 10 2 1 28 3 29 23 30 34 33 35 27 24 18 31 0 25 26 41 20 19 32 21 47 14 48 52 51 22 45 42 36 49 40 43 44 46 38 37 50 39 6 53 16 15 12 4 5 8 3 7 11 10 17 14 13 2 1 31 24 18 34 33 30 0 23 26 21 25 29 28 35 32 42 20 19 27 9 36 52 51 48 40 41 44 39 43 47 46 22 50 49 38 37 45 53 34 33 29 25 30 18 26 21 31 23 35 27 24 28 20 19 47 40 38 37 10 0 36 39 44 46 43 41 48 45 42 49 52 51 50 32 15 16 13 6 14 9 12 4 5 7 8 3 17 11 1 2 22 30 12 34 33 0 31 35 24 18 28 29 32 23 21 20 19 40 25 36 45 38 37 3 27 48 42 39 49 47 50 41 46 52 51 44 22 14 26 15 16 10 5 8 17 9 11 13 53 7 4 1 2 43 6 25 35 17 34 33 27 28 23 30 21 0 29 18 20 19 45 31 26 22 48 50 38 37 53 32 41 36 46 40 47 39 52 51 42 43 44 6 8 24 15 16 3 11 7 14 4 10 13 9 1 2 49 5 12 21 31 25 7 34 33 32 29 35 18 27 30 20 19 50 28 24 0 26 43 22 44 38 37 12 47 48 39 45 36 52 51 41 49 42 40 4 5 6 23 15 16 53 13 8 9 3 14 1 2 46 11 17 10 26 18 28 31 13 34 33 0 25 30 32 20 19 44 21 23 27 35 17 24 49 43 42 38 37 40 22 36 50 52 51 47 46 41 45 48 12 9 11 5 29 15 16 10 6 14 53 1 2 39 4 7 3 8 33 24 30 21 28 10 34 27 31 35 26 19 42 18 29 32 25 20 37 7 23 46 49 41 38 45 43 48 44 51 40 39 47 50 22 52 16 17 14 4 11 0 15 3 5 8 12 2 36 9 13 53 6 1 34 33 23 35 18 21 3 32 28 25 24 41 30 0 26 31 20 19 38 37 13 29 39 46 47 50 49 22 42 45 36 40 44 43 52 51 15 16 7 8 9 4 27 53 11 6 17 48 14 10 12 5 1 2 27 32 26 24 23 29 0 1 19 33 37 21 28 31 25 35 30 18 45 50 44 42 41 47 40 38 34 15 52 46 49 43 22 48 36 39 3 53 12 17 7 13 10 20 2 16 51 4 11 5 6 8 14 9 31 28 21 18 30 35 25 33 15 51 19 24 26 32 27 0 29 23 43 49 46 39 36 48 22 20 52 38 1 42 44 50 45 40 47 41 5 11 4 9 14 8 6 16 34 37 2 17 12 53 3 10 13 7 23 29 0 27 32 26 24 20 52 16 34 31 25 35 30 18 21 28 41 47 40 45 50 44 42 2 37 51 19 43 22 48 36 39 46 49 7 13 10 3 53 12 17 1 38 33 15 5 6 8 14 9 4 11 32 26 24 23 29 0 27 38 34 20 2 28 31 25 35 30 18 21 50 44 42 41 47 40 45 51 16 33 37 49 43 22 48 36 39 46 53 12 17 7 13 10 3 52 15 1 19 11 5 6 8 14 9 4 29 19 20 0 35 18 43 28 23 32 30 4 24 27 31 26 33 34 47 51 52 40 48 39 46 49 41 50 36 22 42 45 6 25 37 38 13 2 1 10 8 9 44 11 7 53 14 21 17 3 5 12 16 15 19 20 29 30 21 22 23 31 24 27 18 34 11 26 0 25 32 33 51 52 47 36 46 49 41 43 42 45 39 38 48 44 40 8 35 37 2 1 13 14 4 50 7 5 17 3 9 15 28 12 10 6 53 16 20 23 18 28 48 24 19 25 26 0 21 33 34 5 32 29 35 27 52 41 39 49 43 42 51 22 44 40 46 37 38 36 50 47 14 30 1 7 9 11 45 17 2 6 12 10 4 16 15 31 53 13 8 3 24 21 31 36 26 19 20 35 32 29 28 0 33 34 6 27 23 30 42 46 43 22 44 51 52 48 50 47 49 18 37 38 39 45 41 9 17 4 5 40 12 2 1 8 53 13 11 10 16 15 25 3 7 14 28 25 39 32 19 20 26 30 27 23 31 18 29 33 34 8 0 24 49 22 48 50 51 52 44 36 45 41 43 4 21 37 38 46 40 42 11 6 47 53 2 1 12 14 3 7 5 9 13 16 15 35 10 17 35 46 27 19 20 32 31 18 0 24 25 26 21 23 33 34 14 29 48 36 45 51 52 50 43 39 40 42 22 44 11 28 37 38 49 47 8 41 3 2 1 53 5 9 10 17 6 12 4 7 16 15 30 13 49 0 19 20 27 25 30 21 29 26 35 23 32 28 24 33 34 9 39 40 51 52 45 22 36 46 47 44 48 41 50 5 31 37 38 43 42 10 2 1 3 6 14 4 13 12 8 7 53 11 17 16 15 18 42 51 52 44 36 46 49 40 43 48 50 39 41 45 22 37 38 32 3 16 15 47 8 9 4 17 11 6 13 14 53 7 5 2 1 12 10 20 19 27 21 31 25 23 35 18 0 28 26 29 30 34 33 24 46 41 51 52 42 48 39 45 49 22 44 47 50 43 37 38 26 36 9 53 16 15 40 6 14 7 4 5 10 12 13 11 2 1 17 8 31 3 20 19 32 18 28 29 25 30 27 24 0 35 34 33 23 21 36 39 47 51 52 41 22 50 46 43 42 44 49 37 38 24 48 40 8 14 12 16 15 45 5 13 9 11 3 10 4 2 1 7 6 17 21 28 53 20 19 26 30 0 31 35 32 27 25 34 33 29 18 23 43 48 36 40 51 52 47 44 39 49 41 46 37 38 23 22 45 42 11 6 8 17 16 15 50 10 14 4 53 9 2 1 13 5 7 3 35 18 21 12 20 19 24 27 28 25 26 31 34 33 0 30 29 32 40 49 22 48 45 51 52 42 36 46 47 37 38 29 43 50 41 39 44 4 5 6 7 16 15 3 8 9 12 2 1 10 11 13 53 14 23 25 30 18 17 20 19 32 21 31 24 34 33 27 35 0 26 28 52 45 46 43 22 50 51 41 48 39 40 38 0 49 44 47 36 37 15 42 9 11 5 13 16 53 6 14 17 1 3 4 10 12 8 2 19 29 31 35 30 7 20 26 18 28 23 33 32 25 27 24 21 34 51 52 50 39 49 43 44 47 22 36 45 27 46 42 40 48 37 38 16 15 41 14 4 11 10 12 5 8 7 53 9 3 17 6 2 1 20 19 0 28 25 35 13 24 30 21 29 26 31 32 23 18 34 33 41 47 40 45 50 44 42 51 38 52 20 43 22 48 36 39 46 49 53 12 17 7 13 10 3 16 1 37 2 11 5 6 8 14 9 4 26 24 23 29 0 27 32 15 33 19 34 35 30 18 21 28 31 25 48 22 43 49 46 39 36 52 37 34 38 45 40 47 41 42 44 50 6 5 11 4 9 14 8 15 2 16 51 7 17 12 53 3 10 13 18 30 35 25 31 28 21 19 1 20 33 29 23 24 26 32 27 0 50 44 42 41 47 40 45 37 33 38 51 48 36 39 46 49 43 22 13 10 3 53 12 17 7 52 15 1 16 6 8 14 9 4 11 5 0 27 32 26 24 23 29 34 19 2 20 18 21 28 31 25 35 30 47 40 45 50 44 42 41 19 51 37 52 22 48 36 39 46 49 43 12 17 7 13 10 3 53 1 38 2 15 5 6 8 14 9 4 11 24 23 29 0 27 32 26 33 20 34 16 30 18 21 28 31 25 35 44 38 37 42 39 49 21 22 50 47 46 36 45 41 48 40 52 51 10 1 2 3 14 4 11 5 13 12 9 8 7 53 43 17 15 16 27 33 34 32 28 25 35 30 0 24 31 6 29 26 18 23 19 20 38 37 44 46 43 28 50 48 45 41 49 51 39 40 42 36 47 52 1 2 10 9 11 5 13 6 7 53 4 16 14 17 3 22 12 15 33 34 27 31 35 30 0 18 29 26 25 20 8 23 32 21 24 19 37 50 49 22 31 45 38 36 40 42 43 52 51 46 47 44 39 41 2 13 4 5 6 7 1 8 17 3 11 15 16 9 12 10 48 53 34 0 25 30 18 29 33 21 23 32 35 19 20 14 24 27 28 26 45 43 48 25 40 38 37 39 47 44 22 42 52 51 49 41 50 46 7 11 6 8 17 1 2 14 12 10 5 3 15 16 4 53 13 36 29 35 18 21 23 33 34 28 24 27 30 32 19 20 9 26 0 31 22 36 35 47 38 37 40 46 41 50 48 49 44 52 51 43 42 45 5 8 14 12 1 2 17 9 53 13 6 39 10 15 16 11 3 7 30 21 28 24 33 34 23 31 26 0 18 25 27 19 20 4 32 29 39 30 41 38 37 47 48 49 42 45 36 40 43 50 52 51 22 44 14 9 53 1 2 12 6 4 3 7 8 17 46 13 15 16 5 10 28 31 26 33 34 24 18 25 32 29 21 23 35 0 19 20 11 27 18 42 38 37 41 36 46 43 44 40 39 50 47 22 45 52 51 48 4 3 1 2 53 8 9 11 10 17 14 13 12 49 7 15 16 6 25 32 33 34 26 21 31 35 27 23 28 0 24 30 29 19 20 5 mate #1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 6 37 16 8 17 14 5 10 15 11 4 12 13 9 3 2 1 22 24 25 34 26 35 7 23 28 33 29 53 30 31 27 21 20 19 18 42 43 52 44 0 50 41 46 51 47 40 48 49 45 39 38 32 36 5 6 52 2 15 1 9 4 3 22 14 13 11 17 8 16 7 12 23 24 28 20 33 19 10 53 21 18 32 31 29 35 26 34 25 30 41 42 46 38 51 37 45 40 39 36 50 49 47 0 44 27 43 48 11 5 6 38 8 3 16 14 17 7 9 22 1 15 2 10 12 13 4 23 24 53 26 21 34 32 35 25 27 18 19 33 20 28 30 31 47 41 42 40 44 39 52 50 0 43 45 36 37 51 29 46 48 49 2 22 5 6 44 15 17 9 1 10 11 16 3 8 4 12 13 7 20 14 23 24 32 33 35 27 19 28 29 34 21 26 53 30 31 25 38 36 41 42 50 51 0 45 37 46 47 52 39 18 40 48 49 43 1 8 7 5 6 51 3 11 16 4 22 17 15 14 12 13 10 2 19 26 9 23 24 27 21 29 34 53 18 35 33 32 30 31 28 20 37 44 43 41 42 45 39 47 52 40 36 0 25 50 48 49 46 38 17 16 15 10 5 6 39 22 2 14 7 3 9 12 13 4 8 1 35 34 33 11 23 24 29 18 20 32 25 21 27 30 31 53 26 19 0 52 51 46 41 42 47 36 38 50 43 28 45 48 49 40 44 37 4 14 9 11 22 7 10 41 6 12 5 15 8 2 16 1 17 3 53 32 27 29 18 25 28 31 13 30 23 33 26 20 34 19 35 21 40 50 45 47 36 43 46 49 42 48 24 51 44 38 52 37 0 39 3 17 1 16 2 8 15 5 42 6 13 9 14 4 10 7 22 11 21 35 19 34 20 26 33 12 30 24 31 27 32 53 28 25 18 29 39 0 37 52 38 44 51 41 48 23 49 45 50 40 46 43 36 47 8 15 3 17 1 16 2 6 13 49 12 10 7 22 11 9 14 4 26 33 21 35 19 34 20 24 31 23 5 28 25 18 29 27 32 53 44 51 39 0 37 52 38 42 30 41 48 46 43 36 47 45 50 40 9 11 22 7 10 4 14 12 5 13 48 1 17 3 15 8 2 16 27 29 18 25 28 53 32 30 23 6 24 19 35 21 33 26 20 34 45 47 36 43 46 40 50 31 41 49 42 37 0 39 51 44 38 52 16 9 4 1 13 12 7 3 14 8 15 43 6 5 22 17 11 10 34 27 53 19 31 30 25 21 32 26 33 20 24 23 18 2 29 28 52 45 40 37 49 48 35 39 50 44 51 38 42 41 36 0 47 46 14 10 17 13 12 22 1 15 4 2 8 7 36 6 5 11 3 9 32 28 35 31 30 18 19 33 53 20 26 25 34 24 23 29 16 27 50 46 0 49 48 21 37 51 40 38 44 43 52 42 41 47 39 45 7 3 13 12 11 17 4 8 10 16 2 14 22 47 6 5 9 15 25 21 31 30 29 35 53 26 28 34 20 32 18 19 24 23 27 1 43 39 49 48 33 0 40 44 46 52 38 50 36 37 42 41 45 51 15 13 12 9 3 10 22 2 7 1 16 8 4 11 45 6 5 14 33 31 30 27 21 28 18 20 25 19 34 17 53 29 35 24 23 32 51 49 48 26 39 46 36 38 43 37 52 44 40 47 0 42 41 50 13 12 14 15 7 11 8 16 22 17 1 4 2 10 9 50 6 5 31 30 32 33 25 29 26 34 18 35 19 53 3 28 27 21 24 23 49 48 20 51 43 47 44 52 36 0 37 40 38 46 45 39 42 41 12 4 8 22 9 2 13 1 11 3 17 5 10 16 7 14 40 6 30 53 26 18 27 20 31 19 29 21 35 23 28 15 25 32 33 24 48 34 44 36 45 38 49 37 47 39 0 41 46 52 43 50 51 42 10 2 11 14 16 13 12 17 9 15 3 6 5 7 1 22 4 46 28 20 29 32 34 31 30 35 27 33 21 24 23 25 8 18 53 26 19 38 47 50 52 49 48 0 45 51 39 42 41 43 37 36 40 44 22 47 43 50 38 49 48 37 46 51 52 39 42 41 44 40 36 21 14 8 3 45 53 12 13 9 17 10 11 4 5 6 7 1 15 2 16 32 29 28 34 24 23 35 18 26 19 33 31 30 20 25 27 0 48 7 36 46 45 44 49 52 40 39 38 42 41 51 50 43 35 0 13 9 15 17 47 32 12 11 1 4 22 5 6 10 16 3 8 14 23 2 27 18 53 20 24 19 25 33 34 31 30 26 28 29 37 21 49 48 10 43 40 47 51 38 50 0 44 41 39 45 46 19 37 42 12 13 11 3 1 36 27 22 16 14 7 6 4 2 17 15 9 5 24 23 8 29 25 32 26 34 28 21 20 30 33 53 18 52 35 31 39 49 48 4 46 50 36 44 45 37 51 0 47 40 34 52 42 41 29 12 13 22 17 16 43 7 2 9 10 14 8 1 3 11 5 6 33 24 23 15 18 28 27 20 53 35 26 21 32 25 38 19 31 30 43 0 49 48 14 40 45 51 47 52 39 36 50 20 38 42 41 37 46 18 12 13 7 1 2 10 8 11 4 15 16 17 22 5 6 9 29 21 24 23 3 25 53 26 32 19 33 27 28 44 34 31 30 35 47 46 37 49 48 9 50 39 36 38 0 45 26 44 42 41 52 43 8 40 25 12 13 10 16 4 15 22 14 2 1 7 5 6 11 3 32 18 35 24 23 17 28 33 27 34 21 53 51 20 31 30 19 29 45 36 40 52 49 48 11 0 43 44 37 33 51 42 41 38 46 47 2 15 50 28 12 13 4 14 3 7 9 16 10 5 6 22 17 8 53 27 25 19 24 23 1 21 29 20 35 39 26 31 30 34 18 32 38 44 51 39 0 37 52 13 48 42 30 40 46 43 36 47 45 50 22 7 10 4 14 9 11 6 24 49 12 1 17 3 15 8 2 16 34 20 26 33 21 35 19 5 23 31 41 25 18 29 27 32 53 28 50 45 47 36 43 46 40 49 12 31 41 51 44 38 52 37 0 39 16 2 8 15 3 17 1 23 5 13 48 10 7 22 11 9 14 4 28 53 32 27 29 18 25 24 6 42 30 26 20 34 19 35 21 33 46 40 50 45 47 36 43 48 24 5 42 52 37 0 39 51 44 38 17 1 16 2 8 15 3 41 6 12 30 11 9 14 4 10 7 22 18 25 28 53 32 27 29 23 49 13 31 19 35 21 33 26 20 34 51 39 0 37 52 38 44 23 49 41 6 47 45 50 40 46 43 36 10 4 14 9 11 22 7 5 42 31 13 8 2 16 1 17 3 15 26 33 21 35 19 34 20 48 24 30 12 32 53 28 25 18 29 27 36 51 38 47 41 42 29 50 44 46 40 2 48 49 0 45 39 52 15 10 22 8 6 5 9 16 7 17 1 3 13 12 37 35 4 11 27 26 34 32 30 31 43 28 20 18 25 14 23 24 21 53 33 19 44 52 45 41 42 27 47 40 38 43 46 37 16 48 49 39 50 51 7 11 2 6 5 14 8 1 22 3 17 9 15 13 12 0 21 10 20 19 53 30 31 36 32 25 34 29 18 35 4 23 24 33 28 26 37 50 41 42 32 45 38 46 52 36 43 44 0 1 48 49 51 40 9 16 6 5 4 2 22 17 11 15 3 7 14 8 13 12 39 33 35 28 30 31 47 53 34 18 19 27 29 20 21 10 23 24 26 25 40 41 42 53 50 52 0 43 37 47 36 46 38 39 17 48 49 44 1 6 5 10 16 11 14 3 9 8 15 26 22 4 2 13 12 51 25 30 31 45 28 19 21 29 35 32 27 18 34 33 7 23 24 20 41 42 28 40 37 39 46 36 0 45 47 38 43 52 51 3 48 49 6 5 7 1 9 4 17 15 14 2 8 44 20 11 10 16 13 12 30 31 50 25 35 33 18 27 21 53 32 34 29 19 26 22 23 24 42 25 46 0 51 43 41 47 39 50 45 49 52 36 37 44 15 48 5 22 17 14 10 3 6 8 4 16 2 12 38 34 9 7 1 13 31 40 18 21 26 29 30 32 33 28 53 24 19 27 35 20 11 23 18 43 39 44 36 41 42 45 51 40 50 48 49 37 47 0 38 8 11 3 4 7 15 6 5 2 10 1 16 13 12 52 19 14 22 17 46 29 33 20 27 30 31 53 26 25 28 23 24 35 32 21 34 9 27 35 34 33 25 30 31 29 20 53 18 32 23 24 28 26 19 45 37 36 46 16 44 42 41 52 40 39 38 0 49 48 51 50 43 47 21 10 14 22 15 13 12 2 9 17 8 1 6 5 3 11 4 7 31 29 19 20 21 28 30 18 26 32 25 23 24 53 33 34 47 27 41 52 43 40 2 51 42 38 50 0 44 49 48 39 45 46 36 37 12 35 4 9 7 3 13 8 11 1 15 6 5 17 22 14 10 16 30 31 18 34 26 35 53 25 33 27 28 24 32 21 20 36 29 23 42 41 38 46 50 8 39 44 45 37 51 48 0 47 40 43 52 49 13 12 19 14 11 10 17 15 22 16 3 5 1 7 9 4 2 6 32 30 31 25 20 33 19 28 21 29 53 27 35 26 43 18 23 24 0 42 41 44 40 45 15 51 47 52 39 37 36 50 46 38 49 48 1 13 12 34 9 22 4 3 7 2 17 16 10 11 14 8 6 5 34 27 30 31 28 26 21 53 35 18 32 19 33 46 25 23 24 29 3 37 42 41 51 50 47 39 36 38 0 43 45 40 44 49 48 52 14 16 13 12 20 11 7 17 10 8 1 4 22 9 15 6 5 2 35 20 29 30 31 53 33 32 19 25 27 21 40 28 23 24 18 34 36 17 52 42 41 39 45 0 43 44 37 47 50 51 49 48 38 46 10 9 2 13 12 26 22 1 4 15 16 7 11 3 6 5 8 14 21 19 26 18 30 31 32 27 34 28 29 50 53 23 24 25 20 35 47 43 1 38 42 41 0 37 46 51 52 45 39 49 48 44 40 36 7 4 11 8 13 12 33 16 14 3 2 22 17 6 5 15 9 10 25 28 53 32 27 29 18 24 31 23 49 26 20 34 19 35 21 33 44 51 39 0 37 52 38 48 41 5 42 50 40 46 43 36 47 45 15 3 17 1 16 2 8 30 12 6 13 11 9 14 4 10 7 22 33 21 35 19 34 20 26 30 23 48 24 53 28 25 18 29 27 32 45 47 36 43 46 40 50 42 49 41 6 39 51 44 38 52 37 0 22 7 10 4 14 9 11 13 31 12 5 17 3 15 8 2 16 1 20 26 33 21 35 19 34 31 41 30 23 18 29 27 32 53 28 25 40 50 45 47 36 43 46 13 48 42 49 38 52 37 0 39 51 44 9 11 22 7 10 4 14 12 5 24 6 8 2 16 1 17 3 15 53 32 27 29 18 25 28 42 30 24 31 35 21 33 26 20 34 19 39 0 37 52 38 44 51 49 12 48 41 36 47 45 50 40 46 43 17 1 16 2 8 15 3 6 13 5 23 10 7 22 11 9 14 4 19 53 25 35 24 23 37 33 28 20 26 34 31 30 27 21 32 18 43 39 44 36 48 49 52 45 51 40 50 46 41 42 14 47 0 38 4 17 15 10 5 6 2 22 3 9 11 29 12 13 16 7 1 8 28 18 21 24 23 0 35 26 25 34 20 29 19 31 30 32 33 53 51 38 47 48 49 37 36 50 44 46 40 52 43 41 42 4 45 39 3 8 7 5 6 16 10 11 15 14 9 2 27 12 13 1 22 17 29 33 24 23 39 21 25 20 18 19 34 28 27 35 31 30 53 26 52 45 48 49 0 47 44 40 38 43 46 51 37 36 41 42 10 50 2 22 5 6 1 7 15 9 8 4 14 3 16 32 12 13 17 11 26 24 23 51 33 18 27 34 29 35 19 20 25 32 21 31 30 28 50 48 49 39 45 38 37 46 52 36 43 40 44 0 47 41 42 7 11 5 6 17 22 8 16 14 2 10 4 9 15 1 53 12 13 3 24 23 44 26 29 32 20 19 27 21 35 25 34 18 53 33 31 30 48 49 51 50 52 0 40 43 37 47 36 22 46 38 39 45 41 42 5 6 3 11 2 1 9 4 16 7 10 15 14 8 17 28 12 13 23 38 20 27 53 34 24 35 32 33 21 30 18 19 29 28 26 31 49 44 40 37 39 46 48 36 0 45 47 42 11 43 52 51 50 41 6 15 9 16 17 14 5 10 1 22 7 13 8 4 2 3 25 12 52 34 32 28 19 24 23 21 53 26 33 31 30 29 35 27 25 20 38 46 0 51 43 48 49 47 39 50 45 41 42 9 36 37 44 40 8 14 1 3 4 5 6 7 17 11 22 12 13 2 10 16 15 18 mate #2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 6 37 16 8 17 14 5 10 15 11 4 12 13 9 3 2 1 22 24 25 34 26 35 7 23 28 33 29 53 30 31 27 21 20 19 18 42 43 52 44 0 50 41 46 51 47 40 48 49 45 39 38 32 36 5 6 52 2 15 1 9 4 3 22 14 13 11 17 8 16 7 12 23 24 28 20 33 19 10 53 21 18 32 31 29 35 26 34 25 30 41 42 46 38 51 37 45 40 39 36 50 49 47 0 44 27 43 48 11 5 6 38 8 3 16 14 17 7 9 22 1 15 2 10 12 13 4 23 24 53 26 21 34 32 35 25 27 18 19 33 20 28 30 31 47 41 42 40 44 39 52 50 0 43 45 36 37 51 29 46 48 49 2 22 5 6 44 15 17 9 1 10 11 16 3 8 4 12 13 7 20 14 23 24 32 33 35 27 19 28 29 34 21 26 53 30 31 25 38 36 41 42 50 51 0 45 37 46 47 52 39 18 40 48 49 43 1 8 7 5 6 51 3 11 16 4 22 17 15 14 12 13 10 2 19 26 9 23 24 27 21 29 34 53 18 35 33 32 30 31 28 20 37 44 43 41 42 45 39 47 52 40 36 0 25 50 48 49 46 38 17 16 15 10 5 6 39 22 2 14 7 3 9 12 13 4 8 1 35 34 33 11 23 24 29 18 20 32 25 21 27 30 31 53 26 19 0 52 51 46 41 42 47 36 38 50 43 28 45 48 49 40 44 37 4 14 9 11 22 7 10 41 6 13 5 15 8 2 16 1 17 3 53 32 27 29 18 25 28 30 12 31 23 33 26 20 34 19 35 21 40 50 45 47 36 43 46 48 42 49 24 51 44 38 52 37 0 39 3 17 1 16 2 8 15 5 42 6 12 9 14 4 10 7 22 11 21 35 19 34 20 26 33 13 31 24 30 27 32 53 28 25 18 29 39 0 37 52 38 44 51 41 49 23 48 45 50 40 46 43 36 47 8 15 3 17 1 16 2 6 12 48 13 10 7 22 11 9 14 4 26 33 21 35 19 34 20 24 30 23 5 28 25 18 29 27 32 53 44 51 39 0 37 52 38 42 31 41 49 46 43 36 47 45 50 40 9 11 22 7 10 4 14 13 5 12 49 1 17 3 15 8 2 16 27 29 18 25 28 53 32 31 23 6 24 19 35 21 33 26 20 34 45 47 36 43 46 40 50 30 41 48 42 37 0 39 51 44 38 52 16 9 4 1 13 12 7 3 14 8 15 43 6 5 22 17 11 10 34 27 53 19 31 30 25 21 32 26 33 20 24 23 18 2 29 28 52 45 40 37 49 48 35 39 50 44 51 38 42 41 36 0 47 46 14 10 17 13 12 22 1 15 4 2 8 7 36 6 5 11 3 9 32 28 35 31 30 18 19 33 53 20 26 25 34 24 23 29 16 27 50 46 0 49 48 21 37 51 40 38 44 43 52 42 41 47 39 45 7 3 13 12 11 17 4 8 10 16 2 14 22 47 6 5 9 15 25 21 31 30 29 35 53 26 28 34 20 32 18 19 24 23 27 1 43 39 49 48 33 0 40 44 46 52 38 50 36 37 42 41 45 51 15 13 12 9 3 10 22 2 7 1 16 8 4 11 45 6 5 14 33 31 30 27 21 28 18 20 25 19 34 17 53 29 35 24 23 32 51 49 48 26 39 46 36 38 43 37 52 44 40 47 0 42 41 50 13 12 14 15 7 11 8 16 22 17 1 4 2 10 9 50 6 5 31 30 32 33 25 29 26 34 18 35 19 53 3 28 27 21 24 23 49 48 20 51 43 47 44 52 36 0 37 40 38 46 45 39 42 41 12 4 8 22 9 2 13 1 11 3 17 5 10 16 7 14 40 6 30 53 26 18 27 20 31 19 29 21 35 23 28 15 25 32 33 24 48 34 44 36 45 38 49 37 47 39 0 41 46 52 43 50 51 42 10 2 11 14 16 13 12 17 9 15 3 6 5 7 1 22 4 46 28 20 29 32 34 31 30 35 27 33 21 24 23 25 8 18 53 26 19 38 47 50 52 49 48 0 45 51 39 42 41 43 37 36 40 44 22 47 43 50 38 48 49 37 46 51 52 39 41 42 44 40 36 21 14 8 3 45 53 13 12 9 17 10 11 4 6 5 7 1 15 2 16 32 29 28 34 24 23 35 18 26 19 33 31 30 20 25 27 0 49 7 36 46 45 44 48 52 40 39 38 41 42 51 50 43 35 0 12 9 15 17 47 32 13 11 1 4 22 6 5 10 16 3 8 14 23 2 27 18 53 20 24 19 25 33 34 31 30 26 28 29 37 21 48 49 10 43 40 47 51 38 50 0 44 42 39 45 46 19 37 41 13 12 11 3 1 36 27 22 16 14 7 5 4 2 17 15 9 6 24 23 8 29 25 32 26 34 28 21 20 30 33 53 18 52 35 31 39 48 49 4 46 50 36 44 45 37 51 0 47 40 34 52 41 42 29 13 12 22 17 16 43 7 2 9 10 14 8 1 3 11 6 5 33 24 23 15 18 28 27 20 53 35 26 21 32 25 38 19 31 30 43 0 48 49 14 40 45 51 47 52 39 36 50 20 38 41 42 37 46 18 13 12 7 1 2 10 8 11 4 15 16 17 22 6 5 9 29 21 24 23 3 25 53 26 32 19 33 27 28 44 34 31 30 35 47 46 37 48 49 9 50 39 36 38 0 45 26 44 41 42 52 43 8 40 25 13 12 10 16 4 15 22 14 2 1 7 6 5 11 3 32 18 35 24 23 17 28 33 27 34 21 53 51 20 31 30 19 29 45 36 40 52 48 49 11 0 43 44 37 33 51 41 42 38 46 47 2 15 50 28 13 12 4 14 3 7 9 16 10 6 5 22 17 8 53 27 25 19 24 23 1 21 29 20 35 39 26 31 30 34 18 32 38 44 51 39 0 37 52 12 49 42 31 40 46 43 36 47 45 50 22 7 10 4 14 9 11 6 24 48 13 1 17 3 15 8 2 16 34 20 26 33 21 35 19 5 23 30 41 25 18 29 27 32 53 28 50 45 47 36 43 46 40 48 13 30 41 51 44 38 52 37 0 39 16 2 8 15 3 17 1 23 5 12 49 10 7 22 11 9 14 4 28 53 32 27 29 18 25 24 6 42 31 26 20 34 19 35 21 33 46 40 50 45 47 36 43 49 24 5 42 52 37 0 39 51 44 38 17 1 16 2 8 15 3 41 6 13 31 11 9 14 4 10 7 22 18 25 28 53 32 27 29 23 48 12 30 19 35 21 33 26 20 34 51 39 0 37 52 38 44 23 48 41 6 47 45 50 40 46 43 36 10 4 14 9 11 22 7 5 42 30 12 8 2 16 1 17 3 15 26 33 21 35 19 34 20 49 24 31 13 32 53 28 25 18 29 27 36 51 38 47 42 41 29 50 44 46 40 2 49 48 0 45 39 52 15 10 22 8 5 6 9 16 7 17 1 3 12 13 37 35 4 11 27 26 34 32 30 31 43 28 20 18 25 14 23 24 21 53 33 19 44 52 45 42 41 27 47 40 38 43 46 37 16 49 48 39 50 51 7 11 2 5 6 14 8 1 22 3 17 9 15 12 13 0 21 10 20 19 53 30 31 36 32 25 34 29 18 35 4 23 24 33 28 26 37 50 42 41 32 45 38 46 52 36 43 44 0 1 49 48 51 40 9 16 5 6 4 2 22 17 11 15 3 7 14 8 12 13 39 33 35 28 30 31 47 53 34 18 19 27 29 20 21 10 23 24 26 25 40 42 41 53 50 52 0 43 37 47 36 46 38 39 17 49 48 44 1 5 6 10 16 11 14 3 9 8 15 26 22 4 2 12 13 51 25 30 31 45 28 19 21 29 35 32 27 18 34 33 7 23 24 20 42 41 28 40 37 39 46 36 0 45 47 38 43 52 51 3 49 48 5 6 7 1 9 4 17 15 14 2 8 44 20 11 10 16 12 13 30 31 50 25 35 33 18 27 21 53 32 34 29 19 26 22 23 24 41 25 46 0 51 43 42 47 39 50 45 48 52 36 37 44 15 49 6 22 17 14 10 3 5 8 4 16 2 13 38 34 9 7 1 12 31 40 18 21 26 29 30 32 33 28 53 24 19 27 35 20 11 23 18 43 39 44 36 42 41 45 51 40 50 49 48 37 47 0 38 8 11 3 4 7 15 5 6 2 10 1 16 12 13 52 19 14 22 17 46 29 33 20 27 30 31 53 26 25 28 23 24 35 32 21 34 9 27 35 34 33 25 31 30 29 20 53 18 32 24 23 28 26 19 45 37 36 46 16 44 42 41 52 40 39 38 0 49 48 51 50 43 47 21 10 14 22 15 12 13 2 9 17 8 1 5 6 3 11 4 7 30 29 19 20 21 28 31 18 26 32 25 24 23 53 33 34 47 27 41 52 43 40 2 51 42 38 50 0 44 49 48 39 45 46 36 37 13 35 4 9 7 3 12 8 11 1 15 5 6 17 22 14 10 16 31 30 18 34 26 35 53 25 33 27 28 23 32 21 20 36 29 24 42 41 38 46 50 8 39 44 45 37 51 48 0 47 40 43 52 49 12 13 19 14 11 10 17 15 22 16 3 6 1 7 9 4 2 5 32 31 30 25 20 33 19 28 21 29 53 27 35 26 43 18 24 23 0 42 41 44 40 45 15 51 47 52 39 37 36 50 46 38 49 48 1 12 13 34 9 22 4 3 7 2 17 16 10 11 14 8 5 6 34 27 31 30 28 26 21 53 35 18 32 19 33 46 25 24 23 29 3 37 42 41 51 50 47 39 36 38 0 43 45 40 44 49 48 52 14 16 12 13 20 11 7 17 10 8 1 4 22 9 15 5 6 2 35 20 29 31 30 53 33 32 19 25 27 21 40 28 24 23 18 34 36 17 52 42 41 39 45 0 43 44 37 47 50 51 49 48 38 46 10 9 2 12 13 26 22 1 4 15 16 7 11 3 5 6 8 14 21 19 26 18 31 30 32 27 34 28 29 50 53 24 23 25 20 35 47 43 1 38 42 41 0 37 46 51 52 45 39 49 48 44 40 36 7 4 11 8 12 13 33 16 14 3 2 22 17 5 6 15 9 10 25 28 53 32 27 29 18 24 30 23 48 26 20 34 19 35 21 33 44 51 39 0 37 52 38 49 41 5 42 50 40 46 43 36 47 45 15 3 17 1 16 2 8 31 13 6 12 11 9 14 4 10 7 22 33 21 35 19 34 20 26 31 23 49 24 53 28 25 18 29 27 32 45 47 36 43 46 40 50 42 48 41 6 39 51 44 38 52 37 0 22 7 10 4 14 9 11 12 30 13 5 17 3 15 8 2 16 1 20 26 33 21 35 19 34 30 41 31 23 18 29 27 32 53 28 25 40 50 45 47 36 43 46 12 49 42 48 38 52 37 0 39 51 44 9 11 22 7 10 4 14 13 5 24 6 8 2 16 1 17 3 15 53 32 27 29 18 25 28 42 31 24 30 35 21 33 26 20 34 19 39 0 37 52 38 44 51 48 13 49 41 36 47 45 50 40 46 43 17 1 16 2 8 15 3 6 12 5 23 10 7 22 11 9 14 4 19 53 25 35 23 24 37 33 28 20 26 34 30 31 27 21 32 18 43 39 44 36 48 49 52 45 51 40 50 46 41 42 14 47 0 38 4 17 15 10 6 5 2 22 3 9 11 29 13 12 16 7 1 8 28 18 21 23 24 0 35 26 25 34 20 29 19 30 31 32 33 53 51 38 47 48 49 37 36 50 44 46 40 52 43 41 42 4 45 39 3 8 7 6 5 16 10 11 15 14 9 2 27 13 12 1 22 17 29 33 23 24 39 21 25 20 18 19 34 28 27 35 30 31 53 26 52 45 48 49 0 47 44 40 38 43 46 51 37 36 41 42 10 50 2 22 6 5 1 7 15 9 8 4 14 3 16 32 13 12 17 11 26 23 24 51 33 18 27 34 29 35 19 20 25 32 21 30 31 28 50 48 49 39 45 38 37 46 52 36 43 40 44 0 47 41 42 7 11 6 5 17 22 8 16 14 2 10 4 9 15 1 53 13 12 3 23 24 44 26 29 32 20 19 27 21 35 25 34 18 53 33 30 31 48 49 51 50 52 0 40 43 37 47 36 22 46 38 39 45 41 42 6 5 3 11 2 1 9 4 16 7 10 15 14 8 17 28 13 12 24 38 20 27 53 34 23 35 32 33 21 31 18 19 29 28 26 30 49 44 40 37 39 46 48 36 0 45 47 42 11 43 52 51 50 41 5 15 9 16 17 14 6 10 1 22 7 12 8 4 2 3 25 13 52 34 32 28 19 23 24 21 53 26 33 30 31 29 35 27 25 20 38 46 0 51 43 48 49 47 39 50 45 41 42 9 36 37 44 40 8 14 1 3 4 6 5 7 17 11 22 13 12 2 10 16 15 18 КлаÑÑ! 66-ка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 54. Итак, оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 54 Ñильно улучшена a(54) >= 66. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
ТÑк-Ñ, ещё надо попробовать Ñнова метод Пелегрино-ЛанÑелотти Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 78 на базе 48-ки 26-го порÑдка. Вдруг получитÑÑ. Завтра Ñ ÑƒÑ‚Ñ€Ð° займуÑÑŒ Ñтим. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ñ‡ÐµÑ€ÐµÐ¿Ð°ÑˆÐºÐµ пора уже отдохнуть. ПоÑле неудачи Ñ Ð¿Ð¾Ñ€Ñдком 20 она уÑтала :( |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
О-о-о!! Harry повторил обработку, ÐºÐ¾Ñ‚Ð¾Ñ€Ð°Ñ Ñƒ черепашки закончилаÑÑŒ неудачно. СпаÑибо! Вот результат Order? 20
Enter the name of the squares file: 20nm-pBCD07ToNFR
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file 20nm-pBCD07ToNFR-orthCounts.txt
..output file 20nm-pBCD07ToNFR-orthNos.txt
.. increasing LS store to 100,000
.. increasing LS store to 200,000
.. increasing LS store to 400,000
squares 221184 total orthogonal pairs 1528823808
Maximum pairs for square 1: 13824
There are 221183 other squares with this maximum number of pairs.
..output file 20nm-pBCD07ToNFR-1orths.txt
Pairs for square 1: 13824
elapsed time 3:55:26У него на обработку потребовалоÑÑŒ чуть менее 4-Ñ… чаÑов. Результат проÑто фантаÑтичеÑкий! Каждый ДЛК набора (а их 221184) имеет 13824 ОДЛК! Ð’Ñего образовано 1528823808 ортогональных пар. Покажу Ñамую первую 13824-ку и неÑколько ортогоналек DLK 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 19 18 17 16 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 17 16 19 18 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 18 19 16 17 12 13 14 15 16 18 17 19 0 1 2 3 4 5 6 7 8 9 10 11 15 14 13 12 19 17 18 16 3 2 1 0 7 6 5 4 11 10 9 8 13 12 15 14 18 16 19 17 1 0 3 2 5 4 7 6 9 8 11 10 14 15 12 13 17 19 16 18 2 3 0 1 6 7 4 5 10 11 8 9 4 5 6 7 8 9 10 11 12 14 13 15 16 17 18 19 0 1 2 3 7 6 5 4 11 10 9 8 15 13 14 12 19 18 17 16 3 2 1 0 5 4 7 6 9 8 11 10 14 12 15 13 17 16 19 18 1 0 3 2 6 7 4 5 10 11 8 9 13 15 12 14 18 19 16 17 2 3 0 1 16 17 18 19 0 1 2 3 4 5 6 7 8 10 9 11 12 13 14 15 19 18 17 16 3 2 1 0 7 6 5 4 11 9 10 8 15 14 13 12 17 16 19 18 1 0 3 2 5 4 7 6 10 8 11 9 13 12 15 14 18 19 16 17 2 3 0 1 6 7 4 5 9 11 8 10 14 15 12 13 8 9 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 11 10 9 8 15 14 13 12 19 18 17 16 3 2 1 0 7 6 5 4 9 8 11 10 13 12 15 14 17 16 19 18 1 0 3 2 5 4 7 6 10 11 8 9 14 15 12 13 18 19 16 17 2 3 0 1 6 7 4 5 mate #1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 18 19 16 17 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 19 18 17 16 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 17 16 19 18 8 9 10 11 12 13 15 14 16 17 18 19 0 1 2 3 4 5 6 7 10 11 8 9 15 14 12 13 18 19 16 17 2 3 0 1 6 7 4 5 11 10 9 8 14 15 13 12 19 18 17 16 3 2 1 0 7 6 5 4 9 8 11 10 13 12 14 15 17 16 19 18 1 0 3 2 5 4 7 6 16 17 18 19 0 1 2 3 4 5 7 6 8 9 10 11 12 13 14 15 18 19 16 17 2 3 0 1 7 6 4 5 10 11 8 9 14 15 12 13 19 18 17 16 3 2 1 0 6 7 5 4 11 10 9 8 15 14 13 12 17 16 19 18 1 0 3 2 5 4 6 7 9 8 11 10 13 12 15 14 4 5 6 7 8 9 10 11 12 13 14 15 16 17 19 18 0 1 2 3 6 7 4 5 10 11 8 9 14 15 12 13 19 18 16 17 2 3 0 1 7 6 5 4 11 10 9 8 15 14 13 12 18 19 17 16 3 2 1 0 5 4 7 6 9 8 11 10 13 12 15 14 17 16 18 19 1 0 3 2 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 10 11 14 15 12 13 18 19 16 17 2 3 0 1 6 7 4 5 10 11 8 9 15 14 13 12 19 18 17 16 3 2 1 0 7 6 5 4 11 10 9 8 13 12 15 14 17 16 19 18 1 0 3 2 5 4 7 6 9 8 11 10 mate #2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 18 19 16 17 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 19 18 17 16 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 17 16 19 18 8 9 10 11 12 13 15 14 16 17 18 19 0 1 2 3 4 5 6 7 10 11 8 9 15 14 12 13 18 19 16 17 2 3 0 1 6 7 4 5 11 10 9 8 14 15 13 12 19 18 17 16 3 2 1 0 7 6 5 4 9 8 11 10 13 12 14 15 17 16 19 18 1 0 3 2 5 4 7 6 16 17 18 19 0 1 2 3 4 5 7 6 8 9 10 11 12 13 14 15 18 19 16 17 2 3 0 1 7 6 4 5 10 11 8 9 14 15 12 13 19 18 17 16 3 2 1 0 6 7 5 4 11 10 9 8 15 14 13 12 17 16 19 18 1 0 3 2 5 4 6 7 9 8 11 10 13 12 15 14 4 5 6 7 8 9 10 11 12 13 14 15 16 18 19 17 0 1 2 3 6 7 4 5 10 11 8 9 14 15 12 13 19 17 16 18 2 3 0 1 7 6 5 4 11 10 9 8 15 14 13 12 17 19 18 16 3 2 1 0 5 4 7 6 9 8 11 10 13 12 15 14 18 16 17 19 1 0 3 2 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 10 11 14 15 12 13 18 19 16 17 2 3 0 1 6 7 4 5 10 11 8 9 15 14 13 12 19 18 17 16 3 2 1 0 7 6 5 4 11 10 9 8 13 12 15 14 17 16 19 18 1 0 3 2 5 4 7 6 9 8 11 10 . . . . . . . mate # 13823 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 18 19 16 17 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 19 18 17 16 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 17 16 19 18 8 9 10 11 14 12 13 15 16 17 18 19 0 1 2 3 4 5 6 7 10 11 8 9 13 15 14 12 18 19 16 17 2 3 0 1 6 7 4 5 11 10 9 8 15 13 12 14 19 18 17 16 3 2 1 0 7 6 5 4 9 8 11 10 12 14 15 13 17 16 19 18 1 0 3 2 5 4 7 6 16 17 18 19 0 1 2 3 6 4 5 7 8 9 10 11 12 13 14 15 18 19 16 17 2 3 0 1 5 7 6 4 10 11 8 9 14 15 12 13 19 18 17 16 3 2 1 0 7 5 4 6 11 10 9 8 15 14 13 12 17 16 19 18 1 0 3 2 4 6 7 5 9 8 11 10 13 12 15 14 4 5 6 7 8 9 10 11 12 13 14 15 18 19 17 16 0 1 2 3 6 7 4 5 10 11 8 9 14 15 12 13 17 16 18 19 2 3 0 1 7 6 5 4 11 10 9 8 15 14 13 12 16 17 19 18 3 2 1 0 5 4 7 6 9 8 11 10 13 12 15 14 19 18 16 17 1 0 3 2 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 10 11 14 15 12 13 18 19 16 17 2 3 0 1 6 7 4 5 10 11 8 9 15 14 13 12 19 18 17 16 3 2 1 0 7 6 5 4 11 10 9 8 13 12 15 14 17 16 19 18 1 0 3 2 5 4 7 6 9 8 11 10 mate # 13824 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 18 19 16 17 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 19 18 17 16 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 17 16 19 18 8 9 10 11 14 12 13 15 16 17 18 19 0 1 2 3 4 5 6 7 10 11 8 9 13 15 14 12 18 19 16 17 2 3 0 1 6 7 4 5 11 10 9 8 15 13 12 14 19 18 17 16 3 2 1 0 7 6 5 4 9 8 11 10 12 14 15 13 17 16 19 18 1 0 3 2 5 4 7 6 16 17 18 19 0 1 2 3 6 4 5 7 8 9 10 11 12 13 14 15 18 19 16 17 2 3 0 1 5 7 6 4 10 11 8 9 14 15 12 13 19 18 17 16 3 2 1 0 7 5 4 6 11 10 9 8 15 14 13 12 17 16 19 18 1 0 3 2 4 6 7 5 9 8 11 10 13 12 15 14 4 5 6 7 8 9 10 11 12 13 14 15 18 16 17 19 0 1 2 3 6 7 4 5 10 11 8 9 14 15 12 13 17 19 18 16 2 3 0 1 7 6 5 4 11 10 9 8 15 14 13 12 19 17 16 18 3 2 1 0 5 4 7 6 9 8 11 10 13 12 15 14 16 18 19 17 1 0 3 2 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 10 11 14 15 12 13 18 19 16 17 2 3 0 1 6 7 4 5 10 11 8 9 15 14 13 12 19 18 17 16 3 2 1 0 7 6 5 4 11 10 9 8 13 12 15 14 17 16 19 18 1 0 3 2 5 4 7 6 9 8 11 10 Грандиозно! И Ñто ещё не предел. ЗдеÑÑŒ макÑÐ¸Ð¼Ð°Ð»ÑŒÐ½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð°, похоже, будет Ñодержать миллионы ОДЛК. ОбÑчитать Ñто на одном ПК нереально. Итак, оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 20 увеличилаÑÑŒ в неÑколько раз a(20) >= 13824. Ðлгоритм замечательно работает. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
СвойÑтва ОДЛК показанной макÑимальной группы Order? 20
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_8.txt
Counts
------
13825 diagonal Latin
192 center symmetric
13825 nfr
1 orthogonal pair
13825 self-orthogonal
768 symmetric parityОÑобых ÑвойÑтв не обнаружено. 192 ОДЛК центрально-Ñимметричные. Ð’Ñе ОДЛК ÑвлÑÑŽÑ‚ÑÑ SODLS. ПоÑмотрите на Ñчётчик ортогональных пар, показываю фрагмент orthogonal
square pairs
------ ----------
1 13824
2 13824
3 13824
4 13824
5 13824
6 13824
7 13824
8 13824
9 13824
10 13824
11 13824
12 13824
13 13824
14 13824
15 13824
16 13824
17 13824
18 13824
19 13824
20 13824
21 13824
22 13824
23 13824
24 13824
25 13824
26 13824
27 13824
28 13824
29 13824
30 13824
. . . . . .
221171 13824
221172 13824
221173 13824
221174 13824
221175 13824
221176 13824
221177 13824
221178 13824
221179 13824
221180 13824
221181 13824
221182 13824
221183 13824
221184 13824У каждого ДЛК 13824 ОДЛК! Офигенно! И вÑе Ñти ОДЛК различные нормализованные. Правда, на изоморфноÑÑ‚ÑŒ они не проверены, канонизатора Ð´Ð»Ñ Ð”Ð›Ðš порÑдка 20 у Ð½Ð°Ñ Ð¿Ð¾ÐºÐ° нет. Ðо в любом Ñлучае 13824-ка найдена! Ðаличие изоморфных ОДЛК допуÑкаетÑÑ ÑоглаÑно Ñтатье в OEIS https://oeis.org/A287695 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
Harry обработал набор из 48*48*48=110592 ДЛК порÑдка 16. СпаÑибо! Поразительно! КоличеÑтва точно такие же, как Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 20 - один к одному! Order? 16
Enter the name of the squares file: 16-pABC07ToNFR
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file 16-pABC07ToNFR-orthCounts.txt
..output file 16-pABC07ToNFR-orthNos.txt
.. increasing LS store to 100,000
.. increasing LS store to 200,000
.. increasing LS store to 400,000
squares 221184 total orthogonal pairs 1528823808
Maximum pairs for square 1: 13824
There are 221183 other squares with this maximum number of pairs.
..output file 16-pABC07ToNFR-1orths.txt
Pairs for square 1: 13824
elapsed time 2:27:34Супер! Показываю оÑновной ДЛК одной из макÑимальных групп ОДЛК, ÑоÑтоÑщей из 13824 ОДЛК, и неÑколько ортогоналек DLK 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2 14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4 9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6 10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5 mate #1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5 11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4 9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6 12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3 14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 mate #2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5 11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4 9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6 12 13 14 15 8 9 10 11 4 7 6 5 0 1 2 3 14 15 12 13 10 11 8 9 6 5 4 7 2 3 0 1 15 14 13 12 11 10 9 8 5 6 7 4 3 2 1 0 13 12 15 14 9 8 11 10 7 4 5 6 1 0 3 2 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 . . . . . . . mate #13823 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 8 9 10 11 15 12 13 14 1 2 3 0 4 5 6 7 10 11 8 9 13 14 15 12 3 0 1 2 6 7 4 5 11 10 9 8 14 13 12 15 0 3 2 1 7 6 5 4 9 8 11 10 12 15 14 13 2 1 0 3 5 4 7 6 12 13 14 15 8 9 10 11 7 6 5 4 1 2 3 0 14 15 12 13 10 11 8 9 5 4 7 6 3 0 1 2 15 14 13 12 11 10 9 8 4 5 6 7 0 3 2 1 13 12 15 14 9 8 11 10 6 7 4 5 2 1 0 3 4 5 6 7 1 2 3 0 12 13 14 15 8 9 10 11 6 7 4 5 3 0 1 2 14 15 12 13 10 11 8 9 7 6 5 4 0 3 2 1 15 14 13 12 11 10 9 8 5 4 7 6 2 1 0 3 13 12 15 14 9 8 11 10 mate #13824 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 8 9 10 11 15 12 13 14 1 2 3 0 4 5 6 7 10 11 8 9 13 14 15 12 3 0 1 2 6 7 4 5 11 10 9 8 14 13 12 15 0 3 2 1 7 6 5 4 9 8 11 10 12 15 14 13 2 1 0 3 5 4 7 6 12 13 14 15 8 9 10 11 7 4 5 6 1 2 3 0 14 15 12 13 10 11 8 9 5 6 7 4 3 0 1 2 15 14 13 12 11 10 9 8 6 5 4 7 0 3 2 1 13 12 15 14 9 8 11 10 4 7 6 5 2 1 0 3 4 5 6 7 1 2 3 0 12 13 14 15 8 9 10 11 6 7 4 5 3 0 1 2 14 15 12 13 10 11 8 9 7 6 5 4 0 3 2 1 15 14 13 12 11 10 9 8 5 4 7 6 2 1 0 3 13 12 15 14 9 8 11 10 И оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 16 Ñильно улучшена a(16) >= 13824. И Ñто далеко не макÑимум. МакÑÐ¸Ð¼Ð°Ð»ÑŒÐ½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° здеÑÑŒ, похоже, будет Ñодержать миллионы ОДЛК. Обработать Ñто на одном ПК невозможно. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
Проверка ÑвойÑтв ОДЛК макÑимальной группы утилитой GetType1 Order? 16
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt
Counts
------
13825 diagonal Latin
1 weakly pandiagonal
2 double axial symmetric
25 center symmetric
13825 nfr
1 orthogonal pair
13825 self-orthogonal
1 axial parity 1-way
384 symmetric parity
Ð’Ñе ОДЛК ÑвлÑÑŽÑ‚ÑÑ SODLS. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
Теперь надо занÑÑ‚ÑŒÑÑ Ð”Ð›Ðš 21-го порÑдка Ñ Ñайта Harry 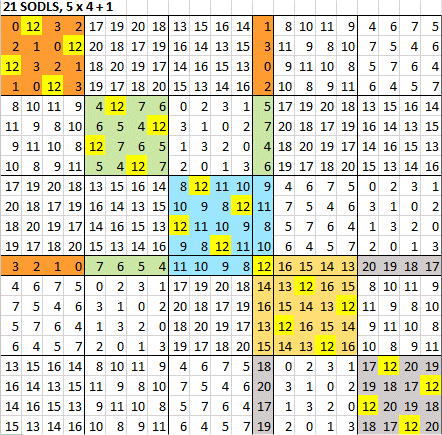 Пока Ñ Ð½Ð°ÑˆÐ»Ð° Ð´Ð»Ñ Ñтого ДЛК только двушку. Ðадо применить алгоритм точно так же, как Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдков 16 и 20. Думаю, Ñто должно Ñработать. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
РаÑкраÑила 4 подквадрата 4Ñ…4, обозначила их A, B, C, D 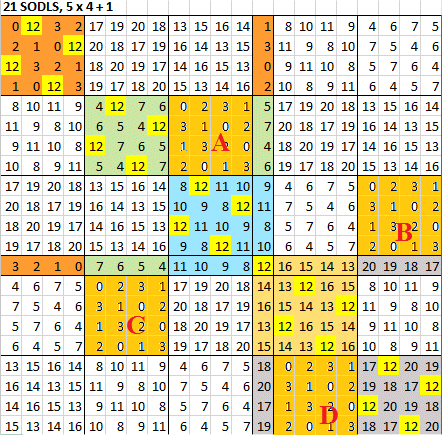 Могу попытатьÑÑ Ð¾Ð±Ñ€Ð°Ð±Ð¾Ñ‚Ð°Ñ‚ÑŒ 48*48=2304 вариантов. Попрошу Harry Ñделать мне Ñти варианты. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
Ðу вот, варианты Harry приÑлал Ð´Ð»Ñ ÐºÐ²Ð°Ð´Ñ€Ð°Ñ‚Ð¸ÐºÐ° 21-го порÑдка. СпаÑибо! Применила алгоритм и получила Order? 21 Enter the name of the squares file: INP Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file INP-orthCounts.txt ..output file INP-orthNos.txt squares 4608 total orthogonal pairs 1327104 Maximum pairs for square 1: 576 There are 4607 other squares with this maximum number of pairs. ..output file INP-1orths.txt Pairs for square 1: 576 elapsed time 0:00:32 Отлично! Образовано 1327104 ортогональных пар. Ðайдено 4608 ДЛК, имеющих 576 ОДЛК, то еÑÑ‚ÑŒ каждый ДЛК набора имеет макÑимальное количеÑтво ОДЛК. Показываю Ñамую первую 576-ку и пару ортогоналек DLK 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2 3 12 0 7 6 5 4 11 10 9 8 1 16 15 14 13 20 19 18 17 12 0 1 2 5 4 7 6 9 8 11 10 3 14 13 16 15 18 17 20 19 1 2 3 12 6 7 4 5 10 11 8 9 0 15 16 13 14 19 20 17 18 8 9 10 11 13 16 2 15 17 18 19 20 14 0 12 3 1 4 5 6 7 11 10 9 8 2 15 14 13 19 20 17 18 16 1 3 12 0 7 6 5 4 9 8 11 10 14 13 16 2 20 19 18 17 15 12 0 1 3 5 4 7 6 10 11 8 9 16 2 15 14 18 17 20 19 13 3 1 0 12 6 7 4 5 17 18 19 20 0 12 3 1 4 7 2 6 5 8 9 10 11 13 14 15 16 20 19 18 17 3 1 0 12 2 6 5 4 7 11 10 9 8 15 16 13 14 18 17 20 19 1 3 12 0 5 4 7 2 6 9 8 11 10 16 15 14 13 19 20 17 18 12 0 1 3 7 2 6 5 4 10 11 8 9 14 13 16 15 3 12 0 1 15 14 13 16 6 5 4 7 2 19 18 17 20 10 9 8 11 4 5 6 7 8 9 10 11 13 14 15 16 18 17 20 2 19 0 12 3 1 7 6 5 4 11 10 9 8 16 15 14 13 20 2 19 18 17 1 3 12 0 5 4 7 6 9 8 11 10 14 13 16 15 19 18 17 20 2 12 0 1 3 6 7 4 5 10 11 8 9 15 16 13 14 17 20 2 19 18 3 1 0 12 13 14 15 16 17 18 19 20 0 12 3 1 9 4 5 6 7 8 11 2 10 16 15 14 13 20 19 18 17 3 1 0 12 11 7 6 5 4 2 10 9 8 14 13 16 15 18 17 20 19 1 3 12 0 10 5 4 7 6 9 8 11 2 15 16 13 14 19 20 17 18 12 0 1 3 8 6 7 4 5 11 2 10 9 mate #1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 3 12 0 1 6 7 4 5 10 11 8 9 2 15 16 13 14 19 20 17 18 1 2 3 12 7 6 5 4 11 10 9 8 0 16 15 14 13 20 19 18 17 12 0 1 2 5 4 7 6 9 8 11 10 3 14 13 16 15 18 17 20 19 13 14 15 16 17 1 19 18 0 2 3 12 20 4 5 6 7 8 9 10 11 15 16 13 14 18 20 17 1 12 3 2 0 19 6 7 4 5 10 11 8 9 16 15 14 13 1 19 18 20 2 0 12 3 17 7 6 5 4 11 10 9 8 14 13 16 15 20 17 1 19 3 12 0 2 18 5 4 7 6 9 8 11 10 4 5 6 7 8 10 9 11 13 1 15 14 16 17 18 19 20 0 2 3 12 6 7 4 5 11 9 10 8 14 16 13 1 15 19 20 17 18 12 3 2 0 7 6 5 4 10 8 11 9 1 15 14 16 13 20 19 18 17 2 0 12 3 5 4 7 6 9 11 8 10 16 13 1 15 14 18 17 20 19 3 12 0 2 2 3 12 0 19 18 20 17 15 14 16 13 1 10 9 11 8 6 5 7 4 17 18 19 20 0 3 2 12 4 5 6 7 11 8 1 10 9 13 14 15 16 19 20 17 18 2 12 0 3 6 7 4 5 10 9 11 8 1 15 16 13 14 20 19 18 17 12 2 3 0 7 6 5 4 8 1 10 9 11 16 15 14 13 18 17 20 19 3 0 12 2 5 4 7 6 9 11 8 1 10 14 13 16 15 8 9 10 11 13 14 15 16 17 19 18 20 7 0 3 2 12 4 1 6 5 10 11 8 9 15 16 13 14 20 18 19 17 6 2 12 0 3 5 7 4 1 11 10 9 8 16 15 14 13 19 17 20 18 4 12 2 3 0 1 6 5 7 9 8 11 10 14 13 16 15 18 20 17 19 5 3 0 12 2 7 4 1 6 mate #2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 3 12 0 1 6 7 4 5 10 11 8 9 2 15 16 13 14 19 20 17 18 1 2 3 12 7 6 5 4 11 10 9 8 0 16 15 14 13 20 19 18 17 12 0 1 2 5 4 7 6 9 8 11 10 3 14 13 16 15 18 17 20 19 13 14 15 16 17 1 19 18 0 2 3 12 20 4 5 6 7 8 9 10 11 15 16 13 14 18 20 17 1 12 3 2 0 19 6 7 4 5 10 11 8 9 16 15 14 13 1 19 18 20 2 0 12 3 17 7 6 5 4 11 10 9 8 14 13 16 15 20 17 1 19 3 12 0 2 18 5 4 7 6 9 8 11 10 4 5 6 7 8 10 9 11 13 1 15 14 16 17 18 19 20 0 2 12 3 6 7 4 5 11 9 10 8 14 16 13 1 15 19 20 17 18 3 12 2 0 7 6 5 4 10 8 11 9 1 15 14 16 13 20 19 18 17 2 0 3 12 5 4 7 6 9 11 8 10 16 13 1 15 14 18 17 20 19 12 3 0 2 2 3 12 0 19 18 20 17 15 14 16 13 1 10 9 11 8 6 5 7 4 17 18 19 20 0 3 2 12 4 5 6 7 11 8 1 10 9 13 14 15 16 19 20 17 18 2 12 0 3 6 7 4 5 10 9 11 8 1 15 16 13 14 20 19 18 17 12 2 3 0 7 6 5 4 8 1 10 9 11 16 15 14 13 18 17 20 19 3 0 12 2 5 4 7 6 9 11 8 1 10 14 13 16 15 8 9 10 11 13 14 15 16 17 19 20 18 7 0 3 2 12 4 1 6 5 10 11 8 9 15 16 13 14 18 20 19 17 6 2 12 0 3 5 7 4 1 11 10 9 8 16 15 14 13 19 17 18 20 4 12 2 3 0 1 6 5 7 9 8 11 10 14 13 16 15 20 18 17 19 5 3 0 12 2 7 4 1 6 И оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 21 Ñильно улучшена a(21) >= 576, Можно ещё больше увеличить нижнюю границу. Я обработала очень маленькое количеÑтво вариантов 48*48=2304. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 24 имеетÑÑ Ð¾Ñ†ÐµÐ½ÐºÐ° a(24) >= 824. Думаю, что её можно улучшить, иÑÐ¿Ð¾Ð»ÑŒÐ·ÑƒÑ Ñтот ДЛК Ñ Ñайта Harry White (ÑÑылка в Ñтартовом поÑте) 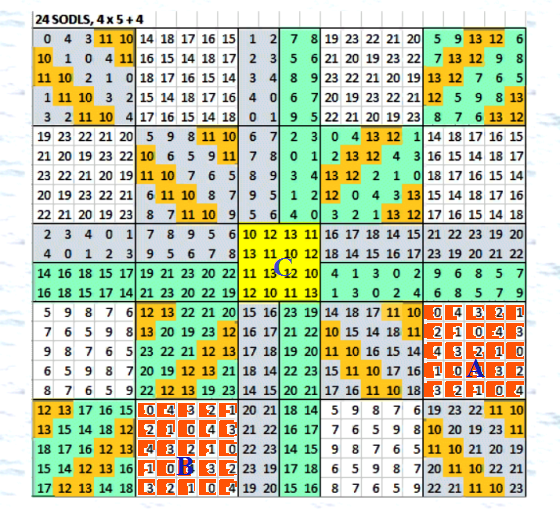 ЕÑли варьировать только центральный подквадрат 4Ñ…4 (обозначен С), поучаетÑÑ Ð²Ñего 48 вариантов. Ðти варианты Ñ ÑƒÐ¶Ðµ попробовала, получила только 24 ОДЛК от одного ДЛК. Можно попробовать варьировать подквадраты 5Ñ…5 (обозначены Ри Ð’). Ðе помню, Ñколько различных вариантов имеет ДЛК 5-го порÑдка. Спрошу у Harry. ЕÑли варьировать три подквадрата - Ð, Ð’ и С - вариантов будет много, черепашка не ÑправитÑÑ. Она может попробовать только варианты от двух подквадратов: Ри С. PS. ПоÑчитала, вроде бы вариантов ДЛК 5-го порÑдка 960. Тогда вариантов при изменении подквадратов Ри С будет 48*960=46080. Отправила Harry заказ на варианты :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
Ой, Harry выполнил ещё ÑкÑперимент Ñ Ñтим ДЛК 16-го порÑдка 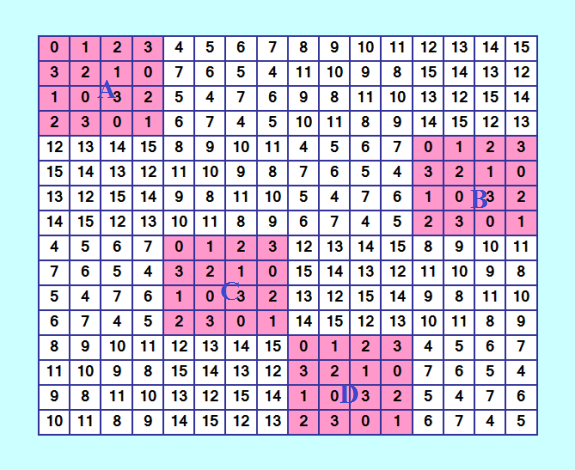 Вот что он получил Order? 16 Enter the name of the squares file: 16-pABC07ToNFR-1orths2 Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file 16-pABC07ToNFR-1orths2-orthCounts.txt ..output file 16-pABC07ToNFR-1orths2-orthNos.txt squares 27625 total orthogonal pairs 27624 Maximum pairs for square 1: 27624 This is the only square with this maximum number of pairs. ..output file 16-pABC07ToNFR-1orths2-1orths.txt Pairs for square 1: 27624 Как Ñ Ð¿Ð¾Ð½Ð¸Ð¼Ð°ÑŽ, здеÑÑŒ уже показана макÑÐ¸Ð¼Ð°Ð»ÑŒÐ½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° ОДЛК от одного ДЛК, и она Ñодержит 27624 ОДЛК! ÐŸÑ€ÐµÐ´Ñ‹Ð´ÑƒÑ‰Ð°Ñ Ð¾Ñ†ÐµÐ½ÐºÐ° была a(16) >= 13824. Почти удвоена! ÐÐ¾Ð²Ð°Ñ Ð¾Ñ†ÐµÐ½ÐºÐ° a(16) >= 27624. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
Показываю оÑновной ДЛК новой макÑимальной группы ОДЛК 16-го порÑдка и неÑколько ортогоналек DLK 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2 14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4 9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6 10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5 mate #1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 8 9 10 11 15 14 13 12 3 2 1 0 4 5 6 7 10 11 8 9 13 12 15 14 1 0 3 2 6 7 4 5 11 10 9 8 12 13 14 15 0 1 2 3 7 6 5 4 9 8 11 10 14 15 12 13 2 3 0 1 5 4 7 6 12 13 14 15 8 9 10 11 7 6 5 4 3 2 1 0 14 15 12 13 10 11 8 9 5 4 7 6 1 0 3 2 15 14 13 12 11 10 9 8 4 5 6 7 0 1 2 3 13 12 15 14 9 8 11 10 6 7 4 5 2 3 0 1 4 5 6 7 3 2 1 0 12 13 14 15 8 9 10 11 6 7 4 5 1 0 3 2 14 15 12 13 10 11 8 9 7 6 5 4 0 1 2 3 15 14 13 12 11 10 9 8 5 4 7 6 2 3 0 1 13 12 15 14 9 8 11 10 mate #2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 8 9 10 11 15 14 13 12 3 2 1 0 4 5 6 7 10 11 8 9 13 12 15 14 1 0 3 2 6 7 4 5 11 10 9 8 12 13 14 15 0 1 2 3 7 6 5 4 9 8 11 10 14 15 12 13 2 3 0 1 5 4 7 6 12 13 14 15 8 9 10 11 7 6 4 5 3 2 1 0 14 15 12 13 10 11 8 9 4 5 7 6 1 0 3 2 15 14 13 12 11 10 9 8 5 4 6 7 0 1 2 3 13 12 15 14 9 8 11 10 6 7 5 4 2 3 0 1 4 5 6 7 3 2 1 0 12 13 14 15 8 9 10 11 6 7 4 5 1 0 3 2 14 15 12 13 10 11 8 9 7 6 5 4 0 1 2 3 15 14 13 12 11 10 9 8 5 4 7 6 2 3 0 1 13 12 15 14 9 8 11 10 . . . . . . mate #27623 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5 11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4 9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6 12 13 14 15 8 9 10 11 4 5 7 6 0 1 2 3 14 15 12 13 10 11 8 9 7 6 4 5 2 3 0 1 15 14 13 12 11 10 9 8 6 7 5 4 3 2 1 0 13 12 15 14 9 8 11 10 5 4 6 7 1 0 3 2 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 mate #27624 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5 11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4 9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6 12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3 14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 Похоже, здеÑÑŒ можно улучшать и улучшать до миллионов ОДЛК от одного ДЛК. Такой вот интереÑный алгоритм поÑвилÑÑ. Сначала Ñ Ð½Ð°ÑˆÐ»Ð° Ñтим алгоритмом только двушечку 18-го порÑдка. И вот как мы Ñ Harry Ñтот алгоритм раÑкрутили. Уже Ñ‚Ñ‹ÑÑчи ОДЛК от одного ДЛК получаем! И Ñто только Ð¼Ð¸Ð·ÐµÑ€Ð½Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ вÑего того, что можно получить. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
Harry обработал набор ДЛК 21-го порÑдка. СпаÑибо! Он варьировал три подквадрата: A$B$C. Вот что у него получилоÑÑŒ Order? 21
Enter the name of the squares file: 21-pABC07ToNFR
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file 21-pABC07ToNFR-orthCounts.txt
..output file 21-pABC07ToNFR-orthNos.txt
.. increasing LS store to 100,000
.. increasing LS store to 200,000
.. increasing LS store to 400,000
squares 221184 total orthogonal pairs 1528823808
Maximum pairs for square 1: 13824
There are 221183 other squares with this maximum number of pairs.
..output file 21-pABC07ToNFR-1orths.txt
Pairs for square 1: 13824
elapsed time 4:02:30КлаÑÑ! Образовано 1528823808 ортогональных пар. Ðайдено 221184 ДЛК, имеющих 13824 ОДЛК! ФантаÑтика! Показываю оÑновной ДЛК одной из макÑимальных групп, Ñодержащих 13824 ОДЛК, и неÑколько ортогоналек DLK 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 3 12 0 1 6 7 4 5 10 11 8 9 2 15 16 13 14 19 20 17 18 1 2 3 12 7 6 5 4 11 10 9 8 0 16 15 14 13 20 19 18 17 12 0 1 2 5 4 7 6 9 8 11 10 3 14 13 16 15 18 17 20 19 13 14 15 16 17 1 19 18 0 12 3 2 20 4 7 5 6 8 9 10 11 15 16 13 14 18 20 17 1 2 3 12 0 19 6 5 7 4 10 11 8 9 16 15 14 13 1 19 18 20 12 0 2 3 17 7 4 6 5 11 10 9 8 14 13 16 15 20 17 1 19 3 2 0 12 18 5 6 4 7 9 8 11 10 4 5 6 7 8 11 9 10 13 1 15 14 16 17 18 19 20 0 12 3 2 6 7 4 5 10 9 11 8 14 16 13 1 15 19 20 17 18 2 3 12 0 7 6 5 4 11 8 10 9 1 15 14 16 13 20 19 18 17 12 0 2 3 5 4 7 6 9 10 8 11 16 13 1 15 14 18 17 20 19 3 2 0 12 2 3 12 0 19 18 20 17 15 14 16 13 1 10 9 11 8 6 5 7 4 17 18 19 20 0 12 3 2 4 5 6 7 11 8 1 10 9 13 14 15 16 19 20 17 18 2 3 12 0 6 7 4 5 10 9 11 8 1 15 16 13 14 20 19 18 17 12 0 2 3 7 6 5 4 8 1 10 9 11 16 15 14 13 18 17 20 19 3 2 0 12 5 4 7 6 9 11 8 1 10 14 13 16 15 8 9 10 11 13 14 15 16 17 20 18 19 7 0 3 2 12 4 1 6 5 10 11 8 9 15 16 13 14 19 18 20 17 6 2 12 0 3 5 7 4 1 11 10 9 8 16 15 14 13 20 17 19 18 4 12 2 3 0 1 6 5 7 9 8 11 10 14 13 16 15 18 19 17 20 5 3 0 12 2 7 4 1 6 mate #1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2 3 12 0 7 6 5 4 11 10 9 8 1 16 15 14 13 20 19 18 17 12 0 1 2 5 4 7 6 9 8 11 10 3 14 13 16 15 18 17 20 19 1 2 3 12 6 7 4 5 10 11 8 9 0 15 16 13 14 19 20 17 18 8 9 10 11 13 16 2 15 17 18 19 20 14 0 12 3 1 4 5 6 7 11 10 9 8 2 15 14 13 19 20 17 18 16 3 1 0 12 7 6 5 4 9 8 11 10 14 13 16 2 20 19 18 17 15 1 3 12 0 5 4 7 6 10 11 8 9 16 2 15 14 18 17 20 19 13 12 0 1 3 6 7 4 5 17 18 19 20 0 12 3 1 4 7 2 6 5 8 9 10 11 13 14 15 16 20 19 18 17 3 1 0 12 2 6 5 4 7 11 10 9 8 15 16 13 14 18 17 20 19 1 3 12 0 5 4 7 2 6 9 8 11 10 16 15 14 13 19 20 17 18 12 0 1 3 7 2 6 5 4 10 11 8 9 14 13 16 15 3 12 0 1 15 14 13 16 6 5 4 7 2 19 18 17 20 10 9 8 11 4 5 6 7 8 9 10 11 13 14 15 16 18 17 20 2 19 0 12 3 1 7 6 5 4 10 11 8 9 16 15 14 13 20 2 19 18 17 1 3 12 0 5 4 7 6 11 10 9 8 14 13 16 15 19 18 17 20 2 12 0 1 3 6 7 4 5 9 8 11 10 15 16 13 14 17 20 2 19 18 3 1 0 12 13 14 15 16 17 18 19 20 0 12 3 1 9 4 5 6 7 8 11 2 10 16 15 14 13 20 19 18 17 3 1 0 12 11 7 6 5 4 2 10 9 8 14 13 16 15 18 17 20 19 1 3 12 0 10 5 4 7 6 9 8 11 2 15 16 13 14 19 20 17 18 12 0 1 3 8 6 7 4 5 11 2 10 9 mate #2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2 3 12 0 7 6 5 4 11 10 9 8 1 16 15 14 13 20 19 18 17 12 0 1 2 5 4 7 6 9 8 11 10 3 14 13 16 15 18 17 20 19 1 2 3 12 6 7 4 5 10 11 8 9 0 15 16 13 14 19 20 17 18 8 9 10 11 13 16 2 15 17 18 19 20 14 0 1 3 12 4 5 6 7 11 10 9 8 2 15 14 13 19 20 17 18 16 3 12 0 1 7 6 5 4 9 8 11 10 14 13 16 2 20 19 18 17 15 12 3 1 0 5 4 7 6 10 11 8 9 16 2 15 14 18 17 20 19 13 1 0 12 3 6 7 4 5 17 18 19 20 0 12 3 1 4 7 2 6 5 8 9 10 11 13 14 15 16 20 19 18 17 3 1 0 12 2 6 5 4 7 11 10 9 8 15 16 13 14 18 17 20 19 1 3 12 0 5 4 7 2 6 9 8 11 10 16 15 14 13 19 20 17 18 12 0 1 3 7 2 6 5 4 10 11 8 9 14 13 16 15 3 12 0 1 15 14 13 16 6 5 4 7 2 19 18 17 20 10 9 8 11 4 5 6 7 8 11 10 9 13 14 15 16 18 17 20 2 19 0 12 3 1 7 6 5 4 10 9 8 11 16 15 14 13 20 2 19 18 17 1 3 12 0 5 4 7 6 9 10 11 8 14 13 16 15 19 18 17 20 2 12 0 1 3 6 7 4 5 11 8 9 10 15 16 13 14 17 20 2 19 18 3 1 0 12 13 14 15 16 17 18 19 20 0 12 3 1 9 4 5 6 7 8 11 2 10 16 15 14 13 20 19 18 17 3 1 0 12 11 7 6 5 4 2 10 9 8 14 13 16 15 18 17 20 19 1 3 12 0 10 5 4 7 6 9 8 11 2 15 16 13 14 19 20 17 18 12 0 1 3 8 6 7 4 5 11 2 10 9 . . . . . . mate #13823 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2 3 12 0 7 6 5 4 11 10 9 8 1 16 15 14 13 20 19 18 17 12 0 1 2 5 4 7 6 9 8 11 10 3 14 13 16 15 18 17 20 19 1 2 3 12 6 7 4 5 10 11 8 9 0 15 16 13 14 19 20 17 18 8 9 10 11 13 16 2 15 20 17 18 19 14 1 3 12 0 4 5 6 7 11 10 9 8 2 15 14 13 18 19 20 17 16 12 0 1 3 7 6 5 4 9 8 11 10 14 13 16 2 19 18 17 20 15 0 12 3 1 5 4 7 6 10 11 8 9 16 2 15 14 17 20 19 18 13 3 1 0 12 6 7 4 5 17 18 19 20 1 0 12 3 4 7 2 6 5 8 9 10 11 16 13 14 15 20 19 18 17 12 3 1 0 2 6 5 4 7 11 10 9 8 14 15 16 13 18 17 20 19 3 12 0 1 5 4 7 2 6 9 8 11 10 15 14 13 16 19 20 17 18 0 1 3 12 7 2 6 5 4 10 11 8 9 13 16 15 14 3 12 0 1 15 14 13 16 6 5 4 7 2 19 18 17 20 10 9 8 11 4 5 6 7 11 10 9 8 13 14 15 16 18 17 20 2 19 0 12 3 1 7 6 5 4 9 8 11 10 16 15 14 13 20 2 19 18 17 1 3 12 0 5 4 7 6 8 9 10 11 14 13 16 15 19 18 17 20 2 12 0 1 3 6 7 4 5 10 11 8 9 15 16 13 14 17 20 2 19 18 3 1 0 12 13 14 15 16 17 18 19 20 1 0 12 3 9 4 5 6 7 8 11 2 10 16 15 14 13 20 19 18 17 12 3 1 0 11 7 6 5 4 2 10 9 8 14 13 16 15 18 17 20 19 3 12 0 1 10 5 4 7 6 9 8 11 2 15 16 13 14 19 20 17 18 0 1 3 12 8 6 7 4 5 11 2 10 9 mate #13824 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2 3 12 0 7 6 5 4 11 10 9 8 1 16 15 14 13 20 19 18 17 12 0 1 2 5 4 7 6 9 8 11 10 3 14 13 16 15 18 17 20 19 1 2 3 12 6 7 4 5 10 11 8 9 0 15 16 13 14 19 20 17 18 8 9 10 11 13 16 2 15 20 17 18 19 14 1 0 12 3 4 5 6 7 11 10 9 8 2 15 14 13 18 19 20 17 16 12 3 1 0 7 6 5 4 9 8 11 10 14 13 16 2 19 18 17 20 15 3 12 0 1 5 4 7 6 10 11 8 9 16 2 15 14 17 20 19 18 13 0 1 3 12 6 7 4 5 17 18 19 20 1 0 12 3 4 7 2 6 5 8 9 10 11 16 13 14 15 20 19 18 17 12 3 1 0 2 6 5 4 7 11 10 9 8 14 15 16 13 18 17 20 19 3 12 0 1 5 4 7 2 6 9 8 11 10 15 14 13 16 19 20 17 18 0 1 3 12 7 2 6 5 4 10 11 8 9 13 16 15 14 3 12 0 1 15 14 13 16 6 5 4 7 2 19 18 17 20 10 9 8 11 4 5 6 7 11 8 9 10 13 14 15 16 18 17 20 2 19 0 12 3 1 7 6 5 4 9 10 11 8 16 15 14 13 20 2 19 18 17 1 3 12 0 5 4 7 6 10 9 8 11 14 13 16 15 19 18 17 20 2 12 0 1 3 6 7 4 5 8 11 10 9 15 16 13 14 17 20 2 19 18 3 1 0 12 13 14 15 16 17 18 19 20 1 0 12 3 9 4 5 6 7 8 11 2 10 16 15 14 13 20 19 18 17 12 3 1 0 11 7 6 5 4 2 10 9 8 14 13 16 15 18 17 20 19 3 12 0 1 10 5 4 7 6 9 8 11 2 15 16 13 14 19 20 17 18 0 1 3 12 8 6 7 4 5 11 2 10 9 И оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 21 улучшена a(21) >= 13824. Покажу иÑходный ДЛК Ñ Ñайта Harry, Ñ ÐºÐ¾Ñ‚Ð¾Ñ€Ð¾Ð³Ð¾ вÑÑ‘ начиналоÑÑŒ  ПонÑтно, что тут ещё можно улучшать и улучшать. Во-первых, ещё не варьировалÑÑ Ð¿Ð¾Ð´ÐºÐ²Ð°Ð´Ñ€Ð°Ñ‚ D. Рпотом и другие подквадраты 4Ñ…4 тоже можно варьировать. Ðо оÑтановимÑÑ Ð¿Ð¾ÐºÐ° на Ñтом результате. Дальше Ñчитать очень Ñложно. Черепашка вообще не может. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
Harry выполнил неÑколько ÑкÑпериментов Ñ Ñтим ДЛК 24-го порÑдка  Лучший результат Ð´Ð»Ñ Ð²Ð°Ñ€ÑŒÐ¸Ñ€Ð¾Ð²Ð°Ð½Ð¸Ñ ÐºÐ²Ð°Ð´Ñ€Ð°Ñ‚Ð¾Ð² Ри С (или Ð’ и С) Ñ Ð¸Ñпользованием 48*480=23040 вариантов и применением поворотов программой Rotate Ñ Ð¿Ð°Ñ€Ð°Ð¼ÐµÑ‚Ñ€Ð¾Ð¼ 8 (вÑе варианты) Order? 24
Enter the name of the squares file: 24-pAC&BCr8soToNFR
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file 24-pAC&BCr8soToNFR-orthCounts.txt
..output file 24-pAC&BCr8soToNFR-orthNos.txt
.. increasing LS store to 100,000
.. increasing LS store to 200,000
squares 184128 total orthogonal pairs 330672384
Maximum pairs for square 1: 5736
There are 45887 other squares with this maximum number of pairs.
..output file 24-pAC&BCr8soToNFR-1orths.txt
Pairs for square 1: 5736
elapsed time 3:12:16[Ð’Ñего у ДЛК 5-го порÑдка 960 вариантов, но Harry иÑпользует только те ДЛК, которые ÑвлÑÑŽÑ‚ÑÑ SODLS, таких вариантов 480.] Образовано 330672384 ортогональных пар. Ðайдено 45888 ДЛК, имеющих 5736 ОДЛК! Супер! Ð¡ÐµÐ¹Ñ‡Ð°Ñ Harry проверÑет ещё один Ñлучай: Ð´Ð»Ñ Ð²Ð°Ñ€ÑŒÐ¸Ñ€Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¿Ð¾Ð´ÐºÐ²Ð°Ð´Ñ€Ð°Ñ‚Ð¾Ð² Ри Ð’, оба Ñти подквадрата 5Ñ…5 (Ñмотрите иллюÑтрацию). Цитирую его пиÑьмо I am also running A and B option for rotations 0 and 7, (460860 squares). Думаю, что результат ещё улучшитÑÑ. Пока покажу оÑновной ДЛК одной из 5736-ок и пару ортогоналек DLK 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 11 3 1 2 10 7 8 9 5 6 4 0 13 21 16 17 18 14 15 20 22 23 12 19 4 0 10 1 2 9 5 6 7 8 11 3 21 22 18 14 15 16 17 23 12 13 19 20 2 11 3 4 1 6 7 8 9 5 0 10 22 23 15 16 17 18 14 13 21 19 20 12 1 2 0 10 11 8 9 5 6 7 3 4 23 12 17 18 14 15 16 22 19 20 13 21 12 13 21 22 23 14 1 2 17 18 15 16 5 6 19 20 7 8 9 11 10 4 3 0 21 22 23 12 13 16 17 1 2 15 18 14 6 7 20 8 9 5 19 4 3 0 11 10 23 12 13 21 22 18 14 15 1 2 16 17 7 8 9 5 6 19 20 0 11 10 4 3 13 21 22 23 12 2 16 17 18 1 14 15 8 9 6 7 19 20 5 10 4 3 0 11 22 23 12 13 21 1 2 14 15 16 17 18 9 5 8 19 20 6 7 3 0 11 10 4 3 10 4 11 0 17 15 18 16 14 20 19 2 1 22 13 23 21 12 8 6 9 7 5 10 4 11 0 3 15 18 16 14 17 2 1 20 19 13 23 21 12 22 6 9 7 5 8 15 14 18 17 16 10 0 4 3 11 1 2 19 20 7 6 5 9 8 21 13 12 23 22 18 17 16 15 14 4 3 11 10 0 19 20 1 2 5 9 8 7 6 12 23 22 21 13 5 6 7 8 9 0 10 20 19 4 13 21 11 3 12 1 2 22 23 14 15 16 17 18 7 8 9 5 6 11 20 19 0 10 23 12 3 4 21 22 1 2 13 16 17 18 14 15 9 5 6 7 8 20 19 10 11 3 21 22 4 0 23 12 13 1 2 18 14 15 16 17 6 7 8 9 5 19 11 3 4 20 12 13 0 10 2 21 22 23 1 15 16 17 18 14 8 9 5 6 7 3 4 0 20 19 22 23 10 11 1 2 12 13 21 17 18 14 15 16 14 15 20 19 18 21 13 23 22 12 6 7 16 17 0 10 11 3 4 5 1 2 8 9 16 20 19 14 15 23 22 12 21 13 9 5 17 18 11 3 4 0 10 7 8 1 2 6 20 19 15 16 17 12 21 13 23 22 7 8 18 14 4 0 10 11 3 9 5 6 1 2 19 16 17 18 20 13 23 22 12 21 5 6 14 15 10 11 3 4 0 2 7 8 9 1 17 18 14 20 19 22 12 21 13 23 8 9 15 16 3 4 0 10 11 1 2 5 6 7 mate #1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 4 10 0 1 3 8 9 5 6 7 11 2 19 23 17 18 14 15 16 12 21 22 20 13 3 4 11 10 0 6 7 8 9 5 2 1 13 20 15 16 17 18 14 21 22 12 23 19 10 3 4 2 11 9 5 6 7 8 1 0 23 12 18 14 15 16 17 22 19 20 13 21 2 11 3 4 1 7 8 9 5 6 0 10 20 19 16 17 18 14 15 13 12 23 21 22 14 15 16 17 18 19 20 13 3 4 23 12 11 2 0 1 21 22 10 9 8 7 6 5 17 18 14 15 16 4 23 19 20 3 12 13 0 10 11 21 22 1 2 6 5 9 8 7 15 16 17 18 14 3 4 12 23 19 13 20 2 1 21 22 11 10 0 8 7 6 5 9 18 14 15 16 17 23 3 4 13 12 20 19 10 11 22 0 1 2 21 5 9 8 7 6 16 17 18 14 15 13 12 3 4 20 19 23 1 0 2 11 10 21 22 7 6 5 9 8 11 2 1 0 10 12 13 20 19 23 22 21 4 3 8 7 6 5 9 17 16 15 14 18 1 0 10 11 2 20 19 23 12 13 3 4 21 22 6 5 9 8 7 15 14 18 17 16 5 8 6 9 7 14 17 15 18 16 21 22 3 4 1 10 2 0 11 20 23 13 19 12 8 6 9 7 5 17 15 18 16 14 4 3 22 21 10 2 0 11 1 23 13 19 12 20 19 20 13 12 23 22 21 16 17 18 9 8 15 14 5 6 7 3 4 0 1 2 11 10 12 23 19 20 13 21 18 14 15 22 8 7 17 16 4 9 5 6 3 11 10 0 1 2 20 13 12 23 19 15 16 17 22 21 7 6 14 18 3 4 8 9 5 1 2 11 10 0 23 19 20 13 12 18 14 22 21 17 6 5 16 15 9 3 4 7 8 10 0 1 2 11 13 12 23 19 20 16 22 21 14 15 5 9 18 17 7 8 3 4 6 2 11 10 0 1 22 21 7 8 9 10 11 2 1 0 18 17 6 5 19 20 13 12 23 14 15 16 3 4 21 9 5 6 22 1 0 10 11 2 17 16 8 7 12 23 19 20 13 4 18 14 15 3 6 7 8 22 21 11 2 1 0 10 16 15 5 9 20 13 12 23 19 3 4 17 18 14 9 5 22 21 8 0 10 11 2 1 15 14 7 6 23 19 20 13 12 18 3 4 16 17 7 22 21 5 6 2 1 0 10 11 14 18 9 8 13 12 23 19 20 16 17 3 4 15 mate #2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 4 10 0 1 3 8 9 5 6 7 11 2 19 23 17 18 14 15 16 12 21 22 20 13 3 4 11 10 0 6 7 8 9 5 2 1 13 20 15 16 17 18 14 21 22 12 23 19 10 3 4 2 11 9 5 6 7 8 1 0 23 12 18 14 15 16 17 22 19 20 13 21 2 11 3 4 1 7 8 9 5 6 0 10 20 19 16 17 18 14 15 13 12 23 21 22 14 15 16 17 18 19 20 13 3 4 23 12 11 2 0 1 21 22 10 9 8 7 6 5 17 18 14 15 16 4 23 19 20 3 12 13 0 10 11 21 22 1 2 6 5 9 8 7 15 16 17 18 14 3 4 12 23 19 13 20 2 1 21 22 11 10 0 8 7 6 5 9 18 14 15 16 17 23 3 4 13 12 20 19 10 11 22 0 1 2 21 5 9 8 7 6 16 17 18 14 15 13 12 3 4 20 19 23 1 0 2 11 10 21 22 7 6 5 9 8 11 2 1 0 10 12 13 20 19 23 22 21 3 4 8 7 6 5 9 17 16 15 14 18 1 0 10 11 2 20 19 23 12 13 4 3 21 22 6 5 9 8 7 15 14 18 17 16 5 8 6 9 7 14 17 15 18 16 21 22 4 3 1 10 2 0 11 20 23 13 19 12 8 6 9 7 5 17 15 18 16 14 3 4 22 21 10 2 0 11 1 23 13 19 12 20 19 20 13 12 23 22 21 16 17 18 9 8 15 14 5 6 7 3 4 0 1 2 11 10 12 23 19 20 13 21 18 14 15 22 8 7 17 16 4 9 5 6 3 11 10 0 1 2 20 13 12 23 19 15 16 17 22 21 7 6 14 18 3 4 8 9 5 1 2 11 10 0 23 19 20 13 12 18 14 22 21 17 6 5 16 15 9 3 4 7 8 10 0 1 2 11 13 12 23 19 20 16 22 21 14 15 5 9 18 17 7 8 3 4 6 2 11 10 0 1 22 21 7 8 9 10 11 2 1 0 18 17 6 5 19 20 13 12 23 14 15 16 3 4 21 9 5 6 22 1 0 10 11 2 17 16 8 7 12 23 19 20 13 4 18 14 15 3 6 7 8 22 21 11 2 1 0 10 16 15 5 9 20 13 12 23 19 3 4 17 18 14 9 5 22 21 8 0 10 11 2 1 15 14 7 6 23 19 20 13 12 18 3 4 16 17 7 22 21 5 6 2 1 0 10 11 14 18 9 8 13 12 23 19 20 16 17 3 4 15 Оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 24 Ñильно улучшена a(24) >= 5736. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
Вот как изменилиÑÑŒ оценки Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдков 12 - 30 a(12) >= 724775546 (1764493860) a(13) >= 248703 a(14) >= 307662 a(15) >= 3 a(16) >= 27624 a(17) >= 829 a(18) >= 96 a(19) >= 471 a(20) >= 13824 a(21) >= 13824 a(22) >= 72 a(23) >= 525 a(24) >= 5736 a(25) >= 50 a(26) >= 48 a(27) >= 23 a(28) >= 3 a(29) >= 112 a(30) >= 24 КраÑным помечены оценки, которые улучшены по Ñравнению Ñ Ð¾Ð¿ÑƒÐ±Ð»Ð¸ÐºÐ¾Ð²Ð°Ð½Ð½Ñ‹Ð¼Ð¸ в OEIS https://oeis.org/A287695 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 27 можно иÑпользовать Ñтот Ñимпатичный квадратик Ñ Ñайта Harry (ÑÑылка в Ñтартовом поÑте) 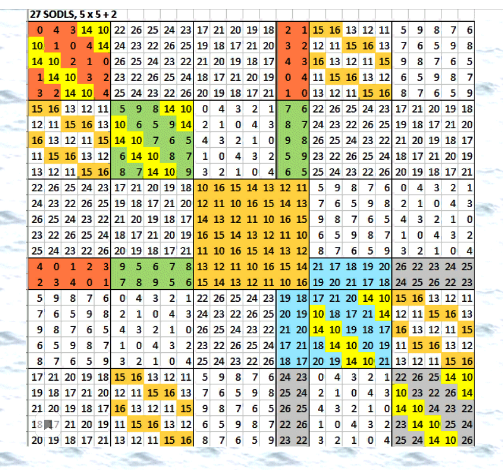 Вариантов море! Можно варьировать один центральный подквадрат 7Ñ…7. Можно варьировать подквадраты 5Ñ…5 в разных комбинациÑÑ…. Так что, тут макÑÐ¸Ð¼Ð°Ð»ÑŒÐ½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° может Ñодержать миллионы ОДЛК. Ðу, нам немножко улучшить бы оценку :) Можно улучшить оценку Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 25, она очень маленькаÑ. Ðичего не могу придумать Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 15 Ñ Ð¿Ñ€Ð¸Ð¼ÐµÐ½ÐµÐ½Ð¸ÐµÐ¼ раÑÑматриваемого тут алгоритма. ЕÑÑ‚ÑŒ две другие идеи, надо опробовать. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
Вот поÑтроила ДЛК 25-го порÑдка методом ÑоÑтавных квадратов, он ÑвлÑетÑÑ SODLS  ЗдеÑÑŒ Ð´Ð»Ñ Ð²Ð°Ñ€ÑŒÐ¸Ñ€Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¿Ð¾Ð´ÐºÐ²Ð°Ð´Ñ€Ð°Ñ‚Ñ‹ 5Ñ…5 в разных комбинациÑÑ…. Ð”Ð»Ñ Ð½Ð°Ñ‡Ð°Ð»Ð° можно Ñделать варьирование только центрального подквадрата, Ñто 480 вариантов и на 8 вариантов от программы Rotate, итого 480*8=3840. Ðто и черепашка может обработать. Ðу, а дальше уже различные комбинации подквадратов 5Ñ…5. И комбинаций много. Следовательно, макÑÐ¸Ð¼Ð°Ð»ÑŒÐ½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° ОДЛК тут будет очень большаÑ, мы не Ñможем её найти. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
Цитата Ð¡ÐµÐ¹Ñ‡Ð°Ñ Harry проверÑет ещё один Ñлучай: Ð´Ð»Ñ Ð²Ð°Ñ€ÑŒÐ¸Ñ€Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¿Ð¾Ð´ÐºÐ²Ð°Ð´Ñ€Ð°Ñ‚Ð¾Ð² Ри Ð’, оба Ñти подквадрата 5Ñ…5 (Ñмотрите иллюÑтрацию). Да! Ðовый результат прибыл Order? 24
Enter the name of the squares file: 24-pAB07ToNFR
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file 24-pAB07ToNFR-orthCounts.txt
..output file 24-pAB07ToNFR-orthNos.txt
.. increasing LS store to 100,000
.. increasing LS store to 200,000
.. increasing LS store to 400,000
.. increasing LS store to 800,000
squares 460800 total orthogonal pairs 1170276352
Maximum pairs for square 1: 14400
There are 460799 other squares with this maximum number of pairs.
..output file 24-pAB07ToNFR-1orths.txt
Pairs for square 1: 14400
elapsed time 22:33:25Отличный ÑкÑперимент! Образовано 1170276352 ортогональных пар. Ðайдено 460800 ДЛК, имеющих 14400 ОДЛК! То еÑÑ‚ÑŒ каждый ДЛК набора имеет 14400 ОДЛК. Поразительно! Покажу оÑновной ДЛК Ñамой первой 14400-ки и неÑколько ортогоналек DLK 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 4 10 0 1 3 8 9 5 6 7 11 2 19 23 17 18 14 15 16 12 21 22 20 13 3 4 11 10 0 6 7 8 9 5 2 1 13 20 15 16 17 18 14 21 22 12 23 19 10 3 4 2 11 9 5 6 7 8 1 0 23 12 18 14 15 16 17 22 19 20 13 21 2 11 3 4 1 7 8 9 5 6 0 10 20 19 16 17 18 14 15 13 12 23 21 22 14 15 16 17 18 19 20 13 3 4 23 12 11 2 0 1 21 22 10 5 9 8 7 6 17 18 14 15 16 4 23 19 20 3 12 13 0 10 11 21 22 1 2 6 8 7 5 9 15 16 17 18 14 3 4 12 23 19 13 20 2 1 21 22 11 10 0 7 6 9 8 5 18 14 15 16 17 23 3 4 13 12 20 19 10 11 22 0 1 2 21 9 7 5 6 8 16 17 18 14 15 13 12 3 4 20 19 23 1 0 2 11 10 21 22 8 5 6 9 7 11 2 1 0 10 12 13 20 19 23 4 22 21 3 8 7 6 5 9 17 16 15 14 18 1 0 10 11 2 20 19 23 12 13 21 3 4 22 6 5 9 8 7 15 14 18 17 16 5 8 6 9 7 14 17 15 18 16 3 21 22 4 1 10 2 0 11 20 23 13 19 12 8 6 9 7 5 17 15 18 16 14 22 4 3 21 10 2 0 11 1 23 13 19 12 20 19 20 13 12 23 22 21 16 17 18 9 8 15 14 5 6 7 3 4 0 10 11 2 1 12 23 19 20 13 21 18 14 15 22 8 7 17 16 4 9 5 6 3 1 11 2 0 10 20 13 12 23 19 15 16 17 22 21 7 6 14 18 3 4 8 9 5 2 1 10 11 0 23 19 20 13 12 18 14 22 21 17 6 5 16 15 9 3 4 7 8 10 2 0 1 11 13 12 23 19 20 16 22 21 14 15 5 9 18 17 7 8 3 4 6 11 0 1 10 2 22 21 7 8 9 0 10 11 2 1 18 17 6 5 19 23 12 13 20 14 15 16 3 4 21 9 5 6 22 1 11 2 0 10 17 16 8 7 20 12 13 19 23 4 18 14 15 3 6 7 8 22 21 2 1 10 11 0 16 15 5 9 13 20 23 12 19 3 4 17 18 14 9 5 22 21 8 10 2 0 1 11 15 14 7 6 23 13 19 20 12 18 3 4 16 17 7 22 21 5 6 11 0 1 10 2 14 18 9 8 12 19 20 23 13 16 17 3 4 15 mate #1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 11 3 1 2 10 7 8 9 5 6 4 0 13 21 16 17 18 14 15 20 22 23 12 19 4 0 10 1 2 9 5 6 7 8 11 3 21 22 18 14 15 16 17 23 12 13 19 20 2 11 3 4 1 6 7 8 9 5 0 10 22 23 15 16 17 18 14 13 21 19 20 12 1 2 0 10 11 8 9 5 6 7 3 4 23 12 17 18 14 15 16 22 19 20 13 21 12 13 21 22 23 14 1 2 17 18 15 16 5 6 19 20 7 8 9 0 11 4 3 10 21 22 23 12 13 16 17 1 2 15 18 14 6 7 20 8 9 5 19 3 10 11 4 0 23 12 13 21 22 18 14 15 1 2 16 17 7 8 9 5 6 19 20 10 4 3 0 11 13 21 22 23 12 2 16 17 18 1 14 15 8 9 6 7 19 20 5 4 0 10 11 3 22 23 12 13 21 1 2 14 15 16 17 18 9 5 8 19 20 6 7 11 3 0 10 4 3 10 4 11 0 17 15 18 16 14 1 20 2 19 22 13 23 21 12 8 6 9 7 5 10 4 11 0 3 15 18 16 14 17 19 2 20 1 13 23 21 12 22 6 9 7 5 8 15 14 18 17 16 10 0 4 3 11 20 1 19 2 7 6 5 9 8 21 13 12 23 22 18 17 16 15 14 4 3 11 10 0 2 19 1 20 5 9 8 7 6 12 23 22 21 13 5 6 7 8 9 0 10 20 19 4 13 21 11 3 12 1 2 22 23 14 16 18 17 15 7 8 9 5 6 11 20 19 0 10 23 12 3 4 21 22 1 2 13 17 15 16 18 14 9 5 6 7 8 20 19 10 11 3 21 22 4 0 23 12 13 1 2 15 18 17 14 16 6 7 8 9 5 19 11 3 4 20 12 13 0 10 2 21 22 23 1 18 14 15 16 17 8 9 5 6 7 3 4 0 20 19 22 23 10 11 1 2 12 13 21 16 17 14 15 18 14 15 20 19 18 12 21 23 22 13 6 7 16 17 0 11 4 3 10 5 1 2 8 9 16 20 19 14 15 22 13 21 23 12 9 5 17 18 3 10 11 4 0 7 8 1 2 6 20 19 15 16 17 13 23 22 12 21 7 8 18 14 10 4 3 0 11 9 5 6 1 2 19 16 17 18 20 23 12 13 21 22 5 6 14 15 4 0 10 11 3 2 7 8 9 1 17 18 14 20 19 21 22 12 13 23 8 9 15 16 11 3 0 10 4 1 2 5 6 7 mate #2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 11 3 1 2 10 7 8 9 5 6 4 0 13 21 16 17 18 14 15 20 22 23 12 19 4 0 10 1 2 9 5 6 7 8 11 3 21 22 18 14 15 16 17 23 12 13 19 20 2 11 3 4 1 6 7 8 9 5 0 10 22 23 15 16 17 18 14 13 21 19 20 12 1 2 0 10 11 8 9 5 6 7 3 4 23 12 17 18 14 15 16 22 19 20 13 21 12 13 21 22 23 14 1 2 17 18 15 16 5 6 19 20 7 8 9 0 4 11 3 10 21 22 23 12 13 16 17 1 2 15 18 14 6 7 20 8 9 5 19 3 10 4 11 0 23 12 13 21 22 18 14 15 1 2 16 17 7 8 9 5 6 19 20 10 11 3 0 4 13 21 22 23 12 2 16 17 18 1 14 15 8 9 6 7 19 20 5 11 0 10 4 3 22 23 12 13 21 1 2 14 15 16 17 18 9 5 8 19 20 6 7 4 3 0 10 11 3 10 4 11 0 17 15 18 16 14 1 20 2 19 22 13 23 21 12 8 6 9 7 5 10 4 11 0 3 15 18 16 14 17 19 2 20 1 13 23 21 12 22 6 9 7 5 8 15 14 18 17 16 10 0 4 3 11 20 1 19 2 7 6 5 9 8 21 13 12 23 22 18 17 16 15 14 4 3 11 10 0 2 19 1 20 5 9 8 7 6 12 23 22 21 13 5 6 7 8 9 0 10 20 19 4 13 21 11 3 12 1 2 22 23 14 16 18 17 15 7 8 9 5 6 11 20 19 0 10 23 12 3 4 21 22 1 2 13 17 15 16 18 14 9 5 6 7 8 20 19 10 11 3 21 22 4 0 23 12 13 1 2 15 18 17 14 16 6 7 8 9 5 19 11 3 4 20 12 13 0 10 2 21 22 23 1 18 14 15 16 17 8 9 5 6 7 3 4 0 20 19 22 23 10 11 1 2 12 13 21 16 17 14 15 18 14 15 20 19 18 12 23 21 22 13 6 7 16 17 0 11 4 3 10 5 1 2 8 9 16 20 19 14 15 22 13 23 21 12 9 5 17 18 3 10 11 4 0 7 8 1 2 6 20 19 15 16 17 13 21 22 12 23 7 8 18 14 10 4 3 0 11 9 5 6 1 2 19 16 17 18 20 21 12 13 23 22 5 6 14 15 4 0 10 11 3 2 7 8 9 1 17 18 14 20 19 23 22 12 13 21 8 9 15 16 11 3 0 10 4 1 2 5 6 7 . . . . . . . mate #14399 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 11 3 1 2 10 7 8 9 5 6 4 0 13 21 16 17 18 14 15 20 22 23 12 19 4 0 10 1 2 9 5 6 7 8 11 3 21 22 18 14 15 16 17 23 12 13 19 20 2 11 3 4 1 6 7 8 9 5 0 10 22 23 15 16 17 18 14 13 21 19 20 12 1 2 0 10 11 8 9 5 6 7 3 4 23 12 17 18 14 15 16 22 19 20 13 21 12 13 21 22 23 14 1 2 17 18 15 16 5 6 19 20 7 8 9 3 4 11 0 10 21 22 23 12 13 16 17 1 2 15 18 14 6 7 20 8 9 5 19 0 10 4 11 3 23 12 13 21 22 18 14 15 1 2 16 17 7 8 9 5 6 19 20 10 11 0 3 4 13 21 22 23 12 2 16 17 18 1 14 15 8 9 6 7 19 20 5 11 3 10 4 0 22 23 12 13 21 1 2 14 15 16 17 18 9 5 8 19 20 6 7 4 0 3 10 11 3 10 4 11 0 17 15 18 16 14 1 20 2 19 22 13 23 21 12 8 6 9 7 5 10 4 11 0 3 15 18 16 14 17 19 2 20 1 13 23 21 12 22 6 9 7 5 8 15 14 18 17 16 10 0 4 3 11 20 1 19 2 7 6 5 9 8 21 13 12 23 22 18 17 16 15 14 4 3 11 10 0 2 19 1 20 5 9 8 7 6 12 23 22 21 13 5 6 7 8 9 0 10 20 19 4 13 21 11 3 12 1 2 22 23 17 16 18 14 15 7 8 9 5 6 11 20 19 0 10 23 12 3 4 21 22 1 2 13 14 15 16 18 17 9 5 6 7 8 20 19 10 11 3 21 22 4 0 23 12 13 1 2 15 18 14 17 16 6 7 8 9 5 19 11 3 4 20 12 13 0 10 2 21 22 23 1 18 17 15 16 14 8 9 5 6 7 3 4 0 20 19 22 23 10 11 1 2 12 13 21 16 14 17 15 18 14 15 20 19 18 22 23 21 12 13 6 7 16 17 3 11 4 0 10 5 1 2 8 9 16 20 19 14 15 12 13 23 21 22 9 5 17 18 0 10 11 4 3 7 8 1 2 6 20 19 15 16 17 13 21 12 22 23 7 8 18 14 10 4 0 3 11 9 5 6 1 2 19 16 17 18 20 21 22 13 23 12 5 6 14 15 4 3 10 11 0 2 7 8 9 1 17 18 14 20 19 23 12 22 13 21 8 9 15 16 11 0 3 10 4 1 2 5 6 7 mate #14400 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 11 3 1 2 10 7 8 9 5 6 4 0 13 21 16 17 18 14 15 20 22 23 12 19 4 0 10 1 2 9 5 6 7 8 11 3 21 22 18 14 15 16 17 23 12 13 19 20 2 11 3 4 1 6 7 8 9 5 0 10 22 23 15 16 17 18 14 13 21 19 20 12 1 2 0 10 11 8 9 5 6 7 3 4 23 12 17 18 14 15 16 22 19 20 13 21 12 13 21 22 23 14 1 2 17 18 15 16 5 6 19 20 7 8 9 3 11 4 0 10 21 22 23 12 13 16 17 1 2 15 18 14 6 7 20 8 9 5 19 0 10 11 4 3 23 12 13 21 22 18 14 15 1 2 16 17 7 8 9 5 6 19 20 10 4 0 3 11 13 21 22 23 12 2 16 17 18 1 14 15 8 9 6 7 19 20 5 4 3 10 11 0 22 23 12 13 21 1 2 14 15 16 17 18 9 5 8 19 20 6 7 11 0 3 10 4 3 10 4 11 0 17 15 18 16 14 1 20 2 19 22 13 23 21 12 8 6 9 7 5 10 4 11 0 3 15 18 16 14 17 19 2 20 1 13 23 21 12 22 6 9 7 5 8 15 14 18 17 16 10 0 4 3 11 20 1 19 2 7 6 5 9 8 21 13 12 23 22 18 17 16 15 14 4 3 11 10 0 2 19 1 20 5 9 8 7 6 12 23 22 21 13 5 6 7 8 9 0 10 20 19 4 13 21 11 3 12 1 2 22 23 17 16 18 14 15 7 8 9 5 6 11 20 19 0 10 23 12 3 4 21 22 1 2 13 14 15 16 18 17 9 5 6 7 8 20 19 10 11 3 21 22 4 0 23 12 13 1 2 15 18 14 17 16 6 7 8 9 5 19 11 3 4 20 12 13 0 10 2 21 22 23 1 18 17 15 16 14 8 9 5 6 7 3 4 0 20 19 22 23 10 11 1 2 12 13 21 16 14 17 15 18 14 15 20 19 18 22 21 23 12 13 6 7 16 17 3 11 4 0 10 5 1 2 8 9 16 20 19 14 15 12 13 21 23 22 9 5 17 18 0 10 11 4 3 7 8 1 2 6 20 19 15 16 17 13 23 12 22 21 7 8 18 14 10 4 0 3 11 9 5 6 1 2 19 16 17 18 20 23 22 13 21 12 5 6 14 15 4 3 10 11 0 2 7 8 9 1 17 18 14 20 19 21 12 22 13 23 8 9 15 16 11 0 3 10 4 1 2 5 6 7 И оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 24 ещё улучшена a(24) >= 14400. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
Ðикаких оÑобых ÑвойÑтв у ОДЛК 14400-ки не обнаружено Order? 24
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
14401 diagonal Latin
14401 nfr
1 orthogonal pair
14401 self-orthogonalкроме того, что вÑе ОДЛК ÑвлÑÑŽÑ‚ÑÑ SODLS. Подтверждение 14400-ки Order? 24 Enter the name of the squares file: inp Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file inp-orthCounts.txt ..output file inp-orthNos.txt squares 14401 total orthogonal pairs 14400 Maximum pairs for square 1: 14400 This is the only square with this maximum number of pairs. ..output file inp-1orths.txt Pairs for square 1: 14400 elapsed time 0:04:15 Ð’ÑÑ‘ чудеÑно! Волшебные квадратики! Ðу и как уже отмечалоÑÑŒ, Ð½Ð°Ð¹Ð´ÐµÐ½Ð½Ð°Ñ Ð½Ð¸Ð¶Ð½ÑÑ Ð³Ñ€Ð°Ð½Ð¸Ñ†Ð° далеко не макÑимальнаÑ. Ðлгоритм открывает удивительные возможноÑти по поиÑку макÑимальных групп ОДЛК разных порÑдков, которые, к Ñожалению, Ð½ÐµÐ»ÑŒÐ·Ñ Ñ€ÐµÐ°Ð»Ð¸Ð·Ð¾Ð²Ð°Ñ‚ÑŒ на одном ПК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3083 Credit: 0 RAC: 0 |
ПопроÑила Harry приÑлать мне иÑходные ДЛК 14-го порÑдка, SODLS. Вот что получилоÑÑŒ Ñ Ñтим набором ДЛК Order? 14 Enter the name of the squares file: inp Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file inp-orthCounts.txt ..output file inp-orthNos.txt squares 1536 total orthogonal pairs 18432 Maximum pairs for square 1: 24 There are 1535 other squares with this maximum number of pairs. ..output file inp-1orths.txt Pairs for square 1: 24 Ðайдены 1536 ДЛК, имеющих 24 ОДЛК. Покажу оÑновной ДЛК первой 24-ки и неÑколько ортогоналек DLK 0 1 2 3 4 5 6 7 8 9 10 11 12 13 3 4 1 2 8 10 9 6 13 5 11 12 7 0 10 6 8 1 2 9 4 5 3 11 12 0 13 7 2 9 5 13 1 3 7 10 6 12 4 8 0 11 1 2 0 10 7 13 5 4 9 8 6 3 11 12 7 13 6 9 0 1 2 11 12 3 8 5 10 4 6 10 13 0 5 11 12 1 2 7 3 4 9 8 8 0 4 7 13 12 11 2 1 6 9 10 5 3 5 3 7 8 9 2 1 12 11 4 0 13 6 10 12 11 9 5 3 4 8 0 7 10 13 6 2 1 11 8 3 6 12 0 13 9 10 1 5 7 4 2 13 7 10 12 11 6 0 3 4 2 1 9 8 5 4 5 12 11 6 7 10 8 0 13 2 1 3 9 9 12 11 4 10 8 3 13 5 0 7 2 1 6 mate #1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 4 6 7 8 3 0 2 1 5 10 12 13 11 9 3 4 1 11 0 13 5 8 2 6 7 12 9 10 11 3 4 2 13 12 1 6 7 0 8 9 10 5 12 13 3 4 5 8 0 11 6 7 9 10 2 1 2 12 8 5 11 3 4 9 10 1 0 6 13 7 13 7 6 1 12 10 9 4 3 8 5 2 0 11 6 5 12 13 7 4 3 10 9 2 11 8 1 0 7 11 0 12 8 9 10 3 4 13 6 1 5 2 5 0 10 9 6 1 13 2 12 11 4 3 7 8 8 10 9 0 2 7 11 12 1 5 13 4 3 6 10 9 5 6 1 11 8 13 0 12 2 7 4 3 9 2 11 7 10 6 12 5 13 3 1 0 8 4 1 8 13 10 9 2 7 0 11 4 3 5 6 12 mate #2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 4 6 7 8 3 0 2 1 5 10 12 13 11 9 3 4 1 11 0 13 5 8 2 6 7 12 9 10 11 3 4 2 13 12 1 6 7 0 8 9 10 5 12 13 3 4 5 8 0 11 6 7 9 10 2 1 2 12 8 5 11 3 4 10 9 1 0 6 13 7 13 7 6 1 12 9 10 4 3 8 5 2 0 11 6 5 12 13 7 4 3 9 10 2 11 8 1 0 7 11 0 12 8 10 9 3 4 13 6 1 5 2 5 0 10 9 6 1 13 2 12 11 4 3 7 8 8 10 9 0 2 7 11 12 1 5 13 4 3 6 10 9 5 6 1 11 8 13 0 12 2 7 4 3 9 2 11 7 10 6 12 5 13 3 1 0 8 4 1 8 13 10 9 2 7 0 11 4 3 5 6 12 . . . . . . . . mate #23 0 1 2 3 4 5 6 7 8 9 10 11 12 13 4 6 7 8 3 0 2 1 5 10 12 13 11 9 3 4 1 11 0 13 5 8 2 6 7 12 9 10 11 3 4 2 13 12 1 6 7 0 8 9 10 5 12 13 3 4 5 8 0 11 6 7 9 10 2 1 2 12 8 5 11 10 9 3 4 1 0 6 13 7 13 7 6 1 12 4 3 9 10 8 5 2 0 11 6 5 12 13 7 9 10 4 3 2 11 8 1 0 7 11 0 12 8 3 4 10 9 13 6 1 5 2 5 0 10 9 6 1 13 2 12 11 4 3 7 8 8 10 9 0 2 7 11 12 1 5 13 4 3 6 10 9 5 6 1 11 8 13 0 12 2 7 4 3 9 2 11 7 10 6 12 5 13 3 1 0 8 4 1 8 13 10 9 2 7 0 11 4 3 5 6 12 mate #24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 4 6 7 8 3 0 2 1 5 10 12 13 11 9 3 4 1 11 0 13 5 8 2 6 7 12 9 10 11 3 4 2 13 12 1 6 7 0 8 9 10 5 12 13 3 4 5 8 0 11 6 7 9 10 2 1 2 12 8 5 11 10 9 4 3 1 0 6 13 7 13 7 6 1 12 3 4 9 10 8 5 2 0 11 6 5 12 13 7 9 10 3 4 2 11 8 1 0 7 11 0 12 8 4 3 10 9 13 6 1 5 2 5 0 10 9 6 1 13 2 12 11 4 3 7 8 8 10 9 0 2 7 11 12 1 5 13 4 3 6 10 9 5 6 1 11 8 13 0 12 2 7 4 3 9 2 11 7 10 6 12 5 13 3 1 0 8 4 1 8 13 10 9 2 7 0 11 4 3 5 6 12 Оценка a(14) >= 24 не актуальна. Я хочу ещё попытатьÑÑ Ð¿Ñ€Ð¸Ð¼ÐµÐ½Ð¸Ñ‚ÑŒ метод Пелегрино-ЛанÑелоти Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 42 на базе 24-ок 14-го порÑдка. ÐеÑколько попыток ранее не увенчалиÑÑŒ уÑпехом: ортогональные пары 42-го порÑдка не ÑтроÑÑ‚ÑÑ. |

©2024 Progger & Stefano Tognon (ice00)