Thread 'ODLS of order n>10'
Message boards : Science : ODLS of order n>10
Message board moderation
Previous · 1 . . . 3 · 4 · 5 · 6 · 7 · 8 · 9 . . . 11 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата У Ð¼ÐµÐ½Ñ Ð¿Ð¾ÑвилÑÑ ÐµÑ‰Ñ‘ один добровольный помощник! Чтобы не забыть и не потерÑÑ‚ÑŒ, обработала результаты от Ñтого квадрата, обÑчитанного тоже полноÑтью добровольным помощником. ДЛК имеет 11128 Д-транÑверÑалей. Ðайдено 812536 ОДЛК. ПоÑчитано программой Белышева. Программа Белышева выдаёт результаты в буквенно-цифровом формате. Канонизатор Harry White работает только Ñ Ñ‡Ð¸Ñловым форматом. ПоÑтому пришлоÑÑŒ преобразовать буквенно-цифровой формат в чиÑловой формат. Делаю Ñ Ñто Ñ Ð¿Ð¾Ð¼Ð¾Ñ‰ÑŒÑŽ программы Tomas Brada dlkconv. Ðу, Ñлава Богу, Ð´Ð»Ñ ÐºÐ¾Ð»Ð¸Ñ‡ÐµÑтва ДЛК в районе миллиона Ñта программа ÑправлÑетÑÑ Ð±Ñ‹Ñтро. Затем запуÑкаю канонизатор Harry White Order? 12 Format, (1: first row or 2: \diagonal)? 2 File name? out .. writing DLS to file output12CF2.txt number of DLS 812536 CFs 275571 elapsed time 0:17:34 Канонизирует за 17 мин 34 Ñек. Отлично! [Может быть, вчера мне надо было Ñразу применить канонизатор Harry White, но решила попробовать канонизатор Tomas Brada, и поÑтигла неудача - ничего не нашла за 17 чаÑов работы программы.] Итак, от Ñтого квадратика найдено 275571 КФ ОДЛК. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð²Ñ‹Ð»Ð¾Ð¶Ñƒ Ñту порцию КФ ОДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Готово! СÑылка https://yadi.sk/d/CTqTUozoLaAD6g Ðрхив объёмом 14 МБ. ОÑталоÑÑŒ выложить результаты моего ÑкÑперимента по второму и третьему уровнÑм. Ðто тоже хорошие порции. Результаты канонизированы. ЗаймуÑÑŒ Ñтим чуть позже. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПытаюÑÑŒ проверить порцию из 812536 ОДЛК 12-го порÑдка на наличие ортогональной пары программой Harry White GetOrthogonal Order? 12 Enter the name of the squares file: inp ..output file inpPairs_2.txt ..output file inpPairNos.txt squares 812536 Пока думает программа :) Да, Ñто Ñложно. Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñ†Ð¸Ð¸ в районе миллиона ОДЛК программа уже ÑправлÑетÑÑ Ñ Ñ‚Ñ€ÑƒÐ´Ð¾Ð¼, то еÑÑ‚ÑŒ, может быть, и ÑправлÑетÑÑ, но за очень большое времÑ. Покручу немножко. Я уже пиÑала выше, что Ñту проверку надо выполнÑÑ‚ÑŒ по чаÑÑ‚Ñм, что вполне возможно. Тройку MODLS 12-го порÑдка Ñтим ÑпоÑобом найти теоретичеÑки возможно, а практичеÑки очень трудно. Порций ОДЛК (от одного ДЛК) можно найти много и гораздо больше проверÑемой ÑÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ñ€Ñ†Ð¸Ð¸. Вот только проверить их данной верÑией программы нереально. Ðеобходимо модифицировать программу. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитирую Ñообщение Ñ Ñ„Ð¾Ñ€ÑƒÐ¼Ð° проекта ОДЛК, чтобы не забыть https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=6131 Цитата Ðто Ñообщение было напиÑано 29 Ð¸ÑŽÐ»Ñ Ð¿Ñ€Ð¾ÑˆÐ»Ð¾Ð³Ð¾ года. Таким образом, Ð¿ÐµÑ€Ð²Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ БД КФ ОДЛК 12-го порÑдка была получена полгода назад. Как видим, Ñто был небольшой набор - вÑего 442696 КФ ОДЛК. Ðа данный момент найдено ещё более миллиона КФ ОДЛК, может быть, даже 2-3 миллиона. Ðе вÑе ОДЛК мне удалоÑÑŒ канонизировать, 2715194 ОДЛК пока не канонизированы. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата ОÑталоÑÑŒ выложить результаты моего ÑкÑперимента по второму и третьему уровнÑм. Выкладываю первую порцию Ñтого ÑкÑперимента https://yadi.sk/d/a8TihFD0kMDTpA ЯндекÑ.ДиÑк, размер файла 25,8 МБ. Результаты канонизированы канонизатором Harry White. ÐŸÐ¾Ñ€Ñ†Ð¸Ñ Ñодержит 606453 КФ ОДЛК. КФ ОДЛК предÑтавлены в формате 2. Ещё Ñоберу одну порцию Ñтого ÑкÑперимента. Кроме того, 79 ОДЛК (от второго уровнÑ) у Ð¼ÐµÐ½Ñ Ð¾ÑталиÑÑŒ не проверенными. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’ÑÑ‘ множеÑтво СРДЛК 12-го порÑдка разделÑетÑÑ Ð½Ð° 596 линеек. Смотрите поÑледовательноÑÑ‚ÑŒ OEIS https://oeis.org/A309283 Результат получен Harry White. О Ñамой первой порции КФ ОДЛК Ñ Ñообщила, что она охватывает 576 линеек, то еÑÑ‚ÑŒ в Ñтой порции еÑÑ‚ÑŒ КФ ОДЛК из 576 линеек. Ðе из вÑех 596 линеек еÑÑ‚ÑŒ КФ ОДЛК в данной порции. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€Ð¸Ð»Ð° только что выложенную порцию из 606453 КФ ОДЛК (Ñто проверÑетÑÑ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð¾Ð¹ Harry White GetDiagonals) Order? 12 File? inp Input file is inp.txt .. writing squares to file inpDiags_2.txt Which \ 1 or / 2? 2 squares 606453 diags 595 ИнтереÑно: только из одной линейки нет КФ ОДЛК. Рвот в первой чаÑти БД, выложенной ранее и Ñодержащей 930337 КФ ОДЛК уже полный комплект предÑтавителей из вÑех 596 линеек Order? 12 File? CF12_part1_930337 Input file is CF12_part1_930337.txt .. writing squares to file CF12_part1_930337Diags.txt Which \ 1 or / 2? 2 squares 930337 diags 596 Отлично! Ядро БД 12-го порÑдка Ñ Ð¿Ð¾Ð»Ð½Ñ‹Ð¼ комплектом КФ ОДЛК из вÑех линеек получено. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Собрала третью порцию от Ñвоего ÑкÑперимента Ñо вторым и третьим уровнÑми, выложила на ЯндекÑ.ДиÑк https://yadi.sk/d/OsftJihEel9p2g Размер файла 30,1 МБ. ÐŸÐ¾Ñ€Ñ†Ð¸Ñ Ñодержит 756976 КФ ОДЛК. Канонизировано программой Harry White. КФ ОДЛК предÑтавлены в формате 2. Итак, в Ñтом ÑкÑперименте Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»Ð° 930337 + 606453 + 756976 = 2293766 КФ ОДЛК Ðапомню: взÑла немного ОДЛК от рекордного по Д-транÑверÑалÑм (на данный момент) ДЛК, нашла к ним ОДЛК, Ñто второй уровень. Затем от ОДЛК второго ÑƒÑ€Ð¾Ð²Ð½Ñ Ð½Ð°ÑˆÐ»Ð° их ОДЛК - Ñто третий уровень. Из ОДЛК второго ÑƒÑ€Ð¾Ð²Ð½Ñ Ð½Ðµ проверила поÑледние 79 ОДЛК. ÐкÑперимент очень интереÑный, но выполнить его в полном объёме на моём ПК нереально. Только первый уровень - Ñто миллионы ОДЛК! Рведь, наверное, на третьем уровне вÑÑ‘ не закончилоÑÑŒ, еÑÑ‚ÑŒ и четвёртый уровень, а может, и пÑтый и далее. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Tomas Brada канонизировал результаты, которые мне не удалоÑÑŒ канонизировать его канонизатором. Ðо Ñделал он Ñто по чаÑÑ‚Ñм. Смотрим его Ñообщение https://boinc.tbrada.eu/forum_thread.php?id=3104&postid=4382 I canonicalized 2715194 mates of Dv8yEzQnSZSx2gbK2JTvcP6FD7Sh7XQ8, in parts. Итак, наконец, Ð´Ð»Ñ Ñтого квадратика  получены КФ ОДЛК. Ðапомню, что Ñ Ð²Ñ‹Ð»Ð¾Ð¶Ð¸Ð»Ð° не канонизированные ОДЛК Ð´Ð»Ñ Ñтого ДЛК здеÑÑŒ https://yadi.sk/d/P-inaoj1R1rC8A По ÑÑылке, указанной в Ñообщении Tomas Brada, можно поÑмотреть полученные им КФ ОДЛК. Позже Ñ Ð²Ñ‹Ð»Ð¾Ð¶Ñƒ Ñто на ЯндекÑ.ДиÑк. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð¡ÐµÐ³Ð¾Ð´Ð½Ñ ÑƒÑ‚Ñ€Ð¾Ð¼ приÑлал результат канонизации и тот добровольный помощник, который Ñтот квадратик обÑчитал. Он канонизировал ОДЛК программой Harry White. Схема такаÑ: 1. Преоборазуем коды ОДЛК в "живые" квадраты, то еÑÑ‚ÑŒ ДЛК в чиÑловом формате; 2. Канонизируем ДЛК программой Harry White; 3. Полученные КФ ОДЛК кодируем в ÑиÑтеме Tomas Brada (в кодах квадраты занимают меньше меÑта). Ð”Ð»Ñ Ð´ÐµÐºÐ¾Ð´Ð¸Ñ€Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¸ ÐºÐ¾Ð´Ð¸Ñ€Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¸ÑпользовалаÑÑŒ программа Tomas Brada dlkconv. Программа Harry White канонизировала 2715194 ОДЛК примерно чаÑ. Ð’ результате канонизации получено 1074990 КФ ОДЛК. Tomas Brada получил такое же количеÑтво КФ ОДЛК. Я немного Ñравнила оба маÑÑива; дело в том, что порÑдок раÑÐ¿Ð¾Ð»Ð¾Ð¶ÐµÐ½Ð¸Ñ ÐºÐ¾Ð´Ð¾Ð² КФ ОДЛК в Ñтих двух маÑÑивах разный. Ðу вот, поÑтому говорю, что Ñравнила немного: проÑто неÑколько кодов из первого файла нашла во втором файле (поиÑком) и наоборот. ÐадеюÑÑŒ, что Ñовпадение результатов полное. Чтобы в Ñтом убедитьÑÑ, надо отÑортировать второй маÑÑив кодов (полученный помощником) и Ñравнить Ñти два маÑÑива. ПоÑкольку Ñвой результат Tomas Brada выложил, Ñ Ð²Ñ‹Ð»Ð¾Ð¶Ð¸Ð»Ð° результат помощника https://yadi.sk/d/2fUWMTJ-IAhwsQ ЯндекÑ.ДиÑк размер архива 24,9 МБ. Файл Ñодержит 1074990 КФ ОДЛК. Канонизировано программой Harry White. КФ ОДЛК предÑтавлены в формате 2 в закодированном виде. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Давно уже по программе Harry White SODLS Ñ Ð½Ð°ÑˆÐ»Ð° 10 аÑÑоциативных SODLS 12-го порÑдка (проÑто проба, за небольшой промежуток времени) 0 2 3 4 9 8 7 6 11 10 5 1 3 1 7 6 8 9 5 10 4 11 0 2 1 9 2 5 7 10 8 11 0 3 6 4 5 4 10 3 11 0 9 8 2 6 1 7 6 7 11 10 4 1 0 5 9 2 8 3 11 0 6 8 2 5 4 1 10 7 3 9 2 8 4 1 10 7 6 9 3 5 11 0 8 3 9 2 6 11 10 7 1 0 4 5 4 10 5 9 3 2 11 0 8 1 7 6 7 5 8 11 0 3 1 4 6 9 2 10 9 11 0 7 1 6 2 3 5 4 10 8 10 6 1 0 5 4 3 2 7 8 9 11 0 2 3 4 9 6 8 11 5 10 7 1 3 1 10 5 7 8 2 6 4 11 0 9 1 7 2 8 11 4 0 10 9 3 6 5 5 10 7 3 8 0 1 9 2 6 11 4 11 9 6 0 4 2 10 5 1 7 8 3 9 6 11 1 10 5 4 8 0 2 3 7 4 8 9 11 3 7 6 1 10 0 5 2 8 3 4 10 6 1 9 7 11 5 2 0 7 0 5 9 2 10 11 3 8 4 1 6 6 5 8 2 1 11 7 0 3 9 4 10 2 11 0 7 5 9 3 4 6 1 10 8 10 4 1 6 0 3 5 2 7 8 9 11 0 2 3 4 11 10 5 8 9 7 6 1 3 1 5 6 7 8 11 2 10 4 0 9 1 10 2 7 8 4 9 11 6 3 5 0 5 9 10 3 1 11 8 6 2 0 7 4 9 0 6 8 4 1 2 5 11 10 3 7 6 7 9 10 2 5 4 1 0 11 8 3 8 3 0 11 10 7 6 9 1 2 4 5 4 8 1 0 6 9 10 7 3 5 11 2 7 4 11 9 5 3 0 10 8 1 2 6 11 6 8 5 0 2 7 3 4 9 1 10 2 11 7 1 9 0 3 4 5 6 10 8 10 5 4 2 3 6 1 0 7 8 9 11 0 2 3 4 9 6 10 8 11 7 5 1 3 1 7 11 2 4 8 10 5 6 0 9 1 8 2 7 5 10 9 11 6 3 4 0 6 5 10 3 8 9 11 4 2 0 1 7 7 0 9 2 4 11 3 5 1 10 8 6 8 9 6 1 10 5 4 0 3 11 7 2 9 4 0 8 11 7 6 1 10 5 2 3 5 3 1 10 6 8 0 7 9 2 11 4 4 10 11 9 7 0 2 3 8 1 6 5 11 7 8 5 0 2 1 6 4 9 3 10 2 11 5 6 1 3 7 9 0 4 10 8 10 6 4 0 3 1 5 2 7 8 9 11 0 2 3 4 10 11 8 9 5 7 6 1 3 1 9 8 5 6 7 10 4 11 0 2 1 7 2 11 8 0 10 4 6 3 5 9 6 4 5 3 0 9 1 8 2 10 11 7 7 9 6 10 4 2 3 5 11 1 8 0 8 10 7 1 11 5 4 2 9 0 3 6 5 8 11 2 9 7 6 0 10 4 1 3 11 3 10 0 6 8 9 7 1 5 2 4 4 0 1 9 3 10 2 11 8 6 7 5 2 6 8 5 7 1 11 3 0 9 4 10 9 11 0 7 1 4 5 6 3 2 10 8 10 5 4 6 2 3 0 1 7 8 9 11 0 2 3 4 11 9 8 6 5 10 7 1 3 1 4 5 2 10 7 8 11 6 0 9 1 10 2 7 8 0 5 4 9 3 11 6 6 9 10 3 1 8 0 11 2 5 4 7 9 8 7 11 4 2 10 5 1 0 6 3 7 6 9 1 10 5 4 2 3 11 8 0 11 3 0 8 9 7 6 1 10 2 5 4 8 5 11 10 6 1 9 7 0 4 3 2 4 7 6 9 0 11 3 10 8 1 2 5 5 0 8 2 7 6 11 3 4 9 1 10 2 11 5 0 3 4 1 9 6 7 10 8 10 4 1 6 5 3 2 0 7 8 9 11 0 2 3 4 8 9 7 10 11 5 6 1 3 1 4 8 5 10 9 2 6 11 0 7 1 0 2 10 11 6 8 4 5 3 7 9 8 6 7 3 10 1 11 9 2 0 4 5 7 9 1 11 4 8 0 5 10 2 3 6 11 3 10 7 0 5 4 8 9 6 1 2 9 10 5 2 3 7 6 11 4 1 8 0 5 8 9 1 6 11 3 7 0 10 2 4 6 7 11 9 2 0 10 1 8 4 5 3 2 4 8 6 7 3 5 0 1 9 11 10 4 11 0 5 9 2 1 6 3 7 10 8 10 5 6 0 1 4 2 3 7 8 9 11 0 2 3 4 8 11 9 6 10 7 5 1 3 1 7 6 10 4 11 8 9 5 0 2 1 0 2 5 9 8 10 11 4 3 7 6 8 9 11 3 7 6 1 0 2 10 4 5 7 3 10 11 4 9 8 5 1 2 6 0 2 10 0 8 1 5 4 9 11 6 3 7 4 8 5 0 2 7 6 10 3 11 1 9 11 5 9 10 6 3 2 7 0 1 8 4 6 7 1 9 11 10 5 4 8 0 2 3 5 4 8 7 0 1 3 2 6 9 11 10 9 11 6 2 3 0 7 1 5 4 10 8 10 6 4 1 5 2 0 3 7 8 9 11 0 2 3 4 10 9 7 8 11 6 5 1 3 1 11 8 7 6 10 9 5 4 0 2 1 4 2 5 9 8 11 10 0 3 6 7 8 7 0 3 11 10 9 6 2 5 1 4 11 9 10 2 4 3 0 5 1 7 8 6 6 8 1 7 0 5 4 3 10 2 11 9 2 0 9 1 8 7 6 11 4 10 3 5 5 3 4 10 6 11 8 7 9 1 2 0 7 10 6 9 5 2 1 0 8 11 4 3 4 5 8 11 1 0 3 2 6 9 7 10 9 11 7 6 2 1 5 4 3 0 10 8 10 6 5 0 3 4 2 1 7 8 9 11 0 2 3 4 7 8 11 9 10 5 6 1 3 1 10 5 11 9 8 2 4 6 0 7 1 6 2 0 8 11 7 10 5 3 4 9 9 10 7 3 5 6 1 11 2 0 8 4 11 9 0 8 4 2 10 5 1 7 3 6 6 0 1 11 10 5 4 8 9 2 7 3 8 4 9 2 3 7 6 1 0 10 11 5 5 8 4 10 6 1 9 7 3 11 2 0 7 3 11 9 0 10 5 6 8 4 1 2 2 7 8 6 1 4 0 3 11 9 5 10 4 11 5 7 9 3 2 0 6 1 10 8 10 5 6 1 2 0 3 4 7 8 9 11 ИнтереÑно, что вÑе аÑÑоциативные SODLS 12-го порÑдка (и не только!) ÑвлÑÑŽÑ‚ÑÑ Ñ‚Ð°ÐºÐ¶Ðµ и DSODLS. Ðто ÑмпиричеÑки полученный факт. ДоказательÑтва ÑƒÑ‚Ð²ÐµÑ€Ð¶Ð´ÐµÐ½Ð¸Ñ Ñƒ Ð¼ÐµÐ½Ñ Ð½ÐµÑ‚. Ð¢Ð°ÐºÐ°Ñ Ð²Ð¾Ñ‚ гипотеза. ИнтереÑно, что Ñти SODLS имеют мало Д-транÑверÑалей order? 12 Type of Latin square, 1 LS or 2 DLS? 2 Get diagonal transversals, (Y or N)? y File name? inp .. writing counts to file 12Transversals_6.txt DLS 8 max transversals 2304 МакÑимум Ñреди Ñтих 10 ДЛК вÑего 2304 Д-транÑверÑалей. Зато Ñто уже готовые ОДЛК! Рвот интереÑно: имеют ли Ñти ДЛК другие ОДЛК, кроме Ñвоего транÑпонированного и анти-транÑпонированного вариантов? Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÑŽ Ð´Ð»Ñ Ð”Ð›Ðš, имеющего 2304 Д-транÑверÑалей. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Готово! [DLK(58):1] 0 2 3 4 8 B 9 6 A 7 5 1 3 1 7 6 A 4 B 8 9 5 0 2 1 0 2 5 9 8 A B 4 3 7 6 8 9 B 3 7 6 1 0 2 A 4 5 7 3 A B 4 9 8 5 1 2 6 0 2 A 0 8 1 5 4 9 B 6 3 7 4 8 5 0 2 7 6 A 3 B 1 9 B 5 9 A 6 3 2 7 0 1 8 4 6 7 1 9 B A 5 4 8 0 2 3 5 4 8 7 0 1 3 2 6 9 B A 9 B 6 2 3 0 7 1 5 4 A 8 A 6 4 1 5 2 0 3 7 8 9 B Квадратик имеет 58 ортогональных диагональных Ñоквадратов. Ðеплохо! Ðти ОДЛК дали 33 КФ ОДЛК. Следующие уровни не проверÑла. Таким образом, поиÑк вÑех SODLS 12-го порÑдка - Ñто очень хороший алгоритм Ð´Ð»Ñ Ð¿Ð¾Ð¿Ð¾Ð»Ð½ÐµÐ½Ð¸Ñ Ð‘Ð” КФ ОДЛК 12-го порÑдка. К тому же, SODLS могут быть и не аÑÑоциативные. ПроÑто в программе Harry White еÑÑ‚ÑŒ отдельно режим поиÑка аÑÑоциативных SODLS, потому что такие SODLS находÑÑ‚ÑÑ Ð±Ñ‹Ñтрее. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ð¿Ñ€Ð¾Ð±ÑƒÑŽ не задавать режим поиÑка аÑÑоциативных SODLS, получитÑÑ Ð»Ð¸ найти не аÑÑоциативный SODLS 12-го порÑдка. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Хм... не хочет программа выдавать не аÑÑоциативный SODLS 12-го порÑдка, три чаÑа работает и... ничего SODLS order? 12 Make SSSOLDS, y (yes) or n (no)? n .. writing SODLS to file SODLS12.txt Second \diagonal value, (2..11)? 2 Прервала. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Рвот однушка, даже не веритÑÑ [DLK(1):1] 0 2 3 4 9 8 7 6 B A 5 1 3 1 7 6 8 9 5 A 4 B 0 2 1 9 2 5 7 A 8 B 0 3 6 4 5 4 A 3 B 0 9 8 2 6 1 7 6 7 B A 4 1 0 5 9 2 8 3 B 0 6 8 2 5 4 1 A 7 3 9 2 8 4 1 A 7 6 9 3 5 B 0 8 3 9 2 6 B A 7 1 0 4 5 4 A 5 9 3 2 B 0 8 1 7 6 7 5 8 B 0 3 1 4 6 9 2 A 9 B 0 7 1 6 2 3 5 4 A 8 A 6 1 0 5 4 3 2 7 8 9 B Ðто тоже от аÑÑоциативного SODLS 12-го порÑдка. ÐепонÑтно, однако, почему однушка, еÑли Ñтот SODLS ортогонален транÑпонированному и анти-транÑпонированному вариантам??? Проверила ортогональноÑÑ‚ÑŒ Ñ Ð°Ð½Ñ‚Ð¸-транÑпонированным вариантом 0 2 3 4 9 8 7 6 11 10 5 1 3 1 7 6 8 9 5 10 4 11 0 2 1 9 2 5 7 10 8 11 0 3 6 4 5 4 10 3 11 0 9 8 2 6 1 7 6 7 11 10 4 1 0 5 9 2 8 3 11 0 6 8 2 5 4 1 10 7 3 9 2 8 4 1 10 7 6 9 3 5 11 0 8 3 9 2 6 11 10 7 1 0 4 5 4 10 5 9 3 2 11 0 8 1 7 6 7 5 8 11 0 3 1 4 6 9 2 10 9 11 0 7 1 6 2 3 5 4 10 8 10 6 1 0 5 4 3 2 7 8 9 11 11 8 10 6 5 0 9 3 7 4 2 1 9 10 2 7 4 11 3 8 1 6 0 5 8 4 9 1 0 5 7 2 6 3 11 10 7 5 6 8 1 3 10 9 2 0 4 11 2 3 4 0 7 9 1 5 8 11 10 6 3 2 1 11 10 6 4 0 9 8 5 7 4 6 3 2 11 7 5 1 0 10 9 8 5 1 0 3 6 10 2 4 11 7 8 9 0 7 11 9 2 1 8 10 3 5 6 4 1 0 8 5 9 4 6 11 10 2 7 3 6 11 5 10 3 8 0 7 4 9 1 2 10 9 7 4 8 2 11 6 5 1 3 0 Ð’ÑÑ‘ нормально, квадраты ортогональны. Ðу, и транÑпонированному варианту, еÑтеÑтвенно, иÑходный ДЛК ортогонален. Тогда почему программа Белышева находит только один ортогональный диагональный Ñоквадрат к Ñтому ДЛК? Ðга, вот в чём дело! Ðормализовала транÑпонированный и анти-транÑпонированный варианты 0 1 2 3 4 5 6 7 8 9 10 11 6 2 10 8 9 0 7 1 11 3 5 4 1 9 6 11 5 4 8 10 3 7 0 2 8 4 3 1 11 7 2 6 10 5 9 0 10 7 9 5 8 6 11 4 1 0 2 3 7 10 11 0 2 3 9 5 6 1 4 8 9 3 7 10 0 8 4 11 5 2 6 1 4 11 5 7 3 2 10 9 0 8 1 6 5 8 0 6 10 11 1 2 7 4 3 9 11 5 1 4 6 9 3 0 2 10 8 7 3 0 4 2 7 1 5 8 9 6 11 10 2 6 8 9 1 10 0 3 4 11 7 5 0 1 2 3 4 5 6 7 8 9 10 11 6 2 10 8 9 0 7 1 11 3 5 4 1 9 6 11 5 4 8 10 3 7 0 2 8 4 3 1 11 7 2 6 10 5 9 0 10 7 9 5 8 6 11 4 1 0 2 3 7 10 11 0 2 3 9 5 6 1 4 8 9 3 7 10 0 8 4 11 5 2 6 1 4 11 5 7 3 2 10 9 0 8 1 6 5 8 0 6 10 11 1 2 7 4 3 9 11 5 1 4 6 9 3 0 2 10 8 7 3 0 4 2 7 1 5 8 9 6 11 10 2 6 8 9 1 10 0 3 4 11 7 5 Совершенно одинаковые ДЛК! Тут, наверное, и кроетÑÑ Ð¿Ñ€Ð¸Ñ‡Ð¸Ð½Ð° того факта, что аÑÑоциативные SODLS ÑвлÑÑŽÑ‚ÑÑ Ñ‚Ð°ÐºÐ¶Ðµ DSODLS. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата Ðапомню: взÑла немного ОДЛК от рекордного по Д-транÑверÑалÑм (на данный момент) ДЛК, нашла к ним ОДЛК, Ñто второй уровень. Вот Ñти 79 квадратиков приглÑнулиÑÑŒ моему новому помощнику :) Да, они не Ñлишком "Ñ‚Ñжёлые", а еÑÑ‚ÑŒ даже и ÑовÑем лёгкие. Однако они дают неплохие результаты. Помощник начал их обÑчитывать. ОбÑчитал на данный момент 13 ОДЛК. Первые 12 ОДЛК дали 666658 ОДЛК. ЗаймуÑÑŒ ÑÐµÐ¹Ñ‡Ð°Ñ Ð¸Ñ… канонизацией. Покажу из Ñтих 12 квадратов Ñамые Ñолидные [DLK(179815):1] 0 8 4 6 2 A 9 3 7 5 B 1 B 1 7 5 9 3 2 8 4 6 0 A 6 4 2 A 0 8 B 1 9 3 5 7 5 7 9 3 B 1 0 A 2 8 6 4 2 A 8 0 4 6 7 5 1 B 9 3 9 3 1 B 7 5 4 6 A 0 2 8 3 9 B 1 5 7 6 4 0 A 8 2 A 2 0 8 6 4 5 7 B 1 3 9 7 5 3 9 1 B A 0 8 2 4 6 4 6 A 2 8 0 1 B 3 9 7 5 1 B 5 7 3 9 8 2 6 4 A 0 8 0 6 4 A 2 3 9 5 7 1 B . . . . . . [DLK(415944):1] 0 A 4 5 2 8 9 3 7 6 B 1 B 1 7 6 9 3 2 8 4 5 0 A 4 5 2 8 1 B A 0 9 3 7 6 7 6 9 3 A 0 1 B 2 8 4 5 3 9 0 A 4 6 7 5 B 1 8 2 8 2 B 1 7 5 4 6 0 A 3 9 2 8 1 B 5 7 6 4 A 0 9 3 9 3 A 0 6 4 5 7 1 B 2 8 5 7 3 9 0 A B 1 8 2 6 4 6 4 8 2 B 1 0 A 3 9 5 7 1 B 6 7 3 9 8 2 5 4 A 0 A 0 5 4 8 2 3 9 6 7 1 B Ð 13-й ОДЛК Ñ Ð½Ðµ включила в Ñту порцию, потому что он имеет м-н-о-о-о-г-о ОДЛК [DLK(771790):1] 0 A 4 5 2 8 9 3 7 6 B 1 B 1 7 6 9 3 2 8 4 5 0 A 4 5 2 8 B 1 0 A 9 3 7 6 7 6 9 3 0 A B 1 2 8 4 5 9 3 0 A 4 6 7 5 B 1 2 8 2 8 B 1 7 5 4 6 0 A 9 3 8 2 1 B 5 7 6 4 A 0 3 9 3 9 A 0 6 4 5 7 1 B 8 2 5 7 3 9 A 0 1 B 8 2 6 4 6 4 8 2 1 B A 0 3 9 5 7 1 B 5 7 3 9 8 2 6 4 A 0 A 0 6 4 8 2 3 9 5 7 1 B Ðтот квадрат имеет больше ОДЛК, чем вÑе предыдущие 12 вмеÑте. Обработаю его отдельно. ИнтереÑный ÑкÑперимент, точнее, завершение моего ÑкÑперимента Ñо вторым и третьим уровнÑми от рекордного ДЛК 12-го порÑдка. Пока ещё не завершён, помощник будет оÑтальные ОДЛК обÑчитывать. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Сначала канонизировала ОДЛК от первых 12 ДЛК Order? 12 Format, (1: first row or 2: \diagonal)? 2 File name? out .. writing DLS to file output12CF2.txt number of DLS 666658 CFs 464619 elapsed time 0:14:34 Затем канонизировала ОДЛК от 13-го ДЛК Order? 12 Format, (1: first row or 2: \diagonal)? 2 File name? out .. writing DLS to file output12CF2_1.txt number of DLS 771790 CFs 264789 elapsed time 0:16:56 Теперь объединила КФ ОДЛК из Ñтих двух порций и Ñнова канонизировала Order? 12 Format, (1: first row or 2: \diagonal)? 2 File name? output12CF2 .. writing DLS to file output12CF2_2.txt number of DLS 729408 CFs 705236 elapsed time 0:16:08 Ð’ итоге получилоÑÑŒ 705236 КФ ОДЛК. Выложила Ñту порцию КФ ОДЛК здеÑÑŒ https://yadi.sk/d/fkxC-TwVWs1hkQ ЯндекÑ.ДиÑк, размер файла 16,4 МБ. КФ ОДЛК предÑтавлены в формате 2 в закодированном виде по ÑиÑтеме Tomas Brada. ПоÑчитано добровольным помощником программой Белышева ortogon_u, канонизировано программой Harry White. Ðапомню: помощник обÑчитал 13 ОДЛК 12-го порÑдка второго ÑƒÑ€Ð¾Ð²Ð½Ñ Ð¸Ð· 79 ОДЛК (из моего ÑкÑперимента). ОДЛК Ñти довольно продуктивные и в то же Ð²Ñ€ÐµÐ¼Ñ Ð½Ðµ Ñильно "Ñ‚Ñжёлые". |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Tomas Brada привёл пример иÑÐ¿Ð¾Ð»ÑŒÐ·Ð¾Ð²Ð°Ð½Ð¸Ñ ÐµÐ³Ð¾ программы ortogonbw Ð´Ð»Ñ Ð¿Ð¾Ð¸Ñка ОДЛК к заданному ДЛК по чаÑÑ‚Ñм https://boinc.tbrada.eu/forum_thread.php?id=3104&postid=4387 Я протеÑтировала программу, дублирую Ñвоё Ñообщение https://boinc.tbrada.eu/forum_thread.php?id=3104&postid=4388 Thanks. Ðе знаю, правильно ли Ñ Ð²ÑÑ‘ понÑла. Вот должен быть ответ на Ñтот поÑÑ‚. ЕÑли вÑÑ‘ правильно понÑла, программа очень интереÑнаÑ. Она позволÑет иÑкать ОДЛК к "Ñ‚Ñжёлым" ДЛК по чаÑÑ‚Ñм. ЕÑли вÑе Ñти чаÑти незавиÑимые и иÑкать их можно в отдельных потоках, Ñто здорово. ПрекраÑно можно раÑпараллелить программу на многоÑдерном процеÑÑоре. Ð’ общем, пока жду ответ на Ñвоё Ñообщение. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата 7. 28496 Д-транÑверÑалей Ðтого монÑтра пока не удалоÑÑŒ обÑчитать полноÑтью. Я чуть-чуть Ñчитала, нашла 211488 ОДЛК. Мой помощник Ñчитал на 40-Ñдерном процеÑÑоре более двух Ñуток. ÐžÐ¿ÐµÑ€Ð°Ñ‚Ð¸Ð²Ð½Ð°Ñ Ð¿Ð°Ð¼ÑÑ‚ÑŒ требуетÑÑ ÐºÐ¾Ð»Ð¾ÑÑальнаÑ! Ð’ программе ortogonb вÑÑ‘ Ñидит в ОЗУ. Ðто плохо. Программу пришлоÑÑŒ прервать во избежание проблем Ñ Ð¿Ð°Ð¼Ñтью. И Ñамое плохое то, что при прерывании вÑе найденные ОДЛК пропали. ЗапуÑкаю Ð´Ð»Ñ Ñтого монÑтра первый шаг в программе ortogonbw ortogonbw DSkEkzZkhtCs22cK3BoLLiYwwc8ZkXd4 1 > output.txt Ðа конÑоль выдаётÑÑ C:\Users\Дом\Downloads\Tomas>ortogonbw DSkEkzZkhtCs22cK3BoLLiYwwc8ZkXd4 1 1>out put.txt init_trans(12) used 495 nodes num_dtrans: 28496 init_disjoint(12) used 145 heads and 342097 nodes L(0) c(28) 1 / 2048 L(1) c(99) X / 818 Ðе выполнила Ñтот шаг полноÑтью, но ОДЛК уже пошли в выходной файл # in: DSkEkzZkhtCs22cK3BoLLiYwwc8ZkXd4 1 # num_dtrans: 28496 DRTrMSrmtgMWUad83WDfEg8YGDL1SZQ9 DJq1LUeGDEq7GY1UwLbej1jSYrwLQQ5H DP7oXqQtvnPteacpK5WhTj7afSyay6i8 Df4GyFEKymxJVft6A639qT6tg6J7HHaY DNMtJJaqn51wwWkXNx2SvKawS2MHoH7N DNkiV9YAnzhSA2meqLSn2vS3KjPK5oA DugRqDKqCbqf2Vyeh3tGxXu6h21PxjRL DaiW3VU2AtRayW1hjrVoc1fQf4tR8349 D7F3Hy1ishXAvXCwo328rxCQpLQbQRFE2 DuidLn5VqkNDD8xnNWBpt5Rnn3YuR7NA DPZGAKnztqZo9TMed7ahu2TC42VJ4rE7 D2gnc8muLHFJQGPJu9gjLnz6sLiy2NZB DU3RKpZ3qtTNwFrb5KEEKxUx9LVxAkUB DnCP4mw7UXPd6XKYNpR65eHRwrUz4FPW DQQm2fKjEVhjPjgmQF9SX81dc1UxXGL8 DMC5aveZWY2wj5LyFgKaP5Kdk9SPm9U4 . . . . . . Ðто хорошо. Как видим, здеÑÑŒ будет 2048 чаÑтей. Ðу, еÑли бы на клаÑтере Ñчитать, на 1000 Ñдер раÑкидать, может, и быÑтро проÑчитаетÑÑ. Ðа 40-Ñдерном процеÑÑоре тоже можно пробовать, но Ñколько времени потребуетÑÑ, трудно Ñказать. ЗдеÑÑŒ Ñ…Ð¾Ñ‚Ñ Ð±Ñ‹ каждую чаÑÑ‚ÑŒ можно проÑчитать отдельно, и вÑе найденные при Ñтом ОДЛК будут запиÑаны в файл и не пропадут уже. PS. Прогноз Ð´Ð»Ñ Ð´Ð°Ð½Ð½Ð¾Ð³Ð¾ ДЛК - 400 миллионов ОДЛК плюÑ/минуÑ. Помощник окреÑтил Ñтот ДЛК квадрозавром :) Очень трудно предÑтавить 400 миллионов ортогональных диагональных Ñоквадратов к одному ДЛК! ИнтереÑно, Ñколько они дадут КФ? Канонизировать такое количеÑтво ОДЛК врÑд ли удаÑÑ‚ÑÑ, даже еÑли их удаÑÑ‚ÑÑ Ð½Ð°Ð¹Ñ‚Ð¸. И опÑÑ‚ÑŒ же ÑÐ¸Ñ‚ÑƒÐ°Ñ†Ð¸Ñ Ð¿Ð¾Ñ…Ð¾Ð¶Ð°Ñ Ð½Ð° Ñитуацию Паркера. Помните? Паркер нашёл 12 миллионов Ñ Ñ…Ð²Ð¾Ñтиком ОЛК к одному ЛК 10-го порÑдка. И потом иÑкал в Ñтом наборе ортогональную пару. И... не нашёл её! Можно предÑтавить его огорчение. Ртеперь предÑтавьте примерно 400 миллионов ортогональных диагональных Ñоквадратов к нашему монÑтру. Предположим, что вÑе Ñти ОДЛК найдены. И поищем в Ñтом наборе ортогональную пару! :) Сможем поиÑкать??? ЕÑли Ñ‚Ð°ÐºÐ°Ñ Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° обнаружитÑÑ Ð² Ñтом наборе ОДЛК, Ñто значит - найдена тройка MODLS 12-го порÑдка. Однако... Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° вполне может и не ÑущеÑтвовать в Ñтом наборе ОДЛК. Ð’ÑÑ‘, как у Паркера :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата Я протеÑтировала программу, дублирую Ñвоё Ñообщение Хм... жду ответ на Ñто Ñообщение, а... Ñамо Ñообщение пропало на форуме Tomas Brada. Странно! Хорошо, что продублировала Ñообщение здеÑÑŒ. Ð’ общем, пока никакого ответа. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð²Ñ‹Ð¿Ð¾Ð»Ð½ÑŽ ещё один теÑÑ‚ Ð´Ð»Ñ Ð»Ñ‘Ð³ÐºÐ¾Ð³Ð¾ квадратика, чтобы убедитьÑÑ Ð² том, что вÑÑ‘ правильно понÑла. Квадратик Ñтот возьму 0 2 4 6 8 B A 9 7 5 3 1 B 1 7 8 3 4 5 2 9 6 0 A 8 A 2 5 7 0 1 6 4 3 B 9 6 5 1 3 B 8 9 A 2 0 4 7 7 9 0 B 4 3 2 5 A 1 8 6 3 6 9 A 0 5 4 1 B 8 7 2 9 4 3 0 A 7 6 B 1 2 5 8 5 3 A 1 6 9 8 7 0 B 2 4 4 7 B 9 1 2 3 0 8 A 6 5 2 0 8 7 5 A B 4 6 9 1 3 1 B 5 2 9 6 7 8 3 4 A 0 A 8 6 4 2 1 0 3 5 7 9 B Я его обÑчитывала в Ñвоём ÑкÑперименте по второму и третьему уровнÑм программой Белышева ortogon_u. Снова обÑчитаю программой Белышева, а потом программой Tomas Brada. Сравню результаты. Программа Белышева обÑчитывает Ñтот ДЛК быÑтро, результат Проверка ДЛК12 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 1 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 2284 Соквадратов: 1305 Ð’Ñ€ÐµÐ¼Ñ Ð² Ñек: 20 Квадратик имеет 2284 Д-транÑверÑалей и 1305 ортогональных диагональных Ñоквадратов. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Теперь обÑчитываю Ñтот квадратик программой Tomas Brada. Первый шаг ÐºÐ¾Ð¼Ð°Ð½Ð´Ð½Ð°Ñ Ñтрока ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 1 > output.txt КонÑоль C:\Users\Дом\Downloads\Tomas>ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 1 1>output.txt init_trans(12) used 495 nodes num_dtrans: 2284 init_disjoint(12) used 145 heads and 27553 nodes L(0) c(63) 1 / 148 L(1) c(82) X / 54 Ðтот шаг мгновенно выполнилÑÑ, результаты запиÑалиÑÑŒ в файл output.txt. Идём дальше. Видим, что здеÑÑŒ 148 чаÑтей. ЗапиÑываю дальше в пакетный файл командные Ñтроки ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 2 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 3 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 4 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 5 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 6 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 7 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 8 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 9 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 10 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 11 >> output.txt . . . . . . ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 141 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 142 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 143 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 144 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 145 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 146 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 147 >> output.txt ortogonbw DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 148 >> output.txt pause ВыполнÑÑŽ пакетный файл. БыÑтро выполнÑетÑÑ, в файл output.txt запиÑаны результаты. Один неудобный момент: перед каждой чаÑтью выводитÑÑ "шапка" # in: DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 2 # num_dtrans: 2284 DH48Cub8CEQwVJiy1QPAad2HgtFUBkG2 DfmrGA15p1SxhxsvdYFMjZEansN6ArZ2 DjXYWL4qcrB87CTVxqFEKcSU5JCRNHA6 D8eYXwR44RaC8A2athsKCYk6nEMRAAF Du3bGDsVmiDhsMU2ZKFyYPmY7qbZHgJ5 DV3fRwRLXhSPDoi8SojJETdvxxRDyLo8 # in: DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 3 # num_dtrans: 2284 DV4wJhpVzgTsjjgqKjiW6iDANhCeeWR D9YCh8Un5darp1rQXMfgvsb1poynZ2a2 DmDWRknEmHA1GfbCRAo78RtxPxuJWvj DyD7o2fPQedLEZ4Mk4W8Bv97NLdXUGW2 # in: DEvRG5oqK7j4UqQT85L8u5xWwrTh5rQ 4 # num_dtrans: 2284 DLFRAgLDsQBKrcsb6aJc1AYHxcxhiSf D4R8cdy4UBseHyD5A7fkwCLfv6BXsfL5 DixgtAJTy5DWSJu97vJQgpHdjCM19bm DQXVWnyt4L4LB8nR5aRPdidnkzEjSy9 DyaHuYaGnBtDpTwPwz4FKQYwZwYsfH5 DWGeSabEa4YZKeitT2JYDKJXi2aaJyA2 DdYteJxq4jPFqEEoqyRiCxTWKFP8WWY DLLvv4TDhxpjdiZgu3FWC6Q3iaojj5Z2 Df9Cm2vhJAFv5eRKbYFPMXmpZ3oZbqW DT9hncdCmfT3yX43zgK3FX4cXqPgzQd D5ci8cjZbU9aDopfgfW4TpqZx4GF4k DtwCRVmaN3NhzTtygX2mdkdKvpnygpd DruNBrnZgD4QD9uQWEmXYc1bggpomkV4 DxAZQH8BMiMt8WeGt1WXVhmVTrzQBLt DfW2BhJSboMYC1zqPK7NfTqJyNSVLhb D7wkM6zhKrSUs8WJXwJrczV8SQkmPoB DEgZBhVee5HepJGRLTvexXgujKSvFGw DW9usGBWLiPtukATLJC5bLupjvfso8K DXmuqecAgmeRRdjDtv32wx2ii5sSHjo8 DhxFZdyRrp31XhRGopSsed8cuowZtAS8 . . . . . Ðто, конечно, лишнÑÑ Ð¸Ð½Ñ„Ð¾Ñ€Ð¼Ð°Ñ†Ð¸Ñ Ð² файле результатов. Чтобы поÑмотреть только на полученные решениÑ, мне пришлоÑÑŒ пропуÑтить файл output.txt через фильтр, удалÑющий Ñтроки, начинающиеÑÑ Ñ Ñимвола #. Решений получено ровно Ñтолько же, Ñколько при обработке программой Белышева - 1305 ОДЛК. Замечательно! КÑтати, Ñтот лёгкий квадратик можно обÑчитать и программой Tomas Brada ortogonb, не по чаÑÑ‚Ñм, а Ñразу веÑÑŒ. Лёгкие квадраты нет ÑмыÑла обÑчитывать по чаÑÑ‚Ñм. Так, теÑÑ‚ вроде удалÑÑ. Ð’Ñ‹Ñвлен один неудобный момент Ñ "шапками". Ð”Ð»Ñ Ð¸Ð·Ð±ÐµÐ¶Ð°Ð½Ð¸Ñ Ð½ÐµÑƒÐ´Ð¾Ð±Ñтв Ñ "шапками", надо проÑчитывать каждую чаÑÑ‚ÑŒ отдельно. Впрочем, Ð´Ð»Ñ "Ñ‚Ñжёлых" квадратов так и надо делать. При Ñтом можно раÑкидать отдельные чаÑти на потоки, еÑли процеÑÑор многоÑдерный. Скажем, Ð´Ð»Ñ 40-Ñдерного процеÑÑора Ñразу Ñчитать 40 чаÑтей. Потом Ñледующие 40 чаÑтей, и так далее. Ð”Ð»Ñ Ñ€ÐµÐºÐ¾Ñ€Ð´Ð½Ð¾Ð³Ð¾ на данный момент ДЛК имеем 2048 чаÑтей. ОÑталоÑÑŒ выÑÑнить, Ñколько времени ÑчитаетÑÑ Ð¾Ð´Ð½Ð° чаÑÑ‚ÑŒ. Тогда можно прикинуть, Ñколько потребуетÑÑ Ð²Ñ€ÐµÐ¼ÐµÐ½Ð¸ Ð´Ð»Ñ Ð¿Ð¾Ð»Ð½Ð¾Ð¹ обработки Ñтого ДЛК. Ðу, и при иÑпользовании Ñтой программы не должно быть проблем Ñ Ð¿Ð°Ð¼Ñтью. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
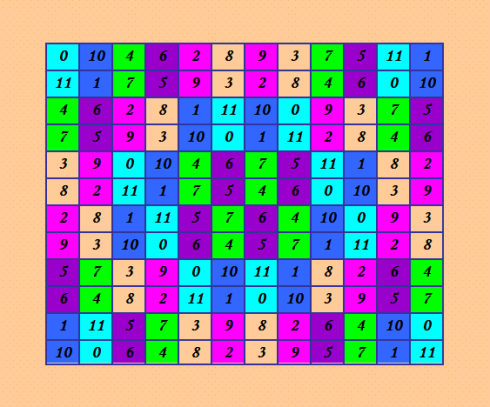
Цитата 4. 24901 Д-транÑверÑалей РаÑÑкажу ещё немного об Ñтом ДЛК. ПриÑмотревшиÑÑŒ к нему повнимательней, Ñ ÑƒÐ²Ð¸Ð´ÐµÐ»Ð° в нём блочную Ñтруктуру; а поначалу увидела только, что он пÑевдоÑимметричный по Гергели/Брауну, что и показано раÑкраÑкой на иллюÑтрации в цитате. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾ÐºÐ°Ð¶Ñƒ другую раÑкраÑку Ñтого ДЛК, ÐºÐ¾Ñ‚Ð¾Ñ€Ð°Ñ Ð¿Ð¾ÐºÐ°Ð·Ñ‹Ð²Ð°ÐµÑ‚ блочную Ñтруктуру. Вот  |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese