Эту тему я создала на форуме проекта ОДЛК совсем недавно и ничего ещё не скопировала.
А написала там уже довольно много.
Не буду здесь всё повторять, надо повторить самое важное, чтобы понимать дальнейшее развитие темы.

Смотрим статью в OEIS https://oeis.org/A338620

A338620 Number of pandiagonal Latin squares of order n with the first row in ascending order.
1, 0, 0, 0, 2, 0, 4, 0, 0, 0, 8, 0, 12386

В статье приведено определение пандиагонального латинского квадрата.
Я дам своё определение, которое мне больше нравится.
Определение: пандиагональным ЛК порядка n называется такой ЛК, в котором главная, побочная и все разломанные диагонали (обоих направлений) суть перестановки элементов 0, 1, 2, ..., n-1.

Из определения следует, что пандиагональный ЛК обязательно является ДЛК.
Из определения также следует, что главная, побочная и все разломанные диагонали (обоих направлений) в пандиагональном ЛК являются трансверсалями.
Именно этим очень интересны пандиагональные ЛК.

Первый важный момент, цитирую статью OEIS

For orders n = 5, 7 and 11 all pandiagonal Latin squares are cyclic.

Все циклические пандиагональные ЛК для указанных (и не только для указанных!) порядков очень легко строятся методом циклического сдвига.
Показываю эти пандиагональные ЛК.

n=5

0 1 2 3 4
2 3 4 0 1
4 0 1 2 3
1 2 3 4 0
3 4 0 1 2

0 1 2 3 4
3 4 0 1 2
1 2 3 4 0
4 0 1 2 3
2 3 4 0 1

Эти ДЛК входят в полную систему MOLS 5-го порядка, которая состоит из четырёх ЛК.

n=7

0 1 2 3 4 5 6
2 3 4 5 6 0 1
4 5 6 0 1 2 3
6 0 1 2 3 4 5
1 2 3 4 5 6 0
3 4 5 6 0 1 2
5 6 0 1 2 3 4

0 1 2 3 4 5 6
3 4 5 6 0 1 2
6 0 1 2 3 4 5
2 3 4 5 6 0 1
5 6 0 1 2 3 4
1 2 3 4 5 6 0
4 5 6 0 1 2 3

0 1 2 3 4 5 6
4 5 6 0 1 2 3
1 2 3 4 5 6 0
5 6 0 1 2 3 4
2 3 4 5 6 0 1
6 0 1 2 3 4 5
3 4 5 6 0 1 2

0 1 2 3 4 5 6
5 6 0 1 2 3 4
3 4 5 6 0 1 2
1 2 3 4 5 6 0
6 0 1 2 3 4 5
4 5 6 0 1 2 3
2 3 4 5 6 0 1

Эти ДЛК входят в полную систему MOLS 7-го порядка, которая состоит из шести ЛК.

n=11

0 1 2 3 4 5 6 7 8 9 10
2 3 4 5 6 7 8 9 10 0 1
4 5 6 7 8 9 10 0 1 2 3
6 7 8 9 10 0 1 2 3 4 5
8 9 10 0 1 2 3 4 5 6 7
10 0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 10 0
3 4 5 6 7 8 9 10 0 1 2
5 6 7 8 9 10 0 1 2 3 4
7 8 9 10 0 1 2 3 4 5 6
9 10 0 1 2 3 4 5 6 7 8

0 1 2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10 0 1 2
6 7 8 9 10 0 1 2 3 4 5
9 10 0 1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8 9 10 0
4 5 6 7 8 9 10 0 1 2 3
7 8 9 10 0 1 2 3 4 5 6
10 0 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9 10 0 1
5 6 7 8 9 10 0 1 2 3 4
8 9 10 0 1 2 3 4 5 6 7

0 1 2 3 4 5 6 7 8 9 10
4 5 6 7 8 9 10 0 1 2 3
8 9 10 0 1 2 3 4 5 6 7
1 2 3 4 5 6 7 8 9 10 0
5 6 7 8 9 10 0 1 2 3 4
9 10 0 1 2 3 4 5 6 7 8
2 3 4 5 6 7 8 9 10 0 1
6 7 8 9 10 0 1 2 3 4 5
10 0 1 2 3 4 5 6 7 8 9
3 4 5 6 7 8 9 10 0 1 2
7 8 9 10 0 1 2 3 4 5 6

0 1 2 3 4 5 6 7 8 9 10
5 6 7 8 9 10 0 1 2 3 4
10 0 1 2 3 4 5 6 7 8 9
4 5 6 7 8 9 10 0 1 2 3
9 10 0 1 2 3 4 5 6 7 8
3 4 5 6 7 8 9 10 0 1 2
8 9 10 0 1 2 3 4 5 6 7
2 3 4 5 6 7 8 9 10 0 1
7 8 9 10 0 1 2 3 4 5 6
1 2 3 4 5 6 7 8 9 10 0
6 7 8 9 10 0 1 2 3 4 5

0 1 2 3 4 5 6 7 8 9 10
6 7 8 9 10 0 1 2 3 4 5
1 2 3 4 5 6 7 8 9 10 0
7 8 9 10 0 1 2 3 4 5 6
2 3 4 5 6 7 8 9 10 0 1
8 9 10 0 1 2 3 4 5 6 7
3 4 5 6 7 8 9 10 0 1 2
9 10 0 1 2 3 4 5 6 7 8
4 5 6 7 8 9 10 0 1 2 3
10 0 1 2 3 4 5 6 7 8 9
5 6 7 8 9 10 0 1 2 3 4

0 1 2 3 4 5 6 7 8 9 10
7 8 9 10 0 1 2 3 4 5 6
3 4 5 6 7 8 9 10 0 1 2
10 0 1 2 3 4 5 6 7 8 9
6 7 8 9 10 0 1 2 3 4 5
2 3 4 5 6 7 8 9 10 0 1
9 10 0 1 2 3 4 5 6 7 8
5 6 7 8 9 10 0 1 2 3 4
1 2 3 4 5 6 7 8 9 10 0
8 9 10 0 1 2 3 4 5 6 7
4 5 6 7 8 9 10 0 1 2 3

0 1 2 3 4 5 6 7 8 9 10
8 9 10 0 1 2 3 4 5 6 7
5 6 7 8 9 10 0 1 2 3 4
2 3 4 5 6 7 8 9 10 0 1
10 0 1 2 3 4 5 6 7 8 9
7 8 9 10 0 1 2 3 4 5 6
4 5 6 7 8 9 10 0 1 2 3
1 2 3 4 5 6 7 8 9 10 0
9 10 0 1 2 3 4 5 6 7 8
6 7 8 9 10 0 1 2 3 4 5
3 4 5 6 7 8 9 10 0 1 2

0 1 2 3 4 5 6 7 8 9 10
9 10 0 1 2 3 4 5 6 7 8
7 8 9 10 0 1 2 3 4 5 6
5 6 7 8 9 10 0 1 2 3 4
3 4 5 6 7 8 9 10 0 1 2
1 2 3 4 5 6 7 8 9 10 0
10 0 1 2 3 4 5 6 7 8 9
8 9 10 0 1 2 3 4 5 6 7
6 7 8 9 10 0 1 2 3 4 5
4 5 6 7 8 9 10 0 1 2 3
2 3 4 5 6 7 8 9 10 0 1

Эти ДЛК входят в полную систему MOLS 11-го порядка, состоящую из 10 ЛК.

Проверим 8 пандиагональных ЛК 11-го порядка утилитой Harry White

Order? 11

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt

Counts
------
         8 diagonal Latin
         8 pandiagonal
         8 center symmetric
         8 nfr
         7 orthogonal pair
         8 self-orthogonal

Интересные свойства у этих ДЛК.

Как уже отмечено выше, пандиагональные ЛК являются ДЛК.
Поэтому мы можем говорить об изоморфизме этих ДЛК, а значит, и о главных классах.

Для порядка n=5 есть только один уникальный пандиагональный ДЛК

0 1 2 3 4
2 3 4 0 1
4 0 1 2 3
1 2 3 4 0
3 4 0 1 2

Следовательно, имеем только один класс пандиагональных ДЛК 5-го порядка.

Для порядка n=7 тоже есть только один уникальный пандиагональный ДЛК

0 1 2 3 4 5 6
2 3 4 5 6 0 1
4 5 6 0 1 2 3
6 0 1 2 3 4 5
1 2 3 4 5 6 0
3 4 5 6 0 1 2
5 6 0 1 2 3 4

Следовательно, есть один главный класс пандиагональных ДЛК 7-го порядка.

Для порядка n=11 есть два уникальных пандиагональных ДЛК

0 1 2 3 4 5 6 7 8 9 10
2 3 4 5 6 7 8 9 10 0 1
4 5 6 7 8 9 10 0 1 2 3
6 7 8 9 10 0 1 2 3 4 5
8 9 10 0 1 2 3 4 5 6 7
10 0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 10 0
3 4 5 6 7 8 9 10 0 1 2
5 6 7 8 9 10 0 1 2 3 4
7 8 9 10 0 1 2 3 4 5 6
9 10 0 1 2 3 4 5 6 7 8

0 1 2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10 0 1 2
6 7 8 9 10 0 1 2 3 4 5
9 10 0 1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8 9 10 0
4 5 6 7 8 9 10 0 1 2 3
7 8 9 10 0 1 2 3 4 5 6
10 0 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9 10 0 1
5 6 7 8 9 10 0 1 2 3 4
8 9 10 0 1 2 3 4 5 6 7

Следовательно, имеется два главных класса пандиагональных ДЛК 11-го порядка.

Для порядка 13, как сказано в статье OEIS, существуют циклические и не циклические (а ещё полуциклические) пандиагональные ЛК.
Цитирую

For order n=13 this is not true and exists 12386 inequivalent squares; of these 10 are cyclic (in all directions) and 1560 are semi-cyclic (cyclic in a single direction).

Показываю 10 циклических пандиагональных ДЛК порядка 13

0 1 2 3 4 5 6 7 8 9 10 11 12
2 3 4 5 6 7 8 9 10 11 12 0 1
4 5 6 7 8 9 10 11 12 0 1 2 3
6 7 8 9 10 11 12 0 1 2 3 4 5
8 9 10 11 12 0 1 2 3 4 5 6 7
10 11 12 0 1 2 3 4 5 6 7 8 9
12 0 1 2 3 4 5 6 7 8 9 10 11
1 2 3 4 5 6 7 8 9 10 11 12 0
3 4 5 6 7 8 9 10 11 12 0 1 2
5 6 7 8 9 10 11 12 0 1 2 3 4
7 8 9 10 11 12 0 1 2 3 4 5 6
9 10 11 12 0 1 2 3 4 5 6 7 8
11 12 0 1 2 3 4 5 6 7 8 9 10

0 1 2 3 4 5 6 7 8 9 10 11 12
3 4 5 6 7 8 9 10 11 12 0 1 2
6 7 8 9 10 11 12 0 1 2 3 4 5
9 10 11 12 0 1 2 3 4 5 6 7 8
12 0 1 2 3 4 5 6 7 8 9 10 11
2 3 4 5 6 7 8 9 10 11 12 0 1
5 6 7 8 9 10 11 12 0 1 2 3 4
8 9 10 11 12 0 1 2 3 4 5 6 7
11 12 0 1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10 11 12 0
4 5 6 7 8 9 10 11 12 0 1 2 3
7 8 9 10 11 12 0 1 2 3 4 5 6
10 11 12 0 1 2 3 4 5 6 7 8 9

0 1 2 3 4 5 6 7 8 9 10 11 12
4 5 6 7 8 9 10 11 12 0 1 2 3
8 9 10 11 12 0 1 2 3 4 5 6 7
12 0 1 2 3 4 5 6 7 8 9 10 11
3 4 5 6 7 8 9 10 11 12 0 1 2
7 8 9 10 11 12 0 1 2 3 4 5 6
11 12 0 1 2 3 4 5 6 7 8 9 10
2 3 4 5 6 7 8 9 10 11 12 0 1
6 7 8 9 10 11 12 0 1 2 3 4 5
10 11 12 0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 10 11 12 0
5 6 7 8 9 10 11 12 0 1 2 3 4
9 10 11 12 0 1 2 3 4 5 6 7 8

0 1 2 3 4 5 6 7 8 9 10 11 12
5 6 7 8 9 10 11 12 0 1 2 3 4
10 11 12 0 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9 10 11 12 0 1
7 8 9 10 11 12 0 1 2 3 4 5 6
12 0 1 2 3 4 5 6 7 8 9 10 11
4 5 6 7 8 9 10 11 12 0 1 2 3
9 10 11 12 0 1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8 9 10 11 12 0
6 7 8 9 10 11 12 0 1 2 3 4 5
11 12 0 1 2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10 11 12 0 1 2
8 9 10 11 12 0 1 2 3 4 5 6 7

0 1 2 3 4 5 6 7 8 9 10 11 12
6 7 8 9 10 11 12 0 1 2 3 4 5
12 0 1 2 3 4 5 6 7 8 9 10 11
5 6 7 8 9 10 11 12 0 1 2 3 4
11 12 0 1 2 3 4 5 6 7 8 9 10
4 5 6 7 8 9 10 11 12 0 1 2 3
10 11 12 0 1 2 3 4 5 6 7 8 9
3 4 5 6 7 8 9 10 11 12 0 1 2
9 10 11 12 0 1 2 3 4 5 6 7 8
2 3 4 5 6 7 8 9 10 11 12 0 1
8 9 10 11 12 0 1 2 3 4 5 6 7
1 2 3 4 5 6 7 8 9 10 11 12 0
7 8 9 10 11 12 0 1 2 3 4 5 6

0 1 2 3 4 5 6 7 8 9 10 11 12
7 8 9 10 11 12 0 1 2 3 4 5 6
1 2 3 4 5 6 7 8 9 10 11 12 0
8 9 10 11 12 0 1 2 3 4 5 6 7
2 3 4 5 6 7 8 9 10 11 12 0 1
9 10 11 12 0 1 2 3 4 5 6 7 8
3 4 5 6 7 8 9 10 11 12 0 1 2
10 11 12 0 1 2 3 4 5 6 7 8 9
4 5 6 7 8 9 10 11 12 0 1 2 3
11 12 0 1 2 3 4 5 6 7 8 9 10
5 6 7 8 9 10 11 12 0 1 2 3 4
12 0 1 2 3 4 5 6 7 8 9 10 11
6 7 8 9 10 11 12 0 1 2 3 4 5

0 1 2 3 4 5 6 7 8 9 10 11 12
8 9 10 11 12 0 1 2 3 4 5 6 7
3 4 5 6 7 8 9 10 11 12 0 1 2
11 12 0 1 2 3 4 5 6 7 8 9 10
6 7 8 9 10 11 12 0 1 2 3 4 5
1 2 3 4 5 6 7 8 9 10 11 12 0
9 10 11 12 0 1 2 3 4 5 6 7 8
4 5 6 7 8 9 10 11 12 0 1 2 3
12 0 1 2 3 4 5 6 7 8 9 10 11
7 8 9 10 11 12 0 1 2 3 4 5 6
2 3 4 5 6 7 8 9 10 11 12 0 1
10 11 12 0 1 2 3 4 5 6 7 8 9
5 6 7 8 9 10 11 12 0 1 2 3 4

0 1 2 3 4 5 6 7 8 9 10 11 12
9 10 11 12 0 1 2 3 4 5 6 7 8
5 6 7 8 9 10 11 12 0 1 2 3 4
1 2 3 4 5 6 7 8 9 10 11 12 0
10 11 12 0 1 2 3 4 5 6 7 8 9
6 7 8 9 10 11 12 0 1 2 3 4 5
2 3 4 5 6 7 8 9 10 11 12 0 1
11 12 0 1 2 3 4 5 6 7 8 9 10
7 8 9 10 11 12 0 1 2 3 4 5 6
3 4 5 6 7 8 9 10 11 12 0 1 2
12 0 1 2 3 4 5 6 7 8 9 10 11
8 9 10 11 12 0 1 2 3 4 5 6 7
4 5 6 7 8 9 10 11 12 0 1 2 3

0 1 2 3 4 5 6 7 8 9 10 11 12
10 11 12 0 1 2 3 4 5 6 7 8 9
7 8 9 10 11 12 0 1 2 3 4 5 6
4 5 6 7 8 9 10 11 12 0 1 2 3
1 2 3 4 5 6 7 8 9 10 11 12 0
11 12 0 1 2 3 4 5 6 7 8 9 10
8 9 10 11 12 0 1 2 3 4 5 6 7
5 6 7 8 9 10 11 12 0 1 2 3 4
2 3 4 5 6 7 8 9 10 11 12 0 1
12 0 1 2 3 4 5 6 7 8 9 10 11
9 10 11 12 0 1 2 3 4 5 6 7 8
6 7 8 9 10 11 12 0 1 2 3 4 5
3 4 5 6 7 8 9 10 11 12 0 1 2

0 1 2 3 4 5 6 7 8 9 10 11 12
11 12 0 1 2 3 4 5 6 7 8 9 10
9 10 11 12 0 1 2 3 4 5 6 7 8
7 8 9 10 11 12 0 1 2 3 4 5 6
5 6 7 8 9 10 11 12 0 1 2 3 4
3 4 5 6 7 8 9 10 11 12 0 1 2
1 2 3 4 5 6 7 8 9 10 11 12 0
12 0 1 2 3 4 5 6 7 8 9 10 11
10 11 12 0 1 2 3 4 5 6 7 8 9
8 9 10 11 12 0 1 2 3 4 5 6 7
6 7 8 9 10 11 12 0 1 2 3 4 5
4 5 6 7 8 9 10 11 12 0 1 2 3
2 3 4 5 6 7 8 9 10 11 12 0 1

Все эти ДЛК входят в полную систему MOLS 13-го порядка, состоящую их 12 ЛК.
Я построила их вручную методом циклического сдвига.
Проверим эти ДЛК утилитой Harry White

Order? 13

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_8.txt

Counts
------
        10 diagonal Latin
        10 pandiagonal
        10 center symmetric
        10 nfr
         9 orthogonal pair
        10 self-orthogonal

Интересно, где можно увидеть 1560 полуциклических пандиагональных ЛК и остальные не циклические пандиагональные ЛК 13-го порядка.

В OEIS приведён один не циклический пандиагональный ДЛК 13-го порядка, который взят из статьи
Vahid Dabbaghian, Tiankuang Wu, Constructing non-cyclic pandiagonal Latin squares of prime orders, Journal of Discrete Algorithms 30, 2015.

7 1 0 3 6 5 12 2 8 9 10 11 4
2 3 4 10 0 7 6 9 12 11 5 8 1
4 11 1 7 8 9 10 3 6 0 12 2 5
6 5 8 11 10 4 7 0 1 2 3 9 12
8 9 2 5 12 11 1 4 3 10 0 6 7
3 6 12 0 1 2 8 11 5 4 7 10 9
10 0 3 2 9 12 5 6 7 8 1 4 11
1 7 10 4 3 6 9 8 2 5 11 12 0
11 4 5 6 7 0 3 10 9 12 2 1 8
5 8 7 1 4 10 11 12 0 6 9 3 2
12 2 9 8 11 1 0 7 10 3 4 5 6
9 10 11 12 5 8 2 1 4 7 6 0 3
0 12 6 9 2 3 4 5 11 1 8 7 10

Да, так вот: я уже давно начала заниматься составлением БД КФ ОДЛК 11-го порядка.
На форуме проекта ОДЛК была создана посвящённая этому тема.
Кроме того, был официально объявлен этот проект.
Проект, конечно, тоже пока работает только в ручном режиме, всего на одном ПК (на моём), да и то эпизодически.

Но я сказать хочу сейчас о пандиагональных ДЛК 11-го порядка.
Сразу подумала, что надо начать с пандиагональных ДЛК, потому что это готовые ОДЛК.
Начала искать к ним подход. И так построю, и этак построю, а они все изоморфные получаются, и только два уникальных.
Очень сильно удивилась такому факту.
Попросила Harry White поискать пандиагональные ДЛК 11-го порядка; он поискал и тоже не нашёл других - не изоморфных двум уникальным пандиагональным ДЛК.

Далее я начала искать SODLS 11-го порядка, которые тоже готовые ОДЛК.
Программу поиска мне прислал Harry White.
Но об этом расскажу в другой теме.

Покажу иллюстрацию не циклического пандиагонального ДЛК 13-го порядка, приведённого в OEIS



Раскраской показана пандиагональность, раскрашены диагонали одного направления - главная и разломанные.
Точно так же можно раскрасить диагонали второго направления.

Дальше я расскажу о слабо пандиагональных ЛК (weakly pandiagonal).
Нашла интересную статью
https://link.springer.com/article/10.1007/s10114-013-2274-1
(читать статью можно прямо по ссылке)

Existence of weakly pandiagonal orthogonal Latin squares
Yong Zhang,
Wen Li &
Jian Guo Lei
Acta Mathematica Sinica, English Series volume 29, pages1089–1094(2013)

Abstract
A weakly pandiagonal Latin square of order n over the number set {0, 1, ..., n − 1} is a Latin square having the property that the sum of the n numbers in each of 2n diagonals is the same. In this paper, we shall prove that a pair of orthogonal weakly pandiagonal Latin squares of order n exists if and only if n ≡ 0, 1,3 (mod 4) and n ≠ 3.

В статье рассматриваются ортогональные пары из слабо пандиагональных ЛК.

Дам своё определение слабо пандиагонального ЛК (более понятное, на мой взгляд).
Определение: латинский квадрат называется слабо пандиагональным, если он пандиагональный как магический квадрат.

Очевидно, что моё определение эквивалентно определению в статье.

Слабо пандиагональные ЛК я встретила очень давно, тогда ещё и не знала, что они так называются.
Первый пример можно посмотреть в моей статье "Совершенные латинские квадраты. Часть I".
Далее покажу этот пример.

В статье на рис. 2 вы видите совершенный ЛК 9-го порядка, а на рис. 3 ортогональный ему ЛК

0 3 6 1 4 7 2 5 8
2 5 8 0 3 6 1 4 7
1 4 7 2 5 8 0 3 6
3 6 0 4 7 1 5 8 2
5 8 2 3 6 0 4 7 1
4 7 1 5 8 2 3 6 0
6 0 3 7 1 4 8 2 5
8 2 5 6 0 3 7 1 4
7 1 4 8 2 5 6 0 3

0 3 6 1 4 7 2 5 8
1 4 7 2 5 8 0 3 6
2 5 8 0 3 6 1 4 7
6 0 3 7 1 4 8 2 5
7 1 4 8 2 5 6 0 3
8 2 5 6 0 3 7 1 4
3 6 0 4 7 1 5 8 2
4 7 1 5 8 2 3 6 0
5 8 2 3 6 0 4 7 1

Далее цитирую статью

Таким образом, мы имеем пару ортогональных совершенных латинских квадратов. Отмечу, что оба совершенных квадрата обладают свойством пандиагональности, поэтому магические квадраты, построенные из данной пары ОЛК, пандиагональны.

Это «свойство пандиагональности», о котором говорится в цитате и есть слабая пандиагональность.

Проверим эти ЛК утилитой Harry White

Order? 9

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt

Counts
------
         2 diagonal Latin
         2 weakly pandiagonal
         2 center symmetric
         1 orthogonal pair
         2 self-orthogonal

Кроме всего прочего, эти ЛК являются ДЛК.
Таким образом, слабо пандиагональные ЛК могут быть и ДЛК.

Понятно, что ортогональная пара слабо пандиагональных ЛК сразу даёт нам пандиагональный магический квадрат, построенный из этой пары методом латинских квадратов.

Далее расскажу о построении ортогональной пары слабо пандиагональных ЛК 12-го порядка.
Это будет уже в Новом Году.

С наступающим Новым Годом!

Просматривала копии тем с форума ОДЛК, наткнулась на интересный пример.
Мне присылали статью
Franklinian Diagonal Latin Squares
Miguel Angel Amela (автор)
Это пример, приведённый в статье



Мы видим слабо пандиагональные ЛК 8-го порядка (они являются ДЛК), из которых составляются магические квадраты.
Оказывается, слабо пандиагональные ЛК умел строить Франклин.
Квадратам Франклина посвящены десятки исследований. Эта статья - одно из них.

Проверим два ДЛК утилитой Harry White, вот эти

0 1 6 7 4 5 2 3
6 7 0 1 2 3 4 5
3 2 5 4 7 6 1 0
5 4 3 2 1 0 7 6
2 3 4 5 6 7 0 1
4 5 2 3 0 1 6 7
1 0 7 6 5 4 3 2
7 6 1 0 3 2 5 4

3 5 0 6 1 7 2 4
2 4 1 7 0 6 3 5
5 3 6 0 7 1 4 2
4 2 7 1 6 0 5 3
7 1 4 2 5 3 6 0
6 0 5 3 4 2 7 1
1 7 2 4 3 5 0 6
0 6 3 5 2 4 1 7

Утилита сообщает

Order? 8

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         2 diagonal Latin
         2 weakly pandiagonal
         2 double axial symmetric
         2 center symmetric
         1 orthogonal pair
         2 self-orthogonal

Очень интересные ДЛК!

Сообщу ещё из той темы, цитата

PS. Сейчас выложу статью "Franklinian Diagonal Latin Squares" на Яндекс.Диск. Интересная статья.
Автор Miguel Angel Amela.
Загрузила, вот ссылка
https://yadi.sk/i/4yQLEKfB3Qsjg2

Попутно. В своё время я много занималась магическими квадратами Франклина. Вот ссылка на мой сборник статей "Квадраты Франклина"
https://yadi.sk/d/-0u4VKR55pXGa

Открыла сборник статей "Квадраты Франклина". Зачиталась! Так интересно.
Сборник довольно большой, 228 страниц (в формате PDF).
И в этом сборнике нашла пандиагональный магический квадрат 4-го порядка



Этот квадрат построен по схеме другого древнего строителя магических квадратов - Френикля.
Разложила этот пандиагональный магический квадрат на два ЛК

0 3 2 1
2 1 0 3
1 2 3 0
3 0 1 2

0 1 2 3
3 2 1 0
1 0 3 2
2 3 0 1

Догадываетесь, что я получила?
Это слабо пандиагональные ЛК (являются ДЛК).
Проверяем утилитой Harry White эти квадратики

Order? 4

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         2 diagonal Latin
         2 weakly pandiagonal
         2 double axial symmetric
         2 center symmetric
         1 nfr
         1 orthogonal pair
         2 self-orthogonal

Вот какая красота! Малюточки квадратики - куча свойств у них, в том числе, слабо пандиагональные.

Ну, пора приступать к построению ортогональной пары слабо пандиагональных ЛК 12-го порядка.

Итак, сначала строим ассоциативный SODLS 12-го порядка по программе Harry White

0 2 3 4 9 8 7 6 11 10 5 1
3 1 7 6 8 9 5 10 4 11 0 2
1 9 2 5 7 10 8 11 0 3 6 4
5 4 10 3 11 0 9 8 2 6 1 7
6 7 11 10 4 1 0 5 9 2 8 3
11 0 6 8 2 5 4 1 10 7 3 9
2 8 4 1 10 7 6 9 3 5 11 0
8 3 9 2 6 11 10 7 1 0 4 5
4 10 5 9 3 2 11 0 8 1 7 6
7 5 8 11 0 3 1 4 6 9 2 10
9 11 0 7 1 6 2 3 5 4 10 8
10 6 1 0 5 4 3 2 7 8 9 11

Теперь применим к этому ДЛК преобразование трёх квадратов.
Описание этого преобразования вы можете посмотреть в моей книге "Волшебный мир магических квадратов".
Скачать книгу можно с Яндекс.Диска
https://yadi.sk/d/ehakE2V6S5TzG

Это преобразование в применении к ассоциативному магическому квадрату порядка n=4k превращает его в пандиагональный квадрат.
Применив преобразование к показанному ассоциативному ДЛК, получаем слабо пандиагональный ЛК, являющийся ДЛК

0 2 3 4 9 8 1 5 10 11 6 7
3 1 7 6 8 9 2 0 11 4 10 5
1 9 2 5 7 10 4 6 3 0 11 8
5 4 10 3 11 0 7 1 6 2 8 9
6 7 11 10 4 1 3 8 2 9 5 0
11 0 6 8 2 5 9 3 7 10 1 4
10 6 1 0 5 4 11 9 8 7 2 3
9 11 0 7 1 6 8 10 4 5 3 2
7 5 8 11 0 3 10 2 9 6 4 1
4 10 5 9 3 2 6 7 1 8 0 11
8 3 9 2 6 11 5 4 0 1 7 10
2 8 4 1 10 7 0 11 5 3 9 6

Проверяем этот ДЛК утилитой Harry White

Order? 12

Enter the name of the squares file: INP
.. writing type information to file INPTypeDetail_5.txt

Counts
------
         1 diagonal Latin
         1 weakly pandiagonal
         1 self-orthogonal

ДЛК является SODLS! Замечательно! Ортогональная пара уже готова.
Транспонированный вариант этого ДЛК

 0  3  1  5  6 11 10  9  7  4  8  2
 2  1  9  4  7  0  6 11  5 10  3  8
 3  7  2 10 11  6  1  0  8  5  9  4
 4  6  5  3 10  8  0  7 11  9  2  1
 9  8  7 11  4  2  5  1  0  3  6 10
 8  9 10  0  1  5  4  6  3  2 11  7
 1  2  4  7  3  9 11  8 10  6  5  0
 5  0  6  1  8  3  9 10  2  7  4 11
10 11  3  6  2  7  8  4  9  1  0  5
11  4  0  2  9 10  7  5  6  8  1  3
 6 10 11  8  5  1  2  3  4  0  7  9
 7  5  8  9  0  4  3  2  1 11 10  6

Этот ДЛК тоже слабо пандиагональный.
Искомая ортогональная пара слабо пандиагональных ЛК построена.

Проверяю утилитой Harry White оба ДЛК построенной ортогональной пары

Order? 12

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt

Counts
------
         2 diagonal Latin
         2 weakly pandiagonal
         1 orthogonal pair
         2 self-orthogonal

Вот так всё просто для порядка 12.
Для порядка 14 ортогональная пара слабо пандиагональных ЛК не существует.
На очереди ортогональная пара слабо пандиагональных ЛК 15-го порядка.

Слабо пандиагональный ЛК 15-го порядка строить не пришлось, я нашла его в своей статье
"ПОСТРОЕНИЕ ИДЕАЛЬНЫХ КВАДРАТОВ 15-ого ПОРЯДКА
С ПОМОЩЬЮ ДВУХ ЛАТИНСКИХ КВАДРАТОВ"
http://www.natalimak1.narod.ru/id15new.htm

Показываю этот слабо пандиагональный ЛК



Офигенно красивый ЛК!
Обратите внимание: этот ЛК построен методом циклического сдвига.
Проверка утилитой Harry White сообщает об этом ЛК

Order? 15

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         1 Latin
         1 weakly pandiagonal
         1 center symmetric

Этот ЛК не является ДЛК.

Далее в статье приведён ЛК ортогональный данному (см. рис. 12)

3 6 10 14 0 4 8 11 2 1 5 7 9 13 12
11 2 1 5 7 9 13 12 3 6 10 14 0 4 8
12 3 6 10 14 0 4 8 11 2 1 5 7 9 13
8 11 2 1 5 7 9 13 12 3 6 10 14 0 4
13 12 3 6 10 14 0 4 8 11 2 1 5 7 9
4 8 11 2 1 5 7 9 13 12 3 6 10 14 0
9 13 12 3 6 10 14 0 4 8 11 2 1 5 7
0 4 8 11 2 1 5 7 9 13 12 3 6 10 14
7 9 13 12 3 6 10 14 0 4 8 11 2 1 5
14 0 4 8 11 2 1 5 7 9 13 12 3 6 10
5 7 9 13 12 3 6 10 14 0 4 8 11 2 1
10 14 0 4 8 11 2 1 5 7 9 13 12 3 6
1 5 7 9 13 12 3 6 10 14 0 4 8 11 2
6 10 14 0 4 8 11 2 1 5 7 9 13 12 3
2 1 5 7 9 13 12 3 6 10 14 0 4 8 11

Проверяю утилитой Harry White сразу оба ЛК построенной ортогональной пары

Order? 15

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt

Counts
------
         2 Latin
         2 weakly pandiagonal
         2 center symmetric
         1 orthogonal pair

Замечательно!

Ортогональная пара слабо пандиагональных ЛК 16-го порядка построена в этой статье

Special Matrices
Volume 6: Issue 1
Existence of strongly symmetrical weakly pandiagonal graeco-latin squares
Yong Zhang 1 , Kejun Chen 2 , and Wen Li 3
1 School of Mathematics and Statistics, Yancheng Teachers University,, Jiangsu, P. R., China
2 School of Mathematics and Information Science, Nanjing Normal University of Special Education, Nanjing,, Jiangsu, P. R., China
3 School of Science, Xichang University,, Sichuan, P. R., China
DOI:
https://doi.org/10.1515/spma-2018-0013

Published online:
15 Sep 2018

https://www.degruyter.com/view/journals/spma/6/1/article-p357.xml?language=en

Сейчас покажу эту пару.

Вот пара ортогональных слабо пандиагональных ЛК 16-го порядка из указанной выше статьи



Выписываю первый ЛК (квадрат А)

0 6 3 5 12 10 15 9 2 4 1 7 14 8 13 11
5 3 6 0 9 15 10 12 7 1 4 2 11 13 8 14
6 0 5 3 10 12 9 15 4 2 7 1 8 14 11 13
3 5 0 6 15 9 12 10 1 7 2 4 13 11 14 8
11 13 8 14 7 1 4 2 9 15 10 12 5 3 6 0
14 8 13 11 2 4 1 7 12 10 15 9 0 6 3 5
13 11 14 8 1 7 2 4 15 9 12 10 3 5 0 6
8 14 11 13 4 2 7 1 10 12 9 15 6 0 5 3
12 10 15 9 0 6 3 5 14 8 13 11 2 4 1 7
9 15 10 12 5 3 6 0 11 13 8 14 7 1 4 2
10 12 9 15 6 0 5 3 8 14 11 13 4 2 7 1
15 9 12 10 3 5 0 6 13 11 14 8 1 7 2 4
7 1 4 2 11 13 8 14 5 3 6 0 9 15 10 12
2 4 1 7 14 8 13 11 0 6 3 5 12 10 15 9
1 7 2 4 13 11 14 8 3 5 0 6 15 9 12 10
4 2 7 1 8 14 11 13 6 0 5 3 10 12 9 15

и проверяю его утилитой Harry White

Order? 16

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         1 diagonal Latin
         1 associative
         1 weakly pandiagonal
         1 ultramagic
         1 double axial symmetric
         1 self-orthogonal

Обалденный квадрат! Он является ДЛК, ассоциативный и слабо пандиагональный, дважды симметричный по Гергели/Брауну (то есть вертикально и горизонтально симметричный); кроме того, он SODLS.
Ну, а если он SODLS, второй ДЛК ортогональной пары уже готов - это транспонированный вариант

 0  5  6  3 11 14 13  8 12  9 10 15  7  2  1  4
 6  3  0  5 13  8 11 14 10 15 12  9  1  4  7  2
 3  6  5  0  8 13 14 11 15 10  9 12  4  1  2  7
 5  0  3  6 14 11  8 13  9 12 15 10  2  7  4  1
12  9 10 15  7  2  1  4  0  5  6  3 11 14 13  8
10 15 12  9  1  4  7  2  6  3  0  5 13  8 11 14
15 10  9 12  4  1  2  7  3  6  5  0  8 13 14 11
 9 12 15 10  2  7  4  1  5  0  3  6 14 11  8 13
 2  7  4  1  9 12 15 10 14 11  8 13  5  0  3  6
 4  1  2  7 15 10  9 12  8 13 14 11  3  6  5  0
 1  4  7  2 10 15 12  9 13  8 11 14  6  3  0  5
 7  2  1  4 12  9 10 15 11 14 13  8  0  5  6  3
14 11  8 13  5  0  3  6  2  7  4  1  9 12 15 10
 8 13 14 11  3  6  5  0  4  1  2  7 15 10  9 12
13  8 11 14  6  3  0  5  1  4  7  2 10 15 12  9
11 14 13  8  0  5  6  3  7  2  1  4 12  9 10 15

Проверяю сразу оба ДЛК построенной ортогональной пары утилитой Harry White

Order? 16

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt

Counts
------
         2 diagonal Latin
         2 associative
         2 weakly pandiagonal
         2 ultramagic
         2 double axial symmetric
         1 orthogonal pair
         2 self-orthogonal

Прекрасно!

В добавление ко всему, квадрат А является DSODLS, то есть ортогонален своему анти-транспонированному варианту

15 10  9 12  4  1  2  7  3  6  5  0  8 13 14 11
 9 12 15 10  2  7  4  1  5  0  3  6 14 11  8 13
12  9 10 15  7  2  1  4  0  5  6  3 11 14 13  8
10 15 12  9  1  4  7  2  6  3  0  5 13  8 11 14
 3  6  5  0  8 13 14 11 15 10  9 12  4  1  2  7
 5  0  3  6 14 11  8 13  9 12 15 10  2  7  4  1
 0  5  6  3 11 14 13  8 12  9 10 15  7  2  1  4
 6  3  0  5 13  8 11 14 10 15 12  9  1  4  7  2
13  8 11 14  6  3  0  5  1  4  7  2 10 15 12  9
11 14 13  8  0  5  6  3  7  2  1  4 12  9 10 15
14 11  8 13  5  0  3  6  2  7  4  1  9 12 15 10
 8 13 14 11  3  6  5  0  4  1  2  7 15 10  9 12
 1  4  7  2 10 15 12  9 13  8 11 14  6  3  0  5
 7  2  1  4 12  9 10 15 11 14 13  8  0  5  6  3
 2  7  4  1  9 12 15 10 14 11  8 13  5  0  3  6
 4  1  2  7 15 10  9 12  8 13 14 11  3  6  5  0

Анти-транспонированный вариант тоже является слабо пандиагональным ДЛК.

А теперь сама построила ортогональную пару слабо пандиагональных ДЛК 16-го порядка.

Малюток помните?

0 1 2 3
3 2 1 0
1 0 3 2
2 3 0 1

0 3 2 1
2 1 0 3
1 2 3 0
3 0 1 2

На основе этой ортогональной пары слабо пандиагональных ДЛК 4-го порядка построила ортогональную пару слабо пандиагональных ДЛК 16-го порядка методом составных квдаратов

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12
1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14
2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13
12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2
14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1
4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11
7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8
5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10
6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9
8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7
11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4
9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6
10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5

0 3 2 1 12 15 14 13 8 11 10 9 4 7 6 5
2 1 0 3 14 13 12 15 10 9 8 11 6 5 4 7
1 2 3 0 13 14 15 12 9 10 11 8 5 6 7 4
3 0 1 2 15 12 13 14 11 8 9 10 7 4 5 6
8 11 10 9 4 7 6 5 0 3 2 1 12 15 14 13
10 9 8 11 6 5 4 7 2 1 0 3 14 13 12 15
9 10 11 8 5 6 7 4 1 2 3 0 13 14 15 12
11 8 9 10 7 4 5 6 3 0 1 2 15 12 13 14
4 7 6 5 8 11 10 9 12 15 14 13 0 3 2 1
6 5 4 7 10 9 8 11 14 13 12 15 2 1 0 3
5 6 7 4 9 10 11 8 13 14 15 12 1 2 3 0
7 4 5 6 11 8 9 10 15 12 13 14 3 0 1 2
12 15 14 13 0 3 2 1 4 7 6 5 8 11 10 9
14 13 12 15 2 1 0 3 6 5 4 7 10 9 8 11
13 14 15 12 1 2 3 0 5 6 7 4 9 10 11 8
15 12 13 14 3 0 1 2 7 4 5 6 11 8 9 10

Проверяю сразу оба ДЛК этой ортогональной пары утилитой Harry White

Order? 16

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_8.txt

Counts
------
         2 diagonal Latin
         2 weakly pandiagonal
         2 double axial symmetric
         2 center symmetric
         1 nfr
         1 orthogonal pair
         2 self-orthogonal

Всё прекрасно, как и должно быть.

Покажу ещё одну ортогональную пару слабо пандиагональных ДЛК 16-го порядка, построенную мной.
Это первый ДЛК пары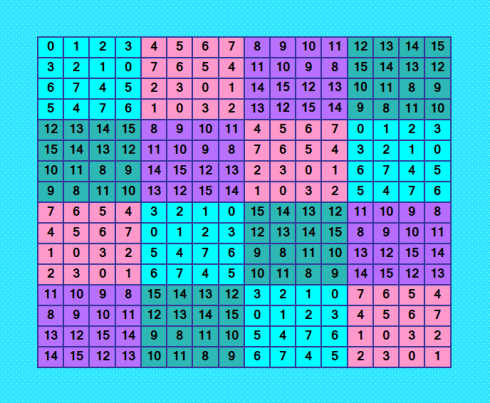



Проверяю его утилитой Harry White

Order? 16

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         1 diagonal Latin
         1 weakly pandiagonal
         1 double axial symmetric
         1 center symmetric
         1 nfr
         1 self-orthogonal

Поскольку этот ДЛК является SODLS, ортогональная пара уже готова.
Это транспонированный вариант

 0  3  6  5 12 15 10  9  7  4  1  2 11  8 13 14
 1  2  7  4 13 14 11  8  6  5  0  3 10  9 12 15
 2  1  4  7 14 13  8 11  5  6  3  0  9 10 15 12
 3  0  5  6 15 12  9 10  4  7  2  1  8 11 14 13
 4  7  2  1  8 11 14 13  3  0  5  6 15 12  9 10
 5  6  3  0  9 10 15 12  2  1  4  7 14 13  8 11
 6  5  0  3 10  9 12 15  1  2  7  4 13 14 11  8
 7  4  1  2 11  8 13 14  0  3  6  5 12 15 10  9
 8 11 14 13  4  7  2  1 15 12  9 10  3  0  5  6
 9 10 15 12  5  6  3  0 14 13  8 11  2  1  4  7
10  9 12 15  6  5  0  3 13 14 11  8  1  2  7  4
11  8 13 14  7  4  1  2 12 15 10  9  0  3  6  5
12 15 10  9  0  3  6  5 11  8 13 14  7  4  1  2
13 14 11  8  1  2  7  4 10  9 12 15  6  5  0  3
14 13  8 11  2  1  4  7  9 10 15 12  5  6  3  0
15 12  9 10  3  0  5  6  8 11 14 13  4  7  2  1

Проверяю утилитой Harry White сразу оба ДЛК построенной ортогональной пары

Order? 16

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_9.txt

Counts
------
         2 diagonal Latin
         2 weakly pandiagonal
         2 double axial symmetric
         2 center symmetric
         1 nfr
         1 nfc
         1 orthogonal pair
         2 self-orthogonal

Всё чудесно!

Не знаю, уникальны ли три показанные ортогональные пары слабо пандиагональных ДЛК 16-го порядка.
У меня нет канонизатора для ДЛК 16-го порядка.
Tomas Brada сообщил на форуме, что он сделал этот канонизатор, но пока не выложил программу.

Ортогональная пара слабо пандиагональных ЛК 18-го порядка не существует.
Для порядков 17 и 19 имеем пандиагональные ДЛК и ортогональные пары таких ДЛК.
На очереди порядок 20.
Попробую построить ортогональную пару слабо пандиагональных ЛК 20-го порядка методом составных квадратов.
Пока не знаю, получится ли.