Thread 'Pandiagonal Latin squares'

Message boards : Science : Pandiagonal Latin squares
Message board moderation

To post messages, you must log in.

Previous · 1 · 2 · 3 · Next

AuthorMessage
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1044 - Posted: 2 Jan 2021, 6:26:07 UTC

Кстати, выше я показала 10 циклических пандиагональных ДЛК порядка 13.
Они строятся очень просто вручную.
Но может быть ещё не все понимают, как это просто.
Поэтому покажу 14 циклических пандиагональных ДЛК 17-го порядка.
А потом вы сами построите 16 циклических пандиагональных ДЛК 19-го порядка. Идёт? :)

Итак, встречайте
14 циклических пандиагональных ДЛК 17-го порядка

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
13 14 15
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
[/code]
Эти ДЛК входят в полную систему MOLS 17-го порядка, состоящую из 16 ЛК, то есть все они взаимно ортогональны.

Проверяю эти ДЛК утилитой Harry White

[code]Order? 17

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
14 diagonal Latin
14 pandiagonal
14 center symmetric
14 nfr
13 orthogonal pair
14 self-orthogonal[/code]
А ещё проверяю эти ДЛК программой Harry White GetOrthogonal, которая составляет все возможные ортогональные пары в заданном множестве ДЛК.
Вот что выдаёт программа
[code]Order? 17

Enter the name of the squares file: inp
..output file inpPairs_1.txt
..output file inpPairNos_1.txt
squares 14 orthogonal pairs 91[/code]
Эти 14 ДЛК образуют 91 ортогональную пару.
И вот таблица ортогональных пар

[code]2: 1
3: 1 2
4: 1 2 3
5: 1 2 3 4
6: 1 2 3 4 5
7: 1 2 3 4 5 6
8: 1 2 3 4 5 6 7
9: 1 2 3 4 5 6 7 8
10: 1 2 3 4 5 6 7 8 9
11: 1 2 3 4 5 6 7 8 9 10
12: 1 2 3 4 5 6 7 8 9 10 11
13: 1 2 3 4 5 6 7 8 9 10 11 12
14: 1 2 3 4 5 6 7 8 9 10 11 12 13[/code]
ID: 1044 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1045 - Posted: 2 Jan 2021, 6:43:38 UTC
Last modified: 2 Jan 2021, 6:45:56 UTC

Из 16 циклических пандиагональных ДЛК 19-го порядка я покажу один, иллюстрация его есть у меня



Этот ДЛК на данный момент рекордсмен по Д-трансверсалям среди ДЛК 19-го порядка, он имеет 11254190082 Д-трансверсалей.
Раскраской показана пандиагональность ДЛК, раскрашены все диагонали одного направления. Точно так же можно раскрасить все диагонали другого направления.
ID: 1045 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1046 - Posted: 2 Jan 2021, 7:52:31 UTC

Ура! Всё получилось. Хорошо работает метод составных квадратов.
В качестве базовой ортогональной пары взяла этих малюток

0 1 2 3
3 2 1 0
1 0 3 2
2 3 0 1

0 3 2 1
2 1 0 3
1 2 3 0
3 0 1 2

Это ортогональная пара слабо пандиагональных ДЛК 4-го порядка.
В качестве основной ортогональной пары взяла эту ортогональную пару пандиагональных ДЛК 5-го порядка

0 1 2 3 4
3 4 0 1 2
1 2 3 4 0
4 0 1 2 3
2 3 4 0 1

0 1 2 3 4
2 3 4 0 1
4 0 1 2 3
1 2 3 4 0
3 4 0 1 2

Первый ДЛК ортогональной пары слабо пандиагональных ДЛК 20-го порядка получился такой

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17
1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15
4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18
2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16
15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4
18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2
16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0
19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3
17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1
5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14
8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12
6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10
9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13
7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11
10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9
13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7
11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5
14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8
12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6

Второй ДЛК ортогональной пары слабо пандиагональных ДЛК 20-го порядка получился такой

0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9
2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6
4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8
1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5
3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7
10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19
12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16
14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18
11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15
13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4
7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1
9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3
6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0
8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2
15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11
19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13
16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10
18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12

Проверяю сразу оба ДЛК построенной ортогональной пары утилитой Harry White

Order? 20

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt

Counts
------
         2 diagonal Latin
         2 weakly pandiagonal
         2 center symmetric
         1 nfr
         1 orthogonal pair
         2 self-orthogonal

Второй ДЛК пары можно было и не строить, а взять транспонированный вариант первого ДЛК.
ID: 1046 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1048 - Posted: 2 Jan 2021, 10:47:48 UTC
Last modified: 2 Jan 2021, 11:53:27 UTC

С ортогональной парой слабо пандиагональных ЛК 21-го порядка повезло.
Не зря я строила давным-давно магические квадраты :)
Вот пандиагональный магический квадрат 21-го порядка из моей статьи "ИДЕАЛЬНЫЕ КВАДРАТЫ Часть IX"
http://www.klassikpoez.narod.ru/idealob9.htm



Красивый квадратик!
Осталось разложить его на два латинских квадрата и - дело в шляпе.
Первый ЛК уже получила

0 1 18 14 7 5 11 17 8 16 10 4 12 3 9 15 13 6 2 19 20
4 12 3 9 15 13 6 2 19 20 0 1 18 14 7 5 11 17 8 16 10
1 18 14 7 5 11 17 8 16 10 4 12 3 9 15 13 6 2 19 20 0
12 3 9 15 13 6 2 19 20 0 1 18 14 7 5 11 17 8 16 10 4
18 14 7 5 11 17 8 16 10 4 12 3 9 15 13 6 2 19 20 0 1
3 9 15 13 6 2 19 20 0 1 18 14 7 5 11 17 8 16 10 4 12
14 7 5 11 17 8 16 10 4 12 3 9 15 13 6 2 19 20 0 1 18
9 15 13 6 2 19 20 0 1 18 14 7 5 11 17 8 16 10 4 12 3
7 5 11 17 8 16 10 4 12 3 9 15 13 6 2 19 20 0 1 18 14
15 13 6 2 19 20 0 1 18 14 7 5 11 17 8 16 10 4 12 3 9
5 11 17 8 16 10 4 12 3 9 15 13 6 2 19 20 0 1 18 14 7
13 6 2 19 20 0 1 18 14 7 5 11 17 8 16 10 4 12 3 9 15
11 17 8 16 10 4 12 3 9 15 13 6 2 19 20 0 1 18 14 7 5
6 2 19 20 0 1 18 14 7 5 11 17 8 16 10 4 12 3 9 15 13
17 8 16 10 4 12 3 9 15 13 6 2 19 20 0 1 18 14 7 5 11
2 19 20 0 1 18 14 7 5 11 17 8 16 10 4 12 3 9 15 13 6
8 16 10 4 12 3 9 15 13 6 2 19 20 0 1 18 14 7 5 11 17
19 20 0 1 18 14 7 5 11 17 8 16 10 4 12 3 9 15 13 6 2
16 10 4 12 3 9 15 13 6 2 19 20 0 1 18 14 7 5 11 17 8
20 0 1 18 14 7 5 11 17 8 16 10 4 12 3 9 15 13 6 2 19
10 4 12 3 9 15 13 6 2 19 20 0 1 18 14 7 5 11 17 8 16

Обратите внимание: ЛК построен методом циклического сдвига.
Проверяю его утилитой Harry White

Order? 21

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         1 Latin
         1 weakly pandiagonal
         1 center symmetric

Да, это слабо пандиагональный ЛК.

Сейчас второй ЛК получу и ортогональная пара готова.
ID: 1048 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1049 - Posted: 2 Jan 2021, 14:02:49 UTC

Второй ЛК ортогональной пары

0 1 18 14 7 5 11 17 8 16 10 4 12 3 9 15 13 6 2 19 20
10 4 12 3 9 15 13 6 2 19 20 0 1 18 14 7 5 11 17 8 16
20 0 1 18 14 7 5 11 17 8 16 10 4 12 3 9 15 13 6 2 19
16 10 4 12 3 9 15 13 6 2 19 20 0 1 18 14 7 5 11 17 8
19 20 0 1 18 14 7 5 11 17 8 16 10 4 12 3 9 15 13 6 2
8 16 10 4 12 3 9 15 13 6 2 19 20 0 1 18 14 7 5 11 17
2 19 20 0 1 18 14 7 5 11 17 8 16 10 4 12 3 9 15 13 6
17 8 16 10 4 12 3 9 15 13 6 2 19 20 0 1 18 14 7 5 11
6 2 19 20 0 1 18 14 7 5 11 17 8 16 10 4 12 3 9 15 13
11 17 8 16 10 4 12 3 9 15 13 6 2 19 20 0 1 18 14 7 5
13 6 2 19 20 0 1 18 14 7 5 11 17 8 16 10 4 12 3 9 15
5 11 17 8 16 10 4 12 3 9 15 13 6 2 19 20 0 1 18 14 7
15 13 6 2 19 20 0 1 18 14 7 5 11 17 8 16 10 4 12 3 9
7 5 11 17 8 16 10 4 12 3 9 15 13 6 2 19 20 0 1 18 14
9 15 13 6 2 19 20 0 1 18 14 7 5 11 17 8 16 10 4 12 3
14 7 5 11 17 8 16 10 4 12 3 9 15 13 6 2 19 20 0 1 18
3 9 15 13 6 2 19 20 0 1 18 14 7 5 11 17 8 16 10 4 12
18 14 7 5 11 17 8 16 10 4 12 3 9 15 13 6 2 19 20 0 1
12 3 9 15 13 6 2 19 20 0 1 18 14 7 5 11 17 8 16 10 4
1 18 14 7 5 11 17 8 16 10 4 12 3 9 15 13 6 2 19 20 0
4 12 3 9 15 13 6 2 19 20 0 1 18 14 7 5 11 17 8 16 10

ЛК тоже построен методом циклического сдвига.

Проверяю сразу оба ЛК утилитой Harry White

Order? 21

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt

Counts
------
         2 Latin
         2 weakly pandiagonal
         2 center symmetric
         1 orthogonal pair

Всё отлично.

Пожалуй, на этом пока закончу с ортогональными парами слабо пандиагональных ЛК.
ID: 1049 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1060 - Posted: 3 Jan 2021, 23:30:12 UTC
Last modified: 3 Jan 2021, 23:31:36 UTC

Расскажу ещё об одном виде пандиагональных ЛК.
Мне такой вид встретился только для ЛК 9-го порядка.
Смотрим иллюстрацию



В этом ЛК все диагонали одного направления удовлетворяют условию пандиагональности, а диагонали другого направления не удовлетворяют.
То есть ЛК пандиагональный в одном направлении.
Раскрашены только три диагонали этого направления - главная и две разломанные.
Назову этот вид полупандиагональные ЛК (semi-pandiagonal LS по-английски).

Надо поискать в Интернете, есть ли там такие ЛК.
Если кто найдёт, сообщите, пожалуйста.
ID: 1060 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1063 - Posted: 4 Jan 2021, 2:13:04 UTC
Last modified: 4 Jan 2021, 5:06:09 UTC

Сейчас писала о совершенном ДЛК 9-го порядка, вспомнила, что в статье у меня построен совершенный ДЛК 16-го порядка.
Я построила его по аналогии с совершенным ДЛК 9-го порядка.
Статья
http://www.natalimak1.narod.ru/perfect1.htm
"СОВЕРШЕННЫЕ ЛАТИНСКИЕ КВАДРАТЫ Часть I"

И есть ещё одна интересная ортогональная пара слабо пандиагональных ЛК 16-го порядка!
Причём здесь ортогональная пара получилась смешанная: один ДЛК и один ЛК.

Иллюстрация совершенного ДЛК 16-го пор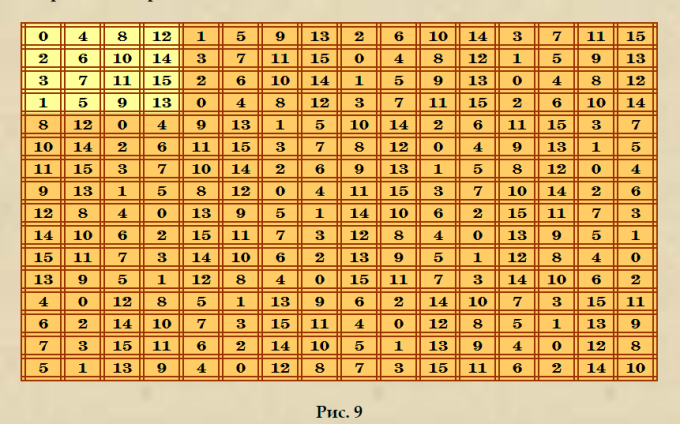ядка



В статье к этому ДЛК построен следующий ортогональный ЛК

0 4 8 12 1 5 9 13 2 6 10 14 3 7 11 15
1 5 9 13 0 4 8 12 3 7 11 15 2 6 10 14
2 6 10 14 3 7 11 15 0 4 8 12 1 5 9 13
3 7 11 15 2 6 10 14 1 5 9 13 0 4 8 12
4 0 12 8 5 1 13 9 6 2 14 10 7 3 15 11
5 1 13 9 4 0 12 8 7 3 15 11 6 2 14 10
6 2 14 10 7 3 15 11 4 0 12 8 5 1 13 9
7 3 15 11 6 2 14 10 5 1 13 9 4 0 12 8
8 12 0 4 9 13 1 5 10 14 2 6 11 15 3 7
9 13 1 5 8 12 0 4 11 15 3 7 10 14 2 6
10 14 2 6 11 15 3 7 8 12 0 4 9 13 1 5
11 15 3 7 10 14 2 6 9 13 1 5 8 12 0 4
12 8 4 0 13 9 5 1 14 10 6 2 15 11 7 3
13 9 5 1 12 8 4 0 15 11 7 3 14 10 6 2
14 10 6 2 15 11 7 3 12 8 4 0 13 9 5 1
15 11 7 3 14 10 6 2 13 9 5 1 12 8 4 0

Проверяю оба ЛК построенной ортогональной пары утилитой Harry White

Order? 16

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt

Counts
------
         1 Latin
         1 diagonal Latin
         2 weakly pandiagonal
         2 double axial symmetric
         2 center symmetric
         1 nfc
         1 orthogonal pair
         1 self-orthogonal

Всё замечательно! Оба ЛК являются слабо пандиагональными.

Кстати, совершенный ДЛК является SODLS. Поэтому ортогональный ЛК можно было и не строить, а взять в качестве ортогонального соквадрата транспонированный вариант.
Но в момент написания статьи я ещё не знала о SODLS.
Кроме того, совершенный ДЛК является и DSODLS, значит, ортогонален своему анти-транспонированному варианту.
И транспонированный, и анти-транспонированный варианты - слабо пандиагональные ДЛК.

Интересно, сколько Д-трансверсалей в совершенном ДЛК 16-го порядка.
Сейчас посчитаю.
ID: 1063 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1064 - Posted: 4 Jan 2021, 2:48:53 UTC
Last modified: 4 Jan 2021, 2:50:02 UTC

Посчитала (программой Tomas Brada)
num_dtrans: 31756544

Много Д-трансверсалей в совершенном ДЛК 16-го порядка, но не рекорд.

Код ДЛК в системе Tomas Brada
HNebk2YrWU5QdkkWgVkwk5cf6jk3dSzGqY9K5XBbFCpznPVv93UCg8nz6dtEeDLdkSahAL
ID: 1064 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1071 - Posted: 4 Jan 2021, 5:47:09 UTC
Last modified: 4 Jan 2021, 5:49:00 UTC

Если мы хотим построить пандиагональный ДЛК порядка n, при этом n=km и существуют пандиагональные ДЛК пордков k и m, можно воспользоваться методом составных квадратов.
В одной из тем на форуме проекта ОДЛК я показывала построение идеального (то есть ассоциативного и пандиагонального) ДЛК 35-го порядка методом составных квадратов (на основе идеальных ДЛК 5-го и 7-го порядков).
Показываю этот идеальный ДЛК

ID: 1071 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1072 - Posted: 4 Jan 2021, 5:52:06 UTC
Last modified: 4 Jan 2021, 5:54:22 UTC

И ещё один идеальный ДЛК 35-го порядка, построенный методом составных квадратов

0  6  5  4  3  2  1 28 34 33 32 31 30 29 21 27 26 25 24 23 22 14 20 19 18 17 16 15  7 13 12 11 10  9  8
2  1  0  6  5  4  3 30 29 28 34 33 32 31 23 22 21 27 26 25 24 16 15 14 20 19 18 17  9  8  7 13 12 11 10
4  3  2  1  0  6  5 32 31 30 29 28 34 33 25 24 23 22 21 27 26 18 17 16 15 14 20 19 11 10  9  8  7 13 12
6  5  4  3  2  1  0 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10  9  8  7
1  0  6  5  4  3  2 29 28 34 33 32 31 30 22 21 27 26 25 24 23 15 14 20 19 18 17 16  8  7 13 12 11 10  9
3  2  1  0  6  5  4 31 30 29 28 34 33 32 24 23 22 21 27 26 25 17 16 15 14 20 19 18 10  9  8  7 13 12 11
5  4  3  2  1  0  6 33 32 31 30 29 28 34 26 25 24 23 22 21 27 19 18 17 16 15 14 20 12 11 10  9  8  7 13
14 20 19 18 17 16 15  7 13 12 11 10  9  8  0  6  5  4  3  2  1 28 34 33 32 31 30 29 21 27 26 25 24 23 22
16 15 14 20 19 18 17  9  8  7 13 12 11 10  2  1  0  6  5  4  3 30 29 28 34 33 32 31 23 22 21 27 26 25 24
18 17 16 15 14 20 19 11 10  9  8  7 13 12  4  3  2  1  0  6  5 32 31 30 29 28 34 33 25 24 23 22 21 27 26
20 19 18 17 16 15 14 13 12 11 10  9  8  7  6  5  4  3  2  1  0 34 33 32 31 30 29 28 27 26 25 24 23 22 21
15 14 20 19 18 17 16  8  7 13 12 11 10  9  1  0  6  5  4  3  2 29 28 34 33 32 31 30 22 21 27 26 25 24 23
17 16 15 14 20 19 18 10  9  8  7 13 12 11  3  2  1  0  6  5  4 31 30 29 28 34 33 32 24 23 22 21 27 26 25
19 18 17 16 15 14 20 12 11 10  9  8  7 13  5  4  3  2  1  0  6 33 32 31 30 29 28 34 26 25 24 23 22 21 27
28 34 33 32 31 30 29 21 27 26 25 24 23 22 14 20 19 18 17 16 15  7 13 12 11 10  9  8  0  6  5  4  3  2  1
30 29 28 34 33 32 31 23 22 21 27 26 25 24 16 15 14 20 19 18 17  9  8  7 13 12 11 10  2  1  0  6  5  4  3
32 31 30 29 28 34 33 25 24 23 22 21 27 26 18 17 16 15 14 20 19 11 10  9  8  7 13 12  4  3  2  1  0  6  5
34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10  9  8  7  6  5  4  3  2  1  0
29 28 34 33 32 31 30 22 21 27 26 25 24 23 15 14 20 19 18 17 16  8  7 13 12 11 10  9  1  0  6  5  4  3  2
31 30 29 28 34 33 32 24 23 22 21 27 26 25 17 16 15 14 20 19 18 10  9  8  7 13 12 11  3  2  1  0  6  5  4
33 32 31 30 29 28 34 26 25 24 23 22 21 27 19 18 17 16 15 14 20 12 11 10  9  8  7 13  5  4  3  2  1  0  6
7 13 12 11 10  9  8  0  6  5  4  3  2  1 28 34 33 32 31 30 29 21 27 26 25 24 23 22 14 20 19 18 17 16 15
9  8  7 13 12 11 10  2  1  0  6  5  4  3 30 29 28 34 33 32 31 23 22 21 27 26 25 24 16 15 14 20 19 18 17
11 10  9  8  7 13 12  4  3  2  1  0  6  5 32 31 30 29 28 34 33 25 24 23 22 21 27 26 18 17 16 15 14 20 19
13 12 11 10  9  8  7  6  5  4  3  2  1  0 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14
8  7 13 12 11 10  9  1  0  6  5  4  3  2 29 28 34 33 32 31 30 22 21 27 26 25 24 23 15 14 20 19 18 17 16
10  9  8  7 13 12 11  3  2  1  0  6  5  4 31 30 29 28 34 33 32 24 23 22 21 27 26 25 17 16 15 14 20 19 18
12 11 10  9  8  7 13  5  4  3  2  1  0  6 33 32 31 30 29 28 34 26 25 24 23 22 21 27 19 18 17 16 15 14 20
21 27 26 25 24 23 22 14 20 19 18 17 16 15  7 13 12 11 10  9  8  0  6  5  4  3  2  1 28 34 33 32 31 30 29
23 22 21 27 26 25 24 16 15 14 20 19 18 17  9  8  7 13 12 11 10  2  1  0  6  5  4  3 30 29 28 34 33 32 31
25 24 23 22 21 27 26 18 17 16 15 14 20 19 11 10  9  8  7 13 12  4  3  2  1  0  6  5 32 31 30 29 28 34 33
27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10  9  8  7  6  5  4  3  2  1  0 34 33 32 31 30 29 28
22 21 27 26 25 24 23 15 14 20 19 18 17 16  8  7 13 12 11 10  9  1  0  6  5  4  3  2 29 28 34 33 32 31 30
24 23 22 21 27 26 25 17 16 15 14 20 19 18 10  9  8  7 13 12 11  3  2  1  0  6  5  4 31 30 29 28 34 33 32
26 25 24 23 22 21 27 19 18 17 16 15 14 20 12 11 10  9  8  7 13  5  4  3  2  1  0  6 33 32 31 30 29 28 34

Проверяю этот ДЛК утилитой Harry White
Order? 35

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         1 diagonal Latin
         1 associative
         1 pandiagonal
         1 ultramagic
         1 natural \diagonal
         1 self-orthogonal

ДЛК является SODLS, значит, имеем ортогональную пару идеальных ДЛК.
ID: 1072 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1073 - Posted: 4 Jan 2021, 6:04:37 UTC

А теперь возьмём ортогональную пару слабо пандиагональных ДЛК 4-го порядка
0 3 2 1
2 1 0 3
1 2 3 0
3 0 1 2

0 1 2 3
3 2 1 0
1 0 3 2
2 3 0 1

и ортогональную пару слабо пандиагональных ДЛК 8-го порядка
0 1 6 7 4 5 2 3
6 7 0 1 2 3 4 5
3 2 5 4 7 6 1 0
5 4 3 2 1 0 7 6
2 3 4 5 6 7 0 1
4 5 2 3 0 1 6 7
1 0 7 6 5 4 3 2
7 6 1 0 3 2 5 4

3 5 0 6 1 7 2 4
2 4 1 7 0 6 3 5
5 3 6 0 7 1 4 2
4 2 7 1 6 0 5 3
7 1 4 2 5 3 6 0
6 0 5 3 4 2 7 1
1 7 2 4 3 5 0 6
0 6 3 5 2 4 1 7

(эти ортогональные пары показаны выше)
и на их основе построим ортогональную пару слабо пандиагональных ДЛК 32-го порядка, используя метод составных квадратов.
ID: 1073 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1074 - Posted: 4 Jan 2021, 6:18:51 UTC
Last modified: 4 Jan 2021, 6:19:29 UTC

Первый ДЛК

  0   1   6   7   4   5   2   3  24  25  30  31  28  29  26  27  16  17  22  23  20  21  18  19   8   9  14  15  12  13  10  11
  6   7   0   1   2   3   4   5  30  31  24  25  26  27  28  29  22  23  16  17  18  19  20  21  14  15   8   9  10  11  12  13
  3   2   5   4   7   6   1   0  27  26  29  28  31  30  25  24  19  18  21  20  23  22  17  16  11  10  13  12  15  14   9   8
  5   4   3   2   1   0   7   6  29  28  27  26  25  24  31  30  21  20  19  18  17  16  23  22  13  12  11  10   9   8  15  14
  2   3   4   5   6   7   0   1  26  27  28  29  30  31  24  25  18  19  20  21  22  23  16  17  10  11  12  13  14  15   8   9
  4   5   2   3   0   1   6   7  28  29  26  27  24  25  30  31  20  21  18  19  16  17  22  23  12  13  10  11   8   9  14  15
  1   0   7   6   5   4   3   2  25  24  31  30  29  28  27  26  17  16  23  22  21  20  19  18   9   8  15  14  13  12  11  10
  7   6   1   0   3   2   5   4  31  30  25  24  27  26  29  28  23  22  17  16  19  18  21  20  15  14   9   8  11  10  13  12
 16  17  22  23  20  21  18  19   8   9  14  15  12  13  10  11   0   1   6   7   4   5   2   3  24  25  30  31  28  29  26  27
 22  23  16  17  18  19  20  21  14  15   8   9  10  11  12  13   6   7   0   1   2   3   4   5  30  31  24  25  26  27  28  29
 19  18  21  20  23  22  17  16  11  10  13  12  15  14   9   8   3   2   5   4   7   6   1   0  27  26  29  28  31  30  25  24
 21  20  19  18  17  16  23  22  13  12  11  10   9   8  15  14   5   4   3   2   1   0   7   6  29  28  27  26  25  24  31  30
 18  19  20  21  22  23  16  17  10  11  12  13  14  15   8   9   2   3   4   5   6   7   0   1  26  27  28  29  30  31  24  25
 20  21  18  19  16  17  22  23  12  13  10  11   8   9  14  15   4   5   2   3   0   1   6   7  28  29  26  27  24  25  30  31
 17  16  23  22  21  20  19  18   9   8  15  14  13  12  11  10   1   0   7   6   5   4   3   2  25  24  31  30  29  28  27  26
 23  22  17  16  19  18  21  20  15  14   9   8  11  10  13  12   7   6   1   0   3   2   5   4  31  30  25  24  27  26  29  28
  8   9  14  15  12  13  10  11  16  17  22  23  20  21  18  19  24  25  30  31  28  29  26  27   0   1   6   7   4   5   2   3
 14  15   8   9  10  11  12  13  22  23  16  17  18  19  20  21  30  31  24  25  26  27  28  29   6   7   0   1   2   3   4   5
 11  10  13  12  15  14   9   8  19  18  21  20  23  22  17  16  27  26  29  28  31  30  25  24   3   2   5   4   7   6   1   0
 13  12  11  10   9   8  15  14  21  20  19  18  17  16  23  22  29  28  27  26  25  24  31  30   5   4   3   2   1   0   7   6
 10  11  12  13  14  15   8   9  18  19  20  21  22  23  16  17  26  27  28  29  30  31  24  25   2   3   4   5   6   7   0   1
 12  13  10  11   8   9  14  15  20  21  18  19  16  17  22  23  28  29  26  27  24  25  30  31   4   5   2   3   0   1   6   7
  9   8  15  14  13  12  11  10  17  16  23  22  21  20  19  18  25  24  31  30  29  28  27  26   1   0   7   6   5   4   3   2
 15  14   9   8  11  10  13  12  23  22  17  16  19  18  21  20  31  30  25  24  27  26  29  28   7   6   1   0   3   2   5   4
 24  25  30  31  28  29  26  27   0   1   6   7   4   5   2   3   8   9  14  15  12  13  10  11  16  17  22  23  20  21  18  19
 30  31  24  25  26  27  28  29   6   7   0   1   2   3   4   5  14  15   8   9  10  11  12  13  22  23  16  17  18  19  20  21
 27  26  29  28  31  30  25  24   3   2   5   4   7   6   1   0  11  10  13  12  15  14   9   8  19  18  21  20  23  22  17  16
 29  28  27  26  25  24  31  30   5   4   3   2   1   0   7   6  13  12  11  10   9   8  15  14  21  20  19  18  17  16  23  22
 26  27  28  29  30  31  24  25   2   3   4   5   6   7   0   1  10  11  12  13  14  15   8   9  18  19  20  21  22  23  16  17
 28  29  26  27  24  25  30  31   4   5   2   3   0   1   6   7  12  13  10  11   8   9  14  15  20  21  18  19  16  17  22  23
 25  24  31  30  29  28  27  26   1   0   7   6   5   4   3   2   9   8  15  14  13  12  11  10  17  16  23  22  21  20  19  18
 31  30  25  24  27  26  29  28   7   6   1   0   3   2   5   4  15  14   9   8  11  10  13  12  23  22  17  16  19  18  21  20

Второй ДЛК

  3   5   0   6   1   7   2   4  11  13   8  14   9  15  10  12  19  21  16  22  17  23  18  20  27  29  24  30  25  31  26  28
  2   4   1   7   0   6   3   5  10  12   9  15   8  14  11  13  18  20  17  23  16  22  19  21  26  28  25  31  24  30  27  29
  5   3   6   0   7   1   4   2  13  11  14   8  15   9  12  10  21  19  22  16  23  17  20  18  29  27  30  24  31  25  28  26
  4   2   7   1   6   0   5   3  12  10  15   9  14   8  13  11  20  18  23  17  22  16  21  19  28  26  31  25  30  24  29  27
  7   1   4   2   5   3   6   0  15   9  12  10  13  11  14   8  23  17  20  18  21  19  22  16  31  25  28  26  29  27  30  24
  6   0   5   3   4   2   7   1  14   8  13  11  12  10  15   9  22  16  21  19  20  18  23  17  30  24  29  27  28  26  31  25
  1   7   2   4   3   5   0   6   9  15  10  12  11  13   8  14  17  23  18  20  19  21  16  22  25  31  26  28  27  29  24  30
  0   6   3   5   2   4   1   7   8  14  11  13  10  12   9  15  16  22  19  21  18  20  17  23  24  30  27  29  26  28  25  31
 27  29  24  30  25  31  26  28  19  21  16  22  17  23  18  20  11  13   8  14   9  15  10  12   3   5   0   6   1   7   2   4
 26  28  25  31  24  30  27  29  18  20  17  23  16  22  19  21  10  12   9  15   8  14  11  13   2   4   1   7   0   6   3   5
 29  27  30  24  31  25  28  26  21  19  22  16  23  17  20  18  13  11  14   8  15   9  12  10   5   3   6   0   7   1   4   2
 28  26  31  25  30  24  29  27  20  18  23  17  22  16  21  19  12  10  15   9  14   8  13  11   4   2   7   1   6   0   5   3
 31  25  28  26  29  27  30  24  23  17  20  18  21  19  22  16  15   9  12  10  13  11  14   8   7   1   4   2   5   3   6   0
 30  24  29  27  28  26  31  25  22  16  21  19  20  18  23  17  14   8  13  11  12  10  15   9   6   0   5   3   4   2   7   1
 25  31  26  28  27  29  24  30  17  23  18  20  19  21  16  22   9  15  10  12  11  13   8  14   1   7   2   4   3   5   0   6
 24  30  27  29  26  28  25  31  16  22  19  21  18  20  17  23   8  14  11  13  10  12   9  15   0   6   3   5   2   4   1   7
 11  13   8  14   9  15  10  12   3   5   0   6   1   7   2   4  27  29  24  30  25  31  26  28  19  21  16  22  17  23  18  20
 10  12   9  15   8  14  11  13   2   4   1   7   0   6   3   5  26  28  25  31  24  30  27  29  18  20  17  23  16  22  19  21
 13  11  14   8  15   9  12  10   5   3   6   0   7   1   4   2  29  27  30  24  31  25  28  26  21  19  22  16  23  17  20  18
 12  10  15   9  14   8  13  11   4   2   7   1   6   0   5   3  28  26  31  25  30  24  29  27  20  18  23  17  22  16  21  19
 15   9  12  10  13  11  14   8   7   1   4   2   5   3   6   0  31  25  28  26  29  27  30  24  23  17  20  18  21  19  22  16
 14   8  13  11  12  10  15   9   6   0   5   3   4   2   7   1  30  24  29  27  28  26  31  25  22  16  21  19  20  18  23  17
  9  15  10  12  11  13   8  14   1   7   2   4   3   5   0   6  25  31  26  28  27  29  24  30  17  23  18  20  19  21  16  22
  8  14  11  13  10  12   9  15   0   6   3   5   2   4   1   7  24  30  27  29  26  28  25  31  16  22  19  21  18  20  17  23
 19  21  16  22  17  23  18  20  27  29  24  30  25  31  26  28   3   5   0   6   1   7   2   4  11  13   8  14   9  15  10  12
 18  20  17  23  16  22  19  21  26  28  25  31  24  30  27  29   2   4   1   7   0   6   3   5  10  12   9  15   8  14  11  13
 21  19  22  16  23  17  20  18  29  27  30  24  31  25  28  26   5   3   6   0   7   1   4   2  13  11  14   8  15   9  12  10
 20  18  23  17  22  16  21  19  28  26  31  25  30  24  29  27   4   2   7   1   6   0   5   3  12  10  15   9  14   8  13  11
 23  17  20  18  21  19  22  16  31  25  28  26  29  27  30  24   7   1   4   2   5   3   6   0  15   9  12  10  13  11  14   8
 22  16  21  19  20  18  23  17  30  24  29  27  28  26  31  25   6   0   5   3   4   2   7   1  14   8  13  11  12  10  15   9
 17  23  18  20  19  21  16  22  25  31  26  28  27  29  24  30   1   7   2   4   3   5   0   6   9  15  10  12  11  13   8  14
 16  22  19  21  18  20  17  23  24  30  27  29  26  28  25  31   0   6   3   5   2   4   1   7   8  14  11  13  10  12   9  15

Проверяю сразу оба ДЛК построенной ортогональной пары утилитой Harry White
Order? 32

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt

Counts
------
         2 diagonal Latin
         2 weakly pandiagonal
         2 double axial symmetric
         2 center symmetric
         1 orthogonal pair
         2 self-orthogonal

Отлично!
ID: 1074 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1075 - Posted: 4 Jan 2021, 6:23:53 UTC
Last modified: 4 Jan 2021, 6:26:07 UTC

А если мы возьмём ортогональную пару пандиагональных ДЛК 7-го порядка и ортогональную пару слабо пандиагональных ДЛК 4-го порядка, получим методом составных квадратов ортогональную пару слабо пандиагональных ДЛК 28-го порядка.
Сейчас проверим :)
Ортогональная пара слабо пандиагональных ДЛК 4-го порядка та же

0 3 2 1
2 1 0 3
1 2 3 0
3 0 1 2

0 1 2 3
3 2 1 0
1 0 3 2
2 3 0 1

Ортогональную пару пандиагональных ДЛК 7-го порядка возьмём эту

0 1 2 3 4 5 6
2 3 4 5 6 0 1
4 5 6 0 1 2 3
6 0 1 2 3 4 5
1 2 3 4 5 6 0
3 4 5 6 0 1 2
5 6 0 1 2 3 4

0 1 2 3 4 5 6
3 4 5 6 0 1 2
6 0 1 2 3 4 5
2 3 4 5 6 0 1
5 6 0 1 2 3 4
1 2 3 4 5 6 0
4 5 6 0 1 2 3
ID: 1075 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1076 - Posted: 4 Jan 2021, 6:36:55 UTC
Last modified: 4 Jan 2021, 6:41:26 UTC

Первый ДЛК
  0   1   2   3   4   5   6  21  22  23  24  25  26  27  14  15  16  17  18  19  20   7   8   9  10  11  12  13
  2   3   4   5   6   0   1  23  24  25  26  27  21  22  16  17  18  19  20  14  15   9  10  11  12  13   7   8
  4   5   6   0   1   2   3  25  26  27  21  22  23  24  18  19  20  14  15  16  17  11  12  13   7   8   9  10
  6   0   1   2   3   4   5  27  21  22  23  24  25  26  20  14  15  16  17  18  19  13   7   8   9  10  11  12
  1   2   3   4   5   6   0  22  23  24  25  26  27  21  15  16  17  18  19  20  14   8   9  10  11  12  13   7
  3   4   5   6   0   1   2  24  25  26  27  21  22  23  17  18  19  20  14  15  16  10  11  12  13   7   8   9
  5   6   0   1   2   3   4  26  27  21  22  23  24  25  19  20  14  15  16  17  18  12  13   7   8   9  10  11
 14  15  16  17  18  19  20   7   8   9  10  11  12  13   0   1   2   3   4   5   6  21  22  23  24  25  26  27
 16  17  18  19  20  14  15   9  10  11  12  13   7   8   2   3   4   5   6   0   1  23  24  25  26  27  21  22
 18  19  20  14  15  16  17  11  12  13   7   8   9  10   4   5   6   0   1   2   3  25  26  27  21  22  23  24
 20  14  15  16  17  18  19  13   7   8   9  10  11  12   6   0   1   2   3   4   5  27  21  22  23  24  25  26
 15  16  17  18  19  20  14   8   9  10  11  12  13   7   1   2   3   4   5   6   0  22  23  24  25  26  27  21
 17  18  19  20  14  15  16  10  11  12  13   7   8   9   3   4   5   6   0   1   2  24  25  26  27  21  22  23
 19  20  14  15  16  17  18  12  13   7   8   9  10  11   5   6   0   1   2   3   4  26  27  21  22  23  24  25
  7   8   9  10  11  12  13  14  15  16  17  18  19  20  21  22  23  24  25  26  27   0   1   2   3   4   5   6
  9  10  11  12  13   7   8  16  17  18  19  20  14  15  23  24  25  26  27  21  22   2   3   4   5   6   0   1
 11  12  13   7   8   9  10  18  19  20  14  15  16  17  25  26  27  21  22  23  24   4   5   6   0   1   2   3
 13   7   8   9  10  11  12  20  14  15  16  17  18  19  27  21  22  23  24  25  26   6   0   1   2   3   4   5
  8   9  10  11  12  13   7  15  16  17  18  19  20  14  22  23  24  25  26  27  21   1   2   3   4   5   6   0
 10  11  12  13   7   8   9  17  18  19  20  14  15  16  24  25  26  27  21  22  23   3   4   5   6   0   1   2
 12  13   7   8   9  10  11  19  20  14  15  16  17  18  26  27  21  22  23  24  25   5   6   0   1   2   3   4
 21  22  23  24  25  26  27   0   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19  20
 23  24  25  26  27  21  22   2   3   4   5   6   0   1   9  10  11  12  13   7   8  16  17  18  19  20  14  15
 25  26  27  21  22  23  24   4   5   6   0   1   2   3  11  12  13   7   8   9  10  18  19  20  14  15  16  17
 27  21  22  23  24  25  26   6   0   1   2   3   4   5  13   7   8   9  10  11  12  20  14  15  16  17  18  19
 22  23  24  25  26  27  21   1   2   3   4   5   6   0   8   9  10  11  12  13   7  15  16  17  18  19  20  14
 24  25  26  27  21  22  23   3   4   5   6   0   1   2  10  11  12  13   7   8   9  17  18  19  20  14  15  16
 26  27  21  22  23  24  25   5   6   0   1   2   3   4  12  13   7   8   9  10  11  19  20  14  15  16  17  18

Второй ДЛК
  0   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19  20  21  22  23  24  25  26  27
  3   4   5   6   0   1   2  10  11  12  13   7   8   9  17  18  19  20  14  15  16  24  25  26  27  21  22  23
  6   0   1   2   3   4   5  13   7   8   9  10  11  12  20  14  15  16  17  18  19  27  21  22  23  24  25  26
  2   3   4   5   6   0   1   9  10  11  12  13   7   8  16  17  18  19  20  14  15  23  24  25  26  27  21  22
  5   6   0   1   2   3   4  12  13   7   8   9  10  11  19  20  14  15  16  17  18  26  27  21  22  23  24  25
  1   2   3   4   5   6   0   8   9  10  11  12  13   7  15  16  17  18  19  20  14  22  23  24  25  26  27  21
  4   5   6   0   1   2   3  11  12  13   7   8   9  10  18  19  20  14  15  16  17  25  26  27  21  22  23  24
 21  22  23  24  25  26  27  14  15  16  17  18  19  20   7   8   9  10  11  12  13   0   1   2   3   4   5   6
 24  25  26  27  21  22  23  17  18  19  20  14  15  16  10  11  12  13   7   8   9   3   4   5   6   0   1   2
 27  21  22  23  24  25  26  20  14  15  16  17  18  19  13   7   8   9  10  11  12   6   0   1   2   3   4   5
 23  24  25  26  27  21  22  16  17  18  19  20  14  15   9  10  11  12  13   7   8   2   3   4   5   6   0   1
 26  27  21  22  23  24  25  19  20  14  15  16  17  18  12  13   7   8   9  10  11   5   6   0   1   2   3   4
 22  23  24  25  26  27  21  15  16  17  18  19  20  14   8   9  10  11  12  13   7   1   2   3   4   5   6   0
 25  26  27  21  22  23  24  18  19  20  14  15  16  17  11  12  13   7   8   9  10   4   5   6   0   1   2   3
  7   8   9  10  11  12  13   0   1   2   3   4   5   6  21  22  23  24  25  26  27  14  15  16  17  18  19  20
 10  11  12  13   7   8   9   3   4   5   6   0   1   2  24  25  26  27  21  22  23  17  18  19  20  14  15  16
 13   7   8   9  10  11  12   6   0   1   2   3   4   5  27  21  22  23  24  25  26  20  14  15  16  17  18  19
  9  10  11  12  13   7   8   2   3   4   5   6   0   1  23  24  25  26  27  21  22  16  17  18  19  20  14  15
 12  13   7   8   9  10  11   5   6   0   1   2   3   4  26  27  21  22  23  24  25  19  20  14  15  16  17  18
  8   9  10  11  12  13   7   1   2   3   4   5   6   0  22  23  24  25  26  27  21  15  16  17  18  19  20  14
 11  12  13   7   8   9  10   4   5   6   0   1   2   3  25  26  27  21  22  23  24  18  19  20  14  15  16  17
 14  15  16  17  18  19  20  21  22  23  24  25  26  27   0   1   2   3   4   5   6   7   8   9  10  11  12  13
 17  18  19  20  14  15  16  24  25  26  27  21  22  23   3   4   5   6   0   1   2  10  11  12  13   7   8   9
 20  14  15  16  17  18  19  27  21  22  23  24  25  26   6   0   1   2   3   4   5  13   7   8   9  10  11  12
 16  17  18  19  20  14  15  23  24  25  26  27  21  22   2   3   4   5   6   0   1   9  10  11  12  13   7   8
 19  20  14  15  16  17  18  26  27  21  22  23  24  25   5   6   0   1   2   3   4  12  13   7   8   9  10  11
 15  16  17  18  19  20  14  22  23  24  25  26  27  21   1   2   3   4   5   6   0   8   9  10  11  12  13   7
 18  19  20  14  15  16  17  25  26  27  21  22  23  24   4   5   6   0   1   2   3  11  12  13   7   8   9  10

Проверяю оба ДЛК построенной ортогональной пары утилитой Harry White
Order? 28

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt

Counts
------
         2 diagonal Latin
         2 weakly pandiagonal
         2 center symmetric
         1 nfr
         1 orthogonal pair
         2 self-orthogonal

Всё прекрасно!
ID: 1076 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1077 - Posted: 4 Jan 2021, 15:59:18 UTC
Last modified: 4 Jan 2021, 16:00:29 UTC

Смотрю свои статьи о ЛК и ДЛК 11-летней давности.
Вот, например, статья
"ГРУППЫ ВЗАИМНО ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ
Mutually Orthogonal Latin squares (MOLS)"
http://www.natalimak1.narod.ru/grolk.htm
написана 19 - 21 января – 4 февраля 2009 г.
Это уже скоро 12 лет будет статье.
А мне до сих пор интересна эта статья, в ней много полезной информации.

Полную систему MOLS 16-го порядка я не построила, а построила вручную два ДЛК из этой системы по аналогии с ДЛК 8-го порядка из полной системы MOLS.
Показываю эту ортогональную пару ДЛК 16-го порядка

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15            
2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13            
4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11            
6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9                      
8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7            
10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5            
12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3            
14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1            
9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6                      
11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4            
13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2            
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0            
1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14            
3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12            
5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10            
7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8            

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12
6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9
5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10           
12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3                      
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0                      
10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5
9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6
7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8           
4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11
1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14
2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13
11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4
8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7
13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2
14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1

Проверяю ДЛК этой ортогональной пары утилитой Harry White
Order? 16

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_9.txt

Counts
------
         2 diagonal Latin
         1 weakly pandiagonal
         2 double axial symmetric
         2 center symmetric
         2 nfr
         1 orthogonal pair
         2 self-orthogonal

Как интересно получилось: один ДЛК слабо пандиагональный, а другой не обладает этим свойством.
Совершенно оригинальная ортогональная пара ДЛК 16-го порядка!
ID: 1077 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1078 - Posted: 4 Jan 2021, 16:02:49 UTC

А кстати...
Господа!
У вас, наверное, есть матпакет Maple.
В этом матпакете можно получить полную систему MOLS 16-го порядка (и не только!).
Пожалуйста, выдайте эту систему MOLS в студию :)
Буду очень признательная.
ID: 1078 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1079 - Posted: 4 Jan 2021, 18:19:18 UTC

Тэк-с, обнаружила, что ортогональной пары слабо пандиагональных ЛК 24-го порядка ещё нет.
И... пришлось с этой парой потрудиться :)
Сначала построила ассоциативный ДЛК

0 8 3 2 20 9 23 22 1 21 16 14 19 18 17 13 12 15 11 10 4 6 7 5
2 1 0 8 22 21 20 9 3 23 18 17 16 14 19 11 10 13 12 15 7 5 4 6
8 3 2 1 9 23 22 21 0 20 14 19 18 17 16 12 15 11 10 13 5 7 6 4
1 0 8 3 21 20 9 23 2 22 17 16 14 19 18 10 13 12 15 11 6 4 5 7
12 9 11 10 4 14 7 6 17 13 0 15 3 2 5 1 20 22 23 21 16 8 19 18
10 13 12 9 6 5 4 14 19 11 2 1 0 15 7 3 23 21 20 22 18 17 16 8
9 11 10 13 14 7 6 5 16 12 15 3 2 1 4 0 21 23 22 20 8 19 18 17
13 12 9 11 5 4 14 7 18 10 1 0 15 3 6 2 22 20 21 23 17 16 8 19
3 2 1 0 11 10 13 12 8 14 23 22 21 20 15 9 7 6 5 4 19 18 17 16
11 10 13 12 23 22 21 20 15 9 7 6 5 4 8 14 19 18 17 16 3 2 1 0
20 14 23 22 16 15 19 18 5 1 12 10 11 13 21 17 4 8 7 6 0 9 3 2
22 21 20 14 18 17 16 15 7 3 11 13 12 10 23 19 6 5 4 8 2 1 0 9
14 23 22 21 15 19 18 17 4 0 13 11 10 12 20 16 8 7 6 5 9 3 2 1
21 20 14 23 17 16 15 19 6 2 10 12 13 11 22 18 5 4 8 7 1 0 9 3
23 22 21 20 7 6 5 4 9 15 19 18 17 16 14 8 3 2 1 0 11 10 13 12
7 6 5 4 19 18 17 16 14 8 3 2 1 0 9 15 11 10 13 12 23 22 21 20
4 15 7 6 0 2 3 1 21 17 20 8 23 22 13 5 16 9 19 18 12 14 11 10
6 5 4 15 3 1 0 2 23 19 22 21 20 8 11 7 18 17 16 9 10 13 12 14
15 7 6 5 1 3 2 0 20 16 8 23 22 21 12 4 9 19 18 17 14 11 10 13
5 4 15 7 2 0 1 3 22 18 21 20 8 23 10 6 17 16 9 19 13 12 14 11
16 18 19 17 12 8 11 10 13 5 4 9 7 6 1 21 0 14 3 2 20 15 23 22
19 17 16 18 10 13 12 8 11 7 6 5 4 9 3 23 2 1 0 14 22 21 20 15
17 19 18 16 8 11 10 13 12 4 9 7 6 5 0 20 14 3 2 1 15 23 22 21
18 16 17 19 13 12 8 11 10 6 5 4 9 7 2 22 1 0 14 3 21 20 15 23

Проверяю утилитой Harry Whine
Order? 24

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_9.txt

Counts
------
         1 diagonal Latin
         1 associative
         1 self-orthogonal

Всё в порядке: ДЛК ассоциативный, а ещё он является SODLS.

Интересно отметить, что ассоциативный ДЛК я построила из ДЛК, полученного программой Harry White, вот этого

 0 12  3  2 20 13 23 22  1 21 16 14 19 18 17  9  8 15 11 10  4  6  7  5
 2  1  0 12 22 21 20 13  3 23 18 17 16 14 19 11 10  9  8 15  7  5  4  6
12  3  2  1 13 23 22 21  0 20 14 19 18 17 16  8 15 11 10  9  5  7  6  4
 1  0 12  3 21 20 13 23  2 22 17 16 14 19 18 10  9  8 15 11  6  4  5  7
 8 13 11 10  4 14  7  6 17  9  0 15  3  2  5  1 20 22 23 21 16 12 19 18
10  9  8 13  6  5  4 14 19 11  2  1  0 15  7  3 23 21 20 22 18 17 16 12
13 11 10  9 14  7  6  5 16  8 15  3  2  1  4  0 21 23 22 20 12 19 18 17
 9  8 13 11  5  4 14  7 18 10  1  0 15  3  6  2 22 20 21 23 17 16 12 19
 3  2  1  0 11 10  9  8 12 14 23 22 21 20 15 13  7  6  5  4 19 18 17 16
11 10  9  8 23 22 21 20 15 13  7  6  5  4 12 14 19 18 17 16  3  2  1  0
20 14 23 22 16 15 19 18  5  1  8 10 11  9 21 17  4 12  7  6  0 13  3  2
22 21 20 14 18 17 16 15  7  3 11  9  8 10 23 19  6  5  4 12  2  1  0 13
14 23 22 21 15 19 18 17  4  0  9 11 10  8 20 16 12  7  6  5 13  3  2  1
21 20 14 23 17 16 15 19  6  2 10  8  9 11 22 18  5  4 12  7  1  0 13  3
23 22 21 20  7  6  5  4 13 15 19 18 17 16 14 12  3  2  1  0 11 10  9  8
 7  6  5  4 19 18 17 16 14 12  3  2  1  0 13 15 11 10  9  8 23 22 21 20
 4 15  7  6  0  2  3  1 21 17 20 12 23 22  9  5 16 13 19 18  8 14 11 10
 6  5  4 15  3  1  0  2 23 19 22 21 20 12 11  7 18 17 16 13 10  9  8 14
15  7  6  5  1  3  2  0 20 16 12 23 22 21  8  4 13 19 18 17 14 11 10  9
 5  4 15  7  2  0  1  3 22 18 21 20 12 23 10  6 17 16 13 19  9  8 14 11
16 18 19 17  8 12 11 10  9  5  4 13  7  6  1 21  0 14  3  2 20 15 23 22
19 17 16 18 10  9  8 12 11  7  6  5  4 13  3 23  2  1  0 14 22 21 20 15
17 19 18 16 12 11 10  9  8  4 13  7  6  5  0 20 14  3  2  1 15 23 22 21
18 16 17 19  9  8 12 11 10  6  5  4 13  7  2 22  1  0 14  3 21 20 15 23

Однако этот ДЛК не является ассоциативным (с точки зрения утилиты Harry White), смотрите
Order? 24

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_10.txt

Counts
------
         1 diagonal Latin
         1 center symmetric
         1 self-orthogonal

Этот ДЛК является центрально-симметричным.
Ну да, вот он - нюанс, о котором я рассказывала на форуме ОДЛК.
С помощью переобозначения элементов я превратила этот ДЛК в ассоциативный (с точки зрения утилиты Harry).
Потому что для дальнейшего преобразования трёх квадратов нужен именно ассоциативный ДЛК.
ID: 1079 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1080 - Posted: 4 Jan 2021, 18:30:46 UTC

Теперь применяю к ассоциативному ДЛК преобразование трёх квадратов и получаю слабо пандиагональный ЛК

0 8 3 2 20 9 23 22 1 21 16 14 5 7 6 4 10 11 15 12 13 17 18 19
2 1 0 8 22 21 20 9 3 23 18 17 6 4 5 7 15 12 13 10 11 19 14 16
8 3 2 1 9 23 22 21 0 20 14 19 4 6 7 5 13 10 11 15 12 16 17 18
1 0 8 3 21 20 9 23 2 22 17 16 7 5 4 6 11 15 12 13 10 18 19 14
12 9 11 10 4 14 7 6 17 13 0 15 18 19 8 16 21 23 22 20 1 5 2 3
10 13 12 9 6 5 4 14 19 11 2 1 8 16 17 18 22 20 21 23 3 7 15 0
9 11 10 13 14 7 6 5 16 12 15 3 17 18 19 8 20 22 23 21 0 4 1 2
13 12 9 11 5 4 14 7 18 10 1 0 19 8 16 17 23 21 20 22 2 6 3 15
3 2 1 0 11 10 13 12 8 14 23 22 16 17 18 19 4 5 6 7 9 15 20 21
11 10 13 12 23 22 21 20 15 9 7 6 0 1 2 3 16 17 18 19 14 8 4 5
20 14 23 22 16 15 19 18 5 1 12 10 2 3 9 0 6 7 8 4 17 21 13 11
22 21 20 14 18 17 16 15 7 3 11 13 9 0 1 2 8 4 5 6 19 23 10 12
18 16 17 19 13 12 8 11 10 6 5 4 23 15 20 21 3 14 0 1 22 2 7 9
17 19 18 16 8 11 10 13 12 4 9 7 21 22 23 15 1 2 3 14 20 0 5 6
19 17 16 18 10 13 12 8 11 7 6 5 15 20 21 22 14 0 1 2 23 3 9 4
16 18 19 17 12 8 11 10 13 5 4 9 22 23 15 20 2 3 14 0 21 1 6 7
5 4 15 7 2 0 1 3 22 18 21 20 11 14 12 13 19 9 16 17 6 10 23 8
15 7 6 5 1 3 2 0 20 16 8 23 13 10 11 14 17 18 19 9 4 12 21 22
6 5 4 15 3 1 0 2 23 19 22 21 14 12 13 10 9 16 17 18 7 11 8 20
4 15 7 6 0 2 3 1 21 17 20 8 10 11 14 12 18 19 9 16 5 13 22 23
7 6 5 4 19 18 17 16 14 8 3 2 20 21 22 23 12 13 10 11 15 9 0 1
23 22 21 20 7 6 5 4 9 15 19 18 12 13 10 11 0 1 2 3 8 14 16 17
21 20 14 23 17 16 15 19 6 2 10 12 3 9 0 1 7 8 4 5 18 22 11 13
14 23 22 21 15 19 18 17 4 0 13 11 1 2 3 9 5 6 7 8 16 20 12 10

О преобразовании трёх квадратов я писала выше.

Проверяю полученный ЛК утилитой Harry White
Order? 24

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt

Counts
------
         1 Latin
         1 weakly pandiagonal
         1 self-orthogonal

Получился слабо пандиагональный ЛК, который является SOLS.
Теперь достаточно взять транспонированный вариант этого ЛК и ортогональная пара слабо пандиагональных ЛК 24-го порядка готова.

Это транспонированный вариант

 0  2  8  1 12 10  9 13  3 11 20 22 18 17 19 16  5 15  6  4  7 23 21 14
 8  1  3  0  9 13 11 12  2 10 14 21 16 19 17 18  4  7  5 15  6 22 20 23
 3  0  2  8 11 12 10  9  1 13 23 20 17 18 16 19 15  6  4  7  5 21 14 22
 2  8  1  3 10  9 13 11  0 12 22 14 19 16 18 17  7  5 15  6  4 20 23 21
20 22  9 21  4  6 14  5 11 23 16 18 13  8 10 12  2  1  3  0 19  7 17 15
 9 21 23 20 14  5  7  4 10 22 15 17 12 11 13  8  0  3  1  2 18  6 16 19
23 20 22  9  7  4  6 14 13 21 19 16  8 10 12 11  1  2  0  3 17  5 15 18
22  9 21 23  6 14  5  7 12 20 18 15 11 13  8 10  3  0  2  1 16  4 19 17
 1  3  0  2 17 19 16 18  8 15  5  7 10 12 11 13 22 20 23 21 14  9  6  4
21 23 20 22 13 11 12 10 14  9  1  3  6  4  7  5 18 16 19 17  8 15  2  0
16 18 14 17  0  2 15  1 23  7 12 11  5  9  6  4 21  8 22 20  3 19 10 13
14 17 19 16 15  1  3  0 22  6 10 13  4  7  5  9 20 23 21  8  2 18 12 11
 5  6  4  7 18  8 17 19 16  0  2  9 23 21 15 22 11 13 14 10 20 12  3  1
 7  4  6  5 19 16 18  8 17  1  3  0 15 22 20 23 14 10 12 11 21 13  9  2
 6  5  7  4  8 17 19 16 18  2  9  1 20 23 21 15 12 11 13 14 22 10  0  3
 4  7  5  6 16 18  8 17 19  3  0  2 21 15 22 20 13 14 10 12 23 11  1  9
10 15 13 11 21 22 20 23  4 16  6  8  3  1 14  2 19 17  9 18 12  0  7  5
11 12 10 15 23 20 22 21  5 17  7  4 14  2  0  3  9 18 16 19 13  1  8  6
15 13 11 12 22 21 23 20  6 18  8  5  0  3  1 14 16 19 17  9 10  2  4  7
12 10 15 13 20 23 21 22  7 19  4  6  1 14  2  0 17  9 18 16 11  3  5  8
13 11 12 10  1  3  0  2  9 14 17 19 22 20 23 21  6  4  7  5 15  8 18 16
17 19 16 18  5  7  4  6 15  8 21 23  2  0  3  1 10 12 11 13  9 14 22 20
18 14 17 19  2 15  1  3 20  4 13 10  7  5  9  6 23 21  8 22  0 16 11 12
19 16 18 14  3  0  2 15 21  5 11 12  9  6  4  7  8 22 20 23  1 17 13 10

Проверяю оба ЛК утилитой Harry White
Order? 24

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt

Counts
------
         2 Latin
         2 weakly pandiagonal
         1 orthogonal pair
         2 self-orthogonal

Что и требовалось получить.
ID: 1080 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1081 - Posted: 4 Jan 2021, 18:53:45 UTC
Last modified: 4 Jan 2021, 18:55:09 UTC

А как насчёт ортогональной пары слабо пандиагональных ЛК 27-го порядка?
Кажется, её тоже нет здесь.

Существует полная система MOLS 27-го порядка, состоящая из 26 ЛК.
Но у меня её тоже нет.
Может, кто-нибудь построит в Maple и выложит сюда?
Было бы здорово!

Однако в одной своей статье я нашла два ДЛК 27-го порядка из полной системы MOLS.
Это очень давно мне прислал друг, у которого был в то время Maple, а мне эти квадраты были нужны для исследования.
Сейчас я покажу эти ДЛК.
ID: 1081 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 1082 - Posted: 4 Jan 2021, 19:04:37 UTC
Last modified: 4 Jan 2021, 19:10:45 UTC

Смотрим мою статью
"ГРУППЫ ВЗАИМНО ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ
Mutually Orthogonal Latin Squares (MOLS)
Часть III"
http://www.natalimak1.narod.ru/grolk2.htm
В статье показаны 4 ЛК из полной системы MOLS 27-го порядка, первые два являются ЛК, а следующие два - ДЛК, вот они

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
3 4 5 6 7 8 0 1 2 12 13 14 15 16 17 9 10 11 21 22 23 24 25 26 18 19 20
6 7 8 0 1 2 3 4 5 15 16 17 9 10 11 12 13 14 24 25 26 18 19 20 21 22 23
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 0 1 2 3 4 5 6 7 8
12 13 14 15 16 17 9 10 11 21 22 23 24 25 26 18 19 20 3 4 5 6 7 8 0 1 2
15 16 17 9 10 11 12 13 14 24 25 26 18 19 20 21 22 23 6 7 8 0 1 2 3 4 5
18 19 20 21 22 23 24 25 26 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
21 22 23 24 25 26 18 19 20 3 4 5 6 7 8 0 1 2 12 13 14 15 16 17 9 10 11
24 25 26 18 19 20 21 22 23 6 7 8 0 1 2 3 4 5 15 16 17 9 10 11 12 13 14
13 14 12 16 17 15 10 11 9 22 23 21 25 26 24 19 20 18 4 5 3 7 8 6 1 2 0
16 17 15 10 11 9 13 14 12 25 26 24 19 20 18 22 23 21 7 8 6 1 2 0 4 5 3
10 11 9 13 14 12 16 17 15 19 20 18 22 23 21 25 26 24 1 2 0 4 5 3 7 8 6
22 23 21 25 26 24 19 20 18 4 5 3 7 8 6 1 2 0 13 14 12 16 17 15 10 11 9
25 26 24 19 20 18 22 23 21 7 8 6 1 2 0 4 5 3 16 17 15 10 11 9 13 14 12
19 20 18 22 23 21 25 26 24 1 2 0 4 5 3 7 8 6 10 11 9 13 14 12 16 17 15
4 5 3 7 8 6 1 2 0 13 14 12 16 17 15 10 11 9 22 23 21 25 26 24 19 20 18
7 8 6 1 2 0 4 5 3 16 17 15 10 11 9 13 14 12 25 26 24 19 20 18 22 23 21
1 2 0 4 5 3 7 8 6 10 11 9 13 14 12 16 17 15 19 20 18 22 23 21 25 26 24
26 24 25 20 18 19 23 21 22 8 6 7 2 0 1 5 3 4 17 15 16 11 9 10 14 12 13
20 18 19 23 21 22 26 24 25 2 0 1 5 3 4 8 6 7 11 9 10 14 12 13 17 15 16
23 21 22 26 24 25 20 18 19 5 3 4 8 6 7 2 0 1 14 12 13 17 15 16 11 9 10
8 6 7 2 0 1 5 3 4 17 15 16 11 9 10 14 12 13 26 24 25 20 18 19 23 21 22
2 0 1 5 3 4 8 6 7 11 9 10 14 12 13 17 15 16 20 18 19 23 21 22 26 24 25
5 3 4 8 6 7 2 0 1 14 12 13 17 15 16 11 9 10 23 21 22 26 24 25 20 18 19
17 15 16 11 9 10 14 12 13 26 24 25 20 18 19 23 21 22 8 6 7 2 0 1 5 3 4
11 9 10 14 12 13 17 15 16 20 18 19 23 21 22 26 24 25 2 0 1 5 3 4 8 6 7
14 12 13 17 15 16 11 9 10 23 21 22 26 24 25 20 18 19 5 3 4 8 6 7 2 0 1

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
4 5 3 7 8 6 1 2 0 13 14 12 16 17 15 10 11 9 22 23 21 25 26 24 19 20 18
8 6 7 2 0 1 5 3 4 17 15 16 11 9 10 14 12 13 26 24 25 20 18 19 23 21 22
12 13 14 15 16 17 9 10 11 21 22 23 24 25 26 18 19 20 3 4 5 6 7 8 0 1 2
16 17 15 10 11 9 13 14 12 25 26 24 19 20 18 22 23 21 7 8 6 1 2 0 4 5 3
11 9 10 14 12 13 17 15 16 20 18 19 23 21 22 26 24 25 2 0 1 5 3 4 8 6 7
24 25 26 18 19 20 21 22 23 6 7 8 0 1 2 3 4 5 15 16 17 9 10 11 12 13 14
19 20 18 22 23 21 25 26 24 1 2 0 4 5 3 7 8 6 10 11 9 13 14 12 16 17 15
23 21 22 26 24 25 20 18 19 5 3 4 8 6 7 2 0 1 14 12 13 17 15 16 11 9 10
22 23 21 25 26 24 19 20 18 4 5 3 7 8 6 1 2 0 13 14 12 16 17 15 10 11 9
26 24 25 20 18 19 23 21 22 8 6 7 2 0 1 5 3 4 17 15 16 11 9 10 14 12 13
18 19 20 21 22 23 24 25 26 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
7 8 6 1 2 0 4 5 3 16 17 15 10 11 9 13 14 12 25 26 24 19 20 18 22 23 21
2 0 1 5 3 4 8 6 7 11 9 10 14 12 13 17 15 16 20 18 19 23 21 22 26 24 25
3 4 5 6 7 8 0 1 2 12 13 14 15 16 17 9 10 11 21 22 23 24 25 26 18 19 20
10 11 9 13 14 12 16 17 15 19 20 18 22 23 21 25 26 24 1 2 0 4 5 3 7 8 6
14 12 13 17 15 16 11 9 10 23 21 22 26 24 25 20 18 19 5 3 4 8 6 7 2 0 1
15 16 17 9 10 11 12 13 14 24 25 26 18 19 20 21 22 23 6 7 8 0 1 2 3 4 5
17 15 16 11 9 10 14 12 13 26 24 25 20 18 19 23 21 22 8 6 7 2 0 1 5 3 4
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 0 1 2 3 4 5 6 7 8
13 14 12 16 17 15 10 11 9 22 23 21 25 26 24 19 20 18 4 5 3 7 8 6 1 2 0
20 18 19 23 21 22 26 24 25 2 0 1 5 3 4 8 6 7 11 9 10 14 12 13 17 15 16
21 22 23 24 25 26 18 19 20 3 4 5 6 7 8 0 1 2 12 13 14 15 16 17 9 10 11
25 26 24 19 20 18 22 23 21 7 8 6 1 2 0 4 5 3 16 17 15 10 11 9 13 14 12
5 3 4 8 6 7 2 0 1 14 12 13 17 15 16 11 9 10 23 21 22 26 24 25 20 18 19
6 7 8 0 1 2 3 4 5 15 16 17 9 10 11 12 13 14 24 25 26 18 19 20 21 22 23
1 2 0 4 5 3 7 8 6 10 11 9 13 14 12 16 17 15 19 20 18 22 23 21 25 26 24

Проверила их утилитой Harry White
Order? 27

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         2 diagonal Latin
         2 center symmetric
         2 nfr
         1 orthogonal pair
         2 self-orthogonal

Эти ДЛК не слабо пандиагональные.

Проверила два первых ЛК из полной системы MOLS, они тоже не слабо пандиагональные.
ID: 1082 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Previous · 1 · 2 · 3 · Next

Message boards : Science : Pandiagonal Latin squares

©2024 ©2024 Progger & Stefano Tognon (ice00) & Reese