Thread 'Pandiagonal Latin squares'
Message boards : Science : Pandiagonal Latin squares
Message board moderation
Previous · 1 · 2 · 3
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Тогда надо попробовать разложить на два ортогональных ЛК идеальный магичеÑкий квадрат 27-го порÑдка, поÑтроенный мной в Ñтатье http://www.klassikpoez.narod.ru/idealob11.htm "ИДЕÐЛЬÐЫЕ КВÐДРÐТЫ ЧаÑÑ‚ÑŒ XI" Показываю Ñтот квадрат  РаÑкладывать его буду завтра :) Рвы можете прÑмо ÑейчаÑ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПриÑматриваюÑÑŒ к идеальному квадратику 27-го порÑдка :) Увидела, что в начальной цепочке не раÑкраÑила одну Ñчейку (давно дело было, а вот только ÑÐµÐ¹Ñ‡Ð°Ñ ÑƒÐ²Ð¸Ð´ÐµÐ»Ð°), Ñодержащую чиÑло 25. ÐÐ°Ñ‡Ð°Ð»ÑŒÐ½Ð°Ñ Ñ†ÐµÐ¿Ð¾Ñ‡ÐºÐ° должна быть замкнутой. Она и еÑÑ‚ÑŒ замкнутаÑ, проÑто забылаÑÑŒ одна Ñчейка при раÑкраÑке начальной цепочки. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð½Ð°Ñ‡Ð½Ñƒ раÑкладывать Ñтот магичеÑкий квадрат на два ортогональных ЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Первый ЛК ортогональной пары, которую даёт показанный идеальный квадрат 27-го порÑдка, готов 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 Обратите внимание: квадрат поÑтроен методом цикличеÑкого Ñдвига. Ðедаром мой метод поÑÑ‚Ñ€Ð¾ÐµÐ½Ð¸Ñ Ð¸Ð´ÐµÐ°Ð»ÑŒÐ½Ñ‹Ñ… магичеÑких квадратов назван методом качелей. ПроверÑÑŽ ЛК утилитой Hqrry White Order? 27
Enter the name of the squares file: INP
.. writing type information to file INPTypeDetail_5.txt
Counts
------
1 Latin
1 weakly pandiagonal
1 center symmetric
Да, как и ожидалоÑÑŒ, ЛК Ñлабо пандиагональный. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ñтрою второй ЛК ортогональной пары. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Второй ЛК готов 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 7 22 20 1 21 24 26 0 2 5 25 6 4 3 7 11 8 10 12 9 13 17 14 16 18 15 19 23 7 11 8 10 12 9 13 17 14 16 18 15 19 23 22 20 1 21 24 26 0 2 5 25 6 4 3 ПроверÑÑŽ Ñразу оба ЛК поÑтроенной ортогональной пары утилитой Harry White Order? 27
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
2 Latin
2 weakly pandiagonal
2 center symmetric
1 orthogonal pairÐ’ÑÑ‘ отлично! ПоÑтроена Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° Ñлабо пандиагональных ЛК 27-го порÑдка. И помог в Ñтом идеальный магичеÑкий квадрат, поÑтроенный мной давным-давно. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Чтобы поÑтроить ортогональную пару Ñлабо пандиагональных ДЛК 40-го порÑдка методом ÑоÑтавных квадратов, возьмите Ñту ортогональную пару пандиагональных ДЛК 5-го порÑдка 0 1 2 3 4 3 4 0 1 2 1 2 3 4 0 4 0 1 2 3 2 3 4 0 1 0 1 2 3 4 2 3 4 0 1 4 0 1 2 3 1 2 3 4 0 3 4 0 1 2 и Ñту ортогональную пару Ñлабо пандиагональных ДЛК 8-го порÑдка 0 1 6 7 4 5 2 3 6 7 0 1 2 3 4 5 3 2 5 4 7 6 1 0 5 4 3 2 1 0 7 6 2 3 4 5 6 7 0 1 4 5 2 3 0 1 6 7 1 0 7 6 5 4 3 2 7 6 1 0 3 2 5 4 3 5 0 6 1 7 2 4 2 4 1 7 0 6 3 5 5 3 6 0 7 1 4 2 4 2 7 1 6 0 5 3 7 1 4 2 5 3 6 0 6 0 5 3 4 2 7 1 1 7 2 4 3 5 0 6 0 6 3 5 2 4 1 7 Попробуйте! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата Покажу иллюÑтрацию не цикличеÑкого пандиагонального ДЛК 13-го порÑдка, приведённого в OEIS Хотела найти Ñ…Ð¾Ñ‚Ñ Ð±Ñ‹ один ортогональный ДЛК к Ñтому ДЛК. Покрутила программу Белышева ortogon_u чаÑа два, ни одного ортогонального диагонального Ñоквадрата не нашлоÑÑŒ. Ðо он должен быть! Тогда применила к Ñтому ДЛК преобразование "Ñтроки - диагонали", найденное мной Ð´Ð»Ñ Ð¿Ð°Ð½Ð´Ð¸Ð°Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ñ‹Ñ… магичеÑких квадратов. Преобразование подробно опиÑано в моей книге "Волшебный мир магичеÑких квадратов" (выше дана ÑÑылка на Ñту книгу). Ðто преобразование превращает пандиагональный магичеÑкий квадрат в другой пандиагональный магичеÑкий квадрат. Я подумала, что преобразование должно работать и Ð´Ð»Ñ Ð»Ð°Ñ‚Ð¸Ð½Ñких квадратов. И оно работает! Показываю новый не цикличеÑкий пандиагональный ДЛК 13-го порÑдка, который Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»Ð° Ñ Ð¿Ð¾Ð¼Ð¾Ñ‰ÑŒÑŽ указанного Ð¿Ñ€ÐµÐ¾Ð±Ñ€Ð°Ð·Ð¾Ð²Ð°Ð½Ð¸Ñ 7 6 12 5 11 10 8 3 4 2 0 1 9 8 1 7 6 4 12 0 11 9 10 5 3 2 3 2 0 8 9 7 5 6 1 12 11 4 10 9 4 5 3 1 2 10 8 7 0 6 12 11 1 12 10 11 6 4 3 9 2 8 7 5 0 6 7 2 0 12 5 11 4 3 1 9 10 8 11 9 8 1 7 0 12 10 5 6 4 2 3 4 10 3 9 8 6 1 2 0 11 12 7 5 12 5 4 2 10 11 9 7 8 3 1 0 6 0 11 6 7 5 3 4 12 10 9 2 8 1 2 3 1 12 0 8 6 5 11 4 10 9 7 10 8 9 4 2 1 7 0 6 5 3 11 12 5 0 11 10 3 9 2 1 12 7 8 6 4 Проверила Ñти два ДЛК, они не изоморфны. Отлично! ЗапуÑтила проверку Ñтого ДЛК на ОДЛК, программа Белышева опÑÑ‚ÑŒ же работает. Ð’ÑÑ‘ ещё работает, ни одного Ñ€ÐµÑˆÐµÐ½Ð¸Ñ Ð½Ðµ найдено Проверка ДЛК13 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 1 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 11386 Соквадратов: 0 Ð’Ñ€ÐµÐ¼Ñ Ð² Ñек: 9340 776 83 99 22 6 2 Ðтот ДЛК имеет чуть больше Д-транÑверÑалей, чем иÑходный ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Выше Ñ ÑƒÐ¶Ðµ показала одну ортогональную пару Ñлабо пандиагональных ЛК 15-го порÑдка. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¼Ð½Ðµ попалаÑÑŒ ещё одна Ñ‚Ð°ÐºÐ°Ñ Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð°, причём очень древнÑÑ. Смотрим мою Ñтатью "ГРУППЫ ВЗÐИМÐО ОРТОГОÐÐЛЬÐЫХ ЛÐТИÐСКИХ КВÐДРÐТОВ Mutually Orthogonal Latin squares (MOLS)" http://www.natalimak1.narod.ru/grolk.htm Цитирую Ðа форуме dxdy.ru в теме “МагичеÑкие квадраты†выложен очень интереÑный цикл Ñтатей “ÐÐ½Ð°Ñ‚Ð¾Ð¼Ð¸Ñ Ð¼Ð°Ð³Ð¸Ñ‡ÐµÑких квадратов†из журнала “Recreational Mathematics†(Ñпешите Ñкачать!). Цикл Ñтатей отноÑитÑÑ Ðº 1938 - 1945 гг. Добавлю, что цикл Ñтатей выложил коллега Ðœ. ÐлекÑеев. Ðтот цикл был выложен мной на ЯндекÑ.ДиÑк. Обратите внимание на годы публикаций! Квадратики очень краÑивые (Ñмотрите в Ñтатье иллюÑтрации; на риÑ. 21 Ð¾Ñ€Ð¸Ð³Ð¸Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¸Ð»Ð»ÑŽÑÑ‚Ñ€Ð°Ñ†Ð¸Ñ Ð¸Ð· журнала) 0 1 8 7 6 13 14 12 3 4 5 9 10 11 2 3 4 5 9 10 11 2 0 1 8 7 6 13 14 12 1 8 7 6 13 14 12 3 4 5 9 10 11 2 0 4 5 9 10 11 2 0 1 8 7 6 13 14 12 3 8 7 6 13 14 12 3 4 5 9 10 11 2 0 1 5 9 10 11 2 0 1 8 7 6 13 14 12 3 4 7 6 13 14 12 3 4 5 9 10 11 2 0 1 8 9 10 11 2 0 1 8 7 6 13 14 12 3 4 5 6 13 14 12 3 4 5 9 10 11 2 0 1 8 7 10 11 2 0 1 8 7 6 13 14 12 3 4 5 9 13 14 12 3 4 5 9 10 11 2 0 1 8 7 6 11 2 0 1 8 7 6 13 14 12 3 4 5 9 10 14 12 3 4 5 9 10 11 2 0 1 8 7 6 13 2 0 1 8 7 6 13 14 12 3 4 5 9 10 11 12 3 4 5 9 10 11 2 0 1 8 7 6 13 14 0 9 10 11 3 4 5 14 12 13 8 7 6 1 2 14 12 13 8 7 6 1 2 0 9 10 11 3 4 5 2 0 9 10 11 3 4 5 14 12 13 8 7 6 1 5 14 12 13 8 7 6 1 2 0 9 10 11 3 4 1 2 0 9 10 11 3 4 5 14 12 13 8 7 6 4 5 14 12 13 8 7 6 1 2 0 9 10 11 3 6 1 2 0 9 10 11 3 4 5 14 12 13 8 7 3 4 5 14 12 13 8 7 6 1 2 0 9 10 11 7 6 1 2 0 9 10 11 3 4 5 14 12 13 8 11 3 4 5 14 12 13 8 7 6 1 2 0 9 10 8 7 6 1 2 0 9 10 11 3 4 5 14 12 13 10 11 3 4 5 14 12 13 8 7 6 1 2 0 9 13 8 7 6 1 2 0 9 10 11 3 4 5 14 12 9 10 11 3 4 5 14 12 13 8 7 6 1 2 0 12 13 8 7 6 1 2 0 9 10 11 3 4 5 14 ПроверÑÑŽ утилитой Harry White Order? 15
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
2 Latin
2 weakly pandiagonal
2 center symmetric
1 orthogonal pair |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата ЗапуÑтила проверку Ñтого ДЛК на ОДЛК, программа Белышева опÑÑ‚ÑŒ же работает. Ð’ÑÑ‘ работает программа, и ни одного решениÑ! Проверка ДЛК13 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 1 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 11386 Соквадратов: 0 Ð’Ñ€ÐµÐ¼Ñ Ð² Ñек: 23795 751 239 2 15 9 1 Прерываю. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата С ортогональной парой Ñлабо пандиагональных ЛК 21-го порÑдка повезло. Ð ÑÐµÐ¹Ñ‡Ð°Ñ ÑƒÐ²Ð¸Ð´ÐµÐ»Ð° в другой Ñтатье очень краÑивый Ñлабо пандиагональный ЛК 21-го порÑдка. И раÑкладывать не надо, уже готовый ЛК. ПоÑтроен по алгоритму, взÑтому из Ñборника "ÐÐ½Ð°Ñ‚Ð¾Ð¼Ð¸Ñ Ð¼Ð°Ð³Ð¸Ñ‡ÐµÑких квадратов". Смотрим мою Ñтатью "ГРУППЫ ВЗÐИМÐО ОРТОГОÐÐЛЬÐЫХ ЛÐТИÐСКИХ КВÐДРÐТОВ ÐЕЧÐТÐОГО ПОРЯДКРили ÐОВЫЕ ÐСПЕКТЫ МЕТОДРЛÐТИÐСКИХ КВÐДРÐТОВ ЧаÑÑ‚ÑŒ VII" http://www.natalimak1.narod.ru/grolk3.htm ЛК 21-го порÑдка изображён на риÑ. 15. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ñ ÐµÐ³Ð¾ покажу тут. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вот он какой краÑивый 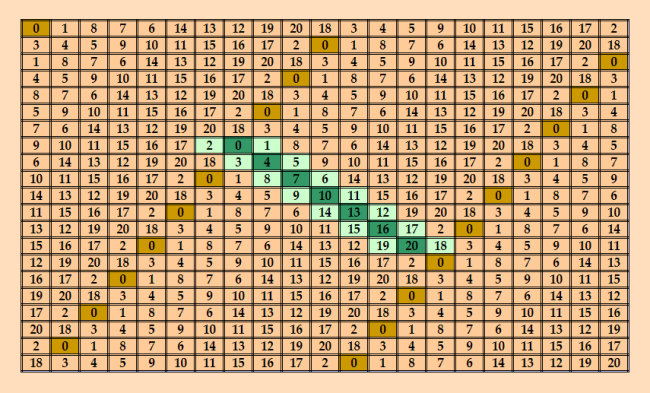 Обратите внимание: ЛК поÑтроен методом цикличеÑкого Ñдвига. Далее в Ñтатье показан ортогональный ЛК к Ñтому ЛК (Ñмотрите риÑ. 16). Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾ÐºÐ°Ð¶Ñƒ оба ЛК в обычном виде и проверю их утилитой Harry Whine. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðто Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° Ñлабо пандиагональных ЛК 21-го порÑдка (алгоритм поÑÑ‚Ñ€Ð¾ÐµÐ½Ð¸Ñ Ð¸Ð· Ñередины прошлого века!) 0 1 8 7 6 14 13 12 19 20 18 3 4 5 9 10 11 15 16 17 2 3 4 5 9 10 11 15 16 17 2 0 1 8 7 6 14 13 12 19 20 18 1 8 7 6 14 13 12 19 20 18 3 4 5 9 10 11 15 16 17 2 0 4 5 9 10 11 15 16 17 2 0 1 8 7 6 14 13 12 19 20 18 3 8 7 6 14 13 12 19 20 18 3 4 5 9 10 11 15 16 17 2 0 1 5 9 10 11 15 16 17 2 0 1 8 7 6 14 13 12 19 20 18 3 4 7 6 14 13 12 19 20 18 3 4 5 9 10 11 15 16 17 2 0 1 8 9 10 11 15 16 17 2 0 1 8 7 6 14 13 12 19 20 18 3 4 5 6 14 13 12 19 20 18 3 4 5 9 10 11 15 16 17 2 0 1 8 7 10 11 15 16 17 2 0 1 8 7 6 14 13 12 19 20 18 3 4 5 9 14 13 12 19 20 18 3 4 5 9 10 11 15 16 17 2 0 1 8 7 6 11 15 16 17 2 0 1 8 7 6 14 13 12 19 20 18 3 4 5 9 10 13 12 19 20 18 3 4 5 9 10 11 15 16 17 2 0 1 8 7 6 14 15 16 17 2 0 1 8 7 6 14 13 12 19 20 18 3 4 5 9 10 11 12 19 20 18 3 4 5 9 10 11 15 16 17 2 0 1 8 7 6 14 13 16 17 2 0 1 8 7 6 14 13 12 19 20 18 3 4 5 9 10 11 15 19 20 18 3 4 5 9 10 11 15 16 17 2 0 1 8 7 6 14 13 12 17 2 0 1 8 7 6 14 13 12 19 20 18 3 4 5 9 10 11 15 16 20 18 3 4 5 9 10 11 15 16 17 2 0 1 8 7 6 14 13 12 19 2 0 1 8 7 6 14 13 12 19 20 18 3 4 5 9 10 11 15 16 17 18 3 4 5 9 10 11 15 16 17 2 0 1 8 7 6 14 13 12 19 20 0 15 16 17 9 10 11 3 4 5 20 18 19 14 13 12 8 7 6 1 2 20 18 19 14 13 12 8 7 6 1 2 0 15 16 17 9 10 11 3 4 5 2 0 15 16 17 9 10 11 3 4 5 20 18 19 14 13 12 8 7 6 1 5 20 18 19 14 13 12 8 7 6 1 2 0 15 16 17 9 10 11 3 4 1 2 0 15 16 17 9 10 11 3 4 5 20 18 19 14 13 12 8 7 6 4 5 20 18 19 14 13 12 8 7 6 1 2 0 15 16 17 9 10 11 3 6 1 2 0 15 16 17 9 10 11 3 4 5 20 18 19 14 13 12 8 7 3 4 5 20 18 19 14 13 12 8 7 6 1 2 0 15 16 17 9 10 11 7 6 1 2 0 15 16 17 9 10 11 3 4 5 20 18 19 14 13 12 8 11 3 4 5 20 18 19 14 13 12 8 7 6 1 2 0 15 16 17 9 10 8 7 6 1 2 0 15 16 17 9 10 11 3 4 5 20 18 19 14 13 12 10 11 3 4 5 20 18 19 14 13 12 8 7 6 1 2 0 15 16 17 9 12 8 7 6 1 2 0 15 16 17 9 10 11 3 4 5 20 18 19 14 13 9 10 11 3 4 5 20 18 19 14 13 12 8 7 6 1 2 0 15 16 17 13 12 8 7 6 1 2 0 15 16 17 9 10 11 3 4 5 20 18 19 14 17 9 10 11 3 4 5 20 18 19 14 13 12 8 7 6 1 2 0 15 16 14 13 12 8 7 6 1 2 0 15 16 17 9 10 11 3 4 5 20 18 19 16 17 9 10 11 3 4 5 20 18 19 14 13 12 8 7 6 1 2 0 15 19 14 13 12 8 7 6 1 2 0 15 16 17 9 10 11 3 4 5 20 18 15 16 17 9 10 11 3 4 5 20 18 19 14 13 12 8 7 6 1 2 0 18 19 14 13 12 8 7 6 1 2 0 15 16 17 9 10 11 3 4 5 20 ПроверÑÑŽ ЛК утилитой Harry White Order? 21
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
2 Latin
2 weakly pandiagonal
2 center symmetric
1 orthogonal pairÐ’ÑÑ‘ замечательно! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðто не цикличеÑкий пандиагональный ДЛК 13-го порÑдка, который Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»Ð° Ñ Ð¿Ð¾Ð¼Ð¾Ñ‰ÑŒÑŽ Ð¿Ñ€ÐµÐ¾Ð±Ñ€Ð°Ð·Ð¾Ð²Ð°Ð½Ð¸Ñ "Ñтроки - диагонали" из квадрата, приведённого в Ñтатье OEIS https://oeis.org/A338620 7 6 12 5 11 10 8 3 4 2 0 1 9 8 1 7 6 4 12 0 11 9 10 5 3 2 3 2 0 8 9 7 5 6 1 12 11 4 10 9 4 5 3 1 2 10 8 7 0 6 12 11 1 12 10 11 6 4 3 9 2 8 7 5 0 6 7 2 0 12 5 11 4 3 1 9 10 8 11 9 8 1 7 0 12 10 5 6 4 2 3 4 10 3 9 8 6 1 2 0 11 12 7 5 12 5 4 2 10 11 9 7 8 3 1 0 6 0 11 6 7 5 3 4 12 10 9 2 8 1 2 3 1 12 0 8 6 5 11 4 10 9 7 10 8 9 4 2 1 7 0 6 5 3 11 12 5 0 11 10 3 9 2 1 12 7 8 6 4 Жаль, что не нашла к Ñтому ДЛК ортогональный ДЛК. Он должен быть, так как ДЛК пандиагональный. ЕÑли мы возьмём Ñтот ДЛК и Ñлабо пандиагональный ДЛК 4-го порÑдка и на их оÑнове поÑтроим ДЛК 52-го порÑдка методом ÑоÑтавных квадратов, Ñтот ДЛК получитÑÑ Ñлабо пандиагональный. ЕÑли мы на оÑнове Ñтого ДЛК и пандиагонального ДЛК 5-го порÑдка поÑтроим ДЛК 65-го порÑдка методом ÑоÑтавных квадратов, получим не цикличеÑкий пандиагональный ДЛК 65-го порÑдка. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÑŽ Ñто поÑтроение. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’Ñтречайте - не цикличеÑкий пандиагональный ДЛК 65-го порÑдка 7 6 12 5 11 10 8 3 4 2 0 1 9 20 19 25 18 24 23 21 16 17 15 13 14 22 33 32 38 31 37 36 34 29 30 28 26 27 35 46 45 51 44 50 49 47 42 43 41 39 40 48 59 58 64 57 63 62 60 55 56 54 52 53 61 8 1 7 6 4 12 0 11 9 10 5 3 2 21 14 20 19 17 25 13 24 22 23 18 16 15 34 27 33 32 30 38 26 37 35 36 31 29 28 47 40 46 45 43 51 39 50 48 49 44 42 41 60 53 59 58 56 64 52 63 61 62 57 55 54 3 2 0 8 9 7 5 6 1 12 11 4 10 16 15 13 21 22 20 18 19 14 25 24 17 23 29 28 26 34 35 33 31 32 27 38 37 30 36 42 41 39 47 48 46 44 45 40 51 50 43 49 55 54 52 60 61 59 57 58 53 64 63 56 62 9 4 5 3 1 2 10 8 7 0 6 12 11 22 17 18 16 14 15 23 21 20 13 19 25 24 35 30 31 29 27 28 36 34 33 26 32 38 37 48 43 44 42 40 41 49 47 46 39 45 51 50 61 56 57 55 53 54 62 60 59 52 58 64 63 1 12 10 11 6 4 3 9 2 8 7 5 0 14 25 23 24 19 17 16 22 15 21 20 18 13 27 38 36 37 32 30 29 35 28 34 33 31 26 40 51 49 50 45 43 42 48 41 47 46 44 39 53 64 62 63 58 56 55 61 54 60 59 57 52 6 7 2 0 12 5 11 4 3 1 9 10 8 19 20 15 13 25 18 24 17 16 14 22 23 21 32 33 28 26 38 31 37 30 29 27 35 36 34 45 46 41 39 51 44 50 43 42 40 48 49 47 58 59 54 52 64 57 63 56 55 53 61 62 60 11 9 8 1 7 0 12 10 5 6 4 2 3 24 22 21 14 20 13 25 23 18 19 17 15 16 37 35 34 27 33 26 38 36 31 32 30 28 29 50 48 47 40 46 39 51 49 44 45 43 41 42 63 61 60 53 59 52 64 62 57 58 56 54 55 4 10 3 9 8 6 1 2 0 11 12 7 5 17 23 16 22 21 19 14 15 13 24 25 20 18 30 36 29 35 34 32 27 28 26 37 38 33 31 43 49 42 48 47 45 40 41 39 50 51 46 44 56 62 55 61 60 58 53 54 52 63 64 59 57 12 5 4 2 10 11 9 7 8 3 1 0 6 25 18 17 15 23 24 22 20 21 16 14 13 19 38 31 30 28 36 37 35 33 34 29 27 26 32 51 44 43 41 49 50 48 46 47 42 40 39 45 64 57 56 54 62 63 61 59 60 55 53 52 58 0 11 6 7 5 3 4 12 10 9 2 8 1 13 24 19 20 18 16 17 25 23 22 15 21 14 26 37 32 33 31 29 30 38 36 35 28 34 27 39 50 45 46 44 42 43 51 49 48 41 47 40 52 63 58 59 57 55 56 64 62 61 54 60 53 2 3 1 12 0 8 6 5 11 4 10 9 7 15 16 14 25 13 21 19 18 24 17 23 22 20 28 29 27 38 26 34 32 31 37 30 36 35 33 41 42 40 51 39 47 45 44 50 43 49 48 46 54 55 53 64 52 60 58 57 63 56 62 61 59 10 8 9 4 2 1 7 0 6 5 3 11 12 23 21 22 17 15 14 20 13 19 18 16 24 25 36 34 35 30 28 27 33 26 32 31 29 37 38 49 47 48 43 41 40 46 39 45 44 42 50 51 62 60 61 56 54 53 59 52 58 57 55 63 64 5 0 11 10 3 9 2 1 12 7 8 6 4 18 13 24 23 16 22 15 14 25 20 21 19 17 31 26 37 36 29 35 28 27 38 33 34 32 30 44 39 50 49 42 48 41 40 51 46 47 45 43 57 52 63 62 55 61 54 53 64 59 60 58 56 33 32 38 31 37 36 34 29 30 28 26 27 35 46 45 51 44 50 49 47 42 43 41 39 40 48 59 58 64 57 63 62 60 55 56 54 52 53 61 7 6 12 5 11 10 8 3 4 2 0 1 9 20 19 25 18 24 23 21 16 17 15 13 14 22 34 27 33 32 30 38 26 37 35 36 31 29 28 47 40 46 45 43 51 39 50 48 49 44 42 41 60 53 59 58 56 64 52 63 61 62 57 55 54 8 1 7 6 4 12 0 11 9 10 5 3 2 21 14 20 19 17 25 13 24 22 23 18 16 15 29 28 26 34 35 33 31 32 27 38 37 30 36 42 41 39 47 48 46 44 45 40 51 50 43 49 55 54 52 60 61 59 57 58 53 64 63 56 62 3 2 0 8 9 7 5 6 1 12 11 4 10 16 15 13 21 22 20 18 19 14 25 24 17 23 35 30 31 29 27 28 36 34 33 26 32 38 37 48 43 44 42 40 41 49 47 46 39 45 51 50 61 56 57 55 53 54 62 60 59 52 58 64 63 9 4 5 3 1 2 10 8 7 0 6 12 11 22 17 18 16 14 15 23 21 20 13 19 25 24 27 38 36 37 32 30 29 35 28 34 33 31 26 40 51 49 50 45 43 42 48 41 47 46 44 39 53 64 62 63 58 56 55 61 54 60 59 57 52 1 12 10 11 6 4 3 9 2 8 7 5 0 14 25 23 24 19 17 16 22 15 21 20 18 13 32 33 28 26 38 31 37 30 29 27 35 36 34 45 46 41 39 51 44 50 43 42 40 48 49 47 58 59 54 52 64 57 63 56 55 53 61 62 60 6 7 2 0 12 5 11 4 3 1 9 10 8 19 20 15 13 25 18 24 17 16 14 22 23 21 37 35 34 27 33 26 38 36 31 32 30 28 29 50 48 47 40 46 39 51 49 44 45 43 41 42 63 61 60 53 59 52 64 62 57 58 56 54 55 11 9 8 1 7 0 12 10 5 6 4 2 3 24 22 21 14 20 13 25 23 18 19 17 15 16 30 36 29 35 34 32 27 28 26 37 38 33 31 43 49 42 48 47 45 40 41 39 50 51 46 44 56 62 55 61 60 58 53 54 52 63 64 59 57 4 10 3 9 8 6 1 2 0 11 12 7 5 17 23 16 22 21 19 14 15 13 24 25 20 18 38 31 30 28 36 37 35 33 34 29 27 26 32 51 44 43 41 49 50 48 46 47 42 40 39 45 64 57 56 54 62 63 61 59 60 55 53 52 58 12 5 4 2 10 11 9 7 8 3 1 0 6 25 18 17 15 23 24 22 20 21 16 14 13 19 26 37 32 33 31 29 30 38 36 35 28 34 27 39 50 45 46 44 42 43 51 49 48 41 47 40 52 63 58 59 57 55 56 64 62 61 54 60 53 0 11 6 7 5 3 4 12 10 9 2 8 1 13 24 19 20 18 16 17 25 23 22 15 21 14 28 29 27 38 26 34 32 31 37 30 36 35 33 41 42 40 51 39 47 45 44 50 43 49 48 46 54 55 53 64 52 60 58 57 63 56 62 61 59 2 3 1 12 0 8 6 5 11 4 10 9 7 15 16 14 25 13 21 19 18 24 17 23 22 20 36 34 35 30 28 27 33 26 32 31 29 37 38 49 47 48 43 41 40 46 39 45 44 42 50 51 62 60 61 56 54 53 59 52 58 57 55 63 64 10 8 9 4 2 1 7 0 6 5 3 11 12 23 21 22 17 15 14 20 13 19 18 16 24 25 31 26 37 36 29 35 28 27 38 33 34 32 30 44 39 50 49 42 48 41 40 51 46 47 45 43 57 52 63 62 55 61 54 53 64 59 60 58 56 5 0 11 10 3 9 2 1 12 7 8 6 4 18 13 24 23 16 22 15 14 25 20 21 19 17 59 58 64 57 63 62 60 55 56 54 52 53 61 7 6 12 5 11 10 8 3 4 2 0 1 9 20 19 25 18 24 23 21 16 17 15 13 14 22 33 32 38 31 37 36 34 29 30 28 26 27 35 46 45 51 44 50 49 47 42 43 41 39 40 48 60 53 59 58 56 64 52 63 61 62 57 55 54 8 1 7 6 4 12 0 11 9 10 5 3 2 21 14 20 19 17 25 13 24 22 23 18 16 15 34 27 33 32 30 38 26 37 35 36 31 29 28 47 40 46 45 43 51 39 50 48 49 44 42 41 55 54 52 60 61 59 57 58 53 64 63 56 62 3 2 0 8 9 7 5 6 1 12 11 4 10 16 15 13 21 22 20 18 19 14 25 24 17 23 29 28 26 34 35 33 31 32 27 38 37 30 36 42 41 39 47 48 46 44 45 40 51 50 43 49 61 56 57 55 53 54 62 60 59 52 58 64 63 9 4 5 3 1 2 10 8 7 0 6 12 11 22 17 18 16 14 15 23 21 20 13 19 25 24 35 30 31 29 27 28 36 34 33 26 32 38 37 48 43 44 42 40 41 49 47 46 39 45 51 50 53 64 62 63 58 56 55 61 54 60 59 57 52 1 12 10 11 6 4 3 9 2 8 7 5 0 14 25 23 24 19 17 16 22 15 21 20 18 13 27 38 36 37 32 30 29 35 28 34 33 31 26 40 51 49 50 45 43 42 48 41 47 46 44 39 58 59 54 52 64 57 63 56 55 53 61 62 60 6 7 2 0 12 5 11 4 3 1 9 10 8 19 20 15 13 25 18 24 17 16 14 22 23 21 32 33 28 26 38 31 37 30 29 27 35 36 34 45 46 41 39 51 44 50 43 42 40 48 49 47 63 61 60 53 59 52 64 62 57 58 56 54 55 11 9 8 1 7 0 12 10 5 6 4 2 3 24 22 21 14 20 13 25 23 18 19 17 15 16 37 35 34 27 33 26 38 36 31 32 30 28 29 50 48 47 40 46 39 51 49 44 45 43 41 42 56 62 55 61 60 58 53 54 52 63 64 59 57 4 10 3 9 8 6 1 2 0 11 12 7 5 17 23 16 22 21 19 14 15 13 24 25 20 18 30 36 29 35 34 32 27 28 26 37 38 33 31 43 49 42 48 47 45 40 41 39 50 51 46 44 64 57 56 54 62 63 61 59 60 55 53 52 58 12 5 4 2 10 11 9 7 8 3 1 0 6 25 18 17 15 23 24 22 20 21 16 14 13 19 38 31 30 28 36 37 35 33 34 29 27 26 32 51 44 43 41 49 50 48 46 47 42 40 39 45 52 63 58 59 57 55 56 64 62 61 54 60 53 0 11 6 7 5 3 4 12 10 9 2 8 1 13 24 19 20 18 16 17 25 23 22 15 21 14 26 37 32 33 31 29 30 38 36 35 28 34 27 39 50 45 46 44 42 43 51 49 48 41 47 40 54 55 53 64 52 60 58 57 63 56 62 61 59 2 3 1 12 0 8 6 5 11 4 10 9 7 15 16 14 25 13 21 19 18 24 17 23 22 20 28 29 27 38 26 34 32 31 37 30 36 35 33 41 42 40 51 39 47 45 44 50 43 49 48 46 62 60 61 56 54 53 59 52 58 57 55 63 64 10 8 9 4 2 1 7 0 6 5 3 11 12 23 21 22 17 15 14 20 13 19 18 16 24 25 36 34 35 30 28 27 33 26 32 31 29 37 38 49 47 48 43 41 40 46 39 45 44 42 50 51 57 52 63 62 55 61 54 53 64 59 60 58 56 5 0 11 10 3 9 2 1 12 7 8 6 4 18 13 24 23 16 22 15 14 25 20 21 19 17 31 26 37 36 29 35 28 27 38 33 34 32 30 44 39 50 49 42 48 41 40 51 46 47 45 43 20 19 25 18 24 23 21 16 17 15 13 14 22 33 32 38 31 37 36 34 29 30 28 26 27 35 46 45 51 44 50 49 47 42 43 41 39 40 48 59 58 64 57 63 62 60 55 56 54 52 53 61 7 6 12 5 11 10 8 3 4 2 0 1 9 21 14 20 19 17 25 13 24 22 23 18 16 15 34 27 33 32 30 38 26 37 35 36 31 29 28 47 40 46 45 43 51 39 50 48 49 44 42 41 60 53 59 58 56 64 52 63 61 62 57 55 54 8 1 7 6 4 12 0 11 9 10 5 3 2 16 15 13 21 22 20 18 19 14 25 24 17 23 29 28 26 34 35 33 31 32 27 38 37 30 36 42 41 39 47 48 46 44 45 40 51 50 43 49 55 54 52 60 61 59 57 58 53 64 63 56 62 3 2 0 8 9 7 5 6 1 12 11 4 10 22 17 18 16 14 15 23 21 20 13 19 25 24 35 30 31 29 27 28 36 34 33 26 32 38 37 48 43 44 42 40 41 49 47 46 39 45 51 50 61 56 57 55 53 54 62 60 59 52 58 64 63 9 4 5 3 1 2 10 8 7 0 6 12 11 14 25 23 24 19 17 16 22 15 21 20 18 13 27 38 36 37 32 30 29 35 28 34 33 31 26 40 51 49 50 45 43 42 48 41 47 46 44 39 53 64 62 63 58 56 55 61 54 60 59 57 52 1 12 10 11 6 4 3 9 2 8 7 5 0 19 20 15 13 25 18 24 17 16 14 22 23 21 32 33 28 26 38 31 37 30 29 27 35 36 34 45 46 41 39 51 44 50 43 42 40 48 49 47 58 59 54 52 64 57 63 56 55 53 61 62 60 6 7 2 0 12 5 11 4 3 1 9 10 8 24 22 21 14 20 13 25 23 18 19 17 15 16 37 35 34 27 33 26 38 36 31 32 30 28 29 50 48 47 40 46 39 51 49 44 45 43 41 42 63 61 60 53 59 52 64 62 57 58 56 54 55 11 9 8 1 7 0 12 10 5 6 4 2 3 17 23 16 22 21 19 14 15 13 24 25 20 18 30 36 29 35 34 32 27 28 26 37 38 33 31 43 49 42 48 47 45 40 41 39 50 51 46 44 56 62 55 61 60 58 53 54 52 63 64 59 57 4 10 3 9 8 6 1 2 0 11 12 7 5 25 18 17 15 23 24 22 20 21 16 14 13 19 38 31 30 28 36 37 35 33 34 29 27 26 32 51 44 43 41 49 50 48 46 47 42 40 39 45 64 57 56 54 62 63 61 59 60 55 53 52 58 12 5 4 2 10 11 9 7 8 3 1 0 6 13 24 19 20 18 16 17 25 23 22 15 21 14 26 37 32 33 31 29 30 38 36 35 28 34 27 39 50 45 46 44 42 43 51 49 48 41 47 40 52 63 58 59 57 55 56 64 62 61 54 60 53 0 11 6 7 5 3 4 12 10 9 2 8 1 15 16 14 25 13 21 19 18 24 17 23 22 20 28 29 27 38 26 34 32 31 37 30 36 35 33 41 42 40 51 39 47 45 44 50 43 49 48 46 54 55 53 64 52 60 58 57 63 56 62 61 59 2 3 1 12 0 8 6 5 11 4 10 9 7 23 21 22 17 15 14 20 13 19 18 16 24 25 36 34 35 30 28 27 33 26 32 31 29 37 38 49 47 48 43 41 40 46 39 45 44 42 50 51 62 60 61 56 54 53 59 52 58 57 55 63 64 10 8 9 4 2 1 7 0 6 5 3 11 12 18 13 24 23 16 22 15 14 25 20 21 19 17 31 26 37 36 29 35 28 27 38 33 34 32 30 44 39 50 49 42 48 41 40 51 46 47 45 43 57 52 63 62 55 61 54 53 64 59 60 58 56 5 0 11 10 3 9 2 1 12 7 8 6 4 46 45 51 44 50 49 47 42 43 41 39 40 48 59 58 64 57 63 62 60 55 56 54 52 53 61 7 6 12 5 11 10 8 3 4 2 0 1 9 20 19 25 18 24 23 21 16 17 15 13 14 22 33 32 38 31 37 36 34 29 30 28 26 27 35 47 40 46 45 43 51 39 50 48 49 44 42 41 60 53 59 58 56 64 52 63 61 62 57 55 54 8 1 7 6 4 12 0 11 9 10 5 3 2 21 14 20 19 17 25 13 24 22 23 18 16 15 34 27 33 32 30 38 26 37 35 36 31 29 28 42 41 39 47 48 46 44 45 40 51 50 43 49 55 54 52 60 61 59 57 58 53 64 63 56 62 3 2 0 8 9 7 5 6 1 12 11 4 10 16 15 13 21 22 20 18 19 14 25 24 17 23 29 28 26 34 35 33 31 32 27 38 37 30 36 48 43 44 42 40 41 49 47 46 39 45 51 50 61 56 57 55 53 54 62 60 59 52 58 64 63 9 4 5 3 1 2 10 8 7 0 6 12 11 22 17 18 16 14 15 23 21 20 13 19 25 24 35 30 31 29 27 28 36 34 33 26 32 38 37 40 51 49 50 45 43 42 48 41 47 46 44 39 53 64 62 63 58 56 55 61 54 60 59 57 52 1 12 10 11 6 4 3 9 2 8 7 5 0 14 25 23 24 19 17 16 22 15 21 20 18 13 27 38 36 37 32 30 29 35 28 34 33 31 26 45 46 41 39 51 44 50 43 42 40 48 49 47 58 59 54 52 64 57 63 56 55 53 61 62 60 6 7 2 0 12 5 11 4 3 1 9 10 8 19 20 15 13 25 18 24 17 16 14 22 23 21 32 33 28 26 38 31 37 30 29 27 35 36 34 50 48 47 40 46 39 51 49 44 45 43 41 42 63 61 60 53 59 52 64 62 57 58 56 54 55 11 9 8 1 7 0 12 10 5 6 4 2 3 24 22 21 14 20 13 25 23 18 19 17 15 16 37 35 34 27 33 26 38 36 31 32 30 28 29 43 49 42 48 47 45 40 41 39 50 51 46 44 56 62 55 61 60 58 53 54 52 63 64 59 57 4 10 3 9 8 6 1 2 0 11 12 7 5 17 23 16 22 21 19 14 15 13 24 25 20 18 30 36 29 35 34 32 27 28 26 37 38 33 31 51 44 43 41 49 50 48 46 47 42 40 39 45 64 57 56 54 62 63 61 59 60 55 53 52 58 12 5 4 2 10 11 9 7 8 3 1 0 6 25 18 17 15 23 24 22 20 21 16 14 13 19 38 31 30 28 36 37 35 33 34 29 27 26 32 39 50 45 46 44 42 43 51 49 48 41 47 40 52 63 58 59 57 55 56 64 62 61 54 60 53 0 11 6 7 5 3 4 12 10 9 2 8 1 13 24 19 20 18 16 17 25 23 22 15 21 14 26 37 32 33 31 29 30 38 36 35 28 34 27 41 42 40 51 39 47 45 44 50 43 49 48 46 54 55 53 64 52 60 58 57 63 56 62 61 59 2 3 1 12 0 8 6 5 11 4 10 9 7 15 16 14 25 13 21 19 18 24 17 23 22 20 28 29 27 38 26 34 32 31 37 30 36 35 33 49 47 48 43 41 40 46 39 45 44 42 50 51 62 60 61 56 54 53 59 52 58 57 55 63 64 10 8 9 4 2 1 7 0 6 5 3 11 12 23 21 22 17 15 14 20 13 19 18 16 24 25 36 34 35 30 28 27 33 26 32 31 29 37 38 44 39 50 49 42 48 41 40 51 46 47 45 43 57 52 63 62 55 61 54 53 64 59 60 58 56 5 0 11 10 3 9 2 1 12 7 8 6 4 18 13 24 23 16 22 15 14 25 20 21 19 17 31 26 37 36 29 35 28 27 38 33 34 32 3019 18 24 17 23 22 20 28 29 27 38 26 34 32 31 37 30 36 35 33 41 42 40 51 39 47 45 44 50 43 49 48 46 62 60 61 56 54 53 59 52 58 57 55 63 64 10 8 9 4 2 1 7 0 6 5 3 11 12 23 21 22 17 15 14 20 13 19 18 16 24 25 36 34 35 30 28 27 33 26 32 31 29 37 38 49 47 48 43 41 40 46 39 45 44 42 50 51 57 52 63 62 55 61 54 53 64 59 60 58 56 5 0 11 10 3 9 2 1 12 7 8 6 4 18 13 24 23 16 22 15 14 25 20 21 19 17 31 26 37 36 29 35 28 27 38 33 34 32 30 44 39 50 49 42 48 41 40 51 46 47 45 43 20 19 25 18 24 23 21 16 17 15 13 14 22 33 32 38 31 37 36 34 29 30 28 26 27 35 46 45 51 44 50 49 47 42 43 41 39 40 48 59 58 64 57 63 62 60 55 56 54 52 53 61 7 6 12 5 11 10 8 3 4 2 0 1 9 21 14 20 19 17 25 13 24 22 23 18 16 15 34 27 33 32 30 38 26 37 35 36 31 29 28 47 40 46 45 43 51 39 50 48 49 44 42 41 60 53 59 58 56 64 52 63 61 62 57 55 54 8 1 7 6 4 12 0 11 9 10 5 3 2 16 15 13 21 22 20 18 19 14 25 24 17 23 29 28 26 34 35 33 31 32 27 38 37 30 36 42 41 39 47 48 46 44 45 40 51 50 43 49 55 54 52 60 61 59 57 58 53 64 63 56 62 3 2 0 8 9 7 5 6 1 12 11 4 10 22 17 18 16 14 15 23 21 20 13 19 25 24 35 30 31 29 27 28 36 34 33 26 32 38 37 48 43 44 42 40 41 49 47 46 39 45 51 50 61 56 57 55 53 54 62 60 59 52 58 64 63 9 4 5 3 1 2 10 8 7 0 6 12 11 14 25 23 24 19 17 16 22 15 21 20 18 13 27 38 36 37 32 30 29 35 28 34 33 31 26 40 51 49 50 45 43 42 48 41 47 46 44 39 53 64 62 63 58 56 55 61 54 60 59 57 52 1 12 10 11 6 4 3 9 2 8 7 5 0 19 20 15 13 25 18 24 17 16 14 22 23 21 32 33 28 26 38 31 37 30 29 27 35 36 34 45 46 41 39 51 44 50 43 42 40 48 49 47 58 59 54 52 64 57 63 56 55 53 61 62 60 6 7 2 0 12 5 11 4 3 1 9 10 8 24 22 21 14 20 13 25 23 18 19 17 15 16 37 35 34 27 33 26 38 36 31 32 30 28 29 50 48 47 40 46 39 51 49 44 45 43 41 42 63 61 60 53 59 52 64 62 57 58 56 54 55 11 9 8 1 7 0 12 10 5 6 4 2 3 17 23 16 22 21 19 14 15 13 24 25 20 18 30 36 29 35 34 32 27 28 26 37 38 33 31 43 49 42 48 47 45 40 41 39 50 51 46 44 56 62 55 61 60 58 53 54 52 63 64 59 57 4 10 3 9 8 6 1 2 0 11 12 7 5 25 18 17 15 23 24 22 20 21 16 14 13 19 38 31 30 28 36 37 35 33 34 29 27 26 32 51 44 43 41 49 50 48 46 47 42 40 39 45 64 57 56 54 62 63 61 59 60 55 53 52 58 12 5 4 2 10 11 9 7 8 3 1 0 6 13 24 19 20 18 16 17 25 23 22 15 21 14 26 37 32 33 31 29 30 38 36 35 28 34 27 39 50 45 46 44 42 43 51 49 48 41 47 40 52 63 58 59 57 55 56 64 62 61 54 60 53 0 11 6 7 5 3 4 12 10 9 2 8 1 15 16 14 25 13 21 19 18 24 17 23 22 20 28 29 27 38 26 34 32 31 37 30 36 35 33 41 42 40 51 39 47 45 44 50 43 49 48 46 54 55 53 64 52 60 58 57 63 56 62 61 59 2 3 1 12 0 8 6 5 11 4 10 9 7 23 21 22 17 15 14 20 13 19 18 16 24 25 36 34 35 30 28 27 33 26 32 31 29 37 38 49 47 48 43 41 40 46 39 45 44 42 50 51 62 60 61 56 54 53 59 52 58 57 55 63 64 10 8 9 4 2 1 7 0 6 5 3 11 12 18 13 24 23 16 22 15 14 25 20 21 19 17 31 26 37 36 29 35 28 27 38 33 34 32 30 44 39 50 49 42 48 41 40 51 46 47 45 43 57 52 63 62 55 61 54 53 64 59 60 58 56 5 0 11 10 3 9 2 1 12 7 8 6 4 46 45 51 44 50 49 47 42 43 41 39 40 48 59 58 64 57 63 62 60 55 56 54 52 53 61 7 6 12 5 11 10 8 3 4 2 0 1 9 20 19 25 18 24 23 21 16 17 15 13 14 22 33 32 38 31 37 36 34 29 30 28 26 27 35 47 40 46 45 43 51 39 50 48 49 44 42 41 60 53 59 58 56 64 52 63 61 62 57 55 54 8 1 7 6 4 12 0 11 9 10 5 3 2 21 14 20 19 17 25 13 24 22 23 18 16 15 34 27 33 32 30 38 26 37 35 36 31 29 28 42 41 39 47 48 46 44 45 40 51 50 43 49 55 54 52 60 61 59 57 58 53 64 63 56 62 3 2 0 8 9 7 5 6 1 12 11 4 10 16 15 13 21 22 20 18 19 14 25 24 17 23 29 28 26 34 35 33 31 32 27 38 37 30 36 48 43 44 42 40 41 49 47 46 39 45 51 50 61 56 57 55 53 54 62 60 59 52 58 64 63 9 4 5 3 1 2 10 8 7 0 6 12 11 22 17 18 16 14 15 23 21 20 13 19 25 24 35 30 31 29 27 28 36 34 33 26 32 38 37 40 51 49 50 45 43 42 48 41 47 46 44 39 53 64 62 63 58 56 55 61 54 60 59 57 52 1 12 10 11 6 4 3 9 2 8 7 5 0 14 25 23 24 19 17 16 22 15 21 20 18 13 27 38 36 37 32 30 29 35 28 34 33 31 26 45 46 41 39 51 44 50 43 42 40 48 49 47 58 59 54 52 64 57 63 56 55 53 61 62 60 6 7 2 0 12 5 11 4 3 1 9 10 8 19 20 15 13 25 18 24 17 16 14 22 23 21 32 33 28 26 38 31 37 30 29 27 35 36 34 50 48 47 40 46 39 51 49 44 45 43 41 42 63 61 60 53 59 52 64 62 57 58 56 54 55 11 9 8 1 7 0 12 10 5 6 4 2 3 24 22 21 14 20 13 25 23 18 19 17 15 16 37 35 34 27 33 26 38 36 31 32 30 28 29 43 49 42 48 47 45 40 41 39 50 51 46 44 56 62 55 61 60 58 53 54 52 63 64 59 57 4 10 3 9 8 6 1 2 0 11 12 7 5 17 23 16 22 21 19 14 15 13 24 25 20 18 30 36 29 35 34 32 27 28 26 37 38 33 31 51 44 43 41 49 50 48 46 47 42 40 39 45 64 57 56 54 62 63 61 59 60 55 53 52 58 12 5 4 2 10 11 9 7 8 3 1 0 6 25 18 17 15 23 24 22 20 21 16 14 13 19 38 31 30 28 36 37 35 33 34 29 27 26 32 39 50 45 46 44 42 43 51 49 48 41 47 40 52 63 58 59 57 55 56 64 62 61 54 60 53 0 11 6 7 5 3 4 12 10 9 2 8 1 13 24 19 20 18 16 17 25 23 22 15 21 14 26 37 32 33 31 29 30 38 36 35 28 34 27 41 42 40 51 39 47 45 44 50 43 49 48 46 54 55 53 64 52 60 58 57 63 56 62 61 59 2 3 1 12 0 8 6 5 11 4 10 9 7 15 16 14 25 13 21 19 18 24 17 23 22 20 28 29 27 38 26 34 32 31 37 30 36 35 33 49 47 48 43 41 40 46 39 45 44 42 50 51 62 60 61 56 54 53 59 52 58 57 55 63 64 10 8 9 4 2 1 7 0 6 5 3 11 12 23 21 22 17 15 14 20 13 19 18 16 24 25 36 34 35 30 28 27 33 26 32 31 29 37 38 44 39 50 49 42 48 41 40 51 46 47 45 43 57 52 63 62 55 61 54 53 64 59 60 58 56 5 0 11 10 3 9 2 1 12 7 8 6 4 18 13 24 23 16 22 15 14 25 20 21 19 17 31 26 37 36 29 35 28 27 38 33 34 32 30[/code] Проверка утилитой Harry White [code]Order? 65 Enter the name of the squares file: inp .. writing type information to file inpTypeDetail_5.txt Counts ------ 1 diagonal Latin 1 pandiagonal[/code] Точно так же можно поÑтроить цикличеÑкий пандиагональный ДЛК 65-го порÑдка методом ÑоÑтавных квадратов, только за оÑнову надо взÑÑ‚ÑŒ цикличеÑкий пандиагональный ДЛК 13-го порÑдка и пандиагональный ДЛК 5-го порÑдка. 10 цикличеÑких пандиагональных ДЛК 13-го порÑдка показаны здеÑÑŒ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=110&postid=1023 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Проект ОДЛК вернулÑÑ! Читайте на форуме проекта тему "Пандиагональные ДЛК" https://boinc.progger.info/odlk/forum_thread.php?id=178 Там было начало, здеÑÑŒ - продолжение. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Создана поÑледовательноÑÑ‚ÑŒ OEIS "Number of main classes of pandiagonal Latin squares of order n" https://oeis.org/A339999 Теперь очень интереÑный вопроÑ: где поÑмотреть вот Ñти пандиагональные ЛК порÑдка 13? For order n=13 this is not true and exists 12386 inequivalent squares; of these 10 are cyclic (in all directions) and 1560 are semi-cyclic (cyclic in a single direction). (Цитата из Ñтатьи OEIS https://oeis.org/A338620 ) Какой ÑмыÑл в голом количеÑтве Ñтих пандиагональных ЛК, еÑли из них нам извеÑтны 10 цикличеÑких и один не цикличеÑкий? Даже нет примера полуцикличеÑкого (semi-cyclic) пандиагонального ЛК 13-го порÑдка. Возможно, автору Ñтатьи извеÑтны вÑе пандиагональные ЛК порÑдка 13 ("12386 inequivalent squares"), но тогда надо их прикрепить к Ñтатье (а-файл), чтобы вÑе видели. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитирую Ñто Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=110&postid=1091 Цитата Мне очень интереÑно: ÑодержитÑÑ Ð»Ð¸ полученный преобразованием (извеÑтного не цикличеÑкого) пандиагональный ЛК 13-го порÑдка в полном наборе вÑех пандиагональных ЛК данного порÑдка? Чтобы ответить на Ñтот вопроÑ, надо иметь полный набор. Пока Ñ ÐµÐ³Ð¾ не имею. И не знаю, где его можно взÑÑ‚ÑŒ. Ð”Ð»Ñ Ñ‚Ð¾Ð³Ð¾ чтобы найти количеÑтво главных клаÑÑов пандиагональных ДЛК 13-го порÑдка, тоже надо иметь полный набор Ñтих ДЛК. Пока Ñ Ð·Ð½Ð°ÑŽ только 5 главных клаÑÑов пандиагональных ДЛК 13-го порÑдка: три клаÑÑа дают цикличеÑкие пандиагональные ДЛК (их вÑего 10 штук, они показаны выше), и два клаÑÑа дают не цикличеÑкие пандиагональные ДЛК, которые мне извеÑтны (они показаны в Ñтом поÑте). |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese
