Thread 'Clique_problem'
Message boards : Science : Clique_problem
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
И Ñнова задача о клике! ЗапоÑтила уже задачу на форуме Math Help Plfnet http://mathhelpplanet.com/viewtopic.php?f=62&t=72879 Ðу, там врÑд ли будут решать. Так, на вÑÑкий Ñлучай запоÑтила. Дальше подробно раÑÑкажу, как Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»Ð° граф, который уже Ñидит на ЯндекÑ.ДиÑке https://yadi.sk/d/ZIddJfJEzueXKg Ðто маленький текÑтовый файл. Граф у Ð¼ÐµÐ½Ñ Ñ…Ð¾Ñ€Ð¾ÑˆÐ¸Ð¹ :) он имеет 1088 вершин и 345 рёбер. ТребуетÑÑ Ð½Ð°Ð¹Ñ‚Ð¸ клику макÑимального размера. ПредполагаетÑÑ, что Ñто будет клика размера 6. Рвдруг найдётÑÑ ÐºÐ»Ð¸ÐºÐ° размера 7. Ðто будет опровержение моей гипотезы, ÐºÐ¾Ñ‚Ð¾Ñ€Ð°Ñ Ð·Ð°Ð¿Ð¸Ñана в Ñтатье OEIS https://oeis.org/A328873 Цитирую Conjecture: a(9) = 6. Natalia Makarova, Dec 24 2020 Добавлю, что задача о клике опиÑана в Википедии https://ru.wikipedia.org/wiki/Задача_о_клике а также в английÑкой Википедии https://en.wikipedia.org/wiki/Clique_problem ИзвеÑтен алгоритм поиÑка клики макÑимального размера. Даже и программа, кажетÑÑ, напиÑана кем-то. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Что такое мой граф? Ðто множеÑтво ортогональных ДЛК, которые предÑтавлÑÑŽÑ‚ Ñобой вершины графа. ДЛК ÑвÑзаны отношением ортогональноÑти; еÑли два ДЛК образуют ортогональную пару (то еÑÑ‚ÑŒ ортогональны друг другу), они ÑоединÑÑŽÑ‚ÑÑ Ñ€ÐµÐ±Ñ€Ð¾Ð¼ графа. Граф предÑтавлÑет Ñобой не что иное как таблицу ортогональноÑти ДЛК данного множеÑтва. Покажу начало таблицы ортогональноÑти 2: 1 3: 1 2 4: 1 2 3 5: 1 2 3 4 6: 1 2 3 4 5 9: 2 214: 4 155 174 269: 120 272: 120 311: 246 317: 5 318: 5 319: 5 320: 5 342: 9 155 . . . . . Ðапример. запиÑÑŒ 6: 1 2 3 4 5 означает, что ДЛК â„–6 ортогонален ДЛК â„–â„– 1, 2, 3, 4, 5. Значит, вершина 6 Ñоединена Ñ Ð²ÐµÑ€ÑˆÐ¸Ð½Ð°Ð¼Ð¸ 1, 2, 3, 4, 5. Ð’Ñе ДЛК â„–â„– 1, 2, 3, 4, 5 тоже взаимно ортогональны. Очевидно, что Ñто Ð¿ÐµÑ€Ð²Ð°Ñ ÐºÐ»Ð¸ÐºÐ° размера 6. ЕÑÑ‚ÑŒ ли другие клики размера 6? Рглавный вопроÑ: еÑÑ‚ÑŒ ли клика размера 7? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Теперь раÑÑкажу, как Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»Ð° множеÑтво ДЛК, предÑтавленное в графе. ВзÑла извеÑтную группу MODLS 9-го порÑдка, ÑоÑтоÑщую из 6 взаимно ортогональных ДЛК, вот она 0 1 2 3 4 5 6 7 8 3 4 5 6 7 8 0 1 2 6 7 8 0 1 2 3 4 5 7 8 6 1 2 0 4 5 3 1 2 0 4 5 3 7 8 6 4 5 3 7 8 6 1 2 0 5 3 4 8 6 7 2 0 1 8 6 7 2 0 1 5 3 4 2 0 1 5 3 4 8 6 7 0 1 2 3 4 5 6 7 8 4 5 3 7 8 6 1 2 0 8 6 7 2 0 1 5 3 4 1 2 0 4 5 3 7 8 6 5 3 4 8 6 7 2 0 1 6 7 8 0 1 2 3 4 5 2 0 1 5 3 4 8 6 7 3 4 5 6 7 8 0 1 2 7 8 6 1 2 0 4 5 3 0 1 2 3 4 5 6 7 8 5 3 4 8 6 7 2 0 1 7 8 6 1 2 0 4 5 3 4 5 3 7 8 6 1 2 0 6 7 8 0 1 2 3 4 5 2 0 1 5 3 4 8 6 7 8 6 7 2 0 1 5 3 4 1 2 0 4 5 3 7 8 6 3 4 5 6 7 8 0 1 2 0 1 2 3 4 5 6 7 8 6 7 8 0 1 2 3 4 5 3 4 5 6 7 8 0 1 2 5 3 4 8 6 7 2 0 1 2 0 1 5 3 4 8 6 7 8 6 7 2 0 1 5 3 4 7 8 6 1 2 0 4 5 3 4 5 3 7 8 6 1 2 0 1 2 0 4 5 3 7 8 6 0 1 2 3 4 5 6 7 8 7 8 6 1 2 0 4 5 3 5 3 4 8 6 7 2 0 1 8 6 7 2 0 1 5 3 4 3 4 5 6 7 8 0 1 2 1 2 0 4 5 3 7 8 6 4 5 3 7 8 6 1 2 0 2 0 1 5 3 4 8 6 7 6 7 8 0 1 2 3 4 5 0 1 2 3 4 5 6 7 8 8 6 7 2 0 1 5 3 4 4 5 3 7 8 6 1 2 0 2 0 1 5 3 4 8 6 7 7 8 6 1 2 0 4 5 3 3 4 5 6 7 8 0 1 2 1 2 0 4 5 3 7 8 6 6 7 8 0 1 2 3 4 5 5 3 4 8 6 7 2 0 1 и нашла макÑимальное раÑширение Ñтой группы. Ðу, еÑли не ошиблаÑÑŒ, конечно. Получила группу из 1088 ОДЛК, Ð²ÐºÐ»ÑŽÑ‡Ð°Ñ 6 иÑходных ДЛК. Первые 6 иÑходных ДЛК раÑположены в начале ÑпиÑка ДЛК. Вот они и образуют первую клику размера 6, о которой Ñ ÑƒÐ¶Ðµ Ñказала выше. Теперь найдите, пожалуйÑта, другие клики макÑимального размера в данном графе. Ðу, клики размера 6, еÑли они ещё еÑÑ‚ÑŒ, не Ñтоль интереÑны. ПонÑтно, что интереÑна клика размера 7. Ðо такой клики, ÑоглаÑно моей гипотезе, не ÑущеÑтвует. Опровергнем гипотезу? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
С ходу нашла клику размера 4, визуальным проÑмотром таблицы ортогональноÑти 198, 489, 535, 922 Ðу, Ñто мало интереÑно. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вообще-то, надо замеÑить ÑкÑперимент покруче. Только пироги печь вÑÑ‘ равно никто не будет :) Ð’ BOINC-проектах найден полный набор КФ ОДЛК 9-го порÑдка. Ðаходим вÑе ОДЛК к Ñтим КФ, нормализуем их, выбраÑываем дубликаты. Вот вам и множеÑтво ОДЛК, в котором надо иÑкать клику макÑимального размера. Ðо Ñта задача врÑд ли решабельна на одном ПК. Так что, ни доказать, ни опровергнуть мою гипотезу пока не получаетÑÑ. Ð Ñ ÑƒÐ²ÐµÑ€ÐµÐ½Ð° в том, что она вернаÑ! Моё доказательÑтво на оÑнове анализа вÑех полных ÑиÑтем MOLS 9-го порÑдка не отменÑетÑÑ! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
У Ð½Ð°Ñ Ð‘Ð” КФ ОДЛК 9-го порÑдка в данный момент Ñодержит 59997 КФ ОДЛК. Ð’ полной БД 75 Ñ‚Ñ‹ÑÑч Ñ Ñ…Ð²Ð¾Ñтиком КФ ОДЛК. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾ÐºÐ°Ð¶Ñƒ, Ñколько ОДЛК имеют вÑе КФ нашей БД. Вот хвоÑÑ‚ выходного файла программы Белышева ortogon_u . . . . . . . . [DLK(4):272592] 0 8 7 6 3 2 5 4 1 4 1 5 8 6 3 7 0 2 7 6 2 5 8 0 3 1 4 8 7 4 3 0 6 1 2 5 6 5 1 2 4 8 0 3 7 2 3 0 7 1 5 4 8 6 1 4 8 0 2 7 6 5 3 3 2 6 1 5 4 8 7 0 5 0 3 4 7 1 2 6 8 [DLK(2):272596] 0 8 7 6 3 2 5 4 1 4 1 5 8 6 3 7 0 2 7 6 2 5 8 0 3 1 4 8 7 4 3 1 6 0 2 5 3 5 0 2 4 8 1 6 7 2 3 1 7 0 5 4 8 6 1 4 8 0 2 7 6 5 3 6 2 3 1 5 4 8 7 0 5 0 6 4 7 1 2 3 8 [DLK(4):272598] 0 8 7 6 3 2 5 4 1 4 1 5 8 6 3 7 0 2 7 6 2 5 8 0 3 1 4 8 7 4 3 1 6 0 2 5 6 5 0 2 4 8 1 3 7 2 3 1 7 0 5 4 8 6 1 4 8 0 2 7 6 5 3 3 2 6 1 5 4 8 7 0 5 0 3 4 7 1 2 6 8 272598 ортогональных диагональных Ñоквадратов! Ðе хило. Конечно, поÑле нормализации чаÑÑ‚ÑŒ квадратов удалитÑÑ. Однако вÑÑ‘ равно очень много. Да к ним нужно ещё добавить вÑе иÑходные КФ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
О-о-о! Ðа форуме Math Help Planet пришёл ответ Программа SageMath говорит, что [1, 2, 3, 4, 5, 6] — единÑÑ‚Ð²ÐµÐ½Ð½Ð°Ñ ÐºÐ»Ð¸ÐºÐ° размера 6, а клик бóльшего размера нет. http://mathhelpplanet.com/viewtopic.php?p=409566#p409566 Ðу, решение ожидаемое, так и должно быть. ОÑталоÑÑŒ замеÑить ÑкÑперимент покруче :) Да, программа указана. Где её можно раздобыть? И как ею пользоватьÑÑ? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðа форуме Math Help Planet дали ÑÑылку на программу, а также на Введение (на руÑÑком Ñзыке). СÑылка на программу SageMath https://www.sagemath.org СÑылка на Введение https://doc.sagemath.org/html/ru/tutorial/index.html УÑтановщик программы Ñкачала, но ещё не уÑтанавливала. Введение чуть-чуть поÑмотрела, одним глазком :) ГоÑпода! ПожалуйÑта, попробуйте тоже Ñту программу, кто ещё не пользуетÑÑ ÐµÑŽ. Ðто должно быть интереÑно и полезно. Заодно мне поможете, еÑли у Ð¼ÐµÐ½Ñ Ñ‡Ñ‚Ð¾-то не пойдёт. Я Ñкачала Ñамую поÑледнюю верÑию (от 5 ÑÐ½Ð²Ð°Ñ€Ñ Ñ‚. г.). Вот ÑÐµÐ¹Ñ‡Ð°Ñ Ñƒ Ð¼ÐµÐ½Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ñ‹ закончат работать, попробую уÑтановить. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ой, как интереÑно! Во Ведении вычитала про Ñтот режим http://sagecell.sagemath.org Там напиÑано, что Ð´Ð»Ñ Ñ€Ð°Ð±Ð¾Ñ‚Ñ‹ в Ñтом режиме можно и не уÑтанавливать программу SageMath. Я попробовала ÑейчаÑ. Вот что у Ð¼ÐµÐ½Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»Ð¾ÑÑŒ 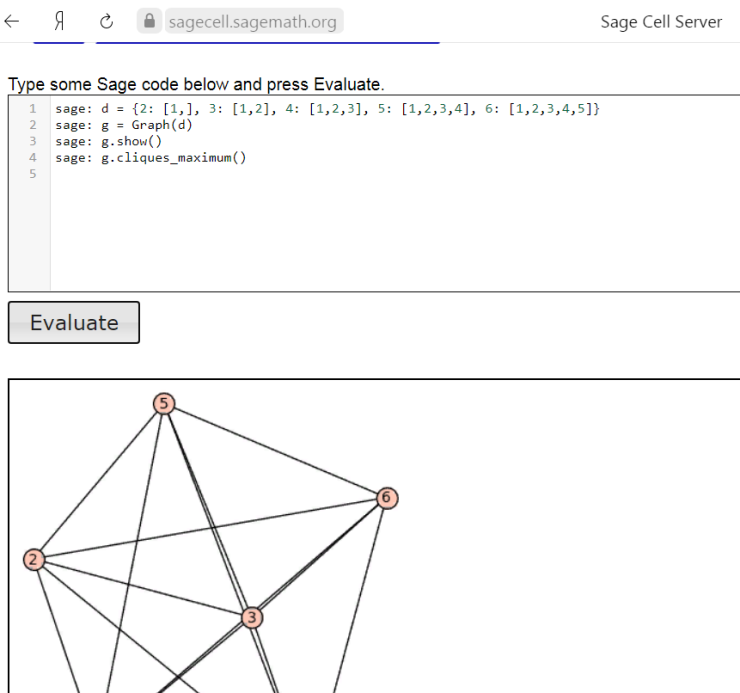 Ðто макÑÐ¸Ð¼Ð°Ð»ÑŒÐ½Ð°Ñ ÐºÐ»Ð¸ÐºÐ° размера 6 в моём графе. ПроÑто задала её вручную (первые шеÑÑ‚ÑŒ вершин графа, которые и образуют Ñту клику). Даже картинку программа нариÑовала :) Ðй-да молодец! ГоÑпода! Ðктуальный, животрепещущий вопроÑ! Как в Ñтом режиме запуÑтить программку из файла? Или как взÑÑ‚ÑŒ граф, запиÑанный в текÑтовый файл? Ðа форуме Math Help Planet форумчанин дал код программки Ð´Ð»Ñ Ð¼Ð¾ÐµÐ¹ задачи. Вот Ñтот код надо запиÑать в текÑтовый файл, а потом запуÑтить программу Sage из Ñтого файла. Ð’ PARI/GP, например, так делаетÑÑ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Подключила второй уровень. Получила граф, в котором больше 18 Ñ‚Ñ‹ÑÑч вершин. Пока ввожу их вручную, по Ñ‚Ñ‹ÑÑче. Ввела уже 13 Ñ‚Ñ‹ÑÑч вершин. Программа выдаёт какую-то ошибку, но клики вычиÑлÑет :) Вот нашла клики размера 5, пÑÑ‚ÑŒ штук [[2795, 12289, 3797, 7668, 8418], [2924, 10300, 12771, 4228, 7611], [10355, 12293, 990, 4702, 7728], [11080, 12271, 992, 7741, 9559], [11614, 12281, 4157, 7974, 8935]] Отлично! Программа работает замечательно! ÐеÑколько Ñекунд и вÑе клики найдены. ИнтереÑно, возьмёт ли программа вÑе 18 Ñ Ñ…Ð²Ð¾Ñтиком вершин? Ðа очереди макÑÐ¸Ð¼Ð°Ð»ÑŒÐ½Ð°Ñ ÐºÐ»Ð¸ÐºÐ° размера 6. Клику размера 7 Ñ Ð½Ðµ ожидаю, её не может быть ÑоглаÑно моей гипотезе. Тему на форуме Math Help Planet Ñмотрите, Ñ Ñ‚Ð°Ð¼ тоже пишу http://mathhelpplanet.com/viewtopic.php?f=62&t=72879 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Добавила ещё Ñ‚Ñ‹ÑÑчу вершин, нашлиÑÑŒ Ñледующие клики размера 5 [[927, 10678, 4619, 7906, 13447], [1045, 4432, 7107, 10204, 13934], [2795, 12289, 3797, 7668, 8418], [2924, 10300, 12771, 4228, 7611], [4394, 7424, 8632, 9992, 13655], [5206, 10774, 2174, 4605, 13717], [5206, 10799, 2169, 4596, 13717], [5546, 10852, 2146, 9498, 13797], [5589, 10852, 2133, 9512, 13785], [5601, 10859, 2133, 9502, 13785], [5782, 2065, 4544, 9069, 13930], [10355, 12293, 990, 4702, 7728], [11080, 12271, 992, 7741, 9559], [11614, 12281, 4157, 7974, 8935]] МакÑимальной клики размера 6 пока нет. Должна быть! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё добавила Ñ‚Ñ‹ÑÑчу вершин, нашлиÑÑŒ опÑÑ‚ÑŒ только клики размера 5, но их теперь больше [[927, 10678, 4619, 7906, 13447], [952, 4187, 5089, 9516, 14287], [1045, 4432, 7107, 10204, 13934], [1280, 7153, 9397, 10154, 14064], [1280, 7171, 9397, 10145, 14071], [1303, 7133, 9403, 10154, 14008], [1303, 7171, 9415, 10122, 14008], [1355, 7133, 9403, 10145, 14071], [1355, 7153, 9415, 10122, 14064], [1430, 6534, 11662, 8409, 14954], [1670, 6226, 4652, 10211, 14771], [1708, 3347, 10679, 7397, 14372], [2561, 5838, 4139, 8754, 14311], [2561, 5856, 4125, 8754, 14320], [2795, 12289, 3797, 7668, 8418], [2924, 10300, 4228, 7611, 12771], [4394, 7424, 8632, 9992, 13655], [5206, 10774, 2174, 4605, 13717], [5206, 10799, 2169, 4596, 13717], [5546, 10852, 2146, 9498, 13797], [5589, 10852, 2133, 9512, 13785], [5601, 10859, 2133, 9502, 13785], [5782, 2065, 4544, 9069, 13930], [5838, 2543, 4130, 8811, 14300], [5856, 2543, 4130, 8784, 14320], [6012, 11604, 4078, 9023, 14977], [6034, 11604, 4078, 8994, 14940], [6422, 2330, 3428, 8597, 14424], [6422, 2334, 3390, 8613, 14442], [6470, 2334, 3390, 8583, 14460], [6778, 10504, 2387, 8623, 14319], [10355, 12293, 990, 4702, 7728], [10584, 4651, 7299, 8625, 14696], [11080, 12271, 992, 7741, 9559], [11614, 12281, 4157, 7974, 8935]] ФантаÑтика! Уже введено 15 Ñ‚Ñ‹ÑÑч вершин, которые Ñоединены N рёбрами. Программа пока работает, правда, выдаёт какие-то ошибки. Может быть, работает некорректно, но клики выдаёт! Возможно, и не вÑе выдаёт из-за ошибок. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Введено 16 Ñ‚Ñ‹ÑÑч вершин! ПоÑвилиÑÑŒ клики размера 6 [[2330, 3428, 6422, 8597, 14424, 15625], [2334, 3390, 6422, 8613, 14442, 15625], [2334, 3390, 6470, 8583, 14460, 15611], [2561, 5838, 4139, 8754, 14311, 15405], [2561, 5856, 4125, 8754, 14320, 15380], [2924, 10300, 4228, 7611, 12771, 15255], [5206, 10774, 2174, 4605, 13717, 15868], [5206, 10799, 2169, 4596, 13717, 15857], [5838, 2543, 4130, 8811, 14300, 15405], [5856, 2543, 4130, 8784, 14320, 15355], [10504, 2387, 6778, 8623, 14319, 15266], [11614, 4157, 7974, 8935, 12281, 15906]] Супер! Ðу, клику 7 Ñ Ð½Ðµ ожидаю, её не может быть ÑоглаÑно моей гипотезе. Однако оÑталоÑÑŒ ввеÑти 2 Ñ‚Ñ‹ÑÑчи Ñ Ñ…Ð²Ð¾Ñтиком вершин. Можно Ð´Ð»Ñ Ñ‡Ð¸Ñтоты ÑкÑперимента попробовать добить до конца Ñтот граф. Ðе лопнет ли программа? :) PS. Да, вот оно раÑширение. РазумеетÑÑ, раÑширение возможно. И в раÑширении неÑколько клик размера 6 найдено. И Ñто ещё не предел! Можно перейти на Ñледующий уровень раÑширениÑ. ПолучитÑÑ Ð¾Ð³Ñ€Ð¾Ð¼Ð½Ð¾Ðµ множеÑтво ОДЛК. И в Ñтом множеÑтве тоже поиÑкать клику размера 7. Только напраÑный труд! Ðет такой клики Ð´Ð»Ñ ÐžÐ”Ð›Ðš 9-го порÑдка. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Введено 17000 вершин! Ðайдены Ñледующие клики размера 6 [[952, 4187, 5089, 9516, 14287, 16206], [1045, 4432, 7107, 10204, 13934, 16086], [1670, 4652, 6226, 10211, 14771, 16514], [2330, 3428, 6422, 8597, 14424, 15625], [2334, 3390, 6422, 8613, 14442, 15625], [2334, 3390, 6470, 8583, 14460, 15611], [2561, 5838, 4139, 8754, 14311, 15405], [2561, 5856, 4125, 8754, 14320, 15380], [2924, 10300, 4228, 7611, 12771, 15255], [4157, 7974, 8935, 11614, 12281, 15906], [5206, 10774, 2174, 4605, 13717, 15868], [5206, 10799, 2169, 4596, 13717, 15857], [5782, 2065, 4544, 9069, 13930, 16205], [5838, 2543, 4130, 8811, 14300, 15405], [5856, 2543, 4130, 8784, 14320, 15355], [10504, 2387, 6778, 8623, 14319, 15266], [10679, 1708, 3347, 7397, 14372, 16183], [11080, 992, 7741, 9559, 12271, 16188]] ОÑталоÑÑŒ чуть-чуть. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’ÑÑ‘! Затолкала вÑе вершины - 18291 штук. И программа не лопнула :) Ðайдены Ñледующие клики размера 6 [[927, 4619, 7906, 10678, 13447, 17465], [952, 4187, 5089, 9516, 14287, 16206], [992, 7741, 9559, 11080, 12271, 16188], [1045, 4432, 7107, 10204, 13934, 16086], [1202, 3988, 6119, 11640, 15067, 18175], [1280, 7153, 9397, 10154, 14064, 17316], [1280, 7171, 9397, 10145, 14071, 17292], [1303, 7133, 9403, 10154, 14008, 17316], [1303, 7171, 9415, 10122, 14008, 17292], [1355, 7133, 9403, 10145, 14071, 17244], [1355, 7153, 9415, 10122, 14064, 17244], [1430, 6534, 8409, 11662, 14954, 18139], [1670, 4652, 6226, 10211, 14771, 16514], [1708, 3347, 7397, 10679, 14372, 16183], [2065, 4544, 5782, 9069, 13930, 16205], [2133, 5589, 9512, 10852, 13785, 17109], [2133, 5601, 9502, 10859, 13785, 17108], [2146, 5546, 9498, 10852, 13797, 17109], [2330, 3428, 6422, 8597, 14424, 15625], [2334, 3390, 6422, 8613, 14442, 15625], [2334, 3390, 6470, 8583, 14460, 15611], [2543, 4130, 5838, 8811, 14300, 15405], [2543, 4130, 5856, 8784, 14320, 15355], [2561, 4125, 5856, 8754, 14320, 15380], [2561, 4139, 5838, 8754, 14311, 15405], [2795, 3797, 7668, 8418, 12289, 17198], [3328, 7005, 8526, 11295, 15118, 17061], [3674, 6661, 8531, 11388, 15051, 18039], [3674, 6677, 8518, 11388, 15062, 18026], [3686, 6632, 8531, 11404, 15047, 18039], [3686, 6677, 8510, 11431, 15047, 18026], [3716, 6632, 8518, 11404, 15062, 17997], [3716, 6661, 8510, 11431, 15051, 17997], [4078, 6012, 9023, 11604, 14977, 17864], [4078, 6034, 8994, 11604, 14940, 17866], [4157, 7974, 8935, 11614, 12281, 15906], [4394, 7424, 8632, 9992, 13655, 17499], [4651, 7299, 8625, 10584, 14696, 17421], [5206, 2169, 4596, 10799, 13717, 15857], [5206, 2174, 4605, 10774, 13717, 15868], [10300, 2924, 4228, 7611, 12771, 15255], [10355, 990, 4702, 7728, 12293, 17160], [10367, 3257, 7656, 8912, 15162, 17546], [10504, 2387, 6778, 8623, 14319, 15266]] Их Ñтало больше. Клики размера 7 в данном раÑширении группы MODLS 9-го порÑдка нет (еÑли, конечно, программа вÑÑ‘ правильно поÑчитала). Ðто ещё раз подтверждает мою гипотезу. Ðу, Ñ Ð´ÑƒÐ¼Ð°ÑŽ, не пройдёт и года, как гоÑподин Ватутин найдёт группу MODLS порÑдка 9, ÑоÑтоÑщую из 7 взаимно ортогональных ДЛК. Я такую группу больше иÑкать не буду, потому что уверна, что Ñ‚Ð°ÐºÐ°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° не ÑущеÑтвует. Ркак хорошо Ñ Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð¾Ð¹ SageMath познакомилаÑÑŒ. КлаÑÑÐ½Ð°Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð°! У Ð¼ÐµÐ½Ñ ÐµÑ‰Ñ‘ задачка была о клике Ð´Ð»Ñ ÐžÐ”Ð›Ðš 8-го порÑдка. Только форум проекта ОДЛК ÑÐµÐ¹Ñ‡Ð°Ñ Ð½ÐµÐ´Ð¾Ñтупен, и данные о задаче взÑÑ‚ÑŒ негде. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðашла у ÑÐµÐ±Ñ Ð² компьютере граф, который делала Ð´Ð»Ñ ÐžÐ”Ð›Ðš 8-го порÑдка. Я его выкладывала в теме на форуме проекта ОДЛК (можно на ЯндекÑ.ДиÑке и ÑÑылку взÑÑ‚ÑŒ). Ð’ графе 5034 вершины. Граф, понÑтно, предÑтавлен таблицей ортогональноÑти заданного множеÑтва ОДЛК, ÑоÑтоÑщего из 5034 квадратов. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð²Ð²ÐµÐ»Ð° Ñтот граф в программу SageMath, вот "хвоÑтик" видно . . . . . . 5032: [762,1453,3028], 5033: [757], 5034: [714,1433,1453,1481,1499,1537,1609,1634,1807,1874, 1925,2016,2082,2191,2247,2874,2998,3028,3118,3349, 3466,3549,3679,3745,3755,3923,3953,4057,4088],} sage: g = Graph(d) sage: g.cliques_maximum() Программа мгновенно выдала единÑтвенную (!) клику размера 6 [761, 1455, 2082, 3068, 4010, 4996] что и требовалоÑÑŒ доказать. Я иÑкала Ñту клику вручную (визуально), и нашла её. Ðо не была уверена в том, что других клик размера 6 нет. Теперь Ñто подтверждено программой. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Проект ОДЛК вернулÑÑ! Дублирую Ñообщение о клике, о которой Ñказано в предыдущем поÑте Рвот и Ð¿ÐµÑ€Ð²Ð°Ñ ÑˆÐµÑтёрка, от показанной выше пÑтёрки произошла, добавилаÑÑŒ вершина 4996 Да! Она та же ÑамаÑ, что найдена программой SageMath! Как быÑтро её можно было найти, а Ñ Ð²Ð¸Ð·ÑƒÐ°Ð»ÑŒÐ½Ð¾ иÑкала долго. И на главный Ð²Ð¾Ð¿Ñ€Ð¾Ñ Ð¾Ñ‚Ð²ÐµÑ‚ программа дала: еÑÑ‚ÑŒ только одна клика размера 6 в Ñтом графе. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese