Thread 'MOLS and MODLS of order 12'
Message boards : Science : MOLS and MODLS of order 12
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Первую группу MOLS 12-го порÑдка из 5 ЛК Ñ ÑоÑтавила очень давно в Ñвоей Ñтатье (по извеÑтному алгоритму) http://www.natalimak1.narod.ru/mols12.htm Показываю Ñту группу 0 1 2 3 4 5 6 7 8 9 10 11 1 2 3 4 5 0 7 8 9 10 11 6 2 3 4 5 0 1 8 9 10 11 6 7 3 4 5 0 1 2 9 10 11 6 7 8 4 5 0 1 2 3 10 11 6 7 8 9 5 0 1 2 3 4 11 6 7 8 9 10 6 7 8 9 10 11 0 1 2 3 4 5 7 8 9 10 11 6 1 2 3 4 5 0 8 9 10 11 6 7 2 3 4 5 0 1 9 10 11 6 7 8 3 4 5 0 1 2 10 11 6 7 8 9 4 5 0 1 2 3 11 6 7 8 9 10 5 0 1 2 3 4 0 6 8 2 7 1 9 11 4 10 5 3 1 7 9 3 8 2 10 6 5 11 0 4 2 8 10 4 9 3 11 7 0 6 1 5 3 9 11 5 10 4 6 8 1 7 2 0 4 10 6 0 11 5 7 9 2 8 3 1 5 11 7 1 6 0 8 10 3 9 4 2 6 0 2 8 1 7 3 5 10 4 11 9 7 1 3 9 2 8 4 0 11 5 6 10 8 2 4 10 3 9 5 1 6 0 7 11 9 3 5 11 4 10 0 2 7 1 8 6 10 4 0 6 5 11 1 3 8 2 9 7 11 5 1 7 0 6 2 4 9 3 10 8 0 3 6 1 9 11 2 8 5 4 7 10 1 4 7 2 10 6 3 9 0 5 8 11 2 5 8 3 11 7 4 10 1 0 9 6 3 0 9 4 6 8 5 11 2 1 10 7 4 1 10 5 7 9 0 6 3 2 11 8 5 2 11 0 8 10 1 7 4 3 6 9 6 9 0 7 3 5 8 2 11 10 1 4 7 10 1 8 4 0 9 3 6 11 2 5 8 11 2 9 5 1 10 4 7 6 3 0 9 6 3 10 0 2 11 5 8 7 4 1 10 7 4 11 1 3 6 0 9 8 5 2 11 8 5 6 2 4 7 1 10 9 0 3 0 8 1 11 5 9 3 10 2 7 6 4 1 9 2 6 0 10 4 11 3 8 7 5 2 10 3 7 1 11 5 6 4 9 8 0 3 11 4 8 2 6 0 7 5 10 9 1 4 6 5 9 3 7 1 8 0 11 10 2 5 7 0 10 4 8 2 9 1 6 11 3 6 2 7 5 11 3 9 4 8 1 0 10 7 3 8 0 6 4 10 5 9 2 1 11 8 4 9 1 7 5 11 0 10 3 2 6 9 5 10 2 8 0 6 1 11 4 3 7 10 0 11 3 9 1 7 2 6 5 4 8 11 1 6 4 10 2 8 3 7 0 5 9 0 4 11 10 2 7 8 6 9 1 3 5 1 5 6 11 3 8 9 7 10 2 4 0 2 0 7 6 4 9 10 8 11 3 5 1 3 1 8 7 5 10 11 9 6 4 0 2 4 2 9 8 0 11 6 10 7 5 1 3 5 3 10 9 1 6 7 11 8 0 2 4 6 10 5 4 8 1 2 0 3 7 9 11 7 11 0 5 9 2 3 1 4 8 10 6 8 6 1 0 10 3 4 2 5 9 11 7 9 7 2 1 11 4 5 3 0 10 6 8 10 8 3 2 6 5 0 4 1 11 7 9 11 9 4 3 7 0 1 5 2 6 8 10 Проверка Ñтих ЛК утилитой Harry White Order? 12
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt
Counts
------
5 Latin
1 center symmetric
1 nfr
5 nfc
1 nfr nfc
1 self-transpose
4 orthogonal pairКак видим, в Ñтой группе MOLS нет ДЛК. Ðе так давно Ñ Ð½ÐµÐ¼Ð½Ð¾Ð³Ð¾ поработала Ñ Ð›Ðš Ñтой группы. С помощью Ð¿Ñ€ÐµÐ¾Ð±Ñ€Ð°Ð·Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¿ÐµÑ€ÐµÑтановки Ñтрок мне удалоÑÑŒ получить неÑколько интереÑных ДЛК Ñ Ñ‚Ð¾Ñ‡ÐºÐ¸ Ð·Ñ€ÐµÐ½Ð¸Ñ ÐºÐ¾Ð»Ð¸Ñ‡ÐµÑтва в них Д-транÑверÑалей. Тогда Ñ Ð¸Ñпользовала только переÑтановку Ñтрок, а можно ещё иÑпользовать переÑтановку Ñтолбцов и одновременную переÑтановку Ñтрок и Ñтолбцов. Рцель у Ð¼ÐµÐ½Ñ Ñ‚Ð°ÐºÐ°Ñ: найти тройку MODLS 12-го порÑдка. Ортогональные пары ДЛК 12-го порÑдка, разумеетÑÑ, ÑущеÑтвуют, нам их уже очень много извеÑтно. Рвот наÑчёт тройки взаимно ортогональных ДЛК данного порÑдка пока ничего неизвеÑтно (по крайней мере, мне). |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’Ñ‚Ð¾Ñ€Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° MOLS 12-го порÑдка тоже из 5 ЛК получена программой SageMath. Команда sage: for x in designs.mutually_orthogonal_latin_squares(5,12): print(x,'\n') Группа MOLS 0 1 2 3 4 5 6 7 8 9 10 11 1 0 3 2 5 4 7 6 9 8 11 10 2 3 0 1 6 7 4 5 10 11 8 9 3 2 1 0 7 6 5 4 11 10 9 8 8 9 10 11 0 1 2 3 4 5 6 7 9 8 11 10 1 0 3 2 5 4 7 6 10 11 8 9 2 3 0 1 6 7 4 5 11 10 9 8 3 2 1 0 7 6 5 4 4 5 6 7 8 9 10 11 0 1 2 3 5 4 7 6 9 8 11 10 1 0 3 2 6 7 4 5 10 11 8 9 2 3 0 1 7 6 5 4 11 10 9 8 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10 11 6 7 4 5 10 11 8 9 2 3 0 1 4 5 6 7 8 9 10 11 0 1 2 3 2 3 0 1 6 7 4 5 10 11 8 9 10 11 8 9 2 3 0 1 6 7 4 5 5 4 7 6 9 8 11 10 1 0 3 2 7 6 5 4 11 10 9 8 3 2 1 0 8 9 10 11 0 1 2 3 4 5 6 7 9 8 11 10 1 0 3 2 5 4 7 6 3 2 1 0 7 6 5 4 11 10 9 8 1 0 3 2 5 4 7 6 9 8 11 10 11 10 9 8 3 2 1 0 7 6 5 4 0 1 2 3 4 5 6 7 8 9 10 11 3 2 1 0 7 6 5 4 11 10 9 8 11 10 9 8 3 2 1 0 7 6 5 4 6 7 4 5 10 11 8 9 2 3 0 1 4 5 6 7 8 9 10 11 0 1 2 3 7 6 5 4 11 10 9 8 3 2 1 0 9 8 11 10 1 0 3 2 5 4 7 6 1 0 3 2 5 4 7 6 9 8 11 10 5 4 7 6 9 8 11 10 1 0 3 2 2 3 0 1 6 7 4 5 10 11 8 9 10 11 8 9 2 3 0 1 6 7 4 5 8 9 10 11 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 10 11 9 8 11 10 1 0 3 2 5 4 7 6 8 9 10 11 0 1 2 3 4 5 6 7 1 0 3 2 5 4 7 6 9 8 11 10 5 4 7 6 9 8 11 10 1 0 3 2 3 2 1 0 7 6 5 4 11 10 9 8 2 3 0 1 6 7 4 5 10 11 8 9 4 5 6 7 8 9 10 11 0 1 2 3 11 10 9 8 3 2 1 0 7 6 5 4 6 7 4 5 10 11 8 9 2 3 0 1 7 6 5 4 11 10 9 8 3 2 1 0 10 11 8 9 2 3 0 1 6 7 4 5 0 1 2 3 4 5 6 7 8 9 10 11 10 11 8 9 2 3 0 1 6 7 4 5 5 4 7 6 9 8 11 10 1 0 3 2 7 6 5 4 11 10 9 8 3 2 1 0 9 8 11 10 1 0 3 2 5 4 7 6 11 10 9 8 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 11 10 9 8 6 7 4 5 10 11 8 9 2 3 0 1 2 3 0 1 6 7 4 5 10 11 8 9 1 0 3 2 5 4 7 6 9 8 11 10 8 9 10 11 0 1 2 3 4 5 6 7 4 5 6 7 8 9 10 11 0 1 2 3 Утилита Harry White Ñообщает об Ñтих ЛК Order? 12
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
5 Latin
1 center symmetric
5 nfr
4 orthogonal pairКак видим, в Ñтой группе тоже нет ДЛК. Итак, мы имеем две группы MOLS 12-го порÑдка из 5 ЛК (возможно, еÑÑ‚ÑŒ и другие, но мне не вÑтречалиÑÑŒ) и не имеем тройки MODLS. Задача: найти тройку MODLS 12-го порÑдка. Ðто задача-минимум. Может быть, ÑущеÑтвуют группы MODLS 12-го порÑдка, Ñодержание более трёх ДЛК. Ðо пока Ñтавлю задачу - найти тройку MODLS. Ðе знаю, ÑущеÑтвует ли иÑÐºÐ¾Ð¼Ð°Ñ Ñ‚Ñ€Ð¾Ð¹ÐºÐ° MODLS. Точно так же, как о тройке MOLS 10-го порÑдка ничего неизвеÑтно (по крайней мере, до недавнего времени было неизвеÑтно; может быть, уже что-то выÑÑнили; математики работают, а мы не вÑегда знаем о полученных результатах). |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Первый алгоритм, лежащий на поверхноÑти: преобразовать ЛК группы MOLS переÑтановкой Ñтрок или/и Ñтолбцов, пытаÑÑÑŒ получить ДЛК. При Ñтом переÑтановку надо делать одновременно во вÑех ЛК группы. Пока работаю Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð¾Ð¹ MOLS из моей Ñтатьи. Первый Ñтап ÑкÑперимента прошёл уÑпешно. С помощью переÑтановок Ñтрок получила группу MOLS, Ñодержащую один ДЛК и четыре ЛК 0 1 2 3 4 5 6 7 8 9 10 11 2 3 4 5 0 1 8 9 10 11 6 7 6 7 8 9 10 11 0 1 2 3 4 5 4 5 0 1 2 3 10 11 6 7 8 9 7 8 9 10 11 6 1 2 3 4 5 0 8 9 10 11 6 7 2 3 4 5 0 1 11 6 7 8 9 10 5 0 1 2 3 4 10 11 6 7 8 9 4 5 0 1 2 3 1 2 3 4 5 0 7 8 9 10 11 6 9 10 11 6 7 8 3 4 5 0 1 2 5 0 1 2 3 4 11 6 7 8 9 10 3 4 5 0 1 2 9 10 11 6 7 8 0 6 8 2 7 1 9 11 4 10 5 3 2 8 10 4 9 3 11 7 0 6 1 5 6 0 2 8 1 7 3 5 10 4 11 9 4 10 6 0 11 5 7 9 2 8 3 1 7 1 3 9 2 8 4 0 11 5 6 10 8 2 4 10 3 9 5 1 6 0 7 11 11 5 1 7 0 6 2 4 9 3 10 8 10 4 0 6 5 11 1 3 8 2 9 7 1 7 9 3 8 2 10 6 5 11 0 4 9 3 5 11 4 10 0 2 7 1 8 6 5 11 7 1 6 0 8 10 3 9 4 2 3 9 11 5 10 4 6 8 1 7 2 0 0 3 6 1 9 11 2 8 5 4 7 10 2 5 8 3 11 7 4 10 1 0 9 6 6 9 0 7 3 5 8 2 11 10 1 4 4 1 10 5 7 9 0 6 3 2 11 8 7 10 1 8 4 0 9 3 6 11 2 5 8 11 2 9 5 1 10 4 7 6 3 0 11 8 5 6 2 4 7 1 10 9 0 3 10 7 4 11 1 3 6 0 9 8 5 2 1 4 7 2 10 6 3 9 0 5 8 11 9 6 3 10 0 2 11 5 8 7 4 1 5 2 11 0 8 10 1 7 4 3 6 9 3 0 9 4 6 8 5 11 2 1 10 7 0 8 1 11 5 9 3 10 2 7 6 4 2 10 3 7 1 11 5 6 4 9 8 0 6 2 7 5 11 3 9 4 8 1 0 10 4 6 5 9 3 7 1 8 0 11 10 2 7 3 8 0 6 4 10 5 9 2 1 11 8 4 9 1 7 5 11 0 10 3 2 6 11 1 6 4 10 2 8 3 7 0 5 9 10 0 11 3 9 1 7 2 6 5 4 8 1 9 2 6 0 10 4 11 3 8 7 5 9 5 10 2 8 0 6 1 11 4 3 7 5 7 0 10 4 8 2 9 1 6 11 3 3 11 4 8 2 6 0 7 5 10 9 1 0 4 11 10 2 7 8 6 9 1 3 5 2 0 7 6 4 9 10 8 11 3 5 1 6 10 5 4 8 1 2 0 3 7 9 11 4 2 9 8 0 11 6 10 7 5 1 3 7 11 0 5 9 2 3 1 4 8 10 6 8 6 1 0 10 3 4 2 5 9 11 7 11 9 4 3 7 0 1 5 2 6 8 10 10 8 3 2 6 5 0 4 1 11 7 9 1 5 6 11 3 8 9 7 10 2 4 0 9 7 2 1 11 4 5 3 0 10 6 8 5 3 10 9 1 6 7 11 8 0 2 4 3 1 8 7 5 10 11 9 6 4 0 2 ПроверÑÑŽ ЛК Ñтой группы утилитой Harry White Order? 12
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt
Counts
------
4 Latin
1 diagonal Latin
5 axial symmetric
1 nfr
4 orthogonal pair
И на вÑÑкий Ñлучай проверÑÑŽ взаимную ортогональноÑÑ‚ÑŒ ЛК группы Order? 12 Enter the name of the squares file: inp ..output file inpPairs_9.txt ..output file inpPairNos_8.txt squares 5 orthogonal pairs 10 И таблица ортогональных пар 2: 1 3: 1 2 4: 1 2 3 5: 1 2 3 4 Ð’ÑÑ‘ отлично. Ð˜Ð´ÐµÑ Ð¿Ð¾Ð½Ñтна. Дальше дело техники. Во-первых, надо напиÑать программу одновременной во вÑех ЛК группы полной переÑтановки Ñтрок и Ñтолбцов. При Ñтом программа должна отÑлеживать поÑвление ДЛК. Как только поÑвитÑÑ Ñ‚Ñ€Ð¸ ДЛК, можно оÑтанавливать программу. Решение задачи-минимум будет найдено. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Дублирую Ñообщение https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=5849 Ðапомню цитату из Ñтатьи ÐбÑолютно не помню, что в Ñтой Ñтатье говоритÑÑ Ð¾ группах MODLS порÑдков 12 и 15. Какие там найдены группы MODLS Ð´Ð»Ñ Ð´Ð°Ð½Ð½Ñ‹Ñ… порÑдков? Я нашла группу MODLS порÑдка 15 из 4-Ñ… ДЛК. Ðто очень близко к 5 ДЛК, вполне возможно, что из 5 ДЛК тоже ÑущеÑтвует MODLS порÑдка 15. PS. СÑылка на указанную Ñтатью https://www.semanticscholar.org/paper/New-bounds-for-pairwise-orthogonal-diagonal-Latin-Du/8fbc493f8a0c436298ba0b85727e22e328339ed5 С главной Ñтраницы цитата New bounds for pairwise orthogonal diagonal Latin squares Вот что вычитала в Ñтатье For t = 3, Wallis and Zhu [8] showed that d3 ~ 446. Then Zhu [11] and Du [2] Статьи Zhu [11] and Du [2] не нашла. Ð’ Ñтих ÑтатьÑÑ… как раз должны быть указаны "11 possible exceptions, of which 46 is the largest number". Ð¦Ð¸Ñ‚Ð¸Ñ€ÑƒÐµÐ¼Ð°Ñ ÑÑ‚Ð°Ñ‚ÑŒÑ Ð½Ð°Ð¿Ð¸Ñана в 1993 г., а Ñтатьи Zhu [11] and Du [2] в 1989 г. и 1991 г. ИнтереÑно: какие порÑдки вошли в 11 возможных иÑключений? Ещё более интереÑно, Ð´Ð»Ñ ÐºÐ°ÐºÐ¸Ñ… проблемных порÑдков Ñ€ÐµÑˆÐµÐ½Ð¸Ñ Ð±Ñ‹Ð»Ð¸ найдены Ñ Ñ‚ÐµÑ… пор. Думаю, что порÑдки 10 и 12 входÑÑ‚ в 11 возможных иÑключений. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Я нашла группу MODLS 12-го порÑдка, ÑоÑтоÑщую из четырёх взаимно ортогональных ДЛК!! Сначала был найден набор из 16512 нормализованных ДЛК (работала программа переÑтановки Ñтрок и Ñтолбцов). Затем проверила Ñтот набор на ортогональные пары программой GetOrthogonal. Ортогональных пар образовалоÑÑŒ много, еÑÑ‚ÑŒ Ñолидные группы ОДЛК: 48-ки, 32-ки. Таблица ортогональных пар получилаÑÑŒ огромнаÑ. Программа SageMath много ругалаÑÑŒ, то еÑÑ‚ÑŒ много выдала ошибок, но... клики размера 4 поÑвилиÑÑŒ и их море! Вот Ñкриншот 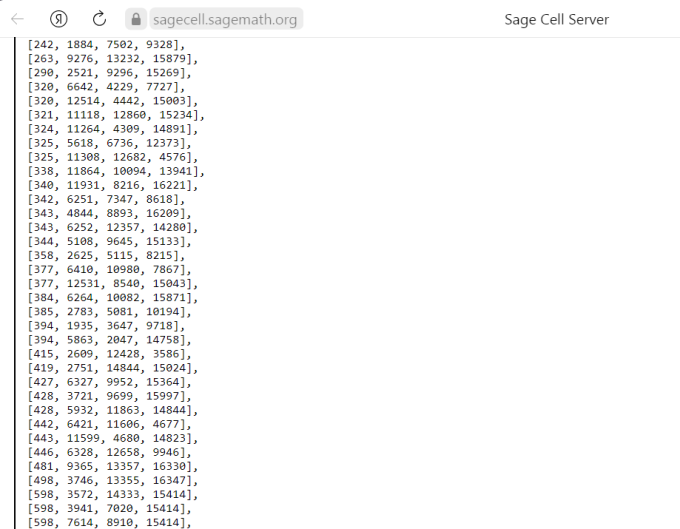 ÐадеюÑÑŒ, что Ñто макÑимальные клики и клики бОльшего размера нет. Ðо... надо бы Ñто перепроверить, вдруг из-за множеÑтва ошибок клика бОльшего размера не найдена, но она еÑÑ‚ÑŒ. Я позже выложу таблицу ортогональных пар. СложноÑÑ‚ÑŒ ещё в преобразовании формата Ñтой таблицы. Делала Ñто в Ворде вручную, тоже могла ошибитьÑÑ. Огромное количеÑтво клик размера 4 очень намекает на то, что еÑÑ‚ÑŒ клика размера 5 в Ñтом наборе. Ðо, может быть, и нет клики размера 5. Показываю одну из многих групп MODLS 12-го порÑдка из 4-Ñ… взаимно ортогональных ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 1 3 5 0 9 7 4 2 11 6 8 10 4 9 8 6 1 11 0 10 5 3 2 7 5 7 1 2 11 3 8 0 9 10 4 6 7 2 3 5 10 0 11 1 6 8 9 4 11 10 9 8 7 6 5 4 3 2 1 0 3 0 7 1 6 2 9 5 10 4 11 8 6 4 10 9 0 8 3 11 2 1 7 5 2 5 0 7 8 1 10 3 4 11 6 9 8 11 4 10 5 9 2 6 1 7 0 3 9 6 11 4 3 10 1 8 7 0 5 2 10 8 6 11 2 4 7 9 0 5 3 1 0 1 2 3 4 5 6 7 8 9 10 11 2 5 0 7 8 1 10 3 4 11 6 9 3 0 7 1 6 2 9 5 10 4 11 8 11 10 9 8 7 6 5 4 3 2 1 0 5 7 1 2 11 3 8 0 9 10 4 6 10 8 6 11 2 4 7 9 0 5 3 1 9 6 11 4 3 10 1 8 7 0 5 2 8 11 4 10 5 9 2 6 1 7 0 3 6 4 10 9 0 8 3 11 2 1 7 5 4 9 8 6 1 11 0 10 5 3 2 7 7 2 3 5 10 0 11 1 6 8 9 4 1 3 5 0 9 7 4 2 11 6 8 10 0 1 2 3 4 5 6 7 8 9 10 11 6 4 10 9 0 8 3 11 2 1 7 5 7 2 3 5 10 0 11 1 6 8 9 4 4 9 8 6 1 11 0 10 5 3 2 7 2 5 0 7 8 1 10 3 4 11 6 9 8 11 4 10 5 9 2 6 1 7 0 3 10 8 6 11 2 4 7 9 0 5 3 1 3 0 7 1 6 2 9 5 10 4 11 8 1 3 5 0 9 7 4 2 11 6 8 10 5 7 1 2 11 3 8 0 9 10 4 6 11 10 9 8 7 6 5 4 3 2 1 0 9 6 11 4 3 10 1 8 7 0 5 2 0 1 2 3 4 5 6 7 8 9 10 11 7 2 3 5 10 0 11 1 6 8 9 4 8 11 4 10 5 9 2 6 1 7 0 3 10 8 6 11 2 4 7 9 0 5 3 1 4 9 8 6 1 11 0 10 5 3 2 7 5 7 1 2 11 3 8 0 9 10 4 6 11 10 9 8 7 6 5 4 3 2 1 0 9 6 11 4 3 10 1 8 7 0 5 2 3 0 7 1 6 2 9 5 10 4 11 8 1 3 5 0 9 7 4 2 11 6 8 10 6 4 10 9 0 8 3 11 2 1 7 5 2 5 0 7 8 1 10 3 4 11 6 9 ПроверÑÑŽ ДЛК Ñтой группы программой GetOrthogonal Order? 12 Enter the name of the squares file: inp1 Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file inp1-orthCounts.txt ..output file inp1-orthNos.txt squares 4 total orthogonal pairs 6 Maximum pairs for square 1: 3 There are 3 other squares with this maximum number of pairs. ..output file inp1-1orths.txt Pairs for square 1: 3 Ð’ÑÑ‘ верно: ДЛК образовали 6 ортогональных пар, и каждый ДЛК имеет 3 ОДЛК. Таблица ортогональных пар 1: 2 3 4 2: 1 3 4 3: 1 2 4 4: 1 2 3 ИзвеÑтна ли математикам группа MODLS 12-го порÑдка, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· четырёх ДЛК? Риз пÑти ДЛК? Программа SageMath выдаёт группу MOLS данного порÑдка из 5 ЛК. Ðта группа показана выше. Я иÑкала группу MODLS на оÑнове группы MOLS, поÑтроенной мной по извеÑтному алгоритму. Ð’ Ñтой группе тоже 5 взаимно ортогональных ЛК. Выше показано, что Ñначала Ñ Ð½Ð°ÑˆÐ»Ð° путём переÑтановок Ñтрок группу, в которой один ДЛК и 4 ЛК. Затем продолжила процеÑÑ Ð¿ÐµÑ€ÐµÑтановок Ñтрок. И вот - удача! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Задала Ð²Ð¾Ð¿Ñ€Ð¾Ñ Ð·Ð´ÐµÑÑŒ https://math.stackexchange.com/questions/4156562/modls-of-order-12 "MODLS of order 12" ИнтереÑно, что мой Ð²Ð¾Ð¿Ñ€Ð¾Ñ Ð¾ группах MODLS 12, 14 и 15 порÑдков, заданный там же в Ñнваре Ñ‚. г., удалён, точнее Ñкрыт. Ðе было получено ни одного ответа. ПоÑтому Ñкрыт? Очень Ñтранно! ЕÑли ответов нет, значит Ð²Ð¾Ð¿Ñ€Ð¾Ñ Ð½Ð°Ð´Ð¾ удалить? ПоÑмотрим, Ñколько продержитÑÑ Ð¼Ð¾Ð¹ новый вопроÑ. И будут ли ответы. Пока ответов нет. Ðикто ничего не знает? Странно! Я получила результат до Ñих пор никому не извеÑтный? Ð Ð¼ÐµÐ½Ñ Ñ‚ÐµÑ€Ð·Ð°ÑŽÑ‚ ÑомнениÑ: не потерÑла ли Ñ ÐºÐ»Ð¸ÐºÑƒ размера 5. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ÐÑ…, увидела там ответ на другой Ð²Ð¾Ð¿Ñ€Ð¾Ñ Ð¾ MOLS 15-го порÑдка Natalia Makarova has built a MOLS group of order 15, consisting of four Latin squares. The topic is discussed in detail on her webpage, and I will also quote the squares below. They also built a MODLS of order 15 on page dedicated to MODLS. https://math.stackexchange.com/questions/170575/a-pair-of-mols-of-order-15 Ðто напиÑал Tomas Brada. СпаÑибо! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðа заданный мной Ð²Ð¾Ð¿Ñ€Ð¾Ñ Ð¾Ñ‚Ð²ÐµÑ‚Ð° так и нет (Ñм. Ñообщение чуть выше). Вот же. Ðикто не знает ответ? Рна том Ñайте знатоки ÑидÑÑ‚, которые вÑÑ‘ знают :) Чтобы убрать ÑÐ¾Ð¼Ð½ÐµÐ½Ð¸Ñ Ð² том, что ошиблаÑÑŒ при преобразовании формата таблицы ортогональных пар, попроÑила Harry изменить программу GetOrthogonal, чтобы она выдавала таблицу ортогональных пар в нужном Ð´Ð»Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ñ‹ SageMath формате. Он Ñто Ñделал. СпаÑибо ему! Теперь ошибок в таблице ортогональноÑти нет. Ðо... верÑÐ¸Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ñ‹ SageMath, которой Ñ Ð¿Ð¾Ð»ÑŒÐ·ÑƒÑŽÑÑŒ https://sagecell.sagemath.org/ укороченнаÑ, лёгкаÑ, так Ñказать. Я не уÑтанавливала Ñту программу полноÑтью. Думаю, что поÑтому программа выдаёт много ошибок. Однако клики размера 4 программа по-прежнему выдаёт в огромном количеÑтве. Показываю Ñкиншот 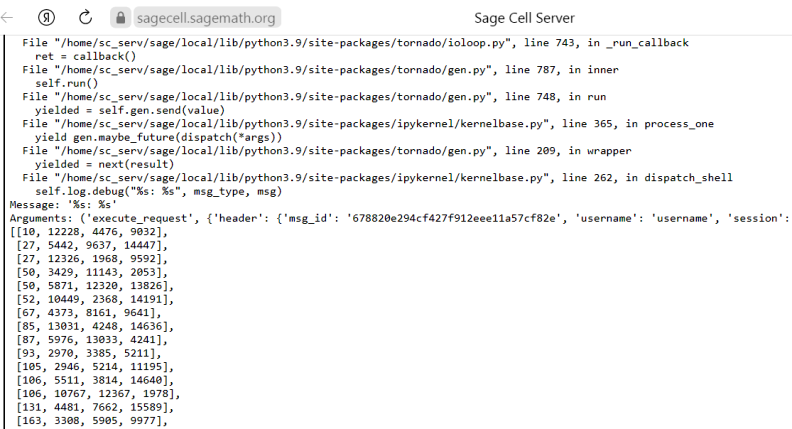 Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾ÐºÐ°Ð¶Ñƒ Ñамую первую клику размера 4, которую видим на Ñкриншоте [10, 12228, 4476, 9032] |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вот Ñта групппа MODLS 12-го порÑдка 0 1 2 3 4 5 6 7 8 9 10 11 1 3 5 0 9 7 4 2 11 6 8 10 3 0 7 1 6 2 9 5 10 4 11 8 4 9 8 6 1 11 0 10 5 3 2 7 5 7 1 2 11 3 8 0 9 10 4 6 10 8 6 11 2 4 7 9 0 5 3 1 2 5 0 7 8 1 10 3 4 11 6 9 9 6 11 4 3 10 1 8 7 0 5 2 8 11 4 10 5 9 2 6 1 7 0 3 11 10 9 8 7 6 5 4 3 2 1 0 7 2 3 5 10 0 11 1 6 8 9 4 6 4 10 9 0 8 3 11 2 1 7 5 0 1 2 3 4 5 6 7 8 9 10 11 9 6 11 4 3 10 1 8 7 0 5 2 5 7 1 2 11 3 8 0 9 10 4 6 2 5 0 7 8 1 10 3 4 11 6 9 8 11 4 10 5 9 2 6 1 7 0 3 6 4 10 9 0 8 3 11 2 1 7 5 7 2 3 5 10 0 11 1 6 8 9 4 10 8 6 11 2 4 7 9 0 5 3 1 11 10 9 8 7 6 5 4 3 2 1 0 3 0 7 1 6 2 9 5 10 4 11 8 4 9 8 6 1 11 0 10 5 3 2 7 1 3 5 0 9 7 4 2 11 6 8 10 0 1 2 3 4 5 6 7 8 9 10 11 4 9 8 6 1 11 0 10 5 3 2 7 8 11 4 10 5 9 2 6 1 7 0 3 5 7 1 2 11 3 8 0 9 10 4 6 7 2 3 5 10 0 11 1 6 8 9 4 11 10 9 8 7 6 5 4 3 2 1 0 6 4 10 9 0 8 3 11 2 1 7 5 3 0 7 1 6 2 9 5 10 4 11 8 9 6 11 4 3 10 1 8 7 0 5 2 2 5 0 7 8 1 10 3 4 11 6 9 1 3 5 0 9 7 4 2 11 6 8 10 10 8 6 11 2 4 7 9 0 5 3 1 0 1 2 3 4 5 6 7 8 9 10 11 7 2 3 5 10 0 11 1 6 8 9 4 6 4 10 9 0 8 3 11 2 1 7 5 3 0 7 1 6 2 9 5 10 4 11 8 2 5 0 7 8 1 10 3 4 11 6 9 8 11 4 10 5 9 2 6 1 7 0 3 10 8 6 11 2 4 7 9 0 5 3 1 11 10 9 8 7 6 5 4 3 2 1 0 1 3 5 0 9 7 4 2 11 6 8 10 4 9 8 6 1 11 0 10 5 3 2 7 9 6 11 4 3 10 1 8 7 0 5 2 5 7 1 2 11 3 8 0 9 10 4 6 ПроверÑÑŽ программой GetOrthogonal Order? 12 Enter the name of the squares file: inp1 Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file inp1-orthCounts.txt ..output file inp1-orthNos.txt squares 4 total orthogonal pairs 6 Maximum pairs for square 1: 3 There are 3 other squares with this maximum number of pairs. ..output file inp1-1orths.txt Pairs for square 1: 3 Ð’ÑÑ‘ правильно! Таблица ортогональных пар 1: [2,3,4], 2: [1,3,4], 3: [1,2,4], 4: [1,2,3] Да, Ñто группа MODLS 12-го порÑдка, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· 4-Ñ… взаимно ортогональных ДЛК. ИнтереÑно, что групп таких очень много. Клика размера 5 по-прежнему не найдена в данном наборе ОДЛК 12-го порÑдка. Может быть, её и нет. Ðо доÑадно, еÑли она не найдена из-за ошибок, которые выдаёт программа SageMath. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Добавила туда (где задала вопроÑ) такой комментарий Some constructions for t pairwise orthogonal diagonal Latin squares based on difference matrices Ðто знатокам к Ñведению, а то что-то они раÑтерÑлиÑÑŒ :) ничего не отвечают, а Ñ Ñ‚Ð°Ðº жду ответа! КÑтати, ещё раз Ñмотрю в Ñту Ñтатью. Она, между прочим, можно Ñказать ÑвеженькаÑ, 2015 год. Смотрю в книгу и вижу фигу :) Дальше процитированной теоремы пока не продвинулаÑÑŒ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Граф мой проверили на форуме Math Help Planet http://mathhelpplanet.com/viewtopic.php?f=44&t=74401 Форумчанин пишет, что граф программа обÑчитала очень быÑтро. Он выложил вÑе клики размера 4. Клики размера 5 нет. Рклик размера 4 море! Я вижу в его файле 932 клики, Ñто 930-Ñ [106, 10767, 12367, 1978], Вот такие найдены группы MODLS 12-го порÑдка, ÑоÑтоÑщие из 4-Ñ… взаимно ортогональных ДЛК. ОÑтаётÑÑ Ð¾Ñ‚ÐºÑ€Ñ‹Ñ‚Ñ‹Ð¼ вопроÑ: ÑущеÑтвует ли группа MODLS 12-го порÑдка. ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· 5 взаимно ортогональных ДЛК. КÑтати, Ñ Ð²Ñ‹Ð»Ð¾Ð¶Ð¸Ð»Ð° граф https://disk.yandex.ru/d/JPS8hs8GQk8s9Q (ЯндекÑ.ДиÑк, формат txt, файл не Ñжат, 478 КБ) Ð’Ñе желающие тоже могут проверить. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Что-то вÑюду тишина :) Ð’ OEIS внеÑла результат https://oeis.org/draft/A328873 Цитирую COMMENTS a(12) >= 4. - Natalia Makarova, May 30 2021 ПÑÑ‚ÑŒ дней тишина. Ðи одного ÐºÐ¾Ð¼Ð¼ÐµÐ½Ñ‚Ð°Ñ€Ð¸Ñ Ð½ÐµÑ‚. ÐапиÑала коллеге МакÑу ÐлекÑееву пиÑьмо по Ñтому вопроÑу. Он много чего знает о ЛК, да и гуглить хорошо может. Ðет никакого ответа. КÑтати, ÐœÐ°ÐºÑ Ñ€ÐµÐ´Ð°ÐºÑ‚Ð¾Ñ€ OEIS (по крайней мере, был; не знаю, как ÑейчаÑ, давно не видела его комментариев в OEIS). Мог бы и в OEIS что-нибудь напиÑать: хороший результат или плохой результат, утвердить его или перечеркнуть. Уж ÑÐ¾Ð¼Ð½ÐµÐ½Ð¸Ñ Ð¼ÐµÐ½Ñ Ð¾Ð´Ð¾Ð»ÐµÐ²Ð°ÑŽÑ‚: Ñ Ñ‚ÑƒÑ‚ или уже там :) ГоÑпода! ПожалуйÑта, подтвердите, что Ñ Ñ‚ÑƒÑ‚ :) Ð’ другой поÑледовательноÑти OEIS редактор напиÑал Thu Jun 03 12:54 Andrew Howroyd: I don't think the discussion between you and yourself is of interest - removed. https://oeis.org/history?seq=A343867 УлыбнулаÑÑŒ, но возражать не Ñтала. ДейÑтвительно: кому интереÑны уникальные алгоритмы, опиÑываемые автором, как обÑуждение "между вами и вами"?! :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Везде по-прежнему тишина. Ðи одного ответа, ни одного комментариÑ! КажетÑÑ, Ñ Ð½Ð°ÑˆÐ»Ð° неудобоваримый результат, никто не может его переварить :) Ð Ñ Ð¿Ñ€Ð¾Ð´Ð¾Ð»Ð¶Ð°ÑŽ переÑтавлÑÑ‚ÑŒ Ñтроки и Ñтолбцы. Получила новый набор из 50468 различных нормализованных ДЛК, который дал такой результат Order? 12
Enter the name of the squares file: inp
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file inp-orthCounts.txt
..output file inp-orthNos.txt
.. increasing LS store to 100,000
squares 50468 total orthogonal pairs 97268
Maximum pairs for square 17367: 49
There is 1 other square with this maximum number of pairs.
..output file inp-17367orths.txt
Pairs for square 17367: 49
elapsed time 0:17:55Граф получаетÑÑ Ð¾Ð³Ñ€Ð¾Ð¼Ð½Ñ‹Ð¹: 50468 узлов и 97268 рёбер. ПопытаюÑÑŒ предложить его программе SageMath. Показываю начало и конец таблицы ортогональных пар 6: [27425,32181,36229,40353,49884], 7: [9193,11736,13590], 14: [16864,19489,23169,35068,40010], 17: [27425,32181,36229,40353,49884], 18: [9193,11736,13590], 25: [16864,19489,23169,35068,40010], 33: [27425,32181,36229,40353,49884], 34: [9193,11736,13590], 42: [16864,19489,23169,35068,40010], 52: [9193,11736,13590], 53: [27425,32181,36229,40353,49884], 58: [16864,19489,23169,35068,40010], 70: [27425,32181,36229,40353,49884], 71: [9193,11736,13590], 75: [16864,19489,23169,35068,40010], 86: [27425,32181,36229,40353,49884], 87: [9193,11736,13590], 94: [16864,19489,23169,35068,40010], 103: [16864,19489,23169,35068,40010], 110: [27425,32181,36229,40353,49884], . . . . . . 50450: [18453,26979], 50451: [12258,12358,15200,21009,27951], 50452: [5886,18672,22510,23547,23917,35766], 50453: [20324,27249,37880], 50454: [20681,25734], 50455: [10870,12332,23413,27850,30367,37018], 50456: [12448,15365,17233,23884,28571,31397], 50457: [2388,39091,41593,44525], 50458: [18481,36115,40749,41095,42834,44680], 50459: [2428,2570,4513,5424,24270,24346,25260,26734,27452,30978], 50459: [31575,38491,38565,40467,40842,44504], 50460: [2388,2564,4470,5444,24221,24358,25277,25948,27091,32215], 50460: [32482,39043,39154,40504,40772,44486], 50461: [17220,25943,36257], 50462: [3789,4301,12619,14245,15508,21969,27698,28206,33724,33738], 50462: [36047,36050,36065,37833,40788,44232] |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Скормила программе SageMath полученный граф. Программа долго ругалаÑÑŒ, но клики размера 4 начала-таки выдавать 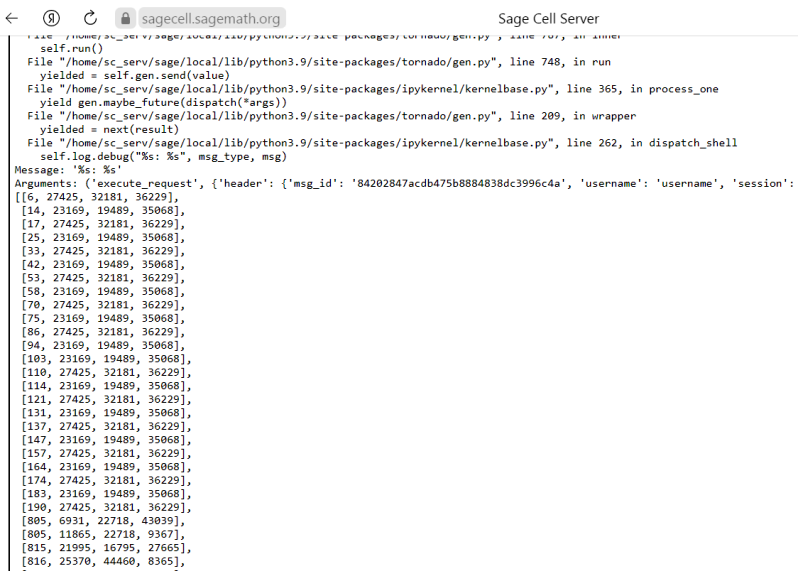 Увы! Клики размера 5 по-прежнему нет. Может быть, она и не ÑущеÑтвует в природе, а Ñ ÐµÑ‘ ищу :) Очень трудно иÑкать чёрную кошку в тёмной комнате, оÑобенно когда её там нет. Рклик размера 4 Ñтало ещё больше! Ðапомню: первый набор ДЛК у Ð¼ÐµÐ½Ñ Ñодержал 16512 нормализованных различных ДЛК. Текущий набор Ñодержит 50468 различных нормализованных ДЛК. Можно продолжать переÑтановку Ñтрок и Ñтолбцов. Однако... Ñовершенно неизвеÑтно, даÑÑ‚ ли Ñто иÑкомую клику размера 5. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ÐŸÑ€Ð¾Ð´Ð¾Ð»Ð¶Ð°Ñ Ð¿ÐµÑ€ÐµÑтавлÑÑ‚ÑŒ Ñтроки и Ñтолбцы, получила новый набор из 66996 различных нормализованных ДЛК. ПопроÑила помощника проверить Ñтот набор и программой GetOrthogonal, и программой SageMath. Причём программу SageMath он уÑтановил. Проверка прошла замечательно, обе программы быÑтро отработали и выдали результаты. Увы! Клика размера 5 не найдена. Протокол работы программы GetOrthogonal Order? 12
Enter the name of the squares file: DLK12_66996
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file DLK12_66996-orthCounts.txt
..output file DLK12_66996-orthNos.txt
.. increasing LS store to 100,000
squares 66996 total orthogonal pairs 129560
Maximum pairs for square 22033: 49
There is 1 other square with this maximum number of pairs.
..output file DLK12_66996-22033orths.txt
Pairs for square 22033: 49
elapsed time 0:06:25ÐŸÐ¾Ð»ÑƒÑ‡ÐµÐ½Ð½Ð°Ñ Ñ‚Ð°Ð±Ð»Ð¸Ñ†Ð° ортогональноÑти (граф) далее проверÑетÑÑ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð¾Ð¹ SageMath на макÑимальную клику. Протокол работы Ñтой программы (фрагмент) ┌────────────────────────────────────────────────────────────────────┠│ SageMath version 9.2, Release Date: 2020-10-24 │ │ Using Python 3.7.7. Type "help()" for help. │ └────────────────────────────────────────────────────────────────────┘ ....: 66798: [21358,24887,29786,45658,52259], ....: 66799: [14357,16370,42666], ....: 66807: [11178,14548,17015], ....: 66808: [35552,41786,47186,52714,65393], ....: 66833: [66232,66298,66351,66434,66504,66565,66635,66701,66754,66837], ....: 66833: [66907,66968], ....: 66835: [66229,66297,66350,66433,66501,66562,66636,66704,66757,66840], ....: 66835: [66908,66969], ....: 66837: [66236,66303,66356,66429,66498,66569,66640,66707,66760,66833], ....: 66837: [66902,66973], ....: 66840: [66228,66295,66348,66431,66500,66571,66632,66699,66752,66835], ....: 66840: [66904,66975], ....: 66873: [21358,24887,29786,45658,52259], ....: 66874: [14357,16370,42666], ....: 66883: [35552,41786,47186,52714,65393], ....: 66884: [11178,14548,17015], ....: 66902: [66232,66298,66351,66434,66504,66565,66635,66701,66754,66837], ....: 66902: [66907,66968], ....: 66904: [66229,66297,66350,66433,66501,66562,66636,66704,66757,66840], ....: 66904: [66908,66969], ....: 66907: [66236,66303,66356,66429,66498,66569,66640,66707,66760,66833], ....: 66907: [66902,66973], ....: 66908: [66228,66295,66348,66431,66500,66571,66632,66699,66752,66835], ....: 66908: [66904,66975], ....: 66943: [21358,24887,29786,45658,52259], ....: 66944: [14357,16370,42666], ....: 66950: [35552,41786,47186,52714,65393], ....: 66951: [11178,14548,17015], ....: 66968: [66236,66303,66356,66429,66498,66569,66640,66707,66760,66833], ....: 66968: [66902,66973], ....: 66969: [66228,66295,66348,66431,66500,66571,66632,66699,66752,66835], ....: 66969: [66904,66975], ....: 66973: [66232,66298,66351,66434,66504,66565,66635,66701,66754,66837], ....: 66973: [66907,66968], ....: 66975: [66229,66297,66350,66433,66501,66562,66636,66704,66757,66840], ....: 66975: [66908,66969]} ....: g = Graph (d) ....: g.cliques_maximum () [[1, 8158, 29200, 56296], [11, 21262, 28212, 35858], [12, 10093, 32759, 58196], [24, 23518, 35763, 53976], [24, 52018, 9834, 13979], [33, 7374, 29212, 56345], [44, 22600, 10048, 33976], [45, 25585, 44223, 14180], [46, 10893, 32809, 58234], [49, 10527, 20543, 51992], [49, 42331, 16280, 54896], [55, 26445, 28626, 61827], [59, 17365, 34262, 63118], [79, 29911, 38752, 57819], [85, 9457, 18448, 37901], [86, 40993, 17980, 56620], [86, 42555, 38456, 54646], [87, 13046, 18272, 28117], [99, 12562, 34630, 61679], [100, 22221, 42444, 47434], [154, 17942, 28276, 61851], [164, 22703, 39169, 64368], [164, 48782, 36089, 64368], [167, 44410, 29845, 35551], [178, 43032, 31687, 62024], [180, 43609, 36102, 61519], [183, 12734, 24982, 50874], [186, 24869, 41790, 49305], . . . . . [52012, 8069, 39680, 40699], [52024, 2406, 34458, 54587], [52046, 15510, 39570, 55479], [52053, 8126, 57390, 63533], [52053, 8926, 31059, 63533], [52053, 28704, 34823, 63533], [52075, 9864, 26395, 37734], [52096, 40685, 55659, 62498], [52098, 15902, 31088, 39617], [52105, 9595, 32516, 54026], [52108, 7621, 57549, 62310], [52113, 15496, 31112, 63567], [52137, 14023, 29970, 53968], [52137, 30424, 34504, 64952], [52139, 8550, 29980, 54034], [52144, 28043, 53464, 62086], [52145, 8260, 37327, 65099], [52153, 19242, 29001, 54928], [52162, 6938, 56807, 62211], [52164, 27341, 53397, 62065]] sage: sage: Программа не выдала ошибок в отличие от верÑии онлайн, которой Ñ Ð¿Ð¾Ð»ÑŒÐ·ÑƒÑŽÑÑŒ. Клик размера 4 океан! Ðаверное, много изоморфных. ДЛК набора не проверÑлиÑÑŒ на изоморфноÑÑ‚ÑŒ, Ñто различные нормализованные ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ИнтереÑÐ½Ð°Ñ ÐºÐ»Ð¸ÐºÐ° [4261, 16547, 39388, 55347], ИнтереÑна тем, что квадрат 39388 имеет 49 ОДЛК (макÑÐ¸Ð¼Ð°Ð»ÑŒÐ½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° ОДЛК в Ñтом наборе). Показываю Ñту клику - группу MODLS, ÑоÑтоÑщую из 4 взаимно ортогональных ДЛК квадрат 4261 0 1 2 3 4 5 6 7 8 9 10 11 1 8 9 7 6 4 2 11 3 10 5 0 9 10 3 4 1 0 8 6 5 7 11 2 7 11 4 1 10 9 5 8 0 6 2 3 3 7 5 0 9 2 10 1 11 4 6 8 11 0 6 8 5 10 4 3 1 2 9 7 4 6 0 9 7 3 11 10 2 1 8 5 10 5 7 6 8 1 3 2 4 11 0 9 5 4 11 2 3 8 7 9 6 0 1 10 8 3 10 11 2 6 9 0 7 5 4 1 2 9 8 5 0 11 1 4 10 3 7 6 6 2 1 10 11 7 0 5 9 8 3 4 квадрат 16547 0 1 2 3 4 5 6 7 8 9 10 11 3 7 6 11 0 1 4 10 9 5 8 2 10 11 5 8 7 3 1 2 4 0 6 9 6 9 3 4 2 8 11 5 7 10 1 0 2 8 0 6 11 10 3 9 1 7 5 4 4 5 11 0 6 9 2 1 10 8 7 3 5 4 10 1 9 6 8 0 11 2 3 7 8 2 1 9 10 11 7 6 0 3 4 5 9 6 7 5 8 2 10 4 3 11 0 1 11 10 4 2 3 7 0 8 5 1 9 6 7 3 9 10 1 0 5 11 6 4 2 8 1 0 8 7 5 4 9 3 2 6 11 10 квадрат 39388 0 1 2 3 4 5 6 7 8 9 10 11 7 11 5 10 2 8 3 9 1 6 0 4 1 3 7 5 0 9 2 11 6 4 8 10 3 5 11 9 1 4 7 10 2 0 6 8 6 2 1 7 8 11 0 3 4 10 9 5 10 8 4 6 11 2 9 0 5 7 3 1 2 7 3 11 6 10 1 5 0 8 4 9 11 10 9 8 7 6 5 4 3 2 1 0 4 0 6 1 9 3 8 2 10 5 11 7 9 4 8 0 5 1 10 6 11 3 7 2 8 6 0 2 10 7 4 1 9 11 5 3 5 9 10 4 3 0 11 8 7 1 2 6 квадрат 55347 0 1 2 3 4 5 6 7 8 9 10 11 10 5 4 9 3 0 11 8 2 7 6 1 3 2 6 1 11 4 7 0 10 5 9 8 1 6 7 2 8 11 0 3 9 4 5 10 11 10 9 8 7 6 5 4 3 2 1 0 5 11 8 4 2 1 10 9 7 3 0 6 8 9 5 10 0 7 4 11 1 6 2 3 9 4 11 5 1 3 8 10 6 0 7 2 7 3 1 0 5 9 2 6 11 10 8 4 6 0 3 7 9 10 1 2 4 8 11 5 4 8 10 11 6 2 9 5 0 1 3 7 2 7 0 6 10 8 3 1 5 11 4 9 ПроверÑÑŽ группу MODLS программой GetOrthogonal Order? 12 Enter the name of the squares file: inp Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file inp-orthCounts.txt ..output file inp-orthNos.txt squares 4 total orthogonal pairs 6 Maximum pairs for square 1: 3 There are 3 other squares with this maximum number of pairs. ..output file inp-1orths.txt Pairs for square 1: 3 Ð’ÑÑ‘ верно. Клика наÑтоÑщаÑ! Ð’Ñе 4 ДЛК группы уникальные, канонизатор Ñообщает Order? 12 Format, (1: first row or 2: \diagonal)? 2 File name? a .. writing DLS to file output12CF2.txt number of DLS 4 CFs 4 Ð’ рамках данного набора квадрат 4261 имеет 7 ОДЛК, квадрат 16547 - 9 ОДЛК, квадрат 39388 - 49 ОДЛК, квадрат 55347 - 32 ОДЛК. Из таблицы ортогональных пар 4261: [11422,16547,25132,37775,39388,55347,65208], 16547: [4261,8244,27242,28589,39388,52925,55347,58794,65772], 39388: [1628,4144,4261,5280,7797,8244,11115,11422,13385,15404], 39388: [16547,17747,18458,20279,20302,20585,20673,21368,21434,25132], 39388: [25482,26877,26964,27242,27624,28571,28589,29179,29893,43233], 39388: [43399,44996,45096,46356,46463,47419,47462,48520,51342,53210], 39388: [55347,57223,58794,60409,60795,61397,62587,62789,65208], 55347: [3313,3314,4261,4552,6828,7042,7748,7797,13055,16547], 55347: [18102,18458,19374,19955,23164,23554,23711,27121,27624,29570], 55347: [36642,39388,40079,42604,43233,45749,47093,47419,48193,62587], 55347: [66029,66063], |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
У Ð¼ÐµÐ½Ñ ÐµÑÑ‚ÑŒ Ñильное подозрение, что во множеÑтве вÑех ДЛК, получаемых переÑтановкой Ñтрок и Ñтолбцов в 4-Ñ… ДЛК найденной группы MODLS 12-го порÑдка, группа MODLS, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· 5 ДЛК, не ÑущеÑтвует. Может быть, ошибочное предположение, но... Ð¸Ð½Ñ‚ÑƒÐ¸Ñ†Ð¸Ñ Ñильно так говорит :) ПоÑтому оÑтановила дальнейшую переÑтановку Ñтрок и Ñтолбцов. Рвдруг группа MODLS 12-го порÑдка, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· 5 взаимно ортогональных ДЛК, вообще не ÑущеÑтвует в природе. Что-то знатоки на Ñайте math.stackexchange.com ничего о ней не говорÑÑ‚. ЕÑли бы она была найдена, то о ней навернÑка знали бы. Значит, не найдена. Может, и не ÑущеÑтвует. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Так, подойдём Ñ Ð´Ñ€ÑƒÐ³Ð¾Ð¹ Ñтороны к Ñтой группе MODLS 12-го порÑдка, ÑоÑтоÑщей из 4-Ñ… взаимно ортогональных ДЛК. Будем иÑкать пÑтый ЛК, который ортогонален вÑем ДЛК группы. Таким образом. мы получим группу MOLS 12-го порÑдка, ÑоÑтоÑщую из пÑти ЛК, четыре из которых ÑвлÑÑŽÑ‚ÑÑ Ð”Ð›Ðš. Мы знаем, что группа MOLS 12-го порÑдка ÑущеÑтвует. Выше показаны две такие группы MOLS. Ðо Ñти группы MOLS не Ñодержат ДЛК. Ð’ Ñамом начале поиÑка группы MODLS Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»Ð° группу MOLS из пÑти ЛК, в которой ÑодержитÑÑ Ð¾Ð´Ð¸Ð½ ДЛК. Покажу ещё раз Ñту группу MOLS ЛК 0 1 2 3 4 5 6 7 8 9 10 11 2 3 4 5 0 1 8 9 10 11 6 7 6 7 8 9 10 11 0 1 2 3 4 5 4 5 0 1 2 3 10 11 6 7 8 9 7 8 9 10 11 6 1 2 3 4 5 0 8 9 10 11 6 7 2 3 4 5 0 1 11 6 7 8 9 10 5 0 1 2 3 4 10 11 6 7 8 9 4 5 0 1 2 3 1 2 3 4 5 0 7 8 9 10 11 6 9 10 11 6 7 8 3 4 5 0 1 2 5 0 1 2 3 4 11 6 7 8 9 10 3 4 5 0 1 2 9 10 11 6 7 8 ЛК 0 6 8 2 7 1 9 11 4 10 5 3 2 8 10 4 9 3 11 7 0 6 1 5 6 0 2 8 1 7 3 5 10 4 11 9 4 10 6 0 11 5 7 9 2 8 3 1 7 1 3 9 2 8 4 0 11 5 6 10 8 2 4 10 3 9 5 1 6 0 7 11 11 5 1 7 0 6 2 4 9 3 10 8 10 4 0 6 5 11 1 3 8 2 9 7 1 7 9 3 8 2 10 6 5 11 0 4 9 3 5 11 4 10 0 2 7 1 8 6 5 11 7 1 6 0 8 10 3 9 4 2 3 9 11 5 10 4 6 8 1 7 2 0 ЛК 0 3 6 1 9 11 2 8 5 4 7 10 2 5 8 3 11 7 4 10 1 0 9 6 6 9 0 7 3 5 8 2 11 10 1 4 4 1 10 5 7 9 0 6 3 2 11 8 7 10 1 8 4 0 9 3 6 11 2 5 8 11 2 9 5 1 10 4 7 6 3 0 11 8 5 6 2 4 7 1 10 9 0 3 10 7 4 11 1 3 6 0 9 8 5 2 1 4 7 2 10 6 3 9 0 5 8 11 9 6 3 10 0 2 11 5 8 7 4 1 5 2 11 0 8 10 1 7 4 3 6 9 3 0 9 4 6 8 5 11 2 1 10 7 ДЛК 0 8 1 11 5 9 3 10 2 7 6 4 2 10 3 7 1 11 5 6 4 9 8 0 6 2 7 5 11 3 9 4 8 1 0 10 4 6 5 9 3 7 1 8 0 11 10 2 7 3 8 0 6 4 10 5 9 2 1 11 8 4 9 1 7 5 11 0 10 3 2 6 11 1 6 4 10 2 8 3 7 0 5 9 10 0 11 3 9 1 7 2 6 5 4 8 1 9 2 6 0 10 4 11 3 8 7 5 9 5 10 2 8 0 6 1 11 4 3 7 5 7 0 10 4 8 2 9 1 6 11 3 3 11 4 8 2 6 0 7 5 10 9 1 ЛК 0 4 11 10 2 7 8 6 9 1 3 5 2 0 7 6 4 9 10 8 11 3 5 1 6 10 5 4 8 1 2 0 3 7 9 11 4 2 9 8 0 11 6 10 7 5 1 3 7 11 0 5 9 2 3 1 4 8 10 6 8 6 1 0 10 3 4 2 5 9 11 7 11 9 4 3 7 0 1 5 2 6 8 10 10 8 3 2 6 5 0 4 1 11 7 9 1 5 6 11 3 8 9 7 10 2 4 0 9 7 2 1 11 4 5 3 0 10 6 8 5 3 10 9 1 6 7 11 8 0 2 4 3 1 8 7 5 10 11 9 6 4 0 2 Смотрите Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=120&postid=1291 Ðта группа MOLS была получена путём переÑтановки Ñтрок в ЛК извеÑтной группы MOLS, ÑоÑтоÑщей из пÑти ЛК, ÐºÐ¾Ñ‚Ð¾Ñ€Ð°Ñ Ð±Ñ‹Ð»Ð° поÑтроена мной давно по извеÑтному алгоритму. Смотрите мою Ñтатью "ПОСТРОЕÐИЕ ГРУППЫ MOLS ДВЕÐÐДЦÐТОГО ПОРЯДКÐ" http://www.natalimak1.narod.ru/mols12.htm Итак, задача понÑтна. Ðлгоритм её Ñ€ÐµÑˆÐµÐ½Ð¸Ñ Ñ‚Ð¾Ð¶Ðµ понÑтен. Ðадо пиÑать программу. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð”Ð»Ñ Ñ€ÐµÑˆÐµÐ½Ð¸Ñ Ð¿Ð¾Ñтавленной задачи возьмём ДЛК группы MODLS в нормализованном виде 0 1 2 3 4 5 6 7 8 9 10 11 1 3 5 0 9 7 4 2 11 6 8 10 4 9 8 6 1 11 0 10 5 3 2 7 5 7 1 2 11 3 8 0 9 10 4 6 7 2 3 5 10 0 11 1 6 8 9 4 11 10 9 8 7 6 5 4 3 2 1 0 3 0 7 1 6 2 9 5 10 4 11 8 6 4 10 9 0 8 3 11 2 1 7 5 2 5 0 7 8 1 10 3 4 11 6 9 8 11 4 10 5 9 2 6 1 7 0 3 9 6 11 4 3 10 1 8 7 0 5 2 10 8 6 11 2 4 7 9 0 5 3 1 0 1 2 3 4 5 6 7 8 9 10 11 2 5 0 7 8 1 10 3 4 11 6 9 3 0 7 1 6 2 9 5 10 4 11 8 11 10 9 8 7 6 5 4 3 2 1 0 5 7 1 2 11 3 8 0 9 10 4 6 10 8 6 11 2 4 7 9 0 5 3 1 9 6 11 4 3 10 1 8 7 0 5 2 8 11 4 10 5 9 2 6 1 7 0 3 6 4 10 9 0 8 3 11 2 1 7 5 4 9 8 6 1 11 0 10 5 3 2 7 7 2 3 5 10 0 11 1 6 8 9 4 1 3 5 0 9 7 4 2 11 6 8 10 0 1 2 3 4 5 6 7 8 9 10 11 6 4 10 9 0 8 3 11 2 1 7 5 7 2 3 5 10 0 11 1 6 8 9 4 4 9 8 6 1 11 0 10 5 3 2 7 2 5 0 7 8 1 10 3 4 11 6 9 8 11 4 10 5 9 2 6 1 7 0 3 10 8 6 11 2 4 7 9 0 5 3 1 3 0 7 1 6 2 9 5 10 4 11 8 1 3 5 0 9 7 4 2 11 6 8 10 5 7 1 2 11 3 8 0 9 10 4 6 11 10 9 8 7 6 5 4 3 2 1 0 9 6 11 4 3 10 1 8 7 0 5 2 0 1 2 3 4 5 6 7 8 9 10 11 7 2 3 5 10 0 11 1 6 8 9 4 8 11 4 10 5 9 2 6 1 7 0 3 10 8 6 11 2 4 7 9 0 5 3 1 4 9 8 6 1 11 0 10 5 3 2 7 5 7 1 2 11 3 8 0 9 10 4 6 11 10 9 8 7 6 5 4 3 2 1 0 9 6 11 4 3 10 1 8 7 0 5 2 3 0 7 1 6 2 9 5 10 4 11 8 1 3 5 0 9 7 4 2 11 6 8 10 6 4 10 9 0 8 3 11 2 1 7 5 2 5 0 7 8 1 10 3 4 11 6 9 ПÑтый ЛК будем иÑкать тоже в нормализованном виде. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
КÑтати, ÑÐµÐ³Ð¾Ð´Ð½Ñ Ð¿Ð¾ÑвилаÑÑŒ Ð½Ð¾Ð²Ð°Ñ Ð¿Ñ€Ð°Ð²ÐºÐ° в поÑледовательноÑти OEIS https://oeis.org/A328873 ГоÑподин Ватутин вÑтавил найденную мной группу MODLS 12-го порÑдка, ÑоÑтоÑщую из 4-Ñ… взаимно ортогональных ДЛК, в Ñвой "Proving list (best known examples)". Правки ещё не утверждены. Показываю добавление гоÑподина Ватутина в "Proving list (best known examples)" n=12, a(12)>=4 Группу MODLS гоÑподин Ватутин на форуме видел (ÑÑылка указана, группа Ñкопирована), однако как группа найдена, он не знает: "Way of finding: ?" Повторю Ñпециально Ð´Ð»Ñ Ð½ÐµÐ³Ð¾: группа MODLS 12-го порÑдка, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· четырёх взаимно ортогональных ДЛК, получена путём переÑтановки Ñтрок и Ñтолбцов в ЛК извеÑтной группы MOLS данного порÑдка, ÑоÑтоÑщей из пÑти взаимно ортогональных ЛК. Ðлгоритм хорошо извеÑтен, Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð½Ð°Ñ Ñ€ÐµÐ°Ð»Ð¸Ð·Ð°Ñ†Ð¸Ñ Ð¼Ð¾Ñ. Так, жду ÑƒÑ‚Ð²ÐµÑ€Ð¶Ð´ÐµÐ½Ð¸Ñ Ñтой поÑледовательноÑти OEIS. Что-то редакторы молчат, ни одного комментариÑ. С момента моей правки прошло две недели. Цитирую COMMENTS СоздаётÑÑ Ð²Ð¿ÐµÑ‡Ð°Ñ‚Ð»ÐµÐ½Ð¸Ðµ, что редакторы правку не видели. По крайней мере, за две недели уже можно приÑвоить поÑледовательноÑти ÑÑ‚Ð°Ñ‚ÑƒÑ "reviewed". |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese