А какую группу MOLS 20-го порядка выдаёт программа SageMath?
Где-то эта группа была показана.

Не нашла, снова составила в программе SageMath

19  8 16  5 13  2 10 18  7 15  6 12  1  4 17  9 14  3 11  0
12 19  9 17  6 14  3 11  0  8 16  7 13  2  5 18 10 15  4  1
 5 13 19 10 18  7 15  4 12  1  9 17  8 14  3  6  0 11 16  2
17  6 14 19 11  0  8 16  5 13  2 10 18  9 15  4  7  1 12  3
13 18  7 15 19 12  1  9 17  6 14  3 11  0 10 16  5  8  2  4
 3 14  0  8 16 19 13  2 10 18  7 15  4 12  1 11 17  6  9  5
10  4 15  1  9 17 19 14  3 11  0  8 16  5 13  2 12 18  7  6
 8 11  5 16  2 10 18 19 15  4 12  1  9 17  6 14  3 13  0  7
 1  9 12  6 17  3 11  0 19 16  5 13  2 10 18  7 15  4 14  8
15  2 10 13  7 18  4 12  1 19 17  6 14  3 11  0  8 16  5  9
 6 16  3 11 14  8  0  5 13  2 19 18  7 15  4 12  1  9 17 10
18  7 17  4 12 15  9  1  6 14  3 19  0  8 16  5 13  2 10 11
11  0  8 18  5 13 16 10  2  7 15  4 19  1  9 17  6 14  3 12
 4 12  1  9  0  6 14 17 11  3  8 16  5 19  2 10 18  7 15 13
16  5 13  2 10  1  7 15 18 12  4  9 17  6 19  3 11  0  8 14
 9 17  6 14  3 11  2  8 16  0 13  5 10 18  7 19  4 12  1 15
 2 10 18  7 15  4 12  3  9 17  1 14  6 11  0  8 19  5 13 16
14  3 11  0  8 16  5 13  4 10 18  2 15  7 12  1  9 19  6 17
 7 15  4 12  1  9 17  6 14  5 11  0  3 16  8 13  2 10 19 18
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 

11  4  0  5 17 10 15 13  9  6 18  2  7 19 14  8 12 16  3  1
 4 12  5  1  6 18 11 16 14 10  7  0  3  8 19 15  9 13 17  2
18  5 13  6  2  7  0 12 17 15 11  8  1  4  9 19 16 10 14  3
15  0  6 14  7  3  8  1 13 18 16 12  9  2  5 10 19 17 11  4
12 16  1  7 15  8  4  9  2 14  0 17 13 10  3  6 11 19 18  5
 0 13 17  2  8 16  9  5 10  3 15  1 18 14 11  4  7 12 19  6
19  1 14 18  3  9 17 10  6 11  4 16  2  0 15 12  5  8 13  7
14 19  2 15  0  4 10 18 11  7 12  5 17  3  1 16 13  6  9  8
10 15 19  3 16  1  5 11  0 12  8 13  6 18  4  2 17 14  7  9
 8 11 16 19  4 17  2  6 12  1 13  9 14  7  0  5  3 18 15 10
16  9 12 17 19  5 18  3  7 13  2 14 10 15  8  1  6  4  0 11
 1 17 10 13 18 19  6  0  4  8 14  3 15 11 16  9  2  7  5 12
 6  2 18 11 14  0 19  7  1  5  9 15  4 16 12 17 10  3  8 13
 9  7  3  0 12 15  1 19  8  2  6 10 16  5 17 13 18 11  4 14
 5 10  8  4  1 13 16  2 19  9  3  7 11 17  6 18 14  0 12 15
13  6 11  9  5  2 14 17  3 19 10  4  8 12 18  7  0 15  1 16
 2 14  7 12 10  6  3 15 18  4 19 11  5  9 13  0  8  1 16 17
17  3 15  8 13 11  7  4 16  0  5 19 12  6 10 14  1  9  2 18
 3 18  4 16  9 14 12  8  5 17  1  6 19 13  7 11 15  2 10  0
 7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6 19 

 7 10  2  0  9 18 16  3 14 13 19  6  4 12 17  8  5 15  1 11
 2  8 11  3  1 10  0 17  4 15 14 19  7  5 13 18  9  6 16 12
17  3  9 12  4  2 11  1 18  5 16 15 19  8  6 14  0 10  7 13
 8 18  4 10 13  5  3 12  2  0  6 17 16 19  9  7 15  1 11 14
12  9  0  5 11 14  6  4 13  3  1  7 18 17 19 10  8 16  2 15
 3 13 10  1  6 12 15  7  5 14  4  2  8  0 18 19 11  9 17 16
18  4 14 11  2  7 13 16  8  6 15  5  3  9  1  0 19 12 10 17
11  0  5 15 12  3  8 14 17  9  7 16  6  4 10  2  1 19 13 18
14 12  1  6 16 13  4  9 15 18 10  8 17  7  5 11  3  2 19  0
19 15 13  2  7 17 14  5 10 16  0 11  9 18  8  6 12  4  3  1
 4 19 16 14  3  8 18 15  6 11 17  1 12 10  0  9  7 13  5  2
 6  5 19 17 15  4  9  0 16  7 12 18  2 13 11  1 10  8 14  3
15  7  6 19 18 16  5 10  1 17  8 13  0  3 14 12  2 11  9  4
10 16  8  7 19  0 17  6 11  2 18  9 14  1  4 15 13  3 12  5
13 11 17  9  8 19  1 18  7 12  3  0 10 15  2  5 16 14  4  6
 5 14 12 18 10  9 19  2  0  8 13  4  1 11 16  3  6 17 15  7
16  6 15 13  0 11 10 19  3  1  9 14  5  2 12 17  4  7 18  8
 0 17  7 16 14  1 12 11 19  4  2 10 15  6  3 13 18  5  8  9
 9  1 18  8 17 15  2 13 12 19  5  3 11 16  7  4 14  0  6 10
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0 19 

 1 14 16  3 10 17  4  9 11  5 18 15  2 12  0 19 13  8  6  7
 7  2 15 17  4 11 18  5 10 12  6  0 16  3 13  1 19 14  9  8
10  8  3 16 18  5 12  0  6 11 13  7  1 17  4 14  2 19 15  9
16 11  9  4 17  0  6 13  1  7 12 14  8  2 18  5 15  3 19 10
19 17 12 10  5 18  1  7 14  2  8 13 15  9  3  0  6 16  4 11
 5 19 18 13 11  6  0  2  8 15  3  9 14 16 10  4  1  7 17 12
18  6 19  0 14 12  7  1  3  9 16  4 10 15 17 11  5  2  8 13
 9  0  7 19  1 15 13  8  2  4 10 17  5 11 16 18 12  6  3 14
 4 10  1  8 19  2 16 14  9  3  5 11 18  6 12 17  0 13  7 15
 8  5 11  2  9 19  3 17 15 10  4  6 12  0  7 13 18  1 14 16
15  9  6 12  3 10 19  4 18 16 11  5  7 13  1  8 14  0  2 17
 3 16 10  7 13  4 11 19  5  0 17 12  6  8 14  2  9 15  1 18
 2  4 17 11  8 14  5 12 19  6  1 18 13  7  9 15  3 10 16  0
17  3  5 18 12  9 15  6 13 19  7  2  0 14  8 10 16  4 11  1
12 18  4  6  0 13 10 16  7 14 19  8  3  1 15  9 11 17  5  2
 6 13  0  5  7  1 14 11 17  8 15 19  9  4  2 16 10 12 18  3
 0  7 14  1  6  8  2 15 12 18  9 16 19 10  5  3 17 11 13  4
14  1  8 15  2  7  9  3 16 13  0 10 17 19 11  6  4 18 12  5
13 15  2  9 16  3  8 10  4 17 14  1 11 18 19 12  7  5  0  6
11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 19

В этой группе MOLS нет ДЛК, она состоит из четырёх взаимно ортогональных ЛК.
ЛК не нормализованы, поэтому перестановок строк не видно.
Надо нормализовать, может быть, тогда появятся перестановки строк. А может быть, и не появятся.

Нормализовала ЛК

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 7 15  4 12  1  9 17  6 14  5 11  0  3 16  8 13  2 10 19 18
14  3 11  0  8 16  5 13  4 10 18  2 15  7 12  1  9 19  6 17
 2 10 18  7 15  4 12  3  9 17  1 14  6 11  0  8 19  5 13 16
 9 17  6 14  3 11  2  8 16  0 13  5 10 18  7 19  4 12  1 15
16  5 13  2 10  1  7 15 18 12  4  9 17  6 19  3 11  0  8 14
 4 12  1  9  0  6 14 17 11  3  8 16  5 19  2 10 18  7 15 13
11  0  8 18  5 13 16 10  2  7 15  4 19  1  9 17  6 14  3 12
18  7 17  4 12 15  9  1  6 14  3 19  0  8 16  5 13  2 10 11
 6 16  3 11 14  8  0  5 13  2 19 18  7 15  4 12  1  9 17 10
15  2 10 13  7 18  4 12  1 19 17  6 14  3 11  0  8 16  5  9
 1  9 12  6 17  3 11  0 19 16  5 13  2 10 18  7 15  4 14  8
 8 11  5 16  2 10 18 19 15  4 12  1  9 17  6 14  3 13  0  7
10  4 15  1  9 17 19 14  3 11  0  8 16  5 13  2 12 18  7  6
 3 14  0  8 16 19 13  2 10 18  7 15  4 12  1 11 17  6  9  5
13 18  7 15 19 12  1  9 17  6 14  3 11  0 10 16  5  8  2  4
17  6 14 19 11  0  8 16  5 13  2 10 18  9 15  4  7  1 12  3
 5 13 19 10 18  7 15  4 12  1  9 17  8 14  3  6  0 11 16  2
12 19  9 17  6 14  3 11  0  8 16  7 13  2  5 18 10 15  4  1
19  8 16  5 13  2 10 18  7 15  6 12  1  4 17  9 14  3 11  0

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
15 11 16  9  2  7  5  1 17 10 13 18 19  6  0  4  8 14  3 12
10 15  8  1  6  4  0 16  9 12 17 19  5 18  3  7 13  2 14 11
14  7  0  5  3 18 15  8 11 16 19  4 17  2  6 12  1 13  9 10
 6 18  4  2 17 14  7 10 15 19  3 16  1  5 11  0 12  8 13  9
17  3  1 16 13  6  9 14 19  2 15  0  4 10 18 11  7 12  5  8
 2  0 15 12  5  8 13 19  1 14 18  3  9 17 10  6 11  4 16  7
18 14 11  4  7 12 19  0 13 17  2  8 16  9  5 10  3 15  1  6
13 10  3  6 11 19 18 12 16  1  7 15  8  4  9  2 14  0 17  5
 9  2  5 10 19 17 11 15  0  6 14  7  3  8  1 13 18 16 12  4
 1  4  9 19 16 10 14 18  5 13  6  2  7  0 12 17 15 11  8  3
 3  8 19 15  9 13 17  4 12  5  1  6 18 11 16 14 10  7  0  2
 7 19 14  8 12 16  3 11  4  0  5 17 10 15 13  9  6 18  2  1
19 13  7 11 15  2 10  3 18  4 16  9 14 12  8  5 17  1  6  0
12  6 10 14  1  9  2 17  3 15  8 13 11  7  4 16  0  5 19 18
 5  9 13  0  8  1 16  2 14  7 12 10  6  3 15 18  4 19 11 17
 8 12 18  7  0 15  1 13  6 11  9  5  2 14 17  3 19 10  4 16
11 17  6 18 14  0 12  5 10  8  4  1 13 16  2 19  9  3  7 15
16  5 17 13 18 11  4  9  7  3  0 12 15  1 19  8  2  6 10 14
 4 16 12 17 10  3  8  6  2 18 11 14  0 19  7  1  5  9 15 13

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 8  0 17  7 16 14  1 12 11 19  4  2 10 15  6  3 13 18  5  9
18 16  6 15 13  0 11 10 19  3  1  9 14  5  2 12 17  4  7  8
15  5 14 12 18 10  9 19  2  0  8 13  4  1 11 16  3  6 17  7
 4 13 11 17  9  8 19  1 18  7 12  3  0 10 15  2  5 16 14  6
12 10 16  8  7 19  0 17  6 11  2 18  9 14  1  4 15 13  3  5
 9 15  7  6 19 18 16  5 10  1 17  8 13  0  3 14 12  2 11  4
14  6  5 19 17 15  4  9  0 16  7 12 18  2 13 11  1 10  8  3
 5  4 19 16 14  3  8 18 15  6 11 17  1 12 10  0  9  7 13  2
 3 19 15 13  2  7 17 14  5 10 16  0 11  9 18  8  6 12  4  1
19 14 12  1  6 16 13  4  9 15 18 10  8 17  7  5 11  3  2  0
13 11  0  5 15 12  3  8 14 17  9  7 16  6  4 10  2  1 19 18
10 18  4 14 11  2  7 13 16  8  6 15  5  3  9  1  0 19 12 17
17  3 13 10  1  6 12 15  7  5 14  4  2  8  0 18 19 11  9 16
 2 12  9  0  5 11 14  6  4 13  3  1  7 18 17 19 10  8 16 15
11  8 18  4 10 13  5  3 12  2  0  6 17 16 19  9  7 15  1 14
 7 17  3  9 12  4  2 11  1 18  5 16 15 19  8  6 14  0 10 13
16  2  8 11  3  1 10  0 17  4 15 14 19  7  5 13 18  9  6 12
 1  7 10  2  0  9 18 16  3 14 13 19  6  4 12 17  8  5 15 11
 6  9  1 18  8 17 15  2 13 12 19  5  3 11 16  7  4 14  0 10

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 2  4 10 17  5 11 16 18 12  6  3  9  0  7 19  1 15 13  8 14
 3  9 16  4 10 15 17 11  5  2  8 18  6 19  0 14 12  7  1 13
 8 15  3  9 14 16 10  4  1  7 17  5 19 18 13 11  6  0  2 12
14  2  8 13 15  9  3  0  6 16  4 19 17 12 10  5 18  1  7 11
 1  7 12 14  8  2 18  5 15  3 19 16 11  9  4 17  0  6 13 10
 6 11 13  7  1 17  4 14  2 19 15 10  8  3 16 18  5 12  0  9
10 12  6  0 16  3 13  1 19 14  9  7  2 15 17  4 11 18  5  8
11  5 18 15  2 12  0 19 13  8  6  1 14 16  3 10 17  4  9  7
 4 17 14  1 11 18 19 12  7  5  0 13 15  2  9 16  3  8 10  6
16 13  0 10 17 19 11  6  4 18 12 14  1  8 15  2  7  9  3  5
12 18  9 16 19 10  5  3 17 11 13  0  7 14  1  6  8  2 15  4
17  8 15 19  9  4  2 16 10 12 18  6 13  0  5  7  1 14 11  3
 7 14 19  8  3  1 15  9 11 17  5 12 18  4  6  0 13 10 16  2
13 19  7  2  0 14  8 10 16  4 11 17  3  5 18 12  9 15  6  1
19  6  1 18 13  7  9 15  3 10 16  2  4 17 11  8 14  5 12  0
 5  0 17 12  6  8 14  2  9 15  1  3 16 10  7 13  4 11 19 18
18 16 11  5  7 13  1  8 14  0  2 15  9  6 12  3 10 19  4 17
15 10  4  6 12  0  7 13 18  1 14  8  5 11  2  9 19  3 17 16
 9  3  5 11 18  6 12 17  0 13  7  4 10  1  8 19  2 16 14 15

Нет, эти ЛК не получаются друг из друга перестановкой строк.
Ладно, оставлю группу MOLS 20-го порядка на будущее.
Надо посмотреть, что у нас с группой MODLS 14-го порядка.
Пока известна только из двух взаимно ортогональных ДЛК.
Нельзя ли найти из трёх взаимно ортогональных ДЛК?

Программа SageMath выдаёт такую группу MOLS 14-го порядка, состоящую из четырёх взаимно ортогональных ЛК

[ 1  9  8  7  6 10  4  2  0 11 13  5 12  3]
[ 5  2 10  9  1  7 11  4  3  8 12  0  6 13]
[12  6  3 11 10  2  1  0  5  4  9 13  8  7]
[ 2 13  7  4 12 11  3  1  8  6  5 10  0  9]
[ 4  3  0  1  5 13 12 10  2  9  7  6 11  8]
[13  5  4  8  2  6  0  9 11  3 10  1  7 12]
[ 8  0  6  5  9  3  7 13 10 12  4 11  2  1]
[ 3 11 13 10  4  0  5  8 12  7  2  9  1  6]
[ 6  4 12  0 11  5  8  7  9 13  1  3 10  2]
[ 9  7  5 13  8 12  6  3  1 10  0  2  4 11]
[ 7 10  1  6  0  9 13 12  4  2 11  8  3  5]
[ 0  1 11  2  7  8 10  6 13  5  3 12  9  4]
[11  8  2 12  3  1  9  5  7  0  6  4 13 10]
[10 12  9  3 13  4  2 11  6  1  8  7  5  0],

[ 1  5 12  2  4 13  8  3  6  9  7  0 11 10]
[ 9  2  6 13  3  5  0 11  4  7 10  1  8 12]
[ 8 10  3  7  0  4  6 13 12  5  1 11  2  9]
[ 7  9 11  4  1  8  5 10  0 13  6  2 12  3]
[ 6  1 10 12  5  2  9  4 11  8  0  7  3 13]
[10  7  2 11 13  6  3  0  5 12  9  8  1  4]
[ 4 11  1  3 12  0  7  5  8  6 13 10  9  2]
[ 2  4  0  1 10  9 13  8  7  3 12  6  5 11]
[ 0  3  5  8  2 11 10 12  9  1  4 13  7  6]
[11  8  4  6  9  3 12  7 13 10  2  5  0  1]
[13 12  9  5  7 10  4  2  1  0 11  3  6  8]
[ 5  0 13 10  6  1 11  9  3  2  8 12  4  7]
[12  6  8  0 11  7  2  1 10  4  3  9 13  5]
[ 3 13  7  9  8 12  1  6  2 11  5  4 10  0],

[ 1  2  3  4  5  6  7  8  9 10 11 12 13  0]
[ 6 13 10  9  3 12  8  2 11  1  7  0  4  5]
[11  8  5  7  1  9  4 12 10  0 13  6  2  3]
[ 3  0 11 12  6 13  1  9  4  7  2  5  8 10]
[13  9  2  0  4  8  5  7  1  3  6 10 12 11]
[12  5  1 10  2  3 11  0  6 13  9  8  7  4]
[ 0  4 12 13  7 10  9  3  2  8  5  1 11  6]
[ 7  3 13  8 10  1  0  6 12  2  4 11  5  9]
[ 2  6  9  5 11  7 13  1  8  4 10  3  0 12]
[ 5 10  8  1 12  0  6  4 13 11  3  7  9  2]
[ 8 12  7 11 13  4  2 10  3  5  0  9  6  1]
[10 11  4  6  0  5  3 13  7  9 12  2  1  8]
[ 9  7  0  3  8  2 12 11  5  6  1  4 10 13]
[ 4  1  6  2  9 11 10  5  0 12  8 13  3  7],

[ 1  2  3  4  5  6  7  8  9 10 11 12 13  0]
[ 9  5 11  7 13 10  0  4  2 12  6  3  8  1]
[ 4 12 10  3  9  1  6  5 13 11  8  0  7  2]
[ 0 13  8  6  7 12  5 11 10  1  3  2  4  9]
[10  4  1  2  0  9  8 12  3  6  5  7 11 13]
[ 2  6 13  5 11  4 12  1  8  7  0 10  9  3]
[ 8 11  0  1 10  3 13  7  5  2  9  4  6 12]
[11  9  6 13  8  7  4  2  1  0 12  5  3 10]
[13  3 12  0  1  2  9  6 11  5  4  8 10  7]
[12  1  7  8  4  5 11  9  0  3 10 13  2  6]
[ 3  8  5  9  2 13 10  0 12  4  7  6  1 11]
[ 6  7  2 10 12 11  1  3  4  8 13  9  0  5]
[ 5  0  9 11  6  8  3 10  7 13  2  1 12  4]
[ 7 10  4 12  3  0  2 13  6  9  1 11  5  8]

Надо поэкспериментировать с этой группой.

Далее смотрите тему
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=141

Цитата

Я попросила помощника выложить таблицу ортогональных пар (этот самый огромный граф) на Яндекс.Диск
Вот здесь
https://disk.yandex.ru/d/wfQVzrZvfW35PQ
текстовый файл сжат, в сжатом виде 172,3 МБ.

Господа!
Вы можете поискать в этом графе максимальную клику.
Пожалуйста, расскажите, если у вас получится.

С этим огромным графом, как я понимаю, глухо.

Недавно я сделала набор ДЛК и ЛК поменьше от найденной мной группы MOLS 12-го порядка, состоящей из четырёх ДЛК и одного ЛК, с целью проверить самой.
Программа GetOrthogonal справилась довольно быстро с этим набором, таблицу ортогональных пар выдала.
Попыталась проверить этот граф в программе SageMath, в версии онлайн, которой я пользуюсь.
Ничего не получилось: программа граф не загружает, выдаёт ошибку о нехватке памяти.
При этом в одной из попыток выдалось такое сообщение: "Браузеру не хватило памяти, чтобы отобразить эту страницу".
Вот как!
Не понимаю: кому памяти не хватает - браузеру или программе SageMath.
Я пыталась обрезать граф, удаляла несколько узлов в конце, ничего не помогло.
Граф начинает загружаться и даже появляется в окне, но всё равно программа вылетает с ошибкой.

В общем, помучила немного программу и обратилась за помощью к помощнику.
У него онлайн версия тоже не загрузила граф.
А установленная версия граф вроде бы загрузила (хотя и не с первого раза), но результат выдала неправильный, она выдала клики размера 3 (как максимальные), хотя в графе точно есть клика размера 5 (исходная группа MOLS).
Наврала программа, нисколько не смущаясь. При этом не выдала никаких ошибок! Вот это особенно удручает.

Дальше решила спросить мнение у форумчанина на форуме Math Help Planet.
Смотрите тему
http://mathhelpplanet.com/viewtopic.php?f=44&t=74646
Форумчанин ответил, но я с его мнением не согласна.
Читайте в теме.
Поразмыслив, я пришла к выводу, что преобразовав граф, форумчанин его резко уменьшил, после чего он нормально загрузился и проверился правильно.

Таким образом, проблема всё-таки в нехватке памяти, а не в синтаксисе, как думает форумчанин.

Я сделала ещё один расширенный набор ДЛК и ЛК по этой же самой группе MOLS, однако он у меня пока лежит без движения.
Даже программой GetOrthogonal я его проверить не могу: очень большой.
О программе SageMath вообще молчу, она этот граф точно не возьмёт.

Таблица ортогональных пар (граф), о которой идёт речь в предыдущем посте, выложена тут
https://disk.yandex.ru/d/h8vaqNmAQ5B5YQ
Яндекс.Диск, текстовый файл сжат, в сжатом виде 2,29 МБ.

Проверяйте, господа.
Попробуйте преобразовать граф, как написал форумчанин.
Как я понимаю, форумчанин говорит, что все значения для одного узла должны быть записаны в одну строку.
А у нас сейчас так записано

1: [2,3,4,5,5696,11175,12760,13893,18905,19490],
1: [24760,26852,27917,31096,34484,34592,34596,34604,34914,36593],
1: [41974,44732,48686,49367,49371,49813,51777,58746,59686,63128],
1: [65825,67566,67576,67750,68058,68787,68883,68924,71942,71954],
1: [71990,72879],

В самом начале работы с программой SageMath я пробовала записывать в одну строку.
Но... попадались узлы, у которых несколько сотен значений, и программа такую длинную строку не читала (выдавала ошибку); приходилось такие длинные строки разбивать вручную.
После чего я решила записывать в несколько строк, по 10 значений в одной строке (так выдаёт программа GetOrthogonal; формат Harry сделал под программу SageMath по моей просьбе).

PS. Результат для этого графа форумчанин получил. Он пишет, что выдалась единственная клика размера 5, та самая исходная группа MOLS
[1, 2, 3, 4, 5].
Других клик размера 5 программа не выдала.

Итак, имеем две открытые проблемы:
1) существует ли группа MOLS 12-го порядка, состоящая из шести взаимно ортогональных ЛК?
2) существует ли группа MODLS 12-го порядка, состоящая из пяти взаимно ортогональных ДЛК?

О бОльшем количестве пока не спрашивается.

В этой таблице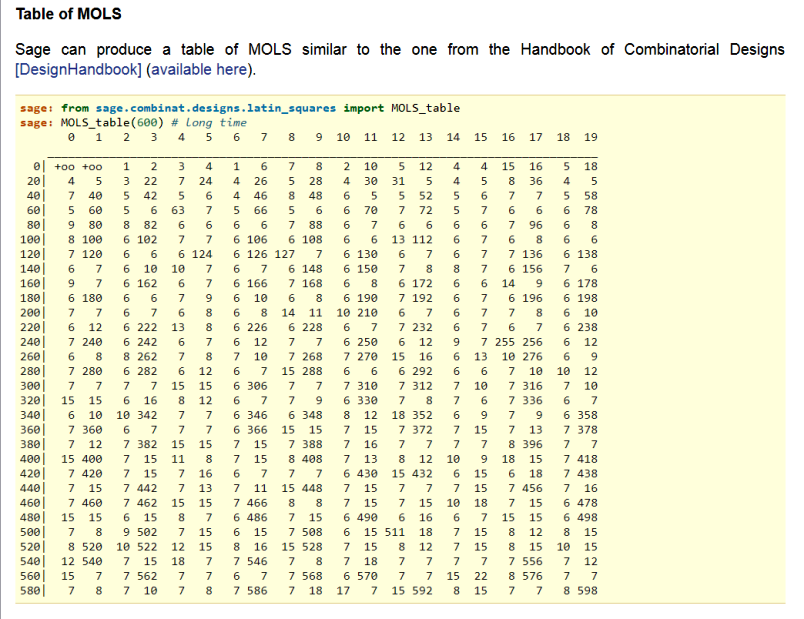



написано, что для порядка 12 известна пока группа MOLS, состоящая из пяти взаимно ортогональных ЛК.

Мной найдена, кроме известных групп, группа MOLS, состоящая из четырёх ДЛК и одного ЛК.
Весьма интересная группа MOLS!

В то же время в статье OEIS
https://oeis.org/A001438
Maximal number of mutually orthogonal Latin squares (or MOLS) of order n.
написано, цитирую

It is also known that a(11) = 10, a(12) >= 5.

Если бы было доказано, что не существует группа MOLS 12-го порядка, состоящая из шести взаимно ортогональных ЛК, было бы написано
a(12) = 5.

Цитата

В общем, помучила немного программу и обратилась за помощью к помощнику.
У него онлайн версия тоже не загрузила граф.
А установленная версия граф вроде бы загрузила (хотя и не с первого раза), но результат выдала неправильный, она выдала клики размера 3 (как максимальные), хотя в графе точно есть клика размера 5 (исходная группа MOLS).
Наврала программа, нисколько не смущаясь. При этом не выдала никаких ошибок! Вот это особенно удручает.

Дальше решила спросить мнение у форумчанина на форуме Math Help Planet.
Смотрите тему
http://mathhelpplanet.com/viewtopic.php?f=44&t=74646
Форумчанин ответил, но я с его мнением не согласна.
Читайте в теме.
Поразмыслив, я пришла к выводу, что преобразовав граф, форумчанин его резко уменьшил, после чего он нормально загрузился и проверился правильно.

Таким образом, проблема всё-таки в нехватке памяти, а не в синтаксисе, как думает форумчанин.

Разобрались в переписке с форумчанином.
Он оказался прав!
Действительно, Питон отбрасывает значения узла во всех предыдущих строках и оставляет только значения в последней строке.

Например, из всех этих значений для узла 1

1: [2,3,4,5,5696,11175,12760,13893,18905,19490],
1: [24760,26852,27917,31096,34484,34592,34596,34604,34914,36593],
1: [41974,44732,48686,49367,49371,49813,51777,58746,59686,63128],
1: [65825,67566,67576,67750,68058,68787,68883,68924,71942,71954],
1: [71990,72879],

останутся только два значения

1: [71990,72879]

Круто!

Цитата из сообщения
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=115&postid=2335

Ссылка на этот вопрос
https://math.stackexchange.com/q/3973469/867143
наверное, не работает.
Интересно, что кто-то влепил минус за этот вопрос.
Что-то не так написала? Вроде вполне корректно задала вопрос, который меня очень интересует.
Хотела бы узнать ответ. Ответа не получила, а вот минус - пожалуйста :)
Злой народ какой-то везде.

Недавно задала вопрос опять, на этот раз о группе MODLS 12-го порядка, в связи с найденной мной группой MODLS данного порядка, состоящей из 4-х взаимно ортогональных ДЛК
https://math.stackexchange.com/questions/4156562/modls-of-order-12
"MODLS of order 12"
Этот вопрос пока висит, не удалён.
Однако нет ни одного ответа.
Слава Богу, хоть минусами не бросаются :) пока.

Ах, кажется, мне за вопрос "MODLS of order 12" выдали серебряную медаль :)
Однако ответов так и не появилось.
Прихожу к выводу, что найденная мной группа MODLS 12-го порядка, состоящая из четырёх взаимно ортогональных ДЛК, не была известна до сих пор.
Соответственно и расширенная группа MOLS данного порядка, состоящая из четырёх ДЛК и одного ЛК, тоже не была известна.