Thread 'DLS with maximum of D-transversals'
Message boards : Science : DLS with maximum of D-transversals
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Решила Ñобрать ДЛК Ñ Ð¼Ð°ÐºÑимальным количеÑтвом Д-транÑверÑалей в одну тему. Смотрим поÑледовательноÑÑ‚ÑŒ OEIS https://oeis.org/A287648 A287648 Maximum number of diagonal transversals in a diagonal Latin square of order n. До порÑдка 9 включительно макÑимальное количеÑтво Д-транÑверÑалей уÑтановлено. Ð”Ð»Ñ Ñледующих порÑдков пока имеем только нижнюю оценку. Далее покажу ДЛК Ñ Ð¼Ð°ÐºÑимальным количеÑтвом транÑверÑалей (уÑтановленным и текущим). |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Итак, показываю ДЛК, имеющие макÑимальное количеÑтво Д-транÑвнрÑалей на данный момент 1. n=9 333 Д-транÑверÑалей Ñовершенный квадрат  Смотрите мою Ñтатью "Совершенные латинÑкие квадраты (чаÑÑ‚ÑŒ 1)", там еÑÑ‚ÑŒ ÑÑылка на Ñтатью, в которой Ñтот квадрат опубликован. Вывод программы Белышева ortogon_u Проверка ДЛК9 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 1 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 333 Соквадратов: 308 2. n=10 866 Д-транÑверÑалей ДЛК Брауна 0 8 5 1 7 3 4 6 9 2 5 1 7 2 9 8 0 3 4 6 1 7 2 9 5 6 8 0 3 4 9 6 4 3 0 2 7 1 5 8 3 0 8 6 4 1 5 9 2 7 4 3 0 8 6 5 9 2 7 1 7 2 9 5 1 4 6 8 0 3 6 4 3 0 8 9 2 7 1 5 2 9 6 4 3 7 1 5 8 0 8 5 1 7 2 0 3 4 6 9 Из Ñтатьи Brown et al. "Completion of the Spectrum of Orthogonal Diagonal Latin Squares". Lecture notes in pure and applied mathematics 139 (1992), 43-49. Вывод программы Белышева ortogon_u Проверка ДЛК10 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 1 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 866 Соквадратов: 4 PS. ГлобальноÑÑ‚ÑŒ макÑимума Ð´Ð»Ñ Ð”Ð›Ðš порÑдка 9 подтверждена в двух BOINC-проектах (Gerasim@Home и Rake Search), которые занималиÑÑŒ ÑоÑтавлением полной БД КФ ОДЛК порÑдка 9. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’Ñтавлю Ñто Ñообщение Рзнаете ли вы, что текущий рекорд по Д-транÑверÑалÑм (Ð´Ð»Ñ Ð”Ð›Ðš 10-го порÑдка) принадлежит знаменитому ДЛК Брауна  Ðтот ДЛК 10-го порÑдка имеет 866 Д-транÑверÑалей. И он принадлежит ÑемейÑтву ЛК блочной Ñтруктуры! Ðто золотое ÑемейÑтво â„–1, которое дало макÑимальное количеÑтво ОДЛК. С него Белышев и начал Ñвоё иÑÑледование ÑемейÑтв ЛК блочной Ñтруктуры. ДЛК Брауна дал нам четвёрку Проверка ДЛК10 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 1 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 866 Соквадратов: 4 Ð’Ñ€ÐµÐ¼Ñ Ð² Ñек: 5 Вот так удачно Ñ Ð¿Ð¾Ð¿Ð°Ð»Ð° на ДЛК 12-го порÑдка блочной Ñтруктуры. ЕÑли Ñто и не окончательный рекордÑмен по Д-транÑверÑалÑм, то довольно близко к рекордному. Однако... поÑмотрите: рекордный ДЛК 10-го порÑдка по Д-транÑверÑалÑм имеет вÑего 4 ортогональных диагональных Ñоквадрата. Ðайденный мной текущий рекордÑмен 12-го порÑдка по Д-транÑверÑалÑм имеет по моему прогнозу неÑколько миллионов ортогональных диагональных Ñоквадратов. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
3. n=11 4828 Д-транÑверÑалей 0 1 2 3 4 5 6 7 8 9 10 1 2 3 5 6 9 7 10 0 4 8 7 10 8 0 3 1 5 9 6 2 4 3 5 9 4 10 6 8 0 2 7 1 4 6 7 10 1 8 2 3 9 0 5 5 9 4 6 8 7 0 1 3 10 2 10 8 0 1 5 2 9 4 7 3 6 6 7 10 8 2 0 3 5 4 1 9 8 0 1 2 9 3 4 6 10 5 7 2 3 5 9 7 4 10 8 1 6 0 9 4 6 7 0 10 1 2 5 8 3 Квадрат нашёл Tomas Brada, Ñмотрите https://boinc.tbrada.eu/forum_thread.php?id=3104&postid=4149 Вывод программы Белышева ortogon_u Проверка ДЛК11 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 1 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 4828 Соквадратов: 32462 Ð’Ñ€ÐµÐ¼Ñ Ð² Ñек: 8000 1 38 15 12 1 1 1 1 1 Ð”Ð»Ñ Ð²Ñ‹Ñ…Ð¾Ð´Ð° нажмите любую клавишу: ПоиÑк выполнен до конца. У ДЛК имеетÑÑ 32462 ОДЛК. 4. n=12 24901 Д-транÑверÑалей Квадрат найден мной 0 9 7 6 10 3 2 11 4 1 8 5 10 1 0 11 5 9 4 3 7 8 6 2 4 11 2 1 7 6 10 8 5 3 9 0 5 8 10 3 2 1 7 9 0 6 11 4 2 6 5 9 4 8 0 1 10 11 3 7 1 2 9 0 8 5 11 10 3 4 7 6 9 5 3 7 1 10 6 0 11 2 4 8 3 10 11 4 9 0 8 7 6 5 2 1 11 0 6 2 3 7 1 4 8 10 5 9 7 3 4 8 0 11 5 6 2 9 1 10 6 7 8 5 11 4 9 2 1 0 10 3 8 4 1 10 6 2 3 5 9 7 0 11 Вывод программы Белышева ortogon_u Проверка ДЛК12 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 1 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 24901 Соквадратов: 2010 Ð’Ñ€ÐµÐ¼Ñ Ð² Ñек: 2025 1994 812 165 28 14 2 Программа прервана. Диагональных Ñоквадратов будет много. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’Ñтавлю Ñто Ñообщение и ещё далее о ДЛК Ñ 24901 Д-транÑверÑалÑми Цитата 4. 24901 Д-транÑверÑалей РаÑÑкажу ещё немного об Ñтом ДЛК. ПриÑмотревшиÑÑŒ к нему повнимательней, Ñ ÑƒÐ²Ð¸Ð´ÐµÐ»Ð° в нём блочную Ñтруктуру; а поначалу увидела только, что он пÑевдоÑимметричный по Гергели/Брауну, что и показано раÑкраÑкой на иллюÑтрации в цитате. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾ÐºÐ°Ð¶Ñƒ другую раÑкраÑку Ñтого ДЛК, ÐºÐ¾Ñ‚Ð¾Ñ€Ð°Ñ Ð¿Ð¾ÐºÐ°Ð·Ñ‹Ð²Ð°ÐµÑ‚ блочную Ñтруктуру. Вот 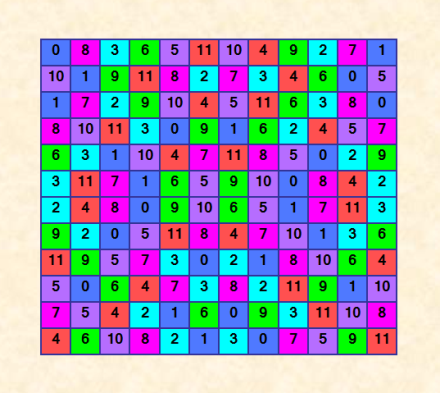 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð Ñто базовый ЛК ÑемейÑтва, которому принадлежит показанный в предыдущем поÑте ДЛК  |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Итак, продолжаю раÑÑказ о ДЛК, имеющем 24901 Д-транÑверÑалей 0 8 3 6 5 B A 4 9 2 7 1 A 1 9 B 8 2 7 3 4 6 0 5 1 7 2 9 A 4 5 B 6 3 8 0 8 A B 3 0 9 1 6 2 4 5 7 6 3 1 A 4 7 B 8 5 0 2 9 3 B 7 1 6 5 9 A 0 8 4 2 2 4 8 0 9 A 6 5 1 7 B 3 9 2 0 5 B 8 4 7 A 1 3 6 B 9 5 7 3 0 2 1 8 A 6 4 5 0 6 4 7 3 8 2 B 9 1 A 7 5 4 2 1 6 0 9 3 B A 8 4 6 A 8 2 1 3 0 7 5 9 B Ðтот ДЛК Ñ Ð½ÐµÐ¼Ð½Ð¾Ð¶ÐºÐ¾ Ñчитала, потом Tomas Brada Ñчитал. Смотрите его Ñообщение https://boinc.tbrada.eu/forum_thread.php?id=3104&postid=4369 Дублирую 98844 ODLK of order 12: Видим его прогноз по количеÑтву ОДЛК у данного ДЛК. Ðаконец, Ñтот "Ñ‚Ñжёлый" квадрат Ñчитал помощник. КÑтати, помощник учаÑтвовал в BOINC-проекте ОДЛК в 2018 г., ник Mynx. Конечно, полноÑтью он не обÑчитал квадрат, но нашёл рекордное количеÑтво ОДЛК от одного ДЛК 12-го порÑдка (на данный момент) - 6 640 729 ОДЛК. Обработка квадрата выполнÑлаÑÑŒ программой Белышева ortogon_u. Я попроÑила его разделить веÑÑŒ файл Ñ Ñ€ÐµÐ·ÑƒÐ»ÑŒÑ‚Ð°Ñ‚Ð°Ð¼Ð¸ на 6 чаÑтей. Он Ñделал Ñто. ПопытаюÑÑŒ канонизировать ОДЛК из каждой чаÑти. Прогноз по количеÑтву вÑех ОДЛК от данного ДЛК Mynx дал такой: примерно 398,9 млн. штук. Как видим, Ñто близко к прогнозу Tomas Brada. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Канонизировала вÑе 6 чаÑтей результатов, которые приÑлал мне Mynx. Очень интереÑно: 5 чаÑтей Ñодержат по 1106769 ОДЛК, и в каждой чаÑти поÑле канонизации получено Ñтолько же КФ ОДЛК. ШеÑÑ‚Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ Ñрдержит 1106884 ОДЛК, поÑле канонизации получилоÑÑŒ Ñтолько же КФ ОДЛК. Покажу канонизацию шеÑтой чаÑти Order? 12 Format, (1: first row or 2: \diagonal)? 2 File name? out .. writing DLS to file output12CF2.txt number of DLS 1106884 CFs 1106884 elapsed time 0:26:57 КФ ОДЛК в каждой чаÑти Ñ Ð¿Ñ€ÐµÐ¾Ð±Ñ€Ð°Ð·Ð¾Ð²Ð°Ð»Ð° в закодированный формат. Теперь мне надо найти ту Ñамую программу Ñортировки, о которой Tomas Brada пиÑал здеÑÑŒ https://boinc.tbrada.eu/forum_thread.php?id=3104&postid=4381 Цитирую I canonicalized 2715194 mates of Dv8yEzQnSZSx2gbK2JTvcP6FD7Sh7XQ8, in parts. Совершенно Ð°Ð½Ð°Ð»Ð¾Ð³Ð¸Ñ‡Ð½Ð°Ñ ÑÐ¸Ñ‚ÑƒÐ°Ñ†Ð¸Ñ Ñƒ него. Он канонизировал результаты по чаÑÑ‚Ñм, а затем объединил вÑе чаÑти и применил к ним программу sort_u, Ñто программа Ñортировки и ÑƒÐ´Ð°Ð»ÐµÐ½Ð¸Ñ Ð´ÑƒÐ±Ð»Ð¸ÐºÐ°Ñ‚Ð¾Ð². Кто-то может подÑказать, где можно взÑÑ‚ÑŒ программу sort_u? РазумеетÑÑ, программу можно напиÑать. Я никогда не работала Ñ Ñимвольными (Ñтроковыми) переменными, поÑтому не имею опыта. Думаю, что программа Ñта довольно проÑтаÑ. ЕÑли тут еÑÑ‚ÑŒ программиÑÑ‚Ñ‹, пожалуйÑта, попробуйте напиÑать программу. Ðапомню, что КФ ОДЛК предÑтавлены в закодированном виде по ÑиÑтеме Tomas Brada. Вот так, например: DhttCvJHdW3FGUACwkztYxyZXMfVQxP DPDzssW2BYDYUVtfUjLehC1uV5uXeZD2 DA2SSUFZWHnvs3UacQqC4cQ3jvNoiu72 D9iC3ReKoZiYEGjqETNimM3AsdRtQM D2KUy2GYgMqmwFwWA2MWjTQotstRPqn Db7SRDpAST2fJmVZHKgrSJFraLShDjF2 DuqJsAkxTQ8SHkwmC2rpioYXv9Sd14eB3 DnuujwG4hUHRw8jTDjttuSnz8m71NFK7 DaMbUnuaLkykTzNC768y3reFDTyjeK4 DSQ4mK2nwEcfkmraGpTx4hnKBWnc7kE . . . . . . Программа Ñортировки должна раÑположить коды квадратов в лекÑикографичеÑком порÑдке и удалить дубликаты. Вообще-то, лекÑикографичеÑкий порÑдок нам не оÑобо нужен, нам нужно только удалить дубликаты. ПоÑле Ñтого мы получим чаÑтичный набор КФ ОДЛК, полученный от ДЛК Ñ 24901 Д-транÑверÑалÑми. Перед канонизацией имелÑÑ Ð½Ð°Ð±Ð¾Ñ€, Ñодержащий 6 640 729 ОДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Так, программу Ñортировки Ñ Ð½Ð°Ð¹Ð´Ñƒ не Ñкоро, еÑли вообще найду. ПоÑтому выкладываю то, что получила (то еÑÑ‚ÑŒ Ñ Ð´ÑƒÐ±Ð»Ð¸ÐºÐ°Ñ‚Ð°Ð¼Ð¸ КФ ОДЛК) https://yadi.sk/d/GnvIaN3dLPEIPg ЯндекÑ.ДиÑк, размер файла 154 МБ. Файл Ñодержит 6640729 КФ ОДЛК, полученных от ДЛК Ñ 24901 Д-транÑверÑалÑми. Возможны дубликаты КФ ОДЛК! Канонизировано программой Harry White. КФ ОДЛК предÑтавлены в формате 2 в закодированном по ÑиÑтеме Tomas Brada виде. ОДЛК найдены программой Белышева. ПоÑчитал добровольный помощник Mynx. PS. Ðто пока рекордное количеÑтво ОДЛК, полученных от одного ДЛК 12-го порÑдка. Ð¥Ð¾Ñ‚Ñ Ð”Ð›Ðš не обÑчитан полноÑтью; вÑего ОДЛК он имеет намного больше, по прогнозам около 400 миллионов. И Ð·Ð°Ð²ÐµÑ€ÑˆÐ°Ñ Ñ€Ð°ÑÑказ о ДЛК Ñ 24901 Д-транÑверÑалÑми, отмечу, что найден новый рекордный ДЛК 12-го порÑдка. Читайте об Ñтом ДЛК далее. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
4a. n=12 28496 Д-транÑверÑалей, квадрат найден мной, Ñто пока текущий рекорд Ð´Ð»Ñ Ð”Ð›Ðš 12-го порÑдка 0 10 4 6 2 8 9 3 7 5 11 1 11 1 7 5 9 3 2 8 4 6 0 10 4 6 2 8 1 11 10 0 9 3 7 5 7 5 9 3 10 0 1 11 2 8 4 6 3 9 0 10 4 6 7 5 11 1 8 2 8 2 11 1 7 5 4 6 0 10 3 9 2 8 1 11 5 7 6 4 10 0 9 3 9 3 10 0 6 4 5 7 1 11 2 8 5 7 3 9 0 10 11 1 8 2 6 4 6 4 8 2 11 1 0 10 3 9 5 7 1 11 5 7 3 9 8 2 6 4 10 0 10 0 6 4 8 2 3 9 5 7 1 11 ИллюÑÑ‚Ñ€Ð°Ñ†Ð¸Ñ 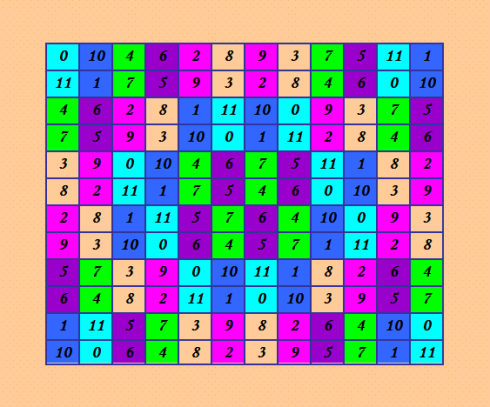 ДЛК имеет клаÑÑичеÑкую блочную Ñтруктуру, как ДЛК Брауна 10-го порÑдка. Ðтого монÑтра пока не удалоÑÑŒ обÑчитать полноÑтью. Я чуть-чуть Ñчитала, нашла 211488 ОДЛК. Мой помощник Ñчитал на 40-Ñдерном процеÑÑоре более двух Ñуток. ÐžÐ¿ÐµÑ€Ð°Ñ‚Ð¸Ð²Ð½Ð°Ñ Ð¿Ð°Ð¼ÑÑ‚ÑŒ требуетÑÑ ÐºÐ¾Ð»Ð¾ÑÑальнаÑ! Ð’ программе ortogonb вÑÑ‘ Ñидит в ОЗУ. Ðто плохо. Программу пришлоÑÑŒ прервать во избежание проблем Ñ Ð¿Ð°Ð¼Ñтью. И Ñамое плохое то, что при прерывании вÑе найденные ОДЛК пропали. ЗапуÑкаю Ð´Ð»Ñ Ñтого монÑтра первый шаг в программе ortogonbw ortogonbw DSkEkzZkhtCs22cK3BoLLiYwwc8ZkXd4 1 > output.txt Ðа конÑоль выдаётÑÑ C:\Users\Дом\Downloads\Tomas>ortogonbw DSkEkzZkhtCs22cK3BoLLiYwwc8ZkXd4 1 1>out put.txt init_trans(12) used 495 nodes num_dtrans: 28496 init_disjoint(12) used 145 heads and 342097 nodes L(0) c(28) 1 / 2048 L(1) c(99) X / 818 Ðе выполнила Ñтот шаг полноÑтью, но ОДЛК уже пошли в выходной файл # in: DSkEkzZkhtCs22cK3BoLLiYwwc8ZkXd4 1 # num_dtrans: 28496 DRTrMSrmtgMWUad83WDfEg8YGDL1SZQ9 DJq1LUeGDEq7GY1UwLbej1jSYrwLQQ5H DP7oXqQtvnPteacpK5WhTj7afSyay6i8 Df4GyFEKymxJVft6A639qT6tg6J7HHaY DNMtJJaqn51wwWkXNx2SvKawS2MHoH7N DNkiV9YAnzhSA2meqLSn2vS3KjPK5oA DugRqDKqCbqf2Vyeh3tGxXu6h21PxjRL DaiW3VU2AtRayW1hjrVoc1fQf4tR8349 D7F3Hy1ishXAvXCwo328rxCQpLQbQRFE2 DuidLn5VqkNDD8xnNWBpt5Rnn3YuR7NA DPZGAKnztqZo9TMed7ahu2TC42VJ4rE7 D2gnc8muLHFJQGPJu9gjLnz6sLiy2NZB DU3RKpZ3qtTNwFrb5KEEKxUx9LVxAkUB DnCP4mw7UXPd6XKYNpR65eHRwrUz4FPW DQQm2fKjEVhjPjgmQF9SX81dc1UxXGL8 DMC5aveZWY2wj5LyFgKaP5Kdk9SPm9U4 . . . . . . Ðто хорошо. Как видим, здеÑÑŒ будет 2048 чаÑтей. Ðу, еÑли бы на клаÑтере Ñчитать, на 1000 Ñдер раÑкидать, может, и быÑтро проÑчитаетÑÑ. Ðа 40-Ñдерном процеÑÑоре тоже можно пробовать, но Ñколько времени потребуетÑÑ, трудно Ñказать. ЗдеÑÑŒ Ñ…Ð¾Ñ‚Ñ Ð±Ñ‹ каждую чаÑÑ‚ÑŒ можно проÑчитать отдельно, и вÑе найденные при Ñтом ОДЛК будут запиÑаны в файл и не пропадут уже. PS. Прогноз Ð´Ð»Ñ Ð´Ð°Ð½Ð½Ð¾Ð³Ð¾ ДЛК - 400 миллионов ОДЛК плюÑ/минуÑ. Помощник окреÑтил Ñтот ДЛК квадрозавром :) Очень трудно предÑтавить 400 миллионов ортогональных диагональных Ñоквадратов к одному ДЛК! ИнтереÑно, Ñколько они дадут КФ? Канонизировать такое количеÑтво ОДЛК врÑд ли удаÑÑ‚ÑÑ, даже еÑли их удаÑÑ‚ÑÑ Ð½Ð°Ð¹Ñ‚Ð¸. И опÑÑ‚ÑŒ же ÑÐ¸Ñ‚ÑƒÐ°Ñ†Ð¸Ñ Ð¿Ð¾Ñ…Ð¾Ð¶Ð°Ñ Ð½Ð° Ñитуацию Паркера. Помните? Паркер нашёл 12 миллионов Ñ Ñ…Ð²Ð¾Ñтиком ОЛК к одному ЛК 10-го порÑдка. И потом иÑкал в Ñтом наборе ортогональную пару. И... не нашёл её! Можно предÑтавить его огорчение. Ртеперь предÑтавьте примерно 400 миллионов ортогональных диагональных Ñоквадратов к нашему монÑтру. Предположим, что вÑе Ñти ОДЛК найдены. И поищем в Ñтом наборе ортогональную пару! :) Сможем поиÑкать??? ЕÑли Ñ‚Ð°ÐºÐ°Ñ Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° обнаружитÑÑ Ð² Ñтом наборе ОДЛК, Ñто значит - найдена тройка MODLS 12-го порÑдка. Однако... Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° вполне может и не ÑущеÑтвовать в Ñтом наборе ОДЛК. Ð’ÑÑ‘, как у Паркера :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
5. n=13 131106 Д-транÑверÑалей ДЛК из полной ÑиÑтемы MOLS 0 1 2 3 4 5 6 7 8 9 10 11 12 2 3 4 5 6 7 8 9 10 11 12 0 1 4 5 6 7 8 9 10 11 12 0 1 2 3 6 7 8 9 10 11 12 0 1 2 3 4 5 8 9 10 11 12 0 1 2 3 4 5 6 7 10 11 12 0 1 2 3 4 5 6 7 8 9 12 0 1 2 3 4 5 6 7 8 9 10 11 1 2 3 4 5 6 7 8 9 10 11 12 0 3 4 5 6 7 8 9 10 11 12 0 1 2 5 6 7 8 9 10 11 12 0 1 2 3 4 7 8 9 10 11 12 0 1 2 3 4 5 6 9 10 11 12 0 1 2 3 4 5 6 7 8 11 12 0 1 2 3 4 5 6 7 8 9 10 Вывод программы Белышева ortogon_u Проверка ДЛК13 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 1 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 131106 Соквадратов: 4937 Ð’Ñ€ÐµÐ¼Ñ Ð² Ñек: 10270 Программа была прервана. Конечно, диагональных Ñоквадратов будет больше. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’Ñтавлю Ñто Ñообщение о рекордном ДЛК 13-го порÑдка ЗдеÑÑŒ https://boinc.tbrada.eu/forum_thread.php?id=3104&postid=4133 нашла обалденный ДЛК 13-го порÑдка EUELx2zmrdPHyTGkGJhedf1cuDmJzqhw6hUme293TPB (13, 131106, >>248703) РаÑкодированный ДЛК 0 9 5 1 10 6 2 11 7 3 12 8 4 5 1 10 6 2 11 7 3 12 8 4 0 9 10 6 2 11 7 3 12 8 4 0 9 5 1 2 11 7 3 12 8 4 0 9 5 1 10 6 7 3 12 8 4 0 9 5 1 10 6 2 11 12 8 4 0 9 5 1 10 6 2 11 7 3 4 0 9 5 1 10 6 2 11 7 3 12 8 9 5 1 10 6 2 11 7 3 12 8 4 0 1 10 6 2 11 7 3 12 8 4 0 9 5 6 2 11 7 3 12 8 4 0 9 5 1 10 11 7 3 12 8 4 0 9 5 1 10 6 2 3 12 8 4 0 9 5 1 10 6 2 11 7 8 4 0 9 5 1 10 6 2 11 7 3 12 Утилита Harry White Ñообщает об Ñтом ДЛК Order? 13
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_4.txt
Counts
------
1 diagonal Latin
1 associative
1 pandiagonal
1 ultramagic
1 natural \diagonal
1 self-orthogonalÐÑÑоциативный и пандиагональный, значит, идеальный (ultramagic), ещё и self orthogonal. ЕÑли Ñ Ð¿Ñ€Ð°Ð²Ð¸Ð»ÑŒÐ½Ð¾ понимаю запиÑÑŒ Tomas Brada, у Ñтого ДЛК 131106 диагональных транÑверÑалей и много больше 248703 ортогональных диагональных Ñоквадратов. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
6. n=14 364596 Д-транÑверÑалей 0 7 6 11 9 3 4 5 2 12 13 8 10 1 6 1 11 5 10 12 2 3 9 7 4 13 0 8 5 11 2 12 8 1 7 10 0 6 9 3 13 4 13 6 5 3 1 10 9 12 7 0 2 4 8 11 12 3 10 1 4 13 8 6 11 5 0 7 2 9 10 12 1 8 2 5 11 13 4 3 6 0 9 7 9 2 7 0 5 11 6 8 13 4 1 10 3 12 4 13 3 9 6 0 10 7 1 8 12 2 11 5 2 4 9 10 11 6 1 0 8 13 7 12 5 3 1 10 8 13 12 2 5 4 3 9 11 6 7 0 3 5 12 7 13 8 0 1 6 11 10 9 4 2 8 0 13 4 7 9 3 2 12 10 5 11 1 6 7 9 0 6 3 4 13 11 5 2 8 1 12 10 11 8 4 2 0 7 12 9 10 1 3 5 6 13 Вывод программы Белышева ortogon_u Проверка ДЛК14 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 1 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 364596 Соквадратов: 1 Ð’Ñ€ÐµÐ¼Ñ Ð² Ñек: 380 25358 10401 3947 1403 267 60 13 3 Программа прервана, поиÑк не выполнÑлÑÑ. Уже понÑтно, что Ñто ОДЛК. Ðтот ОДЛК из моего набора КФ ОДЛК 14-го порÑдка. Ðабор КФ на Д-транÑверÑали проверÑл Harry White Ñвоей программой. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’Ñтавлю Ñто Ñообщение Смотрим Ñтатью в OEIS https://oeis.org/A287648 Цитирую From Natalia Makarova, Oct 04 2020: (Start) The following DLS of order 14 has 364596 diagonal transversals: 0 7 6 11 9 3 4 5 2 12 13 8 10 1 6 1 11 5 10 12 2 3 9 7 4 13 0 8 5 11 2 12 8 1 7 10 0 6 9 3 13 4 13 6 5 3 1 10 9 12 7 0 2 4 8 11 12 3 10 1 4 13 8 6 11 5 0 7 2 9 10 12 1 8 2 5 11 13 4 3 6 0 9 7 9 2 7 0 5 11 6 8 13 4 1 10 3 12 4 13 3 9 6 0 10 7 1 8 12 2 11 5 2 4 9 10 11 6 1 0 8 13 7 12 5 3 1 10 8 13 12 2 5 4 3 9 11 6 7 0 3 5 12 7 13 8 0 1 6 11 10 9 4 2 8 0 13 4 7 9 3 2 12 10 5 11 1 6 7 9 0 6 3 4 13 11 5 2 8 1 12 10 11 8 4 2 0 7 12 9 10 1 3 5 6 13 (End) Ðто текущий рекорд по Д-транÑверÑалÑм Ð´Ð»Ñ Ð”Ð›Ðš 14-го порÑдка, 364596 Д-транÑверÑалей. Ртеперь Ñмотрим иллюÑтрацию  Да! Ðто клаÑÑичеÑÐºÐ°Ñ Ð±Ð»Ð¾Ñ‡Ð½Ð°Ñ Ñтруктура. ВоÑторг! Смотрим ÑвойÑтва Ñтого ДЛК, выданные утилитой Harry White Order? 14
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_11.txt
Counts
------
1 diagonal Latin
1 axial symmetric
1 natural \diagonal
Добавлю, что ДЛК ÑвлÑетÑÑ "брауном". Ðе Ð·Ñ€Ñ ÐºÐ²Ð°Ð´Ñ€Ð°Ñ‚ попал в Ñтатью OEIS. ПоиÑк Ñтого замечательного квадрата опиÑан здеÑÑŒ https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=6513 PS. При проÑмотре темы "ОДЛК Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдков n>10" обнаружила ДЛК 14-го порÑдка, имеющий 370676 Д-транÑверÑалей https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=6339 ПропуÑтила рекордный квадратик!! Дальше Ñ Ñ€Ð°ÑÑкажу об Ñтом ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Итак, цитирую Ñообщение https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=6339 Ð¡ÐµÐ³Ð¾Ð´Ð½Ñ Ñ‡ÐµÑ€ÐµÐ¿Ð°ÑˆÐºÐ° проверÑет Ñтот ДЛК Отлично! Ðовый рекорд по Д-транÑверÑалÑм Ð´Ð»Ñ Ð”Ð›Ðš 14-го порÑдка - 370676 Д-транÑверÑалей. ÐавернÑка Ñтот ДЛК тоже имеет клаÑÑичеÑкую блочную Ñтруктуру. Позже покажу иллюÑтрацию. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
КФ в формате 2 показанного в предыдущем поÑте ДЛК, канонизировано программой Harry White (в предыдушем поÑте тоже показана КФ, только в буквенно-цифровом формате) 0 2 4 6 9 7 13 11 10 12 8 5 3 1 8 1 3 9 7 11 5 4 13 10 12 2 0 6 6 0 2 12 10 13 4 5 11 7 9 3 1 8 4 11 10 3 1 8 12 9 6 0 2 7 13 5 10 12 6 13 4 2 1 0 3 5 11 8 9 7 12 6 0 10 13 5 2 3 4 11 7 1 8 9 13 10 9 4 3 0 6 8 1 2 5 12 7 11 2 5 11 0 8 12 10 7 9 6 1 13 4 3 5 13 7 2 0 6 9 12 8 1 3 10 11 4 1 3 5 8 12 10 11 13 7 9 6 4 2 0 9 8 1 7 11 4 3 2 5 13 10 0 6 12 3 4 13 1 6 9 7 10 12 8 0 11 5 2 7 9 8 11 5 3 0 1 2 4 13 6 12 10 11 7 12 5 2 1 8 6 0 3 4 9 10 13 СвойÑтва Ñтого ДЛК Order? 14
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_12.txt
Counts
------
1 diagonal Latin
1 axial symmetric
1 natural \diagonalИ ещё ДЛК ÑвлÑетÑÑ "брауном". Точно такие же ÑвойÑтва, как у предыдущего рекордного ДЛК. ОÑталоÑÑŒ раÑкраÑить. Готово!  ВоÑхищаюÑÑŒ! ÐžÑ„Ð¸Ð³ÐµÐ½Ð½Ð°Ñ Ð·Ð°ÐºÐ¾Ð½Ð¾Ð¼ÐµÑ€Ð½Ð¾ÑÑ‚ÑŒ! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Уважаемые читатели темы! ПонÑтно, что Ñ Ð´ÐµÐ»Ð°ÑŽ компилÑцию Ñообщений из темы "ОДЛК Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдков n>10" и из темы "ODLS of order n>10". ПоÑтому где-то ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ Ð½Ðµ очень гладко ÑтыкуютÑÑ. Я ÑтараюÑÑŒ дать вÑÑŽ информацию по данной теме. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
7. n=15 389318 Д-транÑверÑалей ДЛК поÑтроен методом Гергели 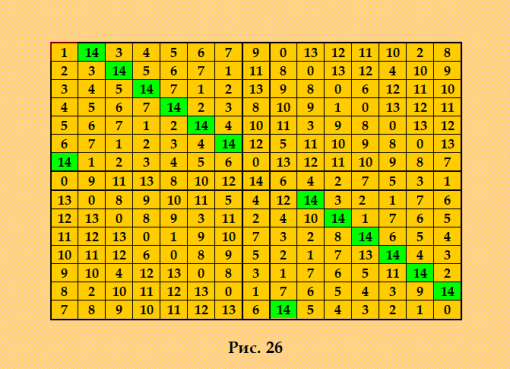 Смотрите мою Ñтатью http://www.natalimak1.narod.ru/dlk.htm Вывод программы Белышева ortogon_u Проверка ДЛК15 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 1 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 389318 Соквадратов: 0 Ð’Ñ€ÐµÐ¼Ñ Ð² Ñек: 4320 20371 8124 2757 857 134 40 12 1 Программа прервана. PS. Ð”Ð»Ñ ÑƒÐ´Ð¾Ð±Ñтва читателей и иÑÑледователей покажу квадрат Гергели в обычном виде 1 14 3 4 5 6 7 9 0 13 12 11 10 2 8 2 3 14 5 6 7 1 11 8 0 13 12 4 10 9 3 4 5 14 7 1 2 13 9 8 0 6 12 11 10 4 5 6 7 14 2 3 8 10 9 1 0 13 12 11 5 6 7 1 2 14 4 10 11 3 9 8 0 13 12 6 7 1 2 3 4 14 12 5 11 10 9 8 0 13 14 1 2 3 4 5 6 0 13 12 11 10 9 8 7 0 9 11 13 8 10 12 14 6 4 2 7 5 3 1 13 0 8 9 10 11 5 4 12 14 3 2 1 7 6 12 13 0 8 9 3 11 2 4 10 14 1 7 6 5 11 12 13 0 1 9 10 7 3 2 8 14 6 5 4 10 11 12 6 0 8 9 5 2 1 7 13 14 4 3 9 10 4 12 13 0 8 3 1 7 6 5 11 14 2 8 2 10 11 12 13 0 1 7 6 5 4 3 9 14 7 8 9 10 11 12 13 6 14 5 4 3 2 1 0 Ð Ñто его КФ в формате 2 0 8 9 14 7 3 4 10 5 2 13 12 6 11 1 9 1 7 4 8 10 2 12 3 13 11 5 14 0 6 4 14 2 13 9 1 7 8 11 0 6 10 3 12 5 7 9 4 3 1 8 13 14 10 11 0 2 5 6 12 10 3 8 1 4 12 9 6 7 14 5 0 11 2 13 8 7 1 9 3 5 14 13 12 4 2 6 0 10 11 13 2 11 0 5 14 6 4 9 12 7 1 8 3 10 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 5 12 3 10 6 0 11 2 8 1 9 13 7 14 4 2 4 13 7 14 6 0 11 1 9 12 8 10 5 3 1 11 6 12 13 2 5 0 4 3 10 14 9 8 7 3 5 10 8 12 7 1 9 0 6 14 11 13 4 2 6 0 14 5 11 13 3 1 2 10 8 4 12 7 9 11 10 0 6 2 4 12 5 14 7 3 9 1 13 8 12 6 5 2 0 11 10 3 13 8 1 7 4 9 14 КФ получена канонизатором Harry White. И код ДЛК по ÑиÑтеме Tomas Brada GLmw2rM2P3TsgRSU2pZNT8z1zFQkWfyMMaFJLbaKMW2xEXTpEeNDsUGW Отмечу, что мне не удалоÑÑŒ найти программой Белышева ortogon_u ни одного ОДЛК к данному ДЛК. Ðо врÑд ли ОДЛК вообще нет - при таком-то количеÑтве Д-транÑверÑалей! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПытаюÑÑŒ запуÑтить первую чаÑÑ‚ÑŒ поиÑка ОДЛК программой Tomas Brada Ð´Ð»Ñ Ð”Ð›Ðš 15-го порÑдка, поÑтроенного методом Гергели ÐšÐ¾Ð¼Ð°Ð½Ð´Ð½Ð°Ñ Ñтрока Ð´Ð»Ñ Ð·Ð°Ð¿ÑƒÑка первой чаÑти программы ortogonbw GLmw2rM2P3TsgRSU2pZNT8z1zFQkWfyMMaFJLbaKMW2xEXTpEeNDsUGW 1 > output.txt КонÑоль C:\Users\Дом\Downloads\Tomas>ortogonbw GLmw2rM2P3TsgRSU2pZNT8z1zFQkWfyMMaFJLbaKM W2xEXTpEeNDsUGW 1 1>output.txt init_trans(15) used 753 nodes num_dtrans: 389318 init_disjoint(15) used 226 heads and 5839996 nodes L(0) c(17) 1 / 20371 L(1) c(127) X / 8035 ПуÑÑ‚ÑŒ чуть-чуть покрутитÑÑ. ИнтереÑно: пойдут ОДЛК или нет. Ðта программа Ñделана так, что ОДЛК Ñразу запиÑываютÑÑ Ð² выходной файл, как только находÑÑ‚ÑÑ. ОбÑчитать Ñтот ДЛК полноÑтью (поиÑк ОДЛК) можно разве что на клаÑтере или Ñуперкомпьютере. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Продолжаю раÑÑказ о ДЛК Ñ Ð¼Ð°ÐºÑимальным количеÑтвом Д-транÑверÑалей (на данный момент). Ðашла рекордный (на данный момент) ДЛК 16-го порÑдка по Д-транÑверÑалÑм. Вот такую он имеет оригинальную блочную Ñтруктуру 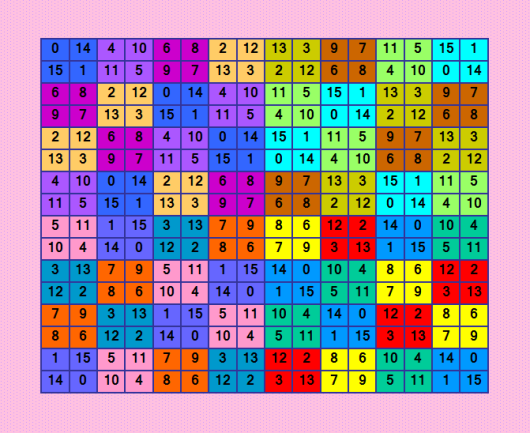 Д-транÑверÑали ÑчиталиÑÑŒ так C:\Users\Дом\Downloads\libr>ortogonb.exe -c HeJsk6HD4zdUUKL8GsPAFGbxN6e4z5b2SeLN XwDproPftBsfzCJ8eDbTSEJ9ZJmh42YUL4 1>out.txt init_trans(16) used 851 nodes dance_mt: using 2 threads for 16 rows in column 1 l(1) 16 / 16 Результат num_dtrans: 32172800 Проверка ДЛК утилитой Harry White Order? 16
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_9.txt
Counts
------
1 diagonal Latin
1 associative
1 double axial symmetric
1 natural \diagonal
1 self-orthogonalОчень интереÑный квадратик! Будет ли побит его рекорд по Д-транÑверÑалÑм? Поживём - увидим :) |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese