Thread 'DLS with maximum of D-transversals'
Message boards : Science : DLS with maximum of D-transversals
Message board moderation
Previous · 1 · 2 · 3 · 4 · 5
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вчера начала редактирование Ñтатьи OEIS. Создала а-файл (загружаетÑÑ Ð² OEIS, как прикрепление к Ñтатье) "DLS of orders n = 11 - 22 with known maximum of D-transversals" Ð’Ñ‹ можете поÑмотреть Ñтот файл на ЯндекÑ.ДиÑке (формат txt, 9,34 КБ) https://disk.yandex.ru/d/rCoMHKXKYswJkQ Ð’ Ñтом файле Ñобрала примеры ДЛК порÑдков n = 11 - 22 Ñ Ñ‚ÐµÐºÑƒÑ‰Ð¸Ð¼ макÑимумом Д-транÑверÑалей. Покажу ДЛК порÑдков 20, 21, 22 n = 20 90010806304 D-transversals 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 ПодробноÑти об Ñтом ДЛК Ñмотрите здеÑÑŒ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=122&postid=1477 Покажу иллюÑтрацию  И напомню: ДЛК поÑтроен программой Harry White. n = 21 51162162017 D-transversals 0 12 3 2 17 19 20 18 13 15 16 14 1 8 10 11 9 4 6 7 5 2 1 0 12 20 18 17 19 16 14 13 15 3 11 9 8 10 7 5 4 6 12 3 2 1 18 20 19 17 14 16 15 13 0 9 11 10 8 5 7 6 4 1 0 12 3 19 17 18 20 15 13 14 16 2 10 8 9 11 6 4 5 7 8 10 11 9 4 12 7 6 0 2 3 1 5 17 19 20 18 13 15 16 14 11 9 8 10 6 5 4 12 3 1 0 2 7 20 18 17 19 16 14 13 15 9 11 10 8 12 7 6 5 1 3 2 0 4 18 20 19 17 14 16 15 13 10 8 9 11 5 4 12 7 2 0 1 3 6 19 17 18 20 15 13 14 16 17 19 20 18 13 15 16 14 8 12 11 10 9 4 6 7 5 0 2 3 1 20 18 17 19 16 14 13 15 10 9 8 12 11 7 5 4 6 3 1 0 2 18 20 19 17 14 16 15 13 12 11 10 9 8 5 7 6 4 1 3 2 0 19 17 18 20 15 13 14 16 9 8 12 11 10 6 4 5 7 2 0 1 3 3 2 1 0 7 6 5 4 11 10 9 8 12 16 15 14 13 20 19 18 17 4 6 7 5 0 2 3 1 17 19 20 18 14 13 12 16 15 8 10 11 9 7 5 4 6 3 1 0 2 20 18 17 19 16 15 14 13 12 11 9 8 10 5 7 6 4 1 3 2 0 18 20 19 17 13 12 16 15 14 9 11 10 8 6 4 5 7 2 0 1 3 19 17 18 20 15 14 13 12 16 10 8 9 11 13 15 16 14 8 10 11 9 4 6 7 5 18 0 2 3 1 17 12 20 19 16 14 13 15 11 9 8 10 7 5 4 6 20 3 1 0 2 19 18 17 12 14 16 15 13 9 11 10 8 5 7 6 4 17 1 3 2 0 12 20 19 18 15 13 14 16 10 8 9 11 6 4 5 7 19 2 0 1 3 18 17 12 20 Ðтот ДЛК поÑтроен программой Harry White, он ÑвлÑетÑÑ SODLS. Значит, у него еÑÑ‚ÑŒ ортогональный диагональный Ñоквадрат (его транÑпонированный вариант) Ñ Ñ‚Ð°ÐºÐ¸Ð¼ же количеÑтвом Д-транÑверÑалей. n = 22 3227747329246 D-transversals 1 13 3 4 5 6 7 8 9 10 11 0 21 20 19 18 17 16 15 14 2 12 2 3 15 5 6 7 8 9 10 11 1 12 0 21 20 19 18 17 16 4 14 13 3 4 5 17 7 8 9 10 11 1 2 13 12 0 21 20 19 18 6 16 15 14 4 5 6 7 19 9 10 11 1 2 3 14 13 12 0 21 20 8 18 17 16 15 5 6 7 8 9 21 11 1 2 3 4 15 14 13 12 0 10 20 19 18 17 16 6 7 8 9 10 11 12 2 3 4 5 16 15 14 13 1 0 21 20 19 18 17 7 8 9 10 11 1 2 14 4 5 6 17 16 15 3 13 12 0 21 20 19 18 8 9 10 11 1 2 3 4 16 6 7 18 17 5 15 14 13 12 0 21 20 19 9 10 11 1 2 3 4 5 6 18 8 19 7 17 16 15 14 13 12 0 21 20 10 11 1 2 3 4 5 6 7 8 20 9 19 18 17 16 15 14 13 12 0 21 0 1 2 3 4 5 6 7 8 9 10 21 20 19 18 17 16 15 14 13 12 11 21 0 12 13 14 15 16 17 18 19 9 20 8 7 6 5 4 3 2 1 11 10 20 21 0 12 13 14 15 16 17 7 19 8 18 6 5 4 3 2 1 11 10 9 19 20 21 0 12 13 14 15 5 17 18 7 6 16 4 3 2 1 11 10 9 8 18 19 20 21 0 12 13 3 15 16 17 6 5 4 14 2 1 11 10 9 8 7 17 18 19 20 21 0 1 13 14 15 16 5 4 3 2 12 11 10 9 8 7 6 16 17 18 19 20 10 0 12 13 14 15 4 3 2 1 11 21 9 8 7 6 5 15 16 17 18 8 20 21 0 12 13 14 3 2 1 11 10 9 19 7 6 5 4 14 15 16 6 18 19 20 21 0 12 13 2 1 11 10 9 8 7 17 5 4 3 13 14 4 16 17 18 19 20 21 0 12 1 11 10 9 8 7 6 5 15 3 2 12 2 14 15 16 17 18 19 20 21 0 11 10 9 8 7 6 5 4 3 13 1 11 12 13 14 15 16 17 18 19 20 21 10 9 8 7 6 5 4 3 2 1 0 ИллюÑÑ‚Ñ€Ð°Ñ†Ð¸Ñ Ð¿Ð¾ÐºÐ°Ð·Ð°Ð½Ð° чуть выше. Ðапомню: Ñтот ДЛК поÑтроен мной методом Гергели. Смотрите Ñтатью "ПОСТРОЕÐИЕ ДИÐГОÐÐЛЬÐЫХ ЛÐТИÐСКИХ КВÐДРÐТОВ" ДЛК 22-го порÑдка изображён в Ñтатье на риÑ. 17. Выражаю огромную благодарноÑÑ‚ÑŒ моему помощнику за обÑчёт Ñтих ДЛК! И конечно, огромное ÑпаÑибо коллеге Tomas Brada за его программу. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Пока Ñ Ð·Ð°ÐºÑ€Ñ‹Ð»Ð° тему о макÑимумах Д-транÑверÑалей. Ð”Ð»Ñ Ð±ÑƒÐ´ÑƒÑ‰ÐµÐ³Ð¾ - еÑÑ‚ÑŒ идеальный ДЛК 23-го порÑдка - кандидат â„–1 на макÑимум Д-транÑверÑалей 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 Смотрите Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=126&postid=1496 Ðтот ДЛК аÑÑоциативный и цикличеÑкий пандиагональный, то еÑÑ‚ÑŒ идеальный. Думаю, что у него будет немало Д-транÑверÑалей. Считать Ñто на одном компьютере очень долго, даже Ñ Ð¼Ð½Ð¾Ð³Ð¾Ñдерным процеÑÑором (как у моего помощника). ЗдеÑÑŒ надо подключать раÑпределённые вычиÑлениÑ. PS. Ð’ полной ÑиÑтеме MOLS 23-го порÑдка не единÑтвенный ДЛК идеальный, а вÑе 20. Вот поÑмотрите проверку утилитой Harry White Order? 23
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_10.txt
Counts
------
20 diagonal Latin
20 associative
20 pandiagonal
20 ultramagic
20 natural \diagonal
19 orthogonal pair
20 self-orthogonalÐо, конечно, Ñреди Ñтих 20 идеальных ДЛК еÑÑ‚ÑŒ изоморфные. Сколько уникальных, Ñ Ð½Ðµ знаю, канонизотора ДЛК 23-го порÑдка у Ð½Ð°Ñ Ð¿Ð¾ÐºÐ° нет. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Кандидат â„–2 - ДЛК 23-го порÑдка, поÑтроенный методом Гергели 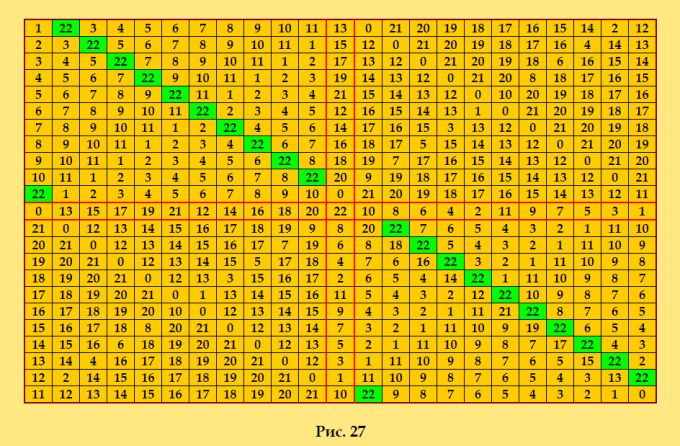 Смотрите ДЛК в Ñтатье http://www.natalimak1.narod.ru/dlk.htm Тоже очень Ñимпатичный квадратик, Ñ…Ð¾Ñ‚Ñ ÑƒÑ‚Ð¸Ð»Ð¸Ñ‚Ð° Harry White никаких ÑвойÑтв в нём не обнаружила. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðу, и далее можно продолжать ÑпиÑок кандидатов Ñледующих порÑдков, но пока Ñчитать негде. ЕÑли иÑÑледователи поÑвÑÑ‚ÑÑ, найти кандидатов ДЛК любого порÑдка не проблема. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата Вчера начала редактирование Ñтатьи OEIS. По непредвиденным обÑтоÑтельÑтвам Ñту правку пришлоÑÑŒ прервать. 17 марта Ñ‚. г. начала новую правку. Ð¡ÐµÐ³Ð¾Ð´Ð½Ñ Ð¿Ð¾ÑледовательноÑÑ‚ÑŒ Ñ Ð½Ð¾Ð²Ñ‹Ð¼Ð¸ оценками утверждена. a(14) >= 380718, a(20) >= 90010806304, a(21) >= 51162162017, a(22) >= 3227747329246. The number of D-transversals for orders 20 - 22 was calculated by a volunteer. - Natalia Makarova, Tomáš Brada, Harry White, Mar 17 2021 Прикреплённый к Ñтатье а-файл "DLS of orders n = 11 - 22 with known maximum of D-transversals" можно поÑмотреть по ÑÑылке https://oeis.org/A287648/a287648_2.txt Ð’ новом а-файле предÑтавлены более подробные данные о ДЛК, имеющих извеÑтные на данный момент макÑимальные Ð·Ð½Ð°Ñ‡ÐµÐ½Ð¸Ñ Ð”-транÑверÑалей. Теперь данный Ñтап ÑкÑперимента по вычиÑлению Д-транÑверÑалей в ДЛК порÑдков n = 11 - 22 полноÑтью завершён. Следующий Ñтап ÑкÑперимента Ð´Ð»Ñ Ð”Ð›Ðš порÑдков n>22 можно будет начинать только Ñ Ð´Ñ€ÑƒÐ³Ð¾Ð¹ программой. Я уже пиÑала выше, что программу подÑчёта Д-транÑверÑалей в ДЛК можно Ñделать по чаÑÑ‚Ñм. Тогда можно будет двигатьÑÑ Ð´Ð°Ð»ÑŒÑˆÐµ. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese