Thread 'Ultramagic DLS'
Message boards : Science : Ultramagic DLS
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
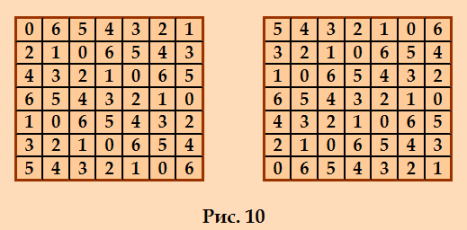
ГҗЕёГҗВҫГ‘вӮ¬ГҗВ° ГҗВҝГҗВҫГ‘ВҒГҗВІГ‘ВҸГ‘вҖҡГҗВёГ‘вҖҡГ‘Е’ ГҗВҫГ‘вҖҡГҗВҙГҗВөГҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ Г‘вҖҡГҗВөГҗВјГ‘Ж’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВј ГҗвҖқГҗвҖәГҗЕЎ (ultramagic DLS). ГҗВҰГҗВёГ‘вҖҡГҗ°ÑвҖҡГҗВ° ГҗВёГҗВ· Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГ‘ВҸ https://boinc.progger.info/odlk/forum_thread.php?id=51&postid=1221 ГҗЕЎГ‘ВҒГ‘вҖҡГҗ°ÑвҖҡГҗВё, ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ ГҗВјГҗВҫГҗВ¶ГҗВҪГҗВҫ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡГ‘Е’ ГҗВҪГҗВө Г‘вҖҡГҗВҫГҗ»ÑŒГҗВәГҗВҫ ГҗВҙГҗВІГҗВ°ГҗВ¶ГҗВҙГ‘вҖ№ Г‘ВҒГҗВёГҗВјГҗВјГҗВөГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ. ГҗВқГҗВ° ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГҗВҫГҗВ№ ГҗВҝГҗВөГ‘вӮ¬ГҗВІГҗВҫГҗВ№ ГҗВёГҗВ»ГҗȄЕҪГ‘ВҒГ‘вҖҡГ‘вӮ¬Гҗ°ÑвҖ ГҗВёГҗВё Г‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘вҖҰГ‘Ж’ ГҗВІГ‘вҖ№ ГҗВІГҗВёГҗВҙГҗВёГ‘вҖҡГҗВө ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ 7-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° (Г‘ВҒ ГҗВјГҗВҫГҗВөГҗВіГҗВҫ Г‘ВҒГҗВ°ГҗВ№Г‘вҖҡГҗВ°) ГҗВё 5-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° (Г‘ВҒ Г‘ВҒГҗВ°ГҗВ№Г‘вҖҡГҗВ° Harry White). ГҗвҖқГҗВ°ГҗВ»ГҗВөГҗВө ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ ГҗВҪГҗВ° ГҗВҫГ‘ВҒГҗВҪГҗВҫГҗВІГҗВө ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 7-ГҗВіГҗВҫ ГҗВё 5-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВҫГҗВІ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 35-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЕҫГҗВҝГ‘вӮ¬ГҗВөГҗВҙГҗВөГҗВ»ГҗВөГҗВҪГҗВёГҗВө: ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВј ГҗвҖқГҗвҖәГҗЕЎ (ultramagic) ГҗВҪГҗВ°ГҗВ·Г‘вҖ№ГҗВІГҗВ°ГҗВөГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҫГҗВҙГҗВҪГҗВҫГҗВІГ‘вӮ¬ГҗВөГҗВјГҗВөГҗВҪГҗВҪГҗВҫ Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВ№ ГҗВё ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№. ГҗвҖ”ГҗВ°ГҗВјГҗВөГ‘вҖЎГҗВ°ГҗВҪГҗВёГҗВө: Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГҗВҪГҗВёГҗВјГҗВ°ГҗВөГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВІ Г‘ВҒГҗВјГ‘вҖ№Г‘ВҒГҗВ»ГҗВө Г‘вҖҡГҗВөГ‘вӮ¬ГҗВјГҗВёГҗВҪГҗВҫГҗВ»ГҗВҫГҗВіГҗВёГҗВё Harry White. ГҗВҜ ГҗВҪГҗВө Г‘вӮ¬ГҗВ°ГҗВ·ГҗВ»ГҗВёГ‘вҖЎГҗ°ÑЕҪ Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВө ГҗВё Г‘вҖ ГҗВөГҗВҪГ‘вҖҡГ‘вӮ¬ГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ-Г‘ВҒГҗВёГҗВјГҗВјГҗВөГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ, ГҗВҝГҗВҫГ‘вҖҡГҗВҫГҗВјГ‘Ж’ Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВҫГҗВҪГҗВё ГҗВёГҗВ·ГҗВҫГҗВјГҗВҫГ‘вӮ¬Г‘вҖһГҗВҪГ‘вҖ№ (ГҗВҝГ‘вӮ¬ГҗВөГҗВІГ‘вӮ¬Гҗ°ÑвҖ°Гҗ°ÑЕҪГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВі ГҗВІ ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВіГҗВ° ГҗВҝГҗВөГ‘вӮ¬ГҗВөГҗВҫГҗВұГҗВҫГҗВ·ГҗВҪГҗ°ÑвҖЎГҗВөГҗВҪГҗВёГҗВөГҗВј Г‘ВҚГҗВ»ГҗВөГҗВјГҗВөГҗВҪГ‘вҖҡГҗВҫГҗВІ). Harry White Г‘вӮ¬ГҗВ°ГҗВ·ГҗВ»ГҗВёГ‘вҖЎГҗВ°ГҗВөГ‘вҖҡ Г‘ВҚГ‘вҖҡГҗВё ГҗВҝГҗВҫГҗВҪГ‘ВҸГ‘вҖҡГҗВёГ‘ВҸ, ГҗВҝГҗВҫГ‘ВҚГ‘вҖҡГҗВҫГҗВјГ‘Ж’ ГҗВұГ‘Ж’ГҗВҙГҗВөГҗВј ГҗВҝГ‘вӮ¬ГҗВёГҗВҙГҗВөГ‘вӮ¬ГҗВ¶ГҗВёГҗВІГҗ°ÑвҖҡГ‘Е’Г‘ВҒГ‘ВҸ ГҗВІ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ Г‘вҖҡГҗВөГҗВјГҗВө Г‘вҖҡГҗВөГ‘вӮ¬ГҗВјГҗВёГҗВҪГҗВҫГҗВ»ГҗВҫГҗВіГҗВёГҗВё Harry White. ГҗвҖҷ Г‘ВҒГ‘вҖҡГҗ°ÑвӮ¬Г‘вҖҡГҗВҫГҗВІГҗВҫГҗВј ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГҗВө ГҗВІГ‘вҖ№ ГҗВІГҗВёГҗВҙГҗВёГ‘вҖҡГҗВө ГҗВҝГ‘вӮ¬ГҗВёГҗВјГҗВөГ‘вӮ¬Г‘вҖ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 5-ГҗВіГҗВҫ, 7-ГҗВіГҗВҫ ГҗВё 35-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВҫГҗВІ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВҜ ГҗВҪГҗВөГҗВјГҗВҪГҗВҫГҗВіГҗВҫ ГҗВ·ГҗВ°ГҗВҪГҗВёГҗВјГҗВ°ГҗВ»Гҗ°ÑВҒГ‘Е’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВјГҗВё ГҗвҖқГҗвҖәГҗЕЎ ГҗВІ Г‘вҖҡГҗВөГҗВјГҗВө ГҗВҪГҗВ° Г‘вҖһГҗВҫГ‘вӮ¬Г‘Ж’ГҗВјГҗВө ГҗВҝГ‘вӮ¬ГҗВҫГҗВөГҗВәГ‘вҖҡГҗВ° ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ, Г‘ВҒ Г‘ВҚГ‘вҖҡГҗВҫГҗВіГҗВҫ Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГ‘ВҸ https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=7171 ГҗВё ГҗВҙГҗВ°ГҗВ»ГҗВөГҗВө. ГҗВқГҗВө ГҗВұГ‘Ж’ГҗВҙГ‘Ж’ ГҗВҝГҗВөГ‘вӮ¬ГҗВөГ‘вҖҡГҗ°ÑВҒГҗВәГҗВёГҗВІГҗ°ÑвҖҡГ‘Е’ Г‘ВҒГ‘ЕҪГҗВҙГҗВ° ГҗВІГ‘ВҒГҗВө Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГ‘ВҸ. ГҗЕёГҗВҫГҗВәГҗВ°Гҗ¶Ñƒ ГҗВҪГҗВөГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬Г‘вҖ№ГҗВө ГҗВёГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҪГ‘вҖ№ГҗВө Г‘вӮ¬ГҗВөГҗВ·Г‘Ж’ГҗȄ΄вҖҡГҗ°ÑвҖҡГ‘вҖ№. ГҗВӯГ‘вҖҡГҗВҫ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 13-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, Г‘вӮ¬ГҗВөГҗВәГҗВҫГ‘вӮ¬ГҗВҙГҗВҪГ‘вҖ№ГҗВ№ ГҗВҪГҗВ° ГҗВҙГҗВ°ГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВҫГҗВјГҗВөГҗВҪГ‘вҖҡ ГҗВҝГҗВҫ ГҗвҖқ-Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°ГҗȄВҸГҗВј (131106 ГҗвҖқ-Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°ГҗВ»ГҗВөГҗВ№)  ГҗВӯГ‘вҖҡГҗВҫ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 19-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, Г‘вҖҡГҗВҫГҗВ¶ГҗВө Г‘вӮ¬ГҗВөГҗВәГҗВҫГ‘вӮ¬ГҗВҙГҗВҪГ‘вҖ№ГҗВ№ ГҗВҪГҗВ° ГҗВҙГҗВ°ГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВҫГҗВјГҗВөГҗВҪГ‘вҖҡ ГҗВҝГҗВҫ ГҗвҖқ-Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°ГҗȄВҸГҗВј (11254190082 ГҗвҖқ-Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°ГҗВ»ГҗВөГҗВ№)  ГҗвҖҷ Г‘ВҚГ‘вҖҡГҗВҫГҗВј ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВ»ГҗВ° Г‘вӮ¬Гҗ°ÑВҒГҗВәГ‘вӮ¬Гҗ°ÑВҒГҗВәГҗВҫГҗВ№ ГҗВҪГҗВөГҗВҫГҗВұГ‘вҖ№Г‘вҖЎГҗВҪГ‘Ж’Г‘ЕҪ Г‘ВҒГ‘вҖҡГ‘вӮ¬Г‘Ж’ГҗВәГ‘вҖҡГ‘Ж’Г‘вӮ¬Г‘Ж’. ГҗвҖқГҗВ°ГҗВ»ГҗВөГҗВө Г‘ВҸ ГҗВёГ‘ВҒГ‘ВҒГҗВ»ГҗВөГҗВҙГҗВҫГҗВІГҗВ°ГҗВ»ГҗВ° ГҗВІГҗВҫГҗВҝГ‘вӮ¬ГҗВҫГ‘ВҒ Г‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГҗВҫГҗВІГҗВ°ГҗВҪГҗВёГ‘ВҸ Г‘вӮ¬ГҗВ°ГҗВ·ГҗВ»ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№Г‘вҖҰ (ГҗВҪГҗВө ГҗВёГҗВ·ГҗВҫГҗВјГҗВҫГ‘вӮ¬Г‘вҖһГҗВҪГ‘вҖ№Г‘вҖҰ) ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВҫГҗВІ 11, 13. ГҗЛң ГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВҪГҗВҫГҗВІГҗВёГҗВ»Гҗ°ÑВҒГ‘Е’ ГҗВҪГҗВ° ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВө 17. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖқГ‘Ж’ГҗВұГҗВ»ГҗВёГ‘вӮ¬Г‘Ж’Г‘ЕҪ Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГҗВө https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=122&postid=1430 ГҗЕЎГҗВ°ГҗВҪГҗВҫГҗВҪГҗВёГҗВ·ГҗВёГ‘вӮ¬ГҗВҫГҗВІГҗВ°ГҗВ»ГҗВ° 14 ГҗвҖқГҗвҖәГҗЕЎ 17-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВІГ‘вҖҰГҗВҫГҗВҙГ‘ВҸГ‘вҖ°ГҗВёГ‘вҖҰ ГҗВІ ГҗВҝГҗВҫГҗВ»ГҗВҪГ‘Ж’Г‘ЕҪ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГ‘Ж’ MOLS, ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВҫГҗВ№ Tomas Brada, ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГҗВ»ГҗВ° Г‘ВҒГҗВ»ГҗВөГҗВҙГ‘Ж’Г‘ЕҪГ‘вҖ°ГҗВёГҗВө 4 ГҗЕЎГҗВӨ J39x3jjhxnHszoQpfcDrAzx27ZgCpvYW9JZU9nm4EozssVGc6mUYnCWuV7HzfwhWK2hEtntURM2pDGa9ins JHep946hdpmD3PbVe64oR1i2JacXn5EZhBapLW1bdkDY4JdXfnDizzcaKLehQmyCFnBMwusRtF4PEhke4 JVUesFePXAN1rG8UWDrmYhv7h3UUqSqVraVEBWcofey2tPsEJpepgvNg8vu32qL8dazxSPiVu1Ttj29tL JZavs7uAV4CURwBtFMoJPcLBijAc1hE3FotZHERYCMPtfJ1PMTFPDqmULKieXppg11yArjb6WbfYS3zYz2 ГҗВЎГҗВ»ГҗВөГҗВҙГҗВҫГҗВІГҗ°ÑвҖҡГҗВөГҗ»ÑŒГҗВҪГҗВҫ, ГҗВёГҗВ· 14 ГҗвҖқГҗвҖәГҗЕЎ Г‘Ж’ГҗВҪГҗВёГҗВәГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ Г‘вҖҡГҗВҫГҗ»ÑŒГҗВәГҗВҫ 4. ГҗВЎГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ ГҗВҝГҗВҫГ‘ВҒГ‘вҖЎГҗВёГ‘вҖҡГҗ°ÑЕҪ ГҗВІ ГҗВҪГҗВёГ‘вҖҰ ГҗвҖқ-Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°ГҗВ»ГҗВё. ГҗвҖңГҗВҫГ‘вҖҡГҗВҫГҗВІГҗВҫ! num_dtrans: 204446127 num_dtrans: 204995269 num_dtrans: 204586817 num_dtrans: 204330233 ГҗВўГҗВҫГҗВҝ-4 ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГҗВ»ГҗВҫГ‘ВҒГ‘Е’ ГҗВҙГҗȄВҸ ГҗвҖқГҗвҖәГҗЕЎ 17-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗвҖҷГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВҫГҗВјГ‘Ж’ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГ‘вӮ¬ГҗВёГҗВҪГҗВ°ГҗВҙГҗВ»ГҗВөГҗВ¶ГҗВёГ‘вҖҡ Г‘вҖҡГҗВөГҗВәГ‘Ж’Г‘вҖ°ГҗВёГҗВ№ Г‘вӮ¬ГҗВөГҗВәГҗВҫГ‘вӮ¬ГҗВҙ. --------- ГҗВўГҗВ°ГҗВәГҗВёГҗВј ГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВј, ГҗВёГҗВ· 14 ГҗвҖқГҗвҖәГҗЕЎ, Г‘ВҒГҗВҫГҗВҙГҗВөГ‘вӮ¬ГҗВ¶Гҗ°ÑвҖ°ГҗВёГ‘вҖҰГ‘ВҒГ‘ВҸ ГҗВІ ГҗВҝГҗВҫГҗВ»ГҗВҪГҗВҫГҗВ№ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГҗВө MOLS 17-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, Г‘вҖҡГҗВҫГҗ»ÑŒГҗВәГҗВҫ 4 Г‘Ж’ГҗВҪГҗВёГҗВәГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ. ГҗВӯГ‘вҖҡГҗВё Г‘Ж’ГҗВҪГҗВёГҗВәГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ Г‘ВҒГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ Г‘вӮ¬Гҗ°ÑВҒГ‘ВҒГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГҗВј. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷ ГҗВҫГ‘вӮ¬ГҗВёГҗВіГҗВёГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВј (ГҗВҪГҗВҫГ‘вӮ¬ГҗВјГҗВ°ГҗВ»ГҗВёГҗВ·ГҗВҫГҗВІГҗВ°ГҗВҪГҗВҪГҗВҫГҗВј) ГҗВІГҗВёГҗВҙГҗВө Г‘ВҚГ‘вҖҡГҗВё 4 ГҗвҖқГҗвҖәГҗЕЎ ГҗВёГҗВ· ГҗВҝГҗВҫГҗВ»ГҗВҪГҗВҫГҗВ№ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГ‘вҖ№ MOLS 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 ГҗВЎГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГҗВј Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ° Г‘ВҚГ‘вҖҡГҗВёГ‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ Г‘Ж’Г‘вҖҡГҗВёГҗВ»ГҗВёГ‘вҖҡГҗВҫГҗВ№ Harry White Order? 17
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt
Counts
------
4 diagonal Latin
4 pandiagonal
4 center symmetric
4 nfr
3 orthogonal pair
4 self-orthogonalГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө, ГҗВҪГҗВҫ ГҗВҪГҗВө Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВө, ГҗВ° ГҗВ·ГҗВҪГҗ°ÑвҖЎГҗВёГ‘вҖҡ, ГҗВҪГҗВө ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө. ГҗЕёГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·Г‘Ж’Г‘ЕҪ Г‘ВҚГ‘вҖҡГҗВё ГҗвҖқГҗвҖәГҗЕЎ ГҗВёГҗВ· ГҗВҪГҗВҫГ‘вӮ¬ГҗВјГҗВ°ГҗВ»ГҗВёГҗВ·ГҗВҫГҗВІГҗВ°ГҗВҪГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВІ ГҗВЎГҗВқ ГҗвҖқГҗвҖәГҗЕЎ (ГҗВёГ‘ВҒГҗВҝГҗВҫГҗ»ÑŒГҗВ·Г‘Ж’Г‘ЕҪ ГҗВҙГҗȄВҸ ГҗВҝГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГҗВ°ГҗВҪГҗВёГ‘ВҸ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГ‘Ж’ Tomas Brada dlkconv), ГҗВҝГҗВҫГҗȄĄвҖЎГҗ°ÑЕҪ Г‘ВҒГҗВ»ГҗВөГҗВҙГ‘Ж’Г‘ЕҪГ‘вҖ°ГҗВёГҗВө ГҗВЎГҗВқ ГҗвҖқГҗвҖәГҗЕЎ 0 6 12 1 7 13 2 8 14 3 9 15 4 10 16 5 11 12 1 7 13 2 8 14 3 9 15 4 10 16 5 11 0 6 7 13 2 8 14 3 9 15 4 10 16 5 11 0 6 12 1 2 8 14 3 9 15 4 10 16 5 11 0 6 12 1 7 13 14 3 9 15 4 10 16 5 11 0 6 12 1 7 13 2 8 9 15 4 10 16 5 11 0 6 12 1 7 13 2 8 14 3 4 10 16 5 11 0 6 12 1 7 13 2 8 14 3 9 15 16 5 11 0 6 12 1 7 13 2 8 14 3 9 15 4 10 11 0 6 12 1 7 13 2 8 14 3 9 15 4 10 16 5 6 12 1 7 13 2 8 14 3 9 15 4 10 16 5 11 0 1 7 13 2 8 14 3 9 15 4 10 16 5 11 0 6 12 13 2 8 14 3 9 15 4 10 16 5 11 0 6 12 1 7 8 14 3 9 15 4 10 16 5 11 0 6 12 1 7 13 2 3 9 15 4 10 16 5 11 0 6 12 1 7 13 2 8 14 15 4 10 16 5 11 0 6 12 1 7 13 2 8 14 3 9 10 16 5 11 0 6 12 1 7 13 2 8 14 3 9 15 4 5 11 0 6 12 1 7 13 2 8 14 3 9 15 4 10 16 0 13 9 5 1 14 10 6 2 15 11 7 3 16 12 8 4 5 1 14 10 6 2 15 11 7 3 16 12 8 4 0 13 9 10 6 2 15 11 7 3 16 12 8 4 0 13 9 5 1 14 15 11 7 3 16 12 8 4 0 13 9 5 1 14 10 6 2 3 16 12 8 4 0 13 9 5 1 14 10 6 2 15 11 7 8 4 0 13 9 5 1 14 10 6 2 15 11 7 3 16 12 13 9 5 1 14 10 6 2 15 11 7 3 16 12 8 4 0 1 14 10 6 2 15 11 7 3 16 12 8 4 0 13 9 5 6 2 15 11 7 3 16 12 8 4 0 13 9 5 1 14 10 11 7 3 16 12 8 4 0 13 9 5 1 14 10 6 2 15 16 12 8 4 0 13 9 5 1 14 10 6 2 15 11 7 3 4 0 13 9 5 1 14 10 6 2 15 11 7 3 16 12 8 9 5 1 14 10 6 2 15 11 7 3 16 12 8 4 0 13 14 10 6 2 15 11 7 3 16 12 8 4 0 13 9 5 1 2 15 11 7 3 16 12 8 4 0 13 9 5 1 14 10 6 7 3 16 12 8 4 0 13 9 5 1 14 10 6 2 15 11 12 8 4 0 13 9 5 1 14 10 6 2 15 11 7 3 16 0 7 14 4 11 1 8 15 5 12 2 9 16 6 13 3 10 11 1 8 15 5 12 2 9 16 6 13 3 10 0 7 14 4 5 12 2 9 16 6 13 3 10 0 7 14 4 11 1 8 15 16 6 13 3 10 0 7 14 4 11 1 8 15 5 12 2 9 10 0 7 14 4 11 1 8 15 5 12 2 9 16 6 13 3 4 11 1 8 15 5 12 2 9 16 6 13 3 10 0 7 14 15 5 12 2 9 16 6 13 3 10 0 7 14 4 11 1 8 9 16 6 13 3 10 0 7 14 4 11 1 8 15 5 12 2 3 10 0 7 14 4 11 1 8 15 5 12 2 9 16 6 13 14 4 11 1 8 15 5 12 2 9 16 6 13 3 10 0 7 8 15 5 12 2 9 16 6 13 3 10 0 7 14 4 11 1 2 9 16 6 13 3 10 0 7 14 4 11 1 8 15 5 12 13 3 10 0 7 14 4 11 1 8 15 5 12 2 9 16 6 7 14 4 11 1 8 15 5 12 2 9 16 6 13 3 10 0 1 8 15 5 12 2 9 16 6 13 3 10 0 7 14 4 11 12 2 9 16 6 13 3 10 0 7 14 4 11 1 8 15 5 6 13 3 10 0 7 14 4 11 1 8 15 5 12 2 9 16 0 3 6 9 12 15 1 4 7 10 13 16 2 5 8 11 14 15 1 4 7 10 13 16 2 5 8 11 14 0 3 6 9 12 13 16 2 5 8 11 14 0 3 6 9 12 15 1 4 7 10 11 14 0 3 6 9 12 15 1 4 7 10 13 16 2 5 8 9 12 15 1 4 7 10 13 16 2 5 8 11 14 0 3 6 7 10 13 16 2 5 8 11 14 0 3 6 9 12 15 1 4 5 8 11 14 0 3 6 9 12 15 1 4 7 10 13 16 2 3 6 9 12 15 1 4 7 10 13 16 2 5 8 11 14 0 1 4 7 10 13 16 2 5 8 11 14 0 3 6 9 12 15 16 2 5 8 11 14 0 3 6 9 12 15 1 4 7 10 13 14 0 3 6 9 12 15 1 4 7 10 13 16 2 5 8 11 12 15 1 4 7 10 13 16 2 5 8 11 14 0 3 6 9 10 13 16 2 5 8 11 14 0 3 6 9 12 15 1 4 7 8 11 14 0 3 6 9 12 15 1 4 7 10 13 16 2 5 6 9 12 15 1 4 7 10 13 16 2 5 8 11 14 0 3 4 7 10 13 16 2 5 8 11 14 0 3 6 9 12 15 1 2 5 8 11 14 0 3 6 9 12 15 1 4 7 10 13 16 ГҗВЎГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГҗВј Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ° Г‘ВҚГ‘вҖҡГҗВёГ‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ Order? 17
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_8.txt
Counts
------
4 diagonal Latin
4 associative
4 pandiagonal
4 ultramagic
4 natural \diagonal
3 orthogonal pair
4 self-orthogonalГҗвҖҷГ‘ВҒГ‘вҖҳ ГҗВҫГ‘вҖҡГҗВ»ГҗВёГ‘вҖЎГҗВҪГҗВҫ! ГҗЕ“Г‘вҖ№ ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГҗВ»ГҗВё ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ. ГҗВқГҗВҫ ГҗВҪГҗВөГҗ»ÑŒГҗВ·Г‘ВҸ Г‘ВҒГҗВәГҗВ°ГҗВ·Гҗ°ÑвҖҡГ‘Е’, Г‘вҖЎГ‘вҖҡГҗВҫ Г‘ВҚГ‘вҖҡГҗВҫ ГҗВІГ‘ВҒГҗВө Г‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГҗВөГҗВҪГҗВҪГҗВҫ Г‘вӮ¬ГҗВ°ГҗВ·ГҗВ»ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№ГҗВө ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ 17-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗвҖқГҗȄВҸ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° 17, ГҗВІГҗВөГ‘вӮ¬ГҗВҫГ‘ВҸГ‘вҖҡГҗВҪГҗВҫ (ГҗВәГҗВ°ГҗВә ГҗВё ГҗВҙГҗȄВҸ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° 13), Г‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГ‘Ж’Г‘ЕҪГ‘вҖҡ ГҗВҝГҗВҫГҗ»Ñƒ-Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВө ГҗВё ГҗВҪГҗВө Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВө ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ. ГҗВЎГ‘вӮ¬ГҗВөГҗВҙГҗВё ГҗВҪГҗВёГ‘вҖҰ, ГҗВјГҗВҫГҗВ¶ГҗВөГ‘вҖҡ ГҗВұГ‘вҖ№Г‘вҖҡГ‘Е’, ГҗВё Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВө ГҗВҪГҗВ°ГҗВ№ГҗВҙГ‘Ж’Г‘вҖҡГ‘ВҒГ‘ВҸ, ГҗВё Г‘ВҚГ‘вҖҡГҗВҫ ГҗВұГ‘Ж’ГҗВҙГ‘Ж’Г‘вҖҡ ГҗВҪГҗВҫГҗВІГ‘вҖ№ГҗВө ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ. ГҗВўГҗВөГҗВәГ‘Ж’Г‘вҖ°ГҗВёГҗВ№ ГҗВјГҗВ°ГҗВәГ‘ВҒГҗВёГҗВјГ‘Ж’ГҗВј ГҗВҝГҗВҫ ГҗвҖқ-Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°ГҗȄВҸГҗВј ГҗВҝГ‘вӮ¬ГҗВёГҗВҪГҗВ°ГҗВҙГҗВ»ГҗВөГҗВ¶ГҗВёГ‘вҖҡ ГҗВҝГҗВөГ‘вӮ¬ГҗВІҗВјГ‘Ж’ ГҗВёГҗВ· 4-Г‘вҖҰ ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ [code]num_dtrans: 204995269[/code] ГҗВ ГҗВөГҗВәГҗВҫГ‘вӮ¬ГҗВҙГҗВҪГҗВҫГҗВјГ‘Ж’ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГҗВ»ГҗВҫГҗВ¶ГҗВөГҗВҪГҗВ° ГҗВёГҗВ»ГҗȄЕҪГ‘ВҒГ‘вҖҡГ‘вӮ¬Гҗ°ÑвҖ ГҗВёГ‘ВҸ :) ГҗВЎГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ ГҗВёГҗВ·ГҗВҫГҗВұГ‘вӮ¬ГҗВ°Гҗ¶Ñƒ. ГҗвҖңГҗВҫГ‘вҖҡГҗВҫГҗВІГҗВҫ! 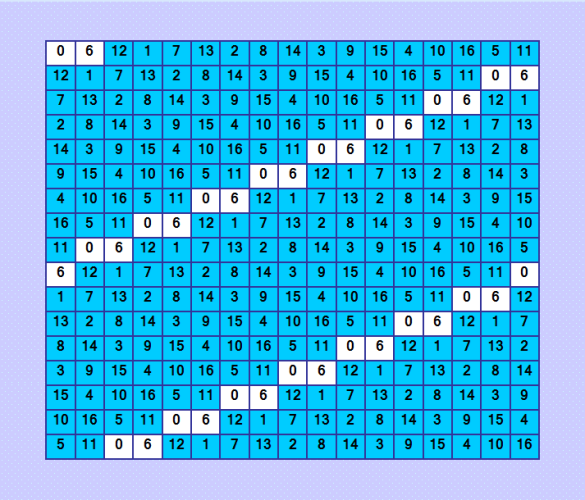 ГҗЕ“ГҗВҫГҗВ¶ГҗВҪГҗВҫ ГҗВұГ‘вҖ№ГҗВ»ГҗВҫ ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·Гҗ°ÑвҖҡГ‘Е’ Г‘вӮ¬Гҗ°ÑВҒГҗВәГ‘вӮ¬Гҗ°ÑВҒГҗВәГҗВҫГҗВ№ Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВёГҗВ»ГҗВё ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’ ГҗвҖқГҗвҖәГҗЕЎ, Г‘ВҸ ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВ»ГҗВ° Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВІ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВәГҗ°ÑвҖҰ. ГҗВӯГ‘вҖҡГҗВҫГ‘вҖҡ ГҗвҖқГҗвҖәГҗЕЎ Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№. ГҗВҗГҗВҪГҗВ°ГҗВ»ГҗВҫГҗВіГҗВёГ‘вҖЎГҗВҪГҗВҫ Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВёГҗВјГҗВөГҗВөГ‘вҖҡ ГҗВјГҗВөГ‘ВҒГ‘вҖҡГҗВҫ ГҗВІ Г‘ВҒГ‘вҖҡГҗВҫГҗВ»ГҗВұГ‘вҖ Гҗ°ÑвҖҰ ГҗВё ГҗВІ ГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°ГҗȄВҸГ‘вҖҰ ГҗВҫГҗВұГҗВҫГҗВёГ‘вҖҰ ГҗВҪГҗВ°ГҗВҝГ‘вӮ¬ГҗВ°ГҗВІГҗВ»ГҗВөГҗВҪГҗВёГҗВ№. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷ ГҗВҝГҗВҫГҗВ»ГҗВҪГҗВҫГҗВ№ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГҗВө MOLS 19-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° Г‘ВҒГҗВҫГҗВҙГҗВөГ‘вӮ¬ГҗВ¶ГҗВёГ‘вҖҡГ‘ВҒГ‘ВҸ 16 ГҗвҖқГҗвҖәГҗЕЎ LNPBNdjGWMGj8q6LJcFJQDE9d3bfxZxELHinjkmjZp9FAqyy8P8Byyzks9rAa4GSffr4GSWyqqvwagd8aKGotS6KZZhYQ1KhesT4XnarJWF83MvkwohSEvKg3 LMocW1vUYvAeZ2EUrrHjD1rTh5YVCPeucSQvrpFiuKG4c7SA8RKK8SXNFJ47UQRShATg7ZMwzffnPeUNvE4pmjVf1P5GjY67SEyFPXbteV7eKxg2j7 Lk5Gt1SvxZZCCeuRUDR3Z7aRVoNSbpDyDqbW1ELDQCfHtqCXPGdydHr3Fk7GskbyXxrCohD4533tdS1CuAXYAGNC1U2DSbzNHADuLkSJK6XVgb4oonN8 LFyGwpMwERA3kjUmpw3QgvVmE3KXMDMZSfT5X2C6hRoKyn2MvhJFSKxwLKKvk8dBRzNWpVX8uWvVKXZxfMwibbVLynBBmjfh2zYTcQByepswFk3GAPTP2 LGeipKTTQKAWgRNLs5HfECkVHmjUW1Hctej7tNR2cDEBWM5N3pHT45dwJhcQVXpmFsg3iLkhqNJRdp5WTCrozp2wYVhVokxxZ2eR7ZR6 LX4vjGAztUkbjLYPB62WKwvMKEaSc6u55HeHue292EaQeqmrYJZd6k3TkrKU7bSKPyDrmf6BwVHEDSc7LXS6NmxeBShkbiWBwuWyychQM1xF9Qz Lcj4oCcBBVdLRBCgmSoWqrSDqxai5ZJRUibbPSN7zjR6VsQWcSTwgaLTZ6Epj4HT58ff6mKPzTiPZBB6bq7o74UQYi4HMeo9uDsgk4pzaf7C LBRLRReVhFDADbACXPM6kMidtYetBv9TbE7stzFV7kQ7NjGATqhiosc4wTRsYwi4qruAxfR9e2vZWjTbvYffLQNNxtoXW8 LCrx6CeA7EU11QNKLpdGTMvs5j2ZNRAYUCUcp7uCRhL6B7EQDN5yqrDAneNtcAfUR3cBPNofq23q9bEZZ4fLAXKuLdShPVKthWsEvokNG9hDwa8znfkrDe Ls2XkSPE5EAmQ2zUn63iD6VLWd7gPYFyMoW1pRAnNHBqJmnxqgH7yqbprMaWSJsR1S4S3fGVXDZCdUfCraCA6dQBEBsT5g6SK1o3CCVwq1x5NYNR LALygJKVaTt9sxSxxTbJEt8hxpNQf3cQGMUb9FkRxsQBnW26DM6cLevv7L1B8bFyCb7UbjjPDXhw7JchYAVsFTbTxd5poPJ9QCcNU7ZuM2h5 Ld8u48CyQKuq9v34TmtMb1ZvNJSwMyg9MHUEYps9SAVTmY8wiTDxsYV6CYM9wQ2bVju617riyBZnsjT7SPQ9T9U1ktDsvzHcximdQngxRNVikfJScB2 LgELmZn4hZE8TWY1UgZbavomVF3GfKHZqPoB7VfuCJSXVnJUfyaiPU7iLHsLatzRddPNsrz2Byqgd6VStBK7V5LnbhqcoepEe64PN28 LudLBmQKpcZUGE9HmCLhyPcDL92fQVLbK4WEMFcgjZFKp8idesKZoPAp1Ch4ufGPjWaDwENnSbQpmgDDCQBRsXyBKyA7fYfjj8mBN6 LUXJjnR46k7ZoLzqWwiTn3hasxJmncMVA8NfcbW5rVBiNAdr7hBQRYo5b6ARrNY8qfT7R18835amHEKgn61pCMxLyai5tRDE3h3s3vL LM6MiG9aWn14qwX7JXNWhZ9asPTZBb4WNjQXUYA77xYFKiafXHgFsfRogaw1SN4pnYSetqBSMBeSf2rjTNQutpj5ZKB7W8 ГҗвҖҷГ‘ВҒГҗВө ГҗВҫГҗВҪГҗВё Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВө ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВё Г‘вҖ ГҗВөГҗВҪГ‘вҖҡГ‘вӮ¬ГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ-Г‘ВҒГҗВёГҗВјГҗВјГҗВөГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№ГҗВө. ГҗЕЎГҗВ°ГҗВҪГҗВҫГҗВҪГҗВёГҗВ·Гҗ°ÑвҖҡГҗВҫГ‘вӮ¬ГҗВ° ГҗвҖқГҗвҖәГҗЕЎ 19-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° Г‘Ж’ ГҗВҪГҗ°ÑВҒ ГҗВҝГҗВҫГҗВәГҗВ° ГҗВҪГҗВөГ‘вҖҡ, ГҗВҝГҗВҫГ‘ВҚГ‘вҖҡГҗВҫГҗВјГ‘Ж’ ГҗВҪГҗВ°ГҗВ№Г‘вҖҡГҗВё Г‘ВҒГ‘вӮ¬ГҗВөГҗВҙГҗВё Г‘ВҚГ‘вҖҡГҗВёГ‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ Г‘Ж’ГҗВҪГҗВёГҗВәГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВҝГҗВҫГҗВәГҗВ° ГҗВҪГҗВө ГҗВјГҗВҫГҗВіГ‘Ж’. ГҗВўГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°ГҗВ»ГҗВё ГҗВІГҗВҫ ГҗВІГ‘ВҒГҗВөГ‘вҖҰ Г‘ВҚГ‘вҖҡГҗВёГ‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГ‘ВҒГ‘вҖЎГҗВёГ‘вҖҡГҗВ°ГҗВ» ГҗВјГҗВҫГҗВ№ ГҗВҝГҗВҫГҗВјГҗВҫГ‘вҖ°ГҗВҪГҗВёГҗВә, ГҗВәГ‘вӮ¬ГҗВҫГҗВјГҗВө ГҗВҫГҗВҙГҗВҪГҗВҫГҗВіГҗВҫ (ГҗВҝГҗВөГ‘вӮ¬ГҗВІГҗВҫГҗВіГҗВҫ), ГҗВІ ГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВҫГҗВј ГҗвҖқ-Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°ГҗВ»ГҗВё ГҗВҝГҗВҫГ‘ВҒГ‘вҖЎГҗВёГ‘вҖҡГҗВ°ГҗВ»ГҗВ° Г‘ВҸ. ГҗЕ“ГҗВ°ГҗВәГ‘ВҒГҗВёГҗВјГ‘Ж’ГҗВј ГҗВҝГҗВҫ ГҗвҖқ-Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°ГҗȄВҸГҗВј (ГҗВҪГҗВ° ГҗВҙГҗВ°ГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВҫГҗВјГҗВөГҗВҪГ‘вҖҡ) ГҗВҝГ‘вӮ¬ГҗВёГҗВҪГҗВ°ГҗВҙГҗВ»ГҗВөГҗВ¶ГҗВёГ‘вҖҡ Г‘ВҚГ‘вҖҡГҗВҫГҗВјГ‘Ж’ ГҗвҖқГҗвҖәГҗЕЎ  ГҗВқГҗВҫ Г‘ВҚГ‘вҖҡГҗВҫ ГҗВҪГҗВө ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ, ГҗВҫГҗВҪ Г‘вҖ ГҗВөГҗВҪГ‘вҖҡГ‘вӮ¬ГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ-Г‘ВҒГҗВёГҗВјГҗВјГҗВөГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№ГҗВ№ ГҗВё ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№. ГҗвҖҷГ‘вҖ№Г‘ЛҶГҗВө Г‘ВҸ Г‘Ж’ГҗВ¶ГҗВө ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВ»ГҗВ° ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВҪГҗВҫГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ Г‘ВҒ Г‘вҖҡГҗВ°ГҗВәГҗВёГҗВј ГҗВ¶ГҗВө ГҗВәГҗВҫГҗВ»ГҗВёГ‘вҖЎГҗВөГ‘ВҒГ‘вҖҡГҗВІГҗВҫГҗВј ГҗвҖқ-Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°ГҗВ»ГҗВөГҗВ№. ГҗВЎГҗВҫГҗВІГҗВөГ‘вӮ¬Г‘ЛҶГҗВөГҗВҪГҗВҪГҗВҫ ГҗВ°ГҗВҪГҗВ°ГҗВ»ГҗВҫГҗВіГҗВёГ‘вҖЎГҗВҪГҗВҫ ГҗВІГ‘ВҒГҗВө 16 ГҗвҖқГҗвҖәГҗЕЎ ГҗВёГҗВ· ГҗВҝГҗВҫГҗВ»ГҗВҪГҗВҫГҗВ№ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГ‘вҖ№ MOLS 19-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬Г‘вҖ№ГҗВө Г‘ВҸГҗВІГҗȄВҸГ‘ЕҪГ‘вҖҡГ‘ВҒГ‘ВҸ Г‘вҖ ГҗВөГҗВҪГ‘вҖҡГ‘вӮ¬ГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ-Г‘ВҒГҗВёГҗВјГҗВјГҗВөГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№ГҗВјГҗВё ГҗВё ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВјГҗВё, ГҗВ»ГҗВөГҗВіГҗВәГҗВҫ ГҗВҝГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГҗ°ÑвҖҡГ‘Е’ ГҗВІ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ, ГҗВҝГ‘вӮ¬ГҗВҫГ‘ВҒГ‘вҖҡГҗВҫ ГҗВҝГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГҗВ°ГҗВІ ГҗВёГ‘вҖҰ ГҗВІ ГҗВЎГҗВқ ГҗвҖқГҗвҖәГҗЕЎ. ГҗВЎГҗВәГҗВҫГҗ»ÑŒГҗВәГҗВҫ ГҗВұГ‘Ж’ГҗВҙГҗВөГ‘вҖҡ ГҗВІ Г‘ВҚГ‘вҖҡГҗВҫГҗВј ГҗВҪГҗВ°ГҗВұГҗВҫГ‘вӮ¬ГҗВө Г‘Ж’ГҗВҪГҗВёГҗВәГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ, ГҗВҝГҗВҫГҗВәГҗВ° ГҗВҪГҗВө ГҗВ·ГҗВҪГҗ°ÑЕҪ. ГҗЕёГ‘вӮ¬ГҗВёГҗВјГҗВөГ‘вӮ¬ ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗВҪГҗВ° ГҗВёГҗВ»ГҗȄЕҪГ‘ВҒГ‘вҖҡГҗ°ÑвҖ ГҗВёГҗВё ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·Г‘Ж’ГҗВөГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВІ Г‘ВҒГҗВ»ГҗВөГҗВҙГ‘Ж’Г‘ЕҪГ‘вҖ°ГҗВёГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 0 13 7 1 14 8 2 15 9 3 16 10 4 17 11 5 18 12 6 7 1 14 8 2 15 9 3 16 10 4 17 11 5 18 12 6 0 13 14 8 2 15 9 3 16 10 4 17 11 5 18 12 6 0 13 7 1 2 15 9 3 16 10 4 17 11 5 18 12 6 0 13 7 1 14 8 9 3 16 10 4 17 11 5 18 12 6 0 13 7 1 14 8 2 15 16 10 4 17 11 5 18 12 6 0 13 7 1 14 8 2 15 9 3 4 17 11 5 18 12 6 0 13 7 1 14 8 2 15 9 3 16 10 11 5 18 12 6 0 13 7 1 14 8 2 15 9 3 16 10 4 17 18 12 6 0 13 7 1 14 8 2 15 9 3 16 10 4 17 11 5 6 0 13 7 1 14 8 2 15 9 3 16 10 4 17 11 5 18 12 13 7 1 14 8 2 15 9 3 16 10 4 17 11 5 18 12 6 0 1 14 8 2 15 9 3 16 10 4 17 11 5 18 12 6 0 13 7 8 2 15 9 3 16 10 4 17 11 5 18 12 6 0 13 7 1 14 15 9 3 16 10 4 17 11 5 18 12 6 0 13 7 1 14 8 2 3 16 10 4 17 11 5 18 12 6 0 13 7 1 14 8 2 15 9 10 4 17 11 5 18 12 6 0 13 7 1 14 8 2 15 9 3 16 17 11 5 18 12 6 0 13 7 1 14 8 2 15 9 3 16 10 4 5 18 12 6 0 13 7 1 14 8 2 15 9 3 16 10 4 17 11 12 6 0 13 7 1 14 8 2 15 9 3 16 10 4 17 11 5 18 ГҗВӯГ‘вҖҡГҗВҫГ‘вҖҡ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВёГҗВ·ГҗВҫГҗВјГҗВҫГ‘вӮ¬Г‘вҖһГҗВөГҗВҪ ГҗвҖқГҗвҖәГҗЕЎ, ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГҗВҫГҗВјГ‘Ж’ ГҗВҪГҗВ° ГҗВёГҗВ»ГҗȄЕҪГ‘ВҒГ‘вҖҡГ‘вӮ¬Гҗ°ÑвҖ ГҗВёГҗВё, ГҗВ° Г‘вҖҡГҗВ°ГҗВәГҗВ¶ГҗВө ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВјГ‘Ж’ ГҗвҖқГҗвҖәГҗЕЎ, ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГҗВҫГҗВјГ‘Ж’ ГҗВ·ГҗВҙГҗВөГ‘ВҒГ‘Е’ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=126&postid=1487 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЛң ГҗВөГ‘вҖ°Г‘вҖҳ ГҗВҫГҗВҙГҗВҪГҗВ° ГҗВёГҗВ»ГҗȄЕҪГ‘ВҒГ‘вҖҡГ‘вӮ¬Гҗ°ÑвҖ ГҗВёГ‘ВҸ - ГҗВҝГҗВҫГ‘ВҒГҗВ»ГҗВөГҗВҙГҗВҪГҗВёГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВёГҗВ· ГҗВҝГ‘вӮ¬ГҗВөГҗВҙГ‘вҖ№ГҗВҙГ‘Ж’Г‘вҖ°ГҗВөГҗВіГҗВҫ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГҗВ°  ГҗВ Гҗ°ÑВҒГҗВәГ‘вӮ¬Гҗ°ÑВҒГҗВәГҗВҫГҗВ№ ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВ° Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВІ Г‘ВҒГ‘вҖҡГҗВҫГҗВ»ГҗВұГ‘вҖ Гҗ°ÑвҖҰ, ГҗвҖқГҗвҖәГҗЕЎ Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№. ГҗВҗГҗВҪГҗВ°ГҗВ»ГҗВҫГҗВіГҗВёГ‘вҖЎГҗВҪГҗ°ÑВҸ Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВёГҗВјГҗВөГҗВөГ‘вҖҡ ГҗВјГҗВөГ‘ВҒГ‘вҖҡГҗВҫ ГҗВІ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВәГҗ°ÑвҖҰ ГҗВё ГҗВІ ГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°ГҗȄВҸГ‘вҖҰ ГҗВҫГҗВұГҗВҫГҗВёГ‘вҖҰ ГҗВҪГҗВ°ГҗВҝГ‘вӮ¬ГҗВ°ГҗВІГҗВ»ГҗВөГҗВҪГҗВёГҗВ№. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷГ‘вҖ№, ГҗВІГҗВөГ‘вӮ¬ГҗВҫГ‘ВҸГ‘вҖҡГҗВҪГҗВҫ, ГҗВ·ГҗВ°ГҗВјГҗВөГ‘вҖҡГҗВёГҗВ»ГҗВё, Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВҝГҗВҫГҗВәГҗВ° Г‘вӮ¬Гҗ°ÑВҒГ‘ВҒГҗВјГҗ°ÑвҖҡГ‘вӮ¬ГҗВёГҗВІГҗ°ÑЕҪГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВҫГҗВІ, Г‘ВҸГҗВІГҗȄВҸГ‘ЕҪГ‘вҖ°ГҗВёГ‘вҖҰГ‘ВҒГ‘ВҸ ГҗВҝГ‘вӮ¬ГҗВҫГ‘ВҒГ‘вҖҡГ‘вҖ№ГҗВјГҗВё Г‘вҖЎГҗВёГ‘ВҒГҗВ»ГҗВ°ГҗВјГҗВё: 5, 7, 11, 13, 17, 19. ГҗвҖқГҗȄВҸ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВҫГҗВІ n=4k+2, k=1, 2, 3, ... ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҪГҗВө Г‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГ‘Ж’ГҗВөГ‘вҖҡ, Г‘вҖҡГҗВ°ГҗВә ГҗВәГҗВ°ГҗВә ГҗВҪГҗВө Г‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГ‘Ж’ГҗВөГ‘вҖҡ ГҗВҪГҗВё Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№Г‘вҖҰ, ГҗВҪГҗВё ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ. ГҗвҖқГҗȄВҸ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВҫГҗВІ n=4k, k=1, 2, 3, ... Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ Г‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГ‘Ж’Г‘ЕҪГ‘вҖҡ, ГҗВҪГҗВҫ ГҗВҪГҗВө Г‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГ‘Ж’ГҗВөГ‘вҖҡ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ, ГҗВ·Гҗ°ÑвҖҡГҗВҫ Г‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГ‘Ж’Г‘ЕҪГ‘вҖҡ Г‘ВҒГҗВ»ГҗВ°ГҗВұГҗВҫ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ. ГҗвҖқГҗȄВҸ ГҗВҝГ‘вӮ¬ГҗВҫГ‘вҖЎГҗВёГ‘вҖҰ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВҫГҗВІ ГҗВҪГҗВ°ГҗВҙГҗВҫ Г‘вӮ¬ГҗВ°ГҗВ·ГҗВұГҗВёГ‘вӮ¬Гҗ°ÑвҖҡГ‘Е’Г‘ВҒГ‘ВҸ ГҗВәГҗВҫГҗВҪГҗВәГ‘вӮ¬ГҗВөГ‘вҖҡГҗВҪГҗВҫ. ГҗВқГҗВ°ГҗВҝГ‘вӮ¬ГҗВёГҗВјГҗВөГ‘вӮ¬, ГҗВҙГҗȄВҸ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° 25 ГҗВҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВҝГ‘вӮ¬ГҗВҫГ‘ВҒГ‘вҖҡГҗВҫ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡГ‘Е’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ ГҗВҪГҗВ° ГҗВҫГ‘ВҒГҗВҪГҗВҫГҗВІГҗВө ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ 5-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗЕёГҗВҫГҗВ·ГҗВ¶ГҗВө ГҗВҝГҗВҫГҗВәГҗВ°Гҗ¶Ñƒ Г‘ВҚГ‘вҖҡГҗВҫГ‘вҖҡ ГҗвҖқГҗвҖәГҗЕЎ. ГҗвҖҷ Г‘ВҒГ‘вҖҡГҗ°ÑвӮ¬Г‘вҖҡГҗВҫГҗВІГҗВҫГҗВј ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГҗВө ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪ ГҗВҝГ‘вӮ¬ГҗВёГҗВјГҗВөГ‘вӮ¬ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВёГ‘ВҸ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ 35-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° Г‘вҖҡГҗВҫГҗВ¶ГҗВө ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ. ГҗВҗ ГҗВІГҗВҫГ‘вҖҡ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВҫГҗВә 27, ГҗВә ГҗВҝГ‘вӮ¬ГҗВёГҗВјГҗВөГ‘вӮ¬Г‘Ж’, ГҗВҝГҗВҫГҗВәГҗВ° ГҗВҝГ‘вӮ¬ГҗВҫГҗВұГҗВ»ГҗВөГҗВјГҗВҪГ‘вҖ№ГҗВ№: ГҗВҪГҗВө ГҗВ·ГҗВҪГҗ°ÑЕҪ, Г‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГ‘Ж’ГҗВөГ‘вҖҡ ГҗВ»ГҗВё ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҙГҗВ°ГҗВҪГҗВҪГҗВҫГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЕёГҗВҫГҗВ»ГҗВҪГҗ°ÑВҸ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГҗВ° MOLS 23-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВ° ГҗВ·ГҗВҙГҗВөГ‘ВҒГ‘Е’ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117&postid=1208 (ГҗВҝГҗВҫГҗȄĄвҖЎГҗВөГҗВҪГҗВҫ ГҗВІ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВө SageMath) ГҗвҖҷ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГҗВө Г‘ВҒГҗВҫГҗВҙГҗВөГ‘вӮ¬ГҗВ¶ГҗВёГ‘вҖҡГ‘ВҒГ‘ВҸ 20 ГҗвҖқГҗвҖәГҗЕЎ, Г‘ВҒГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГҗВј ГҗВёГ‘вҖҰ Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ° Order? 23
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_10.txt
Counts
------
20 diagonal Latin
20 associative
20 pandiagonal
20 ultramagic
20 natural \diagonal
19 orthogonal pair
20 self-orthogonal
ГҗвҖ”ГҗВ°ГҗВјГҗВөГ‘вҖЎГҗ°ÑвҖҡГҗВөГҗ»ÑŒГҗВҪГҗВҫ! ГҗвҖҷГ‘ВҒГҗВө ГҗвҖқГҗвҖәГҗЕЎ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө. ГҗЕёГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВ° SageMath ГҗВҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ Г‘вҖҰГҗВҫГ‘вӮ¬ГҗВҫГ‘ЛҶГ‘Ж’Г‘ЕҪ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГ‘Ж’ MOLS Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВёГҗВ»ГҗВ°: ГҗвҖқГҗвҖәГҗЕЎ ГҗВІ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГҗВө ГҗВҝГ‘вӮ¬ГҗВөГҗВҙГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВ»ГҗВөГҗВҪГ‘вҖ№ ГҗВІ Г‘вҖһГҗВҫГ‘вӮ¬ГҗВјГҗ°ÑвҖҡГҗВө ГҗВЎГҗВқ ГҗвҖқГҗвҖәГҗЕЎ. ГҗвҖҷГҗВҫГ‘вҖҡ - ГҗВё ГҗВҪГҗВёГ‘вҖЎГҗВөГҗВіГҗВҫ ГҗВҪГҗВө ГҗВҪГҗВ°ГҗВҙГҗВҫ ГҗВҝГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГ‘вҖ№ГҗВІГҗ°ÑвҖҡГ‘Е’. ГҗЕёГҗВҫГҗВәГҗВ°Гҗ¶Ñƒ ГҗВҫГҗВҙГҗВёГҗВҪ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 23-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВёГҗВ· ГҗВҝГҗВҫГҗВ»ГҗВҪГҗВҫГҗВ№ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГ‘вҖ№ MOLS 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 5 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 4 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 3 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 2 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 1 2 4 6 8 10 12 14 16 18 20 22 1 3 5 7 9 11 13 15 17 19 21 0 1 3 5 7 9 11 13 15 17 19 21 0 2 4 6 8 10 12 14 16 18 20 22 ГҗВЎГҗВәГҗВҫГҗ»ÑŒГҗВәГҗВҫ Г‘ВҒГ‘вӮ¬ГҗВөГҗВҙГҗВё Г‘ВҚГ‘вҖҡГҗВёГ‘вҖҰ 20 ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ Г‘Ж’ГҗВҪГҗВёГҗВәГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ, ГҗВҝГҗВҫГҗВәГҗВ° ГҗВҪГҗВөГҗВёГҗВ·ГҗВІГҗВөГ‘ВҒГ‘вҖҡГҗВҪГҗВҫ. ГҗЕЎГҗВ°ГҗВҪГҗВҫГҗВҪГҗВёГҗВ·ГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВ° ГҗВҙГҗȄВҸ ГҗвҖқГҗвҖәГҗЕЎ 23-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° Г‘Ж’ ГҗВҪГҗ°ÑВҒ ГҗВҪГҗВөГ‘вҖҡ. ГҗвҖқ-Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°ГҗВ»ГҗВё ГҗВІ ГҗвҖқГҗвҖәГҗЕЎ 23-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВҝГҗВҫГҗВәГҗВ° ГҗВҪГҗВө Г‘ВҒГ‘вҖЎГҗВёГ‘вҖҡГҗВ°ГҗВ»ГҗВё. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖ”ГҗВҙГҗВөГ‘ВҒГ‘Е’ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117&postid=1180 Г‘вӮ¬Гҗ°ÑВҒГ‘ВҒГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҫ, ГҗВәГҗВ°ГҗВә Г‘ВҸ ГҗВҝГ‘вҖ№Г‘вҖҡГҗВ°ГҗВ»Гҗ°ÑВҒГ‘Е’ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡГ‘Е’ ГҗВҝГҗВҫГҗВ»ГҗВҪГ‘Ж’Г‘ЕҪ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГ‘Ж’ MOLS 25-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВҫГҗВіГҗВҫ Г‘ВҒГҗВҙГҗВІГҗВёГҗВіГҗВ°. ГҗВӯГ‘вҖҡГҗВҫ Г‘Ж’ ГҗВјГҗВөГҗВҪГ‘ВҸ ГҗВҪГҗВө ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГҗВ»ГҗВҫГ‘ВҒГ‘Е’. ГҗВқГҗВҫ 10 Г‘вҖ ГҗВөГҗВҪГ‘вҖҡГ‘вӮ¬ГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ-Г‘ВҒГҗВёГҗВјГҗВјГҗВөГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВё ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГҗВ»ГҗВёГ‘ВҒГ‘Е’. ГҗвҖҷГҗВҫГ‘вҖҡ ГҗВҫГҗВҙГҗВёГҗВҪ ГҗВёГҗВ· ГҗВҪГҗВёГ‘вҖҰ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 ГҗВЎГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ° Г‘ВҚГ‘вҖҡГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ Order? 25
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_11.txt
Counts
------
1 diagonal Latin
1 pandiagonal
1 center symmetric
1 nfr
1 self-orthogonalГҗВЎГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ ГҗВҝГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·Г‘Ж’Г‘ЕҪ Г‘ВҚГ‘вҖҡГҗВҫГ‘вҖҡ ГҗвҖқГҗвҖәГҗЕЎ ГҗВІ ГҗВЎГҗВқ ГҗвҖқГҗвҖәГҗЕЎ ГҗВё ГҗВҝГҗВҫГҗȄĄвҖЎГ‘Ж’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 25-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖңГҗВҫГ‘вҖҡГҗВҫГҗВІГҗВҫ! 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 ГҗВЎГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГҗВј Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ° Г‘ВҚГ‘вҖҡГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ Order? 25
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_12.txt
Counts
------
1 diagonal Latin
1 associative
1 pandiagonal
1 ultramagic
1 natural \diagonal
1 self-orthogonalГҗЕёГ‘вӮ¬ГҗВөГҗВәГ‘вӮ¬Гҗ°ÑВҒГҗВҪГҗВҫ! ГҗвҖқГҗВҫГҗВұГҗВ°ГҗВІГҗȄЕҪ: ГҗвҖқГҗвҖәГҗЕЎ Г‘ВҸГҗВІГҗȄВҸГҗВөГ‘вҖҡГ‘ВҒГ‘ВҸ Г‘вҖҡГҗВ°ГҗВәГҗВ¶ГҗВө DSODLS. ГҗВЎГҗВ»ГҗВөГҗВҙГҗВҫГҗВІГҗ°ÑвҖҡГҗВөГҗ»ÑŒГҗВҪГҗВҫ, ГҗВјГҗВҫГҗВ¶ГҗВҪГҗВҫ Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВёГ‘вҖҡГ‘Е’ ГҗВҙГҗВІГҗВө ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ ГҗВёГҗВ· ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 25-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° Г‘ВҒ Г‘Ж’Г‘вҖЎГҗ°ÑВҒГ‘вҖҡГҗВёГҗВөГҗВј ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГҗВҫГҗВіГҗВҫ ГҗВ·ГҗВҙГҗВөГ‘ВҒГ‘Е’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВҜ ГҗВҫГҗВұГҗВөГ‘вҖ°ГҗВ°ГҗВ»ГҗВ° ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·Гҗ°ÑвҖҡГ‘Е’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 25-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ. ГҗВЎГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГ‘ЕҪ ГҗВё ГҗВҝГҗВҫГҗВәГҗВ°Гҗ¶Ñƒ. ГҗвҖқГҗȄВҸ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВёГ‘ВҸ ГҗВІГҗВҫГҗВ·Г‘Е’ГҗВјГ‘Ж’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 5-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВёГҗВ· Г‘ВҒГ‘вҖҡГҗ°ÑвӮ¬Г‘вҖҡГҗВҫГҗВІГҗВҫГҗВіГҗВҫ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГҗВ°. ГҗвҖҷГҗВҫГ‘вҖҡ ГҗВҫГҗВҪ - ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 25-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ 0 4 3 2 1 20 24 23 22 21 15 19 18 17 16 10 14 13 12 11 5 9 8 7 6 2 1 0 4 3 22 21 20 24 23 17 16 15 19 18 12 11 10 14 13 7 6 5 9 8 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 1 0 4 3 2 21 20 24 23 22 16 15 19 18 17 11 10 14 13 12 6 5 9 8 7 3 2 1 0 4 23 22 21 20 24 18 17 16 15 19 13 12 11 10 14 8 7 6 5 9 10 14 13 12 11 5 9 8 7 6 0 4 3 2 1 20 24 23 22 21 15 19 18 17 16 12 11 10 14 13 7 6 5 9 8 2 1 0 4 3 22 21 20 24 23 17 16 15 19 18 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 11 10 14 13 12 6 5 9 8 7 1 0 4 3 2 21 20 24 23 22 16 15 19 18 17 13 12 11 10 14 8 7 6 5 9 3 2 1 0 4 23 22 21 20 24 18 17 16 15 19 20 24 23 22 21 15 19 18 17 16 10 14 13 12 11 5 9 8 7 6 0 4 3 2 1 22 21 20 24 23 17 16 15 19 18 12 11 10 14 13 7 6 5 9 8 2 1 0 4 3 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 21 20 24 23 22 16 15 19 18 17 11 10 14 13 12 6 5 9 8 7 1 0 4 3 2 23 22 21 20 24 18 17 16 15 19 13 12 11 10 14 8 7 6 5 9 3 2 1 0 4 5 9 8 7 6 0 4 3 2 1 20 24 23 22 21 15 19 18 17 16 10 14 13 12 11 7 6 5 9 8 2 1 0 4 3 22 21 20 24 23 17 16 15 19 18 12 11 10 14 13 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 6 5 9 8 7 1 0 4 3 2 21 20 24 23 22 16 15 19 18 17 11 10 14 13 12 8 7 6 5 9 3 2 1 0 4 23 22 21 20 24 18 17 16 15 19 13 12 11 10 14 15 19 18 17 16 10 14 13 12 11 5 9 8 7 6 0 4 3 2 1 20 24 23 22 21 17 16 15 19 18 12 11 10 14 13 7 6 5 9 8 2 1 0 4 3 22 21 20 24 23 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 16 15 19 18 17 11 10 14 13 12 6 5 9 8 7 1 0 4 3 2 21 20 24 23 22 18 17 16 15 19 13 12 11 10 14 8 7 6 5 9 3 2 1 0 4 23 22 21 20 24 ГҗВЎГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГҗВј Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ° Г‘ВҚГ‘вҖҡГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ Order? 25
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_14.txt
Counts
------
1 diagonal Latin
1 associative
1 pandiagonal
1 ultramagic
1 natural \diagonal
1 self-orthogonalГҗвҖҷГ‘ВҒГ‘вҖҳ ГҗВ·ГҗВ°ГҗВјГҗВөГ‘вҖЎГҗ°ÑвҖҡГҗВөГҗ»ÑŒГҗВҪГҗВҫ! ГҗЛң ГҗВҪГҗВө ГҗВјГҗВҫГҗВіГҗВ»ГҗВҫ ГҗВұГ‘вҖ№Г‘вҖҡГ‘Е’ ГҗВёГҗВҪГҗ°ÑвҖЎГҗВө :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВҰГҗВёГ‘вҖҡГҗ°ÑвҖҡГҗВ° ГҗВёГҗВ· Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГ‘ВҸ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=110&postid=1040 ГҗвҖҷГҗВҫГ‘вҖҡ ГҗВҝГҗ°ÑвӮ¬ГҗВ° ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ Г‘ВҒГҗВ»ГҗВ°ГҗВұГҗВҫ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖәГҗЕЎ 16-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВёГҗВ· Г‘Ж’ГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГҗВҫГҗВ№ ГҗВІГ‘вҖ№Г‘ЛҶГҗВө Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ГҗВё ГҗЕЎГҗВ°ГҗВә ГҗВІГҗВёГҗВҙГҗВёГҗВј, Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВө ГҗВё Г‘ВҒГҗВ»ГҗВ°ГҗВұГҗВҫ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ (ГҗВҫГҗВҙГҗВҪГҗВҫГҗВІГ‘вӮ¬ГҗВөГҗВјГҗВөГҗВҪГҗВҪГҗВҫ) Г‘Ж’Г‘вҖҡГҗВёГҗВ»ГҗВёГ‘вҖҡГҗВ° Harry White ГҗВҫГ‘вҖҡГҗВҪГҗВҫГ‘ВҒГҗВёГ‘вҖҡ ГҗВә ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВј ГҗвҖқГҗвҖәГҗЕЎ (ultramagic). ГҗвҖҳГ‘Ж’ГҗВҙГҗВөГҗВј ГҗВҝГ‘вӮ¬ГҗВёГҗВҙГҗВөГ‘вӮ¬ГҗВ¶ГҗВёГҗВІГҗ°ÑвҖҡГ‘Е’Г‘ВҒГ‘ВҸ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВәГҗВ»Гҗ°ÑВҒГ‘ВҒГҗВёГ‘вҖһГҗВёГҗВәГҗ°ÑвҖ ГҗВёГҗВё. ГҗВўГҗВ°ГҗВәГҗВёГҗВј ГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВј, ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 16-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВјГ‘вҖ№ ГҗВІГҗВёГҗВҙГҗВёГҗВј. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВҫГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ Г‘ВҒ ГҗВёГҗВ»ГҗȄЕҪГ‘ВҒГ‘вҖҡГ‘вӮ¬Гҗ°ÑвҖ ГҗВёГҗВё ГҗВҝГ‘вӮ¬ГҗВөГҗВҙГ‘вҖ№ГҗВҙГ‘Ж’Г‘вҖ°ГҗВөГҗВіГҗВҫ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГҗВ° (ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ ГҗвҖҷ) Г‘вҖҡГҗВҫГҗВ¶ГҗВө ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№. ГҗЕёГҗВҫГҗВәГҗВ°Гҗ¶Ñƒ ГҗВөГҗВіГҗВҫ ГҗВІ ГҗВҫГҗВұГ‘вҖ№Г‘вҖЎГҗВҪГҗВҫГҗВј Г‘вҖЎГҗВёГ‘ВҒГҗВ»ГҗВҫГҗВІГҗВҫГҗВј Г‘вҖһГҗВҫГ‘вӮ¬ГҗВјГҗ°ÑвҖҡГҗВө 11 14 13 8 5 0 3 6 7 2 1 4 9 12 15 10 13 8 11 14 3 6 5 0 1 4 7 2 15 10 9 12 8 13 14 11 6 3 0 5 4 1 2 7 10 15 12 9 14 11 8 13 0 5 6 3 2 7 4 1 12 9 10 15 2 7 4 1 12 9 10 15 14 11 8 13 0 5 6 3 4 1 2 7 10 15 12 9 8 13 14 11 6 3 0 5 1 4 7 2 15 10 9 12 13 8 11 14 3 6 5 0 7 2 1 4 9 12 15 10 11 14 13 8 5 0 3 6 9 12 15 10 7 2 1 4 5 0 3 6 11 14 13 8 15 10 9 12 1 4 7 2 3 6 5 0 13 8 11 14 10 15 12 9 4 1 2 7 6 3 0 5 8 13 14 11 12 9 10 15 2 7 4 1 0 5 6 3 14 11 8 13 0 5 6 3 14 11 8 13 12 9 10 15 2 7 4 1 6 3 0 5 8 13 14 11 10 15 12 9 4 1 2 7 3 6 5 0 13 8 11 14 15 10 9 12 1 4 7 2 5 0 3 6 11 14 13 8 9 12 15 10 7 2 1 4 ГҗВЎГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГҗВј Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ° Г‘ВҚГ‘вҖҡГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ Г‘Ж’Г‘вҖҡГҗВёГҗВ»ГҗВёГ‘вҖҡГҗВҫГҗВ№ Harry White Order? 16
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt
Counts
------
1 diagonal Latin
1 associative
1 weakly pandiagonal
1 ultramagic
1 double axial symmetric
1 self-orthogonalГҗВўГҗВ°ГҗВәГҗВёГҗВј ГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВј, ГҗВІ Г‘Ж’ГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГҗВҫГҗВ№ Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ГҗВө ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВ° ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗ°ÑВҸ ГҗВҝГҗ°ÑвӮ¬ГҗВ° ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 16-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗВӯГ‘вҖҰ, ГҗВіГҗВҙГҗВө ГҗВ¶ГҗВө ГҗВұГ‘вҖ№ГҗВ»ГҗВё ГҗВ°ГҗВІГ‘вҖҡГҗВҫГ‘вӮ¬Г‘вҖ№ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ ГҗВІ 2008 ГҗВіГҗВҫГҗВҙГ‘Ж’, ГҗВәГҗВҫГҗВіГҗВҙГҗВ° Г‘ВҸ ГҗВҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВҙГҗВҫГҗВ»ГҗВіГҗВҫ ГҗВё Г‘вҖҡГ‘вӮ¬Г‘Ж’ГҗВҙГҗВҪГҗВҫ ГҗВёГ‘ВҒГҗВәГҗВ°ГҗВ»ГҗВ° Г‘ВҒГҗВҝГҗВҫГ‘ВҒГҗВҫГҗВұ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВёГ‘ВҸ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВіГҗВҫ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВҫГҗВіГҗВҫ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ° 16-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗвҖҷ ГҗВәГҗВҫГҗВҪГ‘вҖ ГҗВө ГҗВәГҗВҫГҗВҪГ‘вҖ ГҗВҫГҗВІ, Г‘ВҸ ГҗВөГҗВіГҗВҫ ГҗВІГ‘ВҒГ‘вҖҳ ГҗВ¶ГҗВө ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГҗВ»ГҗВ°; Г‘ВҚГ‘вҖҡГҗВҫ ГҗВұГ‘вҖ№ГҗВ»ГҗВ° ГҗВҙГҗВҫГ‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗВәГҗВ° (ГҗВҝГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГҗВ°ГҗВҪГҗВёГ‘ВҸГҗВјГҗВё) ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВіГҗВҫ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ° ГҗВӨГ‘вӮ¬ГҗВ°ГҗВҪГҗВәГҗВ»ГҗВёГҗВҪГҗВ°. ГҗЕҫГҗВұ Г‘ВҚГ‘вҖҡГҗВҫГҗВј ГҗВҝГҗВҫГҗВҙГ‘вӮ¬ГҗВҫГҗВұГҗВҪГҗВҫ Г‘вӮ¬Гҗ°ÑВҒГ‘ВҒГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҫ ГҗВІ Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ГҗВө http://www.klassikpoez.narod.ru/idealch.htm ГҗЛңГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ Г‘Ж’ ГҗВјГҗВөГҗВҪГ‘ВҸ ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГҗȄВҒГ‘ВҸ Г‘вҖҡГҗВ°ГҗВәГҗВҫГҗВ№ 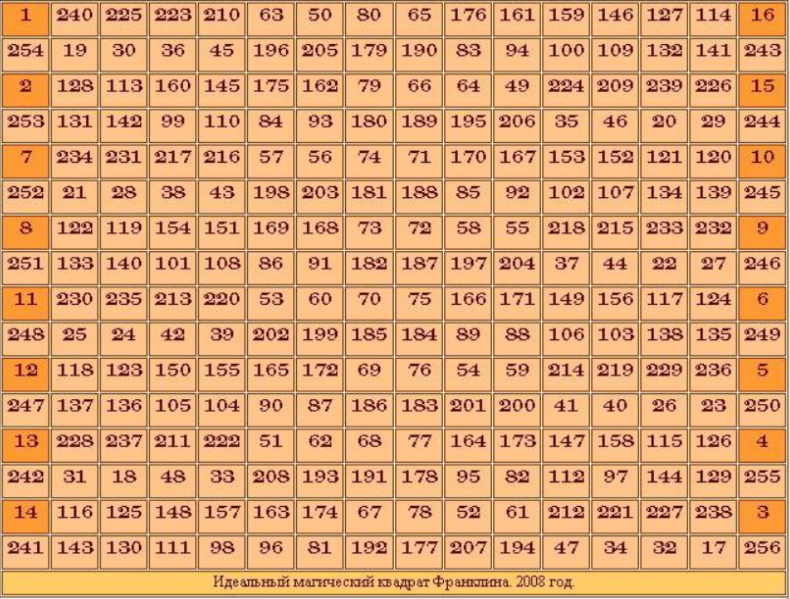 ГҗВқГҗВҫ ГҗВөГ‘ВҒГҗВ»ГҗВё ГҗВІГ‘вҖ№ Г‘вӮ¬ГҗВ°ГҗВ·ГҗВ»ГҗВҫГҗВ¶ГҗВёГ‘вҖҡГҗВө Г‘ВҚГ‘вҖҡГҗВҫГ‘вҖҡ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ ГҗВҪГҗВ° ГҗВҙГҗВІГҗВ° ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖәГҗЕЎ, Г‘Ж’ ГҗВІГҗ°ÑВҒ ГҗВҝГҗВҫГҗȄĄвҖЎГҗ°ÑвҖҡГ‘ВҒГ‘ВҸ ГҗВҫГҗВұГҗВҫГҗВұГ‘вҖ°Г‘вҖҳГҗВҪГҗВҪГ‘вҖ№ГҗВө ГҗвҖәГҗЕЎ! ГҗВҗ Г‘вҖҡГҗВөГҗВҝГҗВөГ‘вӮ¬Г‘Е’ ГҗВёГ‘ВҒГҗВҝГҗВҫГҗ»ÑŒГҗВ·Г‘Ж’ГҗВөГҗВј ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҙГҗȄВҸ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВёГ‘ВҸ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВіГҗВҫ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВҫГҗВіГҗВҫ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ° ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј ГҗВ»Гҗ°ÑвҖҡГҗВёГҗВҪГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ. ГҗВӨГҗВҫГ‘вӮ¬ГҗВјГ‘Ж’ГҗȄвҖ№ ГҗВҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВҝГ‘вӮ¬ГҗВҫГ‘ВҒГ‘вҖҡГ‘вҖ№ГҗВө: ГҗВ»ГҗВёГҗВұГҗВҫ 16A+B+1, ГҗВ»ГҗВёГҗВұГҗВҫ A+16B+1. ГҗвҖҳГ‘Ж’ГҗВҙГ‘Ж’ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡГ‘Е’ ГҗВҝГҗВҫ ГҗВҝГҗВөГ‘вӮ¬ГҗВІГҗВҫГҗВ№ Г‘вҖһГҗВҫГ‘вӮ¬ГҗВјГ‘Ж’ГҗВ»ГҗВө. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷГҗВҫГ‘вҖҡ ГҗВҫГҗВҪ - ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ 16-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј ГҗВ»Гҗ°ÑвҖҡГҗВёГҗВҪГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ 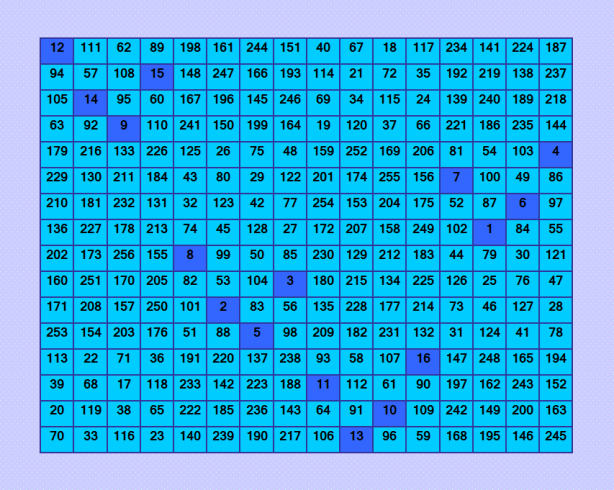 ГҗВҜ ГҗВұГ‘вҖ№ГҗВ»ГҗВ° Г‘ВҒГ‘вҖЎГҗ°ÑВҒГ‘вҖҡГҗВ»ГҗВёГҗВІГҗВ° ГҗВІ 2008 ГҗВіГҗВҫГҗВҙГ‘Ж’, ГҗВәГҗВҫГҗВіГҗВҙГҗВ° ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГҗВ»ГҗВ° ГҗВҝГҗВөГ‘вӮ¬ГҗВІГ‘вҖ№ГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ 16-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗЛң Г‘вҖҡГҗВөГҗВҝГҗВөГ‘вӮ¬Г‘Е’ Г‘ВҒГ‘вҖЎГҗ°ÑВҒГ‘вҖҡГҗВ»ГҗВёГҗВІГҗВ° ГҗВІГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВҫГҗВ№ Г‘вӮ¬ГҗВ°ГҗВ·, ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГҗВІ ГҗВҝГ‘вӮ¬ГҗВёГҗВҪГ‘вҖ ГҗВёГҗВҝГҗВёГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ ГҗВҪГҗВҫГҗВІГ‘вҖ№ГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ ГҗВҙГҗВ°ГҗВҪГҗВҪГҗВҫГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗВқГҗВ° ГҗВёГҗВ»ГҗȄЕҪГ‘ВҒГ‘вҖҡГ‘вӮ¬Гҗ°ÑвҖ ГҗВёГҗВё ГҗВІГ‘вҖ№ГҗВҙГҗВөГҗВ»ГҗВөГҗВҪГҗВ° Г‘вҖҡГҗВ°ГҗВә ГҗВҪГҗВ°ГҗВ·Г‘вҖ№ГҗВІГҗВ°ГҗВөГҗВјГҗ°ÑВҸ ГҗВҪГҗ°ÑвҖЎГҗВ°Гҗ»ÑŒГҗВҪГҗ°ÑВҸ Г‘вҖ ГҗВөГҗВҝГҗВҫГ‘вҖЎГҗВәГҗВ°. ГҗвҖҷ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВҪГҗВҫГҗВј Г‘вӮ¬ГҗВ°ГҗВҪГ‘Е’Г‘ЛҶГҗВө ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВҫГҗВј ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВө ГҗВҪГҗ°ÑвҖЎГҗВ°Гҗ»ÑŒГҗВҪГҗ°ÑВҸ Г‘вҖ ГҗВөГҗВҝГҗВҫГ‘вҖЎГҗВәГҗВ° Г‘вҖҡГҗВҫГҗВ¶ГҗВө ГҗВІГ‘вҖ№ГҗВҙГҗВөГҗВ»ГҗВөГҗВҪГҗВ°. ГҗВЎГ‘вӮ¬ГҗВ°ГҗВІГҗВҪГҗВёГ‘вҖҡГҗВө Г‘вӮ¬Гҗ°ÑВҒГҗВҝГҗВҫГҗВ»ГҗВҫГҗВ¶ГҗВөГҗВҪГҗВёГҗВө ГҗВҪГҗ°ÑвҖЎГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ Г‘вҖ ГҗВөГҗВҝГҗВҫГ‘вҖЎГҗВәГҗВё ГҗВІ Г‘ВҚГ‘вҖҡГҗВёГ‘вҖҰ ГҗВҙГҗВІГ‘Ж’Г‘вҖҰ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗ°ÑвҖҰ. ГҗвҖҷГ‘вҖ№ Г‘Ж’ГҗВІГҗВёГҗВҙГҗВёГ‘вҖҡГҗВө ГҗВҝГ‘вӮ¬ГҗВёГҗВҪГ‘вҖ ГҗВёГҗВҝГҗВёГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВө Г‘вӮ¬ГҗВ°ГҗВ·ГҗВ»ГҗВёГ‘вҖЎГҗВёГҗВө ГҗВІ Г‘вӮ¬Гҗ°ÑВҒГҗВҝГҗВҫГҗВ»ГҗВҫГҗВ¶ГҗВөГҗВҪГҗВёГҗВё ГҗВҪГҗ°ÑвҖЎГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ Г‘вҖ ГҗВөГҗВҝГҗВҫГ‘вҖЎГҗВәГҗВё, Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВё ГҗВҫГҗВҝГ‘вӮ¬ГҗВөГҗВҙГҗВөГҗȄВҸГҗВөГ‘вҖҡ ГҗВҝГ‘вӮ¬ГҗВёГҗВҪГ‘вҖ ГҗВёГҗВҝГҗВёГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВө Г‘вӮ¬ГҗВ°ГҗВ·ГҗВ»ГҗВёГ‘вҖЎГҗВёГҗВө Г‘ВҒГҗВ°ГҗВјГҗВёГ‘вҖҰ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВҰГҗВёГ‘вҖҡГҗ°ÑвҖҡГҗВ° ГҗВӨГҗВҫГ‘вӮ¬ГҗВјГ‘Ж’ГҗȄвҖ№ ГҗВҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВҝГ‘вӮ¬ГҗВҫГ‘ВҒГ‘вҖҡГ‘вҖ№ГҗВө: ГҗВ»ГҗВёГҗВұГҗВҫ 16A+B+1, ГҗВ»ГҗВёГҗВұГҗВҫ A+16B+1. ГҗВқГҗВөГҗВјГҗВҪГҗВҫГҗВіГҗВҫ Г‘вӮ¬ГҗВ°ГҗВ·ГҗВІГҗВөГ‘вӮ¬ГҗВҪГ‘Ж’ Г‘вҖһГҗВҫГ‘вӮ¬ГҗВјГ‘Ж’Гҗ»Ñƒ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВёГ‘ВҸ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВҫГҗВіГҗВҫ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ° ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј ГҗВ»Гҗ°ÑвҖҡГҗВёГҗВҪГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ, ГҗВҙГҗȄВҸ Г‘вҖҡГҗВөГ‘вҖҰ, ГҗВәГ‘вҖҡГҗВҫ Г‘ВҒ Г‘ВҚГ‘вҖҡГҗВёГҗВј ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј ГҗВҪГҗВөГҗВ·ГҗВҪГҗВ°ГҗВәГҗВҫГҗВј. ГҗЕёГ‘Ж’Г‘ВҒГ‘вҖҡГ‘Е’ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ ГҗВҗ ГҗВё ГҗвҖҷ - ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° n. ГҗвҖ”ГҗВ°ГҗВҝГҗВёГ‘ЛҶГҗВөГҗВј Г‘ВҚГ‘вҖҡГҗВё ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ ГҗВІ ГҗВІГҗВёГҗВҙГҗВө A={a(i,j)}, B={b(i,j)}, i,j = 1, 2,..., n Г‘вҖҡГҗВҫ ГҗВөГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВҝГ‘вӮ¬ГҗВөГҗВҙГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВёГҗВј ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ ГҗВёГ‘вҖҰ Г‘ВҚГҗВ»ГҗВөГҗВјГҗВөГҗВҪГ‘вҖҡГҗВ°ГҗВјГҗВё. ГҗВўГҗВҫГҗВіГҗВҙГҗВ° ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ ГҗВЎ=n*A+B+1 ГҗВёГҗВ»ГҗВё ГҗВЎ=A+n*B+1, Г‘ВҚГ‘вҖҡГҗВҫ ГҗВҫГҗВ·ГҗВҪГҗ°ÑвҖЎГҗВ°ГҗВөГ‘вҖҡ, Г‘вҖЎГ‘вҖҡГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ ГҗВІ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ ГҗВҝГҗ°ÑвӮ¬ГҗВө ГҗВјГҗВҫГҗВ¶ГҗВҪГҗВҫ ГҗВҝГҗВҫГҗВјГҗВөГҗВҪГ‘ВҸГ‘вҖҡГ‘Е’ ГҗВјГҗВөГ‘ВҒГ‘вҖҡГҗВ°ГҗВјГҗВё, ГҗВҫГҗВҪГҗВё Г‘вӮ¬ГҗВ°ГҗВІГҗВҪГҗВҫГҗВҝГ‘вӮ¬ГҗВ°ГҗВІГҗВҪГ‘вҖ№. ГҗВЈГҗВјГҗВҪГҗВҫГҗВ¶ГҗВөГҗВҪГҗВёГҗВө ГҗВё Г‘ВҒГҗВ»ГҗВҫГҗВ¶ГҗВөГҗВҪГҗВёГҗВө ГҗВІГ‘вҖ№ГҗВҝГҗВҫГҗВ»ГҗВҪГ‘ВҸГҗВөГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВҝГҗВҫГ‘ВҚГҗВ»ГҗВөГҗВјГҗВөГҗВҪГ‘вҖҡГҗВҪГҗВҫ, Г‘вҖҡГҗВҫ ГҗВөГ‘ВҒГ‘вҖҡГ‘Е’ c(i,j)=n*a(i,j)+b(i,j)+1 ГҗВёГҗВ»ГҗВё c(i,j)=a(i,j)+n*b(i,j)+1 ГҗЕ“ГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВө ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ ГҗВҝГҗВҫ Г‘ВҚГ‘вҖҡГҗВёГҗВј ГҗВҙГҗВІГ‘Ж’ГҗВј Г‘вҖһГҗВҫГ‘вӮ¬ГҗВјГ‘Ж’ГҗВ»ГҗВ°ГҗВј, ГҗВәГҗВҫГҗВҪГҗВөГ‘вҖЎГҗВҪГҗВҫ, ГҗВҝГҗВҫГҗȄĄвҖЎГҗ°ÑвҖҡГ‘ВҒГ‘ВҸ Г‘вӮ¬ГҗВ°ГҗВ·ГҗВҪГ‘вҖ№ГҗВө. ГҗЕ“ГҗВөГ‘вҖҡГҗВҫГҗВҙ ГҗВ»Гҗ°ÑвҖҡГҗВёГҗВҪГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ - Г‘Ж’ГҗВҪГҗВёГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВёГ‘ВҸ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ. ГҗЛңГҗВјГҗВөГҗВҪГҗВҪГҗВҫ ГҗВұГҗВ»ГҗВ°ГҗВіГҗВҫГҗВҙГҗ°ÑвӮ¬Г‘ВҸ Г‘ВҚГ‘вҖҡГҗВҫГҗВјГ‘Ж’ ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГ‘Ж’ Г‘ВҸ ГҗВ·ГҗВ°ГҗВёГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҫГҗВІГҗВ°ГҗВ»Гҗ°ÑВҒГ‘Е’ ГҗВ»Гҗ°ÑвҖҡГҗВёГҗВҪГ‘ВҒГҗВәГҗВёГҗВјГҗВё ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ°ГҗВјГҗВё ГҗВІ Г‘вҖҡГҗВө ГҗВҙГҗВ°ГҗȄвҖҳГҗВәГҗВёГҗВө ГҗВІГ‘вӮ¬ГҗВөГҗВјГҗВөГҗВҪГҗВ°, ГҗВәГҗВҫГҗВіГҗВҙГҗВ° ГҗВ·ГҗВ°ГҗВҪГҗВёГҗВјГҗВ°ГҗВ»Гҗ°ÑВҒГ‘Е’ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВјГҗВё ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ°ГҗВјГҗВё. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВҰГҗВёГ‘вҖҡГҗ°ÑвҖҡГҗВ° ГҗВёГҗВ· Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГ‘ВҸ https://boinc.progger.info/odlk/forum_thread.php?id=178&postid=7105 ГҗЛңГ‘вҖҡГҗВ°ГҗВә, ГҗВҝГҗВҫГ‘ВҒГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГҗВј ГҗВҪГҗВ° Г‘ВҒГҗВҫГҗВІГҗВөГ‘вӮ¬Г‘ЛҶГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 9-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° (ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·Г‘вҖ№ГҗВІГҗ°ÑЕҪ ГҗВөГҗВіГҗВҫ ГҗВІ ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВіГҗВҫГҗВ№ Г‘вӮ¬Гҗ°ÑВҒГҗВәГ‘вӮ¬Гҗ°ÑВҒГҗВәГҗВө) ГҗвҖҷГҗВёГҗВҙГҗВёГҗВј, Г‘вҖЎГ‘вҖҡГҗВҫ Г‘ВҚГ‘вҖҡГҗВҫГ‘вҖҡ ГҗвҖқГҗвҖәГҗЕЎ Г‘вҖ ГҗВөГҗВҪГ‘вҖҡГ‘вӮ¬ГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ-Г‘ВҒГҗВёГҗВјГҗВјГҗВөГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№ГҗВ№ ГҗВё Г‘ВҒГҗВ»ГҗВ°ГҗВұГҗВҫ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№. ГҗвҖқГҗвҖәГҗЕЎ Г‘Ж’ ГҗВҪГҗ°ÑВҒ ГҗВҝГ‘вӮ¬ГҗВөГҗВҙГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВ»ГҗВөГҗВҪ ГҗВІ ГҗВҝГ‘вӮ¬ГҗВҫГҗВёГҗВ·ГҗВІГҗВҫГҗ»ÑŒГҗВҪГҗВҫГҗВј Г‘вҖһГҗВҫГ‘вӮ¬ГҗВјГҗ°ÑвҖҡГҗВө. ГҗЕёГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГҗВ°ГҗВ»ГҗВ° ГҗВөГҗВіГҗВҫ ГҗВІ ГҗВЎГҗВқ ГҗвҖқГҗвҖәГҗЕЎ 0 5 7 8 1 3 4 6 2 8 1 3 4 6 2 0 5 7 4 6 2 0 5 7 8 1 3 7 0 5 3 8 1 2 4 6 3 8 1 2 4 6 7 0 5 2 4 6 7 0 5 3 8 1 5 7 0 1 3 8 6 2 4 1 3 8 6 2 4 5 7 0 6 2 4 5 7 0 1 3 8 ГҗВЎГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГҗВј Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ° Г‘ВҚГ‘вҖҡГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ Order? 9
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_9.txt
Counts
------
1 diagonal Latin
1 associative
1 natural \diagonal
1 self-orthogonalГҗвҖқГҗвҖәГҗЕЎ Г‘ВҒГ‘вҖҡГҗВ°ГҗВ» Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВј, ГҗВҪГҗВҫ... ГҗВёГ‘ВҒГ‘вҖЎГҗВөГҗВ·ГҗВ»ГҗВ° Г‘ВҒГҗВ»ГҗВ°ГҗВұГҗ°ÑВҸ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’. ГҗЕёГҗВҫГҗȄĄвҖЎГҗВёГ‘вҖҡГ‘Е’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВёГҗВ· Г‘ВҒГҗВҫГҗВІГҗВөГ‘вӮ¬Г‘ЛҶГҗВөГҗВҪГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГ‘Ж’Г‘вҖҡГ‘вҖҳГҗВј ГҗВҝГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГҗВ°ГҗВҪГҗВёГ‘ВҸ ГҗВөГҗВіГҗВҫ ГҗВІ ГҗВЎГҗВқ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҪГҗВө Г‘Ж’ГҗВҙГҗВ°ГҗВ»ГҗВҫГ‘ВҒГ‘Е’. ГҗЕ“ГҗВҫГҗВ¶ГҗВөГ‘вҖҡ ГҗВұГ‘вҖ№Г‘вҖҡГ‘Е’, ГҗВәГҗВ°ГҗВәГҗВҫГҗВө-ГҗВҪГҗВёГҗВұГ‘Ж’ГҗВҙГ‘Е’ ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВіГҗВҫГҗВө ГҗВҝГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГҗВ°ГҗВҪГҗВёГҗВө Г‘ВҒГҗВҝГҗВҫГ‘ВҒГҗВҫГҗВұГҗВҪГҗВҫ Г‘ВҚГ‘вҖҡГҗВҫ Г‘ВҒГҗВҙГҗВөГҗВ»Гҗ°ÑвҖҡГ‘Е’. ГҗВҜ ГҗВҝГҗВҫГҗВәГҗВ° ГҗВҪГҗВө ГҗВ·ГҗВҪГҗ°ÑЕҪ Г‘вҖҡГҗВ°ГҗВәГҗВҫГҗВө ГҗВҝГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГҗВ°ГҗВҪГҗВёГҗВө. ГҗвҖ”ГҗВ°ГҗВјГҗВөГ‘вҖЎГ‘Ж’, Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВө ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ 9-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВІ Г‘ВҒГҗВІГҗВҫГ‘вҖҳ ГҗВІГ‘вӮ¬ГҗВөГҗВјГ‘ВҸ ГҗВҙГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВёГҗВ»ГҗВё ГҗВјГҗВҪГҗВҫГҗВіГҗВҫ Г‘вҖҰГҗВ»ГҗВҫГҗВҝГҗВҫГ‘вҖҡ, ГҗВҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВҙГҗВҫГҗВ»ГҗВіГҗВҫ ГҗВҫГҗВҪГҗВё ГҗВІГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВө ГҗВҪГҗВө Г‘вҖҰГҗВҫГ‘вҖҡГҗВөГҗВ»ГҗВё Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡГ‘Е’Г‘ВҒГ‘ВҸ. ГҗВҗГ‘ВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВө ГҗВҝГҗВҫГҗȄĄвҖЎГҗВ°ГҗВ»ГҗВёГ‘ВҒГ‘Е’, ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВҝГҗВҫГҗȄĄвҖЎГҗВ°ГҗВ»ГҗВёГ‘ВҒГ‘Е’, ГҗВ° ГҗВІГҗВҫГ‘вҖҡ ГҗВҫГҗВҙГҗВҪГҗВҫГҗВІГ‘вӮ¬ГҗВөГҗВјГҗВөГҗВҪГҗВҪГҗВҫ Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВө ГҗВё ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВҪГҗВёГҗВәГҗВ°ГҗВә. ГҗвҖҷ ГҗВјГҗВҫГҗВёГ‘вҖҰ Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’Г‘ВҸГ‘вҖҰ ГҗВҝГҗВҫ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВј ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ°ГҗВј ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВј ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВј ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ°ГҗВј 9-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° Г‘Ж’ГҗВҙГҗВөГҗВ»ГҗВөГҗВҪГҗВҫ ГҗВјГҗВҪГҗВҫГҗВіГҗВҫ ГҗВІГҗВҪГҗВёГҗВјГҗВ°ГҗВҪГҗВёГ‘ВҸ. ГҗВЎГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ ГҗВҝГҗВҫГҗВёГ‘вҖ°Г‘Ж’ Г‘ВҒГ‘вӮ¬ГҗВөГҗВҙГҗВё Г‘ВҚГ‘вҖҡГҗВёГ‘вҖҰ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ, ГҗВјГҗВҫГҗВ¶ГҗВөГ‘вҖҡ ГҗВұГ‘вҖ№Г‘вҖҡГ‘Е’, ГҗВҪГҗВ°ГҗВ№ГҗВҙГ‘Ж’ Г‘вҖЎГ‘вҖҡГҗВҫ-ГҗВҪГҗВёГҗВұГ‘Ж’ГҗВҙГ‘Е’ ГҗВҝГҗВҫГҗВҙГ‘вҖҰГҗВҫГҗВҙГ‘ВҸГ‘вҖ°ГҗВөГҗВө :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷГҗВҫГ‘вҖҡ ГҗВҪГҗ°ÑЛҶГҗВ»ГҗВ° ГҗВІ Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ГҗВө ГҗЕёГҗЕҫГҗВЎГҗВўГҗВ ГҗЕҫГҗвҖўГҗВқГҗЛңГҗвҖў ГҗЛңГҗвҖқГҗвҖўГҗВҗГҗвҖәГҗВ¬ГҗВқГҗВ«ГҗВҘ ГҗЕЎГҗвҖҷГҗВҗГҗвҖқГҗВ ГҗВҗГҗВўГҗЕҫГҗвҖҷ ГҗВқГҗвҖўГҗВ§ГҗВҒГҗВўГҗВқГҗЕҫГҗвҖңГҗЕҫ ГҗЕёГҗЕҫГҗВ ГҗВҜГҗвҖқГҗЕЎГҗВҗ ГҗЛңГҗвҖ” ГҗЕҫГҗвҖҳГҗВ ГҗВҗГҗВўГҗЛңГҗЕ“ГҗВ«ГҗВҘ ГҗЕЎГҗвҖҷГҗВҗГҗвҖқГҗВ ГҗВҗГҗВўГҗЕҫГҗвҖҷ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ 9-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° 20 78 5 58 17 48 45 28 70 53 39 36 64 25 74 6 59 13 79 2 60 14 49 44 30 72 19 40 35 66 27 73 7 56 15 50 1 61 11 51 41 31 71 21 81 32 67 26 75 9 55 16 47 42 63 10 52 38 33 68 22 80 3 69 23 76 8 57 18 46 43 29 12 54 37 34 65 24 77 4 62 ГҗВЎГҗВјГҗВҫГ‘вҖҡГҗВёГҗВёГ‘вҖҡГҗВө Г‘вӮ¬ГҗВёГ‘ВҒ. 16 ГҗВІ Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ГҗВө. ГҗВ ГҗВ°ГҗВ·ГҗВ»ГҗВҫГҗВ¶ГҗВёГҗВ»ГҗВ° ГҗВөГҗВіГҗВҫ ГҗВҪГҗВ° ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖәГҗЕЎ 1 5 4 3 7 2 8 0 6 7 2 8 0 6 1 5 4 3 6 1 5 4 3 7 2 8 0 3 7 2 8 0 6 1 5 4 0 6 1 5 4 3 7 2 8 4 3 7 2 8 0 6 1 5 8 0 6 1 5 4 3 7 2 5 4 3 7 2 8 0 6 1 2 8 0 6 1 5 4 3 7 2 8 0 6 1 5 4 3 7 5 4 3 7 2 8 0 6 1 8 0 6 1 5 4 3 7 2 4 3 7 2 8 0 6 1 5 0 6 1 5 4 3 7 2 8 3 7 2 8 0 6 1 5 4 6 1 5 4 3 7 2 8 0 7 2 8 0 6 1 5 4 3 1 5 4 3 7 2 8 0 6 ГҗВЈГҗВІГ‘вҖ№! ГҗВӯГ‘вҖҡГҗВҫ ГҗВҪГҗВө ГҗвҖқГҗвҖәГҗЕЎ. ГҗЕёГҗВҫГҗВәГҗВ° ГҗВҪГҗВө ГҗВ·ГҗВҪГҗ°ÑЕҪ, ГҗВәГҗВ°ГҗВә ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡГ‘Е’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 9-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗвҖқГҗВ° ГҗВё Г‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГ‘Ж’ГҗВөГ‘вҖҡ ГҗВ»ГҗВё Г‘вҖҡГҗВ°ГҗВәГҗВҫГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВқГҗВ° ГҗВҝГҗВҫГҗВјГҗВҫГ‘вҖ°Г‘Е’ ГҗВҝГ‘вӮ¬ГҗВёГ‘ЛҶГҗВ»ГҗВ° ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВ° Harry White LatinSquares. ГҗвҖҷГҗВҫГ‘вҖҡ Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВҫГҗВҪГҗВ° ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГҗВ»ГҗВ° (Г‘ВҸ ГҗВ·ГҗВ°ГҗВҙГҗВ°ГҗВ»ГҗВ° ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡГ‘Е’ 100 ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 9-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°) Order? 9
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_14.txt
Counts
------
72 diagonal Latin
8 associative
72 weakly pandiagonal
8 ultramagic
64 center symmetric
1 nfr
1 nfc
72 self-orthogonalГҗЕёГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВ° ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГҗВ»ГҗВ° 72 ГҗвҖқГҗвҖәГҗЕЎ, ГҗВІГ‘ВҒГҗВө ГҗВҫГҗВҪГҗВё Г‘ВҒГҗВ»ГҗВ°ГҗВұГҗВҫ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө, ГҗВ° 8 ГҗВёГҗВ· ГҗВҪГҗВёГ‘вҖҰ ГҗВөГ‘вҖ°Г‘вҖҳ ГҗВё Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВө! ГҗВЈГ‘вӮ¬ГҗВ°! ГҗЕёГҗВҫГҗȄĄвҖЎГҗВёГҗВ»ГҗВё 8 ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 9-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗЕЎ Г‘вҖҡГҗВҫГҗВјГ‘Ж’ ГҗВ¶ГҗВө ГҗВІГ‘ВҒГҗВө ГҗвҖқГҗвҖәГҗЕЎ Г‘ВҸГҗВІГҗȄВҸГ‘ЕҪГ‘вҖҡГ‘ВҒГ‘ВҸ SODLS, ГҗВ·ГҗВҪГҗ°ÑвҖЎГҗВёГ‘вҖҡ ГҗВёГҗВјГҗВөГҗВөГҗВј ГҗВіГҗВҫГ‘вҖҡГҗВҫГҗВІГ‘вҖ№ГҗВө ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ. ГҗвҖ”ГҗВҙГҗВҫГ‘вӮ¬ГҗВҫГҗВІГҗВҫ! ГҗЕ“ГҗВҫГҗВ»ГҗВҫГҗВҙГҗВөГ‘вҖ Harry White! ГҗВЎГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ ГҗВҝГҗВҫГҗВәГҗВ°Гҗ¶Ñƒ ГҗВҫГҗВҙГҗВёГҗВҪ ГҗВёГҗВ· 8 ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 9-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВҪГ‘вҖ№Г‘вҖҰ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВҫГҗВ№. ГҗвҖҷГҗВҫГ‘вҖҡ 3 5 4 6 8 7 0 2 1 0 2 1 3 5 4 6 8 7 6 8 7 0 2 1 3 5 4 5 4 3 8 7 6 2 1 0 2 1 0 5 4 3 8 7 6 8 7 6 2 1 0 5 4 3 4 3 5 7 6 8 1 0 2 1 0 2 4 3 5 7 6 8 7 6 8 1 0 2 4 3 5 ГҗВқГ‘Ж’, ГҗВё Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВҝГҗВҫГҗВҪГҗВёГ‘вӮ¬ГҗВҫГҗВІГҗВ°ГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗВІГҗ°ÑвӮ¬ГҗВёГҗВ°ГҗВҪГ‘вҖҡ Г‘ВҚГ‘вҖҡГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ ГҗВұГ‘Ж’ГҗВҙГҗВөГ‘вҖҡ ГҗВөГҗВјГ‘Ж’ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°ГҗВ»ГҗВөГҗВҪ, ГҗВё ГҗВҫГҗВҪ Г‘вҖҡГҗВҫГҗВ¶ГҗВө ГҗВұГ‘Ж’ГҗВҙГҗВөГ‘вҖҡ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№. ГҗЛңГҗВјГҗВөГҗВөГҗВј ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ, ГҗВёГҗВ· ГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВҫГҗВ№ ГҗВјГҗВҫГҗВјГҗВөГҗВҪГ‘вҖҡГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ ГҗВҝГҗВҫГҗȄĄвҖЎГҗВ°ГҗВөГҗВј ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј ГҗВ»Гҗ°ÑвҖҡГҗВёГҗВҪГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ. ГҗВӯГ‘вҖҰ, ГҗВіГҗВҙГҗВө ГҗВ¶ГҗВө ГҗВұГ‘вҖ№ГҗВ» Harry White, ГҗВәГҗВҫГҗВіГҗВҙГҗВ° Г‘ВҸ ГҗВјГ‘Ж’Г‘вҖЎГҗВёГҗВ»Гҗ°ÑВҒГ‘Е’ Г‘ВҒ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВёГҗВөГҗВј ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ 9-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° :) ГҗВҘГҗВј... ГҗВ° ГҗВҝГҗВҫ Г‘ВҒГ‘вҖҡГ‘вӮ¬Г‘Ж’ГҗВәГ‘вҖҡГ‘Ж’Г‘вӮ¬ГҗВө Г‘ВҚГ‘вҖҡГҗВҫГ‘вҖҡ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВҝГҗВҫГ‘вҖҰГҗВҫГҗВ¶ ГҗВҪГҗВ° Г‘ВҒГҗВҫГҗВІГҗВөГ‘вӮ¬Г‘ЛҶГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ. ГҗВЎГ‘вӮ¬ГҗВ°ГҗВІГҗВҪГҗВёГ‘вҖҡГҗВө!  ГҗвҖҳГҗВҫГҗВ»ГҗВөГҗВө Г‘вҖҡГҗВҫГҗВіГҗВҫ: Г‘ВҚГ‘вҖҡГҗВё ГҗвҖқГҗвҖәГҗЕЎ ГҗВёГҗВ·ГҗВҫГҗВјГҗВҫГ‘вӮ¬Г‘вҖһГҗВҪГ‘вҖ№! ГҗЕЎГҗВ°ГҗВҪГҗВҫГҗВҪГҗВёГҗВ·Гҗ°ÑвҖҡГҗВҫГ‘вӮ¬ ГҗВІГ‘вҖ№ГҗВҙГҗ°ÑвҖҳГ‘вҖҡ ГҗВҙГҗȄВҸ ГҗВҪГҗВёГ‘вҖҰ ГҗВҫГҗВҙГҗВҪГ‘Ж’ ГҗЕЎГҗВӨ 0 2 7 8 6 3 5 4 1 4 1 6 0 5 2 7 8 3 6 8 2 7 1 4 3 5 0 2 5 4 3 8 6 0 1 7 3 6 0 1 4 7 8 2 5 1 7 8 2 0 5 4 3 6 8 3 5 4 7 1 6 0 2 5 0 1 6 3 8 2 7 4 7 4 3 5 2 0 1 6 8 ГҗвҖ”ГҗВҪГҗ°ÑвҖЎГҗВёГ‘вҖҡ, Г‘ВҒГҗВҫГҗВІГҗВөГ‘вӮ¬Г‘ЛҶГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГ‘вӮ¬ГҗВөГҗВІГ‘вӮ¬Гҗ°ÑвҖ°ГҗВ°ГҗВөГ‘вҖҡГ‘ВҒГ‘ВҸ-Г‘вҖҡГҗВ°ГҗВәГҗВё ГҗВІ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҪГҗВөГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬Г‘вҖ№ГҗВјГҗВё Г‘ВҚГҗВәГҗВІГҗВёГҗВІГҗВ°ГҗВ»ГҗВөГҗВҪГ‘вҖҡГҗВҪГ‘вҖ№ГҗВјГҗВё ГҗВҝГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГҗВ°ГҗВҪГҗВёГ‘ВҸГҗВјГҗВё. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВқГҗВ° ГҗВҫГ‘вҖЎГҗВөГ‘вӮ¬ГҗВөГҗВҙГҗВё ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВёГҗВө ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ 12-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗВӯГ‘вҖҡГҗВҫ Г‘вҖҡГҗВҫГҗВ¶ГҗВө ГҗВҝГ‘вӮ¬ГҗВҫГҗВұГҗВ»ГҗВөГҗВјГҗВҪГ‘вҖ№ГҗВ№ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВҫГҗВә, ГҗВҙГҗȄВҸ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ ГҗВҫГҗВҪ Г‘вҖҡГҗВҫГҗВ¶ГҗВө ГҗВҝГ‘вӮ¬ГҗВҫГҗВұГҗВ»ГҗВөГҗВјГҗВҪГ‘вҖ№ГҗВ№. ГҗВқГҗВҫ, ГҗВәГҗВҫГҗВҪГҗВөГ‘вҖЎГҗВҪГҗВҫ, ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВө ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ ГҗВҙГҗВ°ГҗВҪГҗВҪГҗВҫГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° Г‘ВҸ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГҗВ»ГҗВ° ГҗВІ Г‘вҖҡГҗВө ГҗВІГ‘вӮ¬ГҗВөГҗВјГҗВөГҗВҪГҗВ°. ГҗЕҫГҗВҙГҗВҪГҗВ°ГҗВәГҗВҫ ГҗВІГ‘вӮ¬Г‘ВҸГҗВҙ ГҗВ»ГҗВё ГҗВҫГҗВҪГҗВё ГҗВҙГҗВ°ГҗВҙГ‘Ж’Г‘вҖҡ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГ‘вӮ¬ГҗВё Г‘вӮ¬ГҗВ°ГҗВ·ГҗВ»ГҗВҫГҗВ¶ГҗВөГҗВҪГҗВёГҗВё. ГҗЕёГ‘вӮ¬ГҗВёГҗВјГҗВөГ‘вӮ¬ ГҗВёГҗВ· Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ГҗВё ГҗЕёГҗЕҫГҗВЎГҗВўГҗВ ГҗЕҫГҗвҖўГҗВқГҗЛңГҗвҖў ГҗЛңГҗвҖқГҗвҖўГҗВҗГҗвҖәГҗВ¬ГҗВқГҗВ«ГҗВҘ ГҗЕЎГҗвҖҷГҗВҗГҗвҖқГҗВ ГҗВҗГҗВўГҗЕҫГҗвҖҷ ГҗЕёГҗЕҫГҗВ ГҗВҜГҗвҖқГҗЕЎГҗВҗ n=4k ГҗЛңГҗвҖ” ГҗЕҫГҗвҖҳГҗВ ГҗВҗГҗВўГҗЛңГҗЕ“ГҗВ«ГҗВҘ ГҗЕЎГҗвҖҷГҗВҗГҗвҖқГҗВ ГҗВҗГҗВўГҗЕҫГҗвҖҷ ГҗВӯГ‘вҖҡГҗВҫ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ 12-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° 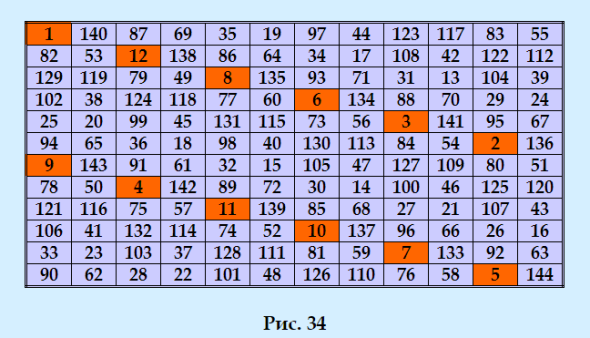 ГҗвҖўГ‘ВҒГҗВ»ГҗВё Г‘вӮ¬ГҗВ°ГҗВ·ГҗВ»ГҗВҫГҗВ¶ГҗВёГ‘вҖҡГ‘Е’ ГҗВөГҗВіГҗВҫ ГҗВҪГҗВ° ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ ГҗвҖәГҗЕЎ, ГҗВҝГҗВҫГҗȄĄвҖЎГҗ°ÑвҖҡГ‘ВҒГ‘ВҸ ГҗВҫГҗВұГҗВҫГҗВұГ‘вҖ°Г‘вҖҳГҗВҪГҗВҪГ‘вҖ№ГҗВө ГҗвҖәГҗЕЎ. ГҗЕёГҗВҫГҗВ№ГҗВҙГ‘Ж’ Г‘ВҒГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВөГ‘вҖҡГ‘Е’, Г‘Ж’ГҗВјГҗВөГҗВөГ‘вҖҡ ГҗВ»ГҗВё ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВ° Harry White Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡГ‘Е’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ 12-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° :) ГҗВқГҗВёГ‘вҖЎГҗВөГҗВіГҗВҫ ГҗВҪГҗВө Г‘Ж’ГҗВҙГҗВ°ГҗВ»ГҗВҫГ‘ВҒГ‘Е’ ГҗВҫГ‘вҖҡ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГ‘вҖ№ ГҗВҙГҗВҫГҗВұГҗВёГ‘вҖҡГ‘Е’Г‘ВҒГ‘ВҸ. ГҗВҰГҗВөГҗВҪГ‘вҖҡГ‘вӮ¬ГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ-Г‘ВҒГҗВёГҗВјГҗВјГҗВөГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡ, Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡ, Г‘ВҒГҗВ»ГҗВ°ГҗВұГҗВҫ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖәГҗЕЎ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡ. ГҗВҗ ГҗВұГҗВҫГҗȄ΄ЛҶГҗВө ГҗВҪГҗВёГ‘вҖЎГҗВөГҗВіГҗВҫ ГҗВҪГҗВө Г‘вҖҰГҗВҫГ‘вҖЎГҗВөГ‘вҖҡ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡГ‘Е’ :( |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese