Thread 'Ultramagic DLS'
Message boards : Science : Ultramagic DLS
Message board moderation
Previous · 1 · 2 · 3 · 4 · 5 . . . 6 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПорÑдок 13 не проблемный, Ð´Ð»Ñ Ð½ÐµÐ³Ð¾ уже поÑтроены идеальные ДЛК. Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 14 идеальные ДЛК не ÑущеÑтвуют. ПорÑдок 15 проблемный (от программы Harry White не Ñмогла ничего добитьÑÑ Ð´Ð»Ñ Ñтого порÑдка). Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 16 идеальные ДЛК найдены в Ñтатье (выше показаны). ПорÑдки 17, 19, 23, 25 не проблемные, Ð´Ð»Ñ Ð½Ð¸Ñ… уже поÑтроены идеальные ДЛК (выше показаны). Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдков 18, 22, 26 идеальных ДЛК не ÑущеÑтвует. ПорÑдки 21, 24, 27 проблемные. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðтот ДЛК 27-го порÑдка из полной ÑиÑтемы MOLS центрально-Ñимметричный и Ñлабо пандиагональный 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 4 5 3 7 8 6 1 2 0 13 14 12 16 17 15 10 11 9 22 23 21 25 26 24 19 20 18 8 6 7 2 0 1 5 3 4 17 15 16 11 9 10 14 12 13 26 24 25 20 18 19 23 21 22 12 13 14 15 16 17 9 10 11 21 22 23 24 25 26 18 19 20 3 4 5 6 7 8 0 1 2 16 17 15 10 11 9 13 14 12 25 26 24 19 20 18 22 23 21 7 8 6 1 2 0 4 5 3 11 9 10 14 12 13 17 15 16 20 18 19 23 21 22 26 24 25 2 0 1 5 3 4 8 6 7 24 25 26 18 19 20 21 22 23 6 7 8 0 1 2 3 4 5 15 16 17 9 10 11 12 13 14 19 20 18 22 23 21 25 26 24 1 2 0 4 5 3 7 8 6 10 11 9 13 14 12 16 17 15 23 21 22 26 24 25 20 18 19 5 3 4 8 6 7 2 0 1 14 12 13 17 15 16 11 9 10 5 3 4 8 6 7 2 0 1 14 12 13 17 15 16 11 9 10 23 21 22 26 24 25 20 18 19 6 7 8 0 1 2 3 4 5 15 16 17 9 10 11 12 13 14 24 25 26 18 19 20 21 22 23 1 2 0 4 5 3 7 8 6 10 11 9 13 14 12 16 17 15 19 20 18 22 23 21 25 26 24 17 15 16 11 9 10 14 12 13 26 24 25 20 18 19 23 21 22 8 6 7 2 0 1 5 3 4 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 0 1 2 3 4 5 6 7 8 13 14 12 16 17 15 10 11 9 22 23 21 25 26 24 19 20 18 4 5 3 7 8 6 1 2 0 20 18 19 23 21 22 26 24 25 2 0 1 5 3 4 8 6 7 11 9 10 14 12 13 17 15 16 21 22 23 24 25 26 18 19 20 3 4 5 6 7 8 0 1 2 12 13 14 15 16 17 9 10 11 25 26 24 19 20 18 22 23 21 7 8 6 1 2 0 4 5 3 16 17 15 10 11 9 13 14 12 7 8 6 1 2 0 4 5 3 16 17 15 10 11 9 13 14 12 25 26 24 19 20 18 22 23 21 2 0 1 5 3 4 8 6 7 11 9 10 14 12 13 17 15 16 20 18 19 23 21 22 26 24 25 3 4 5 6 7 8 0 1 2 12 13 14 15 16 17 9 10 11 21 22 23 24 25 26 18 19 20 10 11 9 13 14 12 16 17 15 19 20 18 22 23 21 25 26 24 1 2 0 4 5 3 7 8 6 14 12 13 17 15 16 11 9 10 23 21 22 26 24 25 20 18 19 5 3 4 8 6 7 2 0 1 15 16 17 9 10 11 12 13 14 24 25 26 18 19 20 21 22 23 6 7 8 0 1 2 3 4 5 22 23 21 25 26 24 19 20 18 4 5 3 7 8 6 1 2 0 13 14 12 16 17 15 10 11 9 26 24 25 20 18 19 23 21 22 8 6 7 2 0 1 5 3 4 17 15 16 11 9 10 14 12 13 18 19 20 21 22 23 24 25 26 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 ÐÑÑоциативноÑти не хватает. Преобразование Ñтого ДЛК в СРДЛК аÑÑоциативноÑÑ‚ÑŒ дало, но... иÑчезла ÑÐ»Ð°Ð±Ð°Ñ Ð¿Ð°Ð½Ð´Ð¸Ð°Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð¾ÑÑ‚ÑŒ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðе могу никак найти идеальный ДЛК 8-го порÑдка. У Ð¼ÐµÐ½Ñ Ð² ÑтатьÑÑ… очень много идеальных магичеÑких ДЛК данного порÑдка. но ни один не раÑкладываетÑÑ Ð² ортогональную пару ДЛК. Попробовала программу Harry White LatinSquare. Задала поÑтроить 3000 пандиагональных ЛК. Программа поÑтроила Ñледующие ЛК Order? 8
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt
Counts
------
2586 Latin
414 diagonal Latin
3000 weakly pandiagonal
64 axial symmetric
8 double axial symmetric
16 center symmetric
8 self-orthogonalÐ’Ñе 3000 ЛК Ñлабо пандиагональные, еÑÑ‚ÑŒ 414 ДЛК, еÑÑ‚ÑŒ 16 центрально-Ñимметричных ЛК, и нет ни одного аÑÑоциативного ЛК! Задала поÑтроить 10000 центрально-Ñимметричных ДЛК. Программа поÑтроила Ñледующие ДЛК Order? 8
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
10000 diagonal Latin
2 weakly pandiagonal
896 double axial symmetric
10000 center symmetric
10000 nfr
28 self-orthogonalÐ’Ñего 2 ДЛК Ñлабо пандиагональные, и нет ни одного аÑÑоциативного ДЛК! Случайно ди Ñто? Или идеального ДЛК 8-го порÑдка не ÑущеÑтвует? Ещё попытка, задала поÑтроить 100000 центрально-Ñимметричных ДЛК, поÑтроено 22528 центрально-Ñимметричных ДЛК Order? 8
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt
Counts
------
22528 diagonal Latin
11 weakly pandiagonal
2048 double axial symmetric
22528 center symmetric
22528 nfr
64 self-orthogonalЕÑÑ‚ÑŒ 11 Ñлабо-пандиагональных ДЛК, нет ни одного аÑÑоциативного ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
У-Ñ€-Ñ€-Ñ€-а-а-а-а! Ðашла! Задала программе Harry White LatinSquares поÑтроить 100000 аÑÑоциативных ДЛК. Программа поÑтроила Ñледующие аÑÑоциативные ДЛК Order? 8
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_8.txt
Counts
------
22528 diagonal Latin
22528 associative
4 weakly pandiagonal
4 ultramagic
2048 double axial symmetric
22528 natural \diagonal
64 self-orthogonalЕÑÑ‚ÑŒ 4 идеальных ДЛК 8-го порÑдка!!! Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ñ Ð¸Ñ… извлеку на Ñвет Божий :) Вот они - идеальные ДЛК 8-го порÑдка 0 2 5 7 1 3 4 6 3 1 6 4 2 0 7 5 6 5 2 1 7 4 3 0 4 7 0 3 5 6 1 2 5 6 1 2 4 7 0 3 7 4 3 0 6 5 2 1 2 0 7 5 3 1 6 4 1 3 4 6 0 2 5 7 0 2 5 7 1 3 4 6 2 1 6 5 3 0 7 4 7 5 2 0 6 4 3 1 4 7 0 3 5 6 1 2 5 6 1 2 4 7 0 3 6 4 3 1 7 5 2 0 3 0 7 4 2 1 6 5 1 3 4 6 0 2 5 7 0 2 7 4 5 6 3 1 3 1 5 6 7 4 0 2 4 6 2 1 0 3 7 5 7 5 0 3 2 1 4 6 1 3 6 5 4 7 2 0 2 0 4 7 6 5 1 3 5 7 3 0 1 2 6 4 6 4 1 2 3 0 5 7 0 2 7 4 5 6 3 1 2 1 5 7 6 4 0 3 5 6 2 0 1 3 7 4 7 5 0 3 2 1 4 6 1 3 6 5 4 7 2 0 3 0 4 6 7 5 1 2 4 7 3 1 0 2 6 5 6 4 1 2 3 0 5 7 ПроверÑÑŽ ÑвойÑтва Order? 8
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_9.txt
Counts
------
4 diagonal Latin
4 associative
4 weakly pandiagonal
4 ultramagic
4 double axial symmetric
4 natural \diagonalÐ’ÑÑ‘ верно. Однако готовой ортогональной пары ДЛК тут не имеетÑÑ, нет SODLS. Проверила ДЛК на изоморфноÑÑ‚ÑŒ, только два уникальных ДЛК здеÑÑŒ еÑÑ‚ÑŒ. ПропуÑтила вÑе 4 идеальных ДЛК через программу Белышева ortogon_u. Ð’Ñе они имеют ОДЛК, но... идеального ДЛК Ñреди ОДЛК нет. Таким образом, Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° идеальных ДЛК 8-го порÑдка пока не найдена. Ð Ñ Ñ‚Ð°Ðº хотела поÑтроить новый идеальный магичеÑкий квадрат 8-го порÑдка! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Попробовала генерировать программой Harry White LatinSquares аÑÑоциативные ДЛК 12-го порÑдка в надежде найти идеальный ДЛК. Ðет, Ñтот финт Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 12 не прошёл. ÐÑÑоциативные ДЛК 12-го порÑдка генерируютÑÑ Ð² огромных количеÑтвах, вÑе их Ñгенерировать и проверить нереально. Вот Ñгенерировала полмиллиона аÑÑоциативных ДЛК Order? 12
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt
Counts
------
500000 diagonal Latin
500000 associative
500000 natural \diagonalИдеального ДЛК Ñреди них нет. Так что, идеальный ДЛК 12-го порÑдка пока не найден. И точно так же Ð´Ð»Ñ Ð°ÑÑоциативных ДЛК порÑдка 15. Вот Ñгенерировала 100000, идеального ДЛК Ñреди них нет Order? 15
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
100000 diagonal Latin
100000 associative
100000 natural \diagonal |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðу вот, пока вÑÑ‘, дальше пошли проблемные порÑдки. Зато теперь можно поÑтроить идеальный ДЛК 40-го порÑдка методом ÑоÑтавных квадратов (40=5*8). Идеальный ДЛК 5-го порÑдка возьму из Ñтартового поÑта, идеальный ДЛК 8-го порÑдка - один из найденных программой Harry White, например, Ñтот 0 2 5 7 1 3 4 6 2 1 6 5 3 0 7 4 7 5 2 0 6 4 3 1 4 7 0 3 5 6 1 2 5 6 1 2 4 7 0 3 6 4 3 1 7 5 2 0 3 0 7 4 2 1 6 5 1 3 4 6 0 2 5 7 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’Ñтречайте - идеальный ДЛК 40-го порÑдка, поÑтроенный методом ÑоÑтавных квадратов 0 2 5 7 1 3 4 6 32 34 37 39 33 35 36 38 24 26 29 31 25 27 28 30 16 18 21 23 17 19 20 22 8 10 13 15 9 11 12 14 2 1 6 5 3 0 7 4 34 33 38 37 35 32 39 36 26 25 30 29 27 24 31 28 18 17 22 21 19 16 23 20 10 9 14 13 11 8 15 12 7 5 2 0 6 4 3 1 39 37 34 32 38 36 35 33 31 29 26 24 30 28 27 25 23 21 18 16 22 20 19 17 15 13 10 8 14 12 11 9 4 7 0 3 5 6 1 2 36 39 32 35 37 38 33 34 28 31 24 27 29 30 25 26 20 23 16 19 21 22 17 18 12 15 8 11 13 14 9 10 5 6 1 2 4 7 0 3 37 38 33 34 36 39 32 35 29 30 25 26 28 31 24 27 21 22 17 18 20 23 16 19 13 14 9 10 12 15 8 11 6 4 3 1 7 5 2 0 38 36 35 33 39 37 34 32 30 28 27 25 31 29 26 24 22 20 19 17 23 21 18 16 14 12 11 9 15 13 10 8 3 0 7 4 2 1 6 5 35 32 39 36 34 33 38 37 27 24 31 28 26 25 30 29 19 16 23 20 18 17 22 21 11 8 15 12 10 9 14 13 1 3 4 6 0 2 5 7 33 35 36 38 32 34 37 39 25 27 28 30 24 26 29 31 17 19 20 22 16 18 21 23 9 11 12 14 8 10 13 15 16 18 21 23 17 19 20 22 8 10 13 15 9 11 12 14 0 2 5 7 1 3 4 6 32 34 37 39 33 35 36 38 24 26 29 31 25 27 28 30 18 17 22 21 19 16 23 20 10 9 14 13 11 8 15 12 2 1 6 5 3 0 7 4 34 33 38 37 35 32 39 36 26 25 30 29 27 24 31 28 23 21 18 16 22 20 19 17 15 13 10 8 14 12 11 9 7 5 2 0 6 4 3 1 39 37 34 32 38 36 35 33 31 29 26 24 30 28 27 25 20 23 16 19 21 22 17 18 12 15 8 11 13 14 9 10 4 7 0 3 5 6 1 2 36 39 32 35 37 38 33 34 28 31 24 27 29 30 25 26 21 22 17 18 20 23 16 19 13 14 9 10 12 15 8 11 5 6 1 2 4 7 0 3 37 38 33 34 36 39 32 35 29 30 25 26 28 31 24 27 22 20 19 17 23 21 18 16 14 12 11 9 15 13 10 8 6 4 3 1 7 5 2 0 38 36 35 33 39 37 34 32 30 28 27 25 31 29 26 24 19 16 23 20 18 17 22 21 11 8 15 12 10 9 14 13 3 0 7 4 2 1 6 5 35 32 39 36 34 33 38 37 27 24 31 28 26 25 30 29 17 19 20 22 16 18 21 23 9 11 12 14 8 10 13 15 1 3 4 6 0 2 5 7 33 35 36 38 32 34 37 39 25 27 28 30 24 26 29 31 32 34 37 39 33 35 36 38 24 26 29 31 25 27 28 30 16 18 21 23 17 19 20 22 8 10 13 15 9 11 12 14 0 2 5 7 1 3 4 6 34 33 38 37 35 32 39 36 26 25 30 29 27 24 31 28 18 17 22 21 19 16 23 20 10 9 14 13 11 8 15 12 2 1 6 5 3 0 7 4 39 37 34 32 38 36 35 33 31 29 26 24 30 28 27 25 23 21 18 16 22 20 19 17 15 13 10 8 14 12 11 9 7 5 2 0 6 4 3 1 36 39 32 35 37 38 33 34 28 31 24 27 29 30 25 26 20 23 16 19 21 22 17 18 12 15 8 11 13 14 9 10 4 7 0 3 5 6 1 2 37 38 33 34 36 39 32 35 29 30 25 26 28 31 24 27 21 22 17 18 20 23 16 19 13 14 9 10 12 15 8 11 5 6 1 2 4 7 0 3 38 36 35 33 39 37 34 32 30 28 27 25 31 29 26 24 22 20 19 17 23 21 18 16 14 12 11 9 15 13 10 8 6 4 3 1 7 5 2 0 35 32 39 36 34 33 38 37 27 24 31 28 26 25 30 29 19 16 23 20 18 17 22 21 11 8 15 12 10 9 14 13 3 0 7 4 2 1 6 5 33 35 36 38 32 34 37 39 25 27 28 30 24 26 29 31 17 19 20 22 16 18 21 23 9 11 12 14 8 10 13 15 1 3 4 6 0 2 5 7 8 10 13 15 9 11 12 14 0 2 5 7 1 3 4 6 32 34 37 39 33 35 36 38 24 26 29 31 25 27 28 30 16 18 21 23 17 19 20 22 10 9 14 13 11 8 15 12 2 1 6 5 3 0 7 4 34 33 38 37 35 32 39 36 26 25 30 29 27 24 31 28 18 17 22 21 19 16 23 20 15 13 10 8 14 12 11 9 7 5 2 0 6 4 3 1 39 37 34 32 38 36 35 33 31 29 26 24 30 28 27 25 23 21 18 16 22 20 19 17 12 15 8 11 13 14 9 10 4 7 0 3 5 6 1 2 36 39 32 35 37 38 33 34 28 31 24 27 29 30 25 26 20 23 16 19 21 22 17 18 13 14 9 10 12 15 8 11 5 6 1 2 4 7 0 3 37 38 33 34 36 39 32 35 29 30 25 26 28 31 24 27 21 22 17 18 20 23 16 19 14 12 11 9 15 13 10 8 6 4 3 1 7 5 2 0 38 36 35 33 39 37 34 32 30 28 27 25 31 29 26 24 22 20 19 17 23 21 18 16 11 8 15 12 10 9 14 13 3 0 7 4 2 1 6 5 35 32 39 36 34 33 38 37 27 24 31 28 26 25 30 29 19 16 23 20 18 17 22 21 9 11 12 14 8 10 13 15 1 3 4 6 0 2 5 7 33 35 36 38 32 34 37 39 25 27 28 30 24 26 29 31 17 19 20 22 16 18 21 23 24 26 29 31 25 27 28 30 16 18 21 23 17 19 20 22 8 10 13 15 9 11 12 14 0 2 5 7 1 3 4 6 32 34 37 39 33 35 36 38 26 25 30 29 27 24 31 28 18 17 22 21 19 16 23 20 10 9 14 13 11 8 15 12 2 1 6 5 3 0 7 4 34 33 38 37 35 32 39 36 31 29 26 24 30 28 27 25 23 21 18 16 22 20 19 17 15 13 10 8 14 12 11 9 7 5 2 0 6 4 3 1 39 37 34 32 38 36 35 33 28 31 24 27 29 30 25 26 20 23 16 19 21 22 17 18 12 15 8 11 13 14 9 10 4 7 0 3 5 6 1 2 36 39 32 35 37 38 33 34 29 30 25 26 28 31 24 27 21 22 17 18 20 23 16 19 13 14 9 10 12 15 8 11 5 6 1 2 4 7 0 3 37 38 33 34 36 39 32 35 30 28 27 25 31 29 26 24 22 20 19 17 23 21 18 16 14 12 11 9 15 13 10 8 6 4 3 1 7 5 2 0 38 36 35 33 39 37 34 32 27 24 31 28 26 25 30 29 19 16 23 20 18 17 22 21 11 8 15 12 10 9 14 13 3 0 7 4 2 1 6 5 35 32 39 36 34 33 38 37 25 27 28 30 24 26 29 31 17 19 20 22 16 18 21 23 9 11 12 14 8 10 13 15 1 3 4 6 0 2 5 7 33 35 36 38 32 34 37 39 ПроверÑÑŽ ÑвойÑтва ДЛК утилитой Harry White Order? 40
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
1 diagonal Latin
1 associative
1 weakly pandiagonal
1 ultramagic
1 natural \diagonalÐ’ÑÑ‘ верно. И не могло быть иначе :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ладно, новый идеальный магичеÑкий квадрат 8-го порÑдка пока не могу поÑтроить. Рвот новый идеальный магичеÑкий квадрат 9-го порÑдка могу поÑтроить! Ðто найденный программой Harry White идеальный ДЛК 9-го порÑдка 3 5 4 6 8 7 0 2 1 0 2 1 3 5 4 6 8 7 6 8 7 0 2 1 3 5 4 5 4 3 8 7 6 2 1 0 2 1 0 5 4 3 8 7 6 8 7 6 2 1 0 5 4 3 4 3 5 7 6 8 1 0 2 1 0 2 4 3 5 7 6 8 7 6 8 1 0 2 4 3 5 Он ÑвлÑетÑÑ SODLS, значит, ортогонален Ñвоему транÑпонированному варианту 3 0 6 5 2 8 4 1 7 5 2 8 4 1 7 3 0 6 4 1 7 3 0 6 5 2 8 6 3 0 8 5 2 7 4 1 8 5 2 7 4 1 6 3 0 7 4 1 6 3 0 8 5 2 0 6 3 2 8 5 1 7 4 2 8 5 1 7 4 0 6 3 1 7 4 0 6 3 2 8 5 Ðтот ДЛК тоже идеальный. ÐžÑ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° идеальных ДЛК готова. Идеальный магичеÑкий квадрат буду Ñтроить по формуле 9Ð+Ð’+1, где Ð - первый идеальный ДЛК, Ð’ - второй идеальный ДЛК (транÑпонированный вариант). |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Готово! Вот он какой краÑивый - новый идеальный магичеÑкий квадрат 9-го порÑдка 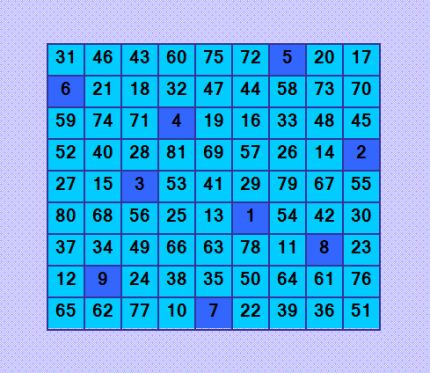 Таких у Ð¼ÐµÐ½Ñ Ð½Ðµ было. Ð’ квадрате выделена так Ð½Ð°Ð·Ñ‹Ð²Ð°ÐµÐ¼Ð°Ñ Ð½Ð°Ñ‡Ð°Ð»ÑŒÐ½Ð°Ñ Ñ†ÐµÐ¿Ð¾Ñ‡ÐºÐ°. Ð¡ÐµÐ¹Ñ‡Ð°Ñ ÐºÐ°ÐºÐ¾Ð¹-нибудь идеальный магичеÑких квадрат 9-го порÑдка покажу из тех, что Ñ Ñтроила давным-давно. Было разработано неÑколько алгоритмов поÑтроениÑ, но ортогональной пары идеальных ДЛК у Ð¼ÐµÐ½Ñ Ð² то Ð²Ñ€ÐµÐ¼Ñ Ð½Ðµ было и применить метод латинÑких квадратов Ñ Ð½Ðµ могла в таком виде. Ð¥Ð¾Ñ‚Ñ Ð¿Ñ€Ð¸Ð¼ÐµÐ½ÑлÑÑ Ð¼ÐµÑ‚Ð¾Ð´ латинÑких квадратов Ñ Ð¸Ñпользованием ортогональных пар обобщённых ЛК и обычных ЛК, не ÑвлÑющихÑÑ Ð”Ð›Ðš. Пример из Ñтатьи ЕЩРРÐЗ ОБ ИДЕÐЛЬÐЫХ КВÐДРÐТÐÐ¥ ДЕВЯТОГО ПОРЯДКРИдеальный магичеÑкий квадрат 9-го порÑдка 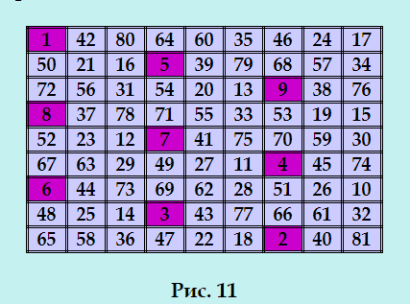 Сравните начальную цепочку Ñ Ð¿Ð¾Ñтроенным выше идеальным магичеÑким квадратом. ЕÑли разложить Ñтот магичеÑкий квадрат на ортогональную пару ЛК, ЛК получатÑÑ Ð¾Ð±Ð¾Ð±Ñ‰Ñ‘Ð½Ð½Ñ‹Ð¼Ð¸. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Теперь можно поÑтроить ортогональную пару идеальных ДЛК 45-го порÑдка на оÑнове ортогональных пар идеальных ДЛК 5-го и 9-го порÑдков. Ортогональную пару идеальных ДЛК 9-го порÑдка возьму показанную чуть выше. Ортогональную пару идеальных ДЛК 5-го порÑдка возьму Ñледующую 0 4 3 2 1 2 1 0 4 3 4 3 2 1 0 1 0 4 3 2 3 2 1 0 4 0 2 4 1 3 4 1 3 0 2 3 0 2 4 1 2 4 1 3 0 1 3 0 2 4 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’Ñтречайте - Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° идеальных ДЛК 45-го порÑдка, поÑÑ‚Ñ€Ð¾ÐµÐ½Ð½Ð°Ñ Ð¼ÐµÑ‚Ð¾Ð´Ð¾Ð¼ ÑоÑтавных квадратов 3 5 4 6 8 7 0 2 1 39 41 40 42 44 43 36 38 37 30 32 31 33 35 34 27 29 28 21 23 22 24 26 25 18 20 19 12 14 13 15 17 16 9 11 10 0 2 1 3 5 4 6 8 7 36 38 37 39 41 40 42 44 43 27 29 28 30 32 31 33 35 34 18 20 19 21 23 22 24 26 25 9 11 10 12 14 13 15 17 16 6 8 7 0 2 1 3 5 4 42 44 43 36 38 37 39 41 40 33 35 34 27 29 28 30 32 31 24 26 25 18 20 19 21 23 22 15 17 16 9 11 10 12 14 13 5 4 3 8 7 6 2 1 0 41 40 39 44 43 42 38 37 36 32 31 30 35 34 33 29 28 27 23 22 21 26 25 24 20 19 18 14 13 12 17 16 15 11 10 9 2 1 0 5 4 3 8 7 6 38 37 36 41 40 39 44 43 42 29 28 27 32 31 30 35 34 33 20 19 18 23 22 21 26 25 24 11 10 9 14 13 12 17 16 15 8 7 6 2 1 0 5 4 3 44 43 42 38 37 36 41 40 39 35 34 33 29 28 27 32 31 30 26 25 24 20 19 18 23 22 21 17 16 15 11 10 9 14 13 12 4 3 5 7 6 8 1 0 2 40 39 41 43 42 44 37 36 38 31 30 32 34 33 35 28 27 29 22 21 23 25 24 26 19 18 20 13 12 14 16 15 17 10 9 11 1 0 2 4 3 5 7 6 8 37 36 38 40 39 41 43 42 44 28 27 29 31 30 32 34 33 35 19 18 20 22 21 23 25 24 26 10 9 11 13 12 14 16 15 17 7 6 8 1 0 2 4 3 5 43 42 44 37 36 38 40 39 41 34 33 35 28 27 29 31 30 32 25 24 26 19 18 20 22 21 23 16 15 17 10 9 11 13 12 14 21 23 22 24 26 25 18 20 19 12 14 13 15 17 16 9 11 10 3 5 4 6 8 7 0 2 1 39 41 40 42 44 43 36 38 37 30 32 31 33 35 34 27 29 28 18 20 19 21 23 22 24 26 25 9 11 10 12 14 13 15 17 16 0 2 1 3 5 4 6 8 7 36 38 37 39 41 40 42 44 43 27 29 28 30 32 31 33 35 34 24 26 25 18 20 19 21 23 22 15 17 16 9 11 10 12 14 13 6 8 7 0 2 1 3 5 4 42 44 43 36 38 37 39 41 40 33 35 34 27 29 28 30 32 31 23 22 21 26 25 24 20 19 18 14 13 12 17 16 15 11 10 9 5 4 3 8 7 6 2 1 0 41 40 39 44 43 42 38 37 36 32 31 30 35 34 33 29 28 27 20 19 18 23 22 21 26 25 24 11 10 9 14 13 12 17 16 15 2 1 0 5 4 3 8 7 6 38 37 36 41 40 39 44 43 42 29 28 27 32 31 30 35 34 33 26 25 24 20 19 18 23 22 21 17 16 15 11 10 9 14 13 12 8 7 6 2 1 0 5 4 3 44 43 42 38 37 36 41 40 39 35 34 33 29 28 27 32 31 30 22 21 23 25 24 26 19 18 20 13 12 14 16 15 17 10 9 11 4 3 5 7 6 8 1 0 2 40 39 41 43 42 44 37 36 38 31 30 32 34 33 35 28 27 29 19 18 20 22 21 23 25 24 26 10 9 11 13 12 14 16 15 17 1 0 2 4 3 5 7 6 8 37 36 38 40 39 41 43 42 44 28 27 29 31 30 32 34 33 35 25 24 26 19 18 20 22 21 23 16 15 17 10 9 11 13 12 14 7 6 8 1 0 2 4 3 5 43 42 44 37 36 38 40 39 41 34 33 35 28 27 29 31 30 32 39 41 40 42 44 43 36 38 37 30 32 31 33 35 34 27 29 28 21 23 22 24 26 25 18 20 19 12 14 13 15 17 16 9 11 10 3 5 4 6 8 7 0 2 1 36 38 37 39 41 40 42 44 43 27 29 28 30 32 31 33 35 34 18 20 19 21 23 22 24 26 25 9 11 10 12 14 13 15 17 16 0 2 1 3 5 4 6 8 7 42 44 43 36 38 37 39 41 40 33 35 34 27 29 28 30 32 31 24 26 25 18 20 19 21 23 22 15 17 16 9 11 10 12 14 13 6 8 7 0 2 1 3 5 4 41 40 39 44 43 42 38 37 36 32 31 30 35 34 33 29 28 27 23 22 21 26 25 24 20 19 18 14 13 12 17 16 15 11 10 9 5 4 3 8 7 6 2 1 0 38 37 36 41 40 39 44 43 42 29 28 27 32 31 30 35 34 33 20 19 18 23 22 21 26 25 24 11 10 9 14 13 12 17 16 15 2 1 0 5 4 3 8 7 6 44 43 42 38 37 36 41 40 39 35 34 33 29 28 27 32 31 30 26 25 24 20 19 18 23 22 21 17 16 15 11 10 9 14 13 12 8 7 6 2 1 0 5 4 3 40 39 41 43 42 44 37 36 38 31 30 32 34 33 35 28 27 29 22 21 23 25 24 26 19 18 20 13 12 14 16 15 17 10 9 11 4 3 5 7 6 8 1 0 2 37 36 38 40 39 41 43 42 44 28 27 29 31 30 32 34 33 35 19 18 20 22 21 23 25 24 26 10 9 11 13 12 14 16 15 17 1 0 2 4 3 5 7 6 8 43 42 44 37 36 38 40 39 41 34 33 35 28 27 29 31 30 32 25 24 26 19 18 20 22 21 23 16 15 17 10 9 11 13 12 14 7 6 8 1 0 2 4 3 5 12 14 13 15 17 16 9 11 10 3 5 4 6 8 7 0 2 1 39 41 40 42 44 43 36 38 37 30 32 31 33 35 34 27 29 28 21 23 22 24 26 25 18 20 19 9 11 10 12 14 13 15 17 16 0 2 1 3 5 4 6 8 7 36 38 37 39 41 40 42 44 43 27 29 28 30 32 31 33 35 34 18 20 19 21 23 22 24 26 25 15 17 16 9 11 10 12 14 13 6 8 7 0 2 1 3 5 4 42 44 43 36 38 37 39 41 40 33 35 34 27 29 28 30 32 31 24 26 25 18 20 19 21 23 22 14 13 12 17 16 15 11 10 9 5 4 3 8 7 6 2 1 0 41 40 39 44 43 42 38 37 36 32 31 30 35 34 33 29 28 27 23 22 21 26 25 24 20 19 18 11 10 9 14 13 12 17 16 15 2 1 0 5 4 3 8 7 6 38 37 36 41 40 39 44 43 42 29 28 27 32 31 30 35 34 33 20 19 18 23 22 21 26 25 24 17 16 15 11 10 9 14 13 12 8 7 6 2 1 0 5 4 3 44 43 42 38 37 36 41 40 39 35 34 33 29 28 27 32 31 30 26 25 24 20 19 18 23 22 21 13 12 14 16 15 17 10 9 11 4 3 5 7 6 8 1 0 2 40 39 41 43 42 44 37 36 38 31 30 32 34 33 35 28 27 29 22 21 23 25 24 26 19 18 20 10 9 11 13 12 14 16 15 17 1 0 2 4 3 5 7 6 8 37 36 38 40 39 41 43 42 44 28 27 29 31 30 32 34 33 35 19 18 20 22 21 23 25 24 26 16 15 17 10 9 11 13 12 14 7 6 8 1 0 2 4 3 5 43 42 44 37 36 38 40 39 41 34 33 35 28 27 29 31 30 32 25 24 26 19 18 20 22 21 23 30 32 31 33 35 34 27 29 28 21 23 22 24 26 25 18 20 19 12 14 13 15 17 16 9 11 10 3 5 4 6 8 7 0 2 1 39 41 40 42 44 43 36 38 37 27 29 28 30 32 31 33 35 34 18 20 19 21 23 22 24 26 25 9 11 10 12 14 13 15 17 16 0 2 1 3 5 4 6 8 7 36 38 37 39 41 40 42 44 43 33 35 34 27 29 28 30 32 31 24 26 25 18 20 19 21 23 22 15 17 16 9 11 10 12 14 13 6 8 7 0 2 1 3 5 4 42 44 43 36 38 37 39 41 40 32 31 30 35 34 33 29 28 27 23 22 21 26 25 24 20 19 18 14 13 12 17 16 15 11 10 9 5 4 3 8 7 6 2 1 0 41 40 39 44 43 42 38 37 36 29 28 27 32 31 30 35 34 33 20 19 18 23 22 21 26 25 24 11 10 9 14 13 12 17 16 15 2 1 0 5 4 3 8 7 6 38 37 36 41 40 39 44 43 42 35 34 33 29 28 27 32 31 30 26 25 24 20 19 18 23 22 21 17 16 15 11 10 9 14 13 12 8 7 6 2 1 0 5 4 3 44 43 42 38 37 36 41 40 39 31 30 32 34 33 35 28 27 29 22 21 23 25 24 26 19 18 20 13 12 14 16 15 17 10 9 11 4 3 5 7 6 8 1 0 2 40 39 41 43 42 44 37 36 38 28 27 29 31 30 32 34 33 35 19 18 20 22 21 23 25 24 26 10 9 11 13 12 14 16 15 17 1 0 2 4 3 5 7 6 8 37 36 38 40 39 41 43 42 44 34 33 35 28 27 29 31 30 32 25 24 26 19 18 20 22 21 23 16 15 17 10 9 11 13 12 14 7 6 8 1 0 2 4 3 5 43 42 44 37 36 38 40 39 41 3 0 6 5 2 8 4 1 7 21 18 24 23 20 26 22 19 25 39 36 42 41 38 44 40 37 43 12 9 15 14 11 17 13 10 16 30 27 33 32 29 35 31 28 34 5 2 8 4 1 7 3 0 6 23 20 26 22 19 25 21 18 24 41 38 44 40 37 43 39 36 42 14 11 17 13 10 16 12 9 15 32 29 35 31 28 34 30 27 33 4 1 7 3 0 6 5 2 8 22 19 25 21 18 24 23 20 26 40 37 43 39 36 42 41 38 44 13 10 16 12 9 15 14 11 17 31 28 34 30 27 33 32 29 35 6 3 0 8 5 2 7 4 1 24 21 18 26 23 20 25 22 19 42 39 36 44 41 38 43 40 37 15 12 9 17 14 11 16 13 10 33 30 27 35 32 29 34 31 28 8 5 2 7 4 1 6 3 0 26 23 20 25 22 19 24 21 18 44 41 38 43 40 37 42 39 36 17 14 11 16 13 10 15 12 9 35 32 29 34 31 28 33 30 27 7 4 1 6 3 0 8 5 2 25 22 19 24 21 18 26 23 20 43 40 37 42 39 36 44 41 38 16 13 10 15 12 9 17 14 11 34 31 28 33 30 27 35 32 29 0 6 3 2 8 5 1 7 4 18 24 21 20 26 23 19 25 22 36 42 39 38 44 41 37 43 40 9 15 12 11 17 14 10 16 13 27 33 30 29 35 32 28 34 31 2 8 5 1 7 4 0 6 3 20 26 23 19 25 22 18 24 21 38 44 41 37 43 40 36 42 39 11 17 14 10 16 13 9 15 12 29 35 32 28 34 31 27 33 30 1 7 4 0 6 3 2 8 5 19 25 22 18 24 21 20 26 23 37 43 40 36 42 39 38 44 41 10 16 13 9 15 12 11 17 14 28 34 31 27 33 30 29 35 32 39 36 42 41 38 44 40 37 43 12 9 15 14 11 17 13 10 16 30 27 33 32 29 35 31 28 34 3 0 6 5 2 8 4 1 7 21 18 24 23 20 26 22 19 25 41 38 44 40 37 43 39 36 42 14 11 17 13 10 16 12 9 15 32 29 35 31 28 34 30 27 33 5 2 8 4 1 7 3 0 6 23 20 26 22 19 25 21 18 24 40 37 43 39 36 42 41 38 44 13 10 16 12 9 15 14 11 17 31 28 34 30 27 33 32 29 35 4 1 7 3 0 6 5 2 8 22 19 25 21 18 24 23 20 26 42 39 36 44 41 38 43 40 37 15 12 9 17 14 11 16 13 10 33 30 27 35 32 29 34 31 28 6 3 0 8 5 2 7 4 1 24 21 18 26 23 20 25 22 19 44 41 38 43 40 37 42 39 36 17 14 11 16 13 10 15 12 9 35 32 29 34 31 28 33 30 27 8 5 2 7 4 1 6 3 0 26 23 20 25 22 19 24 21 18 43 40 37 42 39 36 44 41 38 16 13 10 15 12 9 17 14 11 34 31 28 33 30 27 35 32 29 7 4 1 6 3 0 8 5 2 25 22 19 24 21 18 26 23 20 36 42 39 38 44 41 37 43 40 9 15 12 11 17 14 10 16 13 27 33 30 29 35 32 28 34 31 0 6 3 2 8 5 1 7 4 18 24 21 20 26 23 19 25 22 38 44 41 37 43 40 36 42 39 11 17 14 10 16 13 9 15 12 29 35 32 28 34 31 27 33 30 2 8 5 1 7 4 0 6 3 20 26 23 19 25 22 18 24 21 37 43 40 36 42 39 38 44 41 10 16 13 9 15 12 11 17 14 28 34 31 27 33 30 29 35 32 1 7 4 0 6 3 2 8 5 19 25 22 18 24 21 20 26 23 30 27 33 32 29 35 31 28 34 3 0 6 5 2 8 4 1 7 21 18 24 23 20 26 22 19 25 39 36 42 41 38 44 40 37 43 12 9 15 14 11 17 13 10 16 32 29 35 31 28 34 30 27 33 5 2 8 4 1 7 3 0 6 23 20 26 22 19 25 21 18 24 41 38 44 40 37 43 39 36 42 14 11 17 13 10 16 12 9 15 31 28 34 30 27 33 32 29 35 4 1 7 3 0 6 5 2 8 22 19 25 21 18 24 23 20 26 40 37 43 39 36 42 41 38 44 13 10 16 12 9 15 14 11 17 33 30 27 35 32 29 34 31 28 6 3 0 8 5 2 7 4 1 24 21 18 26 23 20 25 22 19 42 39 36 44 41 38 43 40 37 15 12 9 17 14 11 16 13 10 35 32 29 34 31 28 33 30 27 8 5 2 7 4 1 6 3 0 26 23 20 25 22 19 24 21 18 44 41 38 43 40 37 42 39 36 17 14 11 16 13 10 15 12 9 34 31 28 33 30 27 35 32 29 7 4 1 6 3 0 8 5 2 25 22 19 24 21 18 26 23 20 43 40 37 42 39 36 44 41 38 16 13 10 15 12 9 17 14 11 27 33 30 29 35 32 28 34 31 0 6 3 2 8 5 1 7 4 18 24 21 20 26 23 19 25 22 36 42 39 38 44 41 37 43 40 9 15 12 11 17 14 10 16 13 29 35 32 28 34 31 27 33 30 2 8 5 1 7 4 0 6 3 20 26 23 19 25 22 18 24 21 38 44 41 37 43 40 36 42 39 11 17 14 10 16 13 9 15 12 28 34 31 27 33 30 29 35 32 1 7 4 0 6 3 2 8 5 19 25 22 18 24 21 20 26 23 37 43 40 36 42 39 38 44 41 10 16 13 9 15 12 11 17 14 21 18 24 23 20 26 22 19 25 39 36 42 41 38 44 40 37 43 12 9 15 14 11 17 13 10 16 30 27 33 32 29 35 31 28 34 3 0 6 5 2 8 4 1 7 23 20 26 22 19 25 21 18 24 41 38 44 40 37 43 39 36 42 14 11 17 13 10 16 12 9 15 32 29 35 31 28 34 30 27 33 5 2 8 4 1 7 3 0 6 22 19 25 21 18 24 23 20 26 40 37 43 39 36 42 41 38 44 13 10 16 12 9 15 14 11 17 31 28 34 30 27 33 32 29 35 4 1 7 3 0 6 5 2 8 24 21 18 26 23 20 25 22 19 42 39 36 44 41 38 43 40 37 15 12 9 17 14 11 16 13 10 33 30 27 35 32 29 34 31 28 6 3 0 8 5 2 7 4 1 26 23 20 25 22 19 24 21 18 44 41 38 43 40 37 42 39 36 17 14 11 16 13 10 15 12 9 35 32 29 34 31 28 33 30 27 8 5 2 7 4 1 6 3 0 25 22 19 24 21 18 26 23 20 43 40 37 42 39 36 44 41 38 16 13 10 15 12 9 17 14 11 34 31 28 33 30 27 35 32 29 7 4 1 6 3 0 8 5 2 18 24 21 20 26 23 19 25 22 36 42 39 38 44 41 37 43 40 9 15 12 11 17 14 10 16 13 27 33 30 29 35 32 28 34 31 0 6 3 2 8 5 1 7 4 20 26 23 19 25 22 18 24 21 38 44 41 37 43 40 36 42 39 11 17 14 10 16 13 9 15 12 29 35 32 28 34 31 27 33 30 2 8 5 1 7 4 0 6 3 19 25 22 18 24 21 20 26 23 37 43 40 36 42 39 38 44 41 10 16 13 9 15 12 11 17 14 28 34 31 27 33 30 29 35 32 1 7 4 0 6 3 2 8 5 12 9 15 14 11 17 13 10 16 30 27 33 32 29 35 31 28 34 3 0 6 5 2 8 4 1 7 21 18 24 23 20 26 22 19 25 39 36 42 41 38 44 40 37 43 14 11 17 13 10 16 12 9 15 32 29 35 31 28 34 30 27 33 5 2 8 4 1 7 3 0 6 23 20 26 22 19 25 21 18 24 41 38 44 40 37 43 39 36 42 13 10 16 12 9 15 14 11 17 31 28 34 30 27 33 32 29 35 4 1 7 3 0 6 5 2 8 22 19 25 21 18 24 23 20 26 40 37 43 39 36 42 41 38 44 15 12 9 17 14 11 16 13 10 33 30 27 35 32 29 34 31 28 6 3 0 8 5 2 7 4 1 24 21 18 26 23 20 25 22 19 42 39 36 44 41 38 43 40 37 17 14 11 16 13 10 15 12 9 35 32 29 34 31 28 33 30 27 8 5 2 7 4 1 6 3 0 26 23 20 25 22 19 24 21 18 44 41 38 43 40 37 42 39 36 16 13 10 15 12 9 17 14 11 34 31 28 33 30 27 35 32 29 7 4 1 6 3 0 8 5 2 25 22 19 24 21 18 26 23 20 43 40 37 42 39 36 44 41 38 9 15 12 11 17 14 10 16 13 27 33 30 29 35 32 28 34 31 0 6 3 2 8 5 1 7 4 18 24 21 20 26 23 19 25 22 36 42 39 38 44 41 37 43 40 11 17 14 10 16 13 9 15 12 29 35 32 28 34 31 27 33 30 2 8 5 1 7 4 0 6 3 20 26 23 19 25 22 18 24 21 38 44 41 37 43 40 36 42 39 10 16 13 9 15 12 11 17 14 28 34 31 27 33 30 29 35 32 1 7 4 0 6 3 2 8 5 19 25 22 18 24 21 20 26 23 37 43 40 36 42 39 38 44 4138 43 40 37 42 39 36 17 14 11 16 13 10 15 12 9 34 31 28 33 30 27 35 32 29 7 4 1 6 3 0 8 5 2 25 22 19 24 21 18 26 23 20 43 40 37 42 39 36 44 41 38 16 13 10 15 12 9 17 14 11 27 33 30 29 35 32 28 34 31 0 6 3 2 8 5 1 7 4 18 24 21 20 26 23 19 25 22 36 42 39 38 44 41 37 43 40 9 15 12 11 17 14 10 16 13 29 35 32 28 34 31 27 33 30 2 8 5 1 7 4 0 6 3 20 26 23 19 25 22 18 24 21 38 44 41 37 43 40 36 42 39 11 17 14 10 16 13 9 15 12 28 34 31 27 33 30 29 35 32 1 7 4 0 6 3 2 8 5 19 25 22 18 24 21 20 26 23 37 43 40 36 42 39 38 44 41 10 16 13 9 15 12 11 17 14 21 18 24 23 20 26 22 19 25 39 36 42 41 38 44 40 37 43 12 9 15 14 11 17 13 10 16 30 27 33 32 29 35 31 28 34 3 0 6 5 2 8 4 1 7 23 20 26 22 19 25 21 18 24 41 38 44 40 37 43 39 36 42 14 11 17 13 10 16 12 9 15 32 29 35 31 28 34 30 27 33 5 2 8 4 1 7 3 0 6 22 19 25 21 18 24 23 20 26 40 37 43 39 36 42 41 38 44 13 10 16 12 9 15 14 11 17 31 28 34 30 27 33 32 29 35 4 1 7 3 0 6 5 2 8 24 21 18 26 23 20 25 22 19 42 39 36 44 41 38 43 40 37 15 12 9 17 14 11 16 13 10 33 30 27 35 32 29 34 31 28 6 3 0 8 5 2 7 4 1 26 23 20 25 22 19 24 21 18 44 41 38 43 40 37 42 39 36 17 14 11 16 13 10 15 12 9 35 32 29 34 31 28 33 30 27 8 5 2 7 4 1 6 3 0 25 22 19 24 21 18 26 23 20 43 40 37 42 39 36 44 41 38 16 13 10 15 12 9 17 14 11 34 31 28 33 30 27 35 32 29 7 4 1 6 3 0 8 5 2 18 24 21 20 26 23 19 25 22 36 42 39 38 44 41 37 43 40 9 15 12 11 17 14 10 16 13 27 33 30 29 35 32 28 34 31 0 6 3 2 8 5 1 7 4 20 26 23 19 25 22 18 24 21 38 44 41 37 43 40 36 42 39 11 17 14 10 16 13 9 15 12 29 35 32 28 34 31 27 33 30 2 8 5 1 7 4 0 6 3 19 25 22 18 24 21 20 26 23 37 43 40 36 42 39 38 44 41 10 16 13 9 15 12 11 17 14 28 34 31 27 33 30 29 35 32 1 7 4 0 6 3 2 8 5 12 9 15 14 11 17 13 10 16 30 27 33 32 29 35 31 28 34 3 0 6 5 2 8 4 1 7 21 18 24 23 20 26 22 19 25 39 36 42 41 38 44 40 37 43 14 11 17 13 10 16 12 9 15 32 29 35 31 28 34 30 27 33 5 2 8 4 1 7 3 0 6 23 20 26 22 19 25 21 18 24 41 38 44 40 37 43 39 36 42 13 10 16 12 9 15 14 11 17 31 28 34 30 27 33 32 29 35 4 1 7 3 0 6 5 2 8 22 19 25 21 18 24 23 20 26 40 37 43 39 36 42 41 38 44 15 12 9 17 14 11 16 13 10 33 30 27 35 32 29 34 31 28 6 3 0 8 5 2 7 4 1 24 21 18 26 23 20 25 22 19 42 39 36 44 41 38 43 40 37 17 14 11 16 13 10 15 12 9 35 32 29 34 31 28 33 30 27 8 5 2 7 4 1 6 3 0 26 23 20 25 22 19 24 21 18 44 41 38 43 40 37 42 39 36 16 13 10 15 12 9 17 14 11 34 31 28 33 30 27 35 32 29 7 4 1 6 3 0 8 5 2 25 22 19 24 21 18 26 23 20 43 40 37 42 39 36 44 41 38 9 15 12 11 17 14 10 16 13 27 33 30 29 35 32 28 34 31 0 6 3 2 8 5 1 7 4 18 24 21 20 26 23 19 25 22 36 42 39 38 44 41 37 43 40 11 17 14 10 16 13 9 15 12 29 35 32 28 34 31 27 33 30 2 8 5 1 7 4 0 6 3 20 26 23 19 25 22 18 24 21 38 44 41 37 43 40 36 42 39 10 16 13 9 15 12 11 17 14 28 34 31 27 33 30 29 35 32 1 7 4 0 6 3 2 8 5 19 25 22 18 24 21 20 26 23 37 43 40 36 42 39 38 44 41 [/code] ПроверÑÑŽ ÑвойÑтва ДЛК Ñтой ортогональной пары [code]Order? 45 Enter the name of the squares file: inp .. writing type information to file inpTypeDetail_11.txt Counts ------ 2 diagonal Latin 2 associative 2 weakly pandiagonal 2 ultramagic 1 orthogonal pair 2 self-orthogonal[/code] Ð’ÑÑ‘ верно. И не могло быть иначе :) Конечно, из Ñтой ортогональной пары ДЛК можно поÑтроить идеальный магичеÑкий квадрат 45-го порÑдка методом латинÑких квадратов. Ðу, его можно поÑтроить и из готовых идеальных магичеÑких квадратов 5-го и 9-го порÑдков методом ÑоÑтавных квадратов. Ðаверное, Ñ Ñ‚Ð°ÐºÐ¾Ð¹ магичеÑкий квадрат в то Ð²Ñ€ÐµÐ¼Ñ Ð¿Ð¾Ñтроила. Однако теперь можно взÑÑ‚ÑŒ Ð´Ð»Ñ Ð¿Ð¾ÑÑ‚Ñ€Ð¾ÐµÐ½Ð¸Ñ Ð½Ð¾Ð²Ñ‹Ð¹ идеальный магичеÑкий ДЛК 9-го порÑдка (поÑтроенный здеÑÑŒ), получим новый идеальный магичеÑкий ДЛК 45-го порÑдка. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Выше было показано поÑтроение идеального ДЛК 25-го порÑдка. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾ÐºÐ°Ð¶Ñƒ поÑтроение ортогональной пары идеальных ДЛК 25-го порÑдка. Ð”Ð»Ñ Ð¿Ð¾ÑÑ‚Ñ€Ð¾ÐµÐ½Ð¸Ñ Ð²Ð¾Ð·ÑŒÐ¼Ñƒ Ñледующие ортогональные пары идеальных ДЛК 5-го порÑдка: Ð¿ÐµÑ€Ð²Ð°Ñ ( как SODLS) 0 4 3 2 1 2 1 0 4 3 4 3 2 1 0 1 0 4 3 2 3 2 1 0 4 0 2 4 1 3 4 1 3 0 2 3 0 2 4 1 2 4 1 3 0 1 3 0 2 4 Ð²Ñ‚Ð¾Ñ€Ð°Ñ ( как DSODLS) 4 2 0 3 1 0 3 1 4 2 1 4 2 0 3 2 0 3 1 4 3 1 4 2 0 0 4 3 2 1 2 1 0 4 3 4 3 2 1 0 1 0 4 3 2 3 2 1 0 4 Ð’Ñтречайте - Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° идеальных ДЛК 25-го порÑдка, поÑÑ‚Ñ€Ð¾ÐµÐ½Ð½Ð°Ñ Ð¼ÐµÑ‚Ð¾Ð´Ð¾Ð¼ ÑоÑтавных квадратов 0 4 3 2 1 10 14 13 12 11 20 24 23 22 21 5 9 8 7 6 15 19 18 17 16 2 1 0 4 3 12 11 10 14 13 22 21 20 24 23 7 6 5 9 8 17 16 15 19 18 4 3 2 1 0 14 13 12 11 10 24 23 22 21 20 9 8 7 6 5 19 18 17 16 15 1 0 4 3 2 11 10 14 13 12 21 20 24 23 22 6 5 9 8 7 16 15 19 18 17 3 2 1 0 4 13 12 11 10 14 23 22 21 20 24 8 7 6 5 9 18 17 16 15 19 20 24 23 22 21 5 9 8 7 6 15 19 18 17 16 0 4 3 2 1 10 14 13 12 11 22 21 20 24 23 7 6 5 9 8 17 16 15 19 18 2 1 0 4 3 12 11 10 14 13 24 23 22 21 20 9 8 7 6 5 19 18 17 16 15 4 3 2 1 0 14 13 12 11 10 21 20 24 23 22 6 5 9 8 7 16 15 19 18 17 1 0 4 3 2 11 10 14 13 12 23 22 21 20 24 8 7 6 5 9 18 17 16 15 19 3 2 1 0 4 13 12 11 10 14 15 19 18 17 16 0 4 3 2 1 10 14 13 12 11 20 24 23 22 21 5 9 8 7 6 17 16 15 19 18 2 1 0 4 3 12 11 10 14 13 22 21 20 24 23 7 6 5 9 8 19 18 17 16 15 4 3 2 1 0 14 13 12 11 10 24 23 22 21 20 9 8 7 6 5 16 15 19 18 17 1 0 4 3 2 11 10 14 13 12 21 20 24 23 22 6 5 9 8 7 18 17 16 15 19 3 2 1 0 4 13 12 11 10 14 23 22 21 20 24 8 7 6 5 9 10 14 13 12 11 20 24 23 22 21 5 9 8 7 6 15 19 18 17 16 0 4 3 2 1 12 11 10 14 13 22 21 20 24 23 7 6 5 9 8 17 16 15 19 18 2 1 0 4 3 14 13 12 11 10 24 23 22 21 20 9 8 7 6 5 19 18 17 16 15 4 3 2 1 0 11 10 14 13 12 21 20 24 23 22 6 5 9 8 7 16 15 19 18 17 1 0 4 3 2 13 12 11 10 14 23 22 21 20 24 8 7 6 5 9 18 17 16 15 19 3 2 1 0 4 5 9 8 7 6 15 19 18 17 16 0 4 3 2 1 10 14 13 12 11 20 24 23 22 21 7 6 5 9 8 17 16 15 19 18 2 1 0 4 3 12 11 10 14 13 22 21 20 24 23 9 8 7 6 5 19 18 17 16 15 4 3 2 1 0 14 13 12 11 10 24 23 22 21 20 6 5 9 8 7 16 15 19 18 17 1 0 4 3 2 11 10 14 13 12 21 20 24 23 22 8 7 6 5 9 18 17 16 15 19 3 2 1 0 4 13 12 11 10 14 23 22 21 20 24 4 2 0 3 1 24 22 20 23 21 19 17 15 18 16 14 12 10 13 11 9 7 5 8 6 0 3 1 4 2 20 23 21 24 22 15 18 16 19 17 10 13 11 14 12 5 8 6 9 7 1 4 2 0 3 21 24 22 20 23 16 19 17 15 18 11 14 12 10 13 6 9 7 5 8 2 0 3 1 4 22 20 23 21 24 17 15 18 16 19 12 10 13 11 14 7 5 8 6 9 3 1 4 2 0 23 21 24 22 20 18 16 19 17 15 13 11 14 12 10 8 6 9 7 5 14 12 10 13 11 9 7 5 8 6 4 2 0 3 1 24 22 20 23 21 19 17 15 18 16 10 13 11 14 12 5 8 6 9 7 0 3 1 4 2 20 23 21 24 22 15 18 16 19 17 11 14 12 10 13 6 9 7 5 8 1 4 2 0 3 21 24 22 20 23 16 19 17 15 18 12 10 13 11 14 7 5 8 6 9 2 0 3 1 4 22 20 23 21 24 17 15 18 16 19 13 11 14 12 10 8 6 9 7 5 3 1 4 2 0 23 21 24 22 20 18 16 19 17 15 24 22 20 23 21 19 17 15 18 16 14 12 10 13 11 9 7 5 8 6 4 2 0 3 1 20 23 21 24 22 15 18 16 19 17 10 13 11 14 12 5 8 6 9 7 0 3 1 4 2 21 24 22 20 23 16 19 17 15 18 11 14 12 10 13 6 9 7 5 8 1 4 2 0 3 22 20 23 21 24 17 15 18 16 19 12 10 13 11 14 7 5 8 6 9 2 0 3 1 4 23 21 24 22 20 18 16 19 17 15 13 11 14 12 10 8 6 9 7 5 3 1 4 2 0 9 7 5 8 6 4 2 0 3 1 24 22 20 23 21 19 17 15 18 16 14 12 10 13 11 5 8 6 9 7 0 3 1 4 2 20 23 21 24 22 15 18 16 19 17 10 13 11 14 12 6 9 7 5 8 1 4 2 0 3 21 24 22 20 23 16 19 17 15 18 11 14 12 10 13 7 5 8 6 9 2 0 3 1 4 22 20 23 21 24 17 15 18 16 19 12 10 13 11 14 8 6 9 7 5 3 1 4 2 0 23 21 24 22 20 18 16 19 17 15 13 11 14 12 10 19 17 15 18 16 14 12 10 13 11 9 7 5 8 6 4 2 0 3 1 24 22 20 23 21 15 18 16 19 17 10 13 11 14 12 5 8 6 9 7 0 3 1 4 2 20 23 21 24 22 16 19 17 15 18 11 14 12 10 13 6 9 7 5 8 1 4 2 0 3 21 24 22 20 23 17 15 18 16 19 12 10 13 11 14 7 5 8 6 9 2 0 3 1 4 22 20 23 21 24 18 16 19 17 15 13 11 14 12 10 8 6 9 7 5 3 1 4 2 0 23 21 24 22 20 ПроверÑÑŽ ÑвойÑтва утилитой Harry White Order? 25
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_10.txt
Counts
------
2 diagonal Latin
2 associative
2 pandiagonal
2 ultramagic
1 natural \diagonal
1 orthogonal pair
2 self-orthogonalÐ’ÑÑ‘ верно. И не могло быть иначе :) ИнтереÑно: ÑÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ñмотрю, еÑÑ‚ÑŒ ли в полной MOLS порÑдка 25 идеальные ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ÐŸÐ¾Ð»Ð½Ð°Ñ ÑиÑтема MOLS 25-го порÑдка показана тут https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117&postid=1224 Беру 22 ДЛК из Ñтой ÑиÑтемы MOLS и проверÑÑŽ их утилитой Harry White Order? 25
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_11.txt
Counts
------
22 diagonal Latin
2 pandiagonal
12 weakly pandiagonal
22 center symmetric
22 nfr
21 orthogonal pair
22 self-orthogonal
ИмеютÑÑ 2 пандиагональных ДЛК, 12 Ñлабо пандиагональных ДЛК и 22 центрально-Ñимметричных ДЛК. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ð¿Ñ€Ð¾Ð±ÑƒÑŽ преобразовать вÑе ДЛК в СРДЛК. Преобразовала и проверила ÑвойÑтва полученных СРДЛК Order? 25
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_5.txt
Counts
------
22 diagonal Latin
22 associative
2 pandiagonal
2 ultramagic
22 natural \diagonal
21 orthogonal pair
22 self-orthogonalЗамечательно! Два идеальных ДЛК получены, к тому же они SODLS, а также DSODLS. Кроме того, они ортогональны! Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ñ Ð¸Ñ… извлеку на Ñвет Божий :) отличные квадратики Ð½ÐµÐ»ÑŒÐ·Ñ Ð½Ðµ показать. PS. Обратите внимание: поÑле Ð¿Ñ€ÐµÐ¾Ð±Ñ€Ð°Ð·Ð¾Ð²Ð°Ð½Ð¸Ñ Ð”Ð›Ðš в СРДЛК иÑчезло ÑвойÑтво Ñлабой пандиагональноÑти. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’Ñтречайте - Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° идеальных ДЛК 25-го порÑдка из полной ÑиÑтемы MOLS 0 2 4 1 3 10 12 14 11 13 20 22 24 21 23 5 7 9 6 8 15 17 19 16 18 4 1 3 0 2 14 11 13 10 12 24 21 23 20 22 9 6 8 5 7 19 16 18 15 17 3 0 2 4 1 13 10 12 14 11 23 20 22 24 21 8 5 7 9 6 18 15 17 19 16 2 4 1 3 0 12 14 11 13 10 22 24 21 23 20 7 9 6 8 5 17 19 16 18 15 1 3 0 2 4 11 13 10 12 14 21 23 20 22 24 6 8 5 7 9 16 18 15 17 19 20 22 24 21 23 5 7 9 6 8 15 17 19 16 18 0 2 4 1 3 10 12 14 11 13 24 21 23 20 22 9 6 8 5 7 19 16 18 15 17 4 1 3 0 2 14 11 13 10 12 23 20 22 24 21 8 5 7 9 6 18 15 17 19 16 3 0 2 4 1 13 10 12 14 11 22 24 21 23 20 7 9 6 8 5 17 19 16 18 15 2 4 1 3 0 12 14 11 13 10 21 23 20 22 24 6 8 5 7 9 16 18 15 17 19 1 3 0 2 4 11 13 10 12 14 15 17 19 16 18 0 2 4 1 3 10 12 14 11 13 20 22 24 21 23 5 7 9 6 8 19 16 18 15 17 4 1 3 0 2 14 11 13 10 12 24 21 23 20 22 9 6 8 5 7 18 15 17 19 16 3 0 2 4 1 13 10 12 14 11 23 20 22 24 21 8 5 7 9 6 17 19 16 18 15 2 4 1 3 0 12 14 11 13 10 22 24 21 23 20 7 9 6 8 5 16 18 15 17 19 1 3 0 2 4 11 13 10 12 14 21 23 20 22 24 6 8 5 7 9 10 12 14 11 13 20 22 24 21 23 5 7 9 6 8 15 17 19 16 18 0 2 4 1 3 14 11 13 10 12 24 21 23 20 22 9 6 8 5 7 19 16 18 15 17 4 1 3 0 2 13 10 12 14 11 23 20 22 24 21 8 5 7 9 6 18 15 17 19 16 3 0 2 4 1 12 14 11 13 10 22 24 21 23 20 7 9 6 8 5 17 19 16 18 15 2 4 1 3 0 11 13 10 12 14 21 23 20 22 24 6 8 5 7 9 16 18 15 17 19 1 3 0 2 4 5 7 9 6 8 15 17 19 16 18 0 2 4 1 3 10 12 14 11 13 20 22 24 21 23 9 6 8 5 7 19 16 18 15 17 4 1 3 0 2 14 11 13 10 12 24 21 23 20 22 8 5 7 9 6 18 15 17 19 16 3 0 2 4 1 13 10 12 14 11 23 20 22 24 21 7 9 6 8 5 17 19 16 18 15 2 4 1 3 0 12 14 11 13 10 22 24 21 23 20 6 8 5 7 9 16 18 15 17 19 1 3 0 2 4 11 13 10 12 14 21 23 20 22 24 0 4 3 2 1 20 24 23 22 21 15 19 18 17 16 10 14 13 12 11 5 9 8 7 6 2 1 0 4 3 22 21 20 24 23 17 16 15 19 18 12 11 10 14 13 7 6 5 9 8 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 1 0 4 3 2 21 20 24 23 22 16 15 19 18 17 11 10 14 13 12 6 5 9 8 7 3 2 1 0 4 23 22 21 20 24 18 17 16 15 19 13 12 11 10 14 8 7 6 5 9 10 14 13 12 11 5 9 8 7 6 0 4 3 2 1 20 24 23 22 21 15 19 18 17 16 12 11 10 14 13 7 6 5 9 8 2 1 0 4 3 22 21 20 24 23 17 16 15 19 18 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 11 10 14 13 12 6 5 9 8 7 1 0 4 3 2 21 20 24 23 22 16 15 19 18 17 13 12 11 10 14 8 7 6 5 9 3 2 1 0 4 23 22 21 20 24 18 17 16 15 19 20 24 23 22 21 15 19 18 17 16 10 14 13 12 11 5 9 8 7 6 0 4 3 2 1 22 21 20 24 23 17 16 15 19 18 12 11 10 14 13 7 6 5 9 8 2 1 0 4 3 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 21 20 24 23 22 16 15 19 18 17 11 10 14 13 12 6 5 9 8 7 1 0 4 3 2 23 22 21 20 24 18 17 16 15 19 13 12 11 10 14 8 7 6 5 9 3 2 1 0 4 5 9 8 7 6 0 4 3 2 1 20 24 23 22 21 15 19 18 17 16 10 14 13 12 11 7 6 5 9 8 2 1 0 4 3 22 21 20 24 23 17 16 15 19 18 12 11 10 14 13 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 6 5 9 8 7 1 0 4 3 2 21 20 24 23 22 16 15 19 18 17 11 10 14 13 12 8 7 6 5 9 3 2 1 0 4 23 22 21 20 24 18 17 16 15 19 13 12 11 10 14 15 19 18 17 16 10 14 13 12 11 5 9 8 7 6 0 4 3 2 1 20 24 23 22 21 17 16 15 19 18 12 11 10 14 13 7 6 5 9 8 2 1 0 4 3 22 21 20 24 23 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 16 15 19 18 17 11 10 14 13 12 6 5 9 8 7 1 0 4 3 2 21 20 24 23 22 18 17 16 15 19 13 12 11 10 14 8 7 6 5 9 3 2 1 0 4 23 22 21 20 24 Проверила ÑвойÑтва Ñтих ОДЛК Order? 25
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_6.txt
Counts
------
2 diagonal Latin
2 associative
2 pandiagonal
2 ultramagic
2 natural \diagonal
1 orthogonal pair
2 self-orthogonalРне кажетÑÑ Ð»Ð¸ вам, что Ñти ДЛК очень похожи на ДЛК, поÑтроенные методом ÑоÑтавных квадратов? Мне очень Ñильно кажетÑÑ :) Сравните Ñ Ð¿Ñ€ÐµÐ´Ñтавленной чуть выше ортогональной парой идеальных ДЛК, поÑтроенной методом ÑоÑтавных квдаратов. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ртеперь поÑмотрим на идеальный ДЛК 35-го порÑдка поÑтроенный в Ñтартовом поÑте. Он один. ПоÑтрою ему ортогональный идеальный Ñоквадрат. Ð”Ð»Ñ Ð¿Ð¾ÑÑ‚Ñ€Ð¾ÐµÐ½Ð¸Ñ Ð²Ð¾Ð·ÑŒÐ¼Ñƒ ортогональную пару идеальных ДЛК 7-го порÑдка, показанную на иллюÑтрации в Ñтартовом поÑте, и Ñледующую ортогональную пару идеальных ДЛК 5-го порÑдка 0 4 3 2 1 2 1 0 4 3 4 3 2 1 0 1 0 4 3 2 3 2 1 0 4 0 2 4 1 3 4 1 3 0 2 3 0 2 4 1 2 4 1 3 0 1 3 0 2 4 Ð”Ð»Ñ Ð¿Ð¾ÑÑ‚Ñ€Ð¾ÐµÐ½Ð¸Ñ Ð¾Ñ€Ñ‚Ð³Ð¾Ð½Ð°Ð»ÑŒÐºÐ¸ к поÑтроенному ДЛК 35-го порÑдка берём вторые ДЛК в Ñтих ортогональных парах идеальных ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’Ñтречайте - Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° идеальных ДЛК 35-го порÑдка, поÑÑ‚Ñ€Ð¾ÐµÐ½Ð½Ð°Ñ Ð¼ÐµÑ‚Ð¾Ð´Ð¾Ð¼ ÑоÑтавных квадратов 0 6 5 4 3 2 1 28 34 33 32 31 30 29 21 27 26 25 24 23 22 14 20 19 18 17 16 15 7 13 12 11 10 9 8 2 1 0 6 5 4 3 30 29 28 34 33 32 31 23 22 21 27 26 25 24 16 15 14 20 19 18 17 9 8 7 13 12 11 10 4 3 2 1 0 6 5 32 31 30 29 28 34 33 25 24 23 22 21 27 26 18 17 16 15 14 20 19 11 10 9 8 7 13 12 6 5 4 3 2 1 0 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 1 0 6 5 4 3 2 29 28 34 33 32 31 30 22 21 27 26 25 24 23 15 14 20 19 18 17 16 8 7 13 12 11 10 9 3 2 1 0 6 5 4 31 30 29 28 34 33 32 24 23 22 21 27 26 25 17 16 15 14 20 19 18 10 9 8 7 13 12 11 5 4 3 2 1 0 6 33 32 31 30 29 28 34 26 25 24 23 22 21 27 19 18 17 16 15 14 20 12 11 10 9 8 7 13 14 20 19 18 17 16 15 7 13 12 11 10 9 8 0 6 5 4 3 2 1 28 34 33 32 31 30 29 21 27 26 25 24 23 22 16 15 14 20 19 18 17 9 8 7 13 12 11 10 2 1 0 6 5 4 3 30 29 28 34 33 32 31 23 22 21 27 26 25 24 18 17 16 15 14 20 19 11 10 9 8 7 13 12 4 3 2 1 0 6 5 32 31 30 29 28 34 33 25 24 23 22 21 27 26 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 34 33 32 31 30 29 28 27 26 25 24 23 22 21 15 14 20 19 18 17 16 8 7 13 12 11 10 9 1 0 6 5 4 3 2 29 28 34 33 32 31 30 22 21 27 26 25 24 23 17 16 15 14 20 19 18 10 9 8 7 13 12 11 3 2 1 0 6 5 4 31 30 29 28 34 33 32 24 23 22 21 27 26 25 19 18 17 16 15 14 20 12 11 10 9 8 7 13 5 4 3 2 1 0 6 33 32 31 30 29 28 34 26 25 24 23 22 21 27 28 34 33 32 31 30 29 21 27 26 25 24 23 22 14 20 19 18 17 16 15 7 13 12 11 10 9 8 0 6 5 4 3 2 1 30 29 28 34 33 32 31 23 22 21 27 26 25 24 16 15 14 20 19 18 17 9 8 7 13 12 11 10 2 1 0 6 5 4 3 32 31 30 29 28 34 33 25 24 23 22 21 27 26 18 17 16 15 14 20 19 11 10 9 8 7 13 12 4 3 2 1 0 6 5 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 29 28 34 33 32 31 30 22 21 27 26 25 24 23 15 14 20 19 18 17 16 8 7 13 12 11 10 9 1 0 6 5 4 3 2 31 30 29 28 34 33 32 24 23 22 21 27 26 25 17 16 15 14 20 19 18 10 9 8 7 13 12 11 3 2 1 0 6 5 4 33 32 31 30 29 28 34 26 25 24 23 22 21 27 19 18 17 16 15 14 20 12 11 10 9 8 7 13 5 4 3 2 1 0 6 7 13 12 11 10 9 8 0 6 5 4 3 2 1 28 34 33 32 31 30 29 21 27 26 25 24 23 22 14 20 19 18 17 16 15 9 8 7 13 12 11 10 2 1 0 6 5 4 3 30 29 28 34 33 32 31 23 22 21 27 26 25 24 16 15 14 20 19 18 17 11 10 9 8 7 13 12 4 3 2 1 0 6 5 32 31 30 29 28 34 33 25 24 23 22 21 27 26 18 17 16 15 14 20 19 13 12 11 10 9 8 7 6 5 4 3 2 1 0 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 8 7 13 12 11 10 9 1 0 6 5 4 3 2 29 28 34 33 32 31 30 22 21 27 26 25 24 23 15 14 20 19 18 17 16 10 9 8 7 13 12 11 3 2 1 0 6 5 4 31 30 29 28 34 33 32 24 23 22 21 27 26 25 17 16 15 14 20 19 18 12 11 10 9 8 7 13 5 4 3 2 1 0 6 33 32 31 30 29 28 34 26 25 24 23 22 21 27 19 18 17 16 15 14 20 21 27 26 25 24 23 22 14 20 19 18 17 16 15 7 13 12 11 10 9 8 0 6 5 4 3 2 1 28 34 33 32 31 30 29 23 22 21 27 26 25 24 16 15 14 20 19 18 17 9 8 7 13 12 11 10 2 1 0 6 5 4 3 30 29 28 34 33 32 31 25 24 23 22 21 27 26 18 17 16 15 14 20 19 11 10 9 8 7 13 12 4 3 2 1 0 6 5 32 31 30 29 28 34 33 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 34 33 32 31 30 29 28 22 21 27 26 25 24 23 15 14 20 19 18 17 16 8 7 13 12 11 10 9 1 0 6 5 4 3 2 29 28 34 33 32 31 30 24 23 22 21 27 26 25 17 16 15 14 20 19 18 10 9 8 7 13 12 11 3 2 1 0 6 5 4 31 30 29 28 34 33 32 26 25 24 23 22 21 27 19 18 17 16 15 14 20 12 11 10 9 8 7 13 5 4 3 2 1 0 6 33 32 31 30 29 28 34 5 4 3 2 1 0 6 19 18 17 16 15 14 20 33 32 31 30 29 28 34 12 11 10 9 8 7 13 26 25 24 23 22 21 27 3 2 1 0 6 5 4 17 16 15 14 20 19 18 31 30 29 28 34 33 32 10 9 8 7 13 12 11 24 23 22 21 27 26 25 1 0 6 5 4 3 2 15 14 20 19 18 17 16 29 28 34 33 32 31 30 8 7 13 12 11 10 9 22 21 27 26 25 24 23 6 5 4 3 2 1 0 20 19 18 17 16 15 14 34 33 32 31 30 29 28 13 12 11 10 9 8 7 27 26 25 24 23 22 21 4 3 2 1 0 6 5 18 17 16 15 14 20 19 32 31 30 29 28 34 33 11 10 9 8 7 13 12 25 24 23 22 21 27 26 2 1 0 6 5 4 3 16 15 14 20 19 18 17 30 29 28 34 33 32 31 9 8 7 13 12 11 10 23 22 21 27 26 25 24 0 6 5 4 3 2 1 14 20 19 18 17 16 15 28 34 33 32 31 30 29 7 13 12 11 10 9 8 21 27 26 25 24 23 22 33 32 31 30 29 28 34 12 11 10 9 8 7 13 26 25 24 23 22 21 27 5 4 3 2 1 0 6 19 18 17 16 15 14 20 31 30 29 28 34 33 32 10 9 8 7 13 12 11 24 23 22 21 27 26 25 3 2 1 0 6 5 4 17 16 15 14 20 19 18 29 28 34 33 32 31 30 8 7 13 12 11 10 9 22 21 27 26 25 24 23 1 0 6 5 4 3 2 15 14 20 19 18 17 16 34 33 32 31 30 29 28 13 12 11 10 9 8 7 27 26 25 24 23 22 21 6 5 4 3 2 1 0 20 19 18 17 16 15 14 32 31 30 29 28 34 33 11 10 9 8 7 13 12 25 24 23 22 21 27 26 4 3 2 1 0 6 5 18 17 16 15 14 20 19 30 29 28 34 33 32 31 9 8 7 13 12 11 10 23 22 21 27 26 25 24 2 1 0 6 5 4 3 16 15 14 20 19 18 17 28 34 33 32 31 30 29 7 13 12 11 10 9 8 21 27 26 25 24 23 22 0 6 5 4 3 2 1 14 20 19 18 17 16 15 26 25 24 23 22 21 27 5 4 3 2 1 0 6 19 18 17 16 15 14 20 33 32 31 30 29 28 34 12 11 10 9 8 7 13 24 23 22 21 27 26 25 3 2 1 0 6 5 4 17 16 15 14 20 19 18 31 30 29 28 34 33 32 10 9 8 7 13 12 11 22 21 27 26 25 24 23 1 0 6 5 4 3 2 15 14 20 19 18 17 16 29 28 34 33 32 31 30 8 7 13 12 11 10 9 27 26 25 24 23 22 21 6 5 4 3 2 1 0 20 19 18 17 16 15 14 34 33 32 31 30 29 28 13 12 11 10 9 8 7 25 24 23 22 21 27 26 4 3 2 1 0 6 5 18 17 16 15 14 20 19 32 31 30 29 28 34 33 11 10 9 8 7 13 12 23 22 21 27 26 25 24 2 1 0 6 5 4 3 16 15 14 20 19 18 17 30 29 28 34 33 32 31 9 8 7 13 12 11 10 21 27 26 25 24 23 22 0 6 5 4 3 2 1 14 20 19 18 17 16 15 28 34 33 32 31 30 29 7 13 12 11 10 9 8 19 18 17 16 15 14 20 33 32 31 30 29 28 34 12 11 10 9 8 7 13 26 25 24 23 22 21 27 5 4 3 2 1 0 6 17 16 15 14 20 19 18 31 30 29 28 34 33 32 10 9 8 7 13 12 11 24 23 22 21 27 26 25 3 2 1 0 6 5 4 15 14 20 19 18 17 16 29 28 34 33 32 31 30 8 7 13 12 11 10 9 22 21 27 26 25 24 23 1 0 6 5 4 3 2 20 19 18 17 16 15 14 34 33 32 31 30 29 28 13 12 11 10 9 8 7 27 26 25 24 23 22 21 6 5 4 3 2 1 0 18 17 16 15 14 20 19 32 31 30 29 28 34 33 11 10 9 8 7 13 12 25 24 23 22 21 27 26 4 3 2 1 0 6 5 16 15 14 20 19 18 17 30 29 28 34 33 32 31 9 8 7 13 12 11 10 23 22 21 27 26 25 24 2 1 0 6 5 4 3 14 20 19 18 17 16 15 28 34 33 32 31 30 29 7 13 12 11 10 9 8 21 27 26 25 24 23 22 0 6 5 4 3 2 1 12 11 10 9 8 7 13 26 25 24 23 22 21 27 5 4 3 2 1 0 6 19 18 17 16 15 14 20 33 32 31 30 29 28 34 10 9 8 7 13 12 11 24 23 22 21 27 26 25 3 2 1 0 6 5 4 17 16 15 14 20 19 18 31 30 29 28 34 33 32 8 7 13 12 11 10 9 22 21 27 26 25 24 23 1 0 6 5 4 3 2 15 14 20 19 18 17 16 29 28 34 33 32 31 30 13 12 11 10 9 8 7 27 26 25 24 23 22 21 6 5 4 3 2 1 0 20 19 18 17 16 15 14 34 33 32 31 30 29 28 11 10 9 8 7 13 12 25 24 23 22 21 27 26 4 3 2 1 0 6 5 18 17 16 15 14 20 19 32 31 30 29 28 34 33 9 8 7 13 12 11 10 23 22 21 27 26 25 24 2 1 0 6 5 4 3 16 15 14 20 19 18 17 30 29 28 34 33 32 31 7 13 12 11 10 9 8 21 27 26 25 24 23 22 0 6 5 4 3 2 1 14 20 19 18 17 16 15 28 34 33 32 31 30 29 Смотрим ÑвойÑтва Ñтих ОДЛК Order? 35
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_7.txt
Counts
------
2 diagonal Latin
2 associative
2 pandiagonal
2 ultramagic
1 natural \diagonal
1 orthogonal pair
2 self-orthogonalÐ’ÑÑ‘ верно. И не могло быть иначе :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðапомню: Ð´Ð»Ñ Ð¿Ð¾ÑÑ‚Ñ€Ð¾ÐµÐ½Ð¸Ñ Ð”Ð›Ðš методом ÑоÑтавных квадратов Ñ Ð¿Ð¾Ð»ÑŒÐ·ÑƒÑŽÑÑŒ программой Harry White Composite. Ð’Ñ‹ можете найти Ñту программу на Ñайте Harry White http://budshaw.ca/#top Ртакже вы можете найти на Ñтом Ñайте много других полезных программ. Ðекоторые из них Harry White напиÑал по моей проÑьбе. Раньше Ñ Ð²Ñ‹Ð¿Ð¾Ð»Ð½Ñла поÑтроение методом ÑоÑтавных квдаратов вручную; конечно, Ñто не так быÑтро, как программой. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вчера веÑÑŒ день иÑкала ортогональную пару идеальных ДЛК 8-го порÑдка и... не нашла! Очень удивлена. Одиночных идеальных ДЛК нашла много, но ортогональную пару идеальных ДЛК они не дают, Ñ…Ð¾Ñ‚Ñ Ñƒ них еÑÑ‚ÑŒ ортогональные диагональные Ñоквадраты, но они не идеальные. ИÑпользовала метод переÑтановки Ñтрок и Ñтолбцов в извеÑтных идеальных ДЛК. Ðичего не получилоÑÑŒ. Цитата ПроÑматривала копии тем Ñ Ñ„Ð¾Ñ€ÑƒÐ¼Ð° ОДЛК, наткнулаÑÑŒ на интереÑный пример. ЗдеÑÑŒ мы видим ортогональные пары Ñлабо пандиагональных и центрально-Ñимметричных ДЛК 8-го порÑдка. Проверила вторую ортогональную пару, ДЛК тоже Ñлабо пандиагональные и центрально-Ñимметричные. Где же иÑкать ортогональную пару идеальных ДЛК 8-го порÑдка? СущеÑтвует ли она??? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вот пример покажу. ВзÑла один из идеальных ДЛК 8-го порÑдка, найденных программой Harry White, и переÑтавила в нём Ñтроки и Ñтолбцы, найдено 10240 различных ДЛК (не ÑущеÑтвенно различных! на изоморфноÑÑ‚ÑŒ не проверÑла ДЛК), в том чиÑле 32 идеальных ДЛК. Order? 8
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
10240 diagonal Latin
512 associative
448 weakly pandiagonal
32 ultramagic
6144 axial symmetric
2048 double axial symmetric
2560 center symmetric
2 nfc
2 natural \diagonal
46 orthogonal pairПроверила вÑе Ñти идеальные ДЛК на ОДЛК, ни одной ортогональной пары, ÑоÑтоÑщей из идеальных ДЛК, не нашла. ПоÑмотрите: 512 аÑÑоциативных ДЛК, 448 Ñлабо пандиагональных ДЛК, а одновременно аÑÑоциативных и Ñлабо пандиагональных (ultramagic) вÑего 32. И такие ÑкÑперименты выполнила Ð´Ð»Ñ 4-Ñ… показанных выше идеальных ДЛК 8-го порÑдка. Полный облом! Ðет ортогональной пары идеальных ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Покажу найденные мной в ÑкÑперименте 32 идеальных ДЛК 8-го порÑдка 0 2 5 7 1 3 4 6 2 1 6 5 3 0 7 4 7 5 2 0 6 4 3 1 4 7 0 3 5 6 1 2 5 6 1 2 4 7 0 3 6 4 3 1 7 5 2 0 3 0 7 4 2 1 6 5 1 3 4 6 0 2 5 7 0 2 5 7 1 3 4 6 7 5 2 0 6 4 3 1 2 1 6 5 3 0 7 4 4 7 0 3 5 6 1 2 5 6 1 2 4 7 0 3 3 0 7 4 2 1 6 5 6 4 3 1 7 5 2 0 1 3 4 6 0 2 5 7 0 5 2 7 1 4 3 6 5 1 6 2 4 0 7 3 6 3 4 1 7 2 5 0 2 6 1 5 3 7 0 4 3 7 0 4 2 6 1 5 7 2 5 0 6 3 4 1 4 0 7 3 5 1 6 2 1 4 3 6 0 5 2 7 0 5 2 7 1 4 3 6 6 3 4 1 7 2 5 0 5 1 6 2 4 0 7 3 2 6 1 5 3 7 0 4 3 7 0 4 2 6 1 5 4 0 7 3 5 1 6 2 7 2 5 0 6 3 4 1 1 4 3 6 0 5 2 7 1 3 4 6 0 2 5 7 3 0 7 4 2 1 6 5 6 4 3 1 7 5 2 0 5 6 1 2 4 7 0 3 4 7 0 3 5 6 1 2 7 5 2 0 6 4 3 1 2 1 6 5 3 0 7 4 0 2 5 7 1 3 4 6 1 3 4 6 0 2 5 7 6 4 3 1 7 5 2 0 3 0 7 4 2 1 6 5 5 6 1 2 4 7 0 3 4 7 0 3 5 6 1 2 2 1 6 5 3 0 7 4 7 5 2 0 6 4 3 1 0 2 5 7 1 3 4 6 1 4 3 6 0 5 2 7 4 0 7 3 5 1 6 2 7 2 5 0 6 3 4 1 3 7 0 4 2 6 1 5 2 6 1 5 3 7 0 4 6 3 4 1 7 2 5 0 5 1 6 2 4 0 7 3 0 5 2 7 1 4 3 6 1 4 3 6 0 5 2 7 7 2 5 0 6 3 4 1 4 0 7 3 5 1 6 2 3 7 0 4 2 6 1 5 2 6 1 5 3 7 0 4 5 1 6 2 4 0 7 3 6 3 4 1 7 2 5 0 0 5 2 7 1 4 3 6 2 1 6 5 3 0 7 4 1 3 4 6 0 2 5 7 4 7 0 3 5 6 1 2 6 4 3 1 7 5 2 0 7 5 2 0 6 4 3 1 5 6 1 2 4 7 0 3 0 2 5 7 1 3 4 6 3 0 7 4 2 1 6 5 2 1 6 5 3 0 7 4 4 7 0 3 5 6 1 2 1 3 4 6 0 2 5 7 6 4 3 1 7 5 2 0 7 5 2 0 6 4 3 1 0 2 5 7 1 3 4 6 5 6 1 2 4 7 0 3 3 0 7 4 2 1 6 5 2 6 1 5 3 7 0 4 5 1 6 2 4 0 7 3 6 3 4 1 7 2 5 0 0 5 2 7 1 4 3 6 1 4 3 6 0 5 2 7 7 2 5 0 6 3 4 1 4 0 7 3 5 1 6 2 3 7 0 4 2 6 1 5 2 6 1 5 3 7 0 4 6 3 4 1 7 2 5 0 5 1 6 2 4 0 7 3 0 5 2 7 1 4 3 6 1 4 3 6 0 5 2 7 4 0 7 3 5 1 6 2 7 2 5 0 6 3 4 1 3 7 0 4 2 6 1 5 3 0 7 4 2 1 6 5 0 2 5 7 1 3 4 6 5 6 1 2 4 7 0 3 7 5 2 0 6 4 3 1 6 4 3 1 7 5 2 0 4 7 0 3 5 6 1 2 1 3 4 6 0 2 5 7 2 1 6 5 3 0 7 4 3 0 7 4 2 1 6 5 5 6 1 2 4 7 0 3 0 2 5 7 1 3 4 6 7 5 2 0 6 4 3 1 6 4 3 1 7 5 2 0 1 3 4 6 0 2 5 7 4 7 0 3 5 6 1 2 2 1 6 5 3 0 7 4 3 7 0 4 2 6 1 5 4 0 7 3 5 1 6 2 7 2 5 0 6 3 4 1 1 4 3 6 0 5 2 7 0 5 2 7 1 4 3 6 6 3 4 1 7 2 5 0 5 1 6 2 4 0 7 3 2 6 1 5 3 7 0 4 3 7 0 4 2 6 1 5 7 2 5 0 6 3 4 1 4 0 7 3 5 1 6 2 1 4 3 6 0 5 2 7 0 5 2 7 1 4 3 6 5 1 6 2 4 0 7 3 6 3 4 1 7 2 5 0 2 6 1 5 3 7 0 4 4 0 7 3 5 1 6 2 0 5 2 7 1 4 3 6 3 7 0 4 2 6 1 5 6 3 4 1 7 2 5 0 7 2 5 0 6 3 4 1 2 6 1 5 3 7 0 4 1 4 3 6 0 5 2 7 5 1 6 2 4 0 7 3 4 0 7 3 5 1 6 2 3 7 0 4 2 6 1 5 0 5 2 7 1 4 3 6 6 3 4 1 7 2 5 0 7 2 5 0 6 3 4 1 1 4 3 6 0 5 2 7 2 6 1 5 3 7 0 4 5 1 6 2 4 0 7 3 4 7 0 3 5 6 1 2 2 1 6 5 3 0 7 4 7 5 2 0 6 4 3 1 0 2 5 7 1 3 4 6 1 3 4 6 0 2 5 7 6 4 3 1 7 5 2 0 3 0 7 4 2 1 6 5 5 6 1 2 4 7 0 3 4 7 0 3 5 6 1 2 7 5 2 0 6 4 3 1 2 1 6 5 3 0 7 4 0 2 5 7 1 3 4 6 1 3 4 6 0 2 5 7 3 0 7 4 2 1 6 5 6 4 3 1 7 5 2 0 5 6 1 2 4 7 0 3 5 1 6 2 4 0 7 3 1 4 3 6 0 5 2 7 2 6 1 5 3 7 0 4 7 2 5 0 6 3 4 1 6 3 4 1 7 2 5 0 3 7 0 4 2 6 1 5 0 5 2 7 1 4 3 6 4 0 7 3 5 1 6 2 5 1 6 2 4 0 7 3 2 6 1 5 3 7 0 4 1 4 3 6 0 5 2 7 7 2 5 0 6 3 4 1 6 3 4 1 7 2 5 0 0 5 2 7 1 4 3 6 3 7 0 4 2 6 1 5 4 0 7 3 5 1 6 2 5 6 1 2 4 7 0 3 3 0 7 4 2 1 6 5 6 4 3 1 7 5 2 0 1 3 4 6 0 2 5 7 0 2 5 7 1 3 4 6 7 5 2 0 6 4 3 1 2 1 6 5 3 0 7 4 4 7 0 3 5 6 1 2 5 6 1 2 4 7 0 3 6 4 3 1 7 5 2 0 3 0 7 4 2 1 6 5 1 3 4 6 0 2 5 7 0 2 5 7 1 3 4 6 2 1 6 5 3 0 7 4 7 5 2 0 6 4 3 1 4 7 0 3 5 6 1 2 6 3 4 1 7 2 5 0 0 5 2 7 1 4 3 6 3 7 0 4 2 6 1 5 4 0 7 3 5 1 6 2 5 1 6 2 4 0 7 3 2 6 1 5 3 7 0 4 1 4 3 6 0 5 2 7 7 2 5 0 6 3 4 1 6 3 4 1 7 2 5 0 3 7 0 4 2 6 1 5 0 5 2 7 1 4 3 6 4 0 7 3 5 1 6 2 5 1 6 2 4 0 7 3 1 4 3 6 0 5 2 7 2 6 1 5 3 7 0 4 7 2 5 0 6 3 4 1 6 4 3 1 7 5 2 0 1 3 4 6 0 2 5 7 4 7 0 3 5 6 1 2 2 1 6 5 3 0 7 4 3 0 7 4 2 1 6 5 5 6 1 2 4 7 0 3 0 2 5 7 1 3 4 6 7 5 2 0 6 4 3 1 6 4 3 1 7 5 2 0 4 7 0 3 5 6 1 2 1 3 4 6 0 2 5 7 2 1 6 5 3 0 7 4 3 0 7 4 2 1 6 5 0 2 5 7 1 3 4 6 5 6 1 2 4 7 0 3 7 5 2 0 6 4 3 1 7 2 5 0 6 3 4 1 1 4 3 6 0 5 2 7 2 6 1 5 3 7 0 4 5 1 6 2 4 0 7 3 4 0 7 3 5 1 6 2 3 7 0 4 2 6 1 5 0 5 2 7 1 4 3 6 6 3 4 1 7 2 5 0 7 2 5 0 6 3 4 1 2 6 1 5 3 7 0 4 1 4 3 6 0 5 2 7 5 1 6 2 4 0 7 3 4 0 7 3 5 1 6 2 0 5 2 7 1 4 3 6 3 7 0 4 2 6 1 5 6 3 4 1 7 2 5 0 7 5 2 0 6 4 3 1 0 2 5 7 1 3 4 6 5 6 1 2 4 7 0 3 3 0 7 4 2 1 6 5 2 1 6 5 3 0 7 4 4 7 0 3 5 6 1 2 1 3 4 6 0 2 5 7 6 4 3 1 7 5 2 0 7 5 2 0 6 4 3 1 5 6 1 2 4 7 0 3 0 2 5 7 1 3 4 6 3 0 7 4 2 1 6 5 2 1 6 5 3 0 7 4 1 3 4 6 0 2 5 7 4 7 0 3 5 6 1 2 6 4 3 1 7 5 2 0 Проверка ÑвойÑтв утилитой Harry White Order? 8
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt
Counts
------
32 diagonal Latin
32 associative
32 weakly pandiagonal
32 ultramagic
32 double axial symmetric
1 natural \diagonalМожет быть, квадраты будут полезны в дальнейшем приÑке ортогональной пары идеальных ДЛК 8-го порÑдка. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese
