Thread 'Ultramagic DLS'
Message boards : Science : Ultramagic DLS
Message board moderation
Previous · 1 · 2 · 3 · 4 · 5 · 6 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷГҗВҫГ‘вҖҡ ГҗВәГҗВ°ГҗВәГҗВёГҗВө ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө Г‘ВҒГҗВҫГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ ГҗВёГҗВјГҗВөГ‘ЕҪГ‘вҖҡ Г‘ВҚГ‘вҖҡГҗВё 32 ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ Order? 8
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_8.txt
Counts
------
704 diagonal Latin
8 associative
384 axial symmetric
320 double axial symmetric
312 center symmetricГҗЕҫГҗвҖқГҗвҖәГҗЕЎ ГҗВҙГҗВҫГҗВІГҗВҫГҗ»ÑŒГҗВҪГҗВҫ ГҗВјГҗВҪГҗВҫГҗВіГҗВҫ, ГҗВҪГҗВҫ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВҪГҗВөГ‘вҖҡ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷ ГҗВҝГҗВҫГ‘ВҒГҗВ»ГҗВөГҗВҙГҗВҫГҗВІГҗ°ÑвҖҡГҗВөГҗ»ÑŒГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГҗВё OEIS https://oeis.org/A330391 Г‘Ж’ГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВ° Г‘ВҒГ‘ВҒГ‘вҖ№ГҗВ»ГҗВәГҗВ° ГҗВҪГҗВ° ГҗВҝГҗВҫГҗВ»ГҗВҪГ‘Ж’Г‘ЕҪ ГҗвҖҳГҗвҖқ ГҗЕЎГҗВӨ ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ 8-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° E. I. Vatutin, List of all main classes of orthogonal diagonal Latin squares of orders 1-8. ГҗЕёГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬Г‘ВҸГ‘ЕҪ ГҗВІГ‘ВҒГҗВө Г‘ВҚГ‘вҖҡГҗВё 1105 ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ Г‘Ж’Г‘вҖҡГҗВёГҗВ»ГҗВёГ‘вҖҡГҗВҫГҗВ№ Harry White Order? 8
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_8.txt
Counts
------
1105 diagonal Latin
4 weakly pandiagonal
508 axial symmetric
28 double axial symmetric
69 center symmetric
1105 nfr
8 self-orthogonalГҗВқГҗВё ГҗВҫГҗВҙГҗВҪГҗВҫГҗВіГҗВҫ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ ГҗВ·ГҗВҙГҗВөГ‘ВҒГ‘Е’ ГҗВҪГҗВөГ‘вҖҡ. ГҗВқГҗВҫ Г‘ВҒГҗВ»ГҗВ°ГҗВұГҗВҫ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВё Г‘вҖ ГҗВөГҗВҪГ‘вҖҡГ‘вӮ¬ГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ-Г‘ВҒГҗВёГҗВјГҗВјГҗВөГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№ГҗВө ГҗВөГ‘ВҒГ‘вҖҡГ‘Е’. ГҗЕёГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГҗВ°ГҗВ»ГҗВ° ГҗВІГ‘ВҒГҗВө ГҗвҖқГҗвҖәГҗЕЎ ГҗВІ ГҗВЎГҗВқ ГҗвҖқГҗвҖәГҗЕЎ, Г‘вҖҡГҗВөГҗВҝГҗВөГ‘вӮ¬Г‘Е’ Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ° ГҗВІГ‘вҖ№ГҗВҙГҗВ°ГҗВ»ГҗВёГ‘ВҒГ‘Е’ Г‘вҖҡГҗВ°ГҗВәГҗВёГҗВө Order? 8
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt
Counts
------
1105 diagonal Latin
69 associative
2 weakly pandiagonal
1 ultramagic
508 axial symmetric
28 double axial symmetric
1105 natural \diagonal
8 self-orthogonalГҗЕҫГҗВҙГҗВёГҗВҪ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГҗȄВҒГ‘ВҸ! ГҗвҖҷГҗВҫГ‘вҖҡ ГҗВҫГҗВҪ 0 7 6 1 5 3 2 4 6 1 0 7 2 4 5 3 5 3 2 4 1 6 7 0 2 4 5 3 7 0 1 6 1 6 7 0 4 2 3 5 7 0 1 6 3 5 4 2 4 2 3 5 0 7 6 1 3 5 4 2 6 1 0 7 ГҗВЎГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ ГҗВҪГҗВ°ГҗВ№ГҗВҙГ‘Ж’ ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ ГҗВә Г‘ВҚГ‘вҖҡГҗВҫГҗВјГ‘Ж’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВјГ‘Ж’ ГҗвҖқГҗвҖәГҗЕЎ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЕҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВёГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҪГҗВҫ: ГҗВҪГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ (ГҗВІ ГҗВҝГҗВҫГҗВ»ГҗВҪГҗВҫГҗВ№ ГҗвҖҳГҗвҖқ 8-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°) ГҗВёГҗВјГҗВөГҗВөГ‘вҖҡ ГҗВІГ‘ВҒГҗВөГҗВіГҗВҫ 4 ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ; ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ Г‘ВҒГ‘вӮ¬ГҗВөГҗВҙГҗВё ГҗВҪГҗВёГ‘вҖҰ ГҗВҪГҗВөГ‘вҖҡ, ГҗВҪГҗВҫ ГҗВІГ‘ВҒГҗВө ГҗВҫГҗВҪГҗВё Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВө. ГҗВўГҗВ°ГҗВәГҗВёГҗВј ГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВј, ГҗВҝГҗВҫГҗȄĄвҖЎГҗВ°ГҗВөГҗВј 4 ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ ГҗвҖқГҗвҖәГҗЕЎ; ГҗВІ ГҗВәГҗВ°ГҗВ¶ГҗВҙГҗВҫГҗВ№ ГҗВҝГҗ°ÑвӮ¬ГҗВө ГҗВҫГҗВҙГҗВёГҗВҪ ГҗвҖқГҗвҖәГҗЕЎ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№, ГҗВ° ГҗВІГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВҫГҗВ№ - Г‘вҖҡГҗВҫГҗ»ÑŒГҗВәГҗВҫ Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВ№. ГҗЕёГ‘вӮ¬ГҗВёГҗВјГҗВөГ‘вӮ¬ 0 7 6 1 5 3 2 4 6 1 0 7 2 4 5 3 5 3 2 4 1 6 7 0 2 4 5 3 7 0 1 6 1 6 7 0 4 2 3 5 7 0 1 6 3 5 4 2 4 2 3 5 0 7 6 1 3 5 4 2 6 1 0 7 0 2 4 6 3 1 7 5 3 1 7 5 0 2 4 6 6 4 2 0 5 7 1 3 5 7 1 3 6 4 2 0 7 5 3 1 4 6 0 2 4 6 0 2 7 5 3 1 1 3 5 7 2 0 6 4 2 0 6 4 1 3 5 7 ГҗЕёГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬ГҗВёГҗВ»ГҗВ° Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ° Г‘ВҚГ‘вҖҡГҗВёГ‘вҖҰ ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ Г‘Ж’Г‘вҖҡГҗВёГҗВ»ГҗВёГ‘вҖҡГҗВҫГҗВ№ Harry White Order? 8
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_9.txt
Counts
------
2 diagonal Latin
2 associative
1 weakly pandiagonal
1 ultramagic
1 double axial symmetric
2 natural \diagonal
1 orthogonal pair
1 self-orthogonalSODLS ГҗВ·ГҗВҙГҗВөГ‘ВҒГ‘Е’ ГҗВҪГҗВө ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ. ГҗВЈГҗВІГ‘вҖ№! ГҗВўГҗВ°ГҗВә, ГҗВіГҗВҙГҗВө ГҗВөГ‘вҖ°Г‘вҖҳ ГҗВҝГҗВҫГҗВёГ‘ВҒГҗВәГҗ°ÑвҖҡГ‘Е’ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 8-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВҰГҗВёГ‘вҖҡГҗ°ÑвҖҡГҗВ° n=8 ГҗВўГ‘Ж’Г‘вҖҡ ГҗВёГ‘ВҒГҗВәГҗВ°ГҗВ»ГҗВ° Г‘Ж’ГҗВ¶ГҗВө ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 8-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°? ГҗВқГҗВө ГҗВҝГҗВҫГҗВјГҗВҪГ‘ЕҪ. ГҗВЎГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ ГҗВҝГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬Г‘ЕҪ Г‘ВҚГ‘вҖҡГҗВё ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ-ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ; ГҗВІГҗВёГҗВҙГҗВёГҗВј ГҗВІ Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗ°ÑвҖҰ, Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВІГ‘ВҒГҗВө ГҗВҫГҗВҪГҗВё Г‘вҖ ГҗВөГҗВҪГ‘вҖҡГ‘вӮ¬ГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ-Г‘ВҒГҗВёГҗВјГҗВјГҗВөГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№ГҗВө. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЕёГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГҗВ°ГҗВ»ГҗВ° 6 ГҗвҖқГҗвҖәГҗЕЎ ГҗВёГҗВ· ГҗВҝГҗВҫГҗВ»ГҗВҪГҗВҫГҗВ№ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГ‘вҖ№ MOLS 8-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВІ ГҗВЎГҗВқ ГҗвҖқГҗвҖәГҗЕЎ, ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГҗВ»ГҗВ° ГҗвҖқГҗвҖәГҗЕЎ Г‘ВҒ Г‘вҖҡГҗВ°ГҗВәГҗВёГҗВјГҗВё Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ°ГҗВјГҗВё Order? 8
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt
Counts
------
6 diagonal Latin
6 associative
6 double axial symmetric
6 natural \diagonal
5 orthogonal pair
6 self-orthogonalГҗвҖҷГ‘ВҒГҗВө ГҗВҫГҗВҪГҗВё Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВө, ГҗВ° ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВҪГҗВөГ‘вҖҡ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷГҗВҫГ‘вҖҡ Г‘ВҚГ‘вҖҡГ‘Ж’ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ ГҗВҪГҗВ°ГҗВҙГҗВҫ ГҗВҝГ‘вӮ¬ГҗВҫГ‘вҖ°Г‘Ж’ГҗВҝГҗ°ÑвҖҡГ‘Е’ ГҗВҪГҗВ° ГҗВҝГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГ‘вҖҡГҗВ°ГҗВҪГҗВҫГҗВІГҗВәГ‘Ж’ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВә/Г‘ВҒГ‘вҖҡГҗВҫГҗВ»ГҗВұГ‘вҖ ГҗВҫГҗВІ 0 1 2 3 4 5 6 7 5 4 7 6 1 0 3 2 7 6 5 4 3 2 1 0 2 3 0 1 6 7 4 5 3 2 1 0 7 6 5 4 6 7 4 5 2 3 0 1 4 5 6 7 0 1 2 3 1 0 3 2 5 4 7 6 0 1 2 3 4 5 6 7 6 7 4 5 2 3 0 1 1 0 3 2 5 4 7 6 7 6 5 4 3 2 1 0 2 3 0 1 6 7 4 5 4 5 6 7 0 1 2 3 3 2 1 0 7 6 5 4 5 4 7 6 1 0 3 2 ГҗВЎГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ° Г‘ВҚГ‘вҖҡГҗВёГ‘вҖҰ ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ Order? 8
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt
Counts
------
2 diagonal Latin
2 weakly pandiagonal
2 double axial symmetric
2 center symmetric
2 nfr
1 orthogonal pair
2 self-orthogonalГҗЕёГ‘вӮ¬ГҗВөГҗВІГ‘вӮ¬Гҗ°ÑвҖ°ГҗВөГҗВҪГҗВёГҗВө ГҗВІ ГҗВЎГҗВқ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҪГҗВёГ‘вҖЎГҗВөГҗВіГҗВҫ ГҗВҪГҗВө ГҗВҙГҗ°ÑвҖҳГ‘вҖҡ: ГҗвҖқГҗвҖәГҗЕЎ Г‘ВҒГ‘вҖҡГҗВ°ГҗВҪГҗВҫГҗВІГ‘ВҸГ‘вҖҡГ‘ВҒГ‘ВҸ Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВјГҗВё, ГҗВҪГҗВҫ ГҗВёГ‘ВҒГ‘вҖЎГҗВөГҗВ·ГҗВ°ГҗВөГ‘вҖҡ Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВҫ Г‘ВҒГҗВ»ГҗВ°ГҗВұГҗВҫГҗВ№ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГҗВё. ГҗЕЎГ‘ВҒГ‘вҖҡГҗ°ÑвҖҡГҗВё, Г‘ВҚГ‘вҖҡГ‘Ж’ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ Г‘вҖҡГҗВҫГҗВ¶ГҗВө ГҗВјГҗВҫГҗВ¶ГҗВҪГҗВҫ ГҗВҝГҗВҫГ‘вҖ°Г‘Ж’ГҗВҝГҗ°ÑвҖҡГ‘Е’ ГҗВҝГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГ‘вҖҡГҗВ°ГҗВҪГҗВҫГҗВІГҗВәГҗВҫГҗВ№ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВә/Г‘ВҒГ‘вҖҡГҗВҫГҗВ»ГҗВұГ‘вҖ ГҗВҫГҗВІ 0 7 6 1 5 3 2 4 6 1 0 7 2 4 5 3 5 3 2 4 1 6 7 0 2 4 5 3 7 0 1 6 1 6 7 0 4 2 3 5 7 0 1 6 3 5 4 2 4 2 3 5 0 7 6 1 3 5 4 2 6 1 0 7 0 2 4 6 3 1 7 5 3 1 7 5 0 2 4 6 6 4 2 0 5 7 1 3 5 7 1 3 6 4 2 0 7 5 3 1 4 6 0 2 4 6 0 2 7 5 3 1 1 3 5 7 2 0 6 4 2 0 6 4 1 3 5 7 ГҗЕёГҗВөГ‘вӮ¬ГҗВІГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВІ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ ГҗВҝГҗ°ÑвӮ¬ГҗВө ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№, ГҗВ° ГҗВІГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВҫГҗВ№ - Г‘вҖҡГҗВҫГҗ»ÑŒГҗВәГҗВҫ Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВ№. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖқГҗВІГҗВ° ГҗвҖқГҗвҖәГҗЕЎ ГҗВёГҗВ· Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ 0 1 2 3 4 5 6 7 5 4 7 6 1 0 3 2 7 6 5 4 3 2 1 0 2 3 0 1 6 7 4 5 3 2 1 0 7 6 5 4 6 7 4 5 2 3 0 1 4 5 6 7 0 1 2 3 1 0 3 2 5 4 7 6 0 1 2 3 4 5 6 7 6 7 4 5 2 3 0 1 1 0 3 2 5 4 7 6 7 6 5 4 3 2 1 0 2 3 0 1 6 7 4 5 4 5 6 7 0 1 2 3 3 2 1 0 7 6 5 4 5 4 7 6 1 0 3 2 ГҗВҙГҗВ°ГҗВ»ГҗВё ГҗВҝГ‘вӮ¬ГҗВё ГҗВҝГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГ‘вҖҡГҗВ°ГҗВҪГҗВҫГҗВІГҗВәГҗВө Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВә/Г‘ВҒГ‘вҖҡГҗВҫГҗВ»ГҗВұГ‘вҖ ГҗВҫГҗВІ 18432 Г‘вӮ¬ГҗВ°ГҗВ·ГҗВ»ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ (ГҗВҪГҗВө Г‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГҗВөГҗВҪГҗВҪГҗВҫ Г‘вӮ¬ГҗВ°ГҗВ·ГҗВ»ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№Г‘вҖҰ! ГҗВҪГҗВ° ГҗВёГҗВ·ГҗВҫГҗВјГҗВҫГ‘вӮ¬Г‘вҖһГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВҪГҗВө ГҗВҝГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬Г‘ВҸГҗВ»ГҗВ° Г‘ВҚГ‘вҖҡГҗВё ГҗвҖқГҗвҖәГҗЕЎ), ГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬Г‘вҖ№ГҗВө ГҗВҫГҗВұГҗВ»ГҗВ°ГҗВҙГҗ°ÑЕҪГ‘вҖҡ Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ°ГҗВјГҗВё Order? 8
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_9.txt
Counts
------
18432 diagonal Latin
3072 associative
3904 weakly pandiagonal
192 ultramagic
18432 double axial symmetric
15360 center symmetric
48 nfr
48 natural \diagonal
1894 orthogonal pair
18432 self-orthogonalГҗЕЎГҗВ°ГҗВә ГҗВІГҗВёГҗВҙГҗВёГҗВј, ГҗВҪГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҫ 192 ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ. ГҗВқГҗВҫ ГҗВұГ‘Ж’ГҗВҙГҗВөГ‘вҖҡ ГҗВ»ГҗВё Г‘вҖҰГҗВҫГ‘вҖҡГ‘Е’ ГҗВҫГҗВҙГҗВҪГҗВ° ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗ°ÑВҸ ГҗВҝГҗ°ÑвӮ¬ГҗВ° ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ??? ГҗвҖҷГ‘ВҒГҗВө Г‘ВҚГ‘вҖҡГҗВё ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ ГҗВҪГҗВ°ГҗВІГҗВөГ‘вӮ¬ГҗВҪГ‘ВҸГҗВәГҗВ° ГҗВёГҗВјГҗВөГ‘ЕҪГ‘вҖҡ ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ, ГҗВҪГҗВҫ ГҗВІГҗВҫГ‘вҖҡ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ Г‘ВҒГ‘вӮ¬ГҗВөГҗВҙГҗВё ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ ГҗВјГҗВҫГҗВ¶ГҗВөГ‘вҖҡ ГҗВё ГҗВҪГҗВө ГҗВұГ‘вҖ№Г‘вҖҡГ‘Е’. Гҗ§ÑвҖҡГҗВҫГҗВұГ‘вҖ№ Г‘ВҚГ‘вҖҡГҗВҫ ГҗВҝГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬ГҗВёГ‘вҖҡГ‘Е’, ГҗВҪГҗВ°ГҗВҙГҗВҫ ГҗВІГ‘вҖ№Г‘Ж’ГҗВҙГҗВёГ‘вҖҡГ‘Е’ ГҗВІГ‘ВҒГҗВө 192 ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВёГҗВ· ГҗВҪГҗВ°ГҗВұГҗВҫГ‘вӮ¬ГҗВ°, ГҗВІ ГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВҫГҗВј 18432 ГҗвҖқГҗвҖәГҗЕЎ. ГҗЕёГҗВҫГҗВҪГ‘ВҸГ‘вҖҡГҗВҪГҗВҫ, Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВҙГҗȄВҸ Г‘ВҚГ‘вҖҡГҗВҫГҗВіГҗВҫ ГҗВҪГҗВ°ГҗВҙГҗВҫ ГҗВҪГҗВ°ГҗВҝГҗВёГ‘ВҒГҗ°ÑвҖҡГ‘Е’ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВәГ‘Ж’, ГҗВҝГҗВҫГ‘вҖҡГҗВҫГҗВјГ‘Ж’ Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВІГ‘вӮ¬Г‘Ж’Г‘вҖЎГҗВҪГ‘Ж’Г‘ЕҪ ГҗВІГ‘вҖ№Г‘Ж’ГҗВ¶ГҗВёГҗВІГҗ°ÑвҖҡГ‘Е’ ГҗВҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВҪГ‘Ж’ГҗВҙГҗВҪГҗВҫ. ГҗВҘГҗВј... ГҗЕёГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГҗВ№Г‘вҖҡГҗВө-ГҗВәГҗВ°... ГҗВқГҗВ°ГҗВҝГҗВёГ‘ВҒГҗВ°ГҗВҪГҗВҫ ГҗВІ Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗ°ÑвҖҰ, Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВІГ‘ВҒГҗВө 18432 ГҗвҖқГҗвҖәГҗЕЎ ГҗВҪГҗВ°ГҗВұГҗВҫГ‘вӮ¬ГҗВ° self-orthogonal. ГҗВўГҗВ°ГҗВә ГҗВ·ГҗВҪГҗ°ÑвҖЎГҗВёГ‘вҖҡ, ГҗВё ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ Г‘вҖҡГҗВҫГҗВ¶ГҗВө self-orthogonal, ГҗВё... ГҗВјГ‘вҖ№ ГҗВёГҗВјГҗВөГҗВөГҗВј ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ! ГҗВЎГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ ГҗВІГ‘вҖ№Г‘Ж’Гҗ¶Ñƒ ГҗВҫГҗВҙГҗВёГҗВҪ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВё ГҗВҝГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬Г‘ЕҪ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖқГҗВҗ-ГҗВҗ-ГҗВҗ-ГҗВҗ-ГҗВҗ!!! ГҗвҖҷГҗВҫГ‘вҖҡ ГҗВҫГҗВҪГҗВ° - ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗ°ÑВҸ ГҗВҝГҗ°ÑвӮ¬ГҗВ° ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 8-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° 0 1 6 7 4 5 2 3 3 2 5 4 7 6 1 0 5 4 3 2 1 0 7 6 6 7 0 1 2 3 4 5 2 3 4 5 6 7 0 1 1 0 7 6 5 4 3 2 7 6 1 0 3 2 5 4 4 5 2 3 0 1 6 7 0 3 5 6 2 1 7 4 1 2 4 7 3 0 6 5 6 5 3 0 4 7 1 2 7 4 2 1 5 6 0 3 4 7 1 2 6 5 3 0 5 6 0 3 7 4 2 1 2 1 7 4 0 3 5 6 3 0 6 5 1 2 4 7 ГҗЕёГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬ГҗВәГҗВ° Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІ ГҗвҖқГҗвҖәГҗЕЎ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ Г‘Ж’Г‘вҖҡГҗВёГҗВ»ГҗВёГ‘вҖҡГҗВҫГҗВ№ Harry White Order? 8
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_6.txt
Counts
------
2 diagonal Latin
2 associative
2 weakly pandiagonal
2 ultramagic
2 double axial symmetric
1 orthogonal pair
2 self-orthogonalГҗ§ÑƒГҗВҙГҗВөГ‘ВҒГҗВҪГҗВҫ! ГҗВҗГҗВ»ГҗВіГҗВҫГ‘вӮ¬ГҗВёГ‘вҖҡГҗВј Г‘ВҒГ‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗВ°ГҗВ»! ГҗЛңГ‘вҖҡГҗВ°ГҗВә, ГҗВҪГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҫ 192 ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ. ГҗЕЎГ‘вӮ¬ГҗВҫГҗВјГҗВө Г‘вҖҡГҗВҫГҗВіГҗВҫ, ГҗВІГ‘ВҒГҗВө ГҗВҪГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВө ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ Г‘ВҸГҗВІГҗȄВҸГ‘ЕҪГ‘вҖҡГ‘ВҒГ‘ВҸ DSODLS, ГҗВ° Г‘ВҚГ‘вҖҡГҗВҫ ГҗВөГ‘вҖ°Г‘вҖҳ 192 ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ. ГҗЕҫГҗВ№, Г‘вҖҡГҗВөГҗВҝГҗВөГ‘вӮ¬Г‘Е’ ГҗВјГҗВҫГҗВіГ‘Ж’ ГҗВҫГ‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГҗВёГ‘вҖҡГ‘Е’ Г‘ВҒГҗВІГҗВҫГ‘вҖҳ ГҗВ¶ГҗВөГҗВ»ГҗВ°ГҗВҪГҗВёГҗВө - ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡГ‘Е’ ГҗВҪГҗВҫГҗВІГ‘вҖ№ГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВҙГҗ°ÑвӮ¬Гҗ°ÑвҖҡ 8-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВёГ‘ВҒГҗВҝГҗВҫГҗ»ÑŒГҗВ·Г‘Ж’Г‘ВҸ ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙ ГҗВ»Гҗ°ÑвҖҡГҗВёГҗВҪГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ ГҗВҙГҗȄВҸ ГҗВҪГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҪГҗВҫГҗВ№ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ. ГҗВЎГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ Г‘ВҸ ГҗВөГҗВіГҗВҫ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГ‘ЕҪ :) ГҗВӨГҗВҫГ‘вӮ¬ГҗВјГ‘Ж’Гҗ»Ñƒ ГҗВұГҗВөГ‘вӮ¬Г‘Ж’: ГҗВЎ = 8*ГҗВҗ + ГҗвҖҷ +1, ГҗВіГҗВҙГҗВө ГҗВҗ - ГҗВҝГҗВөГ‘вӮ¬ГҗВІГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВІ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ ГҗВҝГҗ°ÑвӮ¬ГҗВө, ГҗвҖҷ - ГҗВІГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВҫГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВІ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ ГҗВҝГҗ°ÑвӮ¬ГҗВө, ГҗВЎ - ГҗВёГ‘ВҒГҗВәГҗВҫГҗВјГ‘вҖ№ГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВөГ‘вҖЎГҗВ°ГҗВ№Г‘вҖҡГҗВө - ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ 8-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј ГҗВ»Гҗ°ÑвҖҡГҗВёГҗВҪГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ 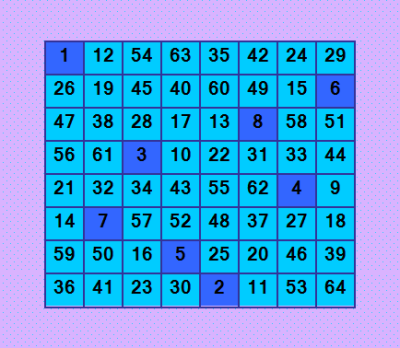 ГҗВўГҗВ°ГҗВәГҗВҫГҗВіГҗВҫ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВіГҗВҫ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВҫГҗВіГҗВҫ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ° 8-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° Г‘Ж’ ГҗВјГҗВөГҗВҪГ‘ВҸ ГҗВөГ‘вҖ°Г‘вҖҳ ГҗВҪГҗВө ГҗВұГ‘вҖ№ГҗВ»ГҗВҫ. ГҗЕҫГҗВұГ‘вӮ¬Гҗ°ÑвҖҡГҗВёГ‘вҖҡГҗВө ГҗВІГҗВҪГҗВёГҗВјГҗВ°ГҗВҪГҗВёГҗВө ГҗВҪГҗВ° ГҗВІГ‘вҖ№ГҗВҙГҗВөГҗВ»ГҗВөГҗВҪГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҪГҗ°ÑвҖЎГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ Г‘вҖ ГҗВөГҗВҝГҗВҫГ‘вҖЎГҗВәГ‘Ж’. ГҗвҖўГ‘ВҒГҗВ»ГҗВё ГҗВІГ‘вҖ№ ГҗВҝГҗВҫГ‘ВҒГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖҡГҗВө ГҗВІ ГҗВјГҗВҫГҗВёГ‘вҖҰ Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’Г‘ВҸГ‘вҖҰ ГҗВІГ‘ВҒГҗВө ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВө Г‘вӮ¬ГҗВ°ГҗВ·ГҗВҪГ‘вҖ№ГҗВјГҗВё ГҗВ°ГҗВ»ГҗВіГҗВҫГ‘вӮ¬ГҗВёГ‘вҖҡГҗВјГҗВ°ГҗВјГҗВё ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВө ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ ГҗВҙГҗВ°ГҗВҪГҗВҪГҗВҫГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, Г‘ВҒ Г‘вҖҡГҗВ°ГҗВәГҗВҫГҗВ№ ГҗВҪГҗ°ÑвҖЎГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ Г‘вҖ ГҗВөГҗВҝГҗВҫГ‘вҖЎГҗВәГҗВҫГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ° ГҗВҪГҗВө ГҗВҪГҗВ°ГҗВ№ГҗВҙГ‘вҖҳГ‘вҖҡГҗВө. ГҗВӯГ‘вҖҡГҗВҫ ГҗВҝГ‘вӮ¬ГҗВёГҗВҪГ‘вҖ ГҗВёГҗВҝГҗВёГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ ГҗВҪГҗВҫГҗВІГ‘вҖ№ГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ 8-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗвҖҷГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВі ГҗВё ГҗВІГҗВҫГ‘ВҒГ‘вҖҰГҗВёГ‘вҖ°ГҗВөГҗВҪГҗВёГҗВө! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷГ‘вҖ№Г‘ЛҶГҗВө ГҗВұГ‘вҖ№ГҗВ» ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪ ГҗВҫГҗВҙГҗВёГҗВҪ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 40-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗВўГҗВөГҗВҝГҗВөГ‘вӮ¬Г‘Е’ ГҗВјГҗВҫГҗВ¶ГҗВҪГҗВҫ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡГ‘Е’ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 40-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗвҖқГҗȄВҸ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВёГ‘ВҸ ГҗВІГҗВҫГҗВ·Г‘Е’ГҗВјГ‘Ж’ Г‘вҖҡГҗВҫГҗ»ÑŒГҗВәГҗВҫ Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВҪГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 8-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВё Г‘ВҚГ‘вҖҡГ‘Ж’ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 5-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° 0 4 3 2 1 2 1 0 4 3 4 3 2 1 0 1 0 4 3 2 3 2 1 0 4 0 2 4 1 3 4 1 3 0 2 3 0 2 4 1 2 4 1 3 0 1 3 0 2 4 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВөГ‘вҖЎГҗВ°ГҗВ№Г‘вҖҡГҗВө - ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗ°ÑВҸ ГҗВҝГҗ°ÑвӮ¬ГҗВ° ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 40-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВҪГҗ°ÑВҸ ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ 0 1 6 7 4 5 2 3 32 33 38 39 36 37 34 35 24 25 30 31 28 29 26 27 16 17 22 23 20 21 18 19 8 9 14 15 12 13 10 11 3 2 5 4 7 6 1 0 35 34 37 36 39 38 33 32 27 26 29 28 31 30 25 24 19 18 21 20 23 22 17 16 11 10 13 12 15 14 9 8 5 4 3 2 1 0 7 6 37 36 35 34 33 32 39 38 29 28 27 26 25 24 31 30 21 20 19 18 17 16 23 22 13 12 11 10 9 8 15 14 6 7 0 1 2 3 4 5 38 39 32 33 34 35 36 37 30 31 24 25 26 27 28 29 22 23 16 17 18 19 20 21 14 15 8 9 10 11 12 13 2 3 4 5 6 7 0 1 34 35 36 37 38 39 32 33 26 27 28 29 30 31 24 25 18 19 20 21 22 23 16 17 10 11 12 13 14 15 8 9 1 0 7 6 5 4 3 2 33 32 39 38 37 36 35 34 25 24 31 30 29 28 27 26 17 16 23 22 21 20 19 18 9 8 15 14 13 12 11 10 7 6 1 0 3 2 5 4 39 38 33 32 35 34 37 36 31 30 25 24 27 26 29 28 23 22 17 16 19 18 21 20 15 14 9 8 11 10 13 12 4 5 2 3 0 1 6 7 36 37 34 35 32 33 38 39 28 29 26 27 24 25 30 31 20 21 18 19 16 17 22 23 12 13 10 11 8 9 14 15 16 17 22 23 20 21 18 19 8 9 14 15 12 13 10 11 0 1 6 7 4 5 2 3 32 33 38 39 36 37 34 35 24 25 30 31 28 29 26 27 19 18 21 20 23 22 17 16 11 10 13 12 15 14 9 8 3 2 5 4 7 6 1 0 35 34 37 36 39 38 33 32 27 26 29 28 31 30 25 24 21 20 19 18 17 16 23 22 13 12 11 10 9 8 15 14 5 4 3 2 1 0 7 6 37 36 35 34 33 32 39 38 29 28 27 26 25 24 31 30 22 23 16 17 18 19 20 21 14 15 8 9 10 11 12 13 6 7 0 1 2 3 4 5 38 39 32 33 34 35 36 37 30 31 24 25 26 27 28 29 18 19 20 21 22 23 16 17 10 11 12 13 14 15 8 9 2 3 4 5 6 7 0 1 34 35 36 37 38 39 32 33 26 27 28 29 30 31 24 25 17 16 23 22 21 20 19 18 9 8 15 14 13 12 11 10 1 0 7 6 5 4 3 2 33 32 39 38 37 36 35 34 25 24 31 30 29 28 27 26 23 22 17 16 19 18 21 20 15 14 9 8 11 10 13 12 7 6 1 0 3 2 5 4 39 38 33 32 35 34 37 36 31 30 25 24 27 26 29 28 20 21 18 19 16 17 22 23 12 13 10 11 8 9 14 15 4 5 2 3 0 1 6 7 36 37 34 35 32 33 38 39 28 29 26 27 24 25 30 31 32 33 38 39 36 37 34 35 24 25 30 31 28 29 26 27 16 17 22 23 20 21 18 19 8 9 14 15 12 13 10 11 0 1 6 7 4 5 2 3 35 34 37 36 39 38 33 32 27 26 29 28 31 30 25 24 19 18 21 20 23 22 17 16 11 10 13 12 15 14 9 8 3 2 5 4 7 6 1 0 37 36 35 34 33 32 39 38 29 28 27 26 25 24 31 30 21 20 19 18 17 16 23 22 13 12 11 10 9 8 15 14 5 4 3 2 1 0 7 6 38 39 32 33 34 35 36 37 30 31 24 25 26 27 28 29 22 23 16 17 18 19 20 21 14 15 8 9 10 11 12 13 6 7 0 1 2 3 4 5 34 35 36 37 38 39 32 33 26 27 28 29 30 31 24 25 18 19 20 21 22 23 16 17 10 11 12 13 14 15 8 9 2 3 4 5 6 7 0 1 33 32 39 38 37 36 35 34 25 24 31 30 29 28 27 26 17 16 23 22 21 20 19 18 9 8 15 14 13 12 11 10 1 0 7 6 5 4 3 2 39 38 33 32 35 34 37 36 31 30 25 24 27 26 29 28 23 22 17 16 19 18 21 20 15 14 9 8 11 10 13 12 7 6 1 0 3 2 5 4 36 37 34 35 32 33 38 39 28 29 26 27 24 25 30 31 20 21 18 19 16 17 22 23 12 13 10 11 8 9 14 15 4 5 2 3 0 1 6 7 8 9 14 15 12 13 10 11 0 1 6 7 4 5 2 3 32 33 38 39 36 37 34 35 24 25 30 31 28 29 26 27 16 17 22 23 20 21 18 19 11 10 13 12 15 14 9 8 3 2 5 4 7 6 1 0 35 34 37 36 39 38 33 32 27 26 29 28 31 30 25 24 19 18 21 20 23 22 17 16 13 12 11 10 9 8 15 14 5 4 3 2 1 0 7 6 37 36 35 34 33 32 39 38 29 28 27 26 25 24 31 30 21 20 19 18 17 16 23 22 14 15 8 9 10 11 12 13 6 7 0 1 2 3 4 5 38 39 32 33 34 35 36 37 30 31 24 25 26 27 28 29 22 23 16 17 18 19 20 21 10 11 12 13 14 15 8 9 2 3 4 5 6 7 0 1 34 35 36 37 38 39 32 33 26 27 28 29 30 31 24 25 18 19 20 21 22 23 16 17 9 8 15 14 13 12 11 10 1 0 7 6 5 4 3 2 33 32 39 38 37 36 35 34 25 24 31 30 29 28 27 26 17 16 23 22 21 20 19 18 15 14 9 8 11 10 13 12 7 6 1 0 3 2 5 4 39 38 33 32 35 34 37 36 31 30 25 24 27 26 29 28 23 22 17 16 19 18 21 20 12 13 10 11 8 9 14 15 4 5 2 3 0 1 6 7 36 37 34 35 32 33 38 39 28 29 26 27 24 25 30 31 20 21 18 19 16 17 22 23 24 25 30 31 28 29 26 27 16 17 22 23 20 21 18 19 8 9 14 15 12 13 10 11 0 1 6 7 4 5 2 3 32 33 38 39 36 37 34 35 27 26 29 28 31 30 25 24 19 18 21 20 23 22 17 16 11 10 13 12 15 14 9 8 3 2 5 4 7 6 1 0 35 34 37 36 39 38 33 32 29 28 27 26 25 24 31 30 21 20 19 18 17 16 23 22 13 12 11 10 9 8 15 14 5 4 3 2 1 0 7 6 37 36 35 34 33 32 39 38 30 31 24 25 26 27 28 29 22 23 16 17 18 19 20 21 14 15 8 9 10 11 12 13 6 7 0 1 2 3 4 5 38 39 32 33 34 35 36 37 26 27 28 29 30 31 24 25 18 19 20 21 22 23 16 17 10 11 12 13 14 15 8 9 2 3 4 5 6 7 0 1 34 35 36 37 38 39 32 33 25 24 31 30 29 28 27 26 17 16 23 22 21 20 19 18 9 8 15 14 13 12 11 10 1 0 7 6 5 4 3 2 33 32 39 38 37 36 35 34 31 30 25 24 27 26 29 28 23 22 17 16 19 18 21 20 15 14 9 8 11 10 13 12 7 6 1 0 3 2 5 4 39 38 33 32 35 34 37 36 28 29 26 27 24 25 30 31 20 21 18 19 16 17 22 23 12 13 10 11 8 9 14 15 4 5 2 3 0 1 6 7 36 37 34 35 32 33 38 39 0 3 5 6 2 1 7 4 16 19 21 22 18 17 23 20 32 35 37 38 34 33 39 36 8 11 13 14 10 9 15 12 24 27 29 30 26 25 31 28 1 2 4 7 3 0 6 5 17 18 20 23 19 16 22 21 33 34 36 39 35 32 38 37 9 10 12 15 11 8 14 13 25 26 28 31 27 24 30 29 6 5 3 0 4 7 1 2 22 21 19 16 20 23 17 18 38 37 35 32 36 39 33 34 14 13 11 8 12 15 9 10 30 29 27 24 28 31 25 26 7 4 2 1 5 6 0 3 23 20 18 17 21 22 16 19 39 36 34 33 37 38 32 35 15 12 10 9 13 14 8 11 31 28 26 25 29 30 24 27 4 7 1 2 6 5 3 0 20 23 17 18 22 21 19 16 36 39 33 34 38 37 35 32 12 15 9 10 14 13 11 8 28 31 25 26 30 29 27 24 5 6 0 3 7 4 2 1 21 22 16 19 23 20 18 17 37 38 32 35 39 36 34 33 13 14 8 11 15 12 10 9 29 30 24 27 31 28 26 25 2 1 7 4 0 3 5 6 18 17 23 20 16 19 21 22 34 33 39 36 32 35 37 38 10 9 15 12 8 11 13 14 26 25 31 28 24 27 29 30 3 0 6 5 1 2 4 7 19 16 22 21 17 18 20 23 35 32 38 37 33 34 36 39 11 8 14 13 9 10 12 15 27 24 30 29 25 26 28 31 32 35 37 38 34 33 39 36 8 11 13 14 10 9 15 12 24 27 29 30 26 25 31 28 0 3 5 6 2 1 7 4 16 19 21 22 18 17 23 20 33 34 36 39 35 32 38 37 9 10 12 15 11 8 14 13 25 26 28 31 27 24 30 29 1 2 4 7 3 0 6 5 17 18 20 23 19 16 22 21 38 37 35 32 36 39 33 34 14 13 11 8 12 15 9 10 30 29 27 24 28 31 25 26 6 5 3 0 4 7 1 2 22 21 19 16 20 23 17 18 39 36 34 33 37 38 32 35 15 12 10 9 13 14 8 11 31 28 26 25 29 30 24 27 7 4 2 1 5 6 0 3 23 20 18 17 21 22 16 19 36 39 33 34 38 37 35 32 12 15 9 10 14 13 11 8 28 31 25 26 30 29 27 24 4 7 1 2 6 5 3 0 20 23 17 18 22 21 19 16 37 38 32 35 39 36 34 33 13 14 8 11 15 12 10 9 29 30 24 27 31 28 26 25 5 6 0 3 7 4 2 1 21 22 16 19 23 20 18 17 34 33 39 36 32 35 37 38 10 9 15 12 8 11 13 14 26 25 31 28 24 27 29 30 2 1 7 4 0 3 5 6 18 17 23 20 16 19 21 22 35 32 38 37 33 34 36 39 11 8 14 13 9 10 12 15 27 24 30 29 25 26 28 31 3 0 6 5 1 2 4 7 19 16 22 21 17 18 20 23 24 27 29 30 26 25 31 28 0 3 5 6 2 1 7 4 16 19 21 22 18 17 23 20 32 35 37 38 34 33 39 36 8 11 13 14 10 9 15 12 25 26 28 31 27 24 30 29 1 2 4 7 3 0 6 5 17 18 20 23 19 16 22 21 33 34 36 39 35 32 38 37 9 10 12 15 11 8 14 13 30 29 27 24 28 31 25 26 6 5 3 0 4 7 1 2 22 21 19 16 20 23 17 18 38 37 35 32 36 39 33 34 14 13 11 8 12 15 9 10 31 28 26 25 29 30 24 27 7 4 2 1 5 6 0 3 23 20 18 17 21 22 16 19 39 36 34 33 37 38 32 35 15 12 10 9 13 14 8 11 28 31 25 26 30 29 27 24 4 7 1 2 6 5 3 0 20 23 17 18 22 21 19 16 36 39 33 34 38 37 35 32 12 15 9 10 14 13 11 8 29 30 24 27 31 28 26 25 5 6 0 3 7 4 2 1 21 22 16 19 23 20 18 17 37 38 32 35 39 36 34 33 13 14 8 11 15 12 10 9 26 25 31 28 24 27 29 30 2 1 7 4 0 3 5 6 18 17 23 20 16 19 21 22 34 33 39 36 32 35 37 38 10 9 15 12 8 11 13 14 27 24 30 29 25 26 28 31 3 0 6 5 1 2 4 7 19 16 22 21 17 18 20 23 35 32 38 37 33 34 36 39 11 8 14 13 9 10 12 15 16 19 21 22 18 17 23 20 32 35 37 38 34 33 39 36 8 11 13 14 10 9 15 12 24 27 29 30 26 25 31 28 0 3 5 6 2 1 7 4 17 18 20 23 19 16 22 21 33 34 36 39 35 32 38 37 9 10 12 15 11 8 14 13 25 26 28 31 27 24 30 29 1 2 4 7 3 0 6 5 22 21 19 16 20 23 17 18 38 37 35 32 36 39 33 34 14 13 11 8 12 15 9 10 30 29 27 24 28 31 25 26 6 5 3 0 4 7 1 2 23 20 18 17 21 22 16 19 39 36 34 33 37 38 32 35 15 12 10 9 13 14 8 11 31 28 26 25 29 30 24 27 7 4 2 1 5 6 0 3 20 23 17 18 22 21 19 16 36 39 33 34 38 37 35 32 12 15 9 10 14 13 11 8 28 31 25 26 30 29 27 24 4 7 1 2 6 5 3 0 21 22 16 19 23 20 18 17 37 38 32 35 39 36 34 33 13 14 8 11 15 12 10 9 29 30 24 27 31 28 26 25 5 6 0 3 7 4 2 1 18 17 23 20 16 19 21 22 34 33 39 36 32 35 37 38 10 9 15 12 8 11 13 14 26 25 31 28 24 27 29 30 2 1 7 4 0 3 5 6 19 16 22 21 17 18 20 23 35 32 38 37 33 34 36 39 11 8 14 13 9 10 12 15 27 24 30 29 25 26 28 31 3 0 6 5 1 2 4 7 8 11 13 14 10 9 15 12 24 27 29 30 26 25 31 28 0 3 5 6 2 1 7 4 16 19 21 22 18 17 23 20 32 35 37 38 34 33 39 36 9 10 12 15 11 8 14 13 25 26 28 31 27 24 30 29 1 2 4 7 3 0 6 5 17 18 20 23 19 16 22 21 33 34 36 39 35 32 38 37 14 13 11 8 12 15 9 10 30 29 27 24 28 31 25 26 6 5 3 0 4 7 1 2 22 21 19 16 20 23 17 18 38 37 35 32 36 39 33 34 15 12 10 9 13 14 8 11 31 28 26 25 29 30 24 27 7 4 2 1 5 6 0 3 23 20 18 17 21 22 16 19 39 36 34 33 37 38 32 35 12 15 9 10 14 13 11 8 28 31 25 26 30 29 27 24 4 7 1 2 6 5 3 0 20 23 17 18 22 21 19 16 36 39 33 34 38 37 35 32 13 14 8 11 15 12 10 9 29 30 24 27 31 28 26 25 5 6 0 3 7 4 2 1 21 22 16 19 23 20 18 17 37 38 32 35 39 36 34 33 10 9 15 12 8 11 13 14 26 25 31 28 24 27 29 30 2 1 7 4 0 3 5 6 18 17 23 20 16 19 21 22 34 33 39 36 32 35 37 38 11 8 14 13 9 10 12 15 27 24 30 29 25 26 28 31 3 0 6 5 1 2 4 7 19 16 22 21 17 18 20 23 35 32 38 37 33 34 36 39 ГҗЕёГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬Г‘ВҸГ‘ЕҪ Г‘В15 12 10 9 13 14 8 11 31 28 26 25 29 30 24 27 7 4 2 1 5 6 0 3 23 20 18 17 21 22 16 19 39 36 34 33 37 38 32 35 12 15 9 10 14 13 11 8 28 31 25 26 30 29 27 24 4 7 1 2 6 5 3 0 20 23 17 18 22 21 19 16 36 39 33 34 38 37 35 32 13 14 8 11 15 12 10 9 29 30 24 27 31 28 26 25 5 6 0 3 7 4 2 1 21 22 16 19 23 20 18 17 37 38 32 35 39 36 34 33 10 9 15 12 8 11 13 14 26 25 31 28 24 27 29 30 2 1 7 4 0 3 5 6 18 17 23 20 16 19 21 22 34 33 39 36 32 35 37 38 11 8 14 13 9 10 12 15 27 24 30 29 25 26 28 31 3 0 6 5 1 2 4 7 19 16 22 21 17 18 20 23 35 32 38 37 33 34 36 39 [/code] ГҗЕёГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬Г‘ВҸГ‘ЕҪ Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ° ГҗвҖқГҗвҖәГҗЕЎ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ [code]Order? 40 Enter the name of the squares file: Inp .. writing type information to file InpTypeDetail_11.txt Counts ------ 2 diagonal Latin 2 associative 2 weakly pandiagonal 2 ultramagic 1 orthogonal pair 2 self-orthogonal[/code] ГҗвҖҷГ‘ВҒГ‘вҖҳ ГҗВІГҗВөГ‘вӮ¬ГҗВҪГҗВҫ. ГҗЛң ГҗВҪГҗВө ГҗВјГҗВҫГҗВіГҗВ»ГҗВҫ ГҗВұГ‘вҖ№Г‘вҖҡГ‘Е’ ГҗВёГҗВҪГҗ°ÑвҖЎГҗВө :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВўГ‘ВҚГҗВә-Г‘ВҒ, Г‘вҖҡГҗВөГҗВҝГҗВөГ‘вӮ¬Г‘Е’ ГҗВҪГҗВ°ГҗВҙГҗВҫ ГҗВҪГҗВ°ГҗВ№Г‘вҖҡГҗВё ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 12-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВөГҗВ¶ГҗВөГҗВ»ГҗВё ГҗВҫГҗВҪ Г‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГ‘Ж’ГҗВөГ‘вҖҡ. ГҗЕёГҗВҫГҗВәГҗВ° ГҗВҪГҗВө ГҗВ·ГҗВҪГҗ°ÑЕҪ, ГҗВәГҗВ°ГҗВә ГҗВөГҗВіГҗВҫ ГҗВёГ‘ВҒГҗВәГҗ°ÑвҖҡГ‘Е’, ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВ° Harry White LatinSquares ГҗВҪГҗВө ГҗВҝГҗВҫГҗВјГҗВҫГҗВіГҗВ°ГҗВөГ‘вҖҡ. ГҗвҖңГҗВҫГ‘ВҒГҗВҝГҗВҫГҗВҙГҗВ°! ГҗЕёГ‘вӮ¬ГҗВөГҗВҙГҗВ»ГҗВ°ГҗВіГҗ°ÑЕҪ ГҗВІГҗВ°ГҗВј ГҗВ·ГҗВ°ГҗВҪГ‘ВҸГ‘вҖҡГ‘Е’Г‘ВҒГ‘ВҸ Г‘ВҚГ‘вҖҡГҗВёГҗВј ГҗВІГҗВҫГҗВҝГ‘вӮ¬ГҗВҫГ‘ВҒГҗВҫГҗВј. ГҗвҖўГ‘ВҒГҗВ»ГҗВё ГҗВөГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВёГҗВҙГҗВөГҗВё, ГҗВҝГҗВҫГҗВ¶ГҗВ°Гҗ»ÑƒГҗВ№Г‘ВҒГ‘вҖҡГҗВ°, ГҗВҝГҗВҫГҗВҙГҗВөГҗВ»ГҗВёГ‘вҖҡГҗВөГ‘ВҒГ‘Е’. ГҗЛңГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ 12-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВІ ГҗВјГҗВҫГҗВёГ‘вҖҰ Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’Г‘ВҸГ‘вҖҰ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВҫ ГҗВјГҗВҪГҗВҫГҗВіГҗВҫ, ГҗВҪГҗВҫ ГҗВҫГҗВҪГҗВё ГҗВҪГҗВө ГҗВҙГҗ°ÑЕҪГ‘вҖҡ ГҗВІ Г‘вӮ¬ГҗВ°ГҗВ·ГҗВ»ГҗВҫГҗВ¶ГҗВөГҗВҪГҗВёГҗВё ГҗВҪГҗВ° ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ ГҗвҖәГҗЕЎ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ. ГҗЕёГ‘вӮ¬ГҗВёГҗВјГҗВөГ‘вӮ¬ Г‘Ж’ГҗВ¶ГҗВө ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·Г‘вҖ№ГҗВІГҗВ°ГҗВ»ГҗВ° ГҗВІГ‘вҖ№Г‘ЛҶГҗВө, ГҗВҝГҗВҫГҗВІГ‘вҖҡГҗВҫГ‘вӮ¬Г‘ЕҪ 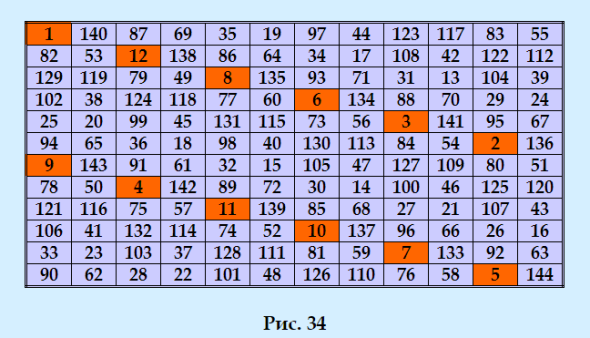 ГҗВ ГҗВ°ГҗВ·ГҗВ»ГҗВҫГҗВ¶ГҗВёГ‘вҖҡГҗВө Г‘ВҚГ‘вҖҡГҗВҫГ‘вҖҡ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ ГҗВҪГҗВ° ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ ГҗвҖәГҗЕЎ, ГҗВІГ‘вҖ№ ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГ‘вҖҡГҗВө ГҗВҫГҗВұГҗВҫГҗВұГ‘вҖ°Г‘вҖҳГҗВҪГҗВҪГ‘вҖ№ГҗВө ГҗвҖәГҗЕЎ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВқГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪ ГҗВҪГҗВҫГҗВІГ‘вҖ№ГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 13-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°! ГҗЕёГҗВҫГҗВҙГ‘вӮ¬ГҗВҫГҗВұГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГҗВё Г‘вҖЎГҗВёГ‘вҖҡГҗВ°ГҗВ№Г‘вҖҡГҗВө ГҗВІ Г‘вҖҡГҗВөГҗВјГҗВө "Experiment (pandiagonal DLS of order 13)" ГҗЕёГҗВҫГҗВәГҗВ°ГҗВ·Г‘вҖ№ГҗВІГҗ°ÑЕҪ Г‘ВҚГ‘вҖҡГҗВҫГ‘вҖҡ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВІ Г‘вҖһГҗВҫГ‘вӮ¬ГҗВјГҗ°ÑвҖҡГҗВө ГҗВЎГҗВқ ГҗвҖқГҗвҖәГҗЕЎ 0 12 3 10 6 4 9 5 11 7 8 1 2 6 1 9 0 11 12 2 10 4 3 5 7 8 11 7 2 8 5 1 0 6 12 10 4 9 3 5 4 12 3 7 9 8 1 0 11 6 2 10 8 6 10 11 4 3 7 2 9 5 1 12 0 1 2 0 6 10 5 11 12 3 8 7 4 9 7 9 1 12 2 8 6 4 10 0 11 3 5 3 8 5 4 9 0 1 7 2 6 12 10 11 12 0 11 7 3 10 5 9 8 1 2 6 4 2 10 6 1 12 11 4 3 5 9 0 8 7 9 3 8 2 0 6 12 11 7 4 10 5 1 4 5 7 9 8 2 10 0 1 12 3 11 6 10 11 4 5 1 7 3 8 6 2 9 0 12 ГҗЛңГҗВ»ГҗȄЕҪГ‘ВҒГ‘вҖҡГ‘вӮ¬Гҗ°ÑвҖ ГҗВёГ‘ВҸ  ГҗВӯГ‘вҖҡГҗВҫГ‘вҖҡ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҪГҗВө Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВё Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВ№. ГҗЕёГҗВҫГҗȄĄвҖЎГҗВөГҗВҪ ГҗВјГҗВҪГҗВҫГҗВ№ ГҗВёГҗВ· ГҗвҖқГҗвҖәГҗЕЎ, ГҗВҝГ‘вӮ¬ГҗВёГҗВІГҗВөГҗВҙГ‘вҖҳГҗВҪГҗВҪГҗВҫГҗВіГҗВҫ ГҗВІ Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ГҗВө OEIS, ГҗВәГҗВҫГҗВјГҗВұГҗВёГҗВҪГҗ°ÑвҖ ГҗВёГҗВөГҗВ№ ГҗВҝГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГҗВ°ГҗВҪГҗВёГҗВ№. ГҗвҖ”ГҗВҙГҗВҫГ‘вӮ¬ГҗВҫГҗВІГҗВҫ Г‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗ°ÑЕҪГ‘вҖҡ ГҗВҝГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГҗВ°ГҗВҪГҗВёГ‘ВҸ, ГҗВёГҗВ·ГҗВІГҗВөГ‘ВҒГ‘вҖҡГҗВҪГ‘вҖ№ГҗВө ГҗВјГҗВҪГҗВө ГҗВҝГҗВҫ Г‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗВө Г‘ВҒ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВјГҗВё ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ°ГҗВјГҗВё. ГҗВ§ГҗВёГ‘вҖҡГҗВ°ГҗВ№Г‘вҖҡГҗВө ГҗВјГҗВҫГ‘ЕҪ ГҗВәГҗВҪГҗВёГҗВіГ‘Ж’ "ГҗвҖҷГҗВҫГҗȄЛҶГҗВөГҗВұГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВёГ‘вӮ¬ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ". ГҗВҗ Г‘вҖҡГҗВ°ГҗВәГҗВ¶ГҗВө ГҗВјГҗВҫГҗВё Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ГҗВё; ГҗВҙГҗВ°ГҗВ»ГҗВөГҗВәГҗВҫ ГҗВҪГҗВө ГҗВІГ‘ВҒГ‘вҖҳ ГҗВұГ‘вҖ№ГҗВ»ГҗВҫ ГҗВІГҗВәГҗȄЕҪГ‘вҖЎГҗВөГҗВҪГҗВҫ ГҗВІ ГҗВәГҗВҪГҗВёГҗВіГ‘Ж’, ГҗВІ Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’Г‘ВҸГ‘вҖҰ ГҗВІГ‘вҖ№ ГҗВҪГҗВ°ГҗВ№ГҗВҙГ‘вҖҳГ‘вҖҡГҗВө ГҗВіГҗВҫГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҙГҗВҫ ГҗВұГҗВҫГҗȄ΄ЛҶГҗВө, ГҗВҪГҗВөГҗВ¶ГҗВөГҗВ»ГҗВё ГҗВІ ГҗВәГҗВҪГҗВёГҗВіГҗВө. ГҗЕЎ Г‘вҖҡГҗВҫГҗВјГ‘Ж’ ГҗВ¶ГҗВө, ГҗВҪГҗВө Г‘вҖҡГҗВҫГҗ»ÑŒГҗВәГҗВҫ ГҗВҫ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГ‘вҖҰ, ГҗВҪГҗВҫ ГҗВё ГҗВҫ ГҗВ»Гҗ°ÑвҖҡГҗВёГҗВҪГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗ°ÑвҖҰ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВқГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҪГҗВө "ГҗВҝГ‘Ж’Г‘ВҒГ‘вҖҡГ‘вҖ№Г‘ЛҶГҗВәГҗВ°", Г‘ВҸ Г‘Ж’ГҗВ¶ГҗВө ГҗВҪГҗ°ÑЛҶГҗВ»ГҗВ° ГҗВҫГҗВҙГҗВёГҗВҪ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ Г‘ВҒГҗВҫГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ ГҗВә ГҗВҪГҗВөГҗВјГ‘Ж’. ГҗВқГҗВҫ... Г‘ВҚГ‘вҖҡГҗВҫГ‘вҖҡ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ Г‘ВҒГҗВҫГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ ГҗВҪГҗВө Г‘ВҸГҗВІГҗȄВҸГҗВөГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВҪГҗВё ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВј, ГҗВҪГҗВё Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВј. ГҗЕҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВёГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҪГҗВҫ ГҗВҫГҗВұГ‘ВҒГ‘вҖЎГҗВёГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ Г‘ВҚГ‘вҖҡГҗВҫГ‘вҖҡ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГҗВ»ГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’Г‘ЕҪ, ГҗВҪГҗВ°ГҗВ№ГҗВҙГ‘вҖҳГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВ»ГҗВё Г‘вҖҰГҗВҫГ‘вҖҡГ‘ВҸ ГҗВұГ‘вҖ№ ГҗВҫГҗВҙГҗВёГҗВҪ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ Г‘ВҒГҗВҫГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ. ГҗЕЎГҗВҫГҗВҙ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГҗВө Tomas Brada EUwk5iiQf7iUNBpDAWeGZBC71RCJazs7RxWdCS2 PS. ГҗвҖқГҗВ°, ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗ°ÑВҸ ГҗВҝГҗ°ÑвӮ¬ГҗВ° ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВјГҗВҪГҗВө ГҗВҪГ‘Ж’ГҗВ¶ГҗВҪГҗВ°. ГҗвҖқГҗȄВҸ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВёГ‘ВҸ ГҗВҝГ‘вӮ¬ГҗВёГҗВҪГ‘вҖ ГҗВёГҗВҝГҗВёГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ ГҗВҪГҗВҫГҗВІГҗВҫГҗВіГҗВҫ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВіГҗВҫ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВҫГҗВіГҗВҫ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ°. ГҗВўГҗВ°ГҗВәГҗВҫГҗВіГҗВҫ Г‘Ж’ ГҗВјГҗВөГҗВҪГ‘ВҸ ГҗВөГ‘вҖ°Г‘вҖҳ ГҗВҪГҗВө ГҗВұГ‘вҖ№ГҗВ»ГҗВҫ :) ГҗЕЎГ‘ВҒГ‘вҖҡГҗ°ÑвҖҡГҗВё, Г‘вӮ¬ГҗВ°ГҗВҪГ‘Е’Г‘ЛҶГҗВө Г‘ВҸ ГҗВҪГҗ°ÑЛҶГҗВ»ГҗВ° ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 13-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВҫГҗВҙГҗВҪГҗВ° ГҗВёГҗВ· ГҗВҪГҗВёГ‘вҖҰ ГҗВұГ‘вҖ№ГҗВ»ГҗВ° ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВ°. ГҗВқГҗВҫ Г‘ВҚГ‘вҖҡГҗВҫ Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВө ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ, ГҗВҫГҗВҪГҗВё ГҗВҪГҗВө ГҗВҙГҗВ°ГҗВҙГ‘Ж’Г‘вҖҡ ГҗВҝГ‘вӮ¬ГҗВёГҗВҪГ‘вҖ ГҗВёГҗВҝГҗВёГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ ГҗВҪГҗВҫГҗВІГҗВҫГҗВіГҗВҫ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВіГҗВҫ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВҫГҗВіГҗВҫ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ°. ГҗвҖқГ‘вӮ¬Г‘Ж’ГҗВіГҗВҫГҗВө ГҗВҙГҗВөГҗВ»ГҗВҫ - ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ, ГҗВҪГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВ№ Г‘вҖҡГҗВөГҗВҝГҗВөГ‘вӮ¬Г‘Е’, ГҗВҫГҗВҪ ГҗВҪГҗВө Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№. ГҗЕЎГҗВҫГҗВјГҗВ°ГҗВҪГҗВҙГҗВҪГҗ°ÑВҸ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВәГҗВ° ГҗВҙГҗȄВҸ ГҗВ·ГҗВ°ГҗВҝГ‘Ж’Г‘ВҒГҗВәГҗВ° ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГ‘вҖ№ Tomas Brada ortogonb.exe EUwk5iiQf7iUNBpDAWeGZBC71RCJazs7RxWdCS2 >out.txt ГҗВқГҗВө ГҗВ·ГҗВҪГҗ°ÑЕҪ, ГҗВәГҗВ°ГҗВә ГҗВұГ‘Ж’ГҗВҙГҗВөГ‘вҖҡ Г‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗ°ÑвҖҡГ‘Е’: ГҗВҪГҗВё Г‘вӮ¬ГҗВ°ГҗВ·Г‘Ж’ ГҗВҪГҗВө ГҗВҝГ‘вӮ¬ГҗВҫГҗВұГҗВҫГҗВІГҗВ°ГҗВ»ГҗВ° ГҗВҫГҗВұГ‘ВҒГ‘вҖЎГҗВёГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ ГҗВҝГҗВҫГҗВ»ГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’Г‘ЕҪ ГҗвҖқГҗвҖәГҗЕЎ 13-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗвҖқ-Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°ГҗВ»ГҗВөГҗВ№ Г‘Ж’ Г‘ВҚГ‘вҖҡГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҪГҗВө ГҗВҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВјГҗВҪГҗВҫГҗВіГҗВҫ. ГҗВЈ ГҗВјГҗВөГҗВҪГ‘ВҸ Г‘ВҚГ‘вҖҡГҗВ° ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВ° ГҗВҪГҗВҫГ‘вӮ¬ГҗВјГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ Г‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗВ°ГҗВөГ‘вҖҡ ГҗВҙГҗȄВҸ ГҗвҖқГҗвҖәГҗЕЎ 11-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗВЎ ГҗвҖқГҗвҖәГҗЕЎ 12-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° Г‘Ж’ГҗВ¶ГҗВө ГҗВҝГ‘вӮ¬ГҗВҫГҗВұГҗВ»ГҗВөГҗВјГ‘вҖ№ Г‘ВҒ ГҗВҝГҗВ°ГҗВјГ‘ВҸГ‘вҖҡГ‘Е’Г‘ЕҪ ГҗВІГҗВҫГҗВ·ГҗВҪГҗВёГҗВәГҗ°ÑЕҪГ‘вҖҡ, ГҗВҪГҗВҫ Г‘ВҸ ГҗВҝГ‘вӮ¬ГҗВҫГҗВұГҗВҫГҗВІГҗВ°ГҗВ»ГҗВ° ГҗвҖқГҗвҖәГҗЕЎ Г‘ВҒ ГҗВұГҗВҫГҗȄ΄ЛҶГҗВёГҗВј ГҗВәГҗВҫГҗВ»ГҗВёГ‘вҖЎГҗВөГ‘ВҒГ‘вҖҡГҗВІГҗВҫГҗВј ГҗвҖқ-Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°ГҗВ»ГҗВөГҗВ№. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЕёГ‘вӮ¬ГҗВёГҗВІГҗВөГҗВҙГ‘Ж’ Г‘вҖ ГҗВёГ‘вҖҡГҗ°ÑвҖҡГ‘Ж’ ГҗЕёГҗВҫГҗВәГҗВ°Гҗ¶Ñƒ Г‘Ж’ГҗВҪГҗВёГҗВәГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ ГҗвҖқГҗвҖәГҗЕЎ 13-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗЕ“ГҗВҫГҗВ¶ГҗВҪГҗВҫ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡГ‘Е’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ, ГҗВёГ‘ВҒГҗВҝГҗВҫГҗ»ÑŒГҗВ·Г‘Ж’Г‘ВҸ Г‘ВҚГ‘вҖҡГ‘Ж’ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ (ГҗВҙГҗВ°ГҗВ¶ГҗВө ГҗВҙГҗВІГҗВө ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№), ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј ГҗВ»Гҗ°ÑвҖҡГҗВёГҗВҪГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ. ГҗВӨГҗВҫГ‘вӮ¬ГҗВјГ‘Ж’Гҗ»Ñƒ ГҗВҪГҗВ°ГҗВҝГҗВҫГҗВјГҗВёГҗВҪГҗ°ÑЕҪ ГҗВЎ = 13*A + B +1 ГҗВқГҗВҫ, ГҗВәГҗВ°ГҗВә Г‘Ж’ГҗВ¶ГҗВө ГҗВҫГ‘вҖҡГҗВјГҗВөГ‘вҖЎГҗВөГҗВҪГҗВҫ ГҗВІГ‘вҖ№Г‘ЛҶГҗВө, Г‘ВҚГ‘вҖҡГҗВҫ ГҗВјГҗВ°ГҗВ»ГҗВҫ ГҗВёГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҪГ‘вҖ№ГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВқГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪ ГҗВөГ‘вҖ°Г‘вҖҳ ГҗВҫГҗВҙГҗВёГҗВҪ Г‘Ж’ГҗВҪГҗВёГҗВәГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 13-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°! 0 3 7 1 9 4 10 6 5 8 12 2 11 2 1 12 0 10 11 5 9 7 6 4 8 3 8 6 2 11 12 9 1 10 4 0 3 7 5 10 11 5 3 2 8 12 0 1 7 9 4 6 5 7 6 8 4 0 3 11 12 2 1 10 9 12 9 4 7 3 5 8 2 6 10 11 0 1 4 0 10 9 1 7 6 5 11 3 2 12 8 11 12 1 2 6 10 4 7 9 5 8 3 0 3 2 11 10 0 1 9 12 8 4 6 5 7 6 8 3 5 11 12 0 4 10 9 7 1 2 7 5 9 12 8 2 11 3 0 1 10 6 4 9 4 8 6 5 3 7 1 2 12 0 11 10 1 10 0 4 7 6 2 8 3 11 5 9 12 ГҗВЎГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖҡГҗВө Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГҗВө https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=128&postid=1589 ГҗЕёГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬ГҗВәГҗВ° Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІ Order? 13
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_15.txt
Counts
------
1 diagonal Latin
1 associative
1 pandiagonal
1 ultramagic
1 natural \diagonalГҗВӯГ‘вҖҡГҗВҫГ‘вҖҡ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҪГҗВө Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№, ГҗВәГҗВ°ГҗВә ГҗВё ГҗВҝГ‘вӮ¬ГҗВөГҗВҙГ‘вҖ№ГҗВҙГ‘Ж’Г‘вҖ°ГҗВёГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ. ГҗвҖқГҗȄВҸ ГҗВҪГҗВөГҗВіГҗВҫ Г‘вҖҡГҗВҫГ‘вҖҡ ГҗВ¶ГҗВө ГҗВІГҗВҫГҗВҝГ‘вӮ¬ГҗВҫГ‘ВҒ: ГҗВёГҗВјГҗВөГҗВөГ‘вҖҡ ГҗВ»ГҗВё ГҗВҫГҗВҪ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ Г‘ВҒГҗВҫГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ? ГҗВқГҗВ°ГҗВҙГҗВҫ ГҗВҫГҗВұГ‘ВҒГ‘вҖЎГҗВёГ‘вҖҡГ‘вҖ№ГҗВІГҗ°ÑвҖҡГ‘Е’. ГҗЕЎГҗВҫГҗВҙ Г‘ВҚГ‘вҖҡГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГҗВө Tomas Brada ETsurYrh4HnfrhyvofvcPgHs7u7QrtgUi4iATH |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВҰГҗВёГ‘вҖҡГҗ°ÑвҖҡГҗВ° ГҗВўГ‘ВҚГҗВә-Г‘ВҒ, Г‘вҖҡГҗВөГҗВҝГҗВөГ‘вӮ¬Г‘Е’ ГҗВҪГҗВ°ГҗВҙГҗВҫ ГҗВҪГҗВ°ГҗВ№Г‘вҖҡГҗВё ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 12-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВөГҗВ¶ГҗВөГҗВ»ГҗВё ГҗВҫГҗВҪ Г‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГ‘Ж’ГҗВөГ‘вҖҡ. ГҗвҖҳГ‘Е’Г‘ЕҪГ‘ВҒГ‘Е’ ГҗВҪГҗВ°ГҗВҙ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВ·ГҗВ°ГҗВҙГҗ°ÑвҖЎГҗВөГҗВ№. ГҗЕёГҗВҫГҗВәГҗВ° ГҗВұГҗВөГҗВ·Г‘Ж’Г‘ВҒГҗВҝГҗВөГ‘ЛҶГҗВҪГҗВҫ. ГҗВқГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҫ ГҗВјГҗВҪГҗВҫГҗВіГҗВҫ Г‘ВҒГҗВ»ГҗВ°ГҗВұГҗВҫ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ, ГҗВҪГҗВҫ ГҗВҫГҗВҪГҗВё ГҗВҪГҗВө Г‘вҖҰГҗВҫГ‘вҖҡГ‘ВҸГ‘вҖҡ ГҗВұГ‘вҖ№Г‘вҖҡГ‘Е’ Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВјГҗВё. 144 ГҗВІГҗ°ÑвӮ¬ГҗВёГҗВ°ГҗВҪГ‘вҖҡГҗВ°, ГҗВҝГҗВҫГҗȄĄвҖЎГҗВ°ГҗВөГҗВјГ‘вҖ№ГҗВө ГҗВҝГҗ°ÑвӮ¬ГҗВ°ГҗВ»ГҗВ»ГҗВөГҗ»ÑŒГҗВҪГ‘вҖ№ГҗВј ГҗВҝГҗВөГ‘вӮ¬ГҗВөГҗВҪГҗВҫГ‘ВҒГҗВҫГҗВј ГҗВҪГҗВ° Г‘вҖҡГҗВҫГ‘вӮ¬ГҗВө, ГҗВҪГҗВө ГҗВҙГҗ°ÑЕҪГ‘вҖҡ Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ. ГҗЕҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗ°ÑВҸ ГҗВҝГҗ°ÑвӮ¬ГҗВ° Г‘ВҒГҗВ»ГҗВ°ГҗВұГҗВҫ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 12-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВҪГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВ° ГҗВјГҗВҪГҗВҫГҗВ№ ГҗВҙГҗВ°ГҗВІГҗВҪГҗВҫ, ГҗВІГҗВҫГ‘вҖҡ ГҗВҫГҗВҪГҗВ° 0 2 3 4 9 8 1 5 10 11 6 7 3 1 7 6 8 9 2 0 11 4 10 5 1 9 2 5 7 10 4 6 3 0 11 8 5 4 10 3 11 0 7 1 6 2 8 9 6 7 11 10 4 1 3 8 2 9 5 0 11 0 6 8 2 5 9 3 7 10 1 4 10 6 1 0 5 4 11 9 8 7 2 3 9 11 0 7 1 6 8 10 4 5 3 2 7 5 8 11 0 3 10 2 9 6 4 1 4 10 5 9 3 2 6 7 1 8 0 11 8 3 9 2 6 11 5 4 0 1 7 10 2 8 4 1 10 7 0 11 5 3 9 6 0 3 1 5 6 11 10 9 7 4 8 2 2 1 9 4 7 0 6 11 5 10 3 8 3 7 2 10 11 6 1 0 8 5 9 4 4 6 5 3 10 8 0 7 11 9 2 1 9 8 7 11 4 2 5 1 0 3 6 10 8 9 10 0 1 5 4 6 3 2 11 7 1 2 4 7 3 9 11 8 10 6 5 0 5 0 6 1 8 3 9 10 2 7 4 11 10 11 3 6 2 7 8 4 9 1 0 5 11 4 0 2 9 10 7 5 6 8 1 3 6 10 11 8 5 1 2 3 4 0 7 9 7 5 8 9 0 4 3 2 1 11 10 6 ГҗВЎГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖҡГҗВө Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГҗВө https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=110&postid=1036 ГҗВқГ‘Ж’, ГҗВёГҗВ· ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ Г‘ВҒГҗВ»ГҗВ°ГҗВұГҗВҫ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВјГҗВҫГҗВ¶ГҗВҪГҗВҫ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡГ‘Е’ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј ГҗВ»Гҗ°ÑвҖҡГҗВёГҗВҪГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ. ГҗВӯГ‘вҖҡГҗВҫ ГҗВұГ‘Ж’ГҗВҙГҗВөГ‘вҖҡ ГҗВҫГ‘вӮ¬ГҗВёГҗВіГҗВёГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ, Г‘вҖҡГҗВ°ГҗВәГҗВёГ‘вҖҰ Г‘Ж’ ГҗВјГҗВөГҗВҪГ‘ВҸ Г‘вӮ¬ГҗВ°ГҗВҪГ‘Е’Г‘ЛҶГҗВө ГҗВҪГҗВө ГҗВұГ‘вҖ№ГҗВ»ГҗВҫ. ГҗВЎГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГ‘ЕҪ ГҗВё ГҗВҝГҗВҫГҗВәГҗВ°Гҗ¶Ñƒ. ГҗВқГҗВҫ ГҗВјГҗВҪГҗВө ГҗВҪГ‘Ж’ГҗВ¶ГҗВөГҗВҪ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ 12-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВ° Г‘вҖҡГҗВ°ГҗВәГҗВ¶ГҗВө ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗ°ÑВҸ ГҗВҝГҗ°ÑвӮ¬ГҗВ° ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ. ГҗЛңГ‘вҖ°ГҗВөГҗВј-Г‘ВҒ :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВөГ‘вҖЎГҗВ°ГҗВ№Г‘вҖҡГҗВө - ГҗВҝГ‘вӮ¬ГҗВёГҗВҪГ‘вҖ ГҗВёГҗВҝГҗВёГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ ГҗВҪГҗВҫГҗВІГ‘вҖ№ГҗВ№ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ 12-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° 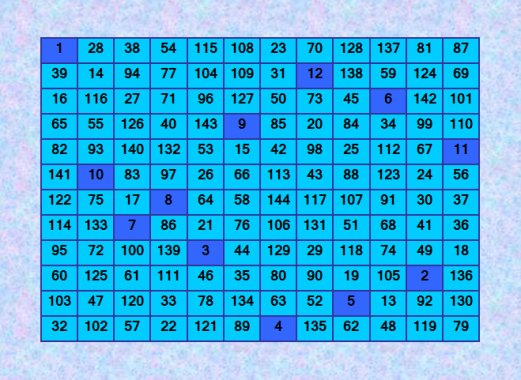 ГҗЕ“ГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪ ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј ГҗВ»Гҗ°ÑвҖҡГҗВёГҗВҪГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ Г‘ВҒ ГҗВёГ‘ВҒГҗВҝГҗВҫГҗ»ÑŒГҗВ·ГҗВҫГҗВІГҗВ°ГҗВҪГҗВёГҗВөГҗВј ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ Г‘ВҒГҗВ»ГҗВ°ГҗВұГҗВҫ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ, ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГҗВҫГҗВ№ ГҗВІ ГҗВҝГ‘вӮ¬ГҗВөГҗВҙГ‘вҖ№ГҗВҙГ‘Ж’Г‘вҖ°ГҗВөГҗВј ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГҗВө. ГҗЕҫГҗВұГ‘вӮ¬Гҗ°ÑвҖҡГҗВёГ‘вҖҡГҗВө ГҗВІГҗВҪГҗВёГҗВјГҗВ°ГҗВҪГҗВёГҗВө ГҗВҪГҗВ° ГҗВІГ‘вҖ№ГҗВҙГҗВөГҗВ»ГҗВөГҗВҪГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҪГҗ°ÑвҖЎГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ Г‘вҖ ГҗВөГҗВҝГҗВҫГ‘вҖЎГҗВәГ‘Ж’. ГҗВқГҗВ°ГҗВ№ГҗВҙГҗВёГ‘вҖҡГҗВө ГҗВҝГ‘вӮ¬ГҗВёГҗВҪГ‘вҖ ГҗВёГҗВҝГҗВёГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВө ГҗВҫГ‘вҖҡГҗВ»ГҗВёГ‘вҖЎГҗВёГҗВө Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВҪГҗ°ÑвҖЎГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ Г‘вҖ ГҗВөГҗВҝГҗВҫГ‘вҖЎГҗВәГҗВё ГҗВҫГ‘вҖҡ ГҗВҪГҗ°ÑвҖЎГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ Г‘вҖ ГҗВөГҗВҝГҗВҫГ‘вҖЎГҗВәГҗВё ГҗВІ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВј ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВҫГҗВј ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВө, ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГҗВҫГҗВј ГҗВІ ГҗВҝГ‘вӮ¬ГҗВөГҗВҙГ‘вҖ№ГҗВҙГ‘Ж’Г‘вҖ°ГҗВөГҗВј ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГҗВө. ГҗВўГҗВөГҗВҝГҗВөГ‘вӮ¬Г‘Е’ ГҗВҪГҗВ°ГҗВҙГҗВҫ ГҗВёГ‘ВҒГҗВәГҗ°ÑвҖҡГ‘Е’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ 12-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗвҖқГ‘Ж’ГҗВјГҗ°ÑЕҪ, Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВҫГҗВҪГҗВё Г‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГ‘Ж’Г‘ЕҪГ‘вҖҡ. ГҗВҗ ГҗВҝГҗВҫГ‘вҖҡГҗВҫГҗВј ГҗВ¶ГҗВөГҗВ»Гҗ°ÑвҖҡГҗВөГҗ»ÑŒГҗВҪГҗВҫ ГҗВҪГҗВ°ГҗВ№Г‘вҖҡГҗВё ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВё ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГ‘вҖҡГ‘Е’ ГҗВҝГ‘вӮ¬ГҗВёГҗВҪГ‘вҖ ГҗВёГҗВҝГҗВёГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ ГҗВҪГҗВҫГҗВІГ‘вҖ№ГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ 12-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. PS. ГҗВқГҗ°ÑвҖЎГҗВ°Гҗ»ÑŒГҗВҪГҗ°ÑВҸ Г‘вҖ ГҗВөГҗВҝГҗВҫГ‘вҖЎГҗВәГҗВ° ГҗВІ ГҗВјГҗВ°ГҗВіГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВҫГҗВј ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВө ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° n - Г‘ВҚГ‘вҖҡГҗВҫ ГҗВҝГҗВөГ‘вӮ¬ГҗВІГ‘вҖ№ГҗВө n Г‘ВҚГҗВ»ГҗВөГҗВјГҗВөГҗВҪГ‘вҖҡГҗВҫГҗВІ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЕёГҗВҫГҗВәГҗВ° ГҗВҫГҗВұ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВј ГҗвҖқГҗвҖәГҗЕЎ 13-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВҪГҗВө Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВҫГҗВј ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВј... ГҗВҰГҗВёГ‘вҖҡГҗ°ÑвҖҡГҗВ° ГҗВқГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҪГҗВө "ГҗВҝГ‘Ж’Г‘ВҒГ‘вҖҡГ‘вҖ№Г‘ЛҶГҗВәГҗВ°", Г‘ВҸ Г‘Ж’ГҗВ¶ГҗВө ГҗВҪГҗ°ÑЛҶГҗВ»ГҗВ° ГҗВҫГҗВҙГҗВёГҗВҪ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ Г‘ВҒГҗВҫГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ ГҗВә ГҗВҪГҗВөГҗВјГ‘Ж’. ГҗЕЎГҗВҫГҗВҪГҗВөГ‘вҖЎГҗВҪГҗВҫ, ГҗȄĄвҖЎГ‘ЛҶГҗВө ГҗВҫГҗВұГ‘ВҒГ‘вҖЎГҗВёГ‘вҖҡГ‘вҖ№ГҗВІГҗ°ÑвҖҡГ‘Е’ Г‘ВҚГ‘вҖҡГҗВҫГ‘вҖҡ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВҫГҗВ№ Tomas Brada, ГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬Гҗ°ÑВҸ ГҗВұГҗВөГ‘вӮ¬Г‘вҖҳГ‘вҖҡ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ ГҗВҝГҗВҫ Г‘вҖЎГҗ°ÑВҒГ‘вҖҡГ‘ВҸГҗВј. ГҗЕЎГҗВҫГҗВјГҗВ°ГҗВҪГҗВҙГҗВҪГҗ°ÑВҸ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВәГҗВ° ГҗВҙГҗȄВҸ ГҗВ·ГҗВ°ГҗВҝГ‘Ж’Г‘ВҒГҗВәГҗВ° ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГ‘вҖ№ ortogonbw.exe EUwk5iiQf7iUNBpDAWeGZBC71RCJazs7RxWdCS2 1 >out.txt ГҗЕёГҗВҫ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВәГҗВҫГҗВјГҗВ°ГҗВҪГҗВҙГҗВө ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВ° ГҗВұГ‘Ж’ГҗВҙГҗВөГ‘вҖҡ ГҗВҝГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬Г‘ВҸГ‘вҖҡГ‘Е’ ГҗВҝГҗВөГ‘вӮ¬ГҗВІГ‘Ж’Г‘ЕҪ Г‘вҖЎГҗ°ÑВҒГ‘вҖҡГ‘Е’. ГҗЕёГҗВҫГ‘ВҒГҗВәГҗВҫГҗ»ÑŒГҗВәГ‘Ж’ Г‘ВҸ Г‘Ж’ГҗВ¶ГҗВө ГҗВҪГҗВөГҗВјГҗВҪГҗВҫГҗВіГҗВҫ ГҗВёГ‘ВҒГҗВәГҗВ°ГҗВ»ГҗВ° ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ ГҗВә Г‘ВҚГ‘вҖҡГҗВҫГҗВјГ‘Ж’ ГҗвҖқГҗвҖәГҗЕЎ (ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВҫГҗВ№ ГҗвҖҳГҗВөГҗȄвҖ№Г‘ЛҶГҗВөГҗВІГҗВ° ortogon_u), Г‘ВҒГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ ГҗВҝГҗВҫГҗВҝГ‘вӮ¬ГҗВҫГҗВұГ‘Ж’Г‘ЕҪ ГҗВ·ГҗВ°ГҗВҝГ‘Ж’Г‘ВҒГ‘вҖҡГҗВёГ‘вҖҡГ‘Е’ ГҗВІГ‘вҖҡГҗВҫГ‘вӮ¬Г‘Ж’Г‘ЕҪ Г‘вҖЎГҗ°ÑВҒГ‘вҖҡГ‘Е’. ГҗвҖ”ГҗВ°ГҗВҝГ‘Ж’Г‘ВҒГ‘вҖҡГҗВёГҗВ»ГҗВ° ГҗВҝГҗВҫГҗВёГ‘ВҒГҗВә ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ ГҗВІГҗВҫ ГҗВІГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВҫГҗВ№ Г‘вҖЎГҗ°ÑВҒГ‘вҖҡГҗВё C:\Users\ГҗвҖқГҗВҫГҗВј\Downloads\libr>ortogonbw.exe EUwk5iiQf7iUNBpDAWeGZBC71RCJazs7RxWdCS2 2 1>out.txt init_trans(13) used 575 nodes num_dtrans: 11061 init_disjoint(13) used 170 heads and 143963 nodes L(0) c(32) 2 / 801 L(1) c(83) X / 310 ГҗВқГ‘Ж’, ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВёГҗВә ГҗВҪГҗВө Г‘ВҒГҗВёГҗ»ÑŒГҗВҪГҗВҫ ГҗВәГ‘вӮ¬Г‘Ж’Г‘вҖҡГҗВҫГҗВ№, ГҗВІГ‘ВҒГҗВөГҗВіГҗВҫ 11061 ГҗвҖқ-Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°ГҗВ»ГҗВөГҗВ№, 801 Г‘вҖЎГҗ°ÑВҒГ‘вҖҡГ‘Е’. ГҗЕҫГҗВҙГҗВҪГҗВ°ГҗВәГҗВҫ ГҗВҪГҗВ° ГҗВјГҗВҫГ‘вҖҳГҗВј ГҗЕёГҗЕЎ ГҗВҫГҗВұГ‘ВҒГ‘вҖЎГҗВёГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ ГҗВөГҗВіГҗВҫ ГҗВҪГҗВөГ‘вӮ¬ГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ. ГҗЕ“ГҗВҫГҗВ¶ГҗВҪГҗВҫ Г‘вҖҡГҗВҫГҗ»ÑŒГҗВәГҗВҫ ГҗВҪГҗВөГ‘ВҒГҗВәГҗВҫГҗ»ÑŒГҗВәГҗВҫ ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГҗВёГ‘ВҒГҗВәГҗ°ÑвҖҡГ‘Е’, ГҗВІГҗВҙГ‘вӮ¬Г‘Ж’ГҗВі ГҗВҝГҗВҫГҗВҝГҗВ°ГҗВҙГ‘вҖҳГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВёГҗВ»ГҗВё Г‘вҖҰГҗВҫГ‘вҖҡГ‘ВҸ ГҗВұГ‘вҖ№ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ. ГҗВЎГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ ГҗВҝГҗВҫГ‘ВҒГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬Г‘ЕҪ, ГҗВәГҗВ°ГҗВә ГҗВұГ‘Ж’ГҗВҙГ‘Ж’Г‘вҖҡ ГҗВҝГҗВҫГ‘ВҸГҗВІГҗȄВҸГ‘вҖҡГ‘Е’Г‘ВҒГ‘ВҸ ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ. ГҗВҗ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВёГҗВә ГҗВҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВәГ‘вӮ¬Гҗ°ÑВҒГҗВёГҗВІГ‘вҖ№ГҗВ№, ГҗВөГ‘вҖ°Г‘вҖҳ Г‘вӮ¬ГҗВ°ГҗВ· ГҗВҝГҗВҫГҗВәГҗВ°Гҗ¶Ñƒ  ГҗВқГҗВө Г‘вҖ ГҗВёГҗВәГҗВ»ГҗВёГ‘вҖЎГҗВөГ‘ВҒГҗВәГҗВёГҗВ№ ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВё Гҗ°ÑВҒГ‘ВҒГҗВҫГ‘вҖ ГҗВёГҗ°ÑвҖҡГҗВёГҗВІГҗВҪГ‘вҖ№ГҗВ№, Г‘вҖҡГҗВҫ ГҗВөГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№. ГҗВ Гҗ°ÑВҒГҗВәГ‘вӮ¬Гҗ°ÑВҒГҗВәГҗВҫГҗВ№ ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВ° ГҗВҝГҗВ°ГҗВҪГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ°, ГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°ГҗВ»ГҗВё ГҗВҫГҗВҙГҗВҪГҗВҫГҗВіГҗВҫ ГҗВҪГҗВ°ГҗВҝГ‘вӮ¬ГҗВ°ГҗВІГҗВ»ГҗВөГҗВҪГҗВёГ‘ВҸ Г‘вӮ¬Гҗ°ÑВҒГҗВәГ‘вӮ¬Гҗ°ÑЛҶГҗВөГҗВҪГ‘вҖ№. ГҗВўГҗВҫГ‘вҖЎГҗВҪГҗВҫ Г‘вҖҡГҗВ°ГҗВә ГҗВ¶ГҗВө ГҗВјГҗВҫГҗВ¶ГҗВҪГҗВҫ Г‘вӮ¬Гҗ°ÑВҒГҗВәГ‘вӮ¬Гҗ°ÑВҒГҗВёГ‘вҖҡГ‘Е’ ГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°ГҗВ»ГҗВё ГҗВІГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВҫГҗВіГҗВҫ ГҗВҪГҗВ°ГҗВҝГ‘вӮ¬ГҗВ°ГҗВІГҗВ»ГҗВөГҗВҪГҗВёГ‘ВҸ. ГҗВЈ ГҗВјГҗВөГҗВҪГ‘ВҸ ГҗВөГ‘вҖ°Г‘вҖҳ ГҗВё ГҗВІГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВҫГҗВ№ ГҗВҝГҗВҫГҗВҙГҗВҫГҗВұГҗВҪГ‘вҖ№ГҗВ№ ГҗвҖқГҗвҖәГҗЕЎ ГҗВөГ‘ВҒГ‘вҖҡГ‘Е’, Г‘Ж’ГҗВҪГҗВёГҗВәГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№. ГҗвҖҷГ‘вҖ№Г‘ЛҶГҗВө ГҗВҫГҗВҪ ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВҘГҗВј... ГҗВ° ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ ГҗВә Г‘ВҚГ‘вҖҡГҗВҫГҗВјГ‘Ж’ ГҗВәГ‘вӮ¬Гҗ°ÑВҒГҗВёГҗВІГҗВҫГҗВјГ‘Ж’ ГҗВёГҗВҙГҗВөГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВјГ‘Ж’ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҪГҗВө Г‘ВҒГҗВҝГҗВөГ‘ЛҶГҗ°ÑвҖҡ ГҗВҝГҗВҫГ‘ВҸГҗВІГҗȄВҸГ‘вҖҡГ‘Е’Г‘ВҒГ‘ВҸ, ГҗВІГ‘вҖ№Г‘вҖҰГҗВҫГҗВҙГҗВҪГҗВҫГҗВ№ Г‘вҖһГҗВ°ГҗВ№ГҗВ» ГҗВҝГҗВҫГҗВәГҗВ° ГҗВҝГ‘Ж’Г‘ВҒГ‘вҖҡГҗВҫГҗВ№. ГҗЕёГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГ‘Ж’ ГҗвҖҳГҗВөГҗȄвҖ№Г‘ЛҶГҗВөГҗВІГҗВ° ГҗВәГ‘вӮ¬Г‘Ж’Г‘вҖҡГҗВёГҗВ»ГҗВ° ГҗВҙГҗВҫГҗВІГҗВҫГҗ»ÑŒГҗВҪГҗВҫ ГҗВҙГҗВҫГҗВ»ГҗВіГҗВҫ, ГҗВҝГҗВҫГҗВәГҗВ° ГҗВҝГҗВөГ‘вӮ¬ГҗВІГ‘вҖ№ГҗВ№ ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГ‘ВҸГҗВІГҗВёГҗȄВҒГ‘ВҸ. ГҗвҖҷГҗВҫГ‘вҖҡ ГҗВәГҗВ°ГҗВә Г‘ЛҶГҗВ»ГҗВ° ГҗВҝГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬ГҗВәГҗВ° ГҗВІ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВө ГҗвҖҳГҗВөГҗȄвҖ№Г‘ЛҶГҗВөГҗВІГҗВ° ГҗЕёГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬ГҗВәГҗВ° ГҗвҖқГҗвҖәГҗЕЎ13 ГҗВҪГҗВ° ГҗВјГҗ°ÑвӮ¬Г‘Е’Г‘ВҸГҗВ¶ГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’ (ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ) ГҗвҖҷГҗВІГҗВөГҗВҙГҗВөГҗВҪГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ: 1 ГҗВқГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҫ ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ: 0 ГҗвҖқ-Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҪГ‘ВҒГҗВІГҗВөГ‘вӮ¬Г‘ВҒГҗВ°ГҗВ»ГҗВөГҗВ№: 11061 ГҗВЎГҗВҫГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ: 1 ГҗвҖҷГ‘вӮ¬ГҗВөГҗВјГ‘ВҸ ГҗВІ Г‘ВҒГҗВөГҗВә: 4650 794 102 56 31 3 1 ГҗЕЎГҗВ°ГҗВә ГҗВҝГҗВөГ‘вӮ¬ГҗВІГ‘вҖ№ГҗВ№ ГҗЕҫГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГ‘ВҸГҗВІГҗВёГҗȄВҒГ‘ВҸ, Г‘ВҒГ‘вӮ¬ГҗВ°ГҗВ·Г‘Ж’ ГҗВҝГ‘вӮ¬ГҗВөГ‘вӮ¬ГҗВІГҗВ°ГҗВ»ГҗВ° ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГ‘Ж’. ГҗВқГҗВө ГҗВ·ГҗВҪГҗ°ÑЕҪ, Г‘ВҒ ГҗВәГҗВ°ГҗВәГҗВҫГҗВ№ Г‘ВҒГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВҫГҗВҪГ‘вҖ№ Г‘вҖЎГҗ°ÑВҒГ‘вҖҡГҗВё ГҗВІ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВө Tomas Brada Г‘ВҒГ‘вҖЎГҗВёГ‘вҖҡГҗ°ÑЕҪГ‘вҖҡГ‘ВҒГ‘ВҸ, ГҗВәГҗВ°ГҗВә Г‘ВҚГ‘вҖҡГҗВҫ Г‘ВҒГҗВҫГҗВҫГ‘вҖҡГҗВҪГҗВҫГ‘ВҒГҗВёГ‘вҖҡГ‘ВҒГ‘ВҸ Г‘ВҒ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВҫГҗВ№ ГҗвҖҳГҗВөГҗȄвҖ№Г‘ЛҶГҗВөГҗВІГҗВ°. ГҗЕёГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВ° ГҗвҖҳГҗВөГҗȄвҖ№Г‘ЛҶГҗВөГҗВІГҗВ° ГҗВҫГ‘вҖҡ 801 Г‘вҖЎГҗ°ÑВҒГ‘вҖҡГҗВөГҗВ№ ГҗВҙГҗВҫГ‘ЛҶГҗВ»ГҗВ° ГҗВҙГҗВҫ 794 Г‘вҖЎГҗ°ÑВҒГ‘вҖҡГҗВөГҗВ№. ГҗЕ“ГҗВҫГҗВ¶ГҗВҪГҗВҫ ГҗВҝГҗВҫГҗВҝГ‘вӮ¬ГҗВҫГҗВұГҗВҫГҗВІГҗ°ÑвҖҡГ‘Е’ ГҗВё ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВҫГҗВ№ ГҗвҖҳГҗВөГҗȄвҖ№Г‘ЛҶГҗВөГҗВІГҗВ° ГҗВҫГҗВұГ‘ВҒГ‘вҖЎГҗВёГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ Г‘ВҚГ‘вҖҡГҗВҫГ‘вҖҡ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВёГҗВә. ГҗВқГҗВҫ ГҗВҪГ‘Ж’ГҗВ¶ГҗВҪГҗВҫ ГҗВёГҗВјГҗВөГ‘вҖҡГ‘Е’ ГҗВІГҗВҫГҗВ·ГҗВјГҗВҫГҗВ¶ГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВҪГҗВөГҗВҝГ‘вӮ¬ГҗВөГ‘вӮ¬Г‘вҖ№ГҗВІГҗВҪГҗВҫГҗВ№ Г‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГ‘вҖ№ ГҗВҪГҗВөГ‘ВҒГҗВәГҗВҫГҗ»ÑŒГҗВәГҗВҫ Г‘ВҒГ‘Ж’Г‘вҖҡГҗВҫГҗВә. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese


