Thread 'Ultramagic DLS'
Message boards : Science : Ultramagic DLS
Message board moderation
Previous · 1 . . . 3 · 4 · 5 · 6
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Выше показан пример из Ñтатьи Existence of strongly symmetrical weakly pandiagonal graeco-latin squares Yong Zhang 1 , Kejun Chen 2 , and Wen Li 3 6 3 7 4 1 5 2 8 0 7 4 1 5 2 8 0 6 3 1 5 2 8 0 6 3 7 4 2 8 0 6 3 7 4 1 5 0 6 3 7 4 1 5 2 8 3 7 4 1 5 2 8 0 6 4 1 5 2 8 0 6 3 7 5 2 8 0 6 3 7 4 1 8 0 6 3 7 4 1 5 2 0 8 2 5 1 4 7 3 6 3 6 0 8 2 5 1 4 7 4 7 3 6 0 8 2 5 1 5 1 4 7 3 6 0 8 2 8 2 5 1 4 7 3 6 0 6 0 8 2 5 1 4 7 3 7 3 6 0 8 2 5 1 4 1 4 7 3 6 0 8 2 5 2 5 1 4 7 3 6 0 8 Ðто Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° аÑÑоциативных и Ñлабо пандиагональных ЛК 9-го порÑдка, очень Ð¿Ð¾Ñ…Ð¾Ð¶Ð°Ñ Ð½Ð° показанную в предыдущем поÑте ортогональную пару ЛК 15-го порÑдка. ПроверÑÑŽ Ñти ЛК утилитой Harry White Order? 9
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
2 Latin
2 weakly pandiagonal
2 center symmetric
1 orthogonal pairÐти аÑÑоциативные ЛК утилита тоже Ñчитает центрально-Ñимметричными, а не аÑÑоциативными. PS. Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 9 Ñ Ð½Ð°ÑˆÐ»Ð° ортогональную пару из идеальных ДЛК (Ñмотрите в том же Ñообщении). Рвот Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдков 12 и 15 такие ортогональные пары пока не найдены; по крайней мере, мне они неизвеÑтны. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Покажу интереÑный набор из 36 идеальных ДЛК 13-го порÑдка, найденных в теме "Experiment (pandiagonal DLS of order 13)" Ñмотрите Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=128&postid=1785 2 3 4 5 6 7 8 9 10 11 12 0 1 6 7 8 9 10 11 12 0 1 2 3 4 5 10 11 12 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 10 11 12 0 5 6 7 8 9 10 11 12 0 1 2 3 4 9 10 11 12 0 1 2 3 4 5 6 7 8 0 1 2 3 4 5 6 7 8 9 10 11 12 4 5 6 7 8 9 10 11 12 0 1 2 3 8 9 10 11 12 0 1 2 3 4 5 6 7 12 0 1 2 3 4 5 6 7 8 9 10 11 3 4 5 6 7 8 9 10 11 12 0 1 2 7 8 9 10 11 12 0 1 2 3 4 5 6 11 12 0 1 2 3 4 5 6 7 8 9 10 2 3 4 5 6 7 8 9 10 11 12 0 1 6 7 8 9 10 11 12 0 1 2 3 4 5 12 0 1 2 3 4 5 6 7 8 9 10 11 9 10 11 12 0 1 2 3 4 5 6 7 8 5 6 7 8 9 10 11 12 0 1 2 3 4 3 4 5 6 7 8 9 10 11 12 0 1 2 0 1 2 3 4 5 6 7 8 9 10 11 12 10 11 12 0 1 2 3 4 5 6 7 8 9 8 9 10 11 12 0 1 2 3 4 5 6 7 4 5 6 7 8 9 10 11 12 0 1 2 3 1 2 3 4 5 6 7 8 9 10 11 12 0 7 8 9 10 11 12 0 1 2 3 4 5 6 11 12 0 1 2 3 4 5 6 7 8 9 10 2 3 4 5 6 7 8 9 10 11 12 0 1 10 11 12 0 1 2 3 4 5 6 7 8 9 6 7 8 9 10 11 12 0 1 2 3 4 5 4 5 6 7 8 9 10 11 12 0 1 2 3 12 0 1 2 3 4 5 6 7 8 9 10 11 8 9 10 11 12 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 10 11 12 5 6 7 8 9 10 11 12 0 1 2 3 4 1 2 3 4 5 6 7 8 9 10 11 12 0 9 10 11 12 0 1 2 3 4 5 6 7 8 7 8 9 10 11 12 0 1 2 3 4 5 6 3 4 5 6 7 8 9 10 11 12 0 1 2 11 12 0 1 2 3 4 5 6 7 8 9 10 4 5 6 7 8 9 10 11 12 0 1 2 3 2 3 4 5 6 7 8 9 10 11 12 0 1 5 6 7 8 9 10 11 12 0 1 2 3 4 12 0 1 2 3 4 5 6 7 8 9 10 11 10 11 12 0 1 2 3 4 5 6 7 8 9 7 8 9 10 11 12 0 1 2 3 4 5 6 0 1 2 3 4 5 6 7 8 9 10 11 12 6 7 8 9 10 11 12 0 1 2 3 4 5 3 4 5 6 7 8 9 10 11 12 0 1 2 1 2 3 4 5 6 7 8 9 10 11 12 0 8 9 10 11 12 0 1 2 3 4 5 6 7 11 12 0 1 2 3 4 5 6 7 8 9 10 9 10 11 12 0 1 2 3 4 5 6 7 8 4 5 6 7 8 9 10 11 12 0 1 2 3 12 0 1 2 3 4 5 6 7 8 9 10 11 3 4 5 6 7 8 9 10 11 12 0 1 2 8 9 10 11 12 0 1 2 3 4 5 6 7 6 7 8 9 10 11 12 0 1 2 3 4 5 11 12 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 11 12 2 3 4 5 6 7 8 9 10 11 12 0 1 7 8 9 10 11 12 0 1 2 3 4 5 6 5 6 7 8 9 10 11 12 0 1 2 3 4 10 11 12 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 10 11 12 0 9 10 11 12 0 1 2 3 4 5 6 7 8 4 5 6 7 8 9 10 11 12 0 1 2 3 12 0 1 2 3 4 5 6 7 8 9 10 11 7 8 9 10 11 12 0 1 2 3 4 5 6 2 3 4 5 6 7 8 9 10 11 12 0 1 10 11 12 0 1 2 3 4 5 6 7 8 9 5 6 7 8 9 10 11 12 0 1 2 3 4 0 1 2 3 4 5 6 7 8 9 10 11 12 8 9 10 11 12 0 1 2 3 4 5 6 7 3 4 5 6 7 8 9 10 11 12 0 1 2 11 12 0 1 2 3 4 5 6 7 8 9 10 6 7 8 9 10 11 12 0 1 2 3 4 5 1 2 3 4 5 6 7 8 9 10 11 12 0 9 10 11 12 0 1 2 3 4 5 6 7 8 4 5 6 7 8 9 10 11 12 0 1 2 3 12 0 1 2 3 4 5 6 7 8 9 10 11 7 8 9 10 11 12 0 1 2 3 4 5 6 11 12 0 1 2 3 4 5 6 7 8 9 10 3 4 5 6 7 8 9 10 11 12 0 1 2 5 6 7 8 9 10 11 12 0 1 2 3 4 0 1 2 3 4 5 6 7 8 9 10 11 12 8 9 10 11 12 0 1 2 3 4 5 6 7 10 11 12 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 10 11 12 0 1 6 7 8 9 10 11 12 0 1 2 3 4 5 1 2 3 4 5 6 7 8 9 10 11 12 0 9 10 11 12 0 1 2 3 4 5 6 7 8 4 5 6 7 8 9 10 11 12 0 1 2 3 1 2 3 4 5 6 7 8 9 10 11 12 0 7 8 9 10 11 12 0 1 2 3 4 5 6 2 3 4 5 6 7 8 9 10 11 12 0 1 10 11 12 0 1 2 3 4 5 6 7 8 9 8 9 10 11 12 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 10 11 12 5 6 7 8 9 10 11 12 0 1 2 3 4 3 4 5 6 7 8 9 10 11 12 0 1 2 11 12 0 1 2 3 4 5 6 7 8 9 10 6 7 8 9 10 11 12 0 1 2 3 4 5 12 0 1 2 3 4 5 6 7 8 9 10 11 9 10 11 12 0 1 2 3 4 5 6 7 8 4 5 6 7 8 9 10 11 12 0 1 2 3 1 2 3 4 5 6 7 8 9 10 11 12 0 7 8 9 10 11 12 0 1 2 3 4 5 6 11 12 0 1 2 3 4 5 6 7 8 9 10 3 4 5 6 7 8 9 10 11 12 0 1 2 8 9 10 11 12 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 10 11 12 5 6 7 8 9 10 11 12 0 1 2 3 4 10 11 12 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 10 11 12 0 1 6 7 8 9 10 11 12 0 1 2 3 4 5 12 0 1 2 3 4 5 6 7 8 9 10 11 9 10 11 12 0 1 2 3 4 5 6 7 8 8 9 10 11 12 0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 8 9 10 11 12 0 11 12 0 1 2 3 4 5 6 7 8 9 10 6 7 8 9 10 11 12 0 1 2 3 4 5 3 4 5 6 7 8 9 10 11 12 0 1 2 9 10 11 12 0 1 2 3 4 5 6 7 8 0 1 2 3 4 5 6 7 8 9 10 11 12 4 5 6 7 8 9 10 11 12 0 1 2 3 10 11 12 0 1 2 3 4 5 6 7 8 9 7 8 9 10 11 12 0 1 2 3 4 5 6 2 3 4 5 6 7 8 9 10 11 12 0 1 12 0 1 2 3 4 5 6 7 8 9 10 11 5 6 7 8 9 10 11 12 0 1 2 3 4 8 9 10 11 12 0 1 2 3 4 5 6 7 11 12 0 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 11 12 0 4 5 6 7 8 9 10 11 12 0 1 2 3 7 8 9 10 11 12 0 1 2 3 4 5 6 10 11 12 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 10 11 12 3 4 5 6 7 8 9 10 11 12 0 1 2 6 7 8 9 10 11 12 0 1 2 3 4 5 9 10 11 12 0 1 2 3 4 5 6 7 8 12 0 1 2 3 4 5 6 7 8 9 10 11 2 3 4 5 6 7 8 9 10 11 12 0 1 5 6 7 8 9 10 11 12 0 1 2 3 4 8 9 10 11 12 0 1 2 3 4 5 6 7 11 12 0 1 2 3 4 5 6 7 8 9 10 3 4 5 6 7 8 9 10 11 12 0 1 2 12 0 1 2 3 4 5 6 7 8 9 10 11 7 8 9 10 11 12 0 1 2 3 4 5 6 4 5 6 7 8 9 10 11 12 0 1 2 3 0 1 2 3 4 5 6 7 8 9 10 11 12 9 10 11 12 0 1 2 3 4 5 6 7 8 6 7 8 9 10 11 12 0 1 2 3 4 5 1 2 3 4 5 6 7 8 9 10 11 12 0 10 11 12 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 10 11 12 0 1 5 6 7 8 9 10 11 12 0 1 2 3 4 10 11 12 0 1 2 3 4 5 6 7 8 9 4 5 6 7 8 9 10 11 12 0 1 2 3 2 3 4 5 6 7 8 9 10 11 12 0 1 8 9 10 11 12 0 1 2 3 4 5 6 7 12 0 1 2 3 4 5 6 7 8 9 10 11 7 8 9 10 11 12 0 1 2 3 4 5 6 0 1 2 3 4 5 6 7 8 9 10 11 12 6 7 8 9 10 11 12 0 1 2 3 4 5 1 2 3 4 5 6 7 8 9 10 11 12 0 5 6 7 8 9 10 11 12 0 1 2 3 4 11 12 0 1 2 3 4 5 6 7 8 9 10 9 10 11 12 0 1 2 3 4 5 6 7 8 3 4 5 6 7 8 9 10 11 12 0 1 2 10 11 12 0 1 2 3 4 5 6 7 8 9 4 5 6 7 8 9 10 11 12 0 1 2 3 11 12 0 1 2 3 4 5 6 7 8 9 10 5 6 7 8 9 10 11 12 0 1 2 3 4 12 0 1 2 3 4 5 6 7 8 9 10 11 6 7 8 9 10 11 12 0 1 2 3 4 5 0 1 2 3 4 5 6 7 8 9 10 11 12 7 8 9 10 11 12 0 1 2 3 4 5 6 1 2 3 4 5 6 7 8 9 10 11 12 0 8 9 10 11 12 0 1 2 3 4 5 6 7 2 3 4 5 6 7 8 9 10 11 12 0 1 9 10 11 12 0 1 2 3 4 5 6 7 8 3 4 5 6 7 8 9 10 11 12 0 1 2 10 11 12 0 1 2 3 4 5 6 7 8 9 6 7 8 9 10 11 12 0 1 2 3 4 5 1 2 3 4 5 6 7 8 9 10 11 12 0 11 12 0 1 2 3 4 5 6 7 8 9 10 4 5 6 7 8 9 10 11 12 0 1 2 3 8 9 10 11 12 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 10 11 12 5 6 7 8 9 10 11 12 0 1 2 3 4 9 10 11 12 0 1 2 3 4 5 6 7 8 2 3 4 5 6 7 8 9 10 11 12 0 1 12 0 1 2 3 4 5 6 7 8 9 10 11 7 8 9 10 11 12 0 1 2 3 4 5 6 3 4 5 6 7 8 9 10 11 12 0 1 2 12 0 1 2 3 4 5 6 7 8 9 10 11 4 5 6 7 8 9 10 11 12 0 1 2 3 6 7 8 9 10 11 12 0 1 2 3 4 5 11 12 0 1 2 3 4 5 6 7 8 9 10 5 6 7 8 9 10 11 12 0 1 2 3 4 10 11 12 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 10 11 12 3 4 5 6 7 8 9 10 11 12 0 1 2 8 9 10 11 12 0 1 2 3 4 5 6 7 2 3 4 5 6 7 8 9 10 11 12 0 1 7 8 9 10 11 12 0 1 2 3 4 5 6 9 10 11 12 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 0 12 0 1 2 3 4 5 6 7 8 9 10 11 10 11 12 0 1 2 3 4 5 6 7 8 9 8 9 10 11 12 0 1 2 3 4 5 6 7 6 7 8 9 10 11 12 0 1 2 3 4 5 4 5 6 7 8 9 10 11 12 0 1 2 3 2 3 4 5 6 7 8 9 10 11 12 0 1 0 1 2 3 4 5 6 7 8 9 10 11 12 11 12 0 1 2 3 4 5 6 7 8 9 10 9 10 11 12 0 1 2 3 4 5 6 7 8 7 8 9 10 11 12 0 1 2 3 4 5 6 5 6 7 8 9 10 11 12 0 1 2 3 4 3 4 5 6 7 8 9 10 11 12 0 1 2 1 2 3 4 5 6 7 8 9 10 11 12 0 12 0 1 2 3 4 5 6 7 8 9 10 11 10 11 12 0 1 2 3 4 5 6 7 8 9 5 6 7 8 9 10 11 12 0 1 2 3 4 7 8 9 10 11 12 0 1 2 3 4 5 6 4 5 6 7 8 9 10 11 12 0 1 2 3 11 12 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 11 12 2 3 4 5 6 7 8 9 10 11 12 0 1 9 10 11 12 0 1 2 3 4 5 6 7 8 6 7 8 9 10 11 12 0 1 2 3 4 5 8 9 10 11 12 0 1 2 3 4 5 6 7 3 4 5 6 7 8 9 10 11 12 0 1 2 1 2 3 4 5 6 7 8 9 10 11 12 0 1 2 3 4 5 6 7 8 9 10 11 12 0 3 4 5 6 7 8 9 10 11 12 0 1 2 8 9 10 11 12 0 1 2 3 4 5 6 7 6 7 8 9 10 11 12 0 1 2 3 4 5 9 10 11 12 0 1 2 3 4 5 6 7 8 2 3 4 5 6 7 8 9 10 11 12 0 1 0 1 2 3 4 5 6 7 8 9 10 11 12 11 12 0 1 2 3 4 5 6 7 8 9 10 4 5 6 7 8 9 10 11 12 0 1 2 3 7 8 9 10 11 12 0 1 2 3 4 5 6 5 6 7 8 9 10 11 12 0 1 2 3 4 10 11 12 0 1 2 3 4 5 6 7 8 9 12 0 1 2 3 4 5 6 7 8 9 10 11 1 2 3 4 5 6 7 8 9 10 11 12 0 3 4 5 6 7 8 9 10 11 12 0 1 2 5 6 7 8 9 10 11 12 0 1 2 3 4 7 8 9 10 11 12 0 1 2 3 4 5 6 9 10 11 12 0 1 2 3 4 5 6 7 8 11 12 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 11 12 2 3 4 5 6 7 8 9 10 11 12 0 1 4 5 6 7 8 9 10 11 12 0 1 2 3 6 7 8 9 10 11 12 0 1 2 3 4 5 8 9 10 11 12 0 1 2 3 4 5 6 7 10 11 12 0 1 2 3 4 5 6 7 8 9 12 0 1 2 3 4 5 6 7 8 9 10 11 1 2 3 4 5 6 7 8 9 10 11 12 0 9 10 11 12 0 1 2 3 4 5 6 7 8 7 8 9 10 11 12 0 1 2 3 4 5 6 2 3 4 5 6 7 8 9 10 11 12 0 1 8 9 10 11 12 0 1 2 3 4 5 6 7 3 4 5 6 7 8 9 10 11 12 0 1 2 0 1 2 3 4 5 6 7 8 9 10 11 12 10 11 12 0 1 2 3 4 5 6 7 8 9 5 6 7 8 9 10 11 12 0 1 2 3 4 11 12 0 1 2 3 4 5 6 7 8 9 10 6 7 8 9 10 11 12 0 1 2 3 4 5 4 5 6 7 8 9 10 11 12 0 1 2 3 12 0 1 2 3 4 5 6 7 8 9 10 11 3 4 5 6 7 8 9 10 11 12 0 1 2 7 8 9 10 11 12 0 1 2 3 4 5 6 12 0 1 2 3 4 5 6 7 8 9 10 11 2 3 4 5 6 7 8 9 10 11 12 0 1 9 10 11 12 0 1 2 3 4 5 6 7 8 5 6 7 8 9 10 11 12 0 1 2 3 4 0 1 2 3 4 5 6 7 8 9 10 11 12 8 9 10 11 12 0 1 2 3 4 5 6 7 4 5 6 7 8 9 10 11 12 0 1 2 3 11 12 0 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 11 12 0 6 7 8 9 10 11 12 0 1 2 3 4 5 10 11 12 0 1 2 3 4 5 6 7 8 9 3 4 5 6 7 8 9 10 11 12 0 1 2 9 10 11 12 0 1 2 3 4 5 6 7 8 2 3 4 5 6 7 8 9 10 11 12 0 1 8 9 10 11 12 0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 8 9 10 11 12 0 7 8 9 10 11 12 0 1 2 3 4 5 6 0 1 2 3 4 5 6 7 8 9 10 11 12 6 7 8 9 10 11 12 0 1 2 3 4 5 12 0 1 2 3 4 5 6 7 8 9 10 11 5 6 7 8 9 10 11 12 0 1 2 3 4 11 12 0 1 2 3 4 5 6 7 8 9 10 4 5 6 7 8 9 10 11 12 0 1 2 3 10 11 12 0 1 2 3 4 5 6 7 8 9 3 4 5 6 7 8 9 10 11 12 0 1 2 9 10 11 12 0 1 2 3 4 5 6 7 8 11 12 0 1 2 3 4 5 6 7 8 9 10 5 6 7 8 9 10 11 12 0 1 2 3 4 1 2 3 4 5 6 7 8 9 10 11 12 0 6 7 8 9 10 11 12 0 1 2 3 4 5 0 1 2 3 4 5 6 7 8 9 10 11 12 7 8 9 10 11 12 0 1 2 3 4 5 6 12 0 1 2 3 4 5 6 7 8 9 10 11 8 9 10 11 12 0 1 2 3 4 5 6 7 2 3 4 5 6 7 8 9 10 11 12 0 1 4 5 6 7 8 9 10 11 12 0 1 2 3 10 11 12 0 1 2 3 4 5 6 7 8 9 5 6 7 8 9 10 11 12 0 1 2 3 4 2 3 4 5 6 7 8 9 10 11 12 0 1 10 11 12 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 10 11 12 0 6 7 8 9 10 11 12 0 1 2 3 4 5 9 10 11 12 0 1 2 3 4 5 6 7 8 0 1 2 3 4 5 6 7 8 9 10 11 12 4 5 6 7 8 9 10 11 12 0 1 2 3 7 8 9 10 11 12 0 1 2 3 4 5 6 12 0 1 2 3 4 5 6 7 8 9 10 11 3 4 5 6 7 8 9 10 11 12 0 1 2 11 12 0 1 2 3 4 5 6 7 8 9 10 8 9 10 11 12 0 1 2 3 4 5 6 7 5 6 7 8 9 10 11 12 0 1 2 3 4 2 3 4 5 6 7 8 9 10 11 12 0 1 12 0 1 2 3 4 5 6 7 8 9 10 11 9 10 11 12 0 1 2 3 4 5 6 7 8 6 7 8 9 10 11 12 0 1 2 3 4 5 3 4 5 6 7 8 9 10 11 12 0 1 2 0 1 2 3 4 5 6 7 8 9 10 11 12 10 11 12 0 1 2 3 4 5 6 7 8 9 7 8 9 10 11 12 0 1 2 3 4 5 6 4 5 6 7 8 9 10 11 12 0 1 2 3 1 2 3 4 5 6 7 8 9 10 11 12 0 11 12 0 1 2 3 4 5 6 7 8 9 10 8 9 10 11 12 0 1 2 3 4 5 6 7 5 6 7 8 9 10 11 12 0 1 2 3 4 12 0 1 2 3 4 5 6 7 8 9 10 11 2 3 4 5 6 7 8 9 10 11 12 0 1 7 8 9 10 11 12 0 1 2 3 4 5 6 10 11 12 0 1 2 3 4 5 6 7 8 9 4 5 6 7 8 9 10 11 12 0 1 2 3 0 1 2 3 4 5 6 7 8 9 10 11 12 9 10 11 12 0 1 2 3 4 5 6 7 8 3 4 5 6 7 8 9 10 11 12 0 1 2 6 7 8 9 10 11 12 0 1 2 3 4 5 11 12 0 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 11 12 0 8 9 10 11 12 0 1 2 3 4 5 6 7 9 10 11 12 0 1 2 3 4 5 6 7 8 12 0 1 2 3 4 5 6 7 8 9 10 11 6 7 8 9 10 11 12 0 1 2 3 4 5 2 3 4 5 6 7 8 9 10 11 12 0 1 10 11 12 0 1 2 3 4 5 6 7 8 9 5 6 7 8 9 10 11 12 0 1 2 3 4 0 1 2 3 4 5 6 7 8 9 10 11 12 8 9 10 11 12 0 1 2 3 4 5 6 7 3 4 5 6 7 8 9 10 11 12 0 1 2 11 12 0 1 2 3 4 5 6 7 8 9 10 7 8 9 10 11 12 0 1 2 3 4 5 6 1 2 3 4 5 6 7 8 9 10 11 12 0 4 5 6 7 8 9 10 11 12 0 1 2 3 9 10 11 12 0 1 2 3 4 5 6 7 8 12 0 1 2 3 4 5 6 7 8 9 10 11 6 7 8 9 10 11 12 0 1 2 3 4 5 11 12 0 1 2 3 4 5 6 7 8 9 10 3 4 5 6 7 8 9 10 11 12 0 1 2 5 6 7 8 9 10 11 12 0 1 2 3 4 0 1 2 3 4 5 6 7 8 9 10 11 12 8 9 10 11 12 0 1 2 3 4 5 6 7 10 11 12 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 10 11 12 0 1 7 8 9 10 11 12 0 1 2 3 4 5 6 1 2 3 4 5 6 7 8 9 10 11 12 0 4 5 6 7 8 9 10 11 12 0 1 2 3 9 10 11 12 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 0 6 7 8 9 10 11 12 0 1 2 3 4 5 2 3 4 5 6 7 8 9 10 11 12 0 1 10 11 12 0 1 2 3 4 5 6 7 8 9 8 9 10 11 12 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 10 11 12 5 6 7 8 9 10 11 12 0 1 2 3 4 3 4 5 6 7 8 9 10 11 12 0 1 2 11 12 0 1 2 3 4 5 6 7 8 9 10 7 8 9 10 11 12 0 1 2 3 4 5 6 12 0 1 2 3 4 5 6 7 8 9 10 11 4 5 6 7 8 9 10 11 12 0 1 2 3 9 10 11 12 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 0 6 7 8 9 10 11 12 0 1 2 3 4 5 11 12 0 1 2 3 4 5 6 7 8 9 10 3 4 5 6 7 8 9 10 11 12 0 1 2 8 9 10 11 12 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 10 11 12 5 6 7 8 9 10 11 12 0 1 2 3 4 10 11 12 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 10 11 12 0 1 7 8 9 10 11 12 0 1 2 3 4 5 6 12 0 1 2 3 4 5 6 7 8 9 10 11 4 5 6 7 8 9 10 11 12 0 1 2 3 9 10 11 12 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 0 10 11 12 0 1 2 3 4 5 6 7 8 9 5 6 7 8 9 10 11 12 0 1 2 3 4 7 8 9 10 11 12 0 1 2 3 4 5 6 2 3 4 5 6 7 8 9 10 11 12 0 1 0 1 2 3 4 5 6 7 8 9 10 11 12 11 12 0 1 2 3 4 5 6 7 8 9 10 6 7 8 9 10 11 12 0 1 2 3 4 5 8 9 10 11 12 0 1 2 3 4 5 6 7 3 4 5 6 7 8 9 10 11 12 0 1 2 12 0 1 2 3 4 5 6 7 8 9 10 11 4 5 6 7 8 9 10 11 12 0 1 2 3 9 10 11 12 0 1 2 3 4 5 6 7 8 11 12 0 1 2 3 4 5 6 7 8 9 10 8 9 10 11 12 0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 8 9 10 11 12 0 3 4 5 6 7 8 9 10 11 12 0 1 2 6 7 8 9 10 11 12 0 1 2 3 4 5 0 1 2 3 4 5 6 7 8 9 10 11 12 7 8 9 10 11 12 0 1 2 3 4 5 6 10 11 12 0 1 2 3 4 5 6 7 8 9 12 0 1 2 3 4 5 6 7 8 9 10 11 5 6 7 8 9 10 11 12 0 1 2 3 4 2 3 4 5 6 7 8 9 10 11 12 0 1 4 5 6 7 8 9 10 11 12 0 1 2 3 11 12 0 1 2 3 4 5 6 7 8 9 10 3 4 5 6 7 8 9 10 11 12 0 1 2 7 8 9 10 11 12 0 1 2 3 4 5 6 9 10 11 12 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 0 5 6 7 8 9 10 11 12 0 1 2 3 4 0 1 2 3 4 5 6 7 8 9 10 11 12 8 9 10 11 12 0 1 2 3 4 5 6 7 12 0 1 2 3 4 5 6 7 8 9 10 11 4 5 6 7 8 9 10 11 12 0 1 2 3 6 7 8 9 10 11 12 0 1 2 3 4 5 10 11 12 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 10 11 12 0 1 11 12 0 1 2 3 4 5 6 7 8 9 10 7 8 9 10 11 12 0 1 2 3 4 5 6 1 2 3 4 5 6 7 8 9 10 11 12 0 4 5 6 7 8 9 10 11 12 0 1 2 3 8 9 10 11 12 0 1 2 3 4 5 6 7 10 11 12 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 10 11 12 3 4 5 6 7 8 9 10 11 12 0 1 2 5 6 7 8 9 10 11 12 0 1 2 3 4 9 10 11 12 0 1 2 3 4 5 6 7 8 12 0 1 2 3 4 5 6 7 8 9 10 11 6 7 8 9 10 11 12 0 1 2 3 4 5 2 3 4 5 6 7 8 9 10 11 12 0 1 11 12 0 1 2 3 4 5 6 7 8 9 10 7 8 9 10 11 12 0 1 2 3 4 5 6 3 4 5 6 7 8 9 10 11 12 0 1 2 12 0 1 2 3 4 5 6 7 8 9 10 11 8 9 10 11 12 0 1 2 3 4 5 6 7 4 5 6 7 8 9 10 11 12 0 1 2 3 0 1 2 3 4 5 6 7 8 9 10 11 12 9 10 11 12 0 1 2 3 4 5 6 7 8 5 6 7 8 9 10 11 12 0 1 2 3 4 1 2 3 4 5 6 7 8 9 10 11 12 0 10 11 12 0 1 2 3 4 5 6 7 8 9 6 7 8 9 10 11 12 0 1 2 3 4 5 2 3 4 5 6 7 8 9 10 11 12 0 1 ЗдеÑÑŒ 10 ДЛК ÑвлÑÑŽÑ‚ÑÑ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡ÐµÑкими пандиагональными и аÑÑоциативными, оÑтальные 26 ДЛК полуцикличеÑкие пандиагональные (Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках) и аÑÑоциативные. ВеÑьма интереÑные квадраты! ЕÑли применить к Ñтим 36 идеальным ДЛК преобразование параллельного переноÑа на торе, в результате получатÑÑ 348 нормализованных пандиагональных ДЛК, Ñреди которых 10 цикличеÑких и 338 полуцикличеÑких Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках. Смотрите также Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=128&postid=1856 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðто подобные идеальные ДЛК 17-го порÑдка, найденные в теме Semi-cyclic pandiagonal DLS of prime order n>11 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 Первый из Ñтих ДЛК цикличеÑкий пандиагональный и аÑÑоциативный, Ñто один из извеÑтных 14 цикличеÑких пандиагональных ДЛК 17-го порÑдка из полной ÑиÑтемы MOLS, преобразованный. ОÑтальные пÑÑ‚ÑŒ ДЛК аÑÑоциативные и полуцикличеÑкие пандиагональные Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках. Я не нашла вÑе подобные идеальные ДЛК 17-го порÑдка, их будет много. ЕÑли найти вÑе такие идеальные ДЛК и применить к ним преобразование параллельного переноÑа на торе, должны получитьÑÑ Ð² результате 8276 нормализованных пандиагональных ДЛК 17-го порÑдка, Ñреди который 14 цикличеÑких, а оÑтальные полуцикличеÑкие Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках. Очень интереÑÐ½Ð°Ñ Ð·Ð°Ð´Ð°Ñ‡Ð°! Покажу паттерн Ñтих идеальных ДЛК 17-го порÑдка  Ð’Ñе показанные 6 идеальных ДЛК ÑоответÑтвуют Ñтому паттерну. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’ Ñообщении https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=132&postid=1847 показан замечательный идеальный ДЛК 19-го порÑдка, ÑвлÑющийÑÑ Ð¿Ð¾Ð»ÑƒÑ†Ð¸ÐºÐ»Ð¸Ñ‡ÐµÑким Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в диагоналÑÑ… параллельных главной диагонали 0 16 18 10 17 15 14 8 13 7 12 6 11 5 4 2 9 1 3 4 1 17 0 11 18 16 15 9 14 8 13 7 12 6 5 3 10 2 3 5 2 18 1 12 0 17 16 10 15 9 14 8 13 7 6 4 11 12 4 6 3 0 2 13 1 18 17 11 16 10 15 9 14 8 7 5 6 13 5 7 4 1 3 14 2 0 18 12 17 11 16 10 15 9 8 9 7 14 6 8 5 2 4 15 3 1 0 13 18 12 17 11 16 10 11 10 8 15 7 9 6 3 5 16 4 2 1 14 0 13 18 12 17 18 12 11 9 16 8 10 7 4 6 17 5 3 2 15 1 14 0 13 14 0 13 12 10 17 9 11 8 5 7 18 6 4 3 16 2 15 1 2 15 1 14 13 11 18 10 12 9 6 8 0 7 5 4 17 3 16 17 3 16 2 15 14 12 0 11 13 10 7 9 1 8 6 5 18 4 5 18 4 17 3 16 15 13 1 12 14 11 8 10 2 9 7 6 0 1 6 0 5 18 4 17 16 14 2 13 15 12 9 11 3 10 8 7 8 2 7 1 6 0 5 18 17 15 3 14 16 13 10 12 4 11 9 10 9 3 8 2 7 1 6 0 18 16 4 15 17 14 11 13 5 12 13 11 10 4 9 3 8 2 7 1 0 17 5 16 18 15 12 14 6 7 14 12 11 5 10 4 9 3 8 2 1 18 6 17 0 16 13 15 16 8 15 13 12 6 11 5 10 4 9 3 2 0 7 18 1 17 14 15 17 9 16 14 13 7 12 6 11 5 10 4 3 1 8 0 2 18 Ðтот ДЛК ÑвлÑетÑÑ SODLS и DSODLS, значит, имеем две ортогональные пары идеальных ДЛК. Из одной ортогональной пары Ñ Ð¿Ð¾Ñтроила оригинальный идеальный магичеÑкий квадрат методом латинÑких квадратов 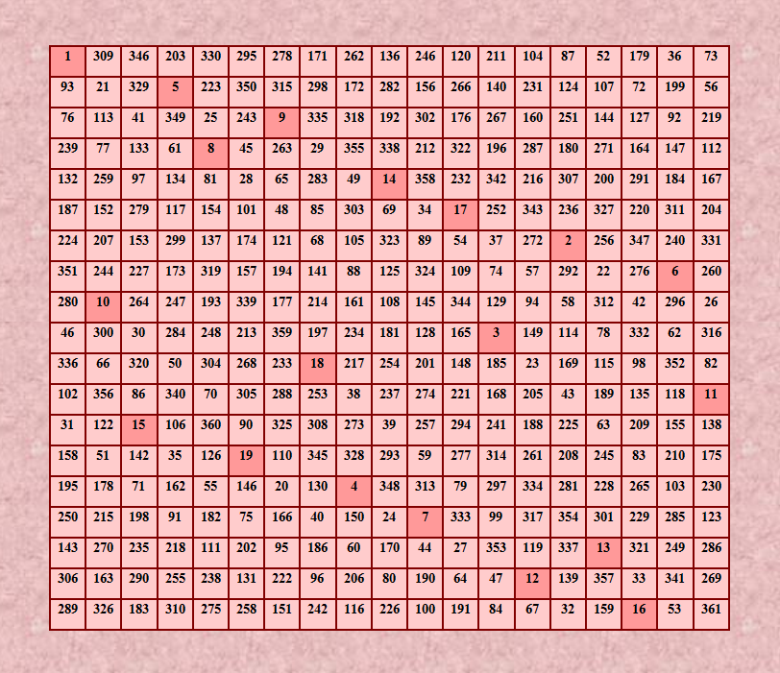 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðадо найти идеальные ДЛК 19-го порÑдка подобные показанным выше идеальным ДЛК порÑдков 13 и 17, Ñреди тех примеров, которые были найдены в теме Semi-cyclic pandiagonal DLS of prime order n>11 Должны быть такие ДЛК. Вот, например, один из таких ДЛК, цитата Прежде вÑего выудила идеальный ДЛК. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ñ ÐµÐ³Ð¾ преобразую в другой формат (чтобы ÑоответÑтвовал показанному выше паттерну Ð´Ð»Ñ Ð¸Ð´ÐµÐ°Ð»ÑŒÐ½Ð¾Ð³Ð¾ ДЛК 17-го порÑдка; аналогичный паттерн будет и Ð´Ð»Ñ Ð¸Ð´ÐµÐ°Ð»ÑŒÐ½Ð¾Ð³Ð¾ ДЛК 19-го порÑдка). Готово! 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 Преобразование выполнÑетÑÑ Ñ Ð¿Ð¾Ð¼Ð¾Ñ‰ÑŒÑŽ Ð¿ÐµÑ€ÐµÐ¾Ð±Ð¾Ð·Ð½Ð°Ñ‡ÐµÐ½Ð¸Ñ Ñлементов. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё один подобный идеальный ДЛК 19-го порÑдка можно получить из цикличеÑкого пандиагонального ДЛК; полный набор из 16 таких ДЛК показан здеÑÑŒ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=132&postid=1824 Беру Ñамый первый ДЛК в Ñтом наборе 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 и преобразую его к нужному формату. Готово! 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 Пока имеем только два идеальных ДЛК 19-го порÑдка Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках, подобные показанным выше идеальным ДЛК порÑдков 13 и 17. ИнтереÑно было бы найти вÑе такие идеальные ДЛК. Ðу, Ñначала надо попытатьÑÑ Ñ€ÐµÑˆÐ¸Ñ‚ÑŒ задачу Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 17. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese