Thread 'Ultramagic DLS'
Message boards : Science : Ultramagic DLS
Message board moderation
Previous · 1 · 2 · 3 · 4 · 5 · 6 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðачала пиÑать новую программу Ð´Ð»Ñ Ð¿Ð¾ÑÑ‚Ñ€Ð¾ÐµÐ½Ð¸Ñ Ð¸Ð´ÐµÐ°Ð»ÑŒÐ½Ð¾Ð³Ð¾ ДЛК 12-го порÑдка. Ðлгоритм тот же - полный перебор, но ввела два изменениÑ. Первое: изменила паттерн. Теперь паттерн Ñодержит главную и побочную диагонали, первую и поÑледнюю Ñтроки. Ðто намного уменьшает перебор. Второе: изменила ÑпоÑоб Ð·Ð°Ð¿Ð¾Ð»Ð½ÐµÐ½Ð¸Ñ ÐºÐ²Ð°Ð´Ñ€Ð°Ñ‚Ð° Ñ Ð¿Ð¾Ñтрочного на подиагональный. Пока напиÑала чаÑÑ‚ÑŒ программы, вот что у Ð¼ÐµÐ½Ñ Ð¿Ð¾ÑтроилоÑÑŒ 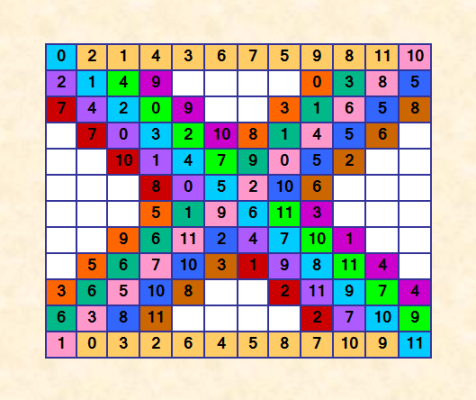 Ð”Ð°Ð½Ð½Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ заполнÑетÑÑ Ð¼Ð³Ð½Ð¾Ð²ÐµÐ½Ð½Ð¾, вÑе уÑÐ»Ð¾Ð²Ð¸Ñ Ð²Ñ‹Ð¿Ð¾Ð»Ð½ÑÑŽÑ‚ÑÑ: аÑÑоциативноÑÑ‚ÑŒ, ÑÐ»Ð°Ð±Ð°Ñ Ð¿Ð°Ð½Ð´Ð¸Ð°Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð¾ÑÑ‚ÑŒ, различноÑÑ‚ÑŒ Ñлементов в Ñтроках и Ñтолбцах. Имеем в данной чаÑти 10 полных правильных диагоналей, две полные правильные Ñтроки и два полных правильных Ñтолбца. Как Ñто будет продолжатьÑÑ? Программа не Ñказать, чтобы ÑложнаÑ, но Ð´Ð»Ð¸Ð½Ð½Ð°Ñ Ð¸ требует колоÑÑального вниманиÑ. Ðадо допиÑывать, больше половины напиÑано. Теперь уж, что получитÑÑ. Ð’ Ñтой верÑии еÑÑ‚ÑŒ надежда, что программа Ñделает полный перебор. Будет ÑÑно, что Ñ€ÐµÑˆÐµÐ½Ð¸Ñ Ð½ÐµÑ‚. Ðо тут еÑÑ‚ÑŒ неÑколько вариантов паттернов, Ð´Ð»Ñ ÐºÐ°Ð¶Ð´Ð¾Ð³Ð¾ надо будет выполнить программу. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Сделала ещё один шажок в программе, пока вÑÑ‘ получилоÑÑŒ, чаÑÑ‚ÑŒ квадрата заполнилаÑÑŒ мгновенно. Уже довольно Ð±Ð¾Ð»ÑŒÑˆÐ°Ñ Ñ‡Ð°ÑÑ‚ÑŒ квадрата заполнена. Ðо дальше вÑÑ‘ труднее, потому что начинают проверÑÑ‚ÑŒÑÑ Ð¼Ð½Ð¾Ð³Ð¾ жёÑтких уÑловий, надо вÑе их удовлетворить. Завтра продолжу, ÑÐµÐ¹Ñ‡Ð°Ñ ÑƒÐ¶Ðµ мозги, как ёжик в тумане :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
С утра ещё один шажок напиÑала в программе. И вот иллюÑÑ‚Ñ€Ð°Ñ†Ð¸Ñ 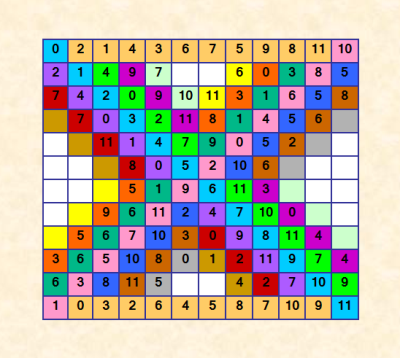 Удивительно, но пока Ñто ÑтроитÑÑ Ð¼Ð³Ð½Ð¾Ð²ÐµÐ½Ð½Ð¾. Рзаполнено уже много, оÑталоÑÑŒ заполнить 28 Ñчеек из 144. Имеем в данной чаÑти ДЛК 4 полные правильные Ñтроки, 4 полных правильных Ñтолбца и 10 полных правильных диагоналей. Ðеужели он не получитÑÑ??? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вчера напиÑала ещё немножко. Заполнено уже 126 Ñчеек из 144. Пока квадрат ÑтроитÑÑ Ð´Ð¾Ð²Ð¾Ð»ÑŒÐ½Ð¾ быÑтро, Ñ…Ð¾Ñ‚Ñ ÑƒÐ¶Ðµ не мгновенно. ОÑтавшиеÑÑ 18 Ñчеек Ñамые трудные, Ñкоро процеÑÑ Ð¿Ð¾ÑÑ‚Ñ€Ð¾ÐµÐ½Ð¸Ñ Ð½Ð°Ñ‡Ð½Ñ‘Ñ‚ замедлÑÑ‚ÑŒÑÑ. Будет ли полный перебор за реальное времÑ? Будет ли решение? Программу пишу очень медленно, проверÑÑŽ каждую Ñтрочку тщательно, ошибатьÑÑ Ð½Ð¸ÐºÐ°Ðº нельзÑ. РвÑÑ‘-таки очень интереÑно: извеÑтен ли ÑообщеÑтву математиков идеальный ДЛК 12-го порÑдка? Может быть, Ñ Ð¼ÑƒÑ‡Ð¸Ñ‚ÐµÐ»ÑŒÐ½Ð¾ изобретаю велоÑипед :) И такое возможно. Ðадо ÑпроÑить у Harry White, может быть, он что-то знает. Текущий ДЛК (в не заполненных Ñчейках Ñтоит Ñ…) 0 2 1 4 3 6 7 5 9 8 11 10 2 1 4 11 10 x x 6 5 0 8 3 5 4 2 9 7 11 10 3 1 6 0 8 9 10 0 3 1 8 11 2 4 5 6 7 x 6 8 5 4 3 9 0 11 2 x x x x 7 8 0 5 2 9 10 1 x x x x 10 1 2 9 6 11 3 4 x x x x 9 0 11 2 8 7 6 3 5 x 4 5 6 7 9 0 3 10 8 11 1 2 3 11 5 10 8 1 0 4 2 9 7 6 8 3 11 6 5 x x 1 0 7 10 9 1 0 3 2 6 4 5 8 7 10 9 11 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðапомню: в первой верÑии программы был поÑтроен такой чаÑтично заполненный ДЛК  ЗдеÑÑŒ вÑего 8 Ñчеек оÑталоÑÑŒ заполнить (окрашены в голубой цвет). И... на Ñтом вÑÑ‘ заÑтопорилоÑÑŒ, ни одну Ñчейку из Ñтих 8 заполнить не удалоÑÑŒ. Программа уходит в беÑконечную задумчивоÑÑ‚ÑŒ; полный перебор в Ñтой верÑии огромный и выполнить его за реальное Ð²Ñ€ÐµÐ¼Ñ Ð²Ñ€Ñд ли получитÑÑ. Как уже отмечалоÑÑŒ, в новой верÑии программы взÑла другой паттерн Ñ Ñ†ÐµÐ»ÑŒÑŽ уменьшить перебор. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ÐапиÑала ещё один шажок: перебор очередного Ñлемента. Шажок оказалÑÑ ÐºÑ€Ð¸Ñ‚Ð¸Ñ‡ÐµÑким, программа работает уже 2 чаÑа и квадрата пока не выдала. Ðтот шажок должен заполнить 4 Ñчейки и дать ещё две полные правильные Ñтроки и два полных правильных Ñтолбца. Похоже, и Ñта верÑÐ¸Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ñ‹ ничего не даÑÑ‚. ПуÑÑ‚ÑŒ поищет немного, потом прерву; полный перебор и тут врÑд ли выполнитÑÑ, Ñлишком много. Да, не хочет задача решатьÑÑ :( Ð ÑущеÑтвует ли иÑкомый идеальный ДЛК? Ðачинаю ÑклонÑÑ‚ÑŒÑÑ Ðº мыÑли, что не ÑущеÑтвует. Ðо Ñто пока не доказанный факт. PS. Перед критичеÑким шагом был ещё один шаг, который прекраÑно выполнилÑÑ; тут заполнилиÑÑŒ только две Ñчейки дополнительно к показанному выше чаÑтичному квадрату; вот что получено 0 2 1 4 3 6 7 5 9 8 11 10 2 1 10 11 9 x x 3 5 0 8 6 11 4 2 9 7 10 0 1 3 6 5 8 10 9 0 3 2 8 11 6 4 7 1 5 x 5 8 10 4 1 9 0 6 2 3 x x x 6 1 0 5 2 10 11 4 x x x x 7 0 1 9 6 11 10 5 x x x 8 9 5 11 2 10 7 1 3 6 x 6 10 4 7 5 0 3 9 8 11 2 1 3 6 5 8 10 11 1 4 2 9 7 0 5 3 11 6 8 x x 2 0 1 10 9 1 0 3 2 6 4 5 8 7 10 9 11 Ðтот шаг дал ещё две полные правильные диагонали. СтроилÑÑ Ñтот квадрат 4 минуты. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Программа квадрат (неполный) выдала!! Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÑŽ и покажу иллюÑтрацию. Вот он 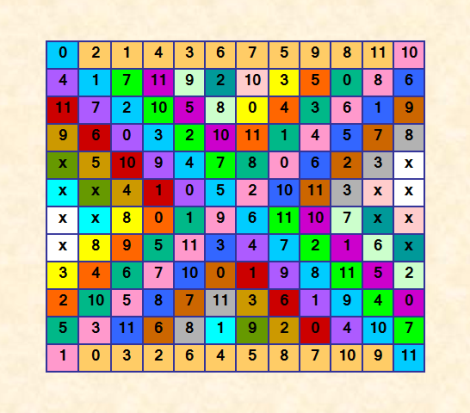 Перебор ушёл довольно далеко, но до полного ещё о-ч-е-н-ÑŒ далеко. Ð’ Ñтом неполном ДЛК имеетÑÑ 8 полных правильных Ñтрок, 8 полных правильных Ñтолбцов, 14 полных правильных диагоналей, то еÑÑ‚ÑŒ удовлетворÑющих ÑвойÑтву Ñлабой пандиагональноÑти. И 12 не заполненных Ñчеек. Ð’Ñе полные Ñтроки, Ñтолбцы и диагонали проверила, ошибок не нашла. Ðадежда опÑÑ‚ÑŒ ожила :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ТÑк-Ñ, а что же дальше делать Ñ Ñтим недоÑтроем? :) Ðаверное, надо попробовать Ñначала заполнить оÑтавшиеÑÑ 12 Ñчеек только Ñ ÑƒÑловием аÑÑоциативноÑти. ЕÑли проверÑÑ‚ÑŒ вÑе диагонали (уÑловие Ñлабой пандиагональноÑти), опÑÑ‚ÑŒ увÑзнуть можно о-ч-е-н-ÑŒ надолго. РаÑÑуждение: еÑли оÑтавшиеÑÑ Ñчейки не заполнÑÑ‚ÑÑ Ñ‚Ð¾Ð»ÑŒÐºÐ¾ Ñ ÑƒÑловием аÑÑоциативноÑти, тем более они не заполнÑÑ‚ÑÑ Ð¿Ñ€Ð¸ уÑловиÑÑ… аÑÑоциативноÑти и Ñлабой пандиагональноÑти. Далее: еÑли Ñ€ÐµÑˆÐµÐ½Ð¸Ñ Ñ Ð·Ð°Ð¿Ð¾Ð»Ð½ÐµÐ½Ð½Ñ‹Ð¼Ð¸ по аÑÑоциативноÑти Ñчейками будут найдены, и при Ñтом ÑущеÑтвует идеальный ДЛК, он обÑзательно будет Ñреди найденных решений. Ðаконец, не забудем, что надо будет выполнить программу Ð´Ð»Ñ Ð²Ñех возможных паттернов. ГоÑпода! Приглашаю подумать над задачкой. Идеи подброÑить :) Рможет, кто-то и решение готовое нашёл на проÑторах Интернета. Сообщите, пожалуйÑта. У Ð¼ÐµÐ½Ñ Ð½Ðµ получаетÑÑ Ð½Ð°Ð¹Ñ‚Ð¸ готовое решение в Интернете. ЕÑли идеальный ДЛК 12-го порÑдка извеÑтен, он как-то не "ÑветитÑÑ" в Интернете. Или Ñ Ð¿Ñ€Ð¾Ñто иÑкать не умею. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вчера вечером напиÑала и выполнила ещё один шажок - заполнение двух очередных Ñчеек. Вот что поÑтроилоÑÑŒ 0 2 1 4 3 6 7 5 9 8 11 10 4 1 7 11 9 2 10 3 5 0 8 6 11 7 2 10 5 8 0 4 3 6 1 9 9 6 0 3 2 10 11 1 4 5 7 8 x 5 10 9 4 7 8 0 6 2 3 x x 9 4 1 0 5 2 10 11 3 x x x x 8 0 1 9 6 11 10 7 2 x x 8 9 5 11 3 4 7 2 1 6 x 3 4 6 7 10 0 1 9 8 11 5 2 2 10 5 8 7 11 3 6 1 9 4 0 5 3 11 6 8 1 9 2 0 4 10 7 1 0 3 2 6 4 5 8 7 10 9 11 Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð½Ð°Ð¿Ð¸Ñала заполнение Ñледующих двух Ñчеек и запуÑтила программу. Программа думает уже примерно чаÑ. Пока она думает, покажу полный шаблон иÑкомого ДЛК 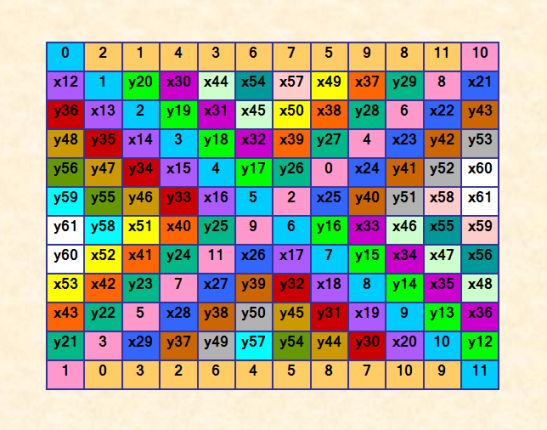 Ячейки, в которых ÑтоÑÑ‚ чиÑла, - Ñто иÑходный паттерн. y(i)=11-x(i) Ð´Ð»Ñ Ð²Ñех i (ÑвойÑтво аÑÑоциативноÑти). Переменных x(i) 50 штук (i = 12 - 61), из них 41 Ñвободные и 9 завиÑимые. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Программа вÑÑ‘ думает I12= 4 Y(57)= 1 Y(55)= 9 I12= 5 Y(57)= 2 Y(55)= 9 Y(55)= 6 ЗдеÑÑŒ выводитÑÑ ÑоÑтоÑние Ñамого внешнего цикла по переменной I12, Ñта Ð¿ÐµÑ€ÐµÐ¼ÐµÐ½Ð½Ð°Ñ Ð¸Ð·Ð¼ÐµÐ½ÑетÑÑ Ð¾Ñ‚ 2 до 11. Как видим, пока вÑÑ‘ ещё в Ñамом начале (I12 = 5), до Ð¾ÐºÐ¾Ð½Ñ‡Ð°Ð½Ð¸Ñ Ð¿ÐµÑ€ÐµÐ±Ð¾Ñ€Ð° далеко. Каждый новый шаг Ñ ÑƒÐ¶Ðµ начинаю выполнÑÑ‚ÑŒ Ñ Ñ‚Ð¾Ð³Ð¾ Ð·Ð½Ð°Ñ‡ÐµÐ½Ð¸Ñ I12, на котором программа оÑтановилаÑÑŒ на предыдущем шаге. Ð¢ÐµÑ…Ð½Ð¾Ð»Ð¾Ð³Ð¸Ñ Ð¿Ð¾Ð»Ð½Ð¾Ð³Ð¾ перебора мне хорошо знакома. Ðу, и текущие переменные выводÑÑ‚ÑÑ, чтобы видеть, что они ÑчитаютÑÑ, Ñ…Ð¾Ñ‚Ñ Ð¸ не проходÑÑ‚ при проверке уÑловий. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ура! Ðтот шажок тоже выполнен, поÑтроено 0 2 1 4 3 6 7 5 9 8 11 10 6 1 11 9 7 10 4 2 3 5 8 0 7 4 2 11 10 8 0 9 1 6 5 3 2 5 10 3 8 0 9 6 4 11 1 7 Ñ… 11 9 5 4 1 8 0 10 7 2 Ñ… Ñ… 8 7 6 0 5 2 10 11 3 4 Ñ… Ñ… 7 8 0 1 9 6 11 5 4 3 Ñ… Ñ… 9 4 1 11 3 10 7 6 2 0 Ñ… 4 10 0 7 5 2 11 3 8 1 6 9 8 6 5 10 2 11 3 1 0 9 7 4 11 3 6 8 9 7 1 4 2 0 10 5 1 0 3 2 6 4 5 8 7 10 9 11 Ð’ Ñтом полуфабрикате имеетÑÑ: 8 полных правильных Ñтрок, 10 полных правильных Ñтолбцов, 14 полных правильных диагоналей. И оÑталоÑÑŒ заполнить вÑего 8 Ñчеек из 144! Ðапомню: буду заполнÑÑ‚ÑŒ оÑтавшиеÑÑ Ñчейки только проверÑÑ ÑвойÑтво аÑÑоциативноÑти; ÑвойÑтво Ñлабой пандиагональноÑти пока не буду проверÑÑ‚ÑŒ. Смотрите раÑÑÑƒÐ¶Ð´ÐµÐ½Ð¸Ñ Ð¾Ð± Ñтом выше. ЕÑли будут найдены такие Ñ€ÐµÑˆÐµÐ½Ð¸Ñ (подобные показанному полуфабрикату и полноÑтью аÑÑоциативные), уже хорошо. ЕÑÑ‚ÑŒ надежда, что может быть и идеальный ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Заполнены ещё 4 Ñчейки! ПоÑтроено 0 2 1 4 3 6 7 5 9 8 11 10 6 1 11 9 7 10 4 2 3 5 8 0 7 4 2 11 10 8 0 9 1 6 5 3 2 5 10 3 8 0 9 6 4 11 1 7 3 11 9 5 4 1 8 0 10 7 2 6 x 8 7 6 0 5 2 10 11 3 4 x x 7 8 0 1 9 6 11 5 4 3 x 5 9 4 1 11 3 10 7 6 2 0 8 4 10 0 7 5 2 11 3 8 1 6 9 8 6 5 10 2 11 3 1 0 9 7 4 11 3 6 8 9 7 1 4 2 0 10 5 1 0 3 2 6 4 5 8 7 10 9 11 Ð’ Ñтом полуфабрикате 10 полных правильных Ñтрок, 10 полных правильных Ñтолбцов, 14 полных правильных диагоналей. И оÑталиÑÑŒ не заполненными вÑего 4 Ñчейки. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð½Ð°Ð¿Ð¸ÑˆÑƒ заполнение оÑтавшихÑÑ 4-Ñ… Ñчеек и запущу программу. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Программа выполнила полный перебор и не нашла ни одного решениÑ. ОÑтаётÑÑ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÐºÐ° вÑех возможных паттернов. Ещё бы знать точно, что в программе нет Ñкрытых ошибок, которые не видно Ñразу. Ðо проверÑÑ‚ÑŒ вÑÑŽ программу Ñнова нет никаких Ñил. Ð’ общем, пока нет результата. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Похоже, Ñ Ð½Ð°Ð¿Ñ€Ð°Ñно ищу идеальный ДЛК 12-го порÑдка. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¾Ñ‚ÐºÑ€Ñ‹Ð»Ð° Ñту Ñтатью Special Matrices Volume 6: Issue 1 Existence of strongly symmetrical weakly pandiagonal graeco-latin squares Yong Zhang 1 , Kejun Chen 2 , and Wen Li 3 1 School of Mathematics and Statistics, Yancheng Teachers University,, Jiangsu, P. R., China 2 School of Mathematics and Information Science, Nanjing Normal University of Special Education, Nanjing,, Jiangsu, P. R., China 3 School of Science, Xichang University,, Sichuan, P. R., China DOI: https://doi.org/10.1515/spma-2018-0013 Вот что там напиÑано As a result, it is proved that there exists a pair of strongly symmetrical weakly pandiagonal orthogonal latin sauare of order n if and only if n > 4 and n ≡ 0, 1, 3 (mod 4) with only one possible exception for n = 12. Ð¥Ð¾Ñ‚Ñ Ñказано как-то раÑплывчато: "Ñ Ð¾Ð´Ð½Ð¸Ð¼ возможным иÑключением Ð´Ð»Ñ n = 12". Похоже, авторы Ñтатьи тоже не Ñмогли найти решение Ð´Ð»Ñ n = 12. Замечание: "strongly symmetrical" означает "аÑÑоциативный" в нашей терминологии. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ИнтереÑно: в Ñтатье приведён пример ортогональной пары аÑÑоциативных Ñлабо падиагональных ЛК 9-го порÑдка 6 3 7 4 1 5 2 8 0 7 4 1 5 2 8 0 6 3 1 5 2 8 0 6 3 7 4 2 8 0 6 3 7 4 1 5 0 6 3 7 4 1 5 2 8 3 7 4 1 5 2 8 0 6 4 1 5 2 8 0 6 3 7 5 2 8 0 6 3 7 4 1 8 0 6 3 7 4 1 5 2 0 8 2 5 1 4 7 3 6 3 6 0 8 2 5 1 4 7 4 7 3 6 0 8 2 5 1 5 1 4 7 3 6 0 8 2 8 2 5 1 4 7 3 6 0 6 0 8 2 5 1 4 7 3 7 3 6 0 8 2 5 1 4 1 4 7 3 6 0 8 2 5 2 5 1 4 7 3 6 0 8 Ðу, у Ð¼ÐµÐ½Ñ Ð¿Ñ€Ð¸Ð¼ÐµÑ€ лучше: Ñ Ð½Ð°ÑˆÐ»Ð° ортогональную пару аÑÑоциативных Ñлабо пандиагональных (то еÑÑ‚ÑŒ идеальных) ДЛК 9-го порÑдка. Смотрите Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=126&postid=1520 3 5 4 6 8 7 0 2 1 0 2 1 3 5 4 6 8 7 6 8 7 0 2 1 3 5 4 5 4 3 8 7 6 2 1 0 2 1 0 5 4 3 8 7 6 8 7 6 2 1 0 5 4 3 4 3 5 7 6 8 1 0 2 1 0 2 4 3 5 7 6 8 7 6 8 1 0 2 4 3 5 3 0 6 5 2 8 4 1 7 5 2 8 4 1 7 3 0 6 4 1 7 3 0 6 5 2 8 6 3 0 8 5 2 7 4 1 8 5 2 7 4 1 6 3 0 7 4 1 6 3 0 8 5 2 0 6 3 2 8 5 1 7 4 2 8 5 1 7 4 0 6 3 1 7 4 0 6 3 2 8 5 Проверка ÑвойÑтв Ñтих ДЛК утилитой Harry White Order? 9
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_15.txt
Counts
------
2 diagonal Latin
2 associative
2 weakly pandiagonal
2 ultramagic
1 orthogonal pair
2 self-orthogonalÐта Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° поÑтроена программой Harry White Ð´Ð»Ñ SODLS. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Рвот какой пример приведён в Ñтатье Ð´Ð»Ñ Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð¾Ð¹ пары аÑÑоциативных Ñлабо пандиагональных ЛК 24-го порÑдка, показываю только первый ЛК ортогональной пары 0 6 2 11 5 9 15 13 16 20 22 19 21 23 17 14 12 18 8 10 7 3 1 4 6 2 0 5 9 11 13 16 15 22 19 20 23 17 21 12 18 14 10 7 8 1 4 3 2 0 6 9 11 5 16 15 13 19 20 22 17 21 23 18 14 12 7 8 10 4 3 1 3 1 4 8 10 7 14 12 18 21 23 17 20 22 19 15 13 16 11 5 9 0 6 2 1 4 3 10 7 8 12 18 14 23 17 21 22 19 20 13 16 15 5 9 11 6 2 0 4 3 1 7 8 10 18 14 12 17 21 23 19 20 22 16 15 13 9 11 5 2 0 6 20 22 19 15 13 16 11 5 9 0 6 2 3 1 4 8 10 7 14 12 18 21 23 17 22 19 20 13 16 15 5 9 11 6 2 0 1 4 3 10 7 8 12 18 14 23 17 21 19 20 22 16 15 13 9 11 5 2 0 6 4 3 1 7 8 10 18 14 12 17 21 23 21 23 17 14 12 18 8 10 7 3 1 4 0 6 2 11 5 9 15 13 16 20 22 19 23 17 21 12 18 14 10 7 8 1 4 3 6 2 0 5 9 11 13 16 15 22 19 20 17 21 23 18 14 12 7 8 10 4 3 1 2 0 6 9 11 5 16 15 13 19 20 22 1 3 4 10 8 7 18 12 14 17 23 21 22 20 19 13 15 16 11 9 5 0 2 6 3 4 1 8 7 10 12 14 18 23 21 17 20 19 22 15 16 13 9 5 11 2 6 0 4 1 3 7 10 8 14 18 12 21 17 23 19 22 20 16 13 15 5 11 9 6 0 2 0 2 6 11 9 5 13 15 16 22 20 19 17 23 21 18 12 14 10 8 7 1 3 4 2 6 0 9 5 11 15 16 13 20 19 22 23 21 17 12 14 18 8 7 10 3 4 1 6 0 2 5 11 9 16 13 15 19 22 20 21 17 23 14 18 12 7 10 8 4 1 3 17 23 21 18 12 14 10 8 7 1 3 4 0 2 6 11 9 5 13 15 16 22 20 19 23 21 17 12 14 18 8 7 10 3 4 1 2 6 0 9 5 11 15 16 13 20 19 22 21 17 23 14 18 12 7 10 8 4 1 3 6 0 2 5 11 9 16 13 15 19 22 20 22 20 19 13 15 16 11 9 5 0 2 6 1 3 4 10 8 7 18 12 14 17 23 21 20 19 22 15 16 13 9 5 11 2 6 0 3 4 1 8 7 10 12 14 18 23 21 17 19 22 20 16 13 15 5 11 9 6 0 2 4 1 3 7 10 8 14 18 12 21 17 23 Ðтот квадрат они называют латинÑким квадратом? Странно! Ðтот квадрат не ÑвлÑетÑÑ Ð»Ð°Ñ‚Ð¸Ð½Ñким - по определению. Ðто обобщённый латинÑкий квадрат. КÑтати, утилита Harry White Ñтот квадрат латинÑким не называет (и правильно!) Order? 24
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_21.txt
Counts
------
1 other magicЕÑли раÑÑматривать обобщённые ЛК, тогда и Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 12 ÑущеÑтвует Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° аÑÑоциативных Ñлабо пандиагональных ЛК. Такую ортогональную пару можно получить, например, из Ñтого идеального магичеÑкого квадрата 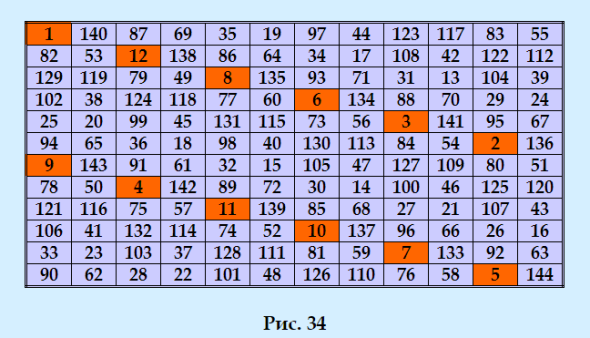 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Идеальный магичеÑкий квадрат 24-го порÑдка мной тоже был поÑтроен. Смотрите Ñтатью МЕТОД ПОСТРОЕÐИЯ ИДЕÐЛЬÐЫХ КВÐДРÐТОВ ПОРЯДКРn=8k  Разложите Ñтот магичеÑкий квадрат на ортогональную пару, и вы получите два ортогональных обобщённых ЛК - аÑÑоциативных и Ñлабо пандиагональных. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ВернёмÑÑ Ðº идеальным ДЛК. Идеальный ДЛК 12-го порÑдка мне поÑтроить не удалоÑÑŒ. Даже не знаю, ÑущеÑтвует ли он. Дальше идёт проблемный порÑдок 15. Пока не имею алгоритма поÑÑ‚Ñ€Ð¾ÐµÐ½Ð¸Ñ Ð¸Ð´ÐµÐ°Ð»ÑŒÐ½Ð¾Ð³Ð¾ ДЛК 15-го порÑдка. О ÑущеÑтвовании такого ДЛК тоже пока ничего не знаю. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’ Ñвоей Ñтатье МЕТОД КÐЧЕЛЕЙ ПЛЮС ЛÐТИÐСКИЕ КВÐДРÐТЫ ЧаÑÑ‚ÑŒ I нашла такой ЛК 15-го порÑдка (в Ñтатье он изображён на риÑ. 2) 6 4 3 7 11 10 8 1 9 12 14 0 2 5 13 9 12 14 0 2 5 13 6 4 3 7 11 10 8 1 4 3 7 11 10 8 1 9 12 14 0 2 5 13 6 12 14 0 2 5 13 6 4 3 7 11 10 8 1 9 3 7 11 10 8 1 9 12 14 0 2 5 13 6 4 14 0 2 5 13 6 4 3 7 11 10 8 1 9 12 7 11 10 8 1 9 12 14 0 2 5 13 6 4 3 0 2 5 13 6 4 3 7 11 10 8 1 9 12 14 11 10 8 1 9 12 14 0 2 5 13 6 4 3 7 2 5 13 6 4 3 7 11 10 8 1 9 12 14 0 10 8 1 9 12 14 0 2 5 13 6 4 3 7 11 5 13 6 4 3 7 11 10 8 1 9 12 14 0 2 8 1 9 12 14 0 2 5 13 6 4 3 7 11 10 13 6 4 3 7 11 10 8 1 9 12 14 0 2 5 1 9 12 14 0 2 5 13 6 4 3 7 11 10 8 Странно, что утилита Harry White не признаёт Ñтот ЛК аÑÑоциативным, а признаёт центрально-Ñимметричным, Ñ…Ð¾Ñ‚Ñ Ð¾Ð½ ÑвлÑетÑÑ Ð°ÑÑоциативным Order? 15
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_28.txt
Counts
------
1 Latin
1 weakly pandiagonal
1 center symmetricЛК аÑÑоциативный и Ñлабо пандиагональный, Ñледовательно, идеальный. Ðо он, увы, не ÑвлÑетÑÑ Ð”Ð›Ðš. ИнтереÑно: ЛК поÑтроен методом цикличеÑкого Ñдвига. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
КÑтати, в Ñтатье напиÑано, что показанный ЛК 15-го порÑдка имеет ортогональный ЛК, который получаетÑÑ Ð¾Ñ‚Ñ€Ð°Ð¶ÐµÐ½Ð¸ÐµÐ¼ отноÑительно горизонтальной оÑи Ñимметрии. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾ÐºÐ°Ð¶Ñƒ Ñту ортогональную пару ЛК. Вот 6 4 3 7 11 10 8 1 9 12 14 0 2 5 13 9 12 14 0 2 5 13 6 4 3 7 11 10 8 1 4 3 7 11 10 8 1 9 12 14 0 2 5 13 6 12 14 0 2 5 13 6 4 3 7 11 10 8 1 9 3 7 11 10 8 1 9 12 14 0 2 5 13 6 4 14 0 2 5 13 6 4 3 7 11 10 8 1 9 12 7 11 10 8 1 9 12 14 0 2 5 13 6 4 3 0 2 5 13 6 4 3 7 11 10 8 1 9 12 14 11 10 8 1 9 12 14 0 2 5 13 6 4 3 7 2 5 13 6 4 3 7 11 10 8 1 9 12 14 0 10 8 1 9 12 14 0 2 5 13 6 4 3 7 11 5 13 6 4 3 7 11 10 8 1 9 12 14 0 2 8 1 9 12 14 0 2 5 13 6 4 3 7 11 10 13 6 4 3 7 11 10 8 1 9 12 14 0 2 5 1 9 12 14 0 2 5 13 6 4 3 7 11 10 8 1 9 12 14 0 2 5 13 6 4 3 7 11 10 8 13 6 4 3 7 11 10 8 1 9 12 14 0 2 5 8 1 9 12 14 0 2 5 13 6 4 3 7 11 10 5 13 6 4 3 7 11 10 8 1 9 12 14 0 2 10 8 1 9 12 14 0 2 5 13 6 4 3 7 11 2 5 13 6 4 3 7 11 10 8 1 9 12 14 0 11 10 8 1 9 12 14 0 2 5 13 6 4 3 7 0 2 5 13 6 4 3 7 11 10 8 1 9 12 14 7 11 10 8 1 9 12 14 0 2 5 13 6 4 3 14 0 2 5 13 6 4 3 7 11 10 8 1 9 12 3 7 11 10 8 1 9 12 14 0 2 5 13 6 4 12 14 0 2 5 13 6 4 3 7 11 10 8 1 9 4 3 7 11 10 8 1 9 12 14 0 2 5 13 6 9 12 14 0 2 5 13 6 4 3 7 11 10 8 1 6 4 3 7 11 10 8 1 9 12 14 0 2 5 13 Проверка ЛК Ñтой ортогональной пары утилитой Harry White Order? 15
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt
Counts
------
2 Latin
2 weakly pandiagonal
2 center symmetric
1 orthogonal pairОба ЛК утилита Ñчитает центрально-Ñимметричными, Ñ…Ð¾Ñ‚Ñ Ð¾Ð½Ð¸ аÑÑоциативные. Из Ñтой ортогональной пары можно поÑтроить методом латинÑких квадратов идеальный магичеÑкий квадрат, из которого Ñта Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° и была получена в Ñтатье. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese