Thread 'Experiment (pandiagonal DLS of order 13)'
Message boards : Science : Experiment (pandiagonal DLS of order 13)
Message board moderation
Previous · 1 · 2 · 3 · 4 · 5 . . . 7 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ЗаинтереÑовали ÑвойÑтва полученных 348 пандиагональных ДЛК, выданные утилитой Harry White Order? 13
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_12.txt
Counts
------
348 diagonal Latin
348 pandiagonal
36 center symmetric
348 nfr
1 orthogonal pair
10 self-orthogonalЕÑÑ‚ÑŒ 36 центрально-Ñимметричных ДЛК. Ðе дадут ли они идеальные ДЛК? Ðадо проверить. ЕÑÑ‚ÑŒ 10 SODLS. Рещё еÑÑ‚ÑŒ одна Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð°, интереÑно, из каких ДЛК она ÑоÑтоит. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð·Ð°Ð¹Ð¼ÑƒÑÑŒ проверкой Ñтих интереÑных пандиагональных квадратиков. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Да!! Беру один из 36 центрально-Ñимметричных ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 2 3 4 5 6 7 8 9 10 11 12 0 1 12 0 1 2 3 4 5 6 7 8 9 10 11 5 6 7 8 9 10 11 12 0 1 2 3 4 7 8 9 10 11 12 0 1 2 3 4 5 6 10 11 12 0 1 2 3 4 5 6 7 8 9 4 5 6 7 8 9 10 11 12 0 1 2 3 11 12 0 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 11 12 0 3 4 5 6 7 8 9 10 11 12 0 1 2 9 10 11 12 0 1 2 3 4 5 6 7 8 6 7 8 9 10 11 12 0 1 2 3 4 5 8 9 10 11 12 0 1 2 3 4 5 6 7 и преобразовываю его в СРДЛК 0 2 5 1 11 7 10 12 3 8 6 4 9 5 1 11 7 10 12 3 8 6 4 9 0 2 9 0 2 5 1 11 7 10 12 3 8 6 4 7 10 12 3 8 6 4 9 0 2 5 1 11 12 3 8 6 4 9 0 2 5 1 11 7 10 6 4 9 0 2 5 1 11 7 10 12 3 8 11 7 10 12 3 8 6 4 9 0 2 5 1 4 9 0 2 5 1 11 7 10 12 3 8 6 2 5 1 11 7 10 12 3 8 6 4 9 0 1 11 7 10 12 3 8 6 4 9 0 2 5 8 6 4 9 0 2 5 1 11 7 10 12 3 10 12 3 8 6 4 9 0 2 5 1 11 7 3 8 6 4 9 0 2 5 1 11 7 10 12 Вот и вÑÑ‘: идеальный ДЛК получен. Проверка утилитой Harry White Order? 13
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_8.txt
Counts
------
1 diagonal Latin
1 associative
1 pandiagonal
1 ultramagic
1 natural \diagonalТакой отличный ДЛК получилÑÑ: аÑÑоциативный и полуцикличеÑкий пандиагональный, то еÑÑ‚ÑŒ идеальный. Теперь надо проверить вÑе оÑтальные центрально-Ñимметричные ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Выудила ортогональную пару 0 1 2 3 4 5 6 7 8 9 10 11 12 10 11 12 0 1 2 3 4 5 6 7 8 9 7 8 9 10 11 12 0 1 2 3 4 5 6 5 6 7 8 9 10 11 12 0 1 2 3 4 1 2 3 4 5 6 7 8 9 10 11 12 0 11 12 0 1 2 3 4 5 6 7 8 9 10 4 5 6 7 8 9 10 11 12 0 1 2 3 8 9 10 11 12 0 1 2 3 4 5 6 7 12 0 1 2 3 4 5 6 7 8 9 10 11 3 4 5 6 7 8 9 10 11 12 0 1 2 9 10 11 12 0 1 2 3 4 5 6 7 8 6 7 8 9 10 11 12 0 1 2 3 4 5 2 3 4 5 6 7 8 9 10 11 12 0 1 0 1 2 3 4 5 6 7 8 9 10 11 12 3 4 5 6 7 8 9 10 11 12 0 1 2 6 7 8 9 10 11 12 0 1 2 3 4 5 8 9 10 11 12 0 1 2 3 4 5 6 7 12 0 1 2 3 4 5 6 7 8 9 10 11 2 3 4 5 6 7 8 9 10 11 12 0 1 9 10 11 12 0 1 2 3 4 5 6 7 8 5 6 7 8 9 10 11 12 0 1 2 3 4 1 2 3 4 5 6 7 8 9 10 11 12 0 10 11 12 0 1 2 3 4 5 6 7 8 9 4 5 6 7 8 9 10 11 12 0 1 2 3 7 8 9 10 11 12 0 1 2 3 4 5 6 11 12 0 1 2 3 4 5 6 7 8 9 10 Здорово: Ñто Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° полуцикличеÑких пандиагональных ДЛК 13-го порÑдка. Можно поÑтроить оригинальный пандиагональный магичеÑкий квадрат Ñ Ð¿Ð¾Ð¼Ð¾Ñ‰ÑŒÑŽ Ñтой ортогональной пары. Такого у Ð¼ÐµÐ½Ñ ÐµÑ‰Ñ‘ не было :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð¥Ð¾Ñ‚Ñ Ð¿Ð¾Ñтроение пандиагональных магичеÑких квадратов 13-го порÑдка не ÑвлÑетÑÑ Ð¿Ñ€Ð¾Ð±Ð»ÐµÐ¼Ð¾Ð¹, покажу вÑÑ‘-таки принципиально новый пандиагональный магичеÑкий квадрат, поÑтроенный Ñ Ð¿Ð¾Ð¼Ð¾Ñ‰ÑŒÑŽ показанной выше ортогональной пары полуцикличеÑких пандиагональных ДЛК методом латинÑких квадратов 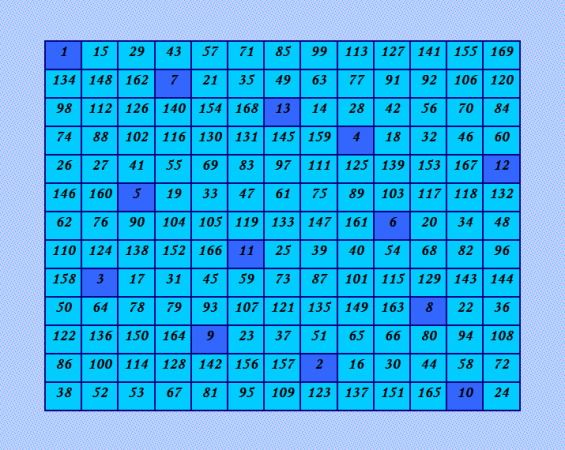 Обратите внимание на начальную цепочку магичеÑкого квадрата, она выделена более тёмным цветом. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Итак, еÑли полуцикличеÑкие пандиагональные ДЛК 13-го порÑдка Ñ Ð¿Ñ€Ð°Ð²Ð¸Ð»ÑŒÐ½Ð¾ понимаю, можно попытатьÑÑ Ð¸Ñ… вÑе найти. Рдалее непонÑтно, как найти вÑе не цикличеÑкие пандиагональные ДЛК, коих много. Цитирую Ñтатью OEIS For order n=13 this is not true and exists 12386 inequivalent squares; of these 10 are cyclic (in all directions) and 1560 are semi-cyclic (cyclic in a single direction). 10 цикличеÑких пандиагональных уже найдены, 1560 полуцикличеÑких можно найти, еÑли Ñ Ð¿Ñ€Ð°Ð²Ð¸Ð»ÑŒÐ½Ð¾ их понÑла. Рвот оÑтальных пандиагональных ДЛК, которые не цикличеÑкие, имеетÑÑ 12386 - 10 - 1560 = 10816 И как же их вÑе найти??? Я уже отмечала выше, что в Ñтатье OEIS пандиагональные ЛК раÑÑматриваютÑÑ "with the first row in ascending order". Однако пример не цикличеÑкого пандиагонального ДЛК, приведённый в Ñтатье, не преобразован к такому виду. Выше был показан преобразованный ДЛК. Повторю 0 1 2 3 4 5 6 7 8 9 10 11 12 7 3 12 10 2 0 4 9 6 11 5 8 1 12 11 1 0 8 9 10 3 4 2 6 7 5 4 5 8 11 10 12 0 2 1 7 3 9 6 8 9 7 5 6 11 1 12 3 10 2 4 0 3 4 6 2 1 7 8 11 5 12 0 10 9 10 2 3 7 9 6 5 4 0 8 1 12 11 1 0 10 12 3 4 9 8 7 5 11 6 2 11 12 5 4 0 2 3 10 9 6 7 1 8 5 8 0 1 12 10 11 6 2 4 9 3 7 6 7 9 8 11 1 2 0 10 3 12 5 4 9 10 11 6 5 8 7 1 12 0 4 2 3 2 6 4 9 7 3 12 5 11 1 8 0 10 ПонÑтно, что и вÑе оÑтальные 10815 не цикличеÑких пандиагональных ДЛК надо иÑкать в таком же виде, то еÑÑ‚ÑŒ нормализованные. Итак, Ñупер-задача: найти 10815 не цикличеÑких нормализованных пандиагональных ДЛК 13-го порÑдка. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðапомню, что Ñ ÑƒÐ¶Ðµ нашла 5 новых не цикличеÑких пандиагональных ДЛК 13-го порÑдка, иÑÐ¿Ð¾Ð»ÑŒÐ·ÑƒÑ Ð¿Ñ€Ð¸Ð²ÐµÐ´Ñ‘Ð½Ð½Ñ‹Ð¹ в Ñтатье OEIS ДЛК, применÑÑ Ðº нему комбинации преобразований. Теперь у Ð¼ÐµÐ½Ñ ÐµÑÑ‚ÑŒ 6 не цикличеÑких пандиагональных ДЛК 13-го порÑдка, Ð²ÐºÐ»ÑŽÑ‡Ð°Ñ Ð¿Ñ€Ð¸Ð¼ÐµÑ€ из Ñтатьи OEIS, вот они 0 1 2 3 4 5 6 7 8 9 10 11 12 6 11 0 1 8 2 10 4 12 5 3 7 9 7 9 10 6 12 0 3 1 11 2 4 8 5 12 8 3 7 11 9 5 6 0 10 1 2 4 11 2 5 4 1 8 7 12 9 6 0 3 10 1 0 9 10 2 3 4 8 7 11 12 5 6 4 12 6 11 0 10 2 5 3 1 8 9 7 8 5 7 12 6 1 11 9 10 4 2 0 3 2 3 8 9 5 4 12 0 6 7 11 10 1 10 4 1 0 3 7 8 2 5 12 9 6 11 9 7 11 2 10 6 1 3 4 8 5 12 0 5 6 12 8 9 11 0 10 1 3 7 4 2 3 10 4 5 7 12 9 11 2 0 6 1 8 0 12 3 10 6 4 9 5 11 7 8 1 2 6 1 9 0 11 12 2 10 4 3 5 7 8 11 7 2 8 5 1 0 6 12 10 4 9 3 5 4 12 3 7 9 8 1 0 11 6 2 10 8 6 10 11 4 3 7 2 9 5 1 12 0 1 2 0 6 10 5 11 12 3 8 7 4 9 7 9 1 12 2 8 6 4 10 0 11 3 5 3 8 5 4 9 0 1 7 2 6 12 10 11 12 0 11 7 3 10 5 9 8 1 2 6 4 2 10 6 1 12 11 4 3 5 9 0 8 7 9 3 8 2 0 6 12 11 7 4 10 5 1 4 5 7 9 8 2 10 0 1 12 3 11 6 10 11 4 5 1 7 3 8 6 2 9 0 12 3 10 6 4 9 5 11 7 8 1 2 0 12 9 0 11 12 2 10 4 3 5 7 8 6 1 2 8 5 1 0 6 12 10 4 9 3 11 7 12 3 7 9 8 1 0 11 6 2 10 5 4 10 11 4 3 7 2 9 5 1 12 0 8 6 0 6 10 5 11 12 3 8 7 4 9 1 2 1 12 2 8 6 4 10 0 11 3 5 7 9 5 4 9 0 1 7 2 6 12 10 11 3 8 11 7 3 10 5 9 8 1 2 6 4 12 0 6 1 12 11 4 3 5 9 0 8 7 2 10 8 2 0 6 12 11 7 4 10 5 1 9 3 7 9 8 2 10 0 1 12 3 11 6 4 5 4 5 1 7 3 8 6 2 9 0 12 10 11 0 3 7 1 9 4 10 6 5 8 12 2 11 2 1 12 0 10 11 5 9 7 6 4 8 3 8 6 2 11 12 9 1 10 4 0 3 7 5 10 11 5 3 2 8 12 0 1 7 9 4 6 5 7 6 8 4 0 3 11 12 2 1 10 9 12 9 4 7 3 5 8 2 6 10 11 0 1 4 0 10 9 1 7 6 5 11 3 2 12 8 11 12 1 2 6 10 4 7 9 5 8 3 0 3 2 11 10 0 1 9 12 8 4 6 5 7 6 8 3 5 11 12 0 4 10 9 7 1 2 7 5 9 12 8 2 11 3 0 1 10 6 4 9 4 8 6 5 3 7 1 2 12 0 11 10 1 10 0 4 7 6 2 8 3 11 5 9 12 0 2 11 1 9 6 4 5 7 8 12 3 10 5 1 10 12 11 0 9 8 4 3 6 7 2 10 3 2 0 7 8 12 1 9 11 4 5 6 9 6 7 3 12 10 0 11 2 5 1 8 4 7 8 5 6 4 3 2 10 1 12 11 9 0 1 9 4 11 2 5 7 3 6 10 0 12 8 12 11 1 5 8 4 6 9 0 7 2 10 3 2 0 12 10 1 9 8 7 5 6 3 4 11 3 10 6 9 0 11 1 12 8 4 5 2 7 6 7 0 2 10 12 3 4 11 9 8 1 5 4 5 8 7 3 2 11 0 12 1 10 6 9 8 12 3 4 6 7 5 2 10 0 9 11 1 11 4 9 8 5 1 10 6 3 2 7 0 12 0 9 7 10 8 12 2 11 5 1 6 3 4 3 1 0 12 7 11 9 8 6 10 4 5 2 8 12 2 4 0 3 7 10 9 5 11 6 1 2 5 1 3 6 10 4 12 7 0 9 8 11 7 11 6 5 4 2 3 0 1 8 12 10 9 6 10 8 11 9 5 1 2 12 4 0 7 3 12 7 9 0 1 8 6 5 11 2 3 4 10 4 0 12 8 10 9 11 7 3 6 1 2 5 1 3 4 2 12 7 10 6 8 11 5 9 0 5 2 11 7 3 0 12 4 10 9 8 1 6 11 6 3 1 2 4 5 9 0 7 10 12 8 9 8 10 6 5 1 0 3 4 12 2 11 7 10 4 5 9 11 6 8 1 2 3 7 0 12 Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð½Ð¾Ñ€Ð¼Ð°Ð»Ð¸Ð·ÑƒÑŽ вÑе Ñти ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Готово! 0 1 2 3 4 5 6 7 8 9 10 11 12 6 11 0 1 8 2 10 4 12 5 3 7 9 7 9 10 6 12 0 3 1 11 2 4 8 5 12 8 3 7 11 9 5 6 0 10 1 2 4 11 2 5 4 1 8 7 12 9 6 0 3 10 1 0 9 10 2 3 4 8 7 11 12 5 6 4 12 6 11 0 10 2 5 3 1 8 9 7 8 5 7 12 6 1 11 9 10 4 2 0 3 2 3 8 9 5 4 12 0 6 7 11 10 1 10 4 1 0 3 7 8 2 5 12 9 6 11 9 7 11 2 10 6 1 3 4 8 5 12 0 5 6 12 8 9 11 0 10 1 3 7 4 2 3 10 4 5 7 12 9 11 2 0 6 1 8 0 1 2 3 4 5 6 7 8 9 10 11 12 4 11 6 0 8 1 12 3 5 2 7 9 10 8 9 12 10 7 11 0 4 1 3 5 6 2 7 5 1 2 9 6 10 11 0 8 4 12 3 10 4 3 8 5 2 9 12 6 7 11 1 0 11 12 0 4 3 7 8 1 2 10 9 5 6 9 6 11 1 12 10 4 5 3 0 8 2 7 2 10 7 5 6 0 11 9 12 4 1 3 8 1 0 8 9 2 3 7 6 10 11 12 4 5 12 3 4 11 1 8 5 2 7 6 0 10 9 6 2 10 12 0 4 1 8 9 5 3 7 11 5 7 9 6 10 12 3 0 11 1 2 8 4 3 8 5 7 11 9 2 10 4 12 6 0 1 0 1 2 3 4 5 6 7 8 9 10 11 12 4 11 6 12 10 1 3 0 5 7 8 2 9 10 8 5 9 11 2 12 1 3 4 0 6 7 12 0 7 4 8 9 11 6 2 10 1 5 3 1 6 3 0 7 10 4 5 9 12 11 8 2 11 2 1 5 6 12 0 8 7 3 4 9 10 9 12 10 8 2 3 1 11 6 0 5 7 4 5 3 4 11 9 7 10 2 12 1 6 0 8 6 7 0 1 5 4 8 9 10 2 3 12 11 2 9 12 6 3 0 5 4 11 8 7 10 1 8 10 11 2 12 6 7 3 1 5 9 4 0 7 4 8 10 1 11 9 12 0 6 2 3 5 3 5 9 7 0 8 2 10 4 11 12 1 6 0 1 2 3 4 5 6 7 8 9 10 11 12 11 3 10 0 6 12 8 4 2 7 5 9 1 9 7 11 12 10 4 3 6 5 0 1 2 8 6 12 8 1 11 9 10 0 3 2 4 5 7 8 2 7 9 5 0 1 12 10 11 3 6 4 10 4 5 2 1 8 9 11 7 6 12 0 3 5 0 6 4 3 2 7 8 12 1 11 10 9 12 10 3 11 7 6 5 2 4 8 9 1 0 1 11 12 6 0 3 4 10 9 5 7 8 2 7 9 1 8 12 10 0 5 6 4 2 3 11 2 8 4 10 9 11 12 1 0 3 6 7 5 4 5 9 7 8 1 2 3 11 10 0 12 6 3 6 0 5 2 7 11 9 1 12 8 4 10 0 1 2 3 4 5 6 7 8 9 10 11 12 7 3 12 10 2 0 4 9 6 11 5 8 1 12 11 1 0 8 9 10 3 4 2 6 7 5 4 5 8 11 10 12 0 2 1 7 3 9 6 8 9 7 5 6 11 1 12 3 10 2 4 0 3 4 6 2 1 7 8 11 5 12 0 10 9 10 2 3 7 9 6 5 4 0 8 1 12 11 1 0 10 12 3 4 9 8 7 5 11 6 2 11 12 5 4 0 2 3 10 9 6 7 1 8 5 8 0 1 12 10 11 6 2 4 9 3 7 6 7 9 8 11 1 2 0 10 3 12 5 4 9 10 11 6 5 8 7 1 12 0 4 2 3 2 6 4 9 7 3 12 5 11 1 8 0 10 0 1 2 3 4 5 6 7 8 9 10 11 12 11 9 0 5 2 7 1 4 10 3 12 8 6 4 5 6 12 0 11 2 3 1 8 7 10 9 6 8 9 11 10 3 12 5 2 0 1 4 7 2 7 10 8 12 6 11 0 9 4 5 3 1 10 3 4 7 1 8 9 6 5 12 0 2 11 5 2 1 0 9 4 10 8 7 6 11 12 3 12 0 5 4 3 1 7 2 11 10 9 6 8 9 11 12 6 5 2 3 10 4 7 8 1 0 8 6 7 2 11 0 5 12 3 1 4 9 10 7 10 11 9 6 12 8 1 0 2 3 5 4 1 4 3 10 8 9 0 11 12 5 6 7 2 3 12 8 1 7 10 4 9 6 11 2 0 5 ПроверÑÑŽ ДЛК утилитой Harry White Order? 13
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_18.txt
Counts
------
6 diagonal Latin
6 pandiagonal
2 center symmetric
6 nfr |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Итак, Ñупер-задачу Ñ ÑƒÐ¶Ðµ чуточку решила, нашла 5 новых не цикличеÑких пандиагональных ДЛК 13-го порÑдка. Из 10816 ÑущеÑтвующих нам извеÑтны теперь 6. Ðадо найти оÑтальные. Ðо... как иÑкать Ñти оÑтальные, Ñ Ð¿Ð¾ÐºÐ° не знаю. ЕÑÑ‚ÑŒ ÑтатьÑ, в которой опиÑываетÑÑ Ð¿Ð¾Ñтроение не цикличеÑких пандиагональных ДЛК 13-го порÑдка (ÑÑылка на Ñтатью указана в OEIS, выше Ñ ÐµÑ‘ привела). Однако разобратьÑÑ Ð² ней непроÑто, тем более что Ñ Ð½Ðµ читаю по-английÑки. Harry White пиÑала про Ñту задачу, от ответил так же: Ñложно разобратьÑÑ Ð² Ñтатье (Ñ…Ð¾Ñ‚Ñ Ð¾Ð½ читает по-английÑки). |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Увидела в Ñтатье OEIS ÑÑылку ещё на одну Ñтатью. Цитирую A.O.L. Atkin, L. Hay, and R. G. Larson, Enumeration and construction of pandiagonal Latin squares of prime order, Computers & Mathematics with Applications, Volume. 9, Iss. 2, 1983, pp. 267-292. Ðту Ñтатью Ñ ÐµÑˆÑ‘ и не Ñмотрела. Abstract- Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ñмотрела, вижу там три пандиагональных ДЛК 13-го порÑдка, как мне кажетÑÑ, не цикличеÑкие. Ðадо Ñкопировать и поÑмотреть приÑтальнее. Ðапример, у Ñтого квадрата 0 B 1 7 5 9 3 A 4 8 6 C 2 9 7 0 3 1 C 2 8 6 A 4 B 5 B 5 C 6 A 8 1 4 2 0 3 9 7 1 4 A 8 C 6 0 7 B 9 2 5 3 A 3 6 4 2 5 B 9 0 7 1 8 C 8 2 9 0 B 4 7 5 3 6 C A 1 7 0 B 2 9 3 A 1 C 5 8 6 4 6 9 7 5 8 1 C 3 A 4 B 2 0 5 C 3 1 7 A 8 6 9 2 0 4 B 3 1 5 C 6 0 4 2 8 B 9 7 A C A 8 B 4 2 6 0 7 1 5 3 9 2 6 4 A 0 B 9 C 5 3 7 1 8 4 8 2 9 3 7 5 B 1 C A 0 6 Ñ‚Ð°ÐºÐ°Ñ Ð¿Ð¾Ð´Ð¿Ð¸ÑÑŒ Fig. I. (A = 10, B = 11, C= 12). A PL-square cyclic in the direction of (1,4): 1 down, 4 across. Хм... "цикличеÑкий в направлении (1,4)". И чего Ñто означает? Конечно, Ñтатью надо читать. Ðо... поÑмотришь на Ñтот текÑÑ‚, прÑмо Ñтрашно аж жуть. Там и знающий английÑкий не Ñразу разберётÑÑ. Как мне кажетÑÑ, приведённый квадрат не цикличеÑкий пандиагональный. Ðо, может, Ñ Ñ‡ÐµÐ³Ð¾-то неправильно понимаю. Преобразовала показанный пандиагональный ДЛК в чиÑловой формат и нормализовала 0 1 2 3 4 5 6 7 8 9 10 11 12 5 3 0 6 2 11 12 9 10 7 8 1 4 1 4 11 10 7 9 2 8 12 0 6 5 3 2 8 7 9 11 10 0 3 1 5 12 4 6 7 6 10 8 12 4 1 5 0 3 2 9 11 9 12 5 0 1 8 3 4 6 10 11 7 2 3 0 1 12 5 6 7 2 11 4 9 10 8 10 5 3 4 9 2 11 6 7 8 1 12 0 4 11 6 2 3 7 9 10 5 12 0 8 1 6 2 4 11 10 0 8 12 9 1 5 3 7 11 7 9 1 8 12 10 0 3 2 4 6 5 12 10 8 7 0 1 5 11 4 6 3 2 9 8 9 12 5 6 3 4 1 2 11 7 0 10 Разве Ñтот ДЛК не ÑвлÑетÑÑ Ð½Ðµ цикличеÑким пандиагональным??? Я думаю, что ÑвлÑетÑÑ. К тому же, у Ð¼ÐµÐ½Ñ Ñ‚Ð°ÐºÐ¾Ð³Ð¾ ещё нет. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё два квадрата Ñкопировала из Ñтатьи 0 1 2 3 4 5 6 7 8 9 A B C 7 C 0 1 B 2 8 9 A 6 5 3 4 3 4 B 2 0 9 A 6 C 8 1 7 5 B 5 8 9 A C 0 1 2 7 3 4 6 8 6 7 5 3 4 B C 0 1 2 9 A 9 A C 6 1 7 3 4 5 B 0 8 2 C 2 1 7 8 6 5 B 3 4 9 A 0 1 0 3 4 9 A 2 8 7 5 6 C B 4 B 5 0 2 8 9 A 6 C 7 1 3 5 3 4 B C 0 1 2 9 A 8 6 7 2 7 9 A 6 B C 0 1 3 4 5 8 A 8 6 C 5 1 7 3 4 0 B 2 9 6 9 A 8 7 3 4 5 B 2 C 0 1 Fig. 2. (A = 10, B = 11, C = 12). T(~, together with 6 shifts of TV*, ,) and 6 shifts of TT~,,, *. 0 1 2 3 4 5 6 7 8 9 A B C A 8 C 9 1 0 2 3 5 B 6 7 4 5 2 6 A 7 C B 1 4 3 0 8 9 4 7 0 B 5 6 A 8 9 1 C 2 3 1 B 3 4 9 8 C 0 2 6 7 A 5 6 C 8 1 3 2 4 A 7 5 B 9 0 2 9 A 6 0 7 5 B 3 4 1 C 8 B 4 7 5 2 9 1 C 6 0 8 3 A 7 0 1 C B 3 8 9 A 2 4 5 6 C 3 5 8 A 4 0 6 B 7 9 1 2 9 A 4 2 6 1 7 5 C 8 3 0 B 8 6 9 0 C B 3 2 1 A 5 4 7 3 5 B 7 8 A 9 4 0 C 2 6 1 Fig. 3. (A = 10, B = 11, C = 12). n(5) together with 3 shifts of T~~,~,, 3 shifts of T~~,~,, 3 shifts of T(~,,,, and 3 shifts of T,,~,~). Ðти пандиагональные ДЛК тоже, по-моему, не цикличеÑкие. Хорошо, что они уже нормализованные, только преобразовать в чиÑловой формат. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Преобразовала два поÑледних ДЛК в чиÑловой формат и проверила утилитой Harry White 0 1 2 3 4 5 6 7 8 9 10 11 12 7 12 0 1 11 2 8 9 10 6 5 3 4 3 4 11 2 0 9 10 6 12 8 1 7 5 11 5 8 9 10 12 0 1 2 7 3 4 6 8 6 7 5 3 4 11 12 0 1 2 9 10 9 10 12 6 1 7 3 4 5 11 0 8 2 12 2 1 7 8 6 5 11 3 4 9 10 0 1 0 3 4 9 10 2 8 7 5 6 12 11 4 11 5 0 2 8 9 10 6 12 7 1 3 5 3 4 11 12 0 1 2 9 10 8 6 7 2 7 9 10 6 11 12 0 1 3 4 5 8 10 8 6 12 5 1 7 3 4 0 11 2 9 6 9 10 8 7 3 4 5 11 2 12 0 1 0 1 2 3 4 5 6 7 8 9 10 11 12 10 8 12 9 1 0 2 3 5 11 6 7 4 5 2 6 10 7 12 11 1 4 3 0 8 9 4 7 0 11 5 6 10 8 9 1 12 2 3 1 11 3 4 9 8 12 0 2 6 7 10 5 6 12 8 1 3 2 4 10 7 5 11 9 0 2 9 10 6 0 7 5 11 3 4 1 12 8 11 4 7 5 2 9 1 12 6 0 8 3 10 7 0 1 12 11 3 8 9 10 2 4 5 6 12 3 5 8 10 4 0 6 11 7 9 1 2 9 10 4 2 6 1 7 5 12 8 3 0 11 8 6 9 0 12 11 3 2 1 10 5 4 7 3 5 11 7 8 10 9 4 0 12 2 6 1 Order? 13
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_21.txt
Counts
------
2 diagonal Latin
2 pandiagonal
2 nfrÐ’ÑÑ‘ прекраÑно, ДЛК пандиагональные, причём, как Ñ Ð²Ð¸Ð¶Ñƒ, не цикличеÑкие. И таких нормализованных не цикличеÑких пандиагональных ДЛК у Ð¼ÐµÐ½Ñ ÐµÑ‰Ñ‘ не было. Теперь можно занÑÑ‚ÑŒÑÑ Ð¿Ñ€ÐµÐ¾Ð±Ñ€Ð°Ð·Ð¾Ð²Ð°Ð½Ð¸ÐµÐ¼ трёх новых не цикличеÑких пандиагональных ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ИнтереÑно, что о ДЛК Ñ Fig.2 говоритÑÑ PROPOSITION 8.5. Ðто об Ñтом ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 7 12 0 1 11 2 8 9 10 6 5 3 4 3 4 11 2 0 9 10 6 12 8 1 7 5 11 5 8 9 10 12 0 1 2 7 3 4 6 8 6 7 5 3 4 11 12 0 1 2 9 10 9 10 12 6 1 7 3 4 5 11 0 8 2 12 2 1 7 8 6 5 11 3 4 9 10 0 1 0 3 4 9 10 2 8 7 5 6 12 11 4 11 5 0 2 8 9 10 6 12 7 1 3 5 3 4 11 12 0 1 2 9 10 8 6 7 2 7 9 10 6 11 12 0 1 3 4 5 8 10 8 6 12 5 1 7 3 4 0 11 2 9 6 9 10 8 7 3 4 5 11 2 12 0 1 Пока ничего не понимаю. Из Ñтого ДЛК можно как-то получить 8112 пандиагональных не цикличеÑких ДЛК, причём ÑущеÑтвенно различных??? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð¡Ð¾Ð¼Ð½ÐµÐ½Ð¸Ñ Ð¾Ð´Ð¾Ð»ÐµÐ²Ð°ÑŽÑ‚ наÑчёт полуцикличеÑких пандиагональных ЛК, которые Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»Ð°. Ð’ Ñтатье OEIS говоритÑÑ Ð¾ неÑквивалентных пандиагональных ЛК 13-го порÑдка For order n=13 this is not true and exists 12386 inequivalent squares; РЛК, получающиеÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок, Ñквивалентны. Решила ÑпроÑить у автора Ñтатьи OEIS, какие же пандиагональные ЛК 13-го порÑдка отноÑÑÑ‚ÑÑ Ðº полуцикличеÑким. Смотрите https://oeis.org/draft/A338620 Может быть, получу какой-нибудь ответ. ХотÑ... Ñтоп! Ð 10 цикличеÑких пандиагональных ЛК 13-го порÑдка тоже получаютÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок. Ðо ведь они вÑе ÑчитаютÑÑ. Почему же они вÑе ÑчитаютÑÑ? Они же Ñквивалентные! Или в Ñтатье OEIS ÑквивалентноÑÑ‚ÑŒ пандиагональных ЛК понимаетÑÑ Ð² каком-то другом ÑмыÑле??? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Рвот ещё одно утверждение PROPOSITION 8.7. Ðто о квадрате Ñ Fig.3 0 1 2 3 4 5 6 7 8 9 10 11 12 10 8 12 9 1 0 2 3 5 11 6 7 4 5 2 6 10 7 12 11 1 4 3 0 8 9 4 7 0 11 5 6 10 8 9 1 12 2 3 1 11 3 4 9 8 12 0 2 6 7 10 5 6 12 8 1 3 2 4 10 7 5 11 9 0 2 9 10 6 0 7 5 11 3 4 1 12 8 11 4 7 5 2 9 1 12 6 0 8 3 10 7 0 1 12 11 3 8 9 10 2 4 5 6 12 3 5 8 10 4 0 6 11 7 9 1 2 9 10 4 2 6 1 7 5 12 8 3 0 11 8 6 9 0 12 11 3 2 1 10 5 4 7 3 5 11 7 8 10 9 4 0 12 2 6 1 И окончательный вывод PROPOSITION 8.8. Очень хочетÑÑ Ð² Ñтом разобратьÑÑ. Пока Ñплошной туман. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё цитата из Ñтатьи (в переводе Google) Программа, напиÑÐ°Ð½Ð½Ð°Ñ Ð½Ð° SNOBOL4, иÑпользовалаÑÑŒ Ð´Ð»Ñ Ð³ÐµÐ½ÐµÑ€Ð°Ñ†Ð¸Ð¸ вÑех возможных нормализованных путей. Ðтот Обратите внимание на количеÑтво "нормализованных путей" - 348. Ðто вам ничего не напоминает? Цитата из Ñтой темы ВзÑла цикличеÑкий пандиагональный ДЛК 13-го порÑдка (нормализованный) и применила к нему программу переÑтановки Ñтрок, Ð¿ÐµÑ€Ð²Ð°Ñ Ñтрока оÑтаётÑÑ Ð½Ð° меÑте. Думаю, что чиÑло 348 у Ð¼ÐµÐ½Ñ Ð½Ðµ Ñлучайно Ñовпадает Ñ Ñ‡Ð¸Ñлом 348 в Ñтатье. Ð¥Ð¾Ñ‚Ñ Ð°Ð±Ñолютно не понимаю, что определÑет Ñто чиÑло в Ñтатье. Что оно определÑет у менÑ, Ñ Ð¾Ñ‡ÐµÐ½ÑŒ хорошо понимаю. Ещё может немного Ñоздавать раÑÑоглаÑование такой момент: Ñ Ð²ÑÑ‘ Ð²Ñ€ÐµÐ¼Ñ Ð³Ð¾Ð²Ð¾Ñ€ÑŽ о пандиагональных ДЛК, а в Ñтатье иÑпользуетÑÑ Ñ‚Ð¾Ð»ÑŒÐºÐ¾ термин "пандиагональные латинÑкие квадраты". Ðо... пандиагональные ЛК вÑе ÑвлÑÑŽÑ‚ÑÑ Ð”Ð›Ðš по определению! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата Решила ÑпроÑить у автора Ñтатьи OEIS, какие же пандиагональные ЛК 13-го порÑдка отноÑÑÑ‚ÑÑ Ðº полуцикличеÑким. Пока ответа нет. Ðу, выходные, понÑтное дело, редакторы OEIS, а также автор Ñтатьи, отдыхают. Так что, надо ещё недельку подождать, пока ÑиÑтема раÑкачаетÑÑ, пока редакторы уведомÑÑ‚ автора Ñтатьи о вопроÑе, пока автор Ñтатьи придумает ответ и даÑÑ‚ его. Хорошо, еÑли вообще ответ будет, Ñ…Ð¾Ñ‚Ñ Ð±Ñ‹ через недельку. Пока начнём Ñначала. Цитирую Ñтатью OEIS For order n=13 this is not true and exists 12386 inequivalent squares; of these 10 are cyclic (in all directions) and 1560 are semi-cyclic (cyclic in a single direction). 1. "of these 10 are cyclic (in all directions)" 10 цикличеÑких пандиагональных ЛК (ДЛК) 13-го порÑдка, цикличеÑкие во вÑех направлениÑÑ…, то еÑÑ‚ÑŒ в Ñтроках, в Ñтолбцах и в диагоналÑÑ… обоих направлений. Я дала в Ñтатье OEIS ÑÑылку на Ñти 10 цикличеÑких пандиагональных ЛК (ДЛК) Natalia Makarova, Ten cyclic pandiagonal Latin squares of order 13 Повторю Ñти пандиагональные ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 2 3 4 5 6 7 8 9 10 11 12 0 1 4 5 6 7 8 9 10 11 12 0 1 2 3 6 7 8 9 10 11 12 0 1 2 3 4 5 8 9 10 11 12 0 1 2 3 4 5 6 7 10 11 12 0 1 2 3 4 5 6 7 8 9 12 0 1 2 3 4 5 6 7 8 9 10 11 1 2 3 4 5 6 7 8 9 10 11 12 0 3 4 5 6 7 8 9 10 11 12 0 1 2 5 6 7 8 9 10 11 12 0 1 2 3 4 7 8 9 10 11 12 0 1 2 3 4 5 6 9 10 11 12 0 1 2 3 4 5 6 7 8 11 12 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 11 12 3 4 5 6 7 8 9 10 11 12 0 1 2 6 7 8 9 10 11 12 0 1 2 3 4 5 9 10 11 12 0 1 2 3 4 5 6 7 8 12 0 1 2 3 4 5 6 7 8 9 10 11 2 3 4 5 6 7 8 9 10 11 12 0 1 5 6 7 8 9 10 11 12 0 1 2 3 4 8 9 10 11 12 0 1 2 3 4 5 6 7 11 12 0 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 11 12 0 4 5 6 7 8 9 10 11 12 0 1 2 3 7 8 9 10 11 12 0 1 2 3 4 5 6 10 11 12 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 10 11 12 4 5 6 7 8 9 10 11 12 0 1 2 3 8 9 10 11 12 0 1 2 3 4 5 6 7 12 0 1 2 3 4 5 6 7 8 9 10 11 3 4 5 6 7 8 9 10 11 12 0 1 2 7 8 9 10 11 12 0 1 2 3 4 5 6 11 12 0 1 2 3 4 5 6 7 8 9 10 2 3 4 5 6 7 8 9 10 11 12 0 1 6 7 8 9 10 11 12 0 1 2 3 4 5 10 11 12 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 10 11 12 0 5 6 7 8 9 10 11 12 0 1 2 3 4 9 10 11 12 0 1 2 3 4 5 6 7 8 0 1 2 3 4 5 6 7 8 9 10 11 12 5 6 7 8 9 10 11 12 0 1 2 3 4 10 11 12 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 10 11 12 0 1 7 8 9 10 11 12 0 1 2 3 4 5 6 12 0 1 2 3 4 5 6 7 8 9 10 11 4 5 6 7 8 9 10 11 12 0 1 2 3 9 10 11 12 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 0 6 7 8 9 10 11 12 0 1 2 3 4 5 11 12 0 1 2 3 4 5 6 7 8 9 10 3 4 5 6 7 8 9 10 11 12 0 1 2 8 9 10 11 12 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 10 11 12 6 7 8 9 10 11 12 0 1 2 3 4 5 12 0 1 2 3 4 5 6 7 8 9 10 11 5 6 7 8 9 10 11 12 0 1 2 3 4 11 12 0 1 2 3 4 5 6 7 8 9 10 4 5 6 7 8 9 10 11 12 0 1 2 3 10 11 12 0 1 2 3 4 5 6 7 8 9 3 4 5 6 7 8 9 10 11 12 0 1 2 9 10 11 12 0 1 2 3 4 5 6 7 8 2 3 4 5 6 7 8 9 10 11 12 0 1 8 9 10 11 12 0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 8 9 10 11 12 0 7 8 9 10 11 12 0 1 2 3 4 5 6 0 1 2 3 4 5 6 7 8 9 10 11 12 7 8 9 10 11 12 0 1 2 3 4 5 6 1 2 3 4 5 6 7 8 9 10 11 12 0 8 9 10 11 12 0 1 2 3 4 5 6 7 2 3 4 5 6 7 8 9 10 11 12 0 1 9 10 11 12 0 1 2 3 4 5 6 7 8 3 4 5 6 7 8 9 10 11 12 0 1 2 10 11 12 0 1 2 3 4 5 6 7 8 9 4 5 6 7 8 9 10 11 12 0 1 2 3 11 12 0 1 2 3 4 5 6 7 8 9 10 5 6 7 8 9 10 11 12 0 1 2 3 4 12 0 1 2 3 4 5 6 7 8 9 10 11 6 7 8 9 10 11 12 0 1 2 3 4 5 0 1 2 3 4 5 6 7 8 9 10 11 12 8 9 10 11 12 0 1 2 3 4 5 6 7 3 4 5 6 7 8 9 10 11 12 0 1 2 11 12 0 1 2 3 4 5 6 7 8 9 10 6 7 8 9 10 11 12 0 1 2 3 4 5 1 2 3 4 5 6 7 8 9 10 11 12 0 9 10 11 12 0 1 2 3 4 5 6 7 8 4 5 6 7 8 9 10 11 12 0 1 2 3 12 0 1 2 3 4 5 6 7 8 9 10 11 7 8 9 10 11 12 0 1 2 3 4 5 6 2 3 4 5 6 7 8 9 10 11 12 0 1 10 11 12 0 1 2 3 4 5 6 7 8 9 5 6 7 8 9 10 11 12 0 1 2 3 4 0 1 2 3 4 5 6 7 8 9 10 11 12 9 10 11 12 0 1 2 3 4 5 6 7 8 5 6 7 8 9 10 11 12 0 1 2 3 4 1 2 3 4 5 6 7 8 9 10 11 12 0 10 11 12 0 1 2 3 4 5 6 7 8 9 6 7 8 9 10 11 12 0 1 2 3 4 5 2 3 4 5 6 7 8 9 10 11 12 0 1 11 12 0 1 2 3 4 5 6 7 8 9 10 7 8 9 10 11 12 0 1 2 3 4 5 6 3 4 5 6 7 8 9 10 11 12 0 1 2 12 0 1 2 3 4 5 6 7 8 9 10 11 8 9 10 11 12 0 1 2 3 4 5 6 7 4 5 6 7 8 9 10 11 12 0 1 2 3 0 1 2 3 4 5 6 7 8 9 10 11 12 10 11 12 0 1 2 3 4 5 6 7 8 9 7 8 9 10 11 12 0 1 2 3 4 5 6 4 5 6 7 8 9 10 11 12 0 1 2 3 1 2 3 4 5 6 7 8 9 10 11 12 0 11 12 0 1 2 3 4 5 6 7 8 9 10 8 9 10 11 12 0 1 2 3 4 5 6 7 5 6 7 8 9 10 11 12 0 1 2 3 4 2 3 4 5 6 7 8 9 10 11 12 0 1 12 0 1 2 3 4 5 6 7 8 9 10 11 9 10 11 12 0 1 2 3 4 5 6 7 8 6 7 8 9 10 11 12 0 1 2 3 4 5 3 4 5 6 7 8 9 10 11 12 0 1 2 0 1 2 3 4 5 6 7 8 9 10 11 12 11 12 0 1 2 3 4 5 6 7 8 9 10 9 10 11 12 0 1 2 3 4 5 6 7 8 7 8 9 10 11 12 0 1 2 3 4 5 6 5 6 7 8 9 10 11 12 0 1 2 3 4 3 4 5 6 7 8 9 10 11 12 0 1 2 1 2 3 4 5 6 7 8 9 10 11 12 0 12 0 1 2 3 4 5 6 7 8 9 10 11 10 11 12 0 1 2 3 4 5 6 7 8 9 8 9 10 11 12 0 1 2 3 4 5 6 7 6 7 8 9 10 11 12 0 1 2 3 4 5 4 5 6 7 8 9 10 11 12 0 1 2 3 2 3 4 5 6 7 8 9 10 11 12 0 1 Обращаю внимание: 1) Ñти ДЛК нормализованные, что удовлетворÑет уÑловию Ñтатьи OEIS "with the first row in ascending order"; 2) вÑе Ñти ДЛК получаютÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок и потому как ЛК вÑе они изоморфные (Ñквивалентные); 3) еÑли раÑÑматривать изоморфноÑÑ‚ÑŒ (ÑквивалентноÑÑ‚ÑŒ) Ñтих квадратов как ДЛК, то уникальных будет вÑего только три, как утверждает канонизатор Harry White Order? 13 Format, (1: first row or 2: \diagonal)? 2 File name? inp .. writing DLS to file output13CF2_4.txt number of DLS 10 CFs 3 Возникает вопроÑ: о какой неÑквивалентноÑти квадратов напиÑано в Ñтой фразе "For order n=13 this is not true and exists 12386 inequivalent squares"? PS. У Ð¼ÐµÐ½Ñ Ñ‚Ð°ÐºÐ°Ñ Ð²ÐµÑ€ÑÐ¸Ñ Ð¾Ñ‚Ð²ÐµÑ‚Ð° на вопроÑ: ÑквивалентноÑÑ‚ÑŒ пандиагональных ЛК раÑÑматриваетÑÑ ÐºÐ°Ðº ДЛК (потому что вÑе пандиагональные ЛК ÑвлÑÑŽÑ‚ÑÑ Ð”Ð›Ðš). Ðто первое. Второе: ÑквивалентноÑÑ‚ÑŒ ДЛК раÑÑматриваетÑÑ Ð½Ðµ в ÑмыÑле нашего канонизатора, который иÑпользует Ðœ-преобразованиÑ, как Ñквивалентные. И тогда - да: вÑе 10 цикличеÑких пандиагональных ДЛК 13-го порÑдка можно Ñчитать неÑквивалентными. И тогда полученные мной полуцикличеÑкие пандиагональные ДЛК тоже можно Ñчитать неÑквивалентными, Ñ…Ð¾Ñ‚Ñ Ð¾Ð½Ð¸ получены из цикличеÑкого пандиагонального ДЛК переÑтановкой Ñтрок. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Далее отмечу, что показанные выше 10 цикличеÑких пандиагональных ДЛК легко превратить в идеальные, Ð´Ð»Ñ Ñтого доÑтаточно преобразовать их в формат СРДЛК. Вот они - 10 идеальных ДЛК 13-го порÑдка, которые цикличеÑкие пандиагональные 0 9 5 1 10 6 2 11 7 3 12 8 4 5 1 10 6 2 11 7 3 12 8 4 0 9 10 6 2 11 7 3 12 8 4 0 9 5 1 2 11 7 3 12 8 4 0 9 5 1 10 6 7 3 12 8 4 0 9 5 1 10 6 2 11 12 8 4 0 9 5 1 10 6 2 11 7 3 4 0 9 5 1 10 6 2 11 7 3 12 8 9 5 1 10 6 2 11 7 3 12 8 4 0 1 10 6 2 11 7 3 12 8 4 0 9 5 6 2 11 7 3 12 8 4 0 9 5 1 10 11 7 3 12 8 4 0 9 5 1 10 6 2 3 12 8 4 0 9 5 1 10 6 2 11 7 8 4 0 9 5 1 10 6 2 11 7 3 12 0 10 7 4 1 11 8 5 2 12 9 6 3 4 1 11 8 5 2 12 9 6 3 0 10 7 8 5 2 12 9 6 3 0 10 7 4 1 11 12 9 6 3 0 10 7 4 1 11 8 5 2 3 0 10 7 4 1 11 8 5 2 12 9 6 7 4 1 11 8 5 2 12 9 6 3 0 10 11 8 5 2 12 9 6 3 0 10 7 4 1 2 12 9 6 3 0 10 7 4 1 11 8 5 6 3 0 10 7 4 1 11 8 5 2 12 9 10 7 4 1 11 8 5 2 12 9 6 3 0 1 11 8 5 2 12 9 6 3 0 10 7 4 5 2 12 9 6 3 0 10 7 4 1 11 8 9 6 3 0 10 7 4 1 11 8 5 2 12 0 8 3 11 6 1 9 4 12 7 2 10 5 6 1 9 4 12 7 2 10 5 0 8 3 11 12 7 2 10 5 0 8 3 11 6 1 9 4 5 0 8 3 11 6 1 9 4 12 7 2 10 11 6 1 9 4 12 7 2 10 5 0 8 3 4 12 7 2 10 5 0 8 3 11 6 1 9 10 5 0 8 3 11 6 1 9 4 12 7 2 3 11 6 1 9 4 12 7 2 10 5 0 8 9 4 12 7 2 10 5 0 8 3 11 6 1 2 10 5 0 8 3 11 6 1 9 4 12 7 8 3 11 6 1 9 4 12 7 2 10 5 0 1 9 4 12 7 2 10 5 0 8 3 11 6 7 2 10 5 0 8 3 11 6 1 9 4 12 0 11 9 7 5 3 1 12 10 8 6 4 2 3 1 12 10 8 6 4 2 0 11 9 7 5 6 4 2 0 11 9 7 5 3 1 12 10 8 9 7 5 3 1 12 10 8 6 4 2 0 11 12 10 8 6 4 2 0 11 9 7 5 3 1 2 0 11 9 7 5 3 1 12 10 8 6 4 5 3 1 12 10 8 6 4 2 0 11 9 7 8 6 4 2 0 11 9 7 5 3 1 12 10 11 9 7 5 3 1 12 10 8 6 4 2 0 1 12 10 8 6 4 2 0 11 9 7 5 3 4 2 0 11 9 7 5 3 1 12 10 8 6 7 5 3 1 12 10 8 6 4 2 0 11 9 10 8 6 4 2 0 11 9 7 5 3 1 12 0 2 4 6 8 10 12 1 3 5 7 9 11 12 1 3 5 7 9 11 0 2 4 6 8 10 11 0 2 4 6 8 10 12 1 3 5 7 9 10 12 1 3 5 7 9 11 0 2 4 6 8 9 11 0 2 4 6 8 10 12 1 3 5 7 8 10 12 1 3 5 7 9 11 0 2 4 6 7 9 11 0 2 4 6 8 10 12 1 3 5 6 8 10 12 1 3 5 7 9 11 0 2 4 5 7 9 11 0 2 4 6 8 10 12 1 3 4 6 8 10 12 1 3 5 7 9 11 0 2 3 5 7 9 11 0 2 4 6 8 10 12 1 2 4 6 8 10 12 1 3 5 7 9 11 0 1 3 5 7 9 11 0 2 4 6 8 10 12 0 5 10 2 7 12 4 9 1 6 11 3 8 9 1 6 11 3 8 0 5 10 2 7 12 4 5 10 2 7 12 4 9 1 6 11 3 8 0 1 6 11 3 8 0 5 10 2 7 12 4 9 10 2 7 12 4 9 1 6 11 3 8 0 5 6 11 3 8 0 5 10 2 7 12 4 9 1 2 7 12 4 9 1 6 11 3 8 0 5 10 11 3 8 0 5 10 2 7 12 4 9 1 6 7 12 4 9 1 6 11 3 8 0 5 10 2 3 8 0 5 10 2 7 12 4 9 1 6 11 12 4 9 1 6 11 3 8 0 5 10 2 7 8 0 5 10 2 7 12 4 9 1 6 11 3 4 9 1 6 11 3 8 0 5 10 2 7 12 0 3 6 9 12 2 5 8 11 1 4 7 10 11 1 4 7 10 0 3 6 9 12 2 5 8 9 12 2 5 8 11 1 4 7 10 0 3 6 7 10 0 3 6 9 12 2 5 8 11 1 4 5 8 11 1 4 7 10 0 3 6 9 12 2 3 6 9 12 2 5 8 11 1 4 7 10 0 1 4 7 10 0 3 6 9 12 2 5 8 11 12 2 5 8 11 1 4 7 10 0 3 6 9 10 0 3 6 9 12 2 5 8 11 1 4 7 8 11 1 4 7 10 0 3 6 9 12 2 5 6 9 12 2 5 8 11 1 4 7 10 0 3 4 7 10 0 3 6 9 12 2 5 8 11 1 2 5 8 11 1 4 7 10 0 3 6 9 12 0 4 8 12 3 7 11 2 6 10 1 5 9 10 1 5 9 0 4 8 12 3 7 11 2 6 7 11 2 6 10 1 5 9 0 4 8 12 3 4 8 12 3 7 11 2 6 10 1 5 9 0 1 5 9 0 4 8 12 3 7 11 2 6 10 11 2 6 10 1 5 9 0 4 8 12 3 7 8 12 3 7 11 2 6 10 1 5 9 0 4 5 9 0 4 8 12 3 7 11 2 6 10 1 2 6 10 1 5 9 0 4 8 12 3 7 11 12 3 7 11 2 6 10 1 5 9 0 4 8 9 0 4 8 12 3 7 11 2 6 10 1 5 6 10 1 5 9 0 4 8 12 3 7 11 2 3 7 11 2 6 10 1 5 9 0 4 8 12 0 6 12 5 11 4 10 3 9 2 8 1 7 8 1 7 0 6 12 5 11 4 10 3 9 2 3 9 2 8 1 7 0 6 12 5 11 4 10 11 4 10 3 9 2 8 1 7 0 6 12 5 6 12 5 11 4 10 3 9 2 8 1 7 0 1 7 0 6 12 5 11 4 10 3 9 2 8 9 2 8 1 7 0 6 12 5 11 4 10 3 4 10 3 9 2 8 1 7 0 6 12 5 11 12 5 11 4 10 3 9 2 8 1 7 0 6 7 0 6 12 5 11 4 10 3 9 2 8 1 2 8 1 7 0 6 12 5 11 4 10 3 9 10 3 9 2 8 1 7 0 6 12 5 11 4 5 11 4 10 3 9 2 8 1 7 0 6 12 0 12 11 10 9 8 7 6 5 4 3 2 1 2 1 0 12 11 10 9 8 7 6 5 4 3 4 3 2 1 0 12 11 10 9 8 7 6 5 6 5 4 3 2 1 0 12 11 10 9 8 7 8 7 6 5 4 3 2 1 0 12 11 10 9 10 9 8 7 6 5 4 3 2 1 0 12 11 12 11 10 9 8 7 6 5 4 3 2 1 0 1 0 12 11 10 9 8 7 6 5 4 3 2 3 2 1 0 12 11 10 9 8 7 6 5 4 5 4 3 2 1 0 12 11 10 9 8 7 6 7 6 5 4 3 2 1 0 12 11 10 9 8 9 8 7 6 5 4 3 2 1 0 12 11 10 11 10 9 8 7 6 5 4 3 2 1 0 12 Проверка ÑвойÑтв Ñтих ДЛК утилитой Harry White Order? 13
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_7.txt
Counts
------
10 diagonal Latin
10 associative
10 pandiagonal
10 ultramagic
10 natural \diagonal
9 orthogonal pair
10 self-orthogonalÐапомню, что Ñти ДЛК из полной ÑиÑтемы MOLS 13-го порÑдка и образуют группу MODLS данного порÑдка. Проверка Ñтой группы ДЛК программой Harry White GetOrthogonal выдаёт Order? 13 Enter the name of the squares file: inp ..output file inpPairs_16.txt ..output file inpPairNos_10.txt squares 10 orthogonal pairs 45 45 ортогональных пар образуют Ñти идеальные ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Теперь думаем над пунктом 2) "1560 are semi-cyclic (cyclic in a single direction)" Выше Ñ Ñ€Ð°ÑÑказала, как получила полуцикличеÑкие пандиагональные ДЛК. ВзÑла цикличеÑкий пандиагональный ДЛК и применила к нему программу переÑтановки Ñтрок, оÑтавлÑÑ Ð½Ð° меÑте первую Ñтроку. Программа выдала 348 ДЛК. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð²Ð½Ð¸Ð¼Ð°Ñ‚ÐµÐ»ÑŒÐ½Ð¾ поÑмотрела на Ñти ДЛК. Два из них цикличеÑкие пандиагональные, Ñто иÑходный ДЛК и ещё вот Ñтот 0 1 2 3 4 5 6 7 8 9 10 11 12 11 12 0 1 2 3 4 5 6 7 8 9 10 9 10 11 12 0 1 2 3 4 5 6 7 8 7 8 9 10 11 12 0 1 2 3 4 5 6 5 6 7 8 9 10 11 12 0 1 2 3 4 3 4 5 6 7 8 9 10 11 12 0 1 2 1 2 3 4 5 6 7 8 9 10 11 12 0 12 0 1 2 3 4 5 6 7 8 9 10 11 10 11 12 0 1 2 3 4 5 6 7 8 9 8 9 10 11 12 0 1 2 3 4 5 6 7 6 7 8 9 10 11 12 0 1 2 3 4 5 4 5 6 7 8 9 10 11 12 0 1 2 3 2 3 4 5 6 7 8 9 10 11 12 0 1 Ð’Ñе оÑтальные ДЛК полуцикличеÑкие пандиагональные. Таким образом, Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»Ð° 346 полуцикличеÑких пандиагональных ДЛК. Где взÑÑ‚ÑŒ оÑтальные 1214? Выше Ñ Ð¿Ð¸Ñала, что надо к каждому цикличеÑкому ДЛК применить программу переÑтановки Ñтрок. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ð½Ñла, что Ñто даÑÑ‚ те же Ñамые 348 ДЛК, потому что вÑе цикличеÑкие пандиагональные ДЛК получаютÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок. Стоп, Ñтоп! Ðеправильно. Ведь вÑе 10 цикличеÑких пандиагональных ДЛК должны быть Ñреди Ñтих 348 ДЛК. Значит, полуцикличеÑких оÑтаётÑÑ 338 ДЛК. Где взÑÑ‚ÑŒ оÑтальные 1222? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Пока больше ничего не придумываетÑÑ, поÑтрою идеальный магичеÑкий квадрат 13-го порÑдка методом латинÑких квадратов, иÑÐ¿Ð¾Ð»ÑŒÐ·ÑƒÑ Ñтот идеальный ДЛК 0 9 5 1 10 6 2 11 7 3 12 8 4 5 1 10 6 2 11 7 3 12 8 4 0 9 10 6 2 11 7 3 12 8 4 0 9 5 1 2 11 7 3 12 8 4 0 9 5 1 10 6 7 3 12 8 4 0 9 5 1 10 6 2 11 12 8 4 0 9 5 1 10 6 2 11 7 3 4 0 9 5 1 10 6 2 11 7 3 12 8 9 5 1 10 6 2 11 7 3 12 8 4 0 1 10 6 2 11 7 3 12 8 4 0 9 5 6 2 11 7 3 12 8 4 0 9 5 1 10 11 7 3 12 8 4 0 9 5 1 10 6 2 3 12 8 4 0 9 5 1 10 6 2 11 7 8 4 0 9 5 1 10 6 2 11 7 3 12 и то, что он ÑвлÑетÑÑ SODLS (можно иÑпользовать и то, что он ÑвлÑетÑÑ DSODLS). ТранÑпонированный вариант Ñтого ДЛК, конечно, тоже идеальный, вот он 0 5 10 2 7 12 4 9 1 6 11 3 8 9 1 6 11 3 8 0 5 10 2 7 12 4 5 10 2 7 12 4 9 1 6 11 3 8 0 1 6 11 3 8 0 5 10 2 7 12 4 9 10 2 7 12 4 9 1 6 11 3 8 0 5 6 11 3 8 0 5 10 2 7 12 4 9 1 2 7 12 4 9 1 6 11 3 8 0 5 10 11 3 8 0 5 10 2 7 12 4 9 1 6 7 12 4 9 1 6 11 3 8 0 5 10 2 3 8 0 5 10 2 7 12 4 9 1 6 11 12 4 9 1 6 11 3 8 0 5 10 2 7 8 0 5 10 2 7 12 4 9 1 6 11 3 4 9 1 6 11 3 8 0 5 10 2 7 12 Ушла Ñтроить магичеÑкий квадрат :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вот он - краÑавец 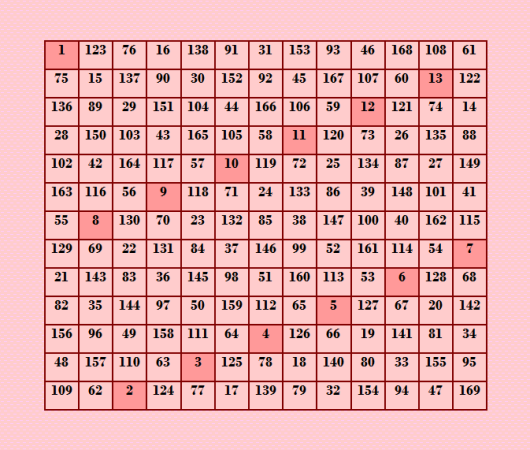 Обратите внимание на начальную цепочку, ÑÑ‚Ð°Ð½Ð´Ð°Ñ€Ñ‚Ð½Ð°Ñ Ð½Ð°Ñ‡Ð°Ð»ÑŒÐ½Ð°Ñ Ñ†ÐµÐ¿Ð¾Ñ‡ÐºÐ° "ход конём". Ðтот магичеÑкий квадрат не ÑвлÑетÑÑ Ð¿Ñ€Ð¸Ð½Ñ†Ð¸Ð¿Ð¸Ð°Ð»ÑŒÐ½Ð¾ новым; такие идеальные магичеÑкие квадраты Ñ Ñтроила в Ñвоё Ð²Ñ€ÐµÐ¼Ñ Ñ€Ð°Ð·Ñ€Ð°Ð±Ð¾Ñ‚Ð°Ð½Ð½Ñ‹Ð¼ мной методом качелей. Смотрите, например, Ñтатью ИДЕÐЛЬÐЫЕ КВÐДРÐТЫ ЧаÑÑ‚ÑŒ I |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese