Thread 'Experiment (pandiagonal DLS of order 13)'
Message boards : Science : Experiment (pandiagonal DLS of order 13)
Message board moderation
Previous · 1 . . . 3 · 4 · 5 · 6 · 7 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ÐŸÐµÑ€ÐµÐ½Ð¾Ñ Ð½Ð° торе выполнила, ÑвойÑтва полученных пандиагональных ДЛК проверила Order? 13
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_44.txt
Counts
------
35152 diagonal Latin
16 associative
35152 pandiagonal
16 ultramagic
2688 center symmetric
208 nfrКвадратики нормальные. ОÑталоÑÑŒ нормализовать их и выброÑить дубликаты. Увы, ничего нового не получено. Итак, пока имеем 208 нормализованных не цикличеÑких пандиагональных ДЛК 13-го порÑдка. До 10816 ДЛК, объÑвленных в Ñтатье OEIS A338620, очень далеко. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПоÑмотрела, как не цикличеÑкие пандиагональные ДЛК 13-го порÑдка вÑтупают в отношение ортогональноÑти внутри одного набора из 208 ДЛК. Программа Harry White GetOrthogonal Ñообщает Order? 13 Enter the name of the squares file: inp ..output file inpPairs.txt ..output file inpPairNos_7.txt squares 208 orthogonal pairs 104 104 ортогональные пары! ИнтереÑÐ½Ð°Ñ Ñ‚Ð°Ð±Ð»Ð¸Ñ†Ð° ортогональных пар 27: 12 28: 13 29: 1 30: 2 31: 3 32: 4 33: 5 34: 6 35: 7 36: 8 37: 9 38: 10 39: 11 40: 25 41: 26 42: 14 43: 15 44: 16 45: 17 46: 18 47: 19 48: 20 49: 21 50: 22 51: 23 52: 24 79: 60 80: 61 81: 62 82: 63 83: 64 84: 65 85: 53 86: 54 87: 55 88: 56 89: 57 90: 58 91: 59 92: 76 93: 77 94: 78 95: 66 96: 67 97: 68 98: 69 99: 70 100: 71 101: 72 102: 73 103: 74 104: 75 131: 116 132: 117 133: 105 134: 106 135: 107 136: 108 137: 109 138: 110 139: 111 140: 112 141: 113 142: 114 143: 115 144: 129 145: 130 146: 118 147: 119 148: 120 149: 121 150: 122 151: 123 152: 124 153: 125 154: 126 155: 127 156: 128 183: 164 184: 165 185: 166 186: 167 187: 168 188: 169 189: 157 190: 158 191: 159 192: 160 193: 161 194: 162 195: 163 196: 180 197: 181 198: 182 199: 170 200: 171 201: 172 202: 173 203: 174 204: 175 205: 176 206: 177 207: 178 208: 179 Ðет ни одного квадратика, который имел бы два ортогональных ДЛК в Ñтом наборе. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
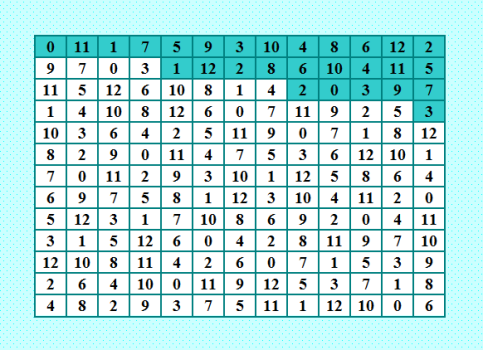
Я квадратики перед проверкой на ортогональные пары превратила в СРДЛК, чтобы иметь идеальные ДЛК. И вот Ð¿ÐµÑ€Ð²Ð°Ñ Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° из таблицы ортогональноÑти 27: 12 Оба Ñти ДЛК идеальные! ЧудеÑно! Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ñ Ð¸Ñ… покажу. Вот они 0 2 9 6 10 12 1 8 3 5 11 7 4 5 1 3 11 7 8 4 2 9 12 6 0 10 4 11 2 10 12 0 5 1 6 3 7 8 9 1 6 8 3 5 7 2 9 11 10 12 4 0 9 3 11 12 4 6 0 10 1 7 8 5 2 6 10 7 8 0 5 9 3 4 11 2 12 1 7 9 12 4 2 1 6 11 10 8 0 3 5 11 0 10 1 8 9 3 7 12 4 5 2 6 10 7 4 5 11 2 12 6 8 0 1 9 3 12 8 0 2 1 3 10 5 7 9 4 6 11 3 4 5 9 6 11 7 12 0 2 10 1 8 2 12 6 0 3 10 8 4 5 1 9 11 7 8 5 1 7 9 4 11 0 2 6 3 10 12 0 5 4 2 8 7 11 9 12 6 3 10 1 12 1 6 9 3 10 8 0 5 2 7 4 11 5 10 2 4 6 11 7 12 1 0 9 3 8 7 12 0 3 1 8 10 11 2 5 4 6 9 10 11 7 5 4 9 12 6 0 1 2 8 3 8 0 12 1 2 5 3 10 7 4 11 9 6 2 7 11 0 9 4 6 8 3 12 1 5 10 6 3 1 8 5 2 9 7 10 11 0 12 4 9 4 10 11 12 6 0 3 8 7 5 1 2 3 6 8 7 10 1 2 4 11 9 12 0 5 4 9 3 12 11 0 5 1 6 8 10 2 7 1 8 5 10 7 12 4 2 9 3 6 11 0 11 2 9 6 0 3 1 5 4 10 8 7 12 Утилита Harry White Ñообщает об Ñтих ДЛК Order? 13
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_10.txt
Counts
------
2 diagonal Latin
2 associative
2 pandiagonal
2 ultramagic
2 natural \diagonal
1 orthogonal pairОтлично! ÐžÑ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° идеальных (не цикличеÑких) ДЛК 13-го порÑдка. Вот теперь можно поÑтроить принципиально новый идеальный магичеÑкий квадрат методом латинÑких квадратов, иÑÐ¿Ð¾Ð»ÑŒÐ·ÑƒÑ Ñту ортогональную пару. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вот он какой краÑивый! 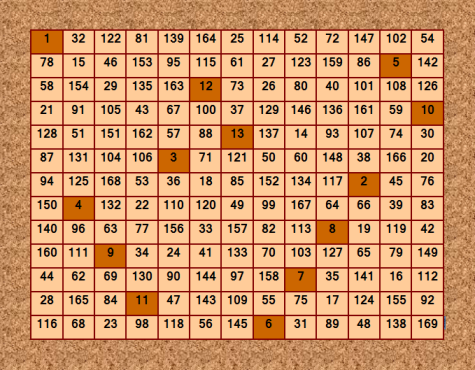 Принципиально новый идеальный магичеÑкий квадрат 13-го порÑдка. Сравните Ñ Ð¸Ð´ÐµÐ°Ð»ÑŒÐ½Ñ‹Ð¼ магичеÑким квадратом, в котором клаÑÑичеÑÐºÐ°Ñ Ð½Ð°Ñ‡Ð°Ð»ÑŒÐ½Ð°Ñ Ñ†ÐµÐ¿Ð¾Ñ‡ÐºÐ° "ход конём" 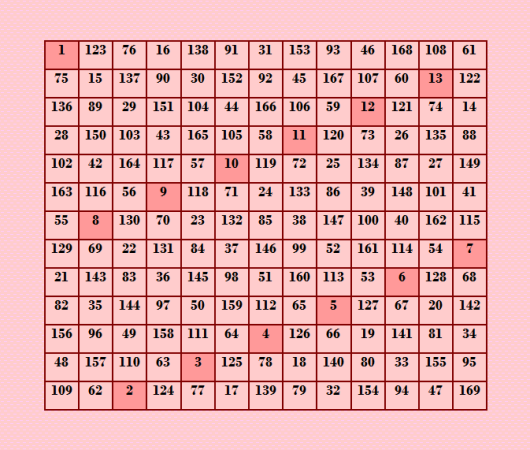 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Теперь поработаю Ñ Ð½Ðµ цикличеÑкими пандиагональными ДЛК 13-го порÑдка по тому же алгоритму, как Ñ Ð¿Ð¾Ð»ÑƒÑ†Ð¸ÐºÐ»Ð¸Ñ‡ÐµÑкими. ВзÑла найденный мной идеальный ДЛК, который ÑвлÑетÑÑ Ð½Ðµ цикличеÑким пандиагональным 0 2 9 6 10 12 1 8 3 5 11 7 4 5 1 3 11 7 8 4 2 9 12 6 0 10 4 11 2 10 12 0 5 1 6 3 7 8 9 1 6 8 3 5 7 2 9 11 10 12 4 0 9 3 11 12 4 6 0 10 1 7 8 5 2 6 10 7 8 0 5 9 3 4 11 2 12 1 7 9 12 4 2 1 6 11 10 8 0 3 5 11 0 10 1 8 9 3 7 12 4 5 2 6 10 7 4 5 11 2 12 6 8 0 1 9 3 12 8 0 2 1 3 10 5 7 9 4 6 11 3 4 5 9 6 11 7 12 0 2 10 1 8 2 12 6 0 3 10 8 4 5 1 9 11 7 8 5 1 7 9 4 11 0 2 6 3 10 12 и переобозначением Ñлементов преобразовала его в Ñледующий идеальный ДЛК 10 4 1 6 8 2 5 9 11 12 7 0 3 12 5 11 7 0 9 3 4 1 2 6 10 8 3 7 4 8 2 10 12 5 6 11 0 9 1 5 6 9 11 12 0 4 1 7 8 2 3 10 1 11 7 2 3 6 10 8 5 0 9 12 4 6 8 0 9 10 12 1 11 3 7 4 2 5 0 1 2 3 4 5 6 7 8 9 10 11 12 7 10 8 5 9 1 11 0 2 3 12 4 6 8 0 3 12 7 4 2 6 9 10 5 1 11 2 9 10 4 5 11 8 12 0 1 3 6 7 11 3 12 1 6 7 0 2 10 4 8 5 9 4 2 6 10 11 8 9 3 12 5 1 7 0 9 12 5 0 1 3 7 10 4 6 11 8 2 Ðналогию видно, да? Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ñ Ð¿Ð°Ñ‚Ñ‚ÐµÑ€Ð½ покажу, ÑовÑем хорошо будет видно. Паттерн 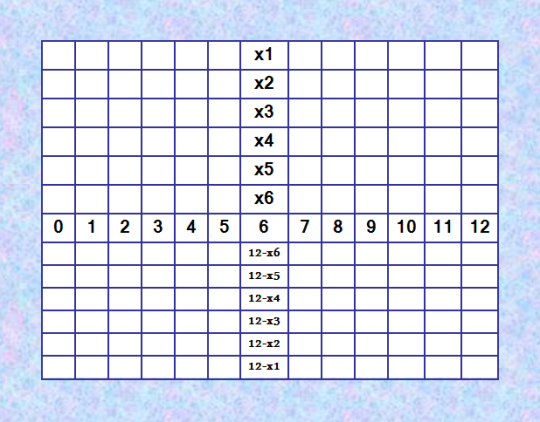 ДЛК должны быть идеальные и при Ñтом не цикличеÑкие пандиагональные. Много ли таких квадратиков? Программу завтра буду пиÑать. Ðапомню: на данный момент у Ð½Ð°Ñ (Ñ Ñ„Ð¾Ñ€ÑƒÐ¼Ñ‡Ð°Ð½Ð¸Ð½Ð¾Ð¼ Ñ Ñ„Ð¾Ñ€ÑƒÐ¼Ð° Math Help Planet) имеетÑÑ 208 нормализованных не цикличеÑких пандиагональных ДЛК 13-го порÑдка. 104 из Ñтих ДЛК показаны в Ñообщении https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=128&postid=1852 Я удвоила Ñтот набор Ñ Ð¿Ð¾Ð¼Ð¾Ñ‰ÑŒÑŽ поворота 104 ДЛК на 90 градуÑов. Ещё: нормализованных не цикличеÑких пандиагональных ДЛК 13-го порÑдка ÑоглаÑно данным в Ñтатье OEIS A338620 должно быть 10816. ÐадеюÑÑŒ, что предложенный ÑÐµÐ¹Ñ‡Ð°Ñ Ð°Ð»Ð³Ð¾Ñ€Ð¸Ñ‚Ð¼ что-нибудь добавит к имеющемуÑÑ Ð½Ð°Ð±Ð¾Ñ€Ñƒ не цикличеÑких пандиагональных ДЛК 13-го порÑдка. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Да-а-а-а, как-то Ñ Ð½Ðµ подумала над показанным выше паттерном. Перебор-то будет не хилый, мой БейÑик его и не потÑнет вообще. Тогда решила немного изменить паттерн. Ð’ найденном наборе из 208 не цикличеÑких пандиагональных ДЛК 13-го порÑдка еÑÑ‚ÑŒ 16 идеальных ДЛК. Я выудила их вÑе из набора и преобразовала к формату паттерна. Показываю Ñти 16 идеальных не цикличеÑких ДЛК уже в преобразованном виде, то еÑÑ‚ÑŒ в формате показанного паттерна 10 4 1 6 8 2 5 9 11 12 7 0 3 12 5 11 7 0 9 3 4 1 2 6 10 8 3 7 4 8 2 10 12 5 6 11 0 9 1 5 6 9 11 12 0 4 1 7 8 2 3 10 1 11 7 2 3 6 10 8 5 0 9 12 4 6 8 0 9 10 12 1 11 3 7 4 2 5 0 1 2 3 4 5 6 7 8 9 10 11 12 7 10 8 5 9 1 11 0 2 3 12 4 6 8 0 3 12 7 4 2 6 9 10 5 1 11 2 9 10 4 5 11 8 12 0 1 3 6 7 11 3 12 1 6 7 0 2 10 4 8 5 9 4 2 6 10 11 8 9 3 12 5 1 7 0 9 12 5 0 1 3 7 10 4 6 11 8 2 9 12 5 0 1 3 7 10 4 6 11 8 2 4 2 6 10 11 8 9 3 12 5 1 7 0 11 3 12 1 6 7 0 2 10 4 8 5 9 2 9 10 4 5 11 8 12 0 1 3 6 7 8 0 3 12 7 4 2 6 9 10 5 1 11 7 10 8 5 9 1 11 0 2 3 12 4 6 0 1 2 3 4 5 6 7 8 9 10 11 12 6 8 0 9 10 12 1 11 3 7 4 2 5 1 11 7 2 3 6 10 8 5 0 9 12 4 5 6 9 11 12 0 4 1 7 8 2 3 10 3 7 4 8 2 10 12 5 6 11 0 9 1 12 5 11 7 0 9 3 4 1 2 6 10 8 10 4 1 6 8 2 5 9 11 12 7 0 3 3 11 5 0 7 1 2 4 9 6 8 12 10 9 10 6 4 8 12 7 3 11 0 1 5 2 11 12 0 5 6 2 1 9 10 3 4 8 7 1 9 3 8 10 7 12 2 0 11 5 6 4 12 2 1 11 5 4 9 6 3 10 0 7 8 7 3 9 10 0 11 8 12 1 5 2 4 6 0 1 2 3 4 5 6 7 8 9 10 11 12 6 8 10 7 11 0 4 1 12 2 3 9 5 4 5 12 2 9 6 3 8 7 1 11 10 0 8 6 7 1 12 10 0 5 2 4 9 3 11 5 4 8 9 2 3 11 10 6 7 12 0 1 10 7 11 12 1 9 5 0 4 8 6 2 3 2 0 4 6 3 8 10 11 5 12 7 1 9 2 0 4 6 3 8 10 11 5 12 7 1 9 10 7 11 12 1 9 5 0 4 8 6 2 3 5 4 8 9 2 3 11 10 6 7 12 0 1 8 6 7 1 12 10 0 5 2 4 9 3 11 4 5 12 2 9 6 3 8 7 1 11 10 0 6 8 10 7 11 0 4 1 12 2 3 9 5 0 1 2 3 4 5 6 7 8 9 10 11 12 7 3 9 10 0 11 8 12 1 5 2 4 6 12 2 1 11 5 4 9 6 3 10 0 7 8 1 9 3 8 10 7 12 2 0 11 5 6 4 11 12 0 5 6 2 1 9 10 3 4 8 7 9 10 6 4 8 12 7 3 11 0 1 5 2 3 11 5 0 7 1 2 4 9 6 8 12 10 1 3 12 11 2 0 8 5 9 4 7 6 10 7 4 0 1 10 9 12 11 6 3 8 5 2 3 8 9 6 7 4 5 10 1 2 11 12 0 4 12 11 5 8 3 2 6 7 0 9 10 1 5 9 10 2 0 12 11 1 3 8 4 7 6 8 11 6 7 1 10 9 4 0 12 5 2 3 0 1 2 3 4 5 6 7 8 9 10 11 12 9 10 7 0 12 8 3 2 11 5 6 1 4 6 5 8 4 9 11 1 0 12 10 2 3 7 11 2 3 12 5 6 10 9 4 7 1 0 8 12 0 1 10 11 2 7 8 5 6 3 4 9 10 7 4 9 6 1 0 3 2 11 12 8 5 2 6 5 8 3 7 4 12 10 1 0 9 11 8 10 7 12 2 0 11 5 6 4 1 9 3 7 12 0 1 5 4 8 9 2 3 11 10 6 1 11 5 4 9 6 3 10 0 7 8 12 2 4 8 6 2 3 10 7 11 12 1 9 5 0 3 9 10 0 11 8 12 1 5 2 4 6 7 11 5 12 7 1 9 2 0 4 6 3 8 10 0 1 2 3 4 5 6 7 8 9 10 11 12 2 4 9 6 8 12 10 3 11 5 0 7 1 5 6 8 10 7 11 0 4 1 12 2 3 9 12 7 3 11 0 1 5 2 9 10 6 4 8 10 0 4 5 12 2 9 6 3 8 7 1 11 6 2 1 9 10 3 4 8 7 11 12 0 5 9 3 11 8 6 7 1 12 10 0 5 2 4 4 12 10 1 0 9 11 2 6 5 8 3 7 1 0 3 2 11 12 8 5 10 7 4 9 6 11 2 7 8 5 6 3 4 9 12 0 1 10 12 5 6 10 9 4 7 1 0 8 11 2 3 8 4 9 11 1 0 12 10 2 3 7 6 5 10 7 0 12 8 3 2 11 5 6 1 4 9 0 1 2 3 4 5 6 7 8 9 10 11 12 3 8 11 6 7 1 10 9 4 0 12 5 2 7 6 5 9 10 2 0 12 11 1 3 8 4 9 10 1 4 12 11 5 8 3 2 6 7 0 2 11 12 0 3 8 9 6 7 4 5 10 1 6 3 8 5 2 7 4 0 1 10 9 12 11 5 9 4 7 6 10 1 3 12 11 2 0 8 11 12 0 4 1 7 8 2 3 10 5 6 9 4 8 5 9 11 3 12 1 6 7 0 2 10 7 2 3 6 10 8 5 0 9 12 4 1 11 12 5 1 7 0 4 2 6 10 11 8 9 3 8 0 9 10 12 1 11 3 7 4 2 5 6 10 4 6 11 8 2 9 12 5 0 1 3 7 0 1 2 3 4 5 6 7 8 9 10 11 12 5 9 11 12 7 0 3 10 4 1 6 8 2 6 7 10 8 5 9 1 11 0 2 3 12 4 9 3 4 1 2 6 10 8 12 5 11 7 0 1 11 8 0 3 12 7 4 2 6 9 10 5 2 10 12 5 6 11 0 9 1 3 7 4 8 3 6 7 2 9 10 4 5 11 8 12 0 1 1 9 5 4 3 0 2 6 7 12 11 10 8 10 4 11 1 2 8 7 3 5 6 0 12 9 12 6 10 8 11 3 4 2 0 1 9 5 7 2 8 7 9 10 12 11 1 4 5 3 0 6 7 5 6 12 0 1 9 8 11 10 4 2 3 11 3 0 5 9 7 12 10 6 2 8 1 4 0 1 2 3 4 5 6 7 8 9 10 11 12 8 11 4 10 6 2 0 5 3 7 12 9 1 9 10 8 2 1 4 3 11 12 0 6 7 5 6 12 9 7 8 11 1 0 2 3 5 4 10 5 7 3 11 12 10 8 9 1 4 2 6 0 3 0 12 6 7 9 5 4 10 11 1 8 2 4 2 1 0 5 6 10 12 9 8 7 3 11 4 2 1 0 5 6 10 12 9 8 7 3 11 3 0 12 6 7 9 5 4 10 11 1 8 2 5 7 3 11 12 10 8 9 1 4 2 6 0 6 12 9 7 8 11 1 0 2 3 5 4 10 9 10 8 2 1 4 3 11 12 0 6 7 5 8 11 4 10 6 2 0 5 3 7 12 9 1 0 1 2 3 4 5 6 7 8 9 10 11 12 11 3 0 5 9 7 12 10 6 2 8 1 4 7 5 6 12 0 1 9 8 11 10 4 2 3 2 8 7 9 10 12 11 1 4 5 3 0 6 12 6 10 8 11 3 4 2 0 1 9 5 7 10 4 11 1 2 8 7 3 5 6 0 12 9 1 9 5 4 3 0 2 6 7 12 11 10 8 12 0 1 7 5 6 3 11 9 10 2 8 4 3 11 5 6 1 7 10 4 12 8 9 0 2 5 2 7 11 9 0 12 8 10 4 3 6 1 6 9 8 10 12 11 4 0 2 7 1 5 3 4 10 12 9 8 2 5 3 1 0 6 7 11 7 8 4 0 6 3 1 2 5 11 12 9 10 0 1 2 3 4 5 6 7 8 9 10 11 12 2 3 0 1 7 10 11 9 6 12 8 4 5 1 5 6 12 11 9 7 10 4 3 0 2 8 9 7 11 5 10 12 8 1 0 2 4 3 6 11 6 9 8 2 4 0 12 3 1 5 10 7 10 12 3 4 0 8 2 5 11 6 7 1 9 8 4 10 2 3 1 9 6 7 5 11 12 0 8 4 10 2 3 1 9 6 7 5 11 12 0 10 12 3 4 0 8 2 5 11 6 7 1 9 11 6 9 8 2 4 0 12 3 1 5 10 7 9 7 11 5 10 12 8 1 0 2 4 3 6 1 5 6 12 11 9 7 10 4 3 0 2 8 2 3 0 1 7 10 11 9 6 12 8 4 5 0 1 2 3 4 5 6 7 8 9 10 11 12 7 8 4 0 6 3 1 2 5 11 12 9 10 4 10 12 9 8 2 5 3 1 0 6 7 11 6 9 8 10 12 11 4 0 2 7 1 5 3 5 2 7 11 9 0 12 8 10 4 3 6 1 3 11 5 6 1 7 10 4 12 8 9 0 2 12 0 1 7 5 6 3 11 9 10 2 8 4 9 3 11 8 6 7 1 12 10 0 5 2 4 6 2 1 9 10 3 4 8 7 11 12 0 5 10 0 4 5 12 2 9 6 3 8 7 1 11 12 7 3 11 0 1 5 2 9 10 6 4 8 5 6 8 10 7 11 0 4 1 12 2 3 9 2 4 9 6 8 12 10 3 11 5 0 7 1 0 1 2 3 4 5 6 7 8 9 10 11 12 11 5 12 7 1 9 2 0 4 6 3 8 10 3 9 10 0 11 8 12 1 5 2 4 6 7 4 8 6 2 3 10 7 11 12 1 9 5 0 1 11 5 4 9 6 3 10 0 7 8 12 2 7 12 0 1 5 4 8 9 2 3 11 10 6 8 10 7 12 2 0 11 5 6 4 1 9 3 2 6 5 8 3 7 4 12 10 1 0 9 11 10 7 4 9 6 1 0 3 2 11 12 8 5 12 0 1 10 11 2 7 8 5 6 3 4 9 11 2 3 12 5 6 10 9 4 7 1 0 8 6 5 8 4 9 11 1 0 12 10 2 3 7 9 10 7 0 12 8 3 2 11 5 6 1 4 0 1 2 3 4 5 6 7 8 9 10 11 12 8 11 6 7 1 10 9 4 0 12 5 2 3 5 9 10 2 0 12 11 1 3 8 4 7 6 4 12 11 5 8 3 2 6 7 0 9 10 1 3 8 9 6 7 4 5 10 1 2 11 12 0 7 4 0 1 10 9 12 11 6 3 8 5 2 1 3 12 11 2 0 8 5 9 4 7 6 10 3 6 7 2 9 10 4 5 11 8 12 0 1 2 10 12 5 6 11 0 9 1 3 7 4 8 1 11 8 0 3 12 7 4 2 6 9 10 5 9 3 4 1 2 6 10 8 12 5 11 7 0 6 7 10 8 5 9 1 11 0 2 3 12 4 5 9 11 12 7 0 3 10 4 1 6 8 2 0 1 2 3 4 5 6 7 8 9 10 11 12 10 4 6 11 8 2 9 12 5 0 1 3 7 8 0 9 10 12 1 11 3 7 4 2 5 6 12 5 1 7 0 4 2 6 10 11 8 9 3 7 2 3 6 10 8 5 0 9 12 4 1 11 4 8 5 9 11 3 12 1 6 7 0 2 10 11 12 0 4 1 7 8 2 3 10 5 6 9 5 9 4 7 6 10 1 3 12 11 2 0 8 6 3 8 5 2 7 4 0 1 10 9 12 11 2 11 12 0 3 8 9 6 7 4 5 10 1 9 10 1 4 12 11 5 8 3 2 6 7 0 7 6 5 9 10 2 0 12 11 1 3 8 4 3 8 11 6 7 1 10 9 4 0 12 5 2 0 1 2 3 4 5 6 7 8 9 10 11 12 10 7 0 12 8 3 2 11 5 6 1 4 9 8 4 9 11 1 0 12 10 2 3 7 6 5 12 5 6 10 9 4 7 1 0 8 11 2 3 11 2 7 8 5 6 3 4 9 12 0 1 10 1 0 3 2 11 12 8 5 10 7 4 9 6 4 12 10 1 0 9 11 2 6 5 8 3 7 Проверила ÑвойÑтва Ñтих ДЛК утилитой Harry White [code]Order? 13 Enter the name of the squares file: inp .. writing type information to file inpTypeDetail_7.txt Counts ------ 16 diagonal Latin 16 associative 16 pandiagonal 16 ultramagic[/code] Таким образом, предÑтавим, что мы напиÑали программу полного перебора Ð´Ð»Ñ Ð¿Ð¾ÑÑ‚Ñ€Ð¾ÐµÐ½Ð¸Ñ Ð¸Ð´ÐµÐ°Ð»ÑŒÐ½Ñ‹Ñ… не цикличеÑких ДЛК 13-го порÑдка по показанному выше паттерну. Программа должна выдать Ñти 16 идеальных не цикличеÑких ДЛК. То еÑÑ‚ÑŒ Ñто решениÑ. Ðо! Ðто ведь навернÑка не вÑе решениÑ! Рнам нужны вÑе. Как их найти? Решила включить в паттерн две извеÑтные Ñтроки - первую и поÑледнюю. Ðто, конечно, Ñильно уменьшит перебор. Можно Ñделать программку, ÐºÐ¾Ñ‚Ð¾Ñ€Ð°Ñ Ð¾Ð¿Ñ€ÐµÐ´ÐµÐ»Ð¸Ñ‚ вÑе потенциальные пары Ñтрок в таких ДЛК, но пока воÑпользуюÑÑŒ уже извеÑтными парами. Беру Ñамый первый из предÑтавленных 16 идеальных не цикличеÑких ДЛК и включаю в паттерн две Ñтроки из него - первую и поÑледнюю. Паттерн теперь приобретает Ñледующий вид [code]10 4 1 6 8 2 5 9 11 12 7 0 3 x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21 x22 x23 x24 x25 x26 x27 x28 x29 x30 x31 x32 x33 x34 x35 x36 x37 x38 x39 x40 x41 x42 x43 x44 x45 x46 x47 x48 x49 x50 x51 x52 x53 x54 x55 x56 x57 x58 x59 x60 x61 x62 x63 x64 x65 0 1 2 3 4 5 6 7 8 9 10 11 12 y65 y64 y63 y62 y61 y60 y59 y58 y57 y56 y55 y54 y53 y52 y51 y50 y49 y48 y47 y46 y45 y44 y43 y42 y41 y40 y39 y38 y37 y36 y35 y34 y33 y32 y31 y30 y29 y28 y27 y26 y25 y24 y23 y22 y21 y20 y19 y18 y17 y16 y15 y14 y13 y12 y11 y10 y9 y8 y7 y6 y5 y4 y3 y2 y1 9 12 5 0 1 3 7 10 4 6 11 8 2[/code] СущеÑтвуют ли другие решениÑ, ÑоответÑтвующие данному паттерну? УÑÐ»Ð¾Ð²Ð¸Ñ Ñ12 11 6 3 8 5 2 1 3 12 11 2 0 8 5 9 4 7 6 10 3 6 7 2 9 10 4 5 11 8 12 0 1 2 10 12 5 6 11 0 9 1 3 7 4 8 1 11 8 0 3 12 7 4 2 6 9 10 5 9 3 4 1 2 6 10 8 12 5 11 7 0 6 7 10 8 5 9 1 11 0 2 3 12 4 5 9 11 12 7 0 3 10 4 1 6 8 2 0 1 2 3 4 5 6 7 8 9 10 11 12 10 4 6 11 8 2 9 12 5 0 1 3 7 8 0 9 10 12 1 11 3 7 4 2 5 6 12 5 1 7 0 4 2 6 10 11 8 9 3 7 2 3 6 10 8 5 0 9 12 4 1 11 4 8 5 9 11 3 12 1 6 7 0 2 10 11 12 0 4 1 7 8 2 3 10 5 6 9 5 9 4 7 6 10 1 3 12 11 2 0 8 6 3 8 5 2 7 4 0 1 10 9 12 11 2 11 12 0 3 8 9 6 7 4 5 10 1 9 10 1 4 12 11 5 8 3 2 6 7 0 7 6 5 9 10 2 0 12 11 1 3 8 4 3 8 11 6 7 1 10 9 4 0 12 5 2 0 1 2 3 4 5 6 7 8 9 10 11 12 10 7 0 12 8 3 2 11 5 6 1 4 9 8 4 9 11 1 0 12 10 2 3 7 6 5 12 5 6 10 9 4 7 1 0 8 11 2 3 11 2 7 8 5 6 3 4 9 12 0 1 10 1 0 3 2 11 12 8 5 10 7 4 9 6 4 12 10 1 0 9 11 2 6 5 8 3 7 [/code] Проверила ÑвойÑтва Ñтих ДЛК утилитой Harry White [code]Order? 13 Enter the name of the squares file: inp .. writing type information to file inpTypeDetail_7.txt Counts ------ 16 diagonal Latin 16 associative 16 pandiagonal 16 ultramagic[/code] Таким образом, предÑтавим, что мы напиÑали программу полного перебора Ð´Ð»Ñ Ð¿Ð¾ÑÑ‚Ñ€Ð¾ÐµÐ½Ð¸Ñ Ð¸Ð´ÐµÐ°Ð»ÑŒÐ½Ñ‹Ñ… не цикличеÑких ДЛК 13-го порÑдка по показанному выше паттерну. Программа должна выдать Ñти 16 идеальных не цикличеÑких ДЛК. То еÑÑ‚ÑŒ Ñто решениÑ. Ðо! Ðто ведь навернÑка не вÑе решениÑ! Рнам нужны вÑе. Как их найти? Решила включить в паттерн две извеÑтные Ñтроки - первую и поÑледнюю. Ðто, конечно, Ñильно уменьшит перебор. Можно Ñделать программку, ÐºÐ¾Ñ‚Ð¾Ñ€Ð°Ñ Ð¾Ð¿Ñ€ÐµÐ´ÐµÐ»Ð¸Ñ‚ вÑе потенциальные пары Ñтрок в таких ДЛК, но пока воÑпользуюÑÑŒ уже извеÑтными парами. Беру Ñамый первый из предÑтавленных 16 идеальных не цикличеÑких ДЛК и включаю в паттерн две Ñтроки из него - первую и поÑледнюю. Паттерн теперь приобретает Ñледующий вид [code]10 4 1 6 8 2 5 9 11 12 7 0 3 x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21 x22 x23 x24 x25 x26 x27 x28 x29 x30 x31 x32 x33 x34 x35 x36 x37 x38 x39 x40 x41 x42 x43 x44 x45 x46 x47 x48 x49 x50 x51 x52 x53 x54 x55 x56 x57 x58 x59 x60 x61 x62 x63 x64 x65 0 1 2 3 4 5 6 7 8 9 10 11 12 y65 y64 y63 y62 y61 y60 y59 y58 y57 y56 y55 y54 y53 y52 y51 y50 y49 y48 y47 y46 y45 y44 y43 y42 y41 y40 y39 y38 y37 y36 y35 y34 y33 y32 y31 y30 y29 y28 y27 y26 y25 y24 y23 y22 y21 y20 y19 y18 y17 y16 y15 y14 y13 y12 y11 y10 y9 y8 y7 y6 y5 y4 y3 y2 y1 9 12 5 0 1 3 7 10 4 6 11 8 2[/code] СущеÑтвуют ли другие решениÑ, ÑоответÑтвующие данному паттерну? УÑÐ»Ð¾Ð²Ð¸Ñ ÑоÑÑ‚Ð°Ð²Ð»ÐµÐ½Ð¸Ñ ÐºÐ²Ð°Ð´Ñ€Ð°Ñ‚Ð° очень жёÑткие: идеальноÑÑ‚ÑŒ означает аÑÑоциативноÑÑ‚ÑŒ и пандиагональноÑÑ‚ÑŒ, причём не цикличеÑкую пандиагональноÑÑ‚ÑŒ. Ðу вот и задача. Супер-задача! Вчера начала пиÑать программу. Программа пишетÑÑ Ð´ÑŒÑвольÑки медленно, приходитÑÑ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÑÑ‚ÑŒ каждый шаг, чтобы не ошибитьÑÑ. Далее покажу, как Ñ Ñ€ÐµÑˆÐ¸Ð»Ð° начать ÑоÑтавление квадрата. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Показываю иллюÑтрацию, как пишу программу  Решила попробовать диагональное заполнение. Вчера почти Ñделала три диагонали: главную и две параллельные ей разломанные. Чуть-чуть оÑталоÑÑŒ допиÑать в Ñтих диагоналÑÑ…. Ð”Ð»Ñ Ð²Ñех yi выполнÑетÑÑ ÑƒÑловие yi = 12 - xi Ðто уÑловие аÑÑоциативноÑти ДЛК. Кроме того, должно выполнÑÑ‚ÑŒÑÑ ÑƒÑловие пандиагональноÑти ДЛК. Ðтот паттерн, понÑтно, имеет решение. Вот оно 10 4 1 6 8 2 5 9 11 12 7 0 3 12 5 11 7 0 9 3 4 1 2 6 10 8 3 7 4 8 2 10 12 5 6 11 0 9 1 5 6 9 11 12 0 4 1 7 8 2 3 10 1 11 7 2 3 6 10 8 5 0 9 12 4 6 8 0 9 10 12 1 11 3 7 4 2 5 0 1 2 3 4 5 6 7 8 9 10 11 12 7 10 8 5 9 1 11 0 2 3 12 4 6 8 0 3 12 7 4 2 6 9 10 5 1 11 2 9 10 4 5 11 8 12 0 1 3 6 7 11 3 12 1 6 7 0 2 10 4 8 5 9 4 2 6 10 11 8 9 3 12 5 1 7 0 9 12 5 0 1 3 7 10 4 6 11 8 2 ЕдинÑтвенное ли Ñто решение??? При очень жёÑтких уÑловиÑÑ… на заполнение квадрата не удивлюÑÑŒ, еÑли решение окажетÑÑ ÐµÐ´Ð¸Ð½Ñтвенным. Ðо лучше бы оно было не единÑтвенное. PS. РазумеетÑÑ, Ñ Ð¿Ð¸ÑˆÑƒ программу Ð´Ð»Ñ Ð¿Ð°Ñ€Ñ‹ Ñтрок (первой и поÑледней) в общем виде, то еÑÑ‚ÑŒ Ð´Ð»Ñ Ð»ÑŽÐ±Ð¾Ð¹ заданной пары Ñтрок программа будет работать. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ñƒ Ð½Ð°Ñ ÐµÑÑ‚ÑŒ 16 извеÑтных пар Ñтрок, но навернÑка их будет больше. Паттерн в общем виде z1 z2 z3 z4 z5 z6 z7 z8 z9 z10 z11 z12 z13 x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21 x22 x23 x24 x25 x26 x27 x28 x29 x30 x31 x32 x33 x34 x35 x36 x37 x38 x39 x40 x41 x42 x43 x44 x45 x46 x47 x48 x49 x50 x51 x52 x53 x54 x55 x56 x57 x58 x59 x60 x61 x62 x63 x64 x65 0 1 2 3 4 5 6 7 8 9 10 11 12 y65 y64 y63 y62 y61 y60 y59 y58 y57 y56 y55 y54 y53 y52 y51 y50 y49 y48 y47 y46 y45 y44 y43 y42 y41 y40 y39 y38 y37 y36 y35 y34 y33 y32 y31 y30 y29 y28 y27 y26 y25 y24 y23 y22 y21 y20 y19 y18 y17 y16 y15 y14 y13 y12 y11 y10 y9 y8 y7 y6 y5 y4 y3 y2 y1 v13 v12 v11 v10 v9 v8 v7 v6 v5 v4 v3 v2 v1 ÐŸÐµÑ€Ð²Ð°Ñ Ñтрока {zi} вводитÑÑ Ð² программу, поÑледнÑÑ Ñтрока {vi} получаетÑÑ Ð¸Ð· первой по ÑвойÑтву аÑÑоциативноÑти: vi = 12 - zi |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Уф! ДопиÑала заполнение двух разломанных диагоналей, они заполнÑÑŽÑ‚ÑÑ Ð¿Ð°Ñ€Ð°Ð»Ð»ÐµÐ»ÑŒÐ½Ð¾ - по аÑÑоциативноÑти. Вот что имею 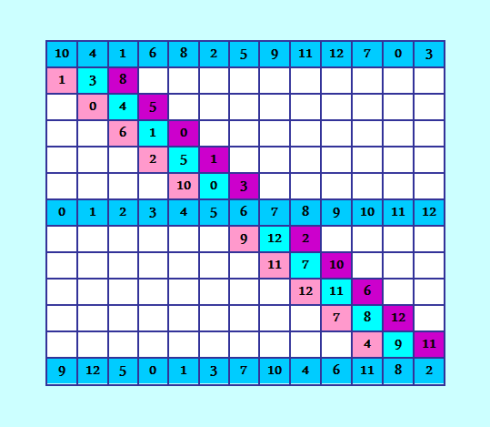 Вроде не наврала. Ðто ж надо каждый Ñлемент проверить, чтобы он не повторилÑÑ Ð½Ð¸ в Ñтроке, ни в Ñтолбце, ни в диагоналÑÑ…. ÐÐµÐ»ÑŒÐ·Ñ Ñказать, что программа очень ÑложнаÑ, но она Ð´Ð»Ð¸Ð½Ð½Ð°Ñ Ð¸ требует колоÑÑального вниманиÑ. Один Ñимвол неправильно напиÑан - и вÑÑ‘ летит Ñобаке под хвоÑÑ‚. Рпотом попробуй-ка найти Ñтот неправильный Ñимвол. Ðо тут еÑÑ‚ÑŒ Ñ…Ð¾Ñ‚Ñ Ð±Ñ‹ возможноÑÑ‚ÑŒ полной верификации программы, потому что еÑÑ‚ÑŒ извеÑтное решение. Ð’ общем, оÑталоÑÑŒ начать и кончить :) Три диагонали заполнила, оÑталоÑÑŒ заполнить 10. Ð’Ñе Ñти диагонали покроют веÑÑŒ квадрат. ГоÑпода! Ð’Ñ‹ можете мне помочь. Вот много пиÑали на форуме boinc.ru о некоем программиÑте ДаниÑле из Польши. Ð’Ñе программы он модифицирует. Ðо ко мне в темы почему-то не приходит. Ðе знает о них? Кто знает контакт Ñтого ДаниÑлÑ, пожалуйÑта, передайте ему моё приглашение. Может быть, его заинтереÑуют и мои программы. Раньше мне очень много помогал коллега из Канады Harry White; он напиÑал деÑÑтки программ по моим алгоритмам. Ðо он Ñвно уÑтал. Потому что Ñ Ð½ÐµÐ¸ÑÑÑкаемый генератор алгоритмов :) Ðто надо пиÑать и пиÑать программы непрерывно по 24 чаÑа в Ñутки, чтобы вÑе мои алгоритмы реализовать. Я беÑконечно благодарна ему за оказанную помощь. Он Ñделал много замечательных инÑтрументов Ð´Ð»Ñ Ñ€Ð°Ð±Ð¾Ñ‚Ñ‹ Ñ Ð”Ð›Ðš/ОДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вчера программу не пиÑала, дела домашние, бытовые... Ð¡ÐµÐ³Ð¾Ð´Ð½Ñ Ð½Ð°Ñ‡Ð°Ð»Ð° Ñ Ñ€Ð°Ð½Ð½ÐµÐ³Ð¾ утречка. ПоÑмотрите на процеÑÑ  Идёт заполнение зелёненьких разломанных диагоналей. Как Ñ ÑƒÐ¶Ðµ говорила, заполнÑÑŽÑ‚ÑÑ Ð¾Ð½Ð¸ параллельно - по аÑÑоциативноÑти. Пока вроде вÑÑ‘ правильно. ЕÑли где-то уже наврала, пожалуйÑта, Ñообщите нам Ñ Ñ‡ÐµÑ€ÐµÐ¿Ð°ÑˆÐºÐ¾Ð¹. Ох и трудно за вÑеми Ñтими Ñлементами уÑледить! :) Рмы будем продолжать. Ð¢Ñ€ÑƒÐ´Ð½Ð°Ñ Ñ€Ð°Ð±Ð¾Ñ‚Ð°, но делать надо. Пока программа не тормозит; Ñто понÑтно, пока перебор-то небольшой. Рчем дальше, тем будет Ñложнее. ОпаÑаюÑÑŒ, что в какой-то момент программа уйдёт в глубокую задумчивоÑÑ‚ÑŒ, и дождатьÑÑ Ð¾Ñ‚ неё Ñ€ÐµÑˆÐµÐ½Ð¸Ñ Ð±ÑƒÐ´ÐµÑ‚ проблематично. Ðу, поÑмотрим. Да, напомню, зачем мне нужны вÑе идеальные ДЛК такого вида. Я потом применю к ним (ко вÑем!) преобразование параллельного переноÑа на торе и получу ещё Ñколько-то не цикличеÑких пандиагональных ДЛК 13-го порÑдка. КÑтати, Ñ Ð¸Ð·Ð²ÐµÑтными 16 идеальными ДЛК такого вида Ñ Ñто проделала (Ð´Ð»Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÐºÐ¸). И да - получены те Ñамые 208 нормализованных не цикличеÑких пандиагональных ДЛК. Ðтот набор и дал извеÑтные 16 идеальных ДЛК. СвÑзь тут очевиднаÑ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПоÑмотрите, что черепашка Ñотворила 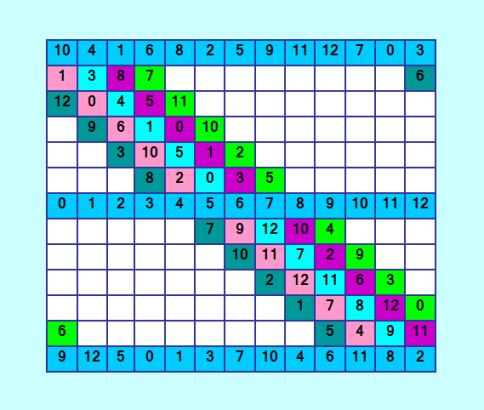 ЕÑÑ‚ÑŒ ошибки у черепашки? ПожалуйÑта, проверьте, гоÑпода. Ðа мой взглÑд пока вÑÑ‘ верно. Уф! Ðу Ñ Ð´Ð¸ÐºÐ¾ уÑтала. ОÑталоÑÑŒ заполнить 8 разломанных диагоналей, вÑего 4 пары, то еÑÑ‚ÑŒ ещё 4 шага. Да, интереÑно: на данный момент в переборе принÑли учаÑтие 23 Ñлемента, 5 Ñлементов при заполнении главной диагонали и по 9 Ñлементов на пару разломанных диагоналей. Вот они - вложенные циклы 956 NEXT J14 958 NEXT J28 960 NEXT J42 962 NEXT J56 964 NEXT I60 966 NEXT I46 968 NEXT I32 970 NEXT I18 972 NEXT I4 974 NEXT J17 976 NEXT J31 978 NEXT I45 980 NEXT J59 982 NEXT I57 984 NEXT I43 986 NEXT I29 988 NEXT I15 990 NEXT I1 992 NEXT I58 994 NEXT I44 996 NEXT I30 998 NEXT I16 1000 NEXT I2 Ðтот Ñтап выполнÑетÑÑ Ð¼Ð³Ð½Ð¾Ð²ÐµÐ½Ð½Ð¾, то еÑÑ‚ÑŒ перебрать 23 Ñлемента программа не затруднÑетÑÑ. У Ð½Ð°Ñ ÐµÑ‰Ñ‘ дождичек, дождичек... Ñпать хочетÑÑ... мозги плохо работают :) Черепашка-то герой, готова и дальше в бой, а Ñ Ð½Ðµ готова. Ðадо Ñделать перерыв. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГоÑпода, черепашка показывает Ñвой новый результат 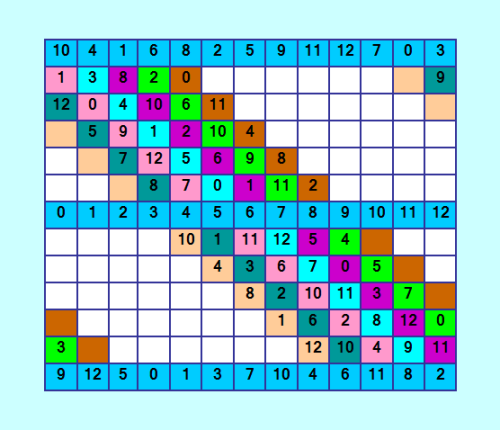 Выполнено ещё полшага, и оÑталоÑÑŒ 3,5 шага. Я проверÑÑŽ картинку поÑле каждого Ñлемента, чтобы визуально отÑледить ошибки. Иногда ошибка Ñразу видна, а иногда - не очень-то разглÑдишь ошибку визуально. ПоÑтому мы Ñ Ñ‡ÐµÑ€ÐµÐ¿Ð°ÑˆÐºÐ¾Ð¹ проÑим Ð²Ð°Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€Ð¸Ñ‚ÑŒ Ñтот промежуточный результат. ПонÑтно, что программа Ñама вÑÑ‘ проверÑет, но... в программе могут быть ошибки. Программа будет делать, что ей напиÑали, а напиÑать можно неправильно. Ðа данный момент в переборе принÑли учаÑтие 28 Ñлементов. Пока программа выполнÑетÑÑ Ð¼Ð³Ð½Ð¾Ð²ÐµÐ½Ð½Ð¾. Так, наÑтраиваюÑÑŒ ещё на полшага :) Ðапомню: один шаг - Ñто заполнение двух параллельных разломанных диагоналей. Полшага - заполнение двух параллельных разломанных диагоналей наполовину. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðе нашли ошибок на предыдущей картинке? У Ð½Ð°Ñ Ñ Ñ‡ÐµÑ€ÐµÐ¿Ð°ÑˆÐºÐ¾Ð¹ Ð½Ð¾Ð²Ð°Ñ ÐºÐ°Ñ€Ñ‚Ð¸Ð½ÐºÐ° готова 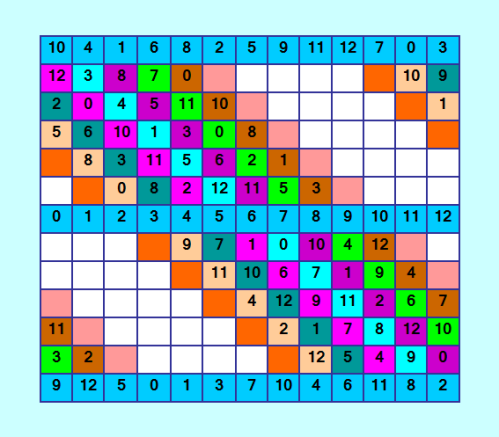 ПолноÑтью заполнена ещё одна пара разломанных диагоналей. ОÑталоÑÑŒ заполнить вÑего 6 диагоналей из 13. ПрогреÑÑ! Более 50% работы Ñделано. Ðа данном Ñтапе в переборе учаÑтвуют 32 Ñлемента. Пока программа не тормозит, мгновенно выполнÑетÑÑ. Уже раÑкраÑила Ñледующую пару разломанных диагоналей. Замечательный процеÑÑ. Вот так - по шажочкам Ñтроить Ñтот идеальный квадратик. Хорошо, еÑли удаÑÑ‚ÑÑ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ñ‚ÑŒ новые Ñ€ÐµÑˆÐµÐ½Ð¸Ñ Ð´Ð¾Ð¿Ð¾Ð»Ð½Ð¸Ñ‚ÐµÐ»ÑŒÐ½Ð¾ к 16 извеÑтным. КÑтати, тут алгоритм грубой Ñилы в чиÑтом виде. Ðо! Ðто только Ð´Ð»Ñ Ð¸Ð´ÐµÐ°Ð»ÑŒÐ½Ñ‹Ñ… ДЛК. ЕÑли отброÑить ÑвойÑтво аÑÑоциативноÑти (и оÑтавить только ÑвойÑтво пандиагональноÑти), перебор Ñильно увеличитÑÑ, и программа безуÑловно захлебнётÑÑ. Я и Ð´Ð»Ñ Ð¸Ð´ÐµÐ°Ð»ÑŒÐ½Ñ‹Ñ… ДЛК волнуюÑÑŒ - не захлебнулаÑÑŒ бы. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата PS. РазумеетÑÑ, Ñ Ð¿Ð¸ÑˆÑƒ программу Ð´Ð»Ñ Ð¿Ð°Ñ€Ñ‹ Ñтрок (первой и поÑледней) в общем виде, то еÑÑ‚ÑŒ Ð´Ð»Ñ Ð»ÑŽÐ±Ð¾Ð¹ заданной пары Ñтрок программа будет работать. Черепашка приÑоветовала: "Давай попробуем Ð´Ð»Ñ Ð´Ñ€ÑƒÐ³Ð¾Ð³Ð¾ варианта паттерна". Умница Ð¼Ð¾Ñ Ñ‡ÐµÑ€ÐµÐ¿Ð°ÑˆÐºÐ° :) Ввожу в программу другую пару Ñтрок (первую и поÑледнюю) из 16 извеÑтных пар. ÐŸÐµÑ€Ð²Ð°Ñ Ñтрока Z(1)=1:Z(2)=3:Z(3)=12:Z(4)=11:Z(5)=2:Z(6)=0:Z(7)=8:Z(8)=5:Z(9)=9:Z(10)=4:Z(11)=7:Z(12)=6:Z(13)=10 ПоÑледнÑÑ Ñтрока получаетÑÑ Ð¸Ð· первой по ÑвойÑтву аÑÑоциативноÑти vi = 12 - zi ЗапуÑкаю программу и мгновенно получаю такой квадратик (полузаполненный) 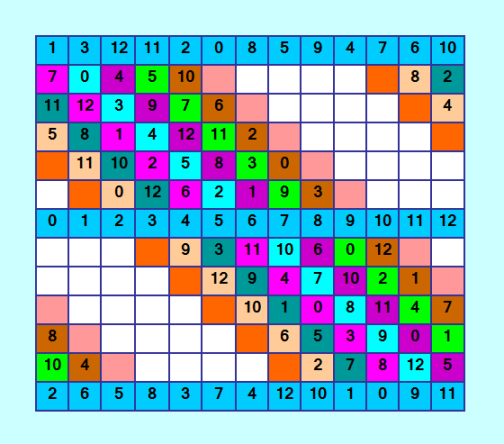 Ð’ÑÑ‘ работает и Ð´Ð»Ñ Ñтой пары Ñтрок. ÐÑ…, ну где же Ñтот великий оптимизатор ДаниÑль? :) ПрÑмо очень нужен он. Вот как бы Ñто мою программу оптимизировать, чтобы вжик-вжик - и готово. Рмне ещё допиÑывать её надо очень долго. Конечно, ковырÑÑŽÑÑŒ Ñ Ð½Ð° Ñвоём БейÑике, как в каменном веке. Рпомочь вÑе ÑтеÑнÑÑŽÑ‚ÑÑ :) Ðа второй картинке нет ли ошибок? Я приÑтально не проверила, за что черепашка Ð¼ÐµÐ½Ñ Ð¾Ñ‚Ñ€ÑƒÐ³Ð°Ð»Ð° :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Мы ползём, бугорки обнимаем, кочки тиÑкаем... © Ð’. Ð’Ñ‹Ñоцкий Да, мы ползём, медленно, но наÑтойчиво. Выполнено ещё полшага, вот что получилоÑÑŒ 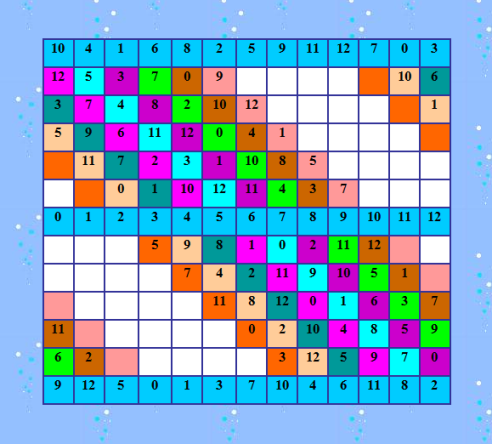 Ошибок не вижу пока. Черепашка ругаетÑÑ: "Смотри лучше! Потом будет труднее иÑкать ошибки". Ðу, ÑтараюÑÑŒ Ñмотреть лучше :) Ðа данном Ñтапе в переборе учаÑтвуют 37 Ñлементов. Уже немало, но пока программа не тормозит, 2-3 Ñекунды задумчивоÑти и результат готов. ОÑталоÑÑŒ текущие две разломанные диагонали заполнить, а потом ещё два шага оÑтанетÑÑ. Однако... квадрат начинает очень Ñильно быть похожим на извеÑтное решение. Сравните Ñ Ñтим извеÑтным решением 10 4 1 6 8 2 5 9 11 12 7 0 3 12 5 11 7 0 9 3 4 1 2 6 10 8 3 7 4 8 2 10 12 5 6 11 0 9 1 5 6 9 11 12 0 4 1 7 8 2 3 10 1 11 7 2 3 6 10 8 5 0 9 12 4 6 8 0 9 10 12 1 11 3 7 4 2 5 0 1 2 3 4 5 6 7 8 9 10 11 12 7 10 8 5 9 1 11 0 2 3 12 4 6 8 0 3 12 7 4 2 6 9 10 5 1 11 2 9 10 4 5 11 8 12 0 1 3 6 7 11 3 12 1 6 7 0 2 10 4 8 5 9 4 2 6 10 11 8 9 3 12 5 1 7 0 9 12 5 0 1 3 7 10 4 6 11 8 2 Ð“Ð»Ð°Ð²Ð½Ð°Ñ Ð´Ð¸Ð°Ð³Ð¾Ð½Ð°Ð»ÑŒ уже один к одному выÑтроилаÑÑŒ. Вот прÑмо очень Ñильно подозреваю, что решение будет единÑтвенное, чего очень не хотелоÑÑŒ бы. Ðу, тогда вÑÑ Ð½Ð°Ð´ÐµÐ¶Ð´Ð° на другие варианты паттернов. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’ÑÑ‘! Приползли! К извеÑтному решению. 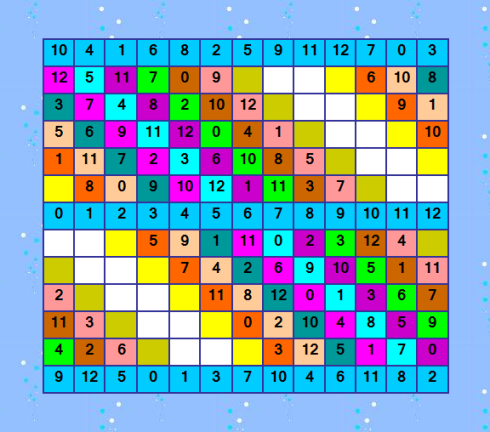 Уже раÑкраÑила две новые разломанные диагонали и ÑобралаÑÑŒ пиÑать дальше. Ðо... Ñравнила полученное решение Ñ Ð¸Ð·Ð²ÐµÑтным решением 10 4 1 6 8 2 5 9 11 12 7 0 3 12 5 11 7 0 9 3 4 1 2 6 10 8 3 7 4 8 2 10 12 5 6 11 0 9 1 5 6 9 11 12 0 4 1 7 8 2 3 10 1 11 7 2 3 6 10 8 5 0 9 12 4 6 8 0 9 10 12 1 11 3 7 4 2 5 0 1 2 3 4 5 6 7 8 9 10 11 12 7 10 8 5 9 1 11 0 2 3 12 4 6 8 0 3 12 7 4 2 6 9 10 5 1 11 2 9 10 4 5 11 8 12 0 1 3 6 7 11 3 12 1 6 7 0 2 10 4 8 5 9 4 2 6 10 11 8 9 3 12 5 1 7 0 9 12 5 0 1 3 7 10 4 6 11 8 2 и вижу, что дальше можно не пиÑать. Решение уже выÑтроилоÑÑŒ, других вариантов программа не находит Ð´Ð»Ñ Ð´Ð°Ð½Ð½Ð¾Ð³Ð¾ варианта паттерна; программа делает полный перебор до конца. Решение единÑтвенное, чего Ñ Ð¸ опаÑалаÑÑŒ. Теперь надо проверить оÑтальные 15 извеÑтных вариантов паттерна. ЕÑли Ð´Ð»Ñ Ð½Ð¸Ñ… тоже нет новых решений, тогда надо напиÑать программку и определить вÑе возможные варианты паттернов, то еÑÑ‚ÑŒ варианты первой и поÑледней Ñтрок в идеальном ДЛК. Думаю, что их должно быть вÑÑ‘-таки больше извеÑтных 16. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðачала проверÑÑ‚ÑŒ извеÑтные 16 вариантов двух Ñтрок. Пару вариантов проверила - одно решение выдала программа. Рвот Ð´Ð»Ñ Ñтого варианта программа выдала два Ñ€ÐµÑˆÐµÐ½Ð¸Ñ (на данном Ñтапе) 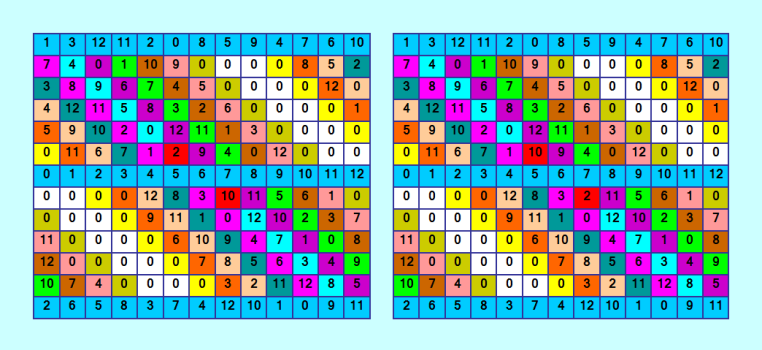 Ð’ краÑных Ñчейках показаны отличиÑ. Ох! ПридётÑÑ Ð´Ð°Ð»ÑŒÑˆÐµ пиÑать программу. Подозреваю, что окончательное решение будет опÑÑ‚ÑŒ-таки одно. Ðо надо убедитьÑÑ Ð² Ñтом, а Ð´Ð»Ñ Ñтого надо допиÑать программу до конца. Ð”Ð»Ñ Ñледующего варианта Ñтрок программа выдала аж 4 Ñ€ÐµÑˆÐµÐ½Ð¸Ñ Ð½Ð° данном Ñтапе 8 10 7 12 2 0 11 5 6 4 1 9 3 7 12 0 1 5 4 0 0 0 0 11 8 6 1 11 5 4 9 6 3 0 0 0 0 12 2 4 8 6 2 3 10 7 11 0 0 0 0 0 3 9 10 0 11 2 12 1 5 0 0 0 0 0 5 12 7 1 3 8 0 2 6 0 0 0 0 1 2 3 4 5 6 7 8 9 10 11 12 0 0 0 6 10 12 4 9 11 5 0 7 0 0 0 0 0 7 11 0 10 1 12 2 3 9 12 0 0 0 0 1 5 2 9 10 6 4 8 10 0 0 0 0 0 9 6 3 8 7 1 11 6 4 1 0 0 0 0 8 7 11 12 0 5 9 3 11 8 6 7 1 12 10 0 5 2 4 8 10 7 12 2 0 11 5 6 4 1 9 3 7 12 0 1 5 4 0 0 0 0 11 10 6 1 11 5 4 9 6 3 0 0 0 0 12 2 4 8 6 2 3 10 7 11 0 0 0 0 0 3 9 10 0 11 8 12 1 5 0 0 0 0 0 5 12 7 1 3 2 0 4 6 0 0 0 0 1 2 3 4 5 6 7 8 9 10 11 12 0 0 0 6 8 12 10 9 11 5 0 7 0 0 0 0 0 7 11 0 4 1 12 2 3 9 12 0 0 0 0 1 5 2 9 10 6 4 8 10 0 0 0 0 0 9 6 3 8 7 1 11 6 2 1 0 0 0 0 8 7 11 12 0 5 9 3 11 8 6 7 1 12 10 0 5 2 4 8 10 7 12 2 0 11 5 6 4 1 9 3 7 12 0 1 5 4 0 0 0 0 11 8 6 1 11 5 4 9 6 3 0 0 0 0 12 2 4 8 6 2 3 10 7 11 0 0 0 0 0 3 9 10 0 11 2 12 1 5 0 0 0 0 0 5 12 7 1 9 8 0 2 6 0 0 0 0 1 2 3 4 5 6 7 8 9 10 11 12 0 0 0 6 10 12 4 3 11 5 0 7 0 0 0 0 0 7 11 0 10 1 12 2 3 9 12 0 0 0 0 1 5 2 9 10 6 4 8 10 0 0 0 0 0 9 6 3 8 7 1 11 6 4 1 0 0 0 0 8 7 11 12 0 5 9 3 11 8 6 7 1 12 10 0 5 2 4 8 10 7 12 2 0 11 5 6 4 1 9 3 7 12 0 1 5 4 0 0 0 0 11 10 6 1 11 5 4 9 6 3 0 0 0 0 12 2 4 8 6 2 3 10 7 11 0 0 0 0 0 3 9 10 0 11 8 12 1 5 0 0 0 0 0 5 12 7 1 9 2 0 4 6 0 0 0 0 1 2 3 4 5 6 7 8 9 10 11 12 0 0 0 6 8 12 10 3 11 5 0 7 0 0 0 0 0 7 11 0 4 1 12 2 3 9 12 0 0 0 0 1 5 2 9 10 6 4 8 10 0 0 0 0 0 9 6 3 8 7 1 11 6 2 1 0 0 0 0 8 7 11 12 0 5 9 3 11 8 6 7 1 12 10 0 5 2 4 Три полуфабриката дальше отÑеютÑÑ, Ñкорее вÑего, и оÑтанетÑÑ Ð¾Ð´Ð½Ð¾ решение. ПоÑмотрим. Итак, пишу заполнение Ñледующей пары разломанных диагоналей, они уже раÑкрашены на иллюÑтрации. Программу вÑÑ‘ равно надо допиÑать. Вдруг найдутÑÑ Ð½Ð¾Ð²Ñ‹Ðµ варианты двух Ñтрок, надо будет их проверÑÑ‚ÑŒ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Программа допиÑываетÑÑ Ñ‚Ñжело. Скоро покажу новую картинку от черепашки. Уже доÑтигли такого Ñтапа, когда два варианта Ñ€ÐµÑˆÐµÐ½Ð¸Ñ Ð¿Ñ€ÐµÐ²Ñ€Ð°Ñ‚Ð¸Ð»Ð¸ÑÑŒ в один вариант Ð´Ð»Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€Ñемых двух Ñтрок (в предыдущем поÑте показаны два полуфабриката Ñ€Ñдом). Ðу вот и картинка  И Ñто уже полноÑтью Ñовпадает Ñ Ð¸Ð·Ð²ÐµÑтным решением. То еÑÑ‚ÑŒ решение опÑÑ‚ÑŒ же единÑтвенное Ð´Ð»Ñ Ñтого варианта паттерна. Теперь проверÑÑ‚ÑŒ дальше и допиÑывать уже программу до конца. УжаÑно долго Ñто пишетÑÑ, чем дальше, тем больше проверок Ð´Ð»Ñ ÐºÐ°Ð¶Ð´Ð¾Ð³Ð¾ Ñлемента. Ðо надо уже добивать. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð”Ð»Ñ Ð´Ð°Ð½Ð½Ð¾Ð³Ð¾ Ñтапа Ð·Ð°Ð¿Ð¾Ð»Ð½ÐµÐ½Ð¸Ñ ÐºÐ²Ð°Ð´Ñ€Ð°Ñ‚Ð° проверила вÑе 16 вариантов паттернов. Полный перебор программа выполнÑет за 3-5 Ñекунд; решение Ð´Ð»Ñ Ð²Ñех вариантов паттерна найдено единÑтвенное. КажетÑÑ, ошибок больше нет в программе. Было неÑколько подводных камней, долго пришлоÑÑŒ их выиÑкивать. Может, и ещё оÑталиÑÑŒ, но на извеÑтных решениÑÑ… они не проÑвлÑÑŽÑ‚ÑÑ. Ðто очень трудно выÑвить, когда ошибки проÑвлÑÑŽÑ‚ÑÑ Ð½Ðµ на вÑех решениÑÑ…. Однако пора занÑÑ‚ÑŒÑÑ Ð´Ð¾Ð¿Ð¸Ñыванием программы :) ОÑталоÑÑŒ напиÑать поиÑк 12 Ñлементов квадрата, оÑтальные 12 Ñлементов определÑÑ‚ÑÑ Ð¿Ð¾ ÑвойÑтву аÑÑоциативноÑти. Ðа данном Ñтапе в переборе учаÑтвуют 43 Ñлемента квадрата; вот вложенные циклы 916 NEXT I21 918 NEXT I7 920 NEXT J25 922 NEXT J39 924 NEXT J40 926 NEXT J54 928 NEXT I62 930 NEXT I48 932 NEXT I34 934 NEXT I20 936 NEXT I6 938 NEXT J26 940 NEXT J27 942 NEXT J41 944 NEXT J55 946 NEXT I61 948 NEXT I47 950 NEXT I33 952 NEXT I19 954 NEXT I5 956 NEXT J14 958 NEXT J28 960 NEXT J42 962 NEXT J56 964 NEXT I60 966 NEXT I46 968 NEXT I32 970 NEXT I18 972 NEXT I4 974 NEXT J17 976 NEXT J31 978 NEXT I45 980 NEXT J59 982 NEXT I57 984 NEXT I43 986 NEXT I29 988 NEXT I15 990 NEXT I1 992 NEXT I58 994 NEXT I44 996 NEXT I30 998 NEXT I16 1000 NEXT I2 Из 12 оÑтавшихÑÑ Ñлементов не вÑе будут Ñвободными (то еÑÑ‚ÑŒ перебиратьÑÑ). |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Дублирую Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=132&postid=2168 Ðу как, гоÑпода, вы разглÑдели цикличноÑÑ‚ÑŒ в Ñтом пандиагональном ДЛК 13-го порÑдка? Буду обÑуждать ÑкÑперимент Ñ Ñтим квадратом дальше. Применив у Ñтому ДЛК преобразование переноÑа на торе, Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»Ð° 13 нормализованных полуцикличеÑких ДЛК Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в направлении (1,4). Покажу их вÑе 0 1 2 3 4 5 6 7 8 9 10 11 12 2 3 0 1 7 10 11 9 6 12 8 4 5 1 5 6 12 11 9 7 10 4 3 0 2 8 9 7 11 5 10 12 8 1 0 2 4 3 6 11 6 9 8 2 4 0 12 3 1 5 10 7 10 12 3 4 0 8 2 5 11 6 7 1 9 8 4 10 2 3 1 9 6 7 5 11 12 0 12 0 1 7 5 6 3 11 9 10 2 8 4 3 11 5 6 1 7 10 4 12 8 9 0 2 5 2 7 11 9 0 12 8 10 4 3 6 1 6 9 8 10 12 11 4 0 2 7 1 5 3 4 10 12 9 8 2 5 3 1 0 6 7 11 7 8 4 0 6 3 1 2 5 11 12 9 10 0 1 2 3 4 5 6 7 8 9 10 11 12 2 12 0 6 9 10 8 5 11 7 3 4 1 4 5 11 10 8 6 9 3 2 12 1 7 0 6 10 4 9 11 7 0 12 1 3 2 5 8 5 8 7 1 3 12 11 2 0 4 9 6 10 11 2 3 12 7 1 4 10 5 6 0 8 9 3 9 1 2 0 8 5 6 4 10 11 12 7 12 0 6 4 5 2 10 8 9 1 7 3 11 10 4 5 0 6 9 3 11 7 8 12 1 2 1 6 10 8 12 11 7 9 3 2 5 0 4 8 7 9 11 10 3 12 1 6 0 4 2 5 9 11 8 7 1 4 2 0 12 5 6 10 3 7 3 12 5 2 0 1 4 10 11 8 9 6 0 1 2 3 4 5 6 7 8 9 10 11 12 2 12 5 1 10 11 8 9 6 7 0 3 4 3 10 9 6 8 1 7 11 12 5 4 2 0 7 6 8 10 9 12 2 0 4 11 3 5 1 5 9 7 11 3 0 4 12 2 1 8 10 6 11 4 12 0 7 2 3 5 9 10 6 1 8 12 0 11 4 5 6 1 10 3 8 9 7 2 4 2 3 8 1 10 5 6 7 0 11 12 9 10 5 1 2 6 8 9 4 11 12 7 0 3 1 3 10 9 12 7 11 8 0 4 2 6 5 6 8 0 7 11 9 12 2 1 3 5 4 10 9 7 6 12 0 4 10 3 5 2 1 8 11 8 11 4 5 2 3 0 1 10 6 12 9 7 0 1 2 3 4 5 6 7 8 9 10 11 12 3 6 7 5 2 8 4 0 1 11 12 9 10 7 5 3 6 0 12 9 11 4 10 1 2 8 6 8 4 10 9 11 0 12 2 5 3 7 1 11 0 9 8 12 10 1 6 3 7 2 5 4 9 4 11 1 7 2 3 10 5 6 8 12 0 12 10 5 2 3 1 7 8 9 4 0 6 11 1 2 12 7 5 6 11 4 0 8 9 10 3 10 3 6 0 8 4 5 9 11 12 7 1 2 5 9 8 4 6 0 12 2 10 1 11 3 7 8 7 0 9 11 3 10 1 12 2 5 4 6 4 11 1 12 10 9 2 3 7 0 6 8 5 2 12 10 11 1 7 8 5 6 3 4 0 9 0 1 2 3 4 5 6 7 8 9 10 11 12 3 12 8 9 6 7 4 5 11 1 2 0 10 7 4 6 12 5 9 10 3 2 0 11 1 8 6 8 7 10 0 11 2 9 1 3 12 5 4 5 9 1 11 2 10 0 12 6 8 4 3 7 10 11 5 0 1 3 7 8 4 12 6 9 2 9 2 3 4 12 8 1 6 7 5 0 10 11 1 6 12 8 3 4 5 11 9 10 7 2 0 12 0 4 6 7 2 9 10 5 11 1 8 3 8 7 10 5 9 6 11 2 0 4 3 12 1 11 5 9 7 10 0 12 1 3 2 8 4 6 4 10 11 2 8 1 3 0 12 6 9 7 5 2 3 0 1 11 12 8 4 10 7 5 6 9 0 1 2 3 4 5 6 7 8 9 10 11 12 5 3 0 6 2 11 12 9 10 7 8 1 4 1 4 11 10 7 9 2 8 12 0 6 5 3 2 8 7 9 11 10 0 3 1 5 12 4 6 7 6 10 8 12 4 1 5 0 3 2 9 11 9 12 5 0 1 8 3 4 6 10 11 7 2 3 0 1 12 5 6 7 2 11 4 9 10 8 10 5 3 4 9 2 11 6 7 8 1 12 0 4 11 6 2 3 7 9 10 5 12 0 8 1 6 2 4 11 10 0 8 12 9 1 5 3 7 11 7 9 1 8 12 10 0 3 2 4 6 5 12 10 8 7 0 1 5 11 4 6 3 2 9 8 9 12 5 6 3 4 1 2 11 7 0 10 0 1 2 3 4 5 6 7 8 9 10 11 12 5 6 4 1 7 3 12 0 10 11 8 9 2 4 2 5 12 11 8 10 3 9 0 1 7 6 7 3 9 8 10 12 11 1 4 2 6 0 5 12 8 7 11 9 0 5 2 6 1 4 3 10 3 10 0 6 1 2 9 4 5 7 11 12 8 9 4 1 2 0 6 7 8 3 12 5 10 11 1 11 6 4 5 10 3 12 7 8 9 2 0 2 5 12 7 3 4 8 10 11 6 0 1 9 8 7 3 5 12 11 1 9 0 10 2 6 4 6 12 8 10 2 9 0 11 1 4 3 5 7 10 0 11 9 8 1 2 6 12 5 7 4 3 11 9 10 0 6 7 4 5 2 3 12 8 1 0 1 2 3 4 5 6 7 8 9 10 11 12 6 3 4 1 2 8 11 12 10 7 0 9 5 9 2 6 7 0 12 10 8 11 5 4 1 3 7 10 8 12 6 11 0 9 2 1 3 5 4 8 12 7 10 9 3 5 1 0 4 2 6 11 10 11 0 4 5 1 9 3 6 12 7 8 2 1 9 5 11 3 4 2 10 7 8 6 12 0 5 0 1 2 8 6 7 4 12 10 11 3 9 3 4 12 6 7 2 8 11 5 0 9 10 1 2 6 3 8 12 10 1 0 9 11 5 4 7 4 7 10 9 11 0 12 5 1 3 8 2 6 12 5 11 0 10 9 3 6 4 2 1 7 8 11 8 9 5 1 7 4 2 3 6 12 0 10 0 1 2 3 4 5 6 7 8 9 10 11 12 6 7 4 5 2 3 9 12 0 11 8 1 10 4 10 3 7 8 1 0 11 9 12 6 5 2 5 8 11 9 0 7 12 1 10 3 2 4 6 12 9 0 8 11 10 4 6 2 1 5 3 7 3 11 12 1 5 6 2 10 4 7 0 8 9 1 2 10 6 12 4 5 3 11 8 9 7 0 10 6 1 2 3 9 7 8 5 0 11 12 4 2 4 5 0 7 8 3 9 12 6 1 10 11 8 3 7 4 9 0 11 2 1 10 12 6 5 7 5 8 11 10 12 1 0 6 2 4 9 3 9 0 6 12 1 11 10 4 7 5 3 2 8 11 12 9 10 6 2 8 5 3 4 7 0 1 0 1 2 3 4 5 6 7 8 9 10 11 12 11 4 0 9 10 7 8 5 6 12 2 3 1 9 8 5 7 0 6 10 11 4 3 1 12 2 5 7 9 8 11 1 12 3 10 2 4 0 6 8 6 10 2 12 3 11 1 0 7 9 5 4 3 11 12 6 1 2 4 8 9 5 0 7 10 12 10 3 4 5 0 9 2 7 8 6 1 11 1 2 7 0 9 4 5 6 12 10 11 8 3 4 0 1 5 7 8 3 10 11 6 12 2 9 2 9 8 11 6 10 7 12 3 1 5 4 0 7 12 6 10 8 11 1 0 2 4 3 9 5 6 5 11 12 3 9 2 4 1 0 7 10 8 10 3 4 1 2 12 0 9 5 11 8 6 7 0 1 2 3 4 5 6 7 8 9 10 11 12 11 4 7 8 6 3 9 5 1 2 12 0 10 9 8 6 4 7 1 0 10 12 5 11 2 3 2 7 9 5 11 10 12 1 0 3 6 4 8 5 12 1 10 9 0 11 2 7 4 8 3 6 1 10 5 12 2 8 3 4 11 6 7 9 0 12 0 11 6 3 4 2 8 9 10 5 1 7 4 2 3 0 8 6 7 12 5 1 9 10 11 3 11 4 7 1 9 5 6 10 12 0 8 2 8 6 10 9 5 7 1 0 3 11 2 12 4 7 9 8 1 10 12 4 11 2 0 3 6 5 6 5 12 2 0 11 10 3 4 8 1 7 9 10 3 0 11 12 2 8 9 6 7 4 5 1 0 1 2 3 4 5 6 7 8 9 10 11 12 11 7 8 5 6 3 4 10 0 1 12 9 2 3 5 11 4 8 9 2 1 12 10 0 7 6 7 6 9 12 10 1 8 0 2 11 4 3 5 8 0 10 1 9 12 11 5 7 3 2 6 4 10 4 12 0 2 6 7 3 11 5 8 1 9 1 2 3 11 7 0 5 6 4 12 9 10 8 5 11 7 2 3 4 10 8 9 6 1 12 0 12 3 5 6 1 8 9 4 10 0 7 2 11 6 9 4 8 5 10 1 12 3 2 11 0 7 4 8 6 9 12 11 0 2 1 7 3 5 10 9 10 1 7 0 2 12 11 5 8 6 4 3 2 12 0 10 11 7 3 9 6 4 5 8 1 0 1 2 3 4 5 6 7 8 9 10 11 12 11 12 5 8 9 7 4 10 6 2 3 0 1 4 10 9 7 5 8 2 1 11 0 6 12 3 9 3 8 10 6 12 11 0 2 1 4 7 5 7 6 0 2 11 10 1 12 3 8 5 9 4 1 2 11 6 0 3 9 4 5 12 7 8 10 8 0 1 12 7 4 5 3 9 10 11 6 2 12 5 3 4 1 9 7 8 0 6 2 10 11 3 4 12 5 8 2 10 6 7 11 0 1 9 5 9 7 11 10 6 8 2 1 4 12 3 0 6 8 10 9 2 11 0 5 12 3 1 4 7 10 7 6 0 3 1 12 11 4 5 9 2 8 2 11 4 1 12 0 3 9 10 7 8 5 6 Отмечу, что поÑле нормализации никакой цикличноÑти вообще не видно в ДЛК. ДЛК, конечно, пандиагональные. Можно ли Ñчитать их полуцикличеÑкими в направлении (1,4)? Будем Ñчитать, что можно. Итак найдены 13 полуцикличеÑких пандиагональынх ДЛК 13-го порÑдка, которые не ÑвлÑÑŽÑ‚ÑÑ Ð¿Ð¾Ð»ÑƒÑ†Ð¸ÐºÐ»Ð¸Ñ‡ÐµÑкими Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках, в Ñтолбцах и в диагоналÑÑ… в ÑмыÑле, раÑÑмотренном ранее. Таким образом, вроде бы Ñто 13 полуцикличеÑких пандиагональных ДЛК из недоÑтающих 208. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ИнтереÑное продолжение. ПопроÑила Harry White напиÑать программу поÑÑ‚Ñ€Ð¾ÐµÐ½Ð¸Ñ Ð¿Ð°Ð½Ð´Ð¸Ð°Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ñ‹Ñ… ДЛК Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в направлении (1,4). Он напиÑал. Его программа нашла 338 таких ДЛК. Показываю неÑколько первых ДЛК 0 1 8 7 9 3 10 12 11 5 6 4 2 6 7 5 3 1 2 9 8 10 4 11 0 12 5 12 1 0 7 8 6 4 2 3 10 9 11 4 11 10 12 6 0 2 1 8 9 7 5 3 10 8 6 4 5 12 11 0 7 1 3 2 9 2 4 3 10 11 9 7 5 6 0 12 1 8 1 0 2 9 3 5 4 11 12 10 8 6 7 11 9 7 8 2 1 3 10 4 6 5 12 0 7 6 0 1 12 10 8 9 3 2 4 11 5 3 5 12 6 8 7 1 2 0 11 9 10 4 12 10 11 5 4 6 0 7 9 8 2 3 1 9 3 4 2 0 11 12 6 5 7 1 8 10 8 2 9 11 10 4 5 3 1 12 0 7 6 0 1 12 10 8 9 3 2 4 11 5 7 6 12 6 8 7 1 2 0 11 9 10 4 3 5 11 5 4 6 0 7 9 8 2 3 1 12 10 4 2 0 11 12 6 5 7 1 8 10 9 3 9 11 10 4 5 3 1 12 0 7 6 8 2 8 7 9 3 10 12 11 5 6 4 2 0 1 5 3 1 2 9 8 10 4 11 0 12 6 7 1 0 7 8 6 4 2 3 10 9 11 5 12 10 12 6 0 2 1 8 9 7 5 3 4 11 6 4 5 12 11 0 7 1 3 2 9 10 8 3 10 11 9 7 5 6 0 12 1 8 2 4 2 9 3 5 4 11 12 10 8 6 7 1 0 7 8 2 1 3 10 4 6 5 12 0 11 9 0 2 1 8 9 7 5 3 4 11 10 12 6 12 11 0 7 1 3 2 9 10 8 6 4 5 9 7 5 6 0 12 1 8 2 4 3 10 11 5 4 11 12 10 8 6 7 1 0 2 9 3 1 3 10 4 6 5 12 0 11 9 7 8 2 10 8 9 3 2 4 11 5 7 6 0 1 12 7 1 2 0 11 9 10 4 3 5 12 6 8 6 0 7 9 8 2 3 1 12 10 11 5 4 11 12 6 5 7 1 8 10 9 3 4 2 0 4 5 3 1 12 0 7 6 8 2 9 11 10 3 10 12 11 5 6 4 2 0 1 8 7 9 2 9 8 10 4 11 0 12 6 7 5 3 1 8 6 4 2 3 10 9 11 5 12 1 0 7 0 2 9 3 5 4 11 12 10 8 6 7 1 9 7 8 2 1 3 10 4 6 5 12 0 11 6 0 1 12 10 8 9 3 2 4 11 5 7 5 12 6 8 7 1 2 0 11 9 10 4 3 10 11 5 4 6 0 7 9 8 2 3 1 12 3 4 2 0 11 12 6 5 7 1 8 10 9 2 9 11 10 4 5 3 1 12 0 7 6 8 1 8 7 9 3 10 12 11 5 6 4 2 0 7 5 3 1 2 9 8 10 4 11 0 12 6 12 1 0 7 8 6 4 2 3 10 9 11 5 11 10 12 6 0 2 1 8 9 7 5 3 4 8 6 4 5 12 11 0 7 1 3 2 9 10 4 3 10 11 9 7 5 6 0 12 1 8 2 0 3 1 12 2 8 6 10 4 11 5 9 7 12 6 10 8 1 4 2 0 3 9 7 11 5 10 8 12 6 0 7 11 9 2 5 3 1 4 6 4 2 5 11 9 0 7 1 8 12 10 3 9 0 11 4 7 5 3 6 12 10 1 8 2 11 2 9 3 10 1 12 5 8 6 4 7 0 7 5 8 1 12 3 10 4 11 2 0 6 9 3 1 7 10 8 6 9 2 0 4 11 5 12 5 12 6 0 4 2 8 11 9 7 10 3 1 8 11 4 2 6 0 7 1 5 3 9 12 10 4 10 0 11 9 12 5 3 7 1 8 2 6 2 9 3 7 5 11 1 12 10 0 6 4 8 1 7 5 9 3 10 4 8 6 12 2 0 11 Смотрим внимательно. Ð’ ДЛК еÑÑ‚ÑŒ ÑƒÐºÐ°Ð·Ð°Ð½Ð½Ð°Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾ÑÑ‚ÑŒ в направлении (1,4), еÑли, конечно, Ñ Ð¿Ñ€Ð°Ð²Ð¸Ð»ÑŒÐ½Ð¾ её понÑла. Ðо почему ДЛК так много? Ðаверное, надо раÑÑматривать только нормализованные ДЛК (?) Ðормализую ДЛК Ñтой порции, удалÑÑŽ дубликаты и... получаю 26 нормализованных ДЛК. ФокуÑ-покуÑ!! То еÑÑ‚ÑŒ еÑÑ‚ÑŒ уже две порции по 13. ОÑтаётÑÑ Ð½Ð°Ð¹Ñ‚Ð¸ ещё 14 порций по 13, и недоÑтающие 208 полуцикличеÑких пандиагональных ДЛК будут в кармане. Ðо как иÑкать другие порции? КÑтати: порциÑ, Ð¿Ð¾Ð»ÑƒÑ‡ÐµÐ½Ð½Ð°Ñ Harry (26 ДЛК), Ñодержит порцию, полученную мной (13 ДЛК). Таким образом, у Ð½Ð°Ñ ÐµÑÑ‚ÑŒ пока только две порции по 13, вÑего 26 полуцикличеÑких пандиагональных ДЛК 13-го порÑдка Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в направлении (1,4). СущеÑтвую ли какие-то другие подобные направлениÑ? Ðапример, (1,5), (1,6)? Или, может быть, увеличивать чиÑла можно не только на 1, а, Ñкажем, на 2, на 3. Ðу, что-то же надо придумать, чтобы найти недоÑтающие полуцикличеÑкие пандиагональные ДЛК 13-го порÑдка. РнедоÑтающих ÑейчаÑ: 208 - 26 = 182, то еÑÑ‚ÑŒ 14 порций по 13. ФантаÑтичеÑÐºÐ°Ñ Ð·Ð°Ð´Ð°Ñ‡Ð°! Я фантазирую :) Ðекто приводит в OEIS количеÑтво 1560 и его Ñовершенно не заботит, как Ñти 1560 "живых" квадратов найти. И Ñто уже в двух ÑтатьÑÑ… OEIS! Ðто ÑовÑем ÑÐ²ÐµÐ¶Ð°Ñ ÑÑ‚Ð°Ñ‚ÑŒÑ https://oeis.org/A343867 Number of semicyclic pandiagonal Latin squares of order 2*n+1 with the first row in ascending order. Приведён единÑтвенный квадрат из извеÑтной Ñтатьи 0 11 1 7 5 9 3 10 4 8 6 12 2 9 7 0 3 1 12 2 8 6 10 4 11 5 11 5 12 6 10 8 1 4 2 0 3 9 7 1 4 10 8 12 6 0 7 11 9 2 5 3 10 3 6 4 2 5 11 9 0 7 1 8 12 8 2 9 0 11 4 7 5 3 6 12 10 1 7 0 11 2 9 3 10 1 12 5 8 6 4 6 9 7 5 8 1 12 3 10 4 11 2 0 5 12 3 1 7 10 8 6 9 2 0 4 11 3 1 5 12 6 0 4 2 8 11 9 7 10 12 10 8 11 4 2 6 0 7 1 5 3 9 2 6 4 10 0 11 9 12 5 3 7 1 8 4 8 2 9 3 7 5 11 1 12 10 0 6 и на Ñтом вÑÑ‘. Как найти Ñти 1560 полуцикличеÑких пандиагональных ДЛК 13-го порÑдка Ñ Ð¿ÐµÑ€Ð²Ð¾Ð¹ Ñтрокой в возраÑтающем порÑдке, одному Богу извеÑтно. Впрочем, может быть, автор Ñтатьи Ñто знает. Ðо... где в Ñтатье хоть какой-нибудь намёк на алгоритм поиÑка??? Да, еÑÑ‚ÑŒ алгоритм поиÑка полуцикличеÑких пандиагональных ДЛК Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках. Ð Ñ Ð´Ñ€ÑƒÐ³Ð¸Ð¼Ð¸ видами цикличноÑти где алгоритм поиÑка? Ð’ÑÑ‘-таки на мой необразованный взглÑд ÑÑ‚Ð°Ñ‚ÑŒÑ Ð´Ð¾Ð»Ð¶Ð½Ð° пиÑатьÑÑ Ñ‚Ð°Ðº, чтобы было понÑтно, что за объекты приведены в Ñтатье и как их можно найти. Я нашла 4 порции нормализованных полуцикличеÑких пандиагональных ДЛК 13-го порÑдка (338*4=1352) по Ñвоему алгоритму и пыталаÑÑŒ добавить их в OEIS (дважды!). Ðе пропуÑтили! Ðе нужны, потому что не комплект Tue May 25 11:57 Ðлки-палки! Так выложите уже, наконец, комплект!!! Мне говорÑÑ‚: в OEIS не нужны квадраты, нужны только количеÑтва. "Мы индекÑ", - говорит редактор. И что делать Ñ Ñтим индекÑом? Кому-то интереÑен голый индекÑ??? |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese