Цитата из сообщения
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=128&postid=1697

Ещё два квадрата скопировала из статьи

0 1 2 3 4 5 6 7 8 9 A B C 
7 C 0 1 B 2 8 9 A 6 5 3 4 
3 4 B 2 0 9 A 6 C 8 1 7 5 
B 5 8 9 A C 0 1 2 7 3 4 6 
8 6 7 5 3 4 B C 0 1 2 9 A 
9 A C 6 1 7 3 4 5 B 0 8 2 
C 2 1 7 8 6 5 B 3 4 9 A 0 
1 0 3 4 9 A 2 8 7 5 6 C B 
4 B 5 0 2 8 9 A 6 C 7 1 3 
5 3 4 B C 0 1 2 9 A 8 6 7 
2 7 9 A 6 B C 0 1 3 4 5 8 
A 8 6 C 5 1 7 3 4 0 B 2 9 
6 9 A 8 7 3 4 5 B 2 C 0 1

Fig. 2. (A = 10, B = 11, C = 12). T(~, together with 6 shifts of TV*, ,) and 6 shifts of TT~,,, *.

0 1 2 3 4 5 6 7 8 9 A B C 
A 8 C 9 1 0 2 3 5 B 6 7 4
5 2 6 A 7 C B 1 4 3 0 8 9 
4 7 0 B 5 6 A 8 9 1 C 2 3 
1 B 3 4 9 8 C 0 2 6 7 A 5 
6 C 8 1 3 2 4 A 7 5 B 9 0 
2 9 A 6 0 7 5 B 3 4 1 C 8 
B 4 7 5 2 9 1 C 6 0 8 3 A 
7 0 1 C B 3 8 9 A 2 4 5 6 
C 3 5 8 A 4 0 6 B 7 9 1 2 
9 A 4 2 6 1 7 5 C 8 3 0 B 
8 6 9 0 C B 3 2 1 A 5 4 7 
3 5 B 7 8 A 9 4 0 C 2 6 1 

Fig. 3. (A = 10, B = 11, C = 12). n(5) together with 3 shifts of T~~,~,, 3 shifts of T~~,~,, 3 shifts of T(~,,,, and 3 shifts of T,,~,~).

Эти квадраты тоже, скорее всего, с какой-то хитрой цикличностью.
Посмотрите подписи под квадратами.
Я ничего в этих подписях не понимаю.
Наверное, выше в статье это всё описывается.
Вот из этих квадратов и могут ещё произойти недостающие полуциклические пандиагональные ДЛК 13-го порядка.

Такой цикл нашла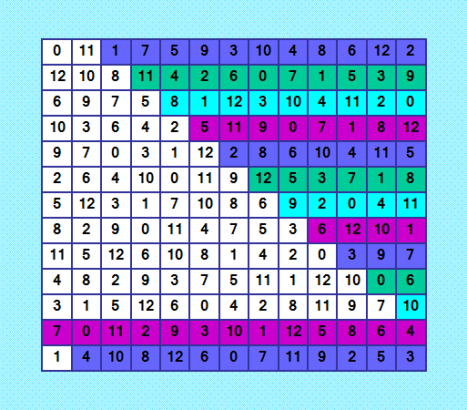



Это полуциклический пандиагональный ДЛК? В каком направлении? (4,4)?

Взяла ДЛК из статьи и свой квадрат, нормализовала их, получила два различных нормализованных ДЛК

0 1 2 3 4 5 6 7 8 9 10 11 12
11 7 9 1 8 12 10 0 3 2 4 6 5
10 5 3 4 9 2 11 6 7 8 1 12 0
7 6 10 8 12 4 1 5 0 3 2 9 11
5 3 0 6 2 11 12 9 10 7 8 1 4
12 10 8 7 0 1 5 11 4 6 3 2 9
4 11 6 2 3 7 9 10 5 12 0 8 1
9 12 5 0 1 8 3 4 6 10 11 7 2
1 4 11 10 7 9 2 8 12 0 6 5 3
8 9 12 5 6 3 4 1 2 11 7 0 10
6 2 4 11 10 0 8 12 9 1 5 3 7
3 0 1 12 5 6 7 2 11 4 9 10 8
2 8 7 9 11 10 0 3 1 5 12 4 6

0 1 2 3 4 5 6 7 8 9 10 11 12
5 3 0 6 2 11 12 9 10 7 8 1 4
1 4 11 10 7 9 2 8 12 0 6 5 3
2 8 7 9 11 10 0 3 1 5 12 4 6
7 6 10 8 12 4 1 5 0 3 2 9 11
9 12 5 0 1 8 3 4 6 10 11 7 2
3 0 1 12 5 6 7 2 11 4 9 10 8
10 5 3 4 9 2 11 6 7 8 1 12 0
4 11 6 2 3 7 9 10 5 12 0 8 1
6 2 4 11 10 0 8 12 9 1 5 3 7
11 7 9 1 8 12 10 0 3 2 4 6 5
12 10 8 7 0 1 5 11 4 6 3 2 9
8 9 12 5 6 3 4 1 2 11 7 0 10

Значит, эти ДЛК не эквивалентные (в смысле переобозначения элементов).

Ой, какая морока! Ну хоть кто-нибудь знает, как эти 208 полуциклических пандиагональных (не эквивалентных) ДЛК 13-го порядка найти???!!!
Я уже всю голову сломала.

Harry мыслит в том же направлении :)
Цитирую его последнее письмо

Attached results for 1 down, x right for x = 0, 1, 2, ... 12.

Да! Именно так и я думала.
А потом 2 вниз и "x right for x = 0, 1, 2, ... 12".
Затем 3 вниз и "x right for x = 0, 1, 2, ... 12".
Приведённый выше пример - это 4 вниз и x = 4.

Ох! Надо разбираться с присланными Harry результатами.
А я ещё со своими не разобралась.
У меня много разных циклов найдено подобных показанному выше направлению (4,4).

Всё осложняется тем, что после нормализации никакой цикличности в ДЛК не видно. То ли это полуциклические пандиагональные ДЛК, то ли это не циклические пандиагональные ДЛК.
Но я так рассуждаю: если исходные ДЛК были полуциклические, то и после нормализации они будут полуциклические.

Нашла с помощью различных преобразований группу из 8788 пандиагональных ДЛК 13-го порядка.
Утилита GetTyp1 ни циклических, ни полуциклических (с цикличностью в строках или в столбцах) пандиагональных ДЛК не обнаружила

Order? 13

Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_2.txt

Counts
------
      8788 diagonal Latin
        52 associative
      8788 pandiagonal
        52 ultramagic
       624 center symmetric
      2366 self-orthogonal
        52 symmetric parity

А теперь проверяю утилитой GetCyclic

Order? 13

Enter the name of the squares file: inp
Count only? y
Get cyclic for, (1 rows, 2 columns, 3 \diagonals, 4 /diagonals)? 3
Get squares with cyclic:  \diagonals
Exact match? y
Number of squares: 8788 number matched 2197

elapsed time 0:00:01

Another order? input y (yes), n (no) or the order: 13

Enter the name of the squares file: inp
Count only? y
Get cyclic for, (1 rows, 2 columns, 3 \diagonals, 4 /diagonals)? 4
Get squares with cyclic:  /diagonals
Exact match? y
Number of squares: 8788 number matched 2197

Очень интересно: есть 2197 поуциклических пандиагональных ДЛК с цикличностью в диагоналях параллельных главной и 2197 поуциклических пандиагональных ДЛК с цикличностью в диагоналях параллельных побочной.
Если эти ДЛК удалить из набора, останутся 4394 пандиагональных ДЛК - ХЗ каких :)
Если все ДЛК набора нормализовать прямо сейчас, вообще ни черта не видно будет никакой цикличности (кроме цикличности в диагоналях).
Вот же фигня какая! Сам чёрт ногу сломит.

Интересно: 4394 = 338*13, магические числа :)

В общем, пока совершенно не знаю, как разобраться с ДЛК в полученном мной наборе из 8788 пандиагональных ДЛК (какие они?).
Попробую разобраться в результатах, которые прислал Harry.
Напомню: Harry прислал такие результаты

Attached results for 1 down, x right for x = 0, 1, 2, ... 12.

Harry показывает, сколько всего у него нашлось пандиагональных ДЛК с такакой цикличностью

total: 17,446 normalized sorted: 1,232
--------------------------------------

down 1 right 0 number of DLS 4524

elapsed time 0:41:53
--------------------------------------
down 1 right 1 number of DLS 4524

elapsed time 0:46:23
--------------------------------------
down 1 right 2 number of DLS 455

elapsed time 0:33:44
--------------------------------------
down 1 right 3 number of DLS 455

elapsed time 0:34:40
--------------------------------------
down 1 right 4 number of DLS 455

elapsed time 0:34:49
--------------------------------------
down 1 right 5 number of DLS 117

elapsed time 0:33:59
--------------------------------------
down 1 right 6 number of DLS 455

elapsed time 0:34:43
--------------------------------------
down 1 right 7 number of DLS 455

elapsed time 0:31:42
--------------------------------------
down 1 right 8 number of DLS 117

elapsed time 0:30:23
--------------------------------------
down 1 right 9 number of DLS 455

elapsed time 0:31:12
--------------------------------------
down 1 right 10 number of DLS 455

elapsed time 0:30:38
--------------------------------------
down 1 right 11 number of DLS 455

elapsed time 0:30:27
--------------------------------------
down 1 right 12 number of DLS 4524

elapsed time 0:39:03

Всего 17446 пандиагональных ДЛК, после нормализации осталось 1232 пандиагональных ДЛК. Это нам много :) какие-то ДЛК тут лишние.

Ещё он свойства 1232 нормализованных пандиагональных ДЛК показывает

Order? 13

Enter the name of the squares file: all13DLS-1dToNFRSortedA

Counts
------
      1232 diagonal Latin
      1232 pandiagonal
        10 cyclic 4-way
       338 semi-cyclic
       104 center symmetric
      1232 nfr
         1 orthogonal pair
       374 self-orthogonal

Ну вот, 10 cyclic 4-way не нужны нам, 338 semi-cyclic тоже не нужны (это, наверное, с цикличностью в строках или в столбцах).
Всё равно много остаётся.
Вот же: мало - плохо, много - тоже плохо :)

Сейчас на квадратики погляжу, может, что-то прояснится.

Проверила все ДЛК набопа (17446 штук) утилитой GetType1

Order? 13

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
     17446 diagonal Latin
       214 associative
     17446 pandiagonal
      1560 cyclic 4-way
      4394 semi-cyclic
       214 ultramagic
      2568 center symmetric
        10 nfr
       348 nfc
       348 natural \diagonal
       545 orthogonal pair
      6292 self-orthogonal
       214 symmetric parity

Прежде всего надо удалить из этого набора 1560 cyclic 4-way и 4394 semi-cyclic. Последние - это с цикличностью в строках или в столбцах.

Удалила, теперь имеем следующие пандиагональные ДЛК - 11492 штук

Order? 13

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt

Counts
------
     11492 diagonal Latin
        68 associative
     11492 pandiagonal
        68 ultramagic
       816 center symmetric
       338 natural \diagonal
       112 orthogonal pair
      4732 self-orthogonal
        68 symmetric parity

Но утилита GetType1 не ищет полуциклические пандиагональные ДЛК с цикличностью в диагоналях.
Надо теперь проверять утилитой GetCyclic.

Проверила

Order? 13

Enter the name of the squares file: inp
Count only? y
Get cyclic for, (1 rows, 2 columns, 3 \diagonals, 4 /diagonals)? 3
Get squares with cyclic:  \diagonals
Exact match? y
Number of squares: 11492 number matched 4394

Another order? input y (yes), n (no) or the order: 13

Enter the name of the squares file: inp
Count only? y
Get cyclic for, (1 rows, 2 columns, 3 \diagonals, 4 /diagonals)? 4
Get squares with cyclic:  /diagonals
Exact match? y
Number of squares: 11492 number matched 4394

С цикличностью в диагоналях обоих направлений имеется 4394*2=8788 ДЛК.
Итак, остаётся:
11492 - 8788 = 2704 пандиагональных ДЛК с ХЗ какой цикличностью :)

Если считать, что остаются полуциклические пандиагональные ДЛК в тех самых направлениях, подобных примеру из статьи с направлением (1,4), тогда можно эти ДЛК нормализовать. И это будет то, что ищем.

Сейчас попробую удалить из набора полуциклические пандиагональные ДЛК с цикличностью в диагоналях обоих направлений.

Удалила.
Осталось 2704 пандиагональных ДЛК, в которых нет цикличности ни в строках, ни в столбцах, ни в диагоналях.
Значит, есть цикличность подобная приведённому в статье направлению (1,4).
Ну, будем так считать.
Утилита GetType1 сообщает об этих квадратиках

Order? 13

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt

Counts
------
      2704 diagonal Latin
        16 associative
      2704 pandiagonal
        16 ultramagic
       192 center symmetric
        16 symmetric parity

Посмотрим на первые три ДЛК в этом наборе

 0  1  4 12  3  7 11  6  9 10  2  5  8
 3  6  9  1  2  5  0  4  8 12  7 10 11
 8 11 12  4  7 10  2  3  6  1  5  9  0
 6 10  1  9 12  0  5  8 11  3  4  7  2
 5  8  3  7 11  2 10  0  1  6  9 12  4
10  0  5  6  9  4  8 12  3 11  1  2  7
 2  3  8 11  1  6  7 10  5  9  0  4 12
 1  5  0  3  4  9 12  2  7  8 11  6 10
12  7 11  2  6  1  4  5 10  0  3  8  9
 4  9 10  0  8 12  3  7  2  5  6 11  1
 7 12  2  5 10 11  1  9  0  4  8  3  6
 9  4  7  8  0  3  6 11 12  2 10  1  5
11  2  6 10  5  8  9  1  4  7 12  0  3

 0  1  5  9 10  4  8 11  7  3 12  2  6
 9 12  8  4  0  3  7  1  2  6 10 11  5
 8  2  3  7 11 12  6 10  0  9  5  1  4
 7 11  1 10  6  2  5  9  3  4  8 12  0
 6 10  4  5  9  0  1  8 12  2 11  7  3
 2  9  0  3 12  8  4  7 11  5  6 10  1
 5  8 12  6  7 11  2  3 10  1  4  0  9
 3  4 11  2  5  1 10  6  9  0  7  8 12
11  7 10  1  8  9  0  4  5 12  3  6  2
 1  5  6  0  4  7  3 12  8 11  2  9 10
 4  0  9 12  3 10 11  2  6  7  1  5  8
12  3  7  8  2  6  9  5  1 10  0  4 11
10  6  2 11  1  5 12  0  4  8  9  3  7

 0  1  5  9 10  4  8 11  7  3 12  2  6
12  8  4  0  3  7  1  2  6 10 11  5  9
 3  7 11 12  6 10  0  9  5  1  4  8  2
10  6  2  5  9  3  4  8 12  0  7 11  1
 9  0  1  8 12  2 11  7  3  6 10  4  5
 8  4  7 11  5  6 10  1  2  9  0  3 12
 2  3 10  1  4  0  9  5  8 12  6  7 11
 6  9  0  7  8 12  3  4 11  2  5  1 10
 5 12  3  6  2 11  7 10  1  8  9  0  4
11  2  9 10  1  5  6  0  4  7  3 12  8
 1  5  8  4  0  9 12  3 10 11  2  6  7
 4 11 12  3  7  8  2  6  9  5  1 10  0
 7 10  6  2 11  1  5 12  0  4  8  9  3

На мой взгляд они цикличные в направлениях подобных направлению (1,4), показанному в статье.

А теперь ВНИМАНИЕ!
Сейчас я нормализую эти ДЛК и удалю дубликаты.

Получено 208 нормализованных полуциклических пандиагональных ДЛК.
Тех самых, которых не хватало.
Теперь, наконец, комплект? Или опять не комплект? :)

Сейчас проверю, есть ли эти квадратики в полученном наборе

0 1 2 3 4 5 6 7 8 9 10 11 12
11 7 9 1 8 12 10 0 3 2 4 6 5
10 5 3 4 9 2 11 6 7 8 1 12 0
7 6 10 8 12 4 1 5 0 3 2 9 11
5 3 0 6 2 11 12 9 10 7 8 1 4
12 10 8 7 0 1 5 11 4 6 3 2 9
4 11 6 2 3 7 9 10 5 12 0 8 1
9 12 5 0 1 8 3 4 6 10 11 7 2
1 4 11 10 7 9 2 8 12 0 6 5 3
8 9 12 5 6 3 4 1 2 11 7 0 10
6 2 4 11 10 0 8 12 9 1 5 3 7
3 0 1 12 5 6 7 2 11 4 9 10 8
2 8 7 9 11 10 0 3 1 5 12 4 6

0 1 2 3 4 5 6 7 8 9 10 11 12
5 3 0 6 2 11 12 9 10 7 8 1 4
1 4 11 10 7 9 2 8 12 0 6 5 3
2 8 7 9 11 10 0 3 1 5 12 4 6
7 6 10 8 12 4 1 5 0 3 2 9 11
9 12 5 0 1 8 3 4 6 10 11 7 2
3 0 1 12 5 6 7 2 11 4 9 10 8
10 5 3 4 9 2 11 6 7 8 1 12 0
4 11 6 2 3 7 9 10 5 12 0 8 1
6 2 4 11 10 0 8 12 9 1 5 3 7
11 7 9 1 8 12 10 0 3 2 4 6 5
12 10 8 7 0 1 5 11 4 6 3 2 9
8 9 12 5 6 3 4 1 2 11 7 0 10

Второй ДЛК есть (это нормализованный ДЛК из статьи), а первого ДЛК нет.
Оказывается у меня получился ДЛК с цикличностью в диагоналях параллельных главной.
Посмотрите-ка на диагонали параллельные главной

Итак, победа!
Мы с Harry нашли все 1560 нормализованных полуциклических пандиагональных ДЛК 13-го порядка.
Теперь комплект.
Но добавлять в OEIS не буду. Не нужны там квадраты. Ну, не нужны так не нужны.
А мне очень нужны! Потому что я - НЕ ИНДЕКС!
Голые количества для меня ничего не значат. Мне интересны "живые" квадраты.

Выложу найденные ДЛК на Яндекс.Диск.

Покажу ещё раз скриншот из OEIS



Я пыталась внести свои результаты для полуциклических пандиагональных ДЛК порядков 13 и 17 (да, в тот момент результаты у меня для обоих порядков были не полные).
Вся правка удалена! Ссылка на тему "Semi-cyclic pandiagonal DLS of prime order n>11" тоже удалена. То есть квадраты не нужны, тема моя не нужна, в которой, между прочим, подробно описывается алгоритм поиска.
Ну и что после этого мне делать в OEIS?!
По-моему, совершенно нечего.

Напомню: полученные мной 1352 нормализованных полуциклических пандиагональных ДЛК 13-го порядка выложены здесь
https://disk.yandex.ru/d/Kb3NZVxFt8NSTA
Яндекс.Диск, формат txt, 577 КБ.

Сейчас добавлю к этим ДЛК новые 208 нормализованных полуциклических пандиагональных ДЛК 13-го порядка и выложу все 1560 ДЛК.

Готово!
https://disk.yandex.ru/d/3KpNZgnH19a0Vg
Яндекс.Диск, 795 КБ, формат txt.

Добавила к 1560 нормализованным полуциклическим пандиагональным ДЛК 13-го порядка 10 нормализованных циклических пандиагональных ДЛК.
Проверила полученный набор из 1570 нормализованных пандиагональных ДЛК на ортогональные пары программой GetOrthogonal

Order? 13

Enter the name of the squares file: a
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file a-orthCounts.txt
..output file a-orthNos.txt
squares 1570 total orthogonal pairs 2905
Maximum pairs for square 1: 165
There are 7 other squares with this maximum number of pairs.
..output file a-1orths.txt
Pairs for square 1: 165

ДЛК образовали 2905 ортогональных пар. Неплохо.
Максимальная группа ОДЛК (165 штук) имеется у восьми ДЛК.

Смотрим счётчик ортогональных пар, первыми идут 10 циклических пандиагональных ДЛК

                orthogonal
      square       pairs
      ------    ----------

           1          165
           2          165
           3          165
           4            9
           5          165
           6          165
           7            9
           8          165
           9          165
          10          165

          11            7
          12            7
          13            1
          14            7
          15            7
          16            1
          17            7
          18            1
          19            1
          20            7
. . . . . . . . 

Оценка a(13) >= 165 для порядка 13 не актуальна.

Так, у нас остались не циклические пандиагональные ДЛК 13-го порядка.
Согласно количествам в последовательности OEIS не циклических (нормализованных) пандиагональных ДЛК должно быть
12386 - 10 - 1560 = 10816

Выше показаны шесть не циклических пандиагональных ДЛК 13-го порядка, которые мне удалось получить, включая пример, приведённый в статье OEIS.
Покажу их ещё раз в нормализованном виде

0 1 2 3 4 5 6 7 8 9 10 11 12
6 11 0 1 8 2 10 4 12 5 3 7 9
7 9 10 6 12 0 3 1 11 2 4 8 5
12 8 3 7 11 9 5 6 0 10 1 2 4
11 2 5 4 1 8 7 12 9 6 0 3 10
1 0 9 10 2 3 4 8 7 11 12 5 6
4 12 6 11 0 10 2 5 3 1 8 9 7
8 5 7 12 6 1 11 9 10 4 2 0 3
2 3 8 9 5 4 12 0 6 7 11 10 1
10 4 1 0 3 7 8 2 5 12 9 6 11
9 7 11 2 10 6 1 3 4 8 5 12 0
5 6 12 8 9 11 0 10 1 3 7 4 2
3 10 4 5 7 12 9 11 2 0 6 1 8

0 1 2 3 4 5 6 7 8 9 10 11 12
4 11 6 0 8 1 12 3 5 2 7 9 10
8 9 12 10 7 11 0 4 1 3 5 6 2
7 5 1 2 9 6 10 11 0 8 4 12 3
10 4 3 8 5 2 9 12 6 7 11 1 0
11 12 0 4 3 7 8 1 2 10 9 5 6
9 6 11 1 12 10 4 5 3 0 8 2 7
2 10 7 5 6 0 11 9 12 4 1 3 8
1 0 8 9 2 3 7 6 10 11 12 4 5
12 3 4 11 1 8 5 2 7 6 0 10 9
6 2 10 12 0 4 1 8 9 5 3 7 11
5 7 9 6 10 12 3 0 11 1 2 8 4
3 8 5 7 11 9 2 10 4 12 6 0 1

0 1 2 3 4 5 6 7 8 9 10 11 12
4 11 6 12 10 1 3 0 5 7 8 2 9
10 8 5 9 11 2 12 1 3 4 0 6 7
12 0 7 4 8 9 11 6 2 10 1 5 3
1 6 3 0 7 10 4 5 9 12 11 8 2
11 2 1 5 6 12 0 8 7 3 4 9 10
9 12 10 8 2 3 1 11 6 0 5 7 4
5 3 4 11 9 7 10 2 12 1 6 0 8
6 7 0 1 5 4 8 9 10 2 3 12 11
2 9 12 6 3 0 5 4 11 8 7 10 1
8 10 11 2 12 6 7 3 1 5 9 4 0
7 4 8 10 1 11 9 12 0 6 2 3 5
3 5 9 7 0 8 2 10 4 11 12 1 6

0 1 2 3 4 5 6 7 8 9 10 11 12
11 3 10 0 6 12 8 4 2 7 5 9 1
9 7 11 12 10 4 3 6 5 0 1 2 8
6 12 8 1 11 9 10 0 3 2 4 5 7
8 2 7 9 5 0 1 12 10 11 3 6 4
10 4 5 2 1 8 9 11 7 6 12 0 3
5 0 6 4 3 2 7 8 12 1 11 10 9
12 10 3 11 7 6 5 2 4 8 9 1 0
1 11 12 6 0 3 4 10 9 5 7 8 2
7 9 1 8 12 10 0 5 6 4 2 3 11
2 8 4 10 9 11 12 1 0 3 6 7 5
4 5 9 7 8 1 2 3 11 10 0 12 6
3 6 0 5 2 7 11 9 1 12 8 4 10

0 1 2 3 4 5 6 7 8 9 10 11 12
7 3 12 10 2 0 4 9 6 11 5 8 1
12 11 1 0 8 9 10 3 4 2 6 7 5
4 5 8 11 10 12 0 2 1 7 3 9 6
8 9 7 5 6 11 1 12 3 10 2 4 0
3 4 6 2 1 7 8 11 5 12 0 10 9
10 2 3 7 9 6 5 4 0 8 1 12 11
1 0 10 12 3 4 9 8 7 5 11 6 2
11 12 5 4 0 2 3 10 9 6 7 1 8
5 8 0 1 12 10 11 6 2 4 9 3 7
6 7 9 8 11 1 2 0 10 3 12 5 4
9 10 11 6 5 8 7 1 12 0 4 2 3
2 6 4 9 7 3 12 5 11 1 8 0 10

0 1 2 3 4 5 6 7 8 9 10 11 12
11 9 0 5 2 7 1 4 10 3 12 8 6
4 5 6 12 0 11 2 3 1 8 7 10 9
6 8 9 11 10 3 12 5 2 0 1 4 7
2 7 10 8 12 6 11 0 9 4 5 3 1
10 3 4 7 1 8 9 6 5 12 0 2 11
5 2 1 0 9 4 10 8 7 6 11 12 3
12 0 5 4 3 1 7 2 11 10 9 6 8
9 11 12 6 5 2 3 10 4 7 8 1 0
8 6 7 2 11 0 5 12 3 1 4 9 10
7 10 11 9 6 12 8 1 0 2 3 5 4
1 4 3 10 8 9 0 11 12 5 6 7 2
3 12 8 1 7 10 4 9 6 11 2 0 5

Как искать остальные не циклические пандиагональные ДЛК?

Ох, ну такая хренотень с этими полуциклическими и не циклическими пандиагональными квадратами 13-го порядка.
Сейчас обнаружила нестыковку.

Итак, у нас есть 1560 нормализованных полуциклических пандиагональных ДЛК 13-го порядка.
Среди них 1352 ДЛК - с цикличностью в строках, или в столбцах, или в диагоналях одного из двух направлений.
С этими ДЛК всё понятно, и в нормализованном виде в этих ДЛК цикличность хорошо видно.
Например, в этом нормализованном ДЛК цикличность в строках

 0  1  2  3  4  5  6  7  8  9 10 11 12
 2  3  4  5  6  7  8  9 10 11 12  0  1
 4  5  6  7  8  9 10 11 12  0  1  2  3
 6  7  8  9 10 11 12  0  1  2  3  4  5
11 12  0  1  2  3  4  5  6  7  8  9 10
 9 10 11 12  0  1  2  3  4  5  6  7  8
12  0  1  2  3  4  5  6  7  8  9 10 11
 5  6  7  8  9 10 11 12  0  1  2  3  4
 3  4  5  6  7  8  9 10 11 12  0  1  2
 1  2  3  4  5  6  7  8  9 10 11 12  0
 7  8  9 10 11 12  0  1  2  3  4  5  6
10 11 12  0  1  2  3  4  5  6  7  8  9
 8  9 10 11 12  0  1  2  3  4  5  6  7

Оставшиеся 208 полуциклических пандиагональных ДЛК обладают весьма странной цикличностью в направлениях (1,4), (1,5) ...
Особенность этой цикличности в том, что после нормализации ДЛК её ни черта уже не видно.
Пример ДЛК из статьи, который с цикличностью в направлении (1,4)

   0 11  1  7  5  9  3 10  4  8  6 12  2
   9  7  0  3  1 12  2  8  6 10  4 11  5
  11  5 12  6 10  8  1  4  2  0  3  9  7
   1  4 10  8 12  6  0  7 11  9  2  5  3
  10  3  6  4  2  5 11  9  0  7  1  8 12
   8  2  9  0 11  4  7  5  3  6 12 10  1
   7  0 11  2  9  3 10  1 12  5  8  6  4
   6  9  7  5  8  1 12  3 10  4 11  2  0
   5 12  3  1  7 10  8  6  9  2  0  4 11
   3  1  5 12  6  0  4  2  8 11  9  7 10
  12 10  8 11  4  2  6  0  7  1  5  3  9
   2  6  4 10  0 11  9 12  5  3  7  1  8
   4  8  2  9  3  7  5 11  1 12 10  0  6

Нормализую этот ДЛК

 0  1  2  3  4  5  6  7  8  9 10 11 12
 5  3  0  6  2 11 12  9 10  7  8  1  4
 1  4 11 10  7  9  2  8 12  0  6  5  3
 2  8  7  9 11 10  0  3  1  5 12  4  6
 7  6 10  8 12  4  1  5  0  3  2  9 11
 9 12  5  0  1  8  3  4  6 10 11  7  2
 3  0  1 12  5  6  7  2 11  4  9 10  8
10  5  3  4  9  2 11  6  7  8  1 12  0
 4 11  6  2  3  7  9 10  5 12  0  8  1
 6  2  4 11 10  0  8 12  9  1  5  3  7
11  7  9  1  8 12 10  0  3  2  4  6  5
12 10  8  7  0  1  5 11  4  6  3  2  9
 8  9 12  5  6  3  4  1  2 11  7  0 10

Вы видите в этом нормализованном ДЛК какую-нибудь цикличность???
Я не вижу никакой цикличности!

Ну ладно, согласились с тем, что эти 208 полуциклических пандиагональных ДЛК имеют место быть, и добавили их к 1352 ранее найденным полуциклическим пандиагональным ДЛК.

Теперь смотрим на не циклический пандиагональный ДЛК, приведённый в статье
Vahid Dabbaghian, Tiankuang Wu, Constructing non-cyclic pandiagonal Latin squares of prime orders, Journal of Discrete Algorithms 30, 2015.

7 1 0 3 6 5 12 2 8 9 10 11 4
2 3 4 10 0 7 6 9 12 11 5 8 1
4 11 1 7 8 9 10 3 6 0 12 2 5
6 5 8 11 10 4 7 0 1 2 3 9 12
8 9 2 5 12 11 1 4 3 10 0 6 7
3 6 12 0 1 2 8 11 5 4 7 10 9
10 0 3 2 9 12 5 6 7 8 1 4 11
1 7 10 4 3 6 9 8 2 5 11 12 0
11 4 5 6 7 0 3 10 9 12 2 1 8
5 8 7 1 4 10 11 12 0 6 9 3 2
12 2 9 8 11 1 0 7 10 3 4 5 6
9 10 11 12 5 8 2 1 4 7 6 0 3
0 12 6 9 2 3 4 5 11 1 8 7 10

Надо понимать, что этот пандиагональный ДЛК не обладает ну никакой цикличностью.
Тогда после нормализации он должен быть совершенно новым ДЛК.
Нормализую этот ДЛК

0 1 2 3 4 5 6 7 8 9 10 11 12
7 3 12 10 2 0 4 9 6 11 5 8 1
12 11 1 0 8 9 10 3 4 2 6 7 5
4 5 8 11 10 12 0 2 1 7 3 9 6
8 9 7 5 6 11 1 12 3 10 2 4 0
3 4 6 2 1 7 8 11 5 12 0 10 9
10 2 3 7 9 6 5 4 0 8 1 12 11
1 0 10 12 3 4 9 8 7 5 11 6 2
11 12 5 4 0 2 3 10 9 6 7 1 8
5 8 0 1 12 10 11 6 2 4 9 3 7
6 7 9 8 11 1 2 0 10 3 12 5 4
9 10 11 6 5 8 7 1 12 0 4 2 3
2 6 4 9 7 3 12 5 11 1 8 0 10

И что же???
Этот нормализованный ДЛК содержится в наборе из 1560 нормализованных полуциклических пандиагональных ДЛК!!!
[И конечно же, он находится в группе из 208 нормалиpованных полуциклических пандиагональных ДЛК, в которых не видна никакая цикличность.]
Но ведь этот ДЛК НЕ ЦИКЛИЧЕСКИЙ!
И как же их тогда различать???

Ой, нет, всё. Я завязываю с этими полуциклическими и не циклическими пандиагональными ДЛК 13-го порядка.
Напридумывали всякой ерунды!

PS. Я вот что думаю:
авторы этой статьи
Vahid Dabbaghian, Tiankuang Wu, Constructing non-cyclic pandiagonal Latin squares of prime orders, Journal of Discrete Algorithms 30, 2015.
назвали "non-cyclic pandiagonal Latin squares" такие пандиагональные ДЛК, которые в статье Аткина называются полуциклическими.
Вполне возможен такой вариант.
Отсюда такая путаница.

Есть циклические пандиагональные ДЛК (вполне понятные, цикличность в них одновременно в строках, в столбцах и в диагоналях обоих направлений).
Все остальные пандиагональные ДЛК, не являющиеся циклическими, надо называть НЕ ЦИКЛИЧЕСКИЕ.
И никаких полуциклических вообще не надо придумывать.