Проверка свойств топовых ДЛК 19-го порядка утилитой Harry White

Order? 19

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_18.txt

Counts
------
         5 diagonal Latin
         4 pandiagonal
         4 center symmetric
         4 nfr
         3 orthogonal pair
         4 self-orthogonal

Топ-3 ДЛК 20-го порядка по Д-трансверсалям
в порядке возрастания

1. 23909627000 Д-трансверсалей
ДЛК построен методом Гергели

 1 12  3  4  5  6  7  8  9 10  0 19 18 17 16 15 14 13  2 11
 9  3 17  5  1 10  6  4  8  2 12 18 14 16  0 11 15  7 13 19
 3  4  5  0  9  2  1  6  7  8 18 17 16 11 12 19 10 15 14 13
 4  5  1  9 18  3  2 10  6  7 17 16  0 12 13  8 19 11 15 14
16  1  9  3  4  7  8  2 10  5 15  0 12 18 17 14 13 19 11  6
 7  6 10  2  3  8 19  1  5  4 14 15 11  9 18 13 12  0 16 17
 8  7  6  1  2  9 10 15  4  3 13 14  5  0 19 12 11 16 17 18
 2  8  4  6 10  1  5  7 13  9 19  3 17 15 11  0 16 14 18 12
10  9  8  7  6  5  4  3  2 11  1 12 13 14 15 16 17 18 19  0
 5 10  2  8  7 14  3  9  1  6 16 11 19 13  4 17 18 12  0 15
 0 19 18 17 16 15 14 13 12  1 11  2  3  4  5  6  7  8  9 10
12 18 14 16  0 11 15 17  3 19  9 13  7  5  1 10  6  4  8  2
18 17 16 11 12 19  0  5 14 13  3  4 15 10  9  2  1  6  7  8
17 16  0 12 13 18  9 11 15 14  4  5  1 19  8  3  2 10  6  7
15  0 12 18 17  4 13 19 11 16  6  1  9  3 14  7  8  2 10  5
14 15 11 19  8 13 12  0 16 17  7  6 10  2  3 18  9  1  5  4
13 14 15 10 19 12 11 16 17 18  8  7  6  1  2  9  0  5  4  3
19 13  7 15 11  0 16 14 18 12  2  8  4  6 10  1  5 17  3  9
11  2 13 14 15 16 17 18 19  0 10  9  8  7  6  5  4  3 12  1
 6 11 19 13 14 17 18 12  0 15  5 10  2  8  7  4  3  9  1 16

Иллюстрация



Смотрите мою статью
ПОСТРОЕНИЕ ДИАГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ

В этом ДЛК Д-трансверсали посчитаны мной; программа Tomas Brada работала 19 часов.
В двух следующих ДЛК Д-трансверсали посчитал помощник.

2. 25314295328 Д-трансверсалей
ДЛК построен мной.
Смотрите статью "ЕЩЁ ОДНА ГРУППА MOLS 20-го ПОРЯДКА"
http://www.natalimak1.narod.ru/mols20a.htm
При построении использовалась квази-разностная матрица, приведённая в статье
M. Wojtas, Discrete Mathematics 140 (1995) 291 - 294

 0 11  9 18 17  6  5 14  3 12  1 10  8 19 16  7  4 15  2 13
10  1 19  8  7 16 15  4 13  2 11  0 18  9  6 17 14  5 12  3
 4 15  2 13 11  0 19  8  7 16  5 14  3 12 10  1 18  9  6 17
14  5 12  3  1 10  9 18 17  6 15  4 13  2  0 11  8 19 16  7
 8 19  6 17  4 15 13  2  1 10  9 18  7 16  5 14 12  3  0 11
18  9 16  7 14  5  3 12 11  0 19  8 17  6 15  4  2 13 10  1
 2 13 10  1  8 19  6 17 15  4  3 12 11  0  9 18  7 16 14  5
12  3  0 11 18  9 16  7  5 14 13  2  1 10 19  8 17  6  4 15
16  7  4 15 12  3 10  1  8 19 17  6  5 14 13  2 11  0  9 18
 6 17 14  5  2 13  0 11 18  9  7 16 15  4  3 12  1 10 19  8
11  0 18  9  6 17 14  5 12  3 10  1 19  8  7 16 15  4 13  2
 1 10  8 19 16  7  4 15  2 13  0 11  9 18 17  6  5 14  3 12
15  4 13  2  0 11  8 19 16  7 14  5 12  3  1 10  9 18 17  6
 5 14  3 12 10  1 18  9  6 17  4 15  2 13 11  0 19  8  7 16
19  8 17  6 15  4  2 13 10  1 18  9 16  7 14  5  3 12 11  0
 9 18  7 16  5 14 12  3  0 11  8 19  6 17  4 15 13  2  1 10
13  2  1 10 19  8 17  6  4 15 12  3  0 11 18  9 16  7  5 14
 3 12 11  0  9 18  7 16 14  5  2 13 10  1  8 19  6 17 15  4
 7 16 15  4  3 12  1 10 19  8  6 17 14  5  2 13  0 11 18  9
17  6  5 14 13  2 11  0  9 18 16  7  4 15 12  3 10  1  8 19

Иллюстрация



В ДЛК своеобразная блочная структура.
И ещё одна иллюстрация, на которой показана классическая блочная структура



3. 90010806304 Д-трансверсалей
ДЛК построен программой Harry White

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 2  3  4  0  1  7  8  9  5  6 12 13 14 10 11 17 18 19 15 16
 4  0  1  2  3  9  5  6  7  8 14 10 11 12 13 19 15 16 17 18
 1  2  3  4  0  6  7  8  9  5 11 12 13 14 10 16 17 18 19 15
 3  4  0  1  2  8  9  5  6  7 13 14 10 11 12 18 19 15 16 17
15 16 17 18 19 10 11 12 13 14  5  6  7  8  9  0  1  2  3  4
17 18 19 15 16 12 13 14 10 11  7  8  9  5  6  2  3  4  0  1
19 15 16 17 18 14 10 11 12 13  9  5  6  7  8  4  0  1  2  3
16 17 18 19 15 11 12 13 14 10  6  7  8  9  5  1  2  3  4  0
18 19 15 16 17 13 14 10 11 12  8  9  5  6  7  3  4  0  1  2
 5  6  7  8  9  0  1  2  3  4 15 16 17 18 19 10 11 12 13 14
 7  8  9  5  6  2  3  4  0  1 17 18 19 15 16 12 13 14 10 11
 9  5  6  7  8  4  0  1  2  3 19 15 16 17 18 14 10 11 12 13
 6  7  8  9  5  1  2  3  4  0 16 17 18 19 15 11 12 13 14 10
 8  9  5  6  7  3  4  0  1  2 18 19 15 16 17 13 14 10 11 12
10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9
12 13 14 10 11 17 18 19 15 16  2  3  4  0  1  7  8  9  5  6
14 10 11 12 13 19 15 16 17 18  4  0  1  2  3  9  5  6  7  8
11 12 13 14 10 16 17 18 19 15  1  2  3  4  0  6  7  8  9  5
13 14 10 11 12 18 19 15 16 17  3  4  0  1  2  8  9  5  6  7

Иллюстрация



Раскраской показана классическая блочная структура

Проверка топовых ДЛК 20-го порядка утилитой Harry White

Order? 20

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_8.txt

Counts
------
         3 diagonal Latin
         1 weakly pandiagonal
         1 axial symmetric
         1 center symmetric
         1 nfr
         1 natural \diagonal
         2 self-orthogonal

Прекрасные квадратики!
Большое спасибо помощнику за подсчёт Д-трансверсалей.

Цитата из сообщения https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=5757

В статье
ГРУППЫ MOLS 20-го и 21-го ПОРЯДКА
http://www.natalimak1.narod.ru/mols20_21.htm
на рис. 12-14 показана группа MOLS 20-го порядка, состоящая из трёх взаимно ортогональных ЛК, построенная методом составных квадратов.

В этой группе два ЛК являются диагональными.
Преобразовала их в традиционную форму

 0  1  2  3  4  5  6  7  8  9  15  16  17  18  19  10  11  12  13  14 
 2  3  4  0  1  7  8  9  5  6  17  18  19  15  16  12  13  14  10  11 
 4  0  1  2  3  9  5  6  7  8  19  15  16  17  18  14  10  11  12  13 
 1  2  3  4  0  6  7  8  9  5  16  17  18  19  15  11  12  13  14  10 
 3  4  0  1  2  8  9  5  6  7  18  19  15  16  17  13  14  10  11  12 
 10  11  12  13  14  15  16  17  18  19  5  6  7  8  9  0  1  2  3  4 
 12  13  14  10  11  17  18  19  15  16  7  8  9  5  6  2  3  4  0  1 
 14  10  11  12  13  19  15  16  17  18  9  5  6  7  8  4  0  1  2  3 
 11  12  13  14  10  16  17  18  19  15  6  7  8  9  5  1  2  3  4  0 
 13  14  10  11  12  18  19  15  16  17  8  9  5  6  7  3  4  0  1  2 
 5  6  7  8  9  0  1  2  3  4  10  11  12  13  14  15  16  17  18  19 
 7  8  9  5  6  2  3  4  0  1  12  13  14  10  11  17  18  19  15  16 
 9  5  6  7  8  4  0  1  2  3  14  10  11  12  13  19  15  16  17  18 
 6  7  8  9  5  1  2  3  4  0  11  12  13  14  10  16  17  18  19  15 
 8  9  5  6  7  3  4  0  1  2  13  14  10  11  12  18  19  15  16  17 
 15  16  17  18  19  10  11  12  13  14  0  1  2  3  4  5  6  7  8  9 
 17  18  19  15  16  12  13  14  10  11  2  3  4  0  1  7  8  9  5  6 
 19  15  16  17  18  14  10  11  12  13  4  0  1  2  3  9  5  6  7  8 
 16  17  18  19  15  11  12  13  14  10  1  2  3  4  0  6  7  8  9  5 
 18  19  15  16  17  13  14  10  11  12  3  4  0  1  2  8  9  5  6  7 

 0  1  2  3  4  10  11  12  13  14  5  6  7  8  9  15  16  17  18  19 
 3  4  0  1  2  13  14  10  11  12  8  9  5  6  7  18  19  15  16  17 
 1  2  3  4  0  11  12  13  14  10  6  7  8  9  5  16  17  18  19  15 
 4  0  1  2  3  14  10  11  12  13  9  5  6  7  8  19  15  16  17  18 
 2  3  4  0  1  12  13  14  10  11  7  8  9  5  6  17  18  19  15  16 
 5  6  7  8  9  15  16  17  18  19  0  1  2  3  4  10  11  12  13  14 
 8  9  5  6  7  18  19  15  16  17  3  4  0  1  2  13  14  10  11  12 
 6  7  8  9  5  16  17  18  19  15  1  2  3  4  0  11  12  13  14  10 
 9  5  6  7  8  19  15  16  17  18  4  0  1  2  3  14  10  11  12  13 
 7  8  9  5  6  17  18  19  15  16  2  3  4  0  1  12  13  14  10  11 
 15  16  17  18  19  5  6  7  8  9  10  11  12  13  14  0  1  2  3  4 
 18  19  15  16  17  8  9  5  6  7  13  14  10  11  12  3  4  0  1  2 
 16  17  18  19  15  6  7  8  9  5  11  12  13  14  10  1  2  3  4  0 
 19  15  16  17  18  9  5  6  7  8  14  10  11  12  13  4  0  1  2  3 
 17  18  19  15  16  7  8  9  5  6  12  13  14  10  11  2  3  4  0  1 
 10  11  12  13  14  0  1  2  3  4  15  16  17  18  19  5  6  7  8  9 
 13  14  10  11  12  3  4  0  1  2  18  19  15  16  17  8  9  5  6  7 
 11  12  13  14  10  1  2  3  4  0  16  17  18  19  15  6  7  8  9  5 
 14  10  11  12  13  4  0  1  2  3  19  15  16  17  18  9  5  6  7  8 
 12  13  14  10  11  2  3  4  0  1  17  18  19  15  16  7  8  9  5  6

Это интересная ортогональная пара.
Нормализовала эти ДЛК и сравнила с первым топовым ДЛК (рекордным на данный момент).
Обнаружила, что один из этих ДЛК с топовым ДЛК совпадает

MaSWzZ2ebdm5cAneAkniTEZhST67FA1uZGAPN7FCp8a6aq6VsJNFegrB5zdWknjNnrJLzVWrCpcPmMscBDbucW6gQ29RktaVRMrY5JUMTepS7hsa64fKN3ry

А второй ДЛК ортогональной пары

ME5FWDZhzcE84xBYSUU1J65AdDUWQbae7DUbVmmzUq6qYZxABbqnHRN7ors7qpKj65c1PXpPrs43dparD7VHaaX7FPHvrCYBmLMwVy4HXsdEkWvUvMT7R3e4

может дать новое количество Д-трансверсалей.
Надо его проверить.

На очереди топовые ДЛК 21-го порядка.
Небольшая пауза.

Господа!
Хотелось бы видеть ваши вопросы, а также замечания и пожелания.

В этом сообщении нашла ортогональную пару ДЛК 18-го порядка подобную ортогональной паре, давшей топовые ДЛК 3 и 4
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117&postid=1245

Преобразовала ДЛК ортогональной пары в традиционную форму

 0  4  14  15  16  17  1  13  12  3  2  6  11  9  7  5  10  8 
 7  1  5  14  15  16  17  0  13  4  3  12  10  8  6  11  9  2 
 13  8  2  6  14  15  16  1  0  5  4  11  9  7  12  10  3  17 
 12  0  9  3  7  14  15  2  1  6  5  10  8  13  11  4  17  16 
 11  13  1  10  4  8  14  3  2  7  6  9  0  12  5  17  16  15 
 10  12  0  2  11  5  9  4  3  8  7  1  13  6  17  16  15  14 
 2  11  13  1  3  12  6  5  4  9  8  0  7  17  16  15  14  10 
 8  9  10  11  12  13  0  14  15  16  17  7  6  5  4  3  2  1 
 6  7  8  9  10  11  12  17  16  15  14  5  4  3  2  1  0  13 
 5  6  7  8  9  10  11  15  14  17  16  4  3  2  1  0  13  12 
 4  5  6  7  8  9  10  16  17  14  15  3  2  1  0  13  12  11 
 3  14  15  16  17  0  7  12  11  2  1  13  5  10  8  6  4  9 
 14  15  16  17  13  6  8  11  10  1  0  2  12  4  9  7  5  3 
 15  16  17  12  5  7  2  10  9  0  13  14  1  11  3  8  6  4 
 16  17  11  4  6  1  3  9  8  13  12  15  14  0  10  2  7  5 
 17  10  3  5  0  2  4  8  7  12  11  16  15  14  13  9  1  6 
 9  2  4  13  1  3  5  7  6  11  10  17  16  15  14  12  8  0 
 1  3  12  0  2  4  13  6  5  10  9  8  17  16  15  14  11  7 

 0  7  13  12  11  10  2  8  4  5  6  3  14  15  16  17  9  1 
 4  1  8  0  13  12  11  9  5  6  7  14  15  16  17  10  2  3 
 14  5  2  9  1  0  13  10  6  7  8  15  16  17  11  3  4  12 
 15  14  6  3  10  2  1  11  7  8  9  16  17  12  4  5  13  0 
 16  15  14  7  4  11  3  12  8  9  10  17  13  5  6  0  1  2 
 17  16  15  14  8  5  12  13  9  10  11  0  6  7  1  2  3  4 
 1  17  16  15  14  9  6  0  10  11  12  7  8  2  3  4  5  13 
 13  0  1  2  3  4  5  14  15  16  17  12  11  10  9  8  7  6 
 2  3  4  5  6  7  8  16  17  14  15  1  0  13  12  11  10  9 
 3  4  5  6  7  8  9  17  16  15  14  2  1  0  13  12  11  10 
 12  13  0  1  2  3  4  15  14  17  16  11  10  9  8  7  6  5 
 6  12  11  10  9  1  0  7  3  4  5  13  2  14  15  16  17  8 
 11  10  9  8  0  13  7  6  2  3  4  5  12  1  14  15  16  17 
 9  8  7  13  12  6  17  5  1  2  3  10  4  11  0  14  15  16 
 7  6  12  11  5  17  16  4  0  1  2  8  9  3  10  13  14  15 
 5  11  10  4  17  16  15  3  13  0  1  6  7  8  2  9  12  14 
 10  9  3  17  16  15  14  2  12  13  0  4  5  6  7  1  8  11 
 8  2  17  16  15  14  10  1  11  12  13  9  3  4  5  6  0  7 

и посчитала в них Д-трансверсали

KG1FUy1EbrZmAKRvHxHTB7KBZsKYMLeHR29ytFenC4bmocDTAvnQQ6inxbqid9vL4317p3BHEMHLcZoA5uc7buwHA2Z51j
num_dtrans: 82629346

K453D5eeuQ5E4Ptku3kDApkLhhXGYwo1g4zvJ2LHvkfhkEDY6nDh6XfwaYd8nnCtb6RejreJMUr2mUtEM2fkSyzeRmV
num_dtrans: 82653006

Это добавление к топовым ДЛК 18-го порядка.
В статье, где строились эти ортогональные пары, написано, что путём варьирования квази-разностной матрицы можно получить 2880 ортогональных пар ДЛК.
Статья здесь
http://www.natalimak1.narod.ru/diagon.htm
Не знаю, сколько среди них будет существенно различных ортогональных пар.
Я тогда написала программу варьирования квази-разностной матрицы и получила 2880 возможных вариантов.
Два из этих вариантов показаны в статье и показаны здесь.

Топ-3 ДЛК 21-го порядка по Д-трансверсалям
в порядке убывания

1. 51162162017 Д-трансверсалей
ДЛК построен программой Harry White (SODLS)

 0 12  3  2 17 19 20 18 13 15 16 14  1  8 10 11  9  4  6  7  5
 2  1  0 12 20 18 17 19 16 14 13 15  3 11  9  8 10  7  5  4  6
12  3  2  1 18 20 19 17 14 16 15 13  0  9 11 10  8  5  7  6  4
 1  0 12  3 19 17 18 20 15 13 14 16  2 10  8  9 11  6  4  5  7
 8 10 11  9  4 12  7  6  0  2  3  1  5 17 19 20 18 13 15 16 14
11  9  8 10  6  5  4 12  3  1  0  2  7 20 18 17 19 16 14 13 15
 9 11 10  8 12  7  6  5  1  3  2  0  4 18 20 19 17 14 16 15 13
10  8  9 11  5  4 12  7  2  0  1  3  6 19 17 18 20 15 13 14 16
17 19 20 18 13 15 16 14  8 12 11 10  9  4  6  7  5  0  2  3  1
20 18 17 19 16 14 13 15 10  9  8 12 11  7  5  4  6  3  1  0  2
18 20 19 17 14 16 15 13 12 11 10  9  8  5  7  6  4  1  3  2  0
19 17 18 20 15 13 14 16  9  8 12 11 10  6  4  5  7  2  0  1  3
 3  2  1  0  7  6  5  4 11 10  9  8 12 16 15 14 13 20 19 18 17
 4  6  7  5  0  2  3  1 17 19 20 18 14 13 12 16 15  8 10 11  9
 7  5  4  6  3  1  0  2 20 18 17 19 16 15 14 13 12 11  9  8 10
 5  7  6  4  1  3  2  0 18 20 19 17 13 12 16 15 14  9 11 10  8
 6  4  5  7  2  0  1  3 19 17 18 20 15 14 13 12 16 10  8  9 11
13 15 16 14  8 10 11  9  4  6  7  5 18  0  2  3  1 17 12 20 19
16 14 13 15 11  9  8 10  7  5  4  6 20  3  1  0  2 19 18 17 12
14 16 15 13  9 11 10  8  5  7  6  4 17  1  3  2  0 12 20 19 18
15 13 14 16 10  8  9 11  6  4  5  7 19  2  0  1  3 18 17 12 20

2. 46228033641 Д-трансверсалей
ДЛК построен методом Гергели

1 20 3 4 5 6 7 8 9 10 12 0 19 18 17 16 15 14 13 2 11
9 3 20 5 1 10 6 4 8 2 17 12 18 14 16 0 11 15 7 13 19
3 4 5 20 9 2 1 6 7 8 0 18 17 16 11 12 19 10 15 14 13
4 5 1 9 20 3 2 10 6 7 18 17 16 0 12 13 8 19 11 15 14
20 1 9 3 4 7 8 2 10 5 16 15 0 12 18 17 14 13 19 11 6
7 6 10 2 3 8 20 1 5 4 19 14 15 11 9 18 13 12 0 16 17
8 7 6 1 2 9 10 20 4 3 15 13 14 5 0 19 12 11 16 17 18
2 8 4 6 10 1 5 7 20 9 13 19 3 17 15 11 0 16 14 18 12
10 9 8 7 6 5 4 3 2 20 11 1 12 13 14 15 16 17 18 19 0
5 10 2 8 7 20 3 9 1 6 14 16 11 19 13 4 17 18 12 0 15
16 12 17 0 18 14 19 15 13 11 20 6 2 7 10 8 4 9 5 3 1
0 19 18 17 16 15 14 13 12 1 2 11 20 3 4 5 6 7 8 9 10
12 18 14 16 0 11 15 17 3 19 7 9 13 20 5 1 10 6 4 8 2
18 17 16 11 12 19 0 5 14 13 10 3 4 15 20 9 2 1 6 7 8
17 16 0 12 13 18 9 11 15 14 8 4 5 1 19 20 3 2 10 6 7
15 0 12 18 17 4 13 19 11 16 6 20 1 9 3 14 7 8 2 10 5
14 15 11 19 8 13 12 0 16 17 9 7 6 10 2 3 18 20 1 5 4
13 14 15 10 19 12 11 16 17 18 5 8 7 6 1 2 9 0 20 4 3
19 13 7 15 11 0 16 14 18 12 3 2 8 4 6 10 1 5 17 20 9
11 2 13 14 15 16 17 18 19 0 1 10 9 8 7 6 5 4 3 12 20
6 11 19 13 14 17 18 12 0 15 4 5 10 2 8 7 20 3 9 1 16

Иллюстрация



Смотрите мою статью
ПОСТРОЕНИЕ ДИАГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ

3. 41515295252 Д-трансверсалей
ДЛК построен методом Линдера по программе А. Чернова

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 
2 10 3 1 0 6 9 8 5 7 4 12 15 14 11 13 17 20 19 16 18 
4 2 1 10 3 7 8 6 9 5 0 13 14 12 15 11 18 19 17 20 16 
1 3 0 4 10 9 7 5 6 8 2 15 13 11 12 14 20 18 16 17 19 
3 4 10 0 2 8 5 9 7 6 1 14 11 15 13 12 19 16 20 18 17 
11 12 13 14 15 20 17 19 3 18 16 10 1 4 2 0 5 6 7 8 9 
12 15 14 11 13 19 16 3 17 20 18 1 0 2 10 4 6 9 8 5 7 
13 14 12 15 11 18 19 17 16 3 20 4 2 1 0 10 7 8 6 9 5 
15 13 11 12 14 17 3 20 18 16 19 0 4 10 1 2 9 7 5 6 8 
14 11 15 13 12 3 18 16 20 19 17 2 10 0 4 1 8 5 9 7 6 
10 0 4 2 1 16 20 18 19 17 3 5 9 7 8 6 11 15 13 14 12 
16 17 18 19 20 11 12 13 14 15 5 9 6 8 3 7 10 1 4 2 0 
17 20 19 16 18 12 15 14 11 13 7 8 5 3 6 9 1 0 2 10 4 
18 19 17 20 16 13 14 12 15 11 9 7 8 6 5 3 4 2 1 0 10 
20 18 16 17 19 15 13 11 12 14 8 6 3 9 7 5 0 4 10 1 2 
19 16 20 18 17 14 11 15 13 12 6 3 7 5 9 8 2 10 0 4 1 
5 6 7 8 9 10 1 4 2 0 11 16 17 18 19 20 15 12 14 3 13 
6 9 8 5 7 1 0 2 10 4 13 17 20 19 16 18 14 11 3 12 15 
7 8 6 9 5 4 2 1 0 10 15 18 19 17 20 16 13 14 12 11 3 
9 7 5 6 8 0 4 10 1 2 14 20 18 16 17 19 12 3 15 13 11 
8 5 9 7 6 2 10 0 4 1 12 19 16 20 18 17 3 13 11 15 14

Иллюстрация



Все три ДЛК обсчитаны моим замечательным помощником.
Спасибо ему!

Проверка свойств топовых ДЛК 21-го порядка утилитой Harry White

Order? 21

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_13.txt

Counts
------
         3 diagonal Latin
         1 nfr
         1 natural \diagonal
         1 self-orthogonal

Никаких особых свойств не обнаружено, кроме того, что один ДЛК является SODLS.
Может быть, поэтому текущий максимум у ДЛК 21-го порядка небольшой, даже меньше, чем у ДЛК 20-го порядка.
Ну, новые рекорды ещё впереди :)

Новый кандидат в топовые ДЛК 21-го порядка

Вот, например, центрально-симметричный ДЛК 21-го порядка, построенный программой Harry White

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
19  2  0  6  1  4  3 10  5  8  7 13  9 16 12 11 14 20 15 18 17
20 19  1  0  2  8  4  3  6 12  5  7 10  9 11 17 13 14 16 15 18
17 20 19  4  0  2  1 12  3  6  8  5  7 18 10  9 11 13 14 16 15
18 17 20 19  3  0  2  1  4 14  6 15  5  8  7 10 12  9 11 13 16
16 15 18 20 19  6  0  2  1  4  3 17  8  5  9  7 10 12 13 11 14
15 18 13 17 20 19  5  0  2 16  1  4  3  6  8 12  7 10  9 14 11
14 11 16 15 18 17 20  8  0  2  4 19  1  3  6  5  9  7 10 12 13
12 13 17 16 14 18 19 11  7 15 20  2  0  1  4  3  6  5  8 10  9
11 14 15 18 17 20 13 19 16 10  0  1  2  4  3  6  5  8  7  9 12
13 16 10  7 15 14 17 20 18 19  9  0  4  2  1  8  3 11 12  6  5
10  9 11 14 13 16 15 18 20 17 19 12  6  0  5  2  1  4  3  8  7
 9 12 14 13 16 15 18 17 19 20  2  3 11  7  0  4  8  6  1  5 10
 5 10 12 11  9 13 16 15 17  0 18 20 19 14  2  1  4  3  6  7  8
 7  8  9 12 11 10 14 16 15 18 17  6 20 19 13  0  2  1  5  4  3
 8  7  5 10 12 11  9 13 14  1 15 18 17 20 19 16  0  2  4  3  6
 6  5  7  9 10 12 11 14 13  3 16  8 18 17 20 19 15  0  2  1  4
 3  6  8  5  7  9 12  4 11 13 14 16 15 10 17 20 19 18  0  2  1
 4  3  6  8  5  1  7  9 12 11 13 10 16 15 18 14 20 19 17  0  2
 1  4  3  2  8  7 10  6  9  5 11 14 13 12 15 18 17 16 19 20  0
 2  0  4  1  6  3  8  5 10  7 12  9 14 11 16 13 18 15 20 17 19

Можно попробовать в этом ДЛК посчитать Д-трансверсали. Вдруг будет новый максимум.
Но это будем делать тогда, когда кто-нибудь модифицирует программу подсчёта Д-трансверсалей, сделав подсчёт по частям.
Сейчас очень неудобно: программа работает несколько суток, а в случае нештатной остановки компьютера всё пропадает.

PS. В моей терминологии этот ДЛК ассоциативный.
Ну, чтобы и утилита Harry White признала его ассоциативным, достаточно преобразовать его в СН ДЛК

 0  2  1  4  3  6  5  8  7 10  9 12 11 14 13 16 15 18 17 20 19
20  1  0  5  2  3  4  9  6  7  8 14 10 15 11 12 13 19 16 17 18
19 20  2  0  1  7  3  4  5 11  6  8  9 10 12 18 14 13 15 16 17
18 19 20  3  0  1  2 11  4  5  7  6  8 17  9 10 12 14 13 15 16
17 18 19 20  4  0  1  2  3 13  5 16  6  7  8  9 11 10 12 14 15
15 16 17 19 20  5  0  1  2  3  4 18  7  6 10  8  9 11 14 12 13
16 17 14 18 19 20  6  0  1 15  2  3  4  5  7 11  8  9 10 13 12
13 12 15 16 17 18 19  7  0  1  3 20  2  4  5  6 10  8  9 11 14
11 14 18 15 13 17 20 12  8 16 19  1  0  2  3  4  5  6  7  9 10
12 13 16 17 18 19 14 20 15  9  0  2  1  3  4  5  6  7  8 10 11
14 15  9  8 16 13 18 19 17 20 10  0  3  1  2  7  4 12 11  5  6
 9 10 12 13 14 15 16 17 19 18 20 11  5  0  6  1  2  3  4  7  8
10 11 13 14 15 16 17 18 20 19  1  4 12  8  0  3  7  5  2  6  9
 6  9 11 12 10 14 15 16 18  0 17 19 20 13  1  2  3  4  5  8  7
 8  7 10 11 12  9 13 15 16 17 18  5 19 20 14  0  1  2  6  3  4
 7  8  6  9 11 12 10 14 13  2 16 17 18 19 20 15  0  1  3  4  5
 5  6  8 10  9 11 12 13 14  4 15  7 17 18 19 20 16  0  1  2  3
 4  5  7  6  8 10 11  3 12 14 13 15 16  9 18 19 20 17  0  1  2
 3  4  5  7  6  2  8 10 11 12 14  9 15 16 17 13 19 20 18  0  1
 2  3  4  1  7  8  9  5 10  6 12 13 14 11 16 17 18 15 20 19  0
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18 20

Теперь утилита Harry White согласна с тем, что этот ДЛК ассоциативный

Order? 21

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_16.txt

Counts
------
         1 diagonal Latin
         1 associative
         1 natural \diagonal

Попутно нашла код этого ДЛК по системе Tomas Brada

NFXFpQ6b9LMSAoJ4b4Y9gsiAnmJRJZtFcmjdeEKmcJf5qHrhKjhRBZZksSni1w9jH3GR6Wz1tHVaGjcyarpzTJ1ouo2XwatET2YLuxxbXm3EjJ4Mqu53

Всё готово, чтобы проверить этого кандидата на новый максимум.
Ну, если не побьёт рекорд, всё равно будет в Топ-4.
А квадратик, между прочим, весьма гармонично сложен, вполне может дать новый рекорд.

Топ-2 ДЛК 22-го порядка по Д-трансверсалям
в порядке убывания

1. 3227747329246 Д-трансверсалей
ДЛК построен методом Гергели

 1 13  3  4  5  6  7  8  9 10 11  0 21 20 19 18 17 16 15 14  2 12
 2  3 15  5  6  7  8  9 10 11  1 12  0 21 20 19 18 17 16  4 14 13
 3  4  5 17  7  8  9 10 11  1  2 13 12  0 21 20 19 18  6 16 15 14
 4  5  6  7 19  9 10 11  1  2  3 14 13 12  0 21 20  8 18 17 16 15
 5  6  7  8  9 21 11  1  2  3  4 15 14 13 12  0 10 20 19 18 17 16
 6  7  8  9 10 11 12  2  3  4  5 16 15 14 13  1  0 21 20 19 18 17
 7  8  9 10 11  1  2 14  4  5  6 17 16 15  3 13 12  0 21 20 19 18
 8  9 10 11  1  2  3  4 16  6  7 18 17  5 15 14 13 12  0 21 20 19
 9 10 11  1  2  3  4  5  6 18  8 19  7 17 16 15 14 13 12  0 21 20
10 11  1  2  3  4  5  6  7  8 20  9 19 18 17 16 15 14 13 12  0 21
 0  1  2  3  4  5  6  7  8  9 10 21 20 19 18 17 16 15 14 13 12 11
21  0 12 13 14 15 16 17 18 19  9 20  8  7  6  5  4  3  2  1 11 10
20 21  0 12 13 14 15 16 17  7 19  8 18  6  5  4  3  2  1 11 10  9
19 20 21  0 12 13 14 15  5 17 18  7  6 16  4  3  2  1 11 10  9  8
18 19 20 21  0 12 13  3 15 16 17  6  5  4 14  2  1 11 10  9  8  7
17 18 19 20 21  0  1 13 14 15 16  5  4  3  2 12 11 10  9  8  7  6
16 17 18 19 20 10  0 12 13 14 15  4  3  2  1 11 21  9  8  7  6  5
15 16 17 18  8 20 21  0 12 13 14  3  2  1 11 10  9 19  7  6  5  4
14 15 16  6 18 19 20 21  0 12 13  2  1 11 10  9  8  7 17  5  4  3
13 14  4 16 17 18 19 20 21  0 12  1 11 10  9  8  7  6  5 15  3  2
12  2 14 15 16 17 18 19 20 21  0 11 10  9  8  7  6  5  4  3 13  1
11 12 13 14 15 16 17 18 19 20 21 10  9  8  7  6  5  4  3  2  1  0

Иллюстрация



Смотрите мою статью
ПОСТРОЕНИЕ ДИАГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ
В статье этот ДЛК изображён на рис. 17 в другой раскраске.
ДЛК имеет классическую блочную структуру, что показано на здешней иллюстрации.

2. 295117333631 Д-трансверсалей
ДЛК построен программой Harry White (SODLS)

0 16 14 8 15 6 17 10 9 1 21 2 3 12 11 5 20 19 4 13 7 18
 9 1 15 13 0 14 7 16 10 2 20 3 4 11 6 19 18 5 21 8 17 12
10 9 2 14 21 1 13 8 15 3 19 4 5 7 18 17 6 20 0 16 12 11
14 10 9 3 13 20 2 21 0 4 18 5 6 17 16 7 19 1 15 12 11 8
 1 13 10 9 4 21 19 3 20 5 17 6 7 15 8 18 2 14 12 11 0 16
19 2 21 10 9 5 20 18 4 6 16 7 8 0 17 3 13 12 11 1 15 14
 5 18 3 20 10 9 6 19 17 7 15 8 0 16 4 21 12 11 2 14 13 1
16 6 17 4 19 10 9 7 18 8 14 0 1 5 20 12 11 3 13 21 2 15
17 15 7 16 5 18 10 9 8 0 13 1 2 19 12 11 4 21 20 3 14 6
 3 4 5 6 7 8 0 1 2 9 11 12 10 21 13 14 15 16 17 18 19 20
20 19 18 17 16 15 14 13 21 12 10 9 11 2 1 0 8 7 6 5 4 3
21 20 19 18 17 16 15 14 13 10 12 11 9 1 0 8 7 6 5 4 3 2
 4 5 6 7 8 0 1 2 3 11 9 10 12 14 15 16 17 18 19 20 21 13
18 7 20 21 2 4 11 12 1 19 5 14 17 13 9 10 3 8 16 15 6 0
 6 21 13 1 3 11 12 0 19 20 4 15 18 8 14 9 10 2 7 17 16 5
13 14 0 2 11 12 8 20 5 21 3 16 19 4 7 15 9 10 1 6 18 17
15 8 1 11 12 7 21 4 14 13 2 17 20 18 3 6 16 9 10 0 5 19
 7 0 11 12 6 13 3 15 16 14 1 18 21 20 19 2 5 17 9 10 8 4
 8 11 12 5 14 2 16 17 6 15 0 19 13 3 21 20 1 4 18 9 10 7
11 12 4 15 1 17 18 5 7 16 8 20 14 6 2 13 21 0 3 19 9 10
12 3 16 0 18 19 4 6 11 17 7 21 15 10 5 1 14 13 8 2 20 9
 2 17 8 19 20 3 5 11 12 18 6 13 16 9 10 4 0 15 14 7 1 21

Оба ДЛК обсчитал мой помощник.
Спасибо!
Первый топовый ДЛК считался очень долго, причём не с первого раза посчитался, потому что произошла нештатная остановка компьютера и всё пропало, пришлось начинать сначала.

Ещё два кандидата в топовые ДЛК 22-го порядка у меня имелись, но обсчитывать эти ДЛК мы не стали.
Кандидатов покажу, это ортогональная пара, построенная методом Ли Жу по программе Чернова

0 21 20 19 18 17 15 14 16 8 6 5 4 3 9 2 11 12 10 7 13 1 
4 1 21 20 19 18 0 16 15 9 7 6 5 10 3 12 13 11 8 14 2 17 
11 5 2 21 20 19 18 1 17 10 8 7 6 4 13 14 12 9 15 3 0 16
5 12 6 3 21 20 19 18 2 11 9 8 7 14 15 13 10 16 4 1 17 0 
15 6 13 7 4 21 20 19 18 12 10 9 8 16 14 11 17 5 2 0 1 3 
17 16 7 14 8 5 21 20 19 13 11 10 9 15 12 0 6 3 1 2 4 18 
16 0 17 8 15 9 6 21 20 14 12 11 10 13 1 7 4 2 3 5 18 19 
14 17 1 0 9 16 10 7 21 15 13 12 11 2 8 5 3 4 6 18 19 20 
3 15 0 2 1 10 17 11 8 16 14 13 12 9 6 4 5 7 18 19 20 21 
13 14 15 16 17 0 1 2 3 19 18 21 20 12 11 10 9 8 7 6 5 4 
6 7 8 9 10 11 12 13 14 20 21 18 19 5 4 3 2 1 0 17 16 15 
2 3 4 5 6 7 8 9 10 18 19 20 21 1 0 17 16 15 14 13 12 11 
1 2 3 4 5 6 7 8 9 21 20 19 18 0 17 16 15 14 13 12 11 10 
21 20 19 18 16 14 13 15 0 7 5 4 3 17 2 8 1 10 11 9 6 12 
20 19 18 15 13 12 14 17 11 6 4 3 2 21 16 1 7 0 9 10 8 5 
19 18 14 12 11 13 16 10 4 5 3 2 1 20 21 15 0 6 17 8 9 7 
18 13 11 10 12 15 9 3 6 4 2 1 0 19 20 21 14 17 5 16 7 8 
12 10 9 11 14 8 2 5 7 3 1 0 17 18 19 20 21 13 16 4 15 6 
9 8 10 13 7 1 4 6 5 2 0 17 16 11 18 19 20 21 12 15 3 14 
7 9 12 6 0 3 5 4 13 1 17 16 15 8 10 18 19 20 21 11 14 2 
8 11 5 17 2 4 3 12 1 0 16 15 14 6 7 9 18 19 20 21 10 13 
10 4 16 1 3 2 11 0 12 17 15 14 13 7 5 6 8 18 19 20 21 9

0 17 16 15 14 21 20 19 18 1 8 10 11 6 4 12 5 3 7 13 9 2 
7 1 0 17 16 15 21 20 19 2 9 11 12 5 13 6 4 8 14 10 3 18 
6 8 2 1 0 17 16 21 20 3 10 12 13 14 7 5 9 15 11 4 18 19
15 7 9 3 2 1 0 17 21 4 11 13 14 8 6 10 16 12 5 18 19 20 
9 16 8 10 4 3 2 1 0 5 12 14 15 7 11 17 13 6 18 19 20 21 
8 10 17 9 11 5 4 3 2 6 13 15 16 12 0 14 7 18 19 20 21 1 
13 9 11 0 10 12 6 5 4 7 14 16 17 1 15 8 18 19 20 21 2 3 
2 14 10 12 1 11 13 7 6 8 15 17 0 16 9 18 19 20 21 3 4 5 
17 3 15 11 13 2 12 14 8 9 16 0 1 10 18 19 20 21 4 5 6 7 
3 4 5 6 7 8 9 10 11 20 21 18 19 2 1 0 17 16 15 14 13 12 
4 5 6 7 8 9 10 11 12 18 19 20 21 3 2 1 0 17 16 15 14 13 
1 2 3 4 5 6 7 8 9 19 18 21 20 0 17 16 15 14 13 12 11 10 
5 6 7 8 9 10 11 12 13 21 20 19 18 4 3 2 1 0 17 16 15 14 
16 15 14 13 21 20 19 18 1 0 7 9 10 17 5 3 11 4 2 6 12 8 
14 13 12 21 20 19 18 0 7 17 6 8 9 15 16 4 2 10 3 1 5 11 
12 11 21 20 19 18 17 6 10 16 5 7 8 13 14 15 3 1 9 2 0 4 
10 21 20 19 18 16 5 9 3 15 4 6 7 11 12 13 14 2 0 8 1 17 
21 20 19 18 15 4 8 2 16 14 3 5 6 9 10 11 12 13 1 17 7 0 
20 19 18 14 3 7 1 15 17 13 2 4 5 21 8 9 10 11 12 0 16 6 
19 18 13 2 6 0 14 16 5 12 1 3 4 20 21 7 8 9 10 11 17 15 
18 12 1 5 17 13 15 4 14 11 0 2 3 19 20 21 6 7 8 9 10 16 
11 0 4 16 12 14 3 13 15 10 17 1 2 18 19 20 21 5 6 7 8 9

Никаких свойств в этих ДЛК утилита Harry White не обнаружила.
Так что, новый рекорд они вряд ли дадут.
Ну, будет Топ-4.

Два топовых ДЛК 22-го порядка обладают свойствами

Order? 22

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         2 diagonal Latin
         1 axial symmetric
         1 natural \diagonal
         1 self-orthogonal

При этом понятно, что первому топовому принадлежит свойство axial symmetric, а второму топовому - свойство self-orthogonal.

Я собрала все топовые ДЛК порядков 11 - 22 по Д-трансверсалям в этой теме.
Старалась ничего не пропустить.
Ну, если что и пропустила, в других темах можно будет посмотреть.
Для порядков n>22 пока ДЛК не обсчитывались.
Я уже объясняла причину.
Нужна модификация программы.
Лучше всего это мог бы сделать Tomas Brada.
Может также и Алексей Белышев, но где он? Я его совсем потеряла.
На boinc.ru он давно не пишет.

Господа!
Кто ещё может модифицировать программу?
Здесь программисты бывают?
Программа подсчёта Д-трансверсалей не сильно сложная.
Главное хорошо понять, что такое Д-трансверсаль.
Разделить на части подсчёт Д-трансверсалей тоже несложно.
Но надо именно разделить на отдельные, автономные части, а не распараллеливать на потоки, как это сделал Tomas Brada.

Покажу полученные на данный момент оценки количества Д-трансверсалей в ДЛК порядков 11 - 22

a(11) ≥ 4828
a(12) ≥ 28496
a(13) ≥ 131106
a(14) ≥ 380718
a(15) ≥ 389318
a(16) ≥ 32172800
a(17) ≥ 204995269
a(18) ≥ 280308432
a(19) ≥ 11254190082
a(20) ≥ 90010806304
a(21) ≥ 51162162017
a(22) ≥ 3227747329246

Смотрите последовательность OEIS
Maximum number of diagonal transversals in a diagonal Latin square of order n.

К статье прикреплён а-файл, в котором приведена полная информация о рекордных на данный момент ДЛК по Д-трансверсалям
"DLS of orders n = 11 - 22 with known maximum of D-transversals"
https://oeis.org/A287648/a287648_2.txt

А теперь о кандидатах в топовые ДЛК порядков n>22.

Цитата

Для будущего -
есть идеальный ДЛК 23-го порядка - кандидат №1 на максимум Д-трансверсалей

 0  2  4  6  8 10 12 14 16 18 20 22  1  3  5  7  9 11 13 15 17 19 21
22  1  3  5  7  9 11 13 15 17 19 21  0  2  4  6  8 10 12 14 16 18 20
21  0  2  4  6  8 10 12 14 16 18 20 22  1  3  5  7  9 11 13 15 17 19
20 22  1  3  5  7  9 11 13 15 17 19 21  0  2  4  6  8 10 12 14 16 18
19 21  0  2  4  6  8 10 12 14 16 18 20 22  1  3  5  7  9 11 13 15 17
18 20 22  1  3  5  7  9 11 13 15 17 19 21  0  2  4  6  8 10 12 14 16
17 19 21  0  2  4  6  8 10 12 14 16 18 20 22  1  3  5  7  9 11 13 15
16 18 20 22  1  3  5  7  9 11 13 15 17 19 21  0  2  4  6  8 10 12 14
15 17 19 21  0  2  4  6  8 10 12 14 16 18 20 22  1  3  5  7  9 11 13
14 16 18 20 22  1  3  5  7  9 11 13 15 17 19 21  0  2  4  6  8 10 12
13 15 17 19 21  0  2  4  6  8 10 12 14 16 18 20 22  1  3  5  7  9 11
12 14 16 18 20 22  1  3  5  7  9 11 13 15 17 19 21  0  2  4  6  8 10
11 13 15 17 19 21  0  2  4  6  8 10 12 14 16 18 20 22  1  3  5  7  9
10 12 14 16 18 20 22  1  3  5  7  9 11 13 15 17 19 21  0  2  4  6  8
 9 11 13 15 17 19 21  0  2  4  6  8 10 12 14 16 18 20 22  1  3  5  7
 8 10 12 14 16 18 20 22  1  3  5  7  9 11 13 15 17 19 21  0  2  4  6
 7  9 11 13 15 17 19 21  0  2  4  6  8 10 12 14 16 18 20 22  1  3  5
 6  8 10 12 14 16 18 20 22  1  3  5  7  9 11 13 15 17 19 21  0  2  4
 5  7  9 11 13 15 17 19 21  0  2  4  6  8 10 12 14 16 18 20 22  1  3
 4  6  8 10 12 14 16 18 20 22  1  3  5  7  9 11 13 15 17 19 21  0  2
 3  5  7  9 11 13 15 17 19 21  0  2  4  6  8 10 12 14 16 18 20 22  1
 2  4  6  8 10 12 14 16 18 20 22  1  3  5  7  9 11 13 15 17 19 21  0
 1  3  5  7  9 11 13 15 17 19 21  0  2  4  6  8 10 12 14 16 18 20 22 

Смотрите сообщение
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=126&postid=1496
Этот ДЛК ассоциативный и циклический пандиагональный, то есть идеальный.
Думаю, что у него будет немало Д-трансверсалей.
Считать это на одном компьютере очень долго, даже с многоядерным процессором (как у моего помощника).
Здесь надо подключать распределённые вычисления.

PS. В полной системе MOLS 23-го порядка не единственный ДЛК идеальный, а все 20.
Вот посмотрите проверку утилитой Harry White

Order? 23

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_10.txt

Counts
------
        20 diagonal Latin
        20 associative
        20 pandiagonal
        20 ultramagic
        20 natural \diagonal
        19 orthogonal pair
        20 self-orthogonal

Но, конечно, среди этих 20 идеальных ДЛК есть изоморфные.
Сколько уникальных, я не знаю, канонизотора ДЛК 23-го порядка у нас пока нет.
_______________________
конец цитаты

И ещё один кандидат - ДЛК 23-го порядка, построенный методом Гергели



Можно найти кандидатов следующих порядков, это не проблема.
Но пока нет нужной программы, подсчёт Д-трансверсалей отложен.

Нашла идеальный ДЛК 17-го порядка нового типа (является полуциклическим пандиагональным)

 0  6 12 11  7  1 13  8  3 15  9  5  4 10 16  2 14
 7  1 13  8  3 15  9  5  4 10 16  2 14  0  6 12 11
10 16  2 14  0  6 12 11  7  1 13  8  3 15  9  5  4
 1 13  8  3 15  9  5  4 10 16  2 14  0  6 12 11  7
 3 15  9  5  4 10 16  2 14  0  6 12 11  7  1 13  8
13  8  3 15  9  5  4 10 16  2 14  0  6 12 11  7  1
 4 10 16  2 14  0  6 12 11  7  1 13  8  3 15  9  5
16  2 14  0  6 12 11  7  1 13  8  3 15  9  5  4 10
14  0  6 12 11  7  1 13  8  3 15  9  5  4 10 16  2
 6 12 11  7  1 13  8  3 15  9  5  4 10 16  2 14  0
11  7  1 13  8  3 15  9  5  4 10 16  2 14  0  6 12
15  9  5  4 10 16  2 14  0  6 12 11  7  1 13  8  3
 8  3 15  9  5  4 10 16  2 14  0  6 12 11  7  1 13
 9  5  4 10 16  2 14  0  6 12 11  7  1 13  8  3 15
12 11  7  1 13  8  3 15  9  5  4 10 16  2 14  0  6
 5  4 10 16  2 14  0  6 12 11  7  1 13  8  3 15  9
 2 14  0  6 12 11  7  1 13  8  3 15  9  5  4 10 16

Годится в топовые ДЛК 17-го порядка по Д-трансверсалям

num_dtrans: 204771973

Смотрите сообщение
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=132&postid=1805

При составлении списка топовых ДЛК 14-го порядка по Д-трансверсалям забыла о ДЛК, построенном методом Гергели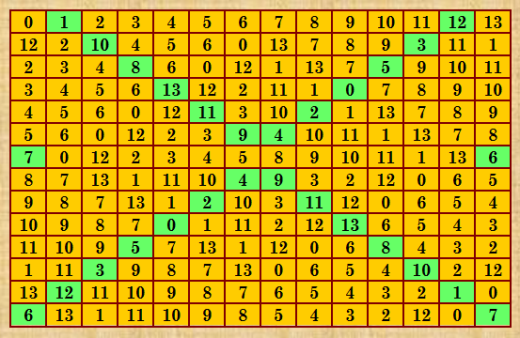



Смотрите статью "ПОСТРОЕНИЕ ДИАГОНАЛЬНЫХ ЛАТИНСКИХ КВДАРАТОВ".
В статье ДЛК изображён на рис. 16.
Здесь ДЛК показан в нормализованном виде.

Этот ДЛК вполне достоин войти в список топовых, он содержит 364252 Д-трансверсалей.
Это самый первый ДЛК 14-го порядка, который я начинала проверять на ОДЛК.
Проверку выполняла программой Белышева ortogon_u.
Покрутила немножко, нашла 290 ОДЛК, затем прервала программу, потому что полностью проверить этот ДЛК на одном ПК нереально.

Сейчас вспомнила об этом ДЛК в связи с задачей о ядре БД КФ ОДЛК 14-го порядка.
Решила ещё немного пощупать этот ДЛК на ОДЛК, теперь программой Tomas Brada; начинаю со второй части

C:\Users\Дом\Downloads\Tomas>ortogonbw FZ6P2fxvxqsd3GrUPmTuqQRE6BCU383vKyutP7TR7
G8whx 2  1>output.txt
init_trans(14) used 661 nodes
num_dtrans: 364252
init_disjoint(14) used 197 heads and 5099725 nodes
L(0) c(7) 2 / 25632
L(1) c(114) X / 10460

Над задачей о ядре БД КФ ОДЛК 14-го порядка постоянно думаю
[задача у меня в стеке записана в моей мозговой ЭВМ :)].
Нам осталось найти КФ ОДЛК всего из двух линеек из известных 5225 линеек.

Добавление к топовым ДЛК 19-го порядка по Д-трансверсалям - идеальный ДЛК, который яаляется полуциклическим с цикличностью в диагоналях параллельных главной диагонали

 0 16 18 10 17 15 14  8 13  7 12  6 11  5  4  2  9  1  3
 4  1 17  0 11 18 16 15  9 14  8 13  7 12  6  5  3 10  2
 3  5  2 18  1 12  0 17 16 10 15  9 14  8 13  7  6  4 11
12  4  6  3  0  2 13  1 18 17 11 16 10 15  9 14  8  7  5
 6 13  5  7  4  1  3 14  2  0 18 12 17 11 16 10 15  9  8
 9  7 14  6  8  5  2  4 15  3  1  0 13 18 12 17 11 16 10
11 10  8 15  7  9  6  3  5 16  4  2  1 14  0 13 18 12 17
18 12 11  9 16  8 10  7  4  6 17  5  3  2 15  1 14  0 13
14  0 13 12 10 17  9 11  8  5  7 18  6  4  3 16  2 15  1
 2 15  1 14 13 11 18 10 12  9  6  8  0  7  5  4 17  3 16
17  3 16  2 15 14 12  0 11 13 10  7  9  1  8  6  5 18  4
 5 18  4 17  3 16 15 13  1 12 14 11  8 10  2  9  7  6  0
 1  6  0  5 18  4 17 16 14  2 13 15 12  9 11  3 10  8  7
 8  2  7  1  6  0  5 18 17 15  3 14 16 13 10 12  4 11  9
10  9  3  8  2  7  1  6  0 18 16  4 15 17 14 11 13  5 12
13 11 10  4  9  3  8  2  7  1  0 17  5 16 18 15 12 14  6
 7 14 12 11  5 10  4  9  3  8  2  1 18  6 17  0 16 13 15
16  8 15 13 12  6 11  5 10  4  9  3  2  0  7 18  1 17 14
15 17  9 16 14 13  7 12  6 11  5 10  4  3  1  8  0  2 18

В этом ДЛК имеется 599698429 Д-трансверсалей.
Оказался всего лишь на последнем месте в топовых ДЛК данного порядка, после ДЛК Гергели.

Спасибо помощнику за подсчёт Д-трансверсалей в этом ДЛК.