Thread 'Semi-cyclic pandiagonal DLS of prime order n>11'
Message boards : Science : Semi-cyclic pandiagonal DLS of prime order n>11
Message board moderation
Previous · 1 · 2 · 3 · 4 · 5 · 6 · 7 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Показываю первые решениÑ, полученные в Ñтом ÑкÑперименте 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 . . . . . . . . Первое решение - иÑходный ДЛК. Так вот, Ñто первый путь Ñ€ÐµÑˆÐµÐ½Ð¸Ñ Ð¿Ñ€Ð¾Ð±Ð»ÐµÐ¼Ñ‹. Он очень долгий, за 12 минут Ð¿Ð¾Ð»Ð½Ð°Ñ Ð¿ÐµÑ€ÐµÑтановка Ñтрок в ДЛК 17-го порÑдка (оÑтавлÑÑ Ð½Ð° меÑте первую Ñтроку) не делаетÑÑ. Или Ñ Ð½Ðµ знаю, как Ñто можно Ñделать за 12 минут. По возможноÑти помощник попытаетÑÑ Ð¿Ð¾Ð²Ñ‚Ð¾Ñ€Ð¸Ñ‚ÑŒ ÑкÑперимент по моей Ñхеме. ЕÑли Ñ Ð½Ðµ ошиблаÑÑŒ Ñ Ñ€Ð°Ñпараллеливанием процеÑÑа, вÑе 8262 полуцикличеÑких пандиагональных ДЛК должны получитьÑÑ. Кто знает другой путь Ñ€ÐµÑˆÐµÐ½Ð¸Ñ Ð¿Ñ€Ð¾Ð±Ð»ÐµÐ¼Ñ‹ (чтобы быÑтрее)? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Когда будут найдены вÑе 8262 нормализованных полуцикличеÑких пандиагональных ДЛК 17-го порÑдка Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках, дальше у Ð¼ÐµÐ½Ñ Ñ€Ð°Ð±Ð¾Ñ‚Ð°ÐµÑ‚ Ñхема Ð¿Ð¾Ð»ÑƒÑ‡ÐµÐ½Ð¸Ñ Ð¸Ð· Ñтих ДЛК пандиагональных полуцикличеÑких ДЛК Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью 1) в Ñтолбцах; 2) в диагоналÑÑ… параллельных главной диагонали; 3) в диагоналÑÑ… параллельных побочной диагонали. Итого будет 8262*4=33048 нормализованных полуцикличеÑких пандиагональных ДЛК 17-го порÑдка. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’Ñпомнила о переноÑе на торе. Применила преобразование к найденным 6779 полуцикличеÑким пандиагональным ДЛК 17-го порÑдка. И у-Ñ€-Ñ€-Ñ€-Ñ€-а-а-а!! Ð’Ñе 8262 нормализованных пандиагональных полуцикличеÑких ДЛК Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках найдены! Order? 17
Enter the name of the squares file: per
.. writing type information to file perTypeDetail_1.txt
Counts
------
8268 diagonal Latin
8268 pandiagonal
6 cyclic 4-way
8262 semi-cyclic
172 center symmetric
8268 nfr
1 orthogonal pair
6 self-orthogonalВот они - 8262 semi-cyclic!!! Тут затеÑалиÑÑŒ 6 цикличеÑких пандиагональных ДЛК, ÑÐµÐ¹Ñ‡Ð°Ñ Ð²Ñ‹Ð±Ñ€Ð¾ÑˆÑƒ их и оÑтанутÑÑ 8262 нормализованных пандиагональных полуцикличеÑких ДЛК Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках. Ðе надо вÑÑ‘ Ñчитать заново. Очень помогло преобразование переноÑа на торе. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Готово! ВыброÑила 6 цикличеÑких пандиагональных ДЛК. Ðто оÑталоÑÑŒ Order? 17
Enter the name of the squares file: per
.. writing type information to file perTypeDetail.txt
Counts
------
8262 diagonal Latin
8262 pandiagonal
8262 semi-cyclic
166 center symmetric
8262 nfr
1 orthogonal pair |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПроверÑÑŽ другой программой Harry White (GetCyclic) Order? 17 Enter the name of the squares file: inp Count only? y Get cyclic for, (1 rows, 2 columns, 3 \diagonals, 4 /diagonals)? 1 Get squares with cyclic: rows Exact match? y Number of squares: 8262 number matched 8262 Ð’ÑÑ‘ замечательно! 8262 полуцикличеÑких пандиагональных ДЛК 17-го порÑдка Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках найдены! Теперь можно найти ещё 3 набора по 8262 полуцикличеÑких пандиагональных ДЛК 17-го порÑдка. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ТÑк-Ñ, поворот ДЛК Ñделала. Ð’ результате получено 8262 нормализованных полуцикличеÑких пандиагональных ДЛК 17-го порÑдка Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтолбцах. Показываю неÑколько первых ДЛК из Ñтого набора 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 10 11 0 15 2 13 14 16 12 7 1 9 4 8 5 6 3 1 9 10 6 0 8 5 3 4 16 11 7 2 12 13 14 15 11 7 1 14 10 12 13 15 2 3 9 16 0 4 8 5 6 9 16 11 5 1 4 8 6 0 15 7 3 10 2 12 13 14 7 3 9 13 11 2 12 14 10 6 16 15 1 0 4 8 5 16 15 7 8 9 0 4 5 1 14 3 6 11 10 2 12 13 3 6 16 12 7 10 2 13 11 5 15 14 9 1 0 4 8 15 14 3 4 16 1 0 8 9 13 6 5 7 11 10 2 12 6 5 15 2 3 11 10 12 7 8 14 13 16 9 1 0 4 14 13 6 0 15 9 1 4 16 12 5 8 3 7 11 10 2 5 8 14 10 6 7 11 2 3 4 13 12 15 16 9 1 0 13 12 5 1 14 16 9 0 15 2 8 4 6 3 7 11 10 8 4 13 11 5 3 7 10 6 0 12 2 14 15 16 9 1 12 2 8 9 13 15 16 1 14 10 4 0 5 6 3 7 11 4 0 12 7 8 6 3 11 5 1 2 10 13 14 15 16 9 2 10 4 16 12 14 15 9 13 11 0 1 8 5 6 3 7 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 12 11 1 14 15 10 3 13 0 16 6 9 7 8 4 5 11 9 6 12 8 4 16 1 7 2 5 10 0 3 13 14 15 6 0 10 9 13 14 5 12 3 11 15 16 2 1 7 8 4 10 2 16 0 7 8 15 9 1 6 4 5 11 12 3 13 14 16 11 5 2 3 13 4 0 12 10 14 15 6 9 1 7 8 5 6 15 11 1 7 14 2 9 16 8 4 10 0 12 3 13 15 10 4 6 12 3 8 11 0 5 13 14 16 2 9 1 7 4 16 14 10 9 1 13 6 2 15 7 8 5 11 0 12 3 14 5 8 16 0 12 7 10 11 4 3 13 15 6 2 9 1 8 15 13 5 2 9 3 16 6 14 1 7 4 10 11 0 12 13 4 7 15 11 0 1 5 10 8 12 3 14 16 6 2 9 7 14 3 4 6 2 12 15 16 13 9 1 8 5 10 11 0 3 8 1 14 10 11 9 4 5 7 0 12 13 15 16 6 2 1 13 12 8 16 6 0 14 15 3 2 9 7 4 5 10 11 12 7 9 13 5 10 2 8 4 1 11 0 3 14 15 16 6 9 3 0 7 15 16 11 13 14 12 6 2 1 8 4 5 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 11 10 6 0 15 16 1 13 14 5 12 9 3 2 7 8 4 9 12 1 11 8 4 10 2 7 16 3 5 0 6 13 14 15 5 3 10 9 14 15 12 6 13 4 0 16 11 1 2 7 8 16 0 12 5 7 8 3 1 2 15 11 4 9 10 6 13 14 4 11 3 16 13 14 0 10 6 8 9 15 5 12 1 2 7 15 9 0 4 2 7 11 12 1 14 5 8 16 3 10 6 13 8 5 11 15 6 13 9 3 10 7 16 14 4 0 12 1 2 14 16 9 8 1 2 5 0 12 13 4 7 15 11 3 10 6 7 4 5 14 10 6 16 11 3 2 15 13 8 9 0 12 1 13 15 16 7 12 1 4 9 0 6 8 2 14 5 11 3 10 2 8 4 13 3 10 15 5 11 1 14 6 7 16 9 0 12 6 14 15 2 0 12 8 16 9 10 7 1 13 4 5 11 3 1 7 8 6 11 3 14 4 5 12 13 10 2 15 16 9 0 10 13 14 1 9 0 7 15 16 3 2 12 6 8 4 5 11 12 2 7 10 5 11 13 8 4 0 6 3 1 14 15 16 9 3 6 13 12 16 9 2 14 15 11 1 0 10 7 8 4 5 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 12 9 0 13 15 11 10 14 5 6 16 2 1 8 3 7 4 1 6 12 8 7 2 16 3 11 10 4 0 9 5 13 14 15 9 10 1 5 14 0 4 13 2 16 15 12 6 11 8 3 7 6 16 9 11 3 12 15 8 0 4 7 1 10 2 5 13 14 10 4 6 2 13 1 7 5 12 15 14 9 16 0 11 8 3 16 15 10 0 8 9 14 11 1 7 3 6 4 12 2 5 13 4 7 16 12 5 6 3 2 9 14 13 10 15 1 0 11 8 15 14 4 1 11 10 13 0 6 3 8 16 7 9 12 2 5 7 3 15 9 2 16 8 12 10 13 5 4 14 6 1 0 11 14 13 7 6 0 4 5 1 16 8 11 15 3 10 9 12 2 3 8 14 10 12 15 11 9 4 5 2 7 13 16 6 1 0 13 5 3 16 1 7 2 6 15 11 0 14 8 4 10 9 12 8 11 13 4 9 14 0 10 7 2 12 3 5 15 16 6 1 5 2 8 15 6 3 12 16 14 0 1 13 11 7 4 10 9 11 0 5 7 10 13 1 4 3 12 9 8 2 14 15 16 6 2 12 11 14 16 8 9 15 13 1 6 5 0 3 7 4 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 12 7 6 11 16 14 3 4 13 15 1 0 10 2 8 5 9 10 4 3 0 9 8 11 16 2 5 7 12 1 6 13 14 15 1 16 11 12 15 13 0 9 6 14 4 10 7 3 2 8 5 7 9 0 10 5 2 12 15 3 8 16 1 4 11 6 13 14 4 15 12 1 14 6 10 5 11 13 9 7 16 0 3 2 8 16 5 10 7 8 3 1 14 0 2 15 4 9 12 11 6 13 9 14 1 4 13 11 7 8 12 6 5 16 15 10 0 3 2 15 8 7 16 2 0 4 13 10 3 14 9 5 1 12 11 6 5 13 4 9 6 12 16 2 1 11 8 15 14 7 10 0 3 14 2 16 15 3 10 9 6 7 0 13 5 8 4 1 12 11 8 6 9 5 11 1 15 3 4 12 2 14 13 16 7 10 0 13 3 15 14 0 7 5 11 16 10 6 8 2 9 4 1 12 2 11 5 8 12 4 14 0 9 1 3 13 6 15 16 7 10 6 0 14 13 10 16 8 12 15 7 11 2 3 5 9 4 1 3 12 8 2 1 9 13 10 5 4 0 6 11 14 15 16 7 11 10 13 6 7 15 2 1 14 16 12 3 0 8 5 9 4 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 4 11 12 1 16 3 14 15 0 13 8 2 10 5 9 6 7 16 2 10 11 7 1 9 6 4 5 0 12 8 3 13 14 15 7 12 8 2 15 11 13 14 16 3 4 10 0 1 5 9 6 15 10 0 12 6 2 5 9 7 1 16 8 4 11 3 13 14 6 8 4 10 14 12 3 13 15 11 7 0 16 2 1 5 9 14 0 16 8 9 10 1 5 6 2 15 4 7 12 11 3 13 9 4 7 0 13 8 11 3 14 12 6 16 15 10 2 1 5 13 16 15 4 5 0 2 1 9 10 14 7 6 8 12 11 3 5 7 6 16 3 4 12 11 13 8 9 15 14 0 10 2 1 3 15 14 7 1 16 10 2 5 0 13 6 9 4 8 12 11 1 6 9 15 11 7 8 12 3 4 5 14 13 16 0 10 2 11 14 13 6 2 15 0 10 1 16 3 9 5 7 4 8 12 2 9 5 14 12 6 4 8 11 7 1 13 3 15 16 0 10 12 13 3 9 10 14 16 0 2 15 11 5 1 6 7 4 8 10 5 1 13 8 9 7 4 12 6 2 3 11 14 15 16 0 8 3 11 5 0 13 15 16 10 14 12 1 2 9 6 7 4 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 7 12 4 16 1 14 13 3 15 11 6 0 9 2 10 5 8 3 9 1 8 12 10 2 16 5 0 13 7 11 4 6 14 15 16 11 12 15 9 6 4 8 14 7 2 3 0 1 13 10 5 8 0 9 5 11 13 1 15 10 3 4 16 7 12 2 6 14 15 7 11 14 0 2 12 5 6 16 1 8 3 9 4 13 10 5 3 0 10 7 4 9 14 13 8 12 15 16 11 1 2 6 14 16 7 6 3 1 11 10 2 15 9 5 8 0 12 4 13 10 8 3 13 16 12 0 6 4 5 11 14 15 7 9 1 2 6 15 16 2 8 9 7 13 1 14 0 10 5 3 11 12 4 13 5 8 4 15 11 3 2 12 10 7 6 14 16 0 9 1 2 14 15 1 5 0 16 4 9 6 3 13 10 8 7 11 12 4 10 5 12 14 7 8 1 11 13 16 2 6 15 3 0 9 1 6 14 9 10 3 15 12 0 2 8 4 13 5 16 7 11 12 13 10 11 6 16 5 9 7 4 15 1 2 14 8 3 0 9 2 6 0 13 8 14 11 3 1 5 12 4 10 15 16 7 11 4 13 7 2 15 10 0 16 12 14 9 1 6 5 8 3 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 12 11 0 1 15 14 13 16 2 7 6 8 9 3 10 5 4 9 8 12 11 5 10 3 4 0 16 13 2 7 1 6 14 15 7 2 9 8 14 6 1 15 12 4 3 0 16 11 13 10 5 16 0 7 2 10 13 11 5 9 15 1 12 4 8 3 6 14 4 12 16 0 6 3 8 14 7 5 11 9 15 2 1 13 10 15 9 4 12 13 1 2 10 16 14 8 7 5 0 11 3 6 5 7 15 9 3 11 0 6 4 10 2 16 14 12 8 1 13 14 16 5 7 1 8 12 13 15 6 0 4 10 9 2 11 3 10 4 14 16 11 2 9 3 5 13 12 15 6 7 0 8 1 6 15 10 4 8 0 7 1 14 3 9 5 13 16 12 2 11 13 5 6 15 2 12 16 11 10 1 7 14 3 4 9 0 8 3 14 13 5 0 9 4 8 6 11 16 10 1 15 7 12 2 1 10 3 14 12 7 15 2 13 8 4 6 11 5 16 9 0 11 6 1 10 9 16 5 0 3 2 15 13 8 14 4 7 12 8 13 11 6 7 4 14 12 1 0 5 3 2 10 15 16 9 2 3 8 13 16 15 10 9 11 12 14 1 0 6 5 4 7 ПроверÑÑŽ программой GetCyclic Ñтот набор ДЛК Order? 17 Enter the name of the squares file: input Count only? y Get cyclic for, (1 rows, 2 columns, 3 \diagonals, 4 /diagonals)? 2 Get squares with cyclic: columns Exact match? y Number of squares: 8262 number matched 8262 Ð’ÑÑ‘ верно. Теперь буду применÑÑ‚ÑŒ Ñвоё преобразование "Ñтроки-диагонали", Ñначала Ð´Ð»Ñ Ð¿ÐµÑ€Ð²Ð¾Ð³Ð¾ набора (Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках), а потом Ð´Ð»Ñ Ð²Ñ‚Ð¾Ñ€Ð¾Ð³Ð¾ набора (Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтолбцах). |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
К порции из 8262 пандиагональных полуцикличеÑких ДЛК 17-го порÑдка Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках применила преобразование "Ñтроки-диагонали". Ð’ результате получено 8262 пандиагональных полуцикличеÑких ДЛК 17-го порÑдка Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в диагоналÑÑ… параллельных главной диагонали. Показываю неÑколько ДЛК из Ñтого набора 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 3 15 0 6 7 1 16 10 14 5 8 4 9 2 11 12 13 11 7 13 15 10 14 0 3 4 12 16 5 1 8 6 9 2 6 9 14 11 13 4 12 15 7 1 2 3 16 0 5 10 8 5 10 8 12 9 11 1 2 13 14 0 6 7 3 15 16 4 1 16 4 5 2 8 9 0 6 11 12 15 10 14 7 13 3 7 0 3 1 16 6 5 8 15 10 9 2 13 4 12 14 11 9 14 15 7 0 3 10 16 5 13 4 8 6 11 1 2 12 2 8 12 13 14 15 7 4 3 16 11 1 5 10 9 0 6 10 6 5 2 11 12 13 14 1 7 3 9 0 16 4 8 15 13 4 10 16 6 9 2 11 12 0 14 7 8 15 3 1 5 16 11 1 4 3 10 8 6 9 2 15 12 14 5 13 7 0 15 3 9 0 1 7 4 5 10 8 6 13 2 12 16 11 14 12 13 7 8 15 0 14 1 16 4 5 10 11 6 2 3 9 8 2 11 14 5 13 15 12 0 3 1 16 4 9 10 6 7 14 5 6 9 12 16 11 13 2 15 7 0 3 1 8 4 10 4 12 16 10 8 2 3 9 11 6 13 14 15 7 0 5 1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 6 15 16 1 14 8 4 0 5 2 12 7 3 10 11 9 13 11 0 13 6 16 9 2 8 15 4 1 10 5 14 7 3 12 10 3 15 11 0 6 12 1 2 13 8 16 7 4 9 5 14 9 7 14 13 3 15 0 10 16 1 11 2 6 5 8 12 4 8 12 5 9 11 14 13 15 7 6 16 3 1 0 4 2 10 7 2 10 4 12 3 9 11 13 5 0 6 14 16 15 8 1 16 5 1 7 8 10 14 12 3 11 4 15 0 9 6 13 2 1 6 4 16 5 2 7 9 10 14 3 8 13 15 12 0 11 3 16 0 8 6 4 1 5 12 7 9 14 2 11 13 10 15 13 14 6 15 2 0 8 16 4 10 5 12 9 1 3 11 7 5 11 9 0 13 1 15 2 6 8 7 4 10 12 16 14 3 14 4 3 12 15 11 16 13 1 0 2 5 8 7 10 6 9 12 9 8 14 10 13 3 6 11 16 15 1 4 2 5 7 0 15 10 12 2 9 7 11 14 0 3 6 13 16 8 1 4 5 4 13 7 10 1 12 5 3 9 15 14 0 11 6 2 16 8 2 8 11 5 7 16 10 4 14 12 13 9 15 3 0 1 6 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 15 16 14 7 1 12 4 6 0 3 9 5 10 11 8 13 11 14 13 2 8 6 16 10 1 4 15 7 3 12 9 5 0 15 5 8 11 14 0 4 2 9 16 1 13 6 7 10 3 12 10 13 12 0 5 8 15 1 14 3 2 16 11 4 6 9 7 6 9 11 10 15 12 0 13 16 8 7 14 2 5 1 4 3 7 4 3 5 9 13 10 15 11 2 0 6 8 14 12 16 1 16 6 1 7 12 3 11 9 13 5 14 15 4 0 8 10 2 14 2 4 16 6 10 7 5 3 11 12 8 13 1 15 0 9 3 8 14 1 2 4 9 6 12 7 5 10 0 11 16 13 15 13 7 0 8 16 14 1 3 4 10 6 12 9 15 5 2 11 5 11 6 15 0 2 8 16 7 1 9 4 10 3 13 12 14 8 12 5 4 13 15 14 0 2 6 16 3 1 9 7 11 10 9 0 10 12 1 11 13 8 15 14 4 2 7 16 3 6 5 12 3 15 9 10 16 5 11 0 13 8 1 14 6 2 7 4 1 10 7 13 3 9 2 12 5 15 11 0 16 8 4 14 6 4 16 9 6 11 7 3 14 10 12 13 5 15 2 0 1 8 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 15 0 6 9 1 16 12 14 5 8 3 7 4 11 10 13 11 6 13 15 12 8 0 2 4 10 16 5 9 14 1 7 3 9 7 12 11 13 4 5 15 6 1 3 2 16 8 10 0 14 10 8 14 4 7 11 1 16 13 12 0 9 6 2 5 3 15 13 3 5 10 1 14 7 0 2 11 4 15 8 12 6 16 9 8 11 9 16 3 0 10 14 15 6 7 1 13 5 4 12 2 6 5 7 8 2 9 15 3 10 13 12 14 0 11 16 1 4 1 12 16 14 5 6 8 13 9 3 11 4 10 15 7 2 0 15 0 4 2 10 16 12 5 11 8 9 7 1 3 13 14 6 12 13 15 1 6 3 2 4 16 7 5 8 14 0 9 11 10 3 4 11 13 0 12 9 6 1 2 14 16 5 10 15 8 7 14 9 1 7 11 15 4 8 12 0 6 10 2 16 3 13 5 16 10 8 0 14 7 13 1 5 4 15 12 3 6 2 9 11 7 2 3 5 15 10 14 11 0 16 1 13 4 9 12 6 8 5 14 6 9 16 13 3 10 7 15 2 0 11 1 8 4 12 4 16 10 12 8 2 11 9 3 14 13 6 15 7 0 5 1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 5 15 14 8 2 0 9 3 16 1 12 7 10 6 11 4 13 11 9 13 4 1 8 15 12 2 5 14 6 16 7 3 10 0 15 10 12 11 0 14 1 13 6 8 9 4 3 5 16 2 7 16 13 7 6 10 15 4 14 11 3 1 12 0 2 9 5 8 1 5 11 16 3 7 13 0 4 10 2 14 6 15 8 12 9 12 14 9 10 5 2 16 11 15 0 7 8 4 3 13 1 6 3 6 4 12 7 9 8 5 10 13 15 16 1 0 2 11 14 4 2 3 0 6 16 12 1 9 7 11 13 5 14 15 8 10 7 0 8 2 15 3 5 6 14 12 16 10 11 9 4 13 1 14 16 15 1 8 13 2 9 3 4 6 5 7 10 12 0 11 10 4 5 13 14 1 11 8 12 2 0 3 9 16 7 6 15 13 7 0 9 11 4 14 10 1 6 8 15 2 12 5 16 3 2 11 16 15 12 10 0 4 7 14 3 1 13 8 6 9 5 9 8 10 5 13 6 7 15 0 16 4 2 14 11 1 3 12 6 12 1 7 9 11 3 16 13 15 5 0 8 4 10 14 2 8 3 6 14 16 12 10 2 5 11 13 9 15 1 0 7 4 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 14 15 5 0 2 8 9 3 1 12 16 7 10 6 11 4 13 11 4 13 9 15 0 12 16 2 5 6 14 1 7 3 10 8 12 10 8 11 16 13 15 6 14 0 9 3 4 5 1 2 7 1 6 7 12 10 14 11 13 3 4 15 16 2 8 9 5 0 15 5 3 1 6 7 4 10 11 2 8 13 14 0 12 16 9 16 13 9 2 5 3 1 8 7 10 0 12 11 4 15 6 14 4 14 11 16 0 9 2 5 12 1 7 15 6 10 8 13 3 2 8 4 10 14 15 16 0 9 6 5 1 13 3 7 12 11 10 0 12 8 7 4 13 14 15 16 3 9 5 11 2 1 6 3 7 15 6 12 1 8 11 4 13 14 2 16 9 10 0 5 9 2 1 13 3 6 5 12 10 8 11 4 0 14 16 7 15 13 16 0 5 11 2 3 9 6 7 12 10 8 15 4 14 1 5 11 14 15 9 10 0 2 16 3 1 6 7 12 13 8 4 8 9 10 4 13 16 7 15 0 14 2 5 3 1 6 11 12 6 12 16 7 8 11 14 1 13 15 4 0 9 2 5 3 10 7 3 6 14 1 12 10 4 5 11 13 8 15 16 0 9 2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 9 15 6 5 16 14 0 4 12 11 7 2 3 1 8 10 13 8 7 13 4 0 9 10 15 14 1 3 12 5 16 6 11 2 5 11 12 8 14 15 7 2 13 10 6 16 1 0 9 4 3 16 0 3 1 11 10 13 12 5 8 2 4 9 6 15 7 14 10 9 15 16 6 3 2 8 1 0 11 5 14 7 4 13 12 1 2 7 13 9 4 16 5 11 6 15 3 0 10 12 14 8 11 6 5 12 8 7 14 9 0 3 4 13 16 15 2 1 10 2 3 4 0 1 11 12 10 7 15 16 14 8 9 13 5 6 4 5 16 14 15 6 3 1 2 12 13 9 10 11 7 8 0 15 14 0 9 10 13 4 16 6 5 1 8 7 2 3 12 11 3 13 10 15 7 2 8 14 9 4 0 6 11 12 5 16 1 6 16 8 2 13 12 5 11 10 7 14 15 4 3 1 0 9 7 4 9 11 5 8 1 0 3 2 12 10 13 14 16 6 15 13 12 14 7 3 0 11 6 15 16 5 1 2 8 10 9 4 14 8 1 10 12 16 15 3 4 13 9 0 6 5 11 2 7 12 10 11 6 2 1 9 13 16 14 8 7 15 4 0 3 5 ПрекраÑно алгоритм работает. ОÑталоÑÑŒ преобразовать ещё одну порцию - Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтолбцах. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Готово! Получено 8262 пандиагональных полуцикличеÑких ДЛК 17-го порÑдка Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в диагоналÑÑ… параллельных побочной диагонали. Показываю неÑколько ДЛК из Ñтого набора 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 11 7 5 14 13 16 12 1 0 15 4 6 8 9 3 10 2 12 13 9 8 10 6 11 2 3 14 16 1 0 5 15 7 4 8 0 1 15 16 4 7 5 9 10 11 2 13 3 12 14 6 2 11 3 10 14 12 13 0 15 4 7 8 5 6 9 16 1 4 5 15 9 6 8 2 3 14 12 1 13 16 0 10 11 7 13 3 0 16 1 7 5 9 6 11 8 10 2 15 4 12 14 5 2 10 11 12 13 0 16 4 1 15 7 3 14 6 9 8 7 15 4 6 8 2 10 14 11 3 12 5 9 16 0 1 13 3 14 16 1 7 15 9 4 5 6 13 0 10 2 11 8 12 9 10 11 12 3 0 14 13 16 8 2 15 7 4 1 6 5 15 4 6 5 2 9 8 10 1 7 3 12 14 11 16 13 0 14 16 13 7 0 1 15 11 12 5 6 9 4 10 8 2 3 10 8 12 2 11 3 4 6 13 16 0 14 15 1 7 5 9 1 6 7 4 5 14 16 8 10 2 9 3 11 12 13 0 15 16 12 14 13 9 10 1 15 7 0 5 4 6 8 2 3 11 6 9 8 0 15 11 3 12 2 13 14 16 1 7 5 4 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 5 12 11 0 13 3 8 14 4 16 2 9 6 15 1 7 10 9 2 10 6 11 14 15 0 7 12 4 3 1 5 8 16 13 12 16 3 2 15 1 10 8 9 0 11 5 13 14 7 6 4 7 11 12 1 5 16 14 4 10 2 13 6 15 8 3 0 9 2 9 5 13 7 15 0 16 12 6 3 1 14 11 10 4 8 4 13 6 8 1 10 7 9 3 11 5 15 2 16 0 14 12 6 3 14 5 16 8 4 11 2 13 1 12 7 10 15 9 0 11 15 13 7 14 0 2 12 6 5 9 8 16 1 4 10 3 1 6 8 15 10 12 9 3 13 4 14 7 5 0 16 11 2 3 14 1 16 9 4 11 6 0 15 8 13 10 7 2 12 5 15 5 7 4 0 2 3 10 1 14 6 16 8 12 9 13 11 13 8 0 10 12 11 16 5 15 3 7 14 9 4 6 2 1 14 10 16 9 2 7 13 1 11 8 15 4 0 3 12 5 6 16 7 4 12 8 6 5 2 14 1 0 10 11 9 13 3 15 8 0 9 14 3 13 12 15 5 10 16 2 4 6 11 1 7 10 4 15 11 6 9 1 13 16 7 12 0 3 2 5 8 14 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 11 6 15 1 13 9 3 14 10 16 2 5 4 7 12 0 8 9 12 11 4 10 15 7 16 0 6 13 1 3 5 8 14 2 5 2 1 16 12 3 0 8 9 4 11 15 13 14 7 6 10 6 11 0 5 15 8 14 10 1 2 12 4 7 3 9 16 13 2 8 13 12 14 7 16 11 6 5 1 3 15 10 0 4 9 14 4 5 7 3 0 2 9 13 11 15 12 16 8 1 10 6 1 13 3 15 8 6 10 4 2 12 5 0 14 11 16 9 7 4 15 12 14 9 16 1 6 5 13 8 7 2 0 10 3 11 12 5 7 10 0 11 9 13 4 14 3 6 8 16 15 2 1 13 3 16 8 2 10 4 1 7 15 9 14 0 12 6 11 5 15 0 14 6 16 1 11 3 12 10 7 8 5 9 2 13 4 8 7 9 0 11 2 15 5 16 3 14 13 10 6 4 1 12 3 10 8 2 6 12 13 0 15 7 4 16 9 1 11 5 14 16 14 6 9 5 4 8 12 3 1 0 10 11 2 13 7 15 7 9 10 13 1 14 5 15 11 8 16 2 6 4 3 12 0 10 16 4 11 7 13 12 2 14 0 6 9 1 15 5 8 3 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 3 14 11 12 16 10 15 5 0 13 4 9 1 8 6 7 2 8 4 9 7 13 6 16 2 1 12 0 3 5 10 15 14 11 12 0 15 1 10 7 14 3 9 2 11 16 13 6 8 4 5 2 6 3 13 15 8 11 0 14 4 7 1 10 5 12 16 9 10 11 1 6 5 4 2 8 12 15 3 13 16 9 7 0 14 4 3 10 16 12 14 5 9 6 11 1 7 0 15 2 8 13 11 13 7 9 8 16 0 10 4 3 15 2 6 14 5 1 12 1 15 0 5 7 2 13 12 11 6 14 10 8 16 3 9 4 6 2 16 15 14 1 9 4 10 8 13 5 7 11 0 12 3 14 7 6 8 3 0 12 13 5 1 16 15 4 2 9 11 10 15 10 5 11 2 9 1 16 3 7 6 12 14 0 4 13 8 13 16 4 14 0 3 7 11 15 10 9 8 2 12 1 5 6 7 12 8 2 11 15 4 6 13 0 5 14 9 3 16 10 1 9 5 14 4 6 12 10 1 2 16 8 0 11 7 13 3 15 16 8 12 10 9 13 3 14 7 5 2 4 15 1 11 6 0 5 9 13 0 1 11 8 15 16 14 12 6 3 4 10 2 7 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 9 16 13 6 7 11 15 2 0 5 14 3 4 1 12 10 8 10 4 11 15 14 12 16 8 7 1 13 6 9 3 5 2 0 6 14 12 1 3 10 2 15 9 4 11 0 13 7 16 8 5 1 3 9 13 5 16 12 0 6 14 8 4 15 10 2 7 11 13 0 4 7 10 3 8 11 1 2 6 12 5 16 15 14 9 8 6 15 5 13 2 14 9 16 11 3 7 10 12 1 0 4 11 12 7 4 16 1 0 10 14 13 15 5 3 9 8 6 2 3 15 6 10 9 8 5 1 4 12 7 13 0 2 11 16 14 12 11 5 0 2 7 9 6 3 15 4 8 16 14 10 1 13 14 7 8 16 15 0 11 13 12 6 2 10 1 5 9 4 3 15 2 10 12 8 14 4 3 11 16 5 9 7 0 6 13 1 16 5 3 2 1 6 13 14 10 7 0 15 8 11 4 9 12 7 13 16 9 11 4 1 5 15 8 12 2 14 6 0 3 10 4 10 0 14 6 9 7 12 2 3 16 1 11 8 13 5 15 5 8 1 11 0 15 3 16 13 10 9 14 2 4 7 12 6 2 9 14 8 12 13 10 4 5 0 1 16 6 15 3 11 7 Ð’Ñе 4 порции по 8262 нормализованных пандиагональных полуцикличеÑких ДЛК 17-го порÑдка получены. Ð’Ñего: 8262*4 = 33048 ДЛК, что и требовалоÑÑŒ получить. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Объединила вÑе 4 порции и проверила вÑе 33048 ДЛК утилитой Harry White GetType1 Order? 17
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_4.txt
Counts
------
33048 diagonal Latin
33048 pandiagonal
16524 semi-cyclic
664 center symmetric
33048 nfr
4 orthogonal pair
8460 self-orthogonalЧудеÑные квадратики! Замечу, что Ñта утилита не Ñчитает полуцикличеÑкими пандиагональными ДЛК Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в диагоналÑÑ…, а Ñчитает только Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках и в Ñтолбцах. ПоÑтому программа выводит "16524 semi-cyclic". Ðе знаю, почему Harry так Ñделал. Может быть, он ориентировалÑÑ Ð½Ð° одну из Ñтатей, где было напиÑано, что полуцикличеÑкие пандиагональные ДЛК - Ñто пандиагональные ДЛК Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках и в Ñтолбцах. Однако позже в иÑÑледованиÑÑ… математиков поÑвилиÑÑŒ и полуцикличеÑкие пандиагональные ДЛК Ñ Ñ†Ð¸ÐµÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в диагоналÑÑ…. Ð”Ñ€ÑƒÐ³Ð°Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð° Harry (GetCyclic) Ñчитает вÑе пандиагональные полуцикличеÑкие ДЛК. Пример проверки программой GetCyclic Order? 17 Enter the name of the squares file: inp Count only? y Get cyclic for, (1 rows, 2 columns, 3 \diagonals, 4 /diagonals)? 3 Get squares with cyclic: \diagonals Exact match? y Number of squares: 33048 number matched 8262 Программа поÑчитала вÑе полуцикличеÑкие пандиагональные ДЛК Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в диагоналÑÑ… параллельных главной диагонали. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Да, пандиагональные ДЛК 17-го порÑдка дейÑтвительно чудеÑные. Они очень хорошо вÑтупают между Ñобой в отношение ортогональноÑти. ПроверÑÑŽ полученный набор из 33048 полуцикличеÑких пандиагональных ДЛК прогhаммой GetOrthogonal Order? 17 Enter the name of the squares file: a Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file a-orthCounts.txt ..output file a-orthNos.txt squares 33048 total orthogonal pairs 21148 Maximum pairs for square 1: 9 There are 679 other squares with this maximum number of pairs. ..output file a-1orths.txt Pairs for square 1: 9 elapsed time 0:15:02 КлаÑÑ! ДЛК образовали между Ñобой 21148 ортогональных пар! ЗдеÑÑŒ макÑÐ¸Ð¼Ð°Ð»ÑŒÐ½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° ОДЛК от одного ДЛК ÑоÑтоит из 9 ОДЛК (девÑтка). ДевÑтка из полуцикличеÑких пандиагональных ДЛК - вот она, как её выводит программа (добавила имена ДЛК) DLK 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 mate #1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 mate #2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 mate #3 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 mate #4 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 mate #5 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 mate #6 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 mate #7 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 mate #8 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 mate #9 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 Ртеперь внимание! Ð’Ñ‹ не забыли о 14 цикличеÑких пандиагональных ДЛК 17-го порÑдка? Я не забыла. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð´Ð¾Ð±Ð°Ð²Ð»ÑŽ их в набор из 33048 полуцикличеÑких пандиагональных ДЛК. ПоÑмотрим, Ñколько ортогональных пар будет в новом наборе пандиагональных ДЛК. 14 цикличеÑких пандиагональных ДЛК 17-го порÑдка показаны в Ñообщении https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=110&postid=1044 Ðти ДЛК из полной ÑиÑтемы MOLS, поÑтому они взаимно ортогональны. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’ Ñтом Ñлучае программа GetOrthogonal выдаёт Order? 17 Enter the name of the squares file: a Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file a-orthCounts.txt ..output file a-orthNos.txt squares 33062 total orthogonal pairs 25047 Maximum pairs for square 4: 421 There are 3 other squares with this maximum number of pairs. ..output file a-4orths.txt Pairs for square 4: 421 elapsed time 0:15:55 ДЛК образовали 25047 ортогональных пар!! МакÑÐ¸Ð¼Ð°Ð»ÑŒÐ½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° ОДЛК от одного ДЛК ÑоÑтоит из 421 ОДЛК. Вот откуда, кÑтати, получена оценка a(17) >= 421. Я уже давно получила Ñту группу ОДЛК от одного ДЛК 17-го порÑдка. По 421 ОДЛК имеют четыре ДЛК в Ñтом наборе. ЗдеÑÑŒ должна быть и клика размера 14. Рбольшего размера не будет ли? Я думаю, что не будет. Вообще Ñильно подозреваю, что группа MODLS порÑдков, Ð´Ð»Ñ ÐºÐ¾Ñ‚Ð¾Ñ€Ñ‹Ñ… ÑущеÑтвует Ð¿Ð¾Ð»Ð½Ð°Ñ ÑиÑтема MOLS, не может Ñодержать больше ДЛК, чем в полной ÑиÑтеме MOLS. Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 9 Ñчитаю, что Ñта гипотеза доказана. ÐžÐ¿Ñ€Ð¾Ð²ÐµÑ€Ð¶ÐµÐ½Ð¸Ñ Ð¿Ð¾ÐºÐ° не поÑледовало. Покажу оÑновной ДЛК 421-ки и неÑколько ортогоналек DLK 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 mate #1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 mate #2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 . . . . . mate #420 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 4 12 16 10 8 2 3 9 11 6 13 14 15 7 0 5 1 14 5 6 9 12 16 11 13 2 15 7 0 3 1 8 4 10 8 2 11 14 5 13 15 12 0 3 1 16 4 9 10 6 7 12 13 7 8 15 0 14 1 16 4 5 10 11 6 2 3 9 15 3 9 0 1 7 4 5 10 8 6 13 2 12 16 11 14 16 11 1 4 3 10 8 6 9 2 15 12 14 5 13 7 0 13 4 10 16 6 9 2 11 12 0 14 7 8 15 3 1 5 10 6 5 2 11 12 13 14 1 7 3 9 0 16 4 8 15 2 8 12 13 14 15 7 4 3 16 11 1 5 10 9 0 6 9 14 15 7 0 3 10 16 5 13 4 8 6 11 1 2 12 7 0 3 1 16 6 5 8 15 10 9 2 13 4 12 14 11 1 16 4 5 2 8 9 0 6 11 12 15 10 14 7 13 3 5 10 8 12 9 11 1 2 13 14 0 6 7 3 15 16 4 6 9 14 11 13 4 12 15 7 1 2 3 16 0 5 10 8 11 7 13 15 10 14 0 3 4 12 16 5 1 8 6 9 2 3 15 0 6 7 1 16 10 14 5 8 4 9 2 11 12 13 mate #421 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 14 8 6 0 1 7 9 4 11 12 13 5 15 3 16 2 10 4 7 10 14 9 11 0 13 5 15 1 16 6 2 8 12 3 9 12 3 11 13 10 15 1 16 14 2 7 8 4 5 6 0 5 6 13 15 12 16 14 2 3 8 9 4 0 1 7 10 11 7 15 16 5 2 3 8 6 4 11 0 10 14 9 12 13 1 16 2 1 8 6 4 7 0 13 10 12 3 11 5 15 14 9 8 14 4 7 0 9 10 15 12 5 6 13 1 16 3 11 2 3 0 9 10 11 12 16 5 1 7 15 14 2 6 13 8 4 10 11 12 13 5 2 1 14 9 16 3 8 7 15 4 0 6 13 5 15 1 8 14 3 11 2 6 4 9 16 0 10 7 12 1 16 14 4 3 6 13 8 7 0 11 2 10 12 9 5 15 2 3 0 6 7 15 4 9 10 13 8 12 5 11 1 16 14 6 10 7 9 16 0 11 12 15 4 5 1 13 14 2 3 8 12 9 11 2 10 13 5 16 0 1 14 15 3 8 6 4 7 11 13 8 12 15 1 2 10 14 3 16 6 4 7 0 9 5 15 4 5 16 14 8 12 3 6 2 7 0 9 10 11 1 13 ОÑновной ДЛК 421-ки цикличеÑкий пандиагональный. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Смотрим Ñчётчик ортогональных пар; в наборе первые 14 ДЛК цикличеÑкие пандиагональные orthogonal
square pairs
------ ----------
1 285
2 285
3 13
4 421
5 285
6 421
7 285
8 285
9 421
10 285
11 421
12 13
13 285
14 285
15 13
16 1
17 1
18 1
19 1
20 13
. . . . . . .Видим, что цикличеÑкие пандиагональные квадраты 4, 6, 9 и 11 имеют 421 ОДЛК. От других цикличеÑких пандиагональных ДЛК тоже Ñолидные группы ОДЛК получаютÑÑ - по 285 ОДЛК; иÑключение ÑоÑтавлÑÑŽÑ‚ квадраты 3 и 12, которые имеют только по 13 ОДЛК. Рквадратики 15 и 20 полуцикличеÑкие пандиагональные, имеют по 13 ОДЛК. ДьÑвольÑки интереÑÐ½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° дьÑвольÑких ДЛК 17-го порÑдка! :) (пандиагональные квадраты математики ещё называют дьÑвольÑкими; например, РоÑÑер так их называл даже в официальной Ñтатье; роÑÑийÑкий математик Ю. Ð’. Чебраков - ныне покойный - был против такого названиÑ, о чём пиÑал С. БелÑеву). |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Выложила 33048 нормализованных полуцикличеÑких пандиагональных ДЛК 17-го порÑдка https://disk.yandex.ru/d/2qqKbnTL2mF7LQ ЯндекÑ.ДиÑк, 4,47 МБ, текÑтовый файл Ñжат. Выражаю благодарноÑÑ‚ÑŒ помощнику; Ñ…Ð¾Ñ‚Ñ Ð¸ Ñ Ð°Ð²Ð°Ñ€Ð¸ÐµÐ¹, но переÑтановку Ñтрок в ДЛК 17-го порÑдка он выполнил. Ðедобор ДЛК оказалÑÑ Ð½ÐµÐ±Ð¾Ð»ÑŒÑˆÐ¾Ð¹; Ñ ÐºÐ¾Ð¼Ð¿ÐµÐ½Ñировала его, применив к полученной порции ДЛК преобразование параллельного переноÑа на торе. Ðто уже второй результат подобного рода, первый получен Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 13. Результат тоже выложен. Цитата из ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=128&postid=1807 Выкладываю полученные мной 1352 нормализованных полуцикличеÑких пандиагональных ДЛК 13-го порÑдка Ðтот результат Ð´Ð»Ñ Ð¿Ð¾Ð»ÑƒÑ†Ð¸ÐºÐ»Ð¸Ñ‡ÐµÑких пандиагональных ДЛК 13-го порÑдка получен Ñовершенно аналогично тому, как получен результат Ð´Ð»Ñ Ð¿Ð¾Ð»ÑƒÑ†Ð¸ÐºÐ»Ð¸Ñ‡ÐµÑких пандиагональных ДЛК 17-го порÑдка, Ñ Ñ‚Ð¾Ð¹ только разницей, что переÑтановку Ñтрок в ДЛК 13-го порÑдка Ñ Ð²Ñ‹Ð¿Ð¾Ð»Ð½Ð¸Ð»Ð° Ñама, она очень быÑтро выполнÑетÑÑ Ð´Ð°Ð¶Ðµ на моём ПК. И в цитате отмечено, что полуцикличеÑких пандиагональных ДЛК 13-го порÑдка вроде бы должно быть 1560. Однако как найти ещё 208 таких ДЛК, Ñ Ð½Ðµ знаю. У Ð¼ÐµÐ½Ñ Ð½ÐµÑ‚ никаких идей. О вÑех полуцикличеÑких пандиагональных ДЛК 17-го порÑдка мне вообще ничего неизвеÑтно. Я не вÑтречала такую информацию. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Тот же Ñамый алгоритм можно применить Ð´Ð»Ñ Ð¿Ð¾Ð¸Ñка полуцикличеÑких пандиагональных ДЛК 19-го порÑдка. Выше Ñ ÑƒÐ¶Ðµ немного пыталаÑÑŒ найти такие ДЛК. ПонÑтно, что Ð¿Ð¾Ð»Ð½Ð°Ñ Ð¿ÐµÑ€ÐµÑтановка Ñтрок в нормализованном цикличеÑком ДЛК 19-го порÑдка (оÑтавлÑÑ Ð½Ð° меÑте первую Ñтроку) будет выполнÑÑ‚ÑŒÑÑ ÐµÑ‰Ñ‘ дольше, чем Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 17. Ðа моём ПК даже переÑтановку Ñтрок Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 17 выполнить нереально за приемлемое времÑ. ЕÑÑ‚ÑŒ ли какой-то другой подход к решению Ñтой проблемы? Можно попробовать алгоритм Ñ Ð¸Ð´ÐµÐ°Ð»ÑŒÐ½Ñ‹Ð¼Ð¸ ДЛК. Ðтот алгоритм Ñ Ñ€ÐµÐ°Ð»Ð¸Ð·Ð¾Ð²Ð°Ð»Ð° Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 17, было получено 180 идеальных ДЛК, но они не дали вÑех полуцикличеÑких ДЛК при переноÑе на торе, дали только некоторую чаÑÑ‚ÑŒ таких ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Смотрим поÑледовательноÑÑ‚ÑŒ OEIS https://oeis.org/A071607 ЕÑли Ñ Ð¿Ñ€Ð°Ð²Ð¸Ð»ÑŒÐ½Ð¾ понимаю, Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 19 мы должны получить при полной переÑтановке Ñтрок в нормализованном цикличеÑком ДЛК 19-го порÑдка (оÑтавлÑÑ Ð½Ð° меÑте первую Ñтроку) 43184 нормализованных пандиагональных ДЛК, Ñреди которых 16 цикличеÑких и 43168 полуцикличеÑких Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках. Потом набор из 43168 полуцикличеÑких пандиагональных ДЛК размножим по моей Ñхеме и получим 43168*4=172672 нормализованных полуцикличеÑких пандиагональных ДЛК 19-го порÑдка. Ðто теоретичеÑкое опиÑание алгоритма. Как реализовать алгоритм, чтобы Ñто было быÑтро? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вот паттерн, по которому Ñ Ð¸Ñкала идеальные ДЛК 17-го порÑдка, нашла их 180 штук  КÑтати, Harry White подтвердил Ñтот результат. Теперь можно попробовать иÑкать идеальные ДЛК 19-го порÑдка по аналогичному паттерну. Затем ко вÑем найденным идеальным ДЛК надо применить преобразование параллельного переноÑа на торе. Ðто даÑÑ‚ Ñколько-то полуцикличеÑких пандиагональных ДЛК, но не вÑе. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Рмежду тем мы перешли на вторую форумную Ñтраницу. Копию первой Ñтраницы Ñделала и положила на ЯндекÑ.ДиÑк https://disk.yandex.ru/d/D73XvHFebR3coA формат html, 607 КБ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вот пример идеального ДЛК 19-го порÑдка, какие надо иÑкать 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 ДЛК аÑÑоциативный и пандиагональный Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡Ð½Ð¾Ñтью в Ñтроках. Утилита Harry White показывает такие ÑвойÑтва Ñтого ДЛК Order? 19
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
1 diagonal Latin
1 associative
1 pandiagonal
1 semi-cyclic
1 ultramagic
1 symmetric parity
Сколько вÑего таких ДЛК 19-го порÑдка? Паттерн Ð´Ð»Ñ Ñ‚Ð°ÐºÐ¸Ñ… ДЛК показан выше (только он Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 17, Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 19 вÑÑ‘ аналогично). |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПопыталаÑÑŒ внеÑти полученные результаты Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдков 13 и 17 в OEIS https://oeis.org/draft/A338620 Показываю Ñкриншот 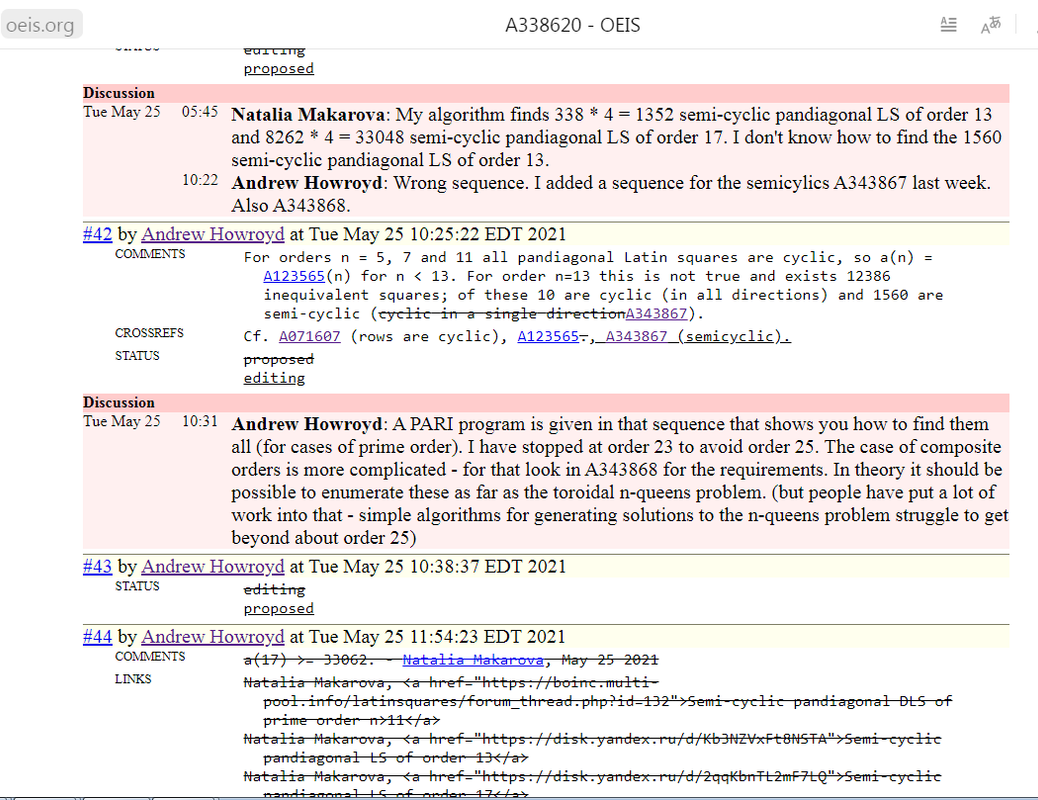 Очень удивил комментарий редактора Andrew Howroyd: Wrong sequence. I added a sequence for the semicylics A343867 last week. Also A343868. Как-то не очень понÑтно. Что значит: "Wrong sequence."? ЕÑли Ð½ÐµÐ¿Ñ€Ð°Ð²Ð¸Ð»ÑŒÐ½Ð°Ñ - иÑправьте! Ðу да ладно. ЕÑли поÑледовательноÑÑ‚ÑŒ неправильнаÑ, то добавлÑÑ‚ÑŒ в неё ничего не надо. И поÑтому, видимо, вÑÑ Ð¼Ð¾Ñ Ð¿Ñ€Ð°Ð²ÐºÐ° летит в топку. Ð’Ñтупать в диÑкуÑÑию не буду. Ðто беÑÑмыÑленно. Редактор вÑегда прав! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’ поÑледовательноÑти A343867 приведён квадрат 0 11 1 7 5 9 3 10 4 8 6 12 2 9 7 0 3 1 12 2 8 6 10 4 11 5 11 5 12 6 10 8 1 4 2 0 3 9 7 1 4 10 8 12 6 0 7 11 9 2 5 3 10 3 6 4 2 5 11 9 0 7 1 8 12 8 2 9 0 11 4 7 5 3 6 12 10 1 7 0 11 2 9 3 10 1 12 5 8 6 4 6 9 7 5 8 1 12 3 10 4 11 2 0 5 12 3 1 7 10 8 6 9 2 0 4 11 3 1 5 12 6 0 4 2 8 11 9 7 10 12 10 8 11 4 2 6 0 7 1 5 3 9 2 6 4 10 0 11 9 12 5 3 7 1 8 4 8 2 9 3 7 5 11 1 12 10 0 6 Я видела Ñтот квадрат давно. Цитата из ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=128&postid=1696 Увидела в Ñтатье OEIS ÑÑылку ещё на одну Ñтатью. При первом знакомÑтве Ñ Ñтим квадратом Ñ Ð½Ð¸ÐºÐ°Ðº не могла понÑÑ‚ÑŒ, почему он "цикличеÑкий в направлении (1,4)" Мне казалоÑÑŒ, что Ñтот квадрат не цикличеÑкий. Ðу да, он не цикличеÑкий ни в Ñтроках, ни в Ñтолбцах, ни в диагоналÑÑ… в том ÑмыÑле, как мы понимали цикличноÑÑ‚ÑŒ раньше. ОказываетÑÑ, он цикличеÑкий ÑовÑем в другом ÑмыÑле. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ñле деÑÑтиминутного разглÑÐ´Ñ‹Ð²Ð°Ð½Ð¸Ñ Ñтого квадрата Ñ Ð¿Ð¾Ð½Ñла, в чём ÑоÑтоит его цикличноÑÑ‚ÑŒ. Рв каких ещё направлениÑÑ… может быть цикличноÑÑ‚ÑŒ в данном ÑмыÑле? (1,5), (1, 6), (1,7)... ??? ВзÑла Ñтот квадрат и применила к нему преобразование параллельного переноÑа на торе. Получила 169 пандиагональных ДЛК (Ð²ÐºÑŽÑ‡Ð°Ñ Ð¸Ñходный). Они тоже вÑе цикличеÑкие в Ñтом ÑмыÑле? Рпочему нет? Ðапример, 169-й ДЛК в Ñтом наборе точно так же цикличеÑкий в направлении (1,4) 6 4 8 2 9 3 7 5 11 1 12 10 0 2 0 11 1 7 5 9 3 10 4 8 6 12 5 9 7 0 3 1 12 2 8 6 10 4 11 7 11 5 12 6 10 8 1 4 2 0 3 9 3 1 4 10 8 12 6 0 7 11 9 2 5 12 10 3 6 4 2 5 11 9 0 7 1 8 1 8 2 9 0 11 4 7 5 3 6 12 10 4 7 0 11 2 9 3 10 1 12 5 8 6 0 6 9 7 5 8 1 12 3 10 4 11 2 11 5 12 3 1 7 10 8 6 9 2 0 4 10 3 1 5 12 6 0 4 2 8 11 9 7 9 12 10 8 11 4 2 6 0 7 1 5 3 8 2 6 4 10 0 11 9 12 5 3 7 1 ПроверÑÑŽ 169 ДЛК Ñтого набора утилитой Harry White Order? 13
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt
Counts
------
169 diagonal Latin
1 associative
169 pandiagonal
1 ultramagic
12 center symmetric
1 symmetric parityРазумеетÑÑ, вÑе ДЛК пандиагональные. ОÑталоÑÑŒ нормализовать Ñти ДЛК и отброÑить дубликаты, еÑли они еÑÑ‚ÑŒ. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese