Thread 'Semi-cyclic pandiagonal DLS of prime order n>11'

Message boards : Science : Semi-cyclic pandiagonal DLS of prime order n>11
Message board moderation

To post messages, you must log in.

Previous · 1 . . . 4 · 5 · 6 · 7

AuthorMessage
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2214 - Posted: 30 May 2021, 7:23:47 UTC
Last modified: 30 May 2021, 7:37:40 UTC

С порядком 31 всё совершенно аналогично.
Имеется полная система MOLS, содержащая 28 ДЛК, которые являются циклическими пандиагональными и образуют группу MODLS.
Если их преобразовать в СН ДЛК, они станут идеальными.
По моему паттерну тоже получились 28 идеальных ДЛК, которые являются циклическими пандиагональными.
Я не буду показывать их все, потому что они входят в набор идеальных ДЛК 31-го порядка, который я выложила выше.
Покажу только один такой ДЛК

17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3
 7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2
 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5
 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1
 5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4
 8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13

Симпатичный квадратик!

Harry прислал по моей просьбе 500 полуциклических идеальных ДЛК 31-го порядка.
Попозже я с ними поиграюсь :)
ID: 2214 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2215 - Posted: 30 May 2021, 7:46:23 UTC

Проверила 28 идеальных цикличных ДЛК 31-го порядка программой GetOrthogonal

Order? 31

Enter the name of the squares file: a
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file a-orthCounts.txt
..output file a-orthNos.txt
squares 28 total orthogonal pairs 378
Maximum pairs for square 1: 27
There are 27 other squares with this maximum number of pairs.
..output file a-1orths.txt
Pairs for square 1: 27

Всё верно: ДЛК образовали 378 ортогональных пар, и каждый ДЛК имеет 27 ОДЛК.
ID: 2215 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2216 - Posted: 30 May 2021, 7:57:12 UTC
Last modified: 30 May 2021, 8:01:48 UTC

Господа!
Напоминаю: я приглашаю всех к обсуждению проблемы.
Ваши вопросы, замечания, пожелания, идеи будут очень полезны.
Мне трудно решать проблемы (а их очень много) без обсуждения, без участия коллег.
К сожалению, большинство моих коллег перестали заниматься квадратами. Устали :)
Это Алексей Чернов, Макс Алексеев, Сергей Беляев, Владимир Чирков, Алексей Белышев, Tomas Brada.
Только Harry White продолжает мне помогать. Спасибо ему!

Если вам интересна тема, регистрируйтесь и участвуйте в форуме.
Для этого совсем не обязательно участвовать в вычислениях, то есть быть кранчером.
ID: 2216 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2229 - Posted: 31 May 2021, 9:43:28 UTC
Last modified: 31 May 2021, 12:14:52 UTC

Ох, добралась-таки до идеальных ДЛК 31-го порядка, присланных Harry.
Я попросила прислать 500 штук.
Прокатила их на торе, получила порцию из 15500 нормализованных полуциклических пандиагональных ДЛК с цикличностью в строках.
Проверила ДЛК этого набора утилитой GetType1

Order? 31

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
     15500 diagonal Latin
     15500 pandiagonal
     15500 semi-cyclic
       500 center symmetric
     15500 nfr

Великолепные квадратики!
500 центрально-симметричных ДЛК, которые легко превратить в идеальные, достаточно преобразовать их в СН ДЛК.
Ну, и посмотреть же надо на такие прекрасные квадратики :)
Вот два из них

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3
 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5
 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0
29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9
 8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11
23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2
30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
 7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6
 5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4
17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13
22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3
 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5
 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9
 8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11
23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2
30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
 7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6
 5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13
18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

Теперь, как вы уже знаете, поверну ДЛК этого набора на 90 градусов.
Что получу от этого - вы тоже уже знаете :)
ID: 2229 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2230 - Posted: 31 May 2021, 10:24:42 UTC

Ну вот, покажу два нормализованных полуциклических пандиагональных ДЛК 31-го порядка с цикличностью в столбцах

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
20 19 22 21 11 23 2 27 14 30 28 18 24 6 26 25 9 29 3 4 16 0 1 13 5 12 15 8 7 10 17
16 4 1 0 18 13 22 8 26 17 7 3 5 2 15 12 30 10 21 11 9 20 19 6 23 24 25 14 27 28 29
9 11 19 20 3 6 1 14 15 29 27 21 23 22 25 24 17 28 0 18 30 16 4 2 13 5 12 26 8 7 10
30 18 4 16 21 2 19 26 25 10 8 0 13 1 12 5 29 7 20 3 17 9 11 22 6 23 24 15 14 27 28
17 3 11 9 0 22 4 15 12 28 14 20 6 19 24 23 10 27 16 21 29 30 18 1 2 13 5 25 26 8 7
29 21 18 30 20 1 11 25 24 7 26 16 2 4 5 13 28 8 9 0 10 17 3 19 22 6 23 12 15 14 27
10 0 3 17 16 19 18 12 5 27 15 9 22 11 23 6 7 14 30 20 28 29 21 4 1 2 13 24 25 26 8
28 20 21 29 9 4 3 24 23 8 25 30 1 18 13 2 27 26 17 16 7 10 0 11 19 22 6 5 12 15 14
7 16 0 10 30 11 21 5 13 14 12 17 19 3 6 22 8 15 29 9 27 28 20 18 4 1 2 23 24 25 26
27 9 20 28 17 18 0 23 6 26 24 29 4 21 2 1 14 25 10 30 8 7 16 3 11 19 22 13 5 12 15
8 30 16 7 29 3 20 13 2 15 5 10 11 0 22 19 26 12 28 17 14 27 9 21 18 4 1 6 23 24 25
14 17 9 27 10 21 16 6 22 25 23 28 18 20 1 4 15 24 7 29 26 8 30 0 3 11 19 2 13 5 12
26 29 30 8 28 0 9 2 1 12 13 7 3 16 19 11 25 5 27 10 15 14 17 20 21 18 4 22 6 23 24
15 10 17 14 7 20 30 22 19 24 6 27 21 9 4 18 12 23 8 28 25 26 29 16 0 3 11 1 2 13 5
25 28 29 26 27 16 17 1 4 5 2 8 0 30 11 3 24 13 14 7 12 15 10 9 20 21 18 19 22 6 23
12 7 10 15 8 9 29 19 11 23 22 14 20 17 18 21 5 6 26 27 24 25 28 30 16 0 3 4 1 2 13
24 27 28 25 14 30 10 4 18 13 1 26 16 29 3 0 23 2 15 8 5 12 7 17 9 20 21 11 19 22 6
5 8 7 12 26 17 28 11 3 6 19 15 9 10 21 20 13 22 25 14 23 24 27 29 30 16 0 18 4 1 2
23 14 27 24 15 29 7 18 21 2 4 25 30 28 0 16 6 1 12 26 13 5 8 10 17 9 20 3 11 19 22
13 26 8 5 25 10 27 3 0 22 11 12 17 7 20 9 2 19 24 15 6 23 14 28 29 30 16 21 18 4 1
6 15 14 23 12 28 8 21 20 1 18 24 29 27 16 30 22 4 5 25 2 13 26 7 10 17 9 0 3 11 19
2 25 26 13 24 7 14 0 16 19 3 5 10 8 9 17 1 11 23 12 22 6 15 27 28 29 30 20 21 18 4
22 12 15 6 5 27 26 20 9 4 21 23 28 14 30 29 19 18 13 24 1 2 25 8 7 10 17 16 0 3 11
1 24 25 2 23 8 15 16 30 11 0 13 7 26 17 10 4 3 6 5 19 22 12 14 27 28 29 9 20 21 18
19 5 12 22 13 14 25 9 17 18 20 6 27 15 29 28 11 21 2 23 4 1 24 26 8 7 10 30 16 0 3
4 23 24 1 6 26 12 30 29 3 16 2 8 25 10 7 18 0 22 13 11 19 5 15 14 27 28 17 9 20 21
11 13 5 19 2 15 24 17 10 21 9 22 14 12 28 27 3 20 1 6 18 4 23 25 26 8 7 29 30 16 0
18 6 23 4 22 25 5 29 28 0 30 1 26 24 7 8 21 16 19 2 3 11 13 12 15 14 27 10 17 9 20
3 2 13 11 1 12 23 10 7 20 17 19 15 5 27 14 0 9 4 22 21 18 6 24 25 26 8 28 29 30 16
21 22 6 18 19 24 13 28 27 16 29 4 25 23 8 26 20 30 11 1 0 3 2 5 12 15 14 7 10 17 9

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
17 19 5 21 11 22 23 27 14 30 28 18 24 2 26 25 29 20 3 4 9 0 1 13 6 12 15 8 7 10 16
20 4 22 0 18 1 13 8 26 16 7 3 6 5 15 12 10 9 21 11 30 17 19 2 23 24 25 14 27 28 29
9 11 1 17 3 19 2 14 15 29 27 21 23 22 25 24 28 30 0 18 16 20 4 5 13 6 12 26 8 7 10
30 18 19 20 21 4 5 26 25 10 8 0 13 1 12 6 7 16 17 3 29 9 11 22 2 23 24 15 14 27 28
16 3 4 9 0 11 22 15 12 28 14 17 2 19 24 23 27 29 20 21 10 30 18 1 5 13 6 25 26 8 7
29 21 11 30 17 18 1 25 24 7 26 20 5 4 6 13 8 10 9 0 28 16 3 19 22 2 23 12 15 14 27
10 0 18 16 20 3 19 12 6 27 15 9 22 11 23 2 14 28 30 17 7 29 21 4 1 5 13 24 25 26 8
28 17 3 29 9 21 4 24 23 8 25 30 1 18 13 5 26 7 16 20 27 10 0 11 19 22 2 6 12 15 14
7 20 21 10 30 0 11 6 13 14 12 16 19 3 2 22 15 27 29 9 8 28 17 18 4 1 5 23 24 25 26
27 9 0 28 16 17 18 23 2 26 24 29 4 21 5 1 25 8 10 30 14 7 20 3 11 19 22 13 6 12 15
8 30 17 7 29 20 3 13 5 15 6 10 11 0 22 19 12 14 28 16 26 27 9 21 18 4 1 2 23 24 25
14 16 20 27 10 9 21 2 22 25 23 28 18 17 1 4 24 26 7 29 15 8 30 0 3 11 19 5 13 6 12
26 29 9 8 28 30 0 5 1 12 13 7 3 20 19 11 6 15 27 10 25 14 16 17 21 18 4 22 2 23 24
15 10 30 14 7 16 17 22 19 24 2 27 21 9 4 18 23 25 8 28 12 26 29 20 0 3 11 1 5 13 6
25 28 16 26 27 29 20 1 4 6 5 8 0 30 11 3 13 12 14 7 24 15 10 9 17 21 18 19 22 2 23
12 7 29 15 8 10 9 19 11 23 22 14 17 16 18 21 2 24 26 27 6 25 28 30 20 0 3 4 1 5 13
24 27 10 25 14 28 30 4 18 13 1 26 20 29 3 0 5 6 15 8 23 12 7 16 9 17 21 11 19 22 2
6 8 28 12 26 7 16 11 3 2 19 15 9 10 21 17 22 23 25 14 13 24 27 29 30 20 0 18 4 1 5
23 14 7 24 15 27 29 18 21 5 4 25 30 28 0 20 1 13 12 26 2 6 8 10 16 9 17 3 11 19 22
13 26 27 6 25 8 10 3 0 22 11 12 16 7 17 9 19 2 24 15 5 23 14 28 29 30 20 21 18 4 1
2 15 8 23 12 14 28 21 17 1 18 24 29 27 20 30 4 5 6 25 22 13 26 7 10 16 9 0 3 11 19
5 25 14 13 24 26 7 0 20 19 3 6 10 8 9 16 11 22 23 12 1 2 15 27 28 29 30 17 21 18 4
22 12 26 2 6 15 27 17 9 4 21 23 28 14 30 29 18 1 13 24 19 5 25 8 7 10 16 20 0 3 11
1 24 15 5 23 25 8 20 30 11 0 13 7 26 16 10 3 19 2 6 4 22 12 14 27 28 29 9 17 21 18
19 6 25 22 13 12 14 9 16 18 17 2 27 15 29 28 21 4 5 23 11 1 24 26 8 7 10 30 20 0 3
4 23 12 1 2 24 26 30 29 3 20 5 8 25 10 7 0 11 22 13 18 19 6 15 14 27 28 16 9 17 21
11 13 24 19 5 6 15 16 10 21 9 22 14 12 28 27 17 18 1 2 3 4 23 25 26 8 7 29 30 20 0
18 2 6 4 22 23 25 29 28 0 30 1 26 24 7 8 20 3 19 5 21 11 13 12 15 14 27 10 16 9 17
3 5 23 11 1 13 12 10 7 17 16 19 15 6 27 14 9 21 4 22 0 18 2 24 25 26 8 28 29 30 20
21 22 13 18 19 2 24 28 27 20 29 4 25 23 8 26 30 0 11 1 17 3 5 6 12 15 14 7 10 16 9

Таких квадратиков тоже получилось 15500, понятное дело.
Теперь соберу пандиагональные циклические (28 штук), пандиагональные полуциклические с цикличностью в строках (15500 штук) и пандиагональные полуциклические с цикличностью в столбцах (15500 штук) и проверю ДЛК этого набора на "товарищей".
ID: 2230 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2231 - Posted: 31 May 2021, 12:07:54 UTC

Готово!

Order? 31

Enter the name of the squares file: inp3
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file inp3-orthCounts_1.txt
..output file inp3-orthNos_1.txt
squares 31028 total orthogonal pairs 502
Maximum pairs for square 6: 58
There are 3 other squares with this maximum number of pairs.
..output file inp3-6orths.txt
Pairs for square 6: 58

ДЛК образовали 502 ортогональные пары.
Нашлись 4 группы по 58 ОДЛК.
Показываю основной ДЛК первой 58-ки (квадрат 6); это циклический пандиагональный ДЛК, он идеальный, я не нормализовала циклические идеальные ДЛК, присланные Harry

22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3
17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11
25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
 7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6
20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9
23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
 5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4
18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12
26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
 8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7
21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10
24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5
19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13
27 28 29 30  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30  0  1  2  3  4  5  6  7  8

И улучшена оценка для порядка 31
a(31) >= 58

Посмотрим на счётчик ортогональных пар для первых 28 ДЛК, это циклические пандиагональные ДЛК

           orthogonal
      square       pairs
      ------    ----------

           1           27
           2           27
           3           27
           4           27
           5           27
           6           58
           7           27
           8           58
           9           58
          10           27

          11           27
          12           27
          13           27
          14           27
          15           27
          16           27
          17           27
          18           27
          19           27
          20           27

          21           27
          22           27
          23           27
          24           58
          25           27
          26           27
          27           27
          28           27

Интересно: четыре 58-ки, остальные 27-ки.
Ну, 27-ки понятно откуда: все циклические пандиагональные ДЛК друг другу ортогональны.
ID: 2231 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2232 - Posted: 31 May 2021, 13:06:07 UTC
Last modified: 31 May 2021, 13:12:43 UTC

Господа!
Отгадайте загадку :)

Этот идеальный ДЛК 35-го порядка какой-нибудь цикличностью обладает?



Или же он не циклический пандиагональный?

Свойства, выданные утилитой GetType1

Order? 35

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt

Counts
------
         1 diagonal Latin
         1 associative
         1 pandiagonal
         1 ultramagic
         1 natural \diagonal
         1 self-orthogonal
         1 symmetric parity

Ни в строках, ни в столбцах цикличность утилитой не обнаружена.
В диагоналях тоже цикличности нет, как утверждает утилита GetCyclic.
Ну, а в каких-нибудь там направлениях (1,х) нет цикличности?

ДЛК построен методом составных квадратов.
ID: 2232 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2233 - Posted: 1 Jun 2021, 1:24:23 UTC
Last modified: 1 Jun 2021, 1:34:43 UTC

Этот нормализованный циклический пандиагональный ДЛК 35-го порядка я построила вручную методом циклического сдвига

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3
 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5
 8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2
 5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4
 7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6
 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

Проверка ДЛК утилитой GetType1

Order? 35

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt

Counts
------
         1 diagonal Latin
         1 pandiagonal
         1 cyclic 4-way
         1 center symmetric
         1 nfr
         1 self-orthogonal

ДЛК центрально-симметричный, значит, его легко превратить в идеальный, достаточно преобразовать его в СН ДЛК.
Вот 

 0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23
24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12
13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1
 2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25
26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14
15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3
 4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27
28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16
17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5
 6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29
30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18
19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7
 8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31
32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20
21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9
10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33
34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22
23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11
12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0
 1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24
25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13
14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2
 3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26
27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15
16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4
 5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28
29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17
18 30  7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6
 7 19 31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30
31  8 20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19
20 32  9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8
 9 21 33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32
33 10 22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21
22 34 11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10
11 23  0 12 24  1 13 25  2 14 26  3 15 27  4 16 28  5 17 29  6 18 30  7 19 31  8 20 32  9 21 33 10 22 34

Утилита GetType1 сообщает для этого ДЛК

Order? 35

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         1 diagonal Latin
         1 associative
         1 pandiagonal
         1 cyclic 4-way
         1 ultramagic
         1 natural \diagonal
         1 self-orthogonal
         1 symmetric parity

Цикличность ДЛК сохранилась, как и должно быть при полной цикличности (в строках, в столбцах и в диагоналях обоих направлений).
Далее переобозначением элементов ДЛК легко превратить в такой идеальный ДЛК, какие я строила по своему паттерну.

Интересный вопрос: сколько нормализованных циклических пандиагональных ДЛК 35-го порядка можно построить методом циклического сдвига?
В своё время я пыталась построить подобные ДЛК для порядка 25.
Сколько-то их у меня получилось, но не 22 ДЛК, содержащихся в полной системе MOLS и образующих группу MODLS.
Для порядка 35 полной системы MOLS не существует.
ID: 2233 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2240 - Posted: 1 Jun 2021, 5:22:51 UTC

Построила второй аналогичный ДЛК 35-го порядка тоже вручную методом циклическиого сдвига.
Проверяю эти два квадратика утилитой GetType1

Order? 35

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         2 diagonal Latin
         2 pandiagonal
         2 cyclic 4-way
         2 center symmetric
         2 nfr
         1 orthogonal pair
         2 self-orthogonal

Чудесно! Оба квадратика правильные да ещё и ортогональные!

И сколько же подобных циклических пандиагональных ДЛК 35-го порядка удастся построить методом циклического сдвига?
ID: 2240 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2241 - Posted: 1 Jun 2021, 5:57:49 UTC
Last modified: 1 Jun 2021, 6:05:34 UTC

Третий квадрат построила методом циклического сдвига; увы, он не получился диагональным.
Но! у меня уже получилась группа MOLS 35-го порядка, в которой два ДЛК и один ЛК.
Можно продолжить построение аналогичных квадратов, может быть, группа MOLS дополнится.

Известную группу MOLS 35-го порядка сейчас покажу, я её, кажется, находила в программе SageMath.

Цитата из сообщения
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117&postid=1254

По команде
sage: for x in designs.mutually_orthogonal_latin_squares(5,35): print(x,'\n')

получаю группу MOLS 35-го порядка из 5 ЛК

. . . . . .

Из 6 ЛК программа пока не знает группы MOLS 35-го порядка.

Проверяю эти ЛК утилитой Harry White
Order? 35

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_9.txt

Counts
------
         4 Latin
         1 diagonal Latin
         1 pandiagonal
         1 center symmetric
         4 natural \diagonal
         4 orthogonal pair

Есть один ДЛК, причём он пандиагональный.
Очень оригинальный последний ЛК, он центрально-симметричный и полупандиагональный; построен методом циклического сдвига.

Ну вот, в известной группе MOLS 35-го порядка 5 ЛК, только один из них ДЛК.
ID: 2241 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2244 - Posted: 2 Jun 2021, 0:33:08 UTC
Last modified: 2 Jun 2021, 0:48:22 UTC

Ох!
Лень было написать программку построения ЛК методом циклического сдвига.
Ну вот и строила их вручную. Ещё не все построила.
Пока имею 6 ДЛК и 12 ЛК.
Вот таблица ортогональных пар

1: [2,5,7,8,9,10,12,13,15,17],
1: [18],
2: [1,3,7,8,9,11,12,14,15,16],
2: [18],
3: [2,5,6,7,8,9,10,11,12,13],
3: [14,17],
4: [5,6,7,8,9,10,11,12,13,14],
4: [15,18],
5: [1,3,4,7,8,11,14,15,16,17],
5: [18],
6: [3,4,7,8,9,12,15,16,17,18],
7: [1,2,3,4,5,6,9,11,13,15],
7: [17],
8: [1,2,3,4,5,6,9,10,11,15],
8: [16,17],
9: [1,2,3,4,6,7,8,10,13,14],
9: [16,18],
10: [1,3,4,8,9,11,12,14,15,17],
10: [18],
11: [2,3,4,5,7,8,10,12,13,16],
11: [18],
12: [1,2,3,4,6,10,11,13,15,16],
12: [17],
13: [1,3,4,7,9,11,12,14,15,16],
13: [17,18],
14: [2,3,4,5,9,10,13,15,16,17],
15: [1,2,4,5,6,7,8,10,12,13],
15: [14,16],
16: [2,5,6,8,9,11,12,13,14,15],
16: [17,18],
17: [1,3,5,6,7,8,10,12,13,14],
17: [16,18],
18: [1,2,4,5,6,9,10,11,13,16],
18: [17]

Здесь уже есть клика размера 4.
Таким образом, найдена группа MOLS 35-го порядка, состоящая из 4-х ЛК, из которых один ДЛК.
Как сказано выше, известная математикам группа MOLS 35-го порядка состоит из 5 ЛК.
Пока не буду делать выводов.
Дострою все ЛК/ДЛК методом циклического сдвига.
Потом посмотрю окончательный результат.
ID: 2244 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2245 - Posted: 2 Jun 2021, 3:58:24 UTC
Last modified: 2 Jun 2021, 4:03:01 UTC

Уф!
Достроила.
Всего получилось у меня 24 ЛК, из которых 8 ДЛК.
Вот свойства

Order? 35

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt

Counts
------
        16 Latin
         8 diagonal Latin
         8 pandiagonal
         8 cyclic 4-way
        24 center symmetric
        24 nfr
         1 nfc
         1 nfr nfc
         1 self-transpose
        20 orthogonal pair
         8 self-orthogonal
         1 transpose parity

8 ДЛК циклические пандиагональные и центрально-симметричные. Отлично!
Сейчас проверю эту группу на ортогональные пары.

Вот
Order? 35

Enter the name of the squares file: inp3
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file inp3-orthCounts.txt
..output file inp3-orthNos.txt
squares 24 total orthogonal pairs 180
Maximum pairs for square 1: 15
There are 23 other squares with this maximum number of pairs.
..output file inp3-1orths.txt
Pairs for square 1: 15

ЛК образовали 180 ортогональных пар.
24 ЛК имеют по 15 ОЛК.
Главный вопрос - клика!
Сейчас пойду спрошу у SageMath.
ID: 2245 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2246 - Posted: 2 Jun 2021, 4:44:20 UTC
Last modified: 2 Jun 2021, 4:48:14 UTC

Вот что сказала программа SageMath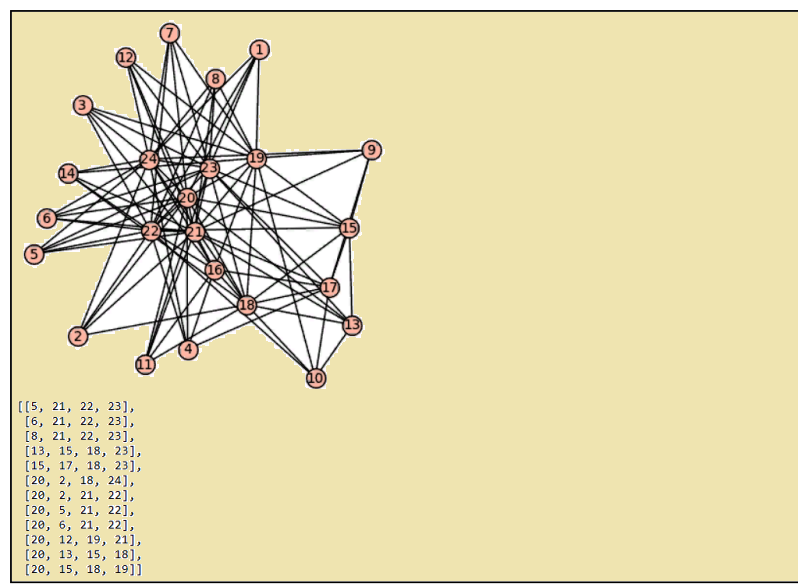



Да, клики только размера 4, клики размера 5 в этом наборе нет.
Зато в некоторых моих группах MOLS есть один ДЛК.
Например, самая первая клика
[5, 21, 22, 23]
содержит ДЛК (квадрат 5).
Сейчас я её покажу.
ID: 2246 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2247 - Posted: 2 Jun 2021, 4:55:00 UTC
Last modified: 2 Jun 2021, 4:56:48 UTC

Группа MOLS 35-го порядка, состоящая из четырёх ЛК, один из которых ДЛК;
построена вручную методом циклического сдвига

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2
21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3
22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4
23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5
24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7
26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8
27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9
28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10
29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11
30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12
31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13
32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2
30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5
33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0
28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3
31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1
29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4
32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4
34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3
33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2
32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1
31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0
30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2
34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1
33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0
32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1
31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0
30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2
34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1
33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0
32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3
[/code]
Проверяю группу программой GetOrthogonal

[code]Order? 35

Enter the name of the squares file: inp1
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file inp1-orthCounts.txt
..output file inp1-orthNos.txt
squares 4 total orthogonal pairs 6
Maximum pairs for square 1: 3
There are 3 other squares with this maximum number of pairs.
..output file inp1-1orths.txt
Pairs for square 1: 3
[/code]
Всё верно: ЛК образовали 6 ортогональных пар, и каждый квадрат имеет 3 ОЛК, то есть все ЛК взаимно ортогональны.

ДЛК, содержащийся в этой группе, циклический пандиагональный и центрально-симметричный, легко может быть превращён в идеальный.
ID: 2247 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2248 - Posted: 2 Jun 2021, 4:58:49 UTC
Last modified: 2 Jun 2021, 5:21:17 UTC

Ну, исследование набора на клику - это попутно.
Теперь займусь исследованием 8 циклических пандиагональных ДЛК, содержащихся в этом наборе.
Покатаю их на торе.

Кстати, выше я нашла тройку ДЛК 35-го порядка методом составных квдаратов.
В полученном сейчас наборе из 8 циклических пандиагональных ДЛК есть 8 троек

Order? 35

Enter the name of the squares file: inp1
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file inp1-orthCounts_1.txt
..output file inp1-orthNos_1.txt
squares 8 total orthogonal pairs 12
Maximum pairs for square 1: 3
There are 7 other squares with this maximum number of pairs.
..output file inp1-1orths_1.txt
Pairs for square 1: 3

Посмотрите таблицу ортогональных пар

1: [2,5,8],
2: [1,3,7],
3: [2,5,6],
4: [5,6,8],
5: [1,3,4],
6: [3,4,7],
7: [2,6,8],
8: [1,4,7]

Каждый из 8 ДЛК имеет 3 ОДЛК.
Замечательные троечки! Очень вкусные!

Тэк-с, ушла катать квадраты на торе :)
ID: 2248 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2249 - Posted: 2 Jun 2021, 5:45:05 UTC
Last modified: 2 Jun 2021, 7:05:11 UTC

Опа!
А катание квадратиков на торе ничего не дало. Неожиданный результат!
[Если хорошо подумать, то ожидаемый результат.]
После нормализации и удаления дубликатов получились исходные 8 ДЛК.
Очень интересно.
Ладно, покажу 8 нормализованных циклических пандиагональных ДЛК 35-го порядка, построенных вручную методом циклического сдвига

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3
 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5
 8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2
 5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4
 7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6
 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2
 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5
 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3
 7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1
 5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4
 8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11
24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12
25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13
26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
 5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
 7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
 8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8
21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9
22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10
23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13
31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12
30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11
29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10
28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9
27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8
26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
 8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7
25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
 7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6
24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5
23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
 5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4
22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3
21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2
21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3
22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
 5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4
23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5
24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
 7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6
25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
 8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7
26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8
27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9
28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10
29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11
30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12
31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13
32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10
34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9
33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8
32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7
31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
 7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6
30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5
29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
 5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4
28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3
27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2
26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1
25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0
24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10
 8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7
 5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1
34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9
 7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0
33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11
 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8
 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10
 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8
 7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6
 5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0
34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11 12 13
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9 10 11
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7  8  9
 8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5  6  7
 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3  4  5
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1  2  3
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34  0  1
4 5 6 7 8 9 10 11 12 13
26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8
21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9
22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10
23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13
31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12
30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11
29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10
28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9
27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8
26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7
25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5
23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4
22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3
21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2
21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3
22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4
23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5
24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7
26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8
27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9
28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10
29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11
30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12
31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13
32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10
34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9
33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8
32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7
31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5
29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4
28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3
27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2
26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1
25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0
24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1
34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0
33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12
11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0
34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1[/code]
Проверка свойств этих ДЛК утилитой GetType1

[code]Order? 35

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
8 diagonal Latin
8 pandiagonal
8 cyclic 4-way
8 center symmetric
8 nfr
5 orthogonal pair
8 self-orthogonal[/code]
Чудесные квадратики!
Все они центрально-симметричные, значит, их легко превратить в идеальные, достаточно преобразовать их в СН ДЛК.
Кроме того, все они являются SODLS и DSODLS.
ID: 2249 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2250 - Posted: 2 Jun 2021, 5:58:19 UTC
Last modified: 2 Jun 2021, 6:06:50 UTC

Посмотрим на троечку, построенную методом составных квадратов тут
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=133&postid=2010

DLK
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
2 3 4 5 6 0 1 9 10 11 12 13 7 8 16 17 18 19 20 14 15 23 24 25 26 27 21 22 30 31 32 33 34 28 29
4 5 6 0 1 2 3 11 12 13 7 8 9 10 18 19 20 14 15 16 17 25 26 27 21 22 23 24 32 33 34 28 29 30 31
6 0 1 2 3 4 5 13 7 8 9 10 11 12 20 14 15 16 17 18 19 27 21 22 23 24 25 26 34 28 29 30 31 32 33
1 2 3 4 5 6 0 8 9 10 11 12 13 7 15 16 17 18 19 20 14 22 23 24 25 26 27 21 29 30 31 32 33 34 28
3 4 5 6 0 1 2 10 11 12 13 7 8 9 17 18 19 20 14 15 16 24 25 26 27 21 22 23 31 32 33 34 28 29 30
5 6 0 1 2 3 4 12 13 7 8 9 10 11 19 20 14 15 16 17 18 26 27 21 22 23 24 25 33 34 28 29 30 31 32
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13
16 17 18 19 20 14 15 23 24 25 26 27 21 22 30 31 32 33 34 28 29 2 3 4 5 6 0 1 9 10 11 12 13 7 8
18 19 20 14 15 16 17 25 26 27 21 22 23 24 32 33 34 28 29 30 31 4 5 6 0 1 2 3 11 12 13 7 8 9 10
20 14 15 16 17 18 19 27 21 22 23 24 25 26 34 28 29 30 31 32 33 6 0 1 2 3 4 5 13 7 8 9 10 11 12
15 16 17 18 19 20 14 22 23 24 25 26 27 21 29 30 31 32 33 34 28 1 2 3 4 5 6 0 8 9 10 11 12 13 7
17 18 19 20 14 15 16 24 25 26 27 21 22 23 31 32 33 34 28 29 30 3 4 5 6 0 1 2 10 11 12 13 7 8 9
19 20 14 15 16 17 18 26 27 21 22 23 24 25 33 34 28 29 30 31 32 5 6 0 1 2 3 4 12 13 7 8 9 10 11
28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
30 31 32 33 34 28 29 2 3 4 5 6 0 1 9 10 11 12 13 7 8 16 17 18 19 20 14 15 23 24 25 26 27 21 22
32 33 34 28 29 30 31 4 5 6 0 1 2 3 11 12 13 7 8 9 10 18 19 20 14 15 16 17 25 26 27 21 22 23 24
34 28 29 30 31 32 33 6 0 1 2 3 4 5 13 7 8 9 10 11 12 20 14 15 16 17 18 19 27 21 22 23 24 25 26
29 30 31 32 33 34 28 1 2 3 4 5 6 0 8 9 10 11 12 13 7 15 16 17 18 19 20 14 22 23 24 25 26 27 21
31 32 33 34 28 29 30 3 4 5 6 0 1 2 10 11 12 13 7 8 9 17 18 19 20 14 15 16 24 25 26 27 21 22 23
33 34 28 29 30 31 32 5 6 0 1 2 3 4 12 13 7 8 9 10 11 19 20 14 15 16 17 18 26 27 21 22 23 24 25
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
9 10 11 12 13 7 8 16 17 18 19 20 14 15 23 24 25 26 27 21 22 30 31 32 33 34 28 29 2 3 4 5 6 0 1
11 12 13 7 8 9 10 18 19 20 14 15 16 17 25 26 27 21 22 23 24 32 33 34 28 29 30 31 4 5 6 0 1 2 3
13 7 8 9 10 11 12 20 14 15 16 17 18 19 27 21 22 23 24 25 26 34 28 29 30 31 32 33 6 0 1 2 3 4 5
8 9 10 11 12 13 7 15 16 17 18 19 20 14 22 23 24 25 26 27 21 29 30 31 32 33 34 28 1 2 3 4 5 6 0
10 11 12 13 7 8 9 17 18 19 20 14 15 16 24 25 26 27 21 22 23 31 32 33 34 28 29 30 3 4 5 6 0 1 2
12 13 7 8 9 10 11 19 20 14 15 16 17 18 26 27 21 22 23 24 25 33 34 28 29 30 31 32 5 6 0 1 2 3 4
21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
23 24 25 26 27 21 22 30 31 32 33 34 28 29 2 3 4 5 6 0 1 9 10 11 12 13 7 8 16 17 18 19 20 14 15
25 26 27 21 22 23 24 32 33 34 28 29 30 31 4 5 6 0 1 2 3 11 12 13 7 8 9 10 18 19 20 14 15 16 17
27 21 22 23 24 25 26 34 28 29 30 31 32 33 6 0 1 2 3 4 5 13 7 8 9 10 11 12 20 14 15 16 17 18 19
22 23 24 25 26 27 21 29 30 31 32 33 34 28 1 2 3 4 5 6 0 8 9 10 11 12 13 7 15 16 17 18 19 20 14
24 25 26 27 21 22 23 31 32 33 34 28 29 30 3 4 5 6 0 1 2 10 11 12 13 7 8 9 17 18 19 20 14 15 16
26 27 21 22 23 24 25 33 34 28 29 30 31 32 5 6 0 1 2 3 4 12 13 7 8 9 10 11 19 20 14 15 16 17 18

mate #1
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
3 4 5 6 0 1 2 10 11 12 13 7 8 9 17 18 19 20 14 15 16 24 25 26 27 21 22 23 31 32 33 34 28 29 30
6 0 1 2 3 4 5 13 7 8 9 10 11 12 20 14 15 16 17 18 19 27 21 22 23 24 25 26 34 28 29 30 31 32 33
2 3 4 5 6 0 1 9 10 11 12 13 7 8 16 17 18 19 20 14 15 23 24 25 26 27 21 22 30 31 32 33 34 28 29
5 6 0 1 2 3 4 12 13 7 8 9 10 11 19 20 14 15 16 17 18 26 27 21 22 23 24 25 33 34 28 29 30 31 32
1 2 3 4 5 6 0 8 9 10 11 12 13 7 15 16 17 18 19 20 14 22 23 24 25 26 27 21 29 30 31 32 33 34 28
4 5 6 0 1 2 3 11 12 13 7 8 9 10 18 19 20 14 15 16 17 25 26 27 21 22 23 24 32 33 34 28 29 30 31
21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
24 25 26 27 21 22 23 31 32 33 34 28 29 30 3 4 5 6 0 1 2 10 11 12 13 7 8 9 17 18 19 20 14 15 16
27 21 22 23 24 25 26 34 28 29 30 31 32 33 6 0 1 2 3 4 5 13 7 8 9 10 11 12 20 14 15 16 17 18 19
23 24 25 26 27 21 22 30 31 32 33 34 28 29 2 3 4 5 6 0 1 9 10 11 12 13 7 8 16 17 18 19 20 14 15
26 27 21 22 23 24 25 33 34 28 29 30 31 32 5 6 0 1 2 3 4 12 13 7 8 9 10 11 19 20 14 15 16 17 18
22 23 24 25 26 27 21 29 30 31 32 33 34 28 1 2 3 4 5 6 0 8 9 10 11 12 13 7 15 16 17 18 19 20 14
25 26 27 21 22 23 24 32 33 34 28 29 30 31 4 5 6 0 1 2 3 11 12 13 7 8 9 10 18 19 20 14 15 16 17
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
10 11 12 13 7 8 9 17 18 19 20 14 15 16 24 25 26 27 21 22 23 31 32 33 34 28 29 30 3 4 5 6 0 1 2
13 7 8 9 10 11 12 20 14 15 16 17 18 19 27 21 22 23 24 25 26 34 28 29 30 31 32 33 6 0 1 2 3 4 5
9 10 11 12 13 7 8 16 17 18 19 20 14 15 23 24 25 26 27 21 22 30 31 32 33 34 28 29 2 3 4 5 6 0 1
12 13 7 8 9 10 11 19 20 14 15 16 17 18 26 27 21 22 23 24 25 33 34 28 29 30 31 32 5 6 0 1 2 3 4
8 9 10 11 12 13 7 15 16 17 18 19 20 14 22 23 24 25 26 27 21 29 30 31 32 33 34 28 1 2 3 4 5 6 0
11 12 13 7 8 9 10 18 19 20 14 15 16 17 25 26 27 21 22 23 24 32 33 34 28 29 30 31 4 5 6 0 1 2 3
28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
31 32 33 34 28 29 30 3 4 5 6 0 1 2 10 11 12 13 7 8 9 17 18 19 20 14 15 16 24 25 26 27 21 22 23
34 28 29 30 31 32 33 6 0 1 2 3 4 5 13 7 8 9 10 11 12 20 14 15 16 17 18 19 27 21 22 23 24 25 26
30 31 32 33 34 28 29 2 3 4 5 6 0 1 9 10 11 12 13 7 8 16 17 18 19 20 14 15 23 24 25 26 27 21 22
33 34 28 29 30 31 32 5 6 0 1 2 3 4 12 13 7 8 9 10 11 19 20 14 15 16 17 18 26 27 21 22 23 24 25
29 30 31 32 33 34 28 1 2 3 4 5 6 0 8 9 10 11 12 13 7 15 16 17 18 19 20 14 22 23 24 25 26 27 21
32 33 34 28 29 30 31 4 5 6 0 1 2 3 11 12 13 7 8 9 10 18 19 20 14 15 16 17 25 26 27 21 22 23 24
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13
17 18 19 20 14 15 16 24 25 26 27 21 22 23 31 32 33 34 28 29 30 3 4 5 6 0 1 2 10 11 12 13 7 8 9
20 14 15 16 17 18 19 27 21 22 23 24 25 26 34 28 29 30 31 32 33 6 0 1 2 3 4 5 13 7 8 9 10 11 12
16 17 18 19 20 14 15 23 24 25 26 27 21 22 30 31 32 33 34 28 29 2 3 4 5 6 0 1 9 10 11 12 13 7 8
19 20 14 15 16 17 18 26 27 21 22 23 24 25 33 34 28 29 30 31 32 5 6 0 1 2 3 4 12 13 7 8 9 10 11
15 16 17 18 19 20 14 22 23 24 25 26 27 21 29 30 31 32 33 34 28 1 2 3 4 5 6 0 8 9 10 11 12 13 7
18 19 20 14 15 16 17 25 26 27 21 22 23 24 32 33 34 28 29 30 31 4 5 6 0 1 2 3 11 12 13 7 8 9 10

mate #2
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
4 5 6 0 1 2 3 11 12 13 7 8 9 10 18 19 20 14 15 16 17 25 26 27 21 22 23 24 32 33 34 28 29 30 31
1 2 3 4 5 6 0 8 9 10 11 12 13 7 15 16 17 18 19 20 14 22 23 24 25 26 27 21 29 30 31 32 33 34 28
5 6 0 1 2 3 4 12 13 7 8 9 10 11 19 20 14 15 16 17 18 26 27 21 22 23 24 25 33 34 28 29 30 31 32
2 3 4 5 6 0 1 9 10 11 12 13 7 8 16 17 18 19 20 14 15 23 24 25 26 27 21 22 30 31 32 33 34 28 29
6 0 1 2 3 4 5 13 7 8 9 10 11 12 20 14 15 16 17 18 19 27 21 22 23 24 25 26 34 28 29 30 31 32 33
3 4 5 6 0 1 2 10 11 12 13 7 8 9 17 18 19 20 14 15 16 24 25 26 27 21 22 23 31 32 33 34 28 29 30
21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
25 26 27 21 22 23 24 32 33 34 28 29 30 31 4 5 6 0 1 2 3 11 12 13 7 8 9 10 18 19 20 14 15 16 17
22 23 24 25 26 27 21 29 30 31 32 33 34 28 1 2 3 4 5 6 0 8 9 10 11 12 13 7 15 16 17 18 19 20 14
26 27 21 22 23 24 25 33 34 28 29 30 31 32 5 6 0 1 2 3 4 12 13 7 8 9 10 11 19 20 14 15 16 17 18
23 24 25 26 27 21 22 30 31 32 33 34 28 29 2 3 4 5 6 0 1 9 10 11 12 13 7 8 16 17 18 19 20 14 15
27 21 22 23 24 25 26 34 28 29 30 31 32 33 6 0 1 2 3 4 5 13 7 8 9 10 11 12 20 14 15 16 17 18 19
24 25 26 27 21 22 23 31 32 33 34 28 29 30 3 4 5 6 0 1 2 10 11 12 13 7 8 9 17 18 19 20 14 15 16
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
11 12 13 7 8 9 10 18 19 20 14 15 16 17 25 26 27 21 22 23 24 32 33 34 28 29 30 31 4 5 6 0 1 2 3
8 9 10 11 12 13 7 15 16 17 18 19 20 14 22 23 24 25 26 27 21 29 30 31 32 33 34 28 1 2 3 4 5 6 0
12 13 7 8 9 10 11 19 20 14 15 16 17 18 26 27 21 22 23 24 25 33 34 28 29 30 31 32 5 6 0 1 2 3 4
9 10 11 12 13 7 8 16 17 18 19 20 14 15 23 24 25 26 27 21 22 30 31 32 33 34 28 29 2 3 4 5 6 0 1
13 7 8 9 10 11 12 20 14 15 16 17 18 19 27 21 22 23 24 25 26 34 28 29 30 31 32 33 6 0 1 2 3 4 5
10 11 12 13 7 8 9 17 18 19 20 14 15 16 24 25 26 27 21 22 23 31 32 33 34 28 29 30 3 4 5 6 0 1 2
28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
32 33 34 28 29 30 31 4 5 6 0 1 2 3 11 12 13 7 8 9 10 18 19 20 14 15 16 17 25 26 27 21 22 23 24
29 30 31 32 33 34 28 1 2 3 4 5 6 0 8 9 10 11 12 13 7 15 16 17 18 19 20 14 22 23 24 25 26 27 21
33 34 28 29 30 31 32 5 6 0 1 2 3 4 12 13 7 8 9 10 11 19 20 14 15 16 17 18 26 27 21 22 23 24 25
30 31 32 33 34 28 29 2 3 4 5 6 0 1 9 10 11 12 13 7 8 16 17 18 19 20 14 15 23 24 25 26 27 21 22
34 28 29 30 31 32 33 6 0 1 2 3 4 5 13 7 8 9 10 11 12 20 14 15 16 17 18 19 27 21 22 23 24 25 26
31 32 33 34 28 29 30 3 4 5 6 0 1 2 10 11 12 13 7 8 9 17 18 19 20 14 15 16 24 25 26 27 21 22 23
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13
18 19 20 14 15 16 17 25 26 27 21 22 23 24 32 33 34 28 29 30 31 4 5 6 0 1 2 3 11 12 13 7 8 9 10
15 16 17 18 19 20 14 22 23 24 25 26 27 21 29 30 31 32 33 34 28 1 2 3 4 5 6 0 8 9 10 11 12 13 7
19 20 14 15 16 17 18 26 27 21 22 23 24 25 33 34 28 29 30 31 32 5 6 0 1 2 3 4 12 13 7 8 9 10 11
16 17 18 19 20 14 15 23 24 25 26 27 21 22 30 31 32 33 34 28 29 2 3 4 5 6 0 1 9 10 11 12 13 7 8
20 14 15 16 17 18 19 27 21 22 23 24 25 26 34 28 29 30 31 32 33 6 0 1 2 3 4 5 13 7 8 9 10 11 12
17 18 19 20 14 15 16 24 25 26 27 21 22 23 31 32 33 34 28 29 30 3 4 5 6 0 1 2 10 11 12 13 7 8 9

mate #3
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
5 6 0 1 2 3 4 12 13 7 8 9 10 11 19 20 14 15 16 17 18 26 27 21 22 23 24 25 33 34 28 29 30 31 32
3 4 5 6 0 1 2 10 11 12 13 7 8 9 17 18 19 20 14 15 16 24 25 26 27 21 22 23 31 32 33 34 28 29 30
1 2 3 4 5 6 0 8 9 10 11 12 13 7 15 16 17 18 19 20 14 22 23 24 25 26 27 21 29 30 31 32 33 34 28
6 0 1 2 3 4 5 13 7 8 9 10 11 12 20 14 15 16 17 18 19 27 21 22 23 24 25 26 34 28 29 30 31 32 33
4 5 6 0 1 2 3 11 12 13 7 8 9 10 18 19 20 14 15 16 17 25 26 27 21 22 23 24 32 33 34 28 29 30 31
2 3 4 5 6 0 1 9 10 11 12 13 7 8 16 17 18 19 20 14 15 23 24 25 26 27 21 22 30 31 32 33 34 28 29
21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
26 27 21 22 23 24 25 33 34 28 29 30 31 32 5 6 0 1 2 3 4 12 13 7 8 9 10 11 19 20 14 15 16 17 18
24 25 26 27 21 22 23 31 32 33 34 28 29 30 3 4 5 6 0 1 2 10 11 12 13 7 8 9 17 18 19 20 14 15 16
22 23 24 25 26 27 21 29 30 31 32 33 34 28 1 2 3 4 5 6 0 8 9 10 11 12 13 7 15 16 17 18 19 20 14
27 21 22 23 24 25 26 34 28 29 30 31 32 33 6 0 1 2 3 4 5 13 7 8 9 10 11 12 20 14 15 16 17 18 19
25 26 27 21 22 23 24 32 33 34 28 29 30 31 4 5 6 0 1 2 3 11 12 13 7 8 9 10 18 19 20 14 15 16 17
23 24 25 26 27 21 22 30 31 32 33 34 28 29 2 3 4 5 6 0 1 9 10 11 12 13 7 8 16 17 18 19 20 14 15
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6
12 13 7 8 9 10 11 19 20 14 15 16 17 18 26 27 21 22 23 24 25 33 34 28 29 30 31 32 5 6 0 1 2 3 4
10 11 12 13 7 8 9 17 18 19 20 14 15 16 24 25 26 27 21 22 23 31 32 33 34 28 29 30 3 4 5 6 0 1 2
8 9 10 11 12 13 7 15 16 17 18 19 20 14 22 23 24 25 26 27 21 29 30 31 32 33 34 28 1 2 3 4 5 6 0
13 7 8 9 10 11 12 20 14 15 16 17 18 19 27 21 22 23 24 25 26 34 28 29 30 31 32 33 6 0 1 2 3 4 5
11 12 13 7 8 9 10 18 19 20 14 15 16 17 25 26 27 21 22 23 24 32 33 34 28 29 30 31 4 5 6 0 1 2 3
9 10 11 12 13 7 8 16 17 18 19 20 14 15 23 24 25 26 27 21 22 30 31 32 33 34 28 29 2 3 4 5 6 0 1
28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
33 34 28 29 30 31 32 5 6 0 1 2 3 4 12 13 7 8 9 10 11 19 20 14 15 16 17 18 26 27 21 22 23 24 25
31 32 33 34 28 29 30 3 4 5 6 0 1 2 10 11 12 13 7 8 9 17 18 19 20 14 15 16 24 25 26 27 21 22 23
29 30 31 32 33 34 28 1 2 3 4 5 6 0 8 9 10 11 12 13 7 15 16 17 18 19 20 14 22 23 24 25 26 27 21
34 28 29 30 31 32 33 6 0 1 2 3 4 5 13 7 8 9 10 11 12 20 14 15 16 17 18 19 27 21 22 23 24 25 26
32 33 34 28 29 30 31 4 5 6 0 1 2 3 11 12 13 7 8 9 10 18 19 20 14 15 16 17 25 26 27 21 22 23 24
30 31 32 33 34 28 29 2 3 4 5 6 0 1 9 10 11 12 13 7 8 16 17 18 19 20 14 15 23 24 25 26 27 21 22
14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0 1 2 3 4 5 6 7 8 9 10 11 12 13
19 20 14 15 16 17 18 26 27 21 22 23 24 25 33 34 28 29 30 31 32 5 6 0 1 2 3 4 12 13 7 8 9 10 11
17 18 19 20 14 15 16 24 25 26 27 21 22 23 31 32 33 34 28 29 30 3 4 5 6 0 1 2 10 11 12 13 7 8 9
15 16 17 18 19 20 14 22 23 24 25 26 27 21 29 30 31 32 33 34 28 1 2 3 4 5 6 0 8 9 10 11 12 13 7
20 14 15 16 17 18 19 27 21 22 23 24 25 26 34 28 29 30 31 32 33 6 0 1 2 3 4 5 13 7 8 9 10 11 12
18 19 20 14 15 16 17 25 26 27 21 22 23 24 32 33 34 28 29 30 31 4 5 6 0 1 2 3 11 12 13 7 8 9 10
16 17 18 19 20 14 15 23 24 25 26 27 21 22 30 31 32 33 34 28 29 2 3 4 5 6 0 1 9 10 11 12 13 7 8

Эти ДЛК пандиагональные и центрально-симметричные.
А есть ли в них какая-нибудь цикличность?
Ещё одна загадка, господа :) Попробуйте-ка разгадать.

Проверила эти ДЛК утилитой GetCyclic, цикличности в строках, или в столбцах, или в диагоналях одного из двух направлений утилита не обнаружила.
Следовательно, если и есть цикличность, то в направлениях (1,х).
А скорее всего, это не циклические пандиагональные ДЛК.
ID: 2250 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2251 - Posted: 2 Jun 2021, 7:00:34 UTC
Last modified: 2 Jun 2021, 12:57:38 UTC

По команде
sage: for x in designs.mutually_orthogonal_latin_squares(36,37): print(x,'\n')

построила в программе SageMath полную систему MOLS 37-го порядка, состоящую из 36 ЛК, среди которых 34 являются ДЛК.
Свойства ЛК этой полной сиcnемы MOLS, выданные утилитой GetType1

Order? 37

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt

Counts
------
         2 Latin
        34 diagonal Latin
        34 associative
        34 pandiagonal
        34 cyclic 4-way
        34 ultramagic
         2 center symmetric
         1 nfr
        35 natural \diagonal
         1 self-transpose
        35 orthogonal pair
        34 self-orthogonal
        35 symmetric parity
         1 transpose parity

Тут всё прекрасно: 34 циклических пандиагональных (к тому же, идеальных) ДЛК.
Показываю первые два ДЛК

 0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35
36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34
35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33
34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32
33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31
32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30
31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29
30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28
29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27
28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26
27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25
26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24
25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23
24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22
23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21
22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20
21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19
20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18
19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17
18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16
17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15
16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14
15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13
14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12
13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11
12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10
11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9
10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8
 9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7
 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6
 7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5
 6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4
 5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3
 4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2
 3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1
 2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36  1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0
 1  3  5  7  9 11 13 15 17 19 21 23 25 27 29 31 33 35  0  2  4  6  8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 

 0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34
35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32
33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30
31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28
29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26
27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24
25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22
23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20
21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18
19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16
17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14
15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12
13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10
11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8
 9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6
 7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4
 5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2
 3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0
 1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35
36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33
34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31
32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29
30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27
28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25
26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23
24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21
22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19
20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17
18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15
16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13
14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11
12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9
10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7
 8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5
 6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3
 4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36  2  5  8 11 14 17 20 23 26 29 32 35  1
 2  5  8 11 14 17 20 23 26 29 32 35  1  4  7 10 13 16 19 22 25 28 31 34  0  3  6  9 12 15 18 21 24 27 30 33 36

Ну, до полуциклических пандиагональных ДЛК 37-го порядка мы ещё не доросли :)
Я даже для порядка 19 не нашла все полуциклические пандиагональные ДЛК.

PS. Заметьте: ДЛК здесь представлены в формате СН ДЛК, поэтому они уже идеальные (ассоциативные и пандиагональные).
ID: 2251 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Previous · 1 . . . 4 · 5 · 6 · 7

Message boards : Science : Semi-cyclic pandiagonal DLS of prime order n>11

©2024 ©2024 Progger & Stefano Tognon (ice00) & Reese