Thread 'Алгоритм получения двушек для порядков n=4k+2'

Message boards : Science : Алгоритм получения двушек для порядков n=4k+2
Message board moderation

To post messages, you must log in.

Previous · 1 · 2 · 3 · 4 · 5 . . . 11 · Next

AuthorMessage
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2276 - Posted: 5 Jun 2021, 10:05:32 UTC

Показываю основной ДЛК 11-ки 20-го порядка и три ортогональки

DLK
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17
 3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7
10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5
11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4
 9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6
16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13
19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12
17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3
 6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1
 7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0
 5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2
12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11
14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9
15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8
13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10

mate #1
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17
12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11
15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8
13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10
14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3
 7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0
 5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2
 6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1
16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12
17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13
 8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7
11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4
 9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6
10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5

mate #2
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17
12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11
15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8
13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10
14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3
 7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0
 5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2
 6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1
16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12
17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13
 8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  7  5  6  4
11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0  4  6  5  7
 9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  7  4  6
10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1  6  4  7  5

mate #3
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17
12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11
15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8
13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10
14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3
 7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0
 5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2
 6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1
16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12
17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13
 8  9 10 11 12 13 14 15 16 17 18 19  0  2  1  3  4  5  6  7
11 10  9  8 15 14 13 12 19 18 17 16  3  1  2  0  7  6  5  4
 9  8 11 10 13 12 15 14 17 16 19 18  2  0  3  1  5  4  7  6
10 11  8  9 14 15 12 13 18 19 16 17  1  3  0  2  6  7  4  5

Вот для порядка 20 11-ку нашла легко, а для порядка 10 нету 11-ки до сих пор :(
ID: 2276 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2277 - Posted: 5 Jun 2021, 10:40:27 UTC

А между тем метод Пелегрино-Ланселотти для порядка 66 сработал!
Найдены 6-ка и 18-ка 66-го порядка!

Order? 66

Enter the name of the squares file: inp
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file inp-orthCounts.txt
..output file inp-orthNos.txt
squares 26 total orthogonal pairs 24
Maximum pairs for square 25: 18
This is the only square with this maximum number of pairs.
..output file inp-25orths.txt
Pairs for square 25: 18

Смотрим таблицу ортогональных пар

1: [25],
2: [25],
3: [25],
4: [25],
5: [25],
6: [25],
7: [26],
8: [26],
9: [26],
10: [26],
11: [26],
12: [26],
13: [25],
14: [25],
15: [25],
16: [25],
17: [25],
18: [25],
19: [25],
20: [25],
21: [25],
22: [25],
23: [25],
24: [25],
25: [1,2,3,4,5,6,13,14,15,16],
25: [17,18,19,20,21,22,23,24],
26: [7,8,9,10,11,12]

Квадрат 25 имеет 18 ОДЛК, квадрат 26 имеет 6 ОДЛК.
Остальные однушки.
Грандиозный результат!
Сейчас нарисую эту конфигурацию ОДЛК 66-го порядка.
ID: 2277 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2278 - Posted: 5 Jun 2021, 10:53:53 UTC
Last modified: 5 Jun 2021, 18:19:59 UTC

Готово!



Собственно, здесь две отдельные конфигурации: шестёрка и 18-ка.
Интересно: ожидалась 24-ка, но она распалась на шестёрку и 18-ку.

Итак, для порядка 66 оценка очень хорошо улучшена
a(66) >= 18.

Попозже выложу 18-ку 66-го порядка на Яндекс.Диск.
ID: 2278 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2279 - Posted: 5 Jun 2021, 16:31:53 UTC
Last modified: 5 Jun 2021, 16:38:29 UTC

Harry White применил алгоритм к большому количеству ДЛК порядков 18, 22 и 26.
Цитирую его письмо
I did this using the files sent to you:
10,000 order 18; 5,886 order 22; 2986 order 26.
These numbers doubled with their transposed squares added.
Then with the centers replaced by all the order 4 SODLS, the numbers are 960,000; 565,056; and 286,656.
I normalized these and sorted to confirm that there were no duplicates.

Грандиозно!

Обработка полученного набора ДЛК 26-го порядка завершилась.
Протокол работы программы GetOrthogonal

Order? 26
 
Enter the name of the squares file: 26aAllCenter4ToNFR
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file 26aAllCenter4ToNFR-orthCounts.txt
..output file 26aAllCenter4ToNFR-orthNos.txt
    .. increasing LS store to     100,000
    .. increasing LS store to     200,000
    .. increasing LS store to     400,000
squares 286656 total orthogonal pairs 3545856
Maximum pairs for square 913: 48
There are 8831 other squares with this maximum number of pairs.
..output file 26aAllCenter4ToNFR-913orths.txt
Pairs for square 913: 48
 
elapsed time 11:32:42

Найдено 8832 ДЛК, имеющих 48 ОДЛК!!!
Это рекордный результат на данный момент.

Обработка наборов ДЛК порядков 18 и 22 ещё не завершена.

Показываю основной ДЛК первой 48-ки 26-го порядка и несколько ортогоналек

DLK
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
10 11 23  1 12  3 25 24 22 15  9 13 21 14 20 16 17  7  0  8  5 19  4  2  6 18
 9 10 13  4 23 21 12  6  2 19 18 14  5 20  8 17 22 11 15 25  0  3  1 24  7 16
 7  9 10 14  3  4  5 21 24  1  0 20 25  8 15 19 13 18  6 11 12 23  2 22 16 17
11 22  9 10 20 12  3 25  5  2 23  8  6 15 18 14  7 24 13 21  4  1 19 16 17  0
 4 13 19  9 10  8 21 12  6 25  1 15 24 18  7 22  2 14  5  3 23  0 16 17 11 20
23  3 14  0  9 10 15  5 21 24  6 18  2  7 22  1 20 25 12  4 11 16 17 13  8 19
24  4 12 20 11  9 10 18 25  5  2  7  1 22 19  8  6 21  3 13 16 17 14 15  0 23
 1  2  3 21  8 13  9 10  7  6 25 22 23 19  0 24  5 12 14 16 17 20 18 11  4 15
 6 23  1 12  5 15 14  9 10 22 24 19  4  0 11 25 21 20 16 17  8  7 13  3 18  2
 2 24  4 23 21 25 18 20  9 10 19  0  3 11 13  5  8 16 17 15 22 14 12  7  1  6
14 20  8 15 18  7 22 19  0 11 13 10  9 17 16 12  3  4 23  1  2 24  6 25  5 21
21  5 25  6 24  2  1 23  4  3 12 16 17  9 10  0 19 22  7 18 15  8 20 14 13 11
12 21  5 25  6 24  2  1 23  4  3  9 10 16 17 11  0 19 22  7 18 15  8 20 14 13
20  8 15 18  7 22 19  0 11 13 14 17 16 10  9 21 12  3  4 23  1  2 24  6 25  5
19 18  0  2 22  6 13  4 17 16 11  5 14 12  1  3 10  9 24 20 21 25 23  8 15  7
15 19 24  7 25 11 23 17 16  0 22 21 13  3  2 18  4 10  9  6 14 12  5  1 20  8
22  6 18  5  0  1 17 16 19  7  8 12 11  4 24 20 15 23 10  9 25 13  3 21  2 14
25 15 21 19  2 17 16 22 18 20  7  3  0 23  6 13 14  8  1 10  9  5 11  4 12 24
 8 12 22 24 17 16  7 15 14 18  5  4 19  1 25  6 11 13 20  2 10  9 21  0 23  3
 3  7  6 17 16 18  8 13 15 21 20 23 22  2  5  4 25  0 11 14 24 10  9 12 19  1
18 25 17 16 15 20 11  8 12 14  4  1  7 24 21  2 23  5 19  0 13  6 10  9  3 22
 5 17 16  8 14  0 20  3 13 23 15  2 18  6 12  7 24  1 21 22 19 11 25 10  9  4
17 16 20 13 19 14  4 11  1  8 21 24 15 25  3 23 18  6  2 12  7 22  0  5 10  9
16 14 11 22 13 23  0  2 20 12 17  6  8  5  4  9  1 15 25 24  3 18  7 19 21 10
13  0  7 11  1 19 24 14  3 17 16 25 20 21 23 10  9  2  8  5  6  4 15 18 22 12

mate #1
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
 8  4  1  2 17 25 20  5 10  6  7 14 22 12 19 21 15  9 16 13  3 18 23 24 11  0
10  6 25  1  2 15 11 13 20  8  5 19 18 22 16  0  7 21 12 17  9 23 24 14  4  3
20  8  5 11  1  2  0 14 12 13  6 16  9 18 21 10  3 22 15  7 23 24 19 25 17  4
 5 13  6 20 14  1  2  4 19 22 12 21  7  9  3 17 18  0 10 23 24 16 11 15 25  8
22 20 12  5 13 19  1  2 25 16 18  3 10  7 17  9  4  8 23 24 21 14  0 11  6 15
 9 18 13 22 20 12 16  1  2 11 21 17  8 10 15 25  6 23 24  3 19  4 14  5  0  7
 3  7  9 12 18 13 22 21  1  2 14 15  6  8  0  5 23 24 17 16 25 19 20  4 10 11
19 17 10  7 22  9 12 18  3  1  2  0  5  6  4 23 24 15 21 11 16 13 25  8 14 20
 2 16 15  8 10 18  7 22  9 17  1  4 20  5 25 24  0  3 14 21 12 11  6 19 13 23
 1  2 21  0  6  8  9 10 18  7 15 25 13 20 11  4 17 19  3 22 14  5 16 12 23 24
 4 25 11 14 19 16 21  3 17 15  0  1  2 23 24 22 12 13 20  5  6  8 10  7  9 18
13 12 22 18  9  7 10  8  6  5 20 23 24  1  2 11 25  4  0 15 17  3 21 16 19 14
25 11 14 19 16 21  3 17 15  0  4 24 23  2  1 13 20  5  6  8 10  7  9 18 22 12
11 14 19 16 21  3 17 15  0  4 25  2  1 24 23  8 10  7  9 18 22 12 13 20  5  6
16 24 23 15 11 17  8 19  7 18 22 13  0  4 12 20 21 14 25  9  5 10  3  6  2  1
24 23 17 25  3 10 14  9 22 12 19 20 15  0 13  1  5 16 11  4 18  6  7 21  8  2
23  3  4 21  7 11 18 12 13 14 24  5 17 15 20  2  1  6 19 25  0 22  8  9 16 10
21  0 16  9 25 22 13 20 11 24 23  6  3 17  5  7  2  1  8 14  4 15 12 10 18 19
15 19 18  4 12 20  5 25 24 23 16  8 21  3  6 14  9  2  1 10 11  0 17 13  7 22
14 22  0 13  5  6  4 24 23 19 17 10 16 21  8 12 11 18  2  1  7 25 15  3 20  9
12 15 20  6  8  0 24 23 14  3 11  7 19 16 10 18 13 25 22  2  1  9  4 17 21  5
17  5  8 10 15 24 23 11 21 25 13  9 14 19  7  6 22 20  4 12  2  1 18  0  3 16
 6 10  7 17 24 23 25 16  4 20  3 18 11 14  9 19  8 12  5  0 13  2  1 22 15 21
 7  9  3 24 23  4 19  0  5 21  8 22 25 11 18 16 14 10 13  6 15 20  2  1 12 17
18 21 24 23  0 14 15  6 16 10  9 12  4 25 22  3 19 11  7 20  8 17  5  2  1 13

mate #2
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
 8  4  1  2 17 25 20  5 10  6  7 14 22 12 19 21 15  9 16 13  3 18 23 24 11  0
10  6 25  1  2 15 11 13 20  8  5 19 18 22 16  0  7 21 12 17  9 23 24 14  4  3
20  8  5 11  1  2  0 14 12 13  6 16  9 18 21 10  3 22 15  7 23 24 19 25 17  4
 5 13  6 20 14  1  2  4 19 22 12 21  7  9  3 17 18  0 10 23 24 16 11 15 25  8
22 20 12  5 13 19  1  2 25 16 18  3 10  7 17  9  4  8 23 24 21 14  0 11  6 15
 9 18 13 22 20 12 16  1  2 11 21 17  8 10 15 25  6 23 24  3 19  4 14  5  0  7
 3  7  9 12 18 13 22 21  1  2 14 15  6  8  0  5 23 24 17 16 25 19 20  4 10 11
19 17 10  7 22  9 12 18  3  1  2  0  5  6  4 23 24 15 21 11 16 13 25  8 14 20
 2 16 15  8 10 18  7 22  9 17  1  4 20  5 25 24  0  3 14 21 12 11  6 19 13 23
 1  2 21  0  6  8  9 10 18  7 15 25 13 20 11  4 17 19  3 22 14  5 16 12 23 24
 4 25 11 14 19 16 21  3 17 15  0  1  2 24 23 22 12 13 20  5  6  8 10  7  9 18
13 12 22 18  9  7 10  8  6  5 20 24 23  1  2 11 25  4  0 15 17  3 21 16 19 14
25 11 14 19 16 21  3 17 15  0  4 23 24  2  1 13 20  5  6  8 10  7  9 18 22 12
11 14 19 16 21  3 17 15  0  4 25  2  1 23 24  8 10  7  9 18 22 12 13 20  5  6
16 24 23 15 11 17  8 19  7 18 22 13  0  4 12 20 21 14 25  9  5 10  3  6  2  1
24 23 17 25  3 10 14  9 22 12 19 20 15  0 13  1  5 16 11  4 18  6  7 21  8  2
23  3  4 21  7 11 18 12 13 14 24  5 17 15 20  2  1  6 19 25  0 22  8  9 16 10
21  0 16  9 25 22 13 20 11 24 23  6  3 17  5  7  2  1  8 14  4 15 12 10 18 19
15 19 18  4 12 20  5 25 24 23 16  8 21  3  6 14  9  2  1 10 11  0 17 13  7 22
14 22  0 13  5  6  4 24 23 19 17 10 16 21  8 12 11 18  2  1  7 25 15  3 20  9
12 15 20  6  8  0 24 23 14  3 11  7 19 16 10 18 13 25 22  2  1  9  4 17 21  5
17  5  8 10 15 24 23 11 21 25 13  9 14 19  7  6 22 20  4 12  2  1 18  0  3 16
 6 10  7 17 24 23 25 16  4 20  3 18 11 14  9 19  8 12  5  0 13  2  1 22 15 21
 7  9  3 24 23  4 19  0  5 21  8 22 25 11 18 16 14 10 13  6 15 20  2  1 12 17
18 21 24 23  0 14 15  6 16 10  9 12  4 25 22  3 19 11  7 20  8 17  5  2  1 13
. . . . . 

mate #47
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
 7  4  1  2 17 25 20  5  9  6  8 14 22 12 19 21 15 10 16 13  3 18 23 24 11  0
 6  9 25  1  2 15 11 13 20  8  5 19 18 22 16  0  7 21 12 17 10 23 24 14  4  3
20  5  8 11  1  2  0 14 12 13  6 16 10 18 21  9  3 22 15  7 23 24 19 25 17  4
 5 13 20  6 14  1  2  4 19 22 12 21  7 10  3 17 18  0  9 23 24 16 11 15 25  8
22 20 12 13  5 19  1  2 25 16 18  3  9  7 17 10  4  8 23 24 21 14  0 11  6 15
10 18 13 22 12 20 16  1  2 11 21 17  8  9 15 25  6 23 24  3 19  4 14  5  0  7
 3  7 10 12 18 22 13 21  1  2 14 15  6  8  0  5 23 24 17 16 25 19 20  4  9 11
19 17  9  7 22 10 18 12  3  1  2  0  5  6  4 23 24 15 21 11 16 13 25  8 14 20
 2 16 15  8  9 18  7 10 22 17  1  4 20  5 25 24  0  3 14 21 12 11  6 19 13 23
 1  2 21  0  6  8 10  9  7 18 15 25 13 20 11  4 17 19  3 22 14  5 16 12 23 24
 4 25 11 14 19 16 21  3 17 15  0 23 24  1  2 22 12 13 20  5  6  8  9  7 10 18
13 12 22 18 10  7  9  8  6  5 20  1  2 23 24 11 25  4  0 15 17  3 21 16 19 14
25 11 14 19 16 21  3 17 15  0  4  2  1 24 23 13 20  5  6  8  9  7 10 18 22 12
11 14 19 16 21  3 17 15  0  4 25 24 23  2  1  8  9  7 10 18 22 12 13 20  5  6
16 24 23 15 11 17  8 19 18  7 22 13  0  4 12 20 21 14 25 10  5  9  3  6  2  1
24 23 17 25  3  9 14 22 10 12 19 20 15  0 13  1  5 16 11  4 18  6  7 21  8  2
23  3  4 21  7 11 12 18 13 14 24  5 17 15 20  2  1  6 19 25  0 22  8 10 16  9
21  0 16 10 25 13 22 20 11 24 23  6  3 17  5  7  2  1  8 14  4 15 12  9 18 19
15 19 18  4 20 12  5 25 24 23 16  8 21  3  6 14 10  2  1  9 11  0 17 13  7 22
14 22  0  5 13  6  4 24 23 19 17  9 16 21  8 12 11 18  2  1  7 25 15  3 20 10
12 15  6 20  8  0 24 23 14  3 11  7 19 16  9 18 13 25 22  2  1 10  4 17 21  5
17  8  5  9 15 24 23 11 21 25 13 10 14 19  7  6 22 20  4 12  2  1 18  0  3 16
 9  6  7 17 24 23 25 16  4 20  3 18 11 14 10 19  8 12  5  0 13  2  1 22 15 21
 8 10  3 24 23  4 19  0  5 21  7 22 25 11 18 16 14  9 13  6 15 20  2  1 12 17
18 21 24 23  0 14 15  6 16 10  9 12  4 25 22  3 19 11  7 20  8 17  5  2  1 13

mate #48
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
 7  4  1  2 17 25 20  5  9  6  8 14 22 12 19 21 15 10 16 13  3 18 23 24 11  0
 6  9 25  1  2 15 11 13 20  8  5 19 18 22 16  0  7 21 12 17 10 23 24 14  4  3
20  5  8 11  1  2  0 14 12 13  6 16 10 18 21  9  3 22 15  7 23 24 19 25 17  4
 5 13 20  6 14  1  2  4 19 22 12 21  7 10  3 17 18  0  9 23 24 16 11 15 25  8
22 20 12 13  5 19  1  2 25 16 18  3  9  7 17 10  4  8 23 24 21 14  0 11  6 15
10 18 13 22 12 20 16  1  2 11 21 17  8  9 15 25  6 23 24  3 19  4 14  5  0  7
 3  7 10 12 18 22 13 21  1  2 14 15  6  8  0  5 23 24 17 16 25 19 20  4  9 11
19 17  9  7 22 10 18 12  3  1  2  0  5  6  4 23 24 15 21 11 16 13 25  8 14 20
 2 16 15  8  9 18  7 10 22 17  1  4 20  5 25 24  0  3 14 21 12 11  6 19 13 23
 1  2 21  0  6  8 10  9  7 18 15 25 13 20 11  4 17 19  3 22 14  5 16 12 23 24
 4 25 11 14 19 16 21  3 17 15  0 23 24  2  1 22 12 13 20  5  6  8  9  7 10 18
13 12 22 18 10  7  9  8  6  5 20  2  1 23 24 11 25  4  0 15 17  3 21 16 19 14
25 11 14 19 16 21  3 17 15  0  4  1  2 24 23 13 20  5  6  8  9  7 10 18 22 12
11 14 19 16 21  3 17 15  0  4 25 24 23  1  2  8  9  7 10 18 22 12 13 20  5  6
16 24 23 15 11 17  8 19 18  7 22 13  0  4 12 20 21 14 25 10  5  9  3  6  2  1
24 23 17 25  3  9 14 22 10 12 19 20 15  0 13  1  5 16 11  4 18  6  7 21  8  2
23  3  4 21  7 11 12 18 13 14 24  5 17 15 20  2  1  6 19 25  0 22  8 10 16  9
21  0 16 10 25 13 22 20 11 24 23  6  3 17  5  7  2  1  8 14  4 15 12  9 18 19
15 19 18  4 20 12  5 25 24 23 16  8 21  3  6 14 10  2  1  9 11  0 17 13  7 22
14 22  0  5 13  6  4 24 23 19 17  9 16 21  8 12 11 18  2  1  7 25 15  3 20 10
12 15  6 20  8  0 24 23 14  3 11  7 19 16  9 18 13 25 22  2  1 10  4 17 21  5
17  8  5  9 15 24 23 11 21 25 13 10 14 19  7  6 22 20  4 12  2  1 18  0  3 16
 9  6  7 17 24 23 25 16  4 20  3 18 11 14 10 19  8 12  5  0 13  2  1 22 15 21
 8 10  3 24 23  4 19  0  5 21  7 22 25 11 18 16 14  9 13  6 15 20  2  1 12 17
18 21 24 23  0 14 15  6 16 10  9 12  4 25 22  3 19 11  7 20  8 17  5  2  1 13

И оценка для порядка 26 снова улучшена, в два раза
a(26) >= 48.

Ждём результаты для порядков 18 и 22.
ID: 2279 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2280 - Posted: 5 Jun 2021, 17:58:23 UTC

Показываю основной ДЛК найденной мной 18-ки 66-го порядка

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65
8 31 4 19 22 2 20 1 7 11 16 12 18 14 5 17 21 15 10 3 6 13 30 9 26 41 0 24 42 23 29 33 38 34 40 36 27 39 65 37 32 25 50 35 52 53 48 63 44 46 64 45 51 55 60 56 62 58 49 61 43 59 54 47 28 57
7 8 33 2 10 9 19 3 4 12 17 18 15 20 21 6 5 16 22 1 13 14 29 30 11 24 32 31 41 25 26 34 39 40 37 42 65 28 27 38 0 45 35 36 51 52 55 46 54 53 63 47 48 56 61 62 59 64 43 50 49 60 44 23 57 58
2 7 8 34 19 16 11 10 22 18 21 15 5 6 1 20 17 9 4 13 14 3 24 29 30 12 41 38 33 32 0 40 65 37 27 28 23 42 39 31 48 35 36 25 46 51 52 56 63 60 55 54 44 62 43 59 49 50 45 64 61 53 26 57 58 47
9 19 7 8 40 10 17 12 16 15 6 5 20 4 3 21 11 2 13 14 22 1 31 41 29 30 18 32 39 34 38 37 28 27 42 26 25 65 33 46 35 36 0 23 53 63 51 52 62 54 61 56 60 59 50 49 64 48 47 43 55 24 57 58 44 45
17 11 10 7 8 37 16 21 18 5 1 20 3 22 6 12 19 13 14 9 4 2 39 33 32 29 30 15 38 65 40 27 23 42 25 0 28 34 63 35 36 31 26 24 61 55 54 51 52 59 60 43 62 49 45 64 47 44 50 56 41 57 58 53 48 46
15 21 12 16 7 8 27 17 6 20 4 3 22 1 18 10 13 14 11 2 19 9 37 65 34 38 29 30 5 39 28 42 26 25 0 23 40 54 35 36 33 24 41 31 59 43 56 60 51 52 49 61 50 64 48 47 44 45 62 32 57 58 55 46 63 53
1 5 6 18 17 7 8 42 21 3 2 22 9 15 16 13 14 12 19 10 11 4 23 27 28 40 39 29 30 20 65 25 24 0 31 37 60 35 36 34 41 32 33 26 45 49 50 62 61 51 52 64 43 47 46 44 53 59 38 57 58 56 63 54 55 48
6 4 20 1 15 21 7 8 25 22 19 9 11 17 13 14 18 10 16 12 2 5 28 26 42 23 37 65 29 30 3 0 41 31 33 61 35 36 40 32 38 34 24 27 50 48 64 45 59 43 51 52 47 44 63 53 55 39 57 58 62 54 60 56 46 49
12 18 15 5 20 3 22 9 11 30 7 14 13 10 19 2 4 1 6 21 17 16 34 40 37 27 42 25 0 31 33 8 29 36 57 32 41 24 26 23 28 65 39 38 56 62 59 49 64 47 44 53 55 52 51 58 35 54 63 46 48 45 50 43 61 60
16 17 21 6 1 4 2 19 10 13 36 7 8 11 9 22 3 20 5 15 18 12 38 39 65 28 23 26 24 41 32 35 14 51 30 33 31 0 25 42 27 37 40 34 60 61 43 50 45 48 46 63 54 57 58 29 52 55 53 44 47 64 49 59 62 56
10 16 17 21 6 1 4 2 19 7 8 35 14 9 22 3 20 5 15 18 12 11 32 38 39 65 28 23 26 24 41 29 52 13 36 31 0 25 42 27 37 40 34 33 54 60 61 43 50 45 48 46 63 51 30 57 58 53 44 47 64 49 59 62 56 55
18 15 5 20 3 22 9 11 12 14 13 8 29 2 4 1 6 21 17 16 10 19 40 37 27 42 25 0 31 33 34 58 35 30 7 24 26 23 28 65 39 38 32 41 62 59 49 64 47 44 53 55 56 36 57 52 51 46 48 45 50 43 61 60 54 63
21 20 16 10 11 18 14 13 9 17 15 2 6 41 8 7 12 3 1 4 5 22 65 42 38 32 33 40 36 35 53 39 37 24 28 19 30 29 34 25 23 26 27 0 43 64 60 54 55 62 58 57 31 61 59 46 50 63 52 51 56 47 45 48 49 44
5 10 19 9 12 14 13 22 17 16 18 4 21 3 24 8 7 11 20 6 1 15 27 32 41 31 34 36 35 44 39 38 40 26 65 25 2 30 29 33 42 28 23 37 49 54 63 53 56 58 57 0 61 60 62 48 43 47 46 52 51 55 64 50 45 59
19 2 22 11 14 13 3 16 15 10 12 1 17 18 20 26 8 7 9 5 21 6 41 24 0 33 36 35 47 38 37 32 34 23 39 40 42 4 30 29 31 27 65 28 63 46 44 55 58 57 25 60 59 54 56 45 61 62 64 48 52 51 53 49 43 50
4 3 9 14 13 20 10 18 2 19 11 6 16 21 12 5 23 8 7 22 15 17 26 25 31 36 35 64 32 40 24 41 33 28 38 65 34 27 1 30 29 0 37 39 48 47 53 58 57 42 54 62 46 63 55 50 60 43 56 49 45 52 51 44 59 61
20 22 14 13 5 19 12 4 1 2 9 21 10 16 17 11 15 28 8 7 3 18 42 0 36 35 49 41 34 26 23 24 31 65 32 38 39 33 37 6 30 29 25 40 64 44 58 57 27 63 56 48 45 46 53 43 54 60 61 55 59 50 52 51 47 62
3 14 13 15 2 11 1 6 5 4 22 17 19 12 10 16 9 18 65 8 7 20 25 36 35 59 24 33 23 28 27 26 0 39 41 34 32 38 31 40 21 30 29 42 47 58 57 37 46 55 45 50 49 48 44 61 63 56 54 60 53 62 43 52 51 64
14 13 18 4 9 6 21 15 20 1 3 16 2 5 11 19 10 22 12 39 8 7 36 35 62 26 31 28 65 37 42 23 25 38 24 27 33 41 32 0 34 17 30 29 58 57 40 48 53 50 43 59 64 45 47 60 46 49 55 63 54 44 56 61 52 51
13 12 1 22 21 17 18 5 14 6 20 10 4 7 15 9 2 19 3 11 38 8 35 56 23 0 65 39 40 27 36 28 42 32 26 29 37 31 24 41 25 33 16 30 57 34 45 44 43 61 62 49 58 50 64 54 48 51 59 53 46 63 47 55 60 52
11 6 3 17 16 12 15 14 13 21 5 19 1 8 7 18 22 4 2 20 9 32 55 28 25 39 38 34 37 36 35 65 27 41 23 30 29 40 0 26 24 42 31 10 33 50 47 61 60 56 59 58 57 43 49 63 45 52 51 62 44 48 46 64 53 54
33 59 23 40 34 25 26 37 0 24 41 32 27 39 28 38 65 30 36 35 29 42 49 31 22 51 47 63 52 60 48 46 58 45 53 54 64 44 43 55 50 57 56 61 11 9 62 7 18 17 8 6 10 16 14 19 5 21 12 15 4 20 2 13 3 1
48 24 34 35 33 23 29 31 37 32 65 27 36 28 25 30 42 38 41 40 26 39 0 46 47 57 11 62 56 59 60 45 43 53 50 64 63 55 61 44 58 51 52 54 10 16 18 13 49 22 3 9 6 19 4 5 2 12 17 20 1 15 14 7 8 21
37 0 32 23 41 24 35 40 34 27 30 36 38 29 42 52 25 65 33 31 39 28 60 48 45 62 58 46 57 51 47 53 55 50 44 56 61 26 17 43 49 59 54 64 6 10 19 22 14 16 13 7 18 5 20 2 15 3 1 8 63 4 11 9 21 12
23 37 0 27 35 65 32 41 33 36 42 38 25 26 31 29 30 24 34 54 28 40 62 60 48 53 57 43 45 58 49 50 61 44 63 52 59 56 55 16 47 39 64 51 22 6 10 5 13 4 19 14 11 2 1 15 17 8 9 3 20 46 18 21 12 7
24 35 37 0 36 41 30 27 65 38 26 25 56 34 40 42 32 23 39 28 33 31 46 57 60 48 50 58 55 53 43 44 8 63 29 47 51 61 45 62 54 64 49 59 16 13 6 10 2 14 20 5 4 15 52 17 3 18 7 1 19 22 21 12 11 9
30 32 41 37 0 38 65 61 36 25 31 29 40 33 26 27 35 39 28 24 34 23 20 45 58 60 48 44 43 42 50 63 59 56 51 49 52 53 57 54 64 46 47 62 55 19 14 6 10 15 4 1 2 17 9 3 7 11 8 5 13 21 12 16 18 22
38 42 27 65 37 0 25 30 26 29 34 40 33 31 36 41 39 64 32 23 35 24 44 61 53 43 60 48 63 55 52 56 47 7 49 59 50 58 54 28 45 62 57 46 15 1 5 4 6 10 17 20 8 3 18 51 11 9 2 14 21 12 19 22 13 16
31 25 26 36 30 60 0 29 42 40 23 33 24 38 65 39 28 27 35 41 32 34 59 63 52 50 55 37 48 56 61 51 62 49 46 44 43 21 64 53 57 58 45 47 9 17 8 2 20 6 10 3 1 7 22 11 16 15 4 54 12 5 13 14 19 18
26 34 29 31 38 42 37 0 40 33 35 24 32 30 39 28 36 41 43 27 23 25 52 47 56 9 44 61 60 48 51 49 57 46 45 55 54 64 50 58 65 53 62 63 8 18 3 59 15 1 6 10 7 11 13 16 19 20 21 12 2 14 4 5 22 17
27 36 38 25 29 40 33 24 32 0 37 28 39 58 35 23 34 31 26 42 30 65 53 50 44 63 56 51 49 46 45 48 60 64 54 41 57 62 47 59 52 61 55 4 5 2 15 17 3 7 11 16 19 10 6 12 21 14 13 22 18 9 8 1 20 43
65 30 42 26 31 34 23 35 41 39 28 37 0 32 46 33 40 29 25 38 36 27 43 55 61 52 59 47 62 57 58 54 64 60 48 45 24 49 51 56 63 44 2 53 4 20 1 8 9 18 22 13 14 21 12 6 10 19 16 11 7 3 17 15 50 5
41 65 30 42 26 31 34 23 35 37 0 39 28 24 33 40 29 25 38 36 27 45 58 43 55 61 52 59 18 62 57 60 48 54 64 46 49 51 56 63 44 50 53 32 14 4 20 1 8 9 47 22 13 6 10 21 12 16 11 7 3 17 15 2 5 19
36 38 25 29 51 33 24 32 27 28 39 0 37 23 34 31 26 42 30 65 41 35 50 44 63 56 40 49 46 45 5 64 54 48 60 62 47 59 52 61 55 43 58 57 2 15 17 3 7 11 16 19 53 12 21 10 6 22 18 9 8 1 20 4 14 13
42 29 65 41 32 36 28 39 24 55 38 23 26 35 0 37 27 40 31 34 25 33 61 3 43 58 45 50 64 54 46 30 44 62 52 57 48 60 53 51 59 47 63 49 1 56 4 14 19 2 12 21 16 20 15 22 8 13 10 6 5 7 9 18 17 11
25 41 35 24 27 28 39 33 30 65 50 34 42 40 23 0 37 32 29 26 31 38 63 58 57 46 53 12 54 49 55 43 36 47 61 51 62 48 60 45 56 52 59 44 17 14 13 16 5 64 21 11 20 4 2 18 1 7 22 10 6 19 3 8 9 15
35 23 49 32 28 39 40 65 38 41 27 31 30 36 29 34 0 37 24 25 42 26 57 62 33 45 64 54 51 43 44 14 53 59 55 50 56 47 48 60 46 63 61 52 13 22 11 19 12 21 7 4 15 58 5 9 20 2 3 18 10 6 16 17 1 8
34 40 24 28 39 29 41 36 23 35 32 26 65 42 27 25 31 0 37 33 44 30 47 51 46 64 54 56 58 50 62 57 45 52 43 1 53 63 59 48 60 49 38 55 18 7 16 12 21 3 14 2 22 13 19 8 4 61 5 17 9 10 6 11 15 20
29 33 28 39 25 35 53 34 31 23 24 42 41 65 30 32 38 26 0 37 40 36 56 49 64 54 63 57 27 47 59 62 46 61 58 43 55 45 44 52 10 60 51 50 3 11 12 21 17 13 5 18 9 22 16 1 14 4 20 19 15 8 48 6 7 2
40 28 39 38 23 32 31 26 63 34 33 30 35 27 41 65 24 36 42 0 37 29 51 64 54 44 62 45 59 52 25 47 49 55 13 53 58 43 46 50 61 48 60 56 7 12 21 15 22 19 9 8 17 18 11 20 57 5 14 4 16 2 1 10 6 3
28 39 36 47 24 26 42 38 29 31 40 65 23 25 32 35 41 33 27 30 0 37 64 54 50 34 46 52 61 15 56 59 51 43 62 63 45 57 58 49 53 55 48 60 12 21 2 18 16 8 1 44 3 9 7 4 22 17 19 13 14 11 5 20 10 6
39 27 31 33 42 30 36 25 28 26 29 41 34 37 38 24 62 35 40 32 65 0 54 53 59 49 61 55 50 63 64 52 56 58 47 60 44 46 23 57 51 19 43 48 21 5 9 11 1 20 2 17 12 8 3 14 18 6 15 16 22 13 7 45 4 10
32 26 40 30 65 27 38 28 39 42 25 57 31 0 37 36 33 34 23 29 24 41 45 52 51 55 43 53 44 64 54 61 63 35 59 48 6 50 49 47 62 56 46 58 19 8 7 20 4 5 15 12 21 1 17 13 9 10 60 2 11 18 22 3 16 14
61 54 64 53 43 51 44 57 50 63 52 48 59 56 55 47 46 58 49 62 60 10 33 17 6 5 21 18 16 13 14 3 4 22 9 7 8 12 2 19 11 1 15 45 20 41 38 31 32 25 24 35 36 34 65 40 37 29 30 42 28 23 27 39 0 26
50 63 43 62 61 64 60 54 57 48 46 59 49 55 51 58 45 47 52 53 16 56 14 34 21 1 20 6 15 17 13 22 2 9 11 8 18 19 10 12 4 5 44 7 36 3 32 39 33 38 0 41 35 40 28 37 27 30 25 23 26 42 65 31 24 29
57 50 48 64 52 63 62 53 43 59 58 49 47 60 45 44 51 46 61 17 56 55 13 14 40 6 4 3 1 5 21 9 19 11 12 15 10 16 18 2 20 54 7 8 35 36 22 38 65 34 39 31 32 37 23 27 42 0 26 24 25 28 33 41 29 30
64 57 50 59 62 46 48 52 61 49 45 47 51 44 54 60 58 63 21 56 55 53 6 13 14 37 1 2 22 4 20 11 10 12 18 16 17 15 19 3 43 7 8 5 38 35 36 9 39 28 40 65 33 27 26 42 25 24 41 0 23 34 32 29 30 31
63 62 57 50 49 52 58 59 46 47 44 51 60 43 53 45 48 6 56 55 61 54 3 1 13 14 27 4 19 9 2 12 16 18 15 21 5 10 22 64 7 8 20 17 34 39 35 36 11 65 23 37 28 42 24 25 0 32 31 26 40 38 29 30 33 41
58 48 52 57 50 47 46 45 49 51 54 60 53 61 44 59 1 56 55 63 43 64 19 22 4 13 14 42 2 10 11 18 17 15 5 20 16 9 62 7 8 3 21 6 23 40 65 35 36 12 28 26 27 25 41 0 31 33 24 37 39 29 30 34 32 38
47 45 59 46 57 50 51 58 44 60 43 53 61 54 49 4 56 55 48 64 62 63 12 10 9 2 13 14 25 19 16 15 21 5 20 17 11 52 7 8 22 6 1 3 42 26 37 28 35 36 18 23 24 0 32 31 33 41 27 65 29 30 40 38 39 34
54 51 44 49 58 57 50 60 45 53 64 61 63 47 2 56 55 59 62 52 48 43 17 18 16 11 19 13 14 0 10 5 6 20 3 12 46 7 8 9 1 4 22 21 41 25 24 27 23 35 36 15 26 31 38 33 34 42 28 29 30 37 39 65 40 32
44 43 60 54 47 45 57 50 53 61 62 63 48 19 56 55 49 52 46 59 64 51 16 21 15 17 12 10 13 14 31 20 1 3 22 58 7 8 11 4 2 9 6 18 24 32 0 41 42 26 35 36 5 33 39 34 40 23 29 30 27 65 28 37 38 25
59 49 47 51 60 53 61 63 48 50 57 55 7 52 62 64 43 54 44 45 58 46 9 11 12 18 15 5 20 3 22 36 13 8 56 4 1 6 21 17 16 10 19 2 37 27 42 25 0 31 33 34 40 14 35 30 29 65 39 38 32 41 24 26 23 28
46 58 45 44 54 43 64 62 52 56 55 13 50 48 63 61 53 60 51 47 49 59 2 19 10 16 17 21 6 1 4 7 30 57 14 22 3 20 5 15 18 12 11 9 28 23 26 24 41 32 38 39 65 29 8 35 36 40 34 33 31 0 25 42 27 37
52 46 58 45 44 54 43 64 62 57 14 56 55 63 61 53 60 51 47 49 59 48 4 2 19 10 16 17 21 6 1 13 50 29 8 3 20 5 15 18 12 11 9 22 65 28 23 26 24 41 32 38 39 35 36 7 30 34 33 31 0 25 42 27 37 40
49 47 51 60 53 61 63 48 59 8 56 50 57 64 43 54 44 45 58 46 52 62 11 12 18 15 5 20 3 22 9 55 7 14 35 6 21 17 16 10 19 2 4 1 27 42 25 0 31 33 34 40 37 30 29 36 13 38 32 41 24 26 23 28 65 39
45 60 46 52 48 49 55 56 3 58 47 64 44 62 50 57 59 53 54 43 51 61 10 15 2 4 22 11 8 7 63 19 12 6 16 39 14 13 9 5 17 21 18 20 26 0 28 65 40 27 30 29 34 23 42 38 24 1 36 35 37 31 41 32 25 33
51 52 62 63 59 55 56 20 58 46 49 43 45 53 64 50 57 48 60 44 54 47 18 4 1 3 9 8 7 61 19 2 11 21 10 5 38 14 13 22 15 16 17 12 25 65 39 34 37 30 29 33 23 28 27 32 26 31 6 36 35 40 0 24 41 42
62 64 61 48 55 56 5 46 47 52 59 54 58 49 60 43 50 57 63 51 45 44 1 6 20 22 8 7 53 2 12 4 9 17 19 11 15 32 14 13 3 18 10 16 39 38 33 40 30 29 31 28 42 65 37 41 23 27 0 21 36 35 34 25 26 24
43 53 63 55 56 15 52 49 64 62 48 44 46 45 59 51 54 50 57 61 47 58 21 5 3 8 7 60 4 11 6 1 22 16 2 10 9 18 41 14 13 20 12 19 32 31 34 30 29 0 65 27 38 39 40 24 28 26 37 25 17 36 35 33 42 23
60 61 55 56 18 62 59 43 54 64 63 45 52 46 58 48 47 44 50 57 53 49 15 20 8 7 51 1 9 21 17 6 3 10 4 2 19 22 12 24 14 13 5 11 0 33 30 29 25 39 37 32 41 38 34 26 65 28 23 40 42 16 36 35 31 27
53 55 56 12 64 48 54 44 51 43 61 58 62 59 52 46 63 49 45 50 57 60 5 8 7 47 6 22 17 16 18 21 20 19 1 9 4 2 3 11 26 14 13 15 31 30 29 42 38 40 41 24 25 32 33 23 39 37 65 28 34 27 10 36 35 0
55 56 11 43 63 44 45 47 60 54 53 46 64 51 48 62 52 61 59 58 50 57 8 7 49 21 3 16 10 12 15 17 5 2 6 18 22 1 4 20 9 23 14 13 30 29 27 32 34 24 26 42 0 41 31 28 38 25 40 39 65 33 37 19 36 35
56 9 54 61 45 58 49 51 55 44 60 52 43 57 47 63 64 62 53 48 46 50 7 59 17 20 10 19 11 18 8 16 15 4 21 13 12 3 6 1 5 22 28 14 29 37 41 33 26 23 27 25 30 24 0 65 32 35 42 34 38 39 31 40 2 36
22 44 53 58 46 59 47 55 56 45 51 62 54 50 57 49 61 43 64 60 63 52 48 16 5 19 2 9 12 8 7 10 18 1 17 14 13 11 20 21 6 15 3 65 40 24 31 23 28 37 42 30 29 26 25 39 41 36 35 27 33 32 38 0 34 4

Всю 18-ку ещё не выложила, руки не дошли :)
Но я помню, что надо выложить.
ID: 2280 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2281 - Posted: 6 Jun 2021, 5:16:47 UTC
Last modified: 6 Jun 2021, 5:34:15 UTC

Выложила очаровательную 18-ку 66-го порядка
https://disk.yandex.ru/d/uw8UbH9OELqPRw
Яндекс.Диск, формат txt, файл не сжат, 244 КБ.

Это, пожалуй, самая солидная группа ОДЛК для большого порядка (в этой теме).
Нашлась очень легко на базе 24-ки 22-го порядка методом Пелегрино-Ланселотти.

Для порядка 78 метод Пелегрино-Ланселотти пока не сработал, была одна попытка.
ID: 2281 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2282 - Posted: 6 Jun 2021, 7:43:11 UTC

Ещё поигралась вручную с квадратиком 20-го порядка, получила 148 37-ок.
Очень интересно: каждый из 148 ДЛК в наборе имеет 37 ОДЛК.
Показываю основной ДЛК одной из этих 37-ок и пару ортогоналек

DLK
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17
 3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7
10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5
11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4
 9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6
16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13
19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12
17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3
 6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1
 7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0
 5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2
12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11
14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9
15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8
13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10

mate #1
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17
12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11
15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8
13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10
14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3
 7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0
 5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2
 6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1
16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12
17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13
 8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7
11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4
 9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6
10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5

mate #2
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17
12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11
15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8
13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10
14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3
 7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0
 5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2
 6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1
16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12
17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13
 8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  7  6
11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0  6  7  5  4
 9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  6  7
10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1  7  6  4  5

Сильно подозреваю, что этим способом можно получить море ОДЛК от одного ДЛК 20-го порядка.
Но варьировать вручную очень нудно да и нереально все варианты сделать вручную.
Написала Harry, чтобы он сделал программку, но он меня пока не сразу понял.
Я сейчас покажу исходный квадрат и что в нём надо варьировать.

Итак, пока оценка для порядка 20 такая
a(20) >= 37.
ID: 2282 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2283 - Posted: 6 Jun 2021, 7:46:15 UTC
Last modified: 6 Jun 2021, 8:07:47 UTC

Вот посмотрите на таблицу ортогональных пар (фрагмент)

1: [112,113,114,115,116,117,118,119,120,121],
1: [122,123,124,125,126,127,128,129,130,131],
1: [132,133,134,135,136,137,138,139,140,141],
1: [142,143,144,145,146,147,148],
2: [112,113,114,115,116,117,118,119,120,121],
2: [122,123,124,125,126,127,128,129,130,131],
2: [132,133,134,135,136,137,138,139,140,141],
2: [142,143,144,145,146,147,148],
3: [112,113,114,115,116,117,118,119,120,121],
3: [122,123,124,125,126,127,128,129,130,131],
3: [132,133,134,135,136,137,138,139,140,141],
3: [142,143,144,145,146,147,148],
4: [112,113,114,115,116,117,118,119,120,121],
4: [122,123,124,125,126,127,128,129,130,131],
4: [132,133,134,135,136,137,138,139,140,141],
4: [142,143,144,145,146,147,148],
5: [112,113,114,115,116,117,118,119,120,121],
5: [122,123,124,125,126,127,128,129,130,131],
5: [132,133,134,135,136,137,138,139,140,141],
5: [142,143,144,145,146,147,148],
6: [112,113,114,115,116,117,118,119,120,121],
6: [122,123,124,125,126,127,128,129,130,131],
6: [132,133,134,135,136,137,138,139,140,141],
6: [142,143,144,145,146,147,148],
7: [112,113,114,115,116,117,118,119,120,121],
7: [122,123,124,125,126,127,128,129,130,131],
7: [132,133,134,135,136,137,138,139,140,141],
7: [142,143,144,145,146,147,148],
. . . . . . 
144: [1,2,3,4,5,6,7,8,9,10],
144: [11,12,13,14,15,16,17,18,19,20],
144: [21,22,23,24,25,26,27,28,29,30],
144: [31,32,33,34,35,36,37],
145: [1,2,3,4,5,6,7,8,9,10],
145: [11,12,13,14,15,16,17,18,19,20],
145: [21,22,23,24,25,26,27,28,29,30],
145: [31,32,33,34,35,36,37],
146: [1,2,3,4,5,6,7,8,9,10],
146: [11,12,13,14,15,16,17,18,19,20],
146: [21,22,23,24,25,26,27,28,29,30],
146: [31,32,33,34,35,36,37],
147: [1,2,3,4,5,6,7,8,9,10],
147: [11,12,13,14,15,16,17,18,19,20],
147: [21,22,23,24,25,26,27,28,29,30],
147: [31,32,33,34,35,36,37],
148: [1,2,3,4,5,6,7,8,9,10],
148: [11,12,13,14,15,16,17,18,19,20],
148: [21,22,23,24,25,26,27,28,29,30],
148: [31,32,33,34,35,36,37]

Но клики размера 3, наверное, нет.
Сейчас проверю.

Проверила.
Клики размера 3 нет, как я и предполагала.
ID: 2283 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2284 - Posted: 6 Jun 2021, 7:57:38 UTC
Last modified: 6 Jun 2021, 8:18:52 UTC

А пока посмотрите на исходный ДЛК 20-го порядка, он построен методом составных квадратов и является SODLS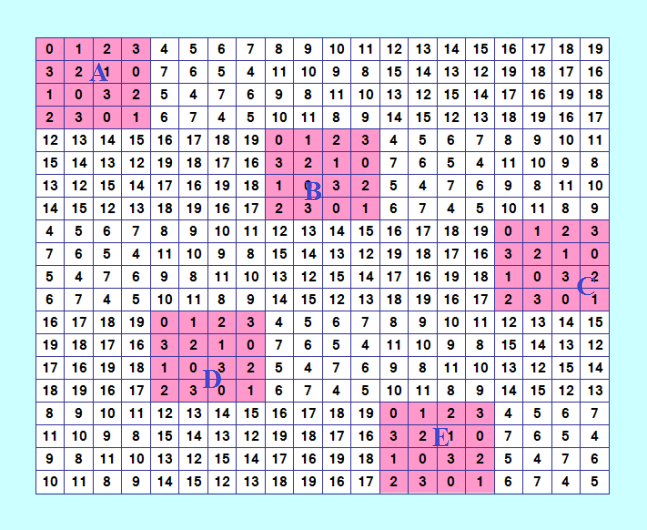



Я подквадраты 4х4 обозначила A, B, C, D, E, чтобы Harry было понятнее, что надо варьировать.
Теперь считаем, господа.
У меня что-то ум за разум заходит.
Один подквадрат 4х4 имеет 48 вариантов, считая его самого.
Сколько всего вариантов можно получить из исходного ДЛК, если сделать все возможные комбинации изменений пяти подквадратов?
Простенькая комбинаторная задачка, но я что-то туплю.
А Harry пока вообще меня не понял - о каких вариантах я говорю.
Вот и играюсь вручную, так как программки нет у меня.

Господа!
Пожалуйста, скажите, сколько вариантов вы насчитали :)
Я насчитала 48*120=5760 вариантов, но что-то не уверена.
ID: 2284 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2285 - Posted: 6 Jun 2021, 10:43:13 UTC

Точно, недаром я была не уверена.
Что-то не то посчитала :)
Сейчас Harry прислал письмо; он пишет, что вариантов будет 48*48*48*48*48.
Но поскольку подквадрат А имеет особенность расположения (в углу квадрата), то для него существенно различные только два варианта.
Итак, всего вариантов будет 2*48*48*48*48.
О-о-о-ой!!!
ID: 2285 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2286 - Posted: 6 Jun 2021, 13:19:05 UTC
Last modified: 6 Jun 2021, 13:24:09 UTC

У Harry завершилась обработка набора ДЛК 22-го порядка!
Грандиозные результаты!!
Протокол работы программы GetOrthogonal

Order? 22
 
Enter the name of the squares file: 22aAllCenter4ToNFR
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file 22aAllCenter4ToNFR-orthCounts.txt
..output file 22aAllCenter4ToNFR-orthNos.txt
    .. increasing LS store to     100,000
    .. increasing LS store to     200,000
    .. increasing LS store to     400,000
    .. increasing LS store to     800,000
squares 565056 total orthogonal pairs 6859008
Maximum pairs for square 5617: 72
There are 287 other squares with this maximum number of pairs.
..output file 22aAllCenter4ToNFR-5617orths.txt
Pairs for square 5617: 72
 
elapsed time 33:40:50

Программа работала почти 34 часа!
Образовано 6859008 ортогональных пар.
Найдено 288 ДЛК, у которых 72 ОДЛК!
Это рекорд для порядка 22 на данный момент.

Показываю основной ДЛК одной из 72-ек и несколько ортогоналек

DLK
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
 8  9  6  0 18 10 17 20  7 11  5 12  3 14 15  4 21 13  2 16  1 19
 7  8 11 20  9 13  5 21 16 12 17  3 18 15 10  1 19  0  4  6  2 14
 4  7  8 12 16 11 19 17  1  3 21 18 13  5  6  2  9 10 20  0 14 15
 6 10  7  8  3  4 12  2 21 18  1 13 19 20  0 11  5 16  9 14 15 17
 1 20  5  7  8 18 10  3  0 13  6 19  2  9 12 17  4 11 14 15 21 16
 9  6 16 17  7  8 13  5 18 19 20  2  0  3 21 10 12 14 15  1  4 11
13 11 20  4 21  7  8 19 17  2 16  0  9  1  5  3 14 15  6 10 12 18
21 19 12 16 10  1  7  8  2  0  4  9 11 17 18 14 15 20  5  3 13  6
12  3 18 13 19  2  0  9 11  8  7 15 14 10  4 16 20  6  1 21 17  5
 5 17 21  1  6 20 16  4 10 14 15  7  8 12 11  9  0  2 19 13 18  3
10  5 17 21  1  6 20 16  4  7  8 14 15 11  9  0  2 19 13 18  3 12
 3 18 13 19  2  0  9 11 12 15 14  8  7  6  1 21 17  5 10  4 16 20
20  2  1 11  0 21 15 14  9 17 19 16 10  4  8  7  3 18 12  5  6 13
19 21  9  2 17 15 14  0  6  5 13 20  4 18 16  8  7 12  3 11 10  1
17  0 19  5 15 14  2  1 13 10 18  6 16 21  3 20  8  7 11 12  9  4
 2 13 10 15 14 19 21 18  5  4  3  1 20 16 17 12  6  8  7  9 11  0
18  4 15 14 13 17  3 10 19 16 12 21  6  2 20  5 11  1  8  7  0  9
16 15 14 18  5 12  4 13  3 20 11 17  1  0 19  6 10  9 21  8  7  2
15 14  3 10 11 16 18 12 20  6  9  5 21 19  2 13  1  4  0 17  8  7
14 12  4  9 20  3 11  6 15  1  0 10 17  7 13 19 18 21 16  2  5  8
11 16  0  6 12  9  1 15 14 21  2  4  5  8  7 18 13  3 17 20 19 10

mate #1
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
 5  6  1  2 11 13  4 21 14 12 15 10 17 16  8  0  7  3 19 20  9 18
16  4 21  1  2 10 18 13  9 17  8 15  7  5  6 14 11 19 20 12  3  0
12  0 13  9  1  2 15  3 18  7  5  8 14 21 16 10 19 20 17 11  6  4
 3 17  6 18 12  1  2  8 11 14  4  5 16  0 15 19 20  7 10 21 13  9
10 11  7 21  3 17  1  2  5 16 13  4  0  8 19 20 14 15  9 18 12  6
 4 15 10 14  9 11  7  1  2  0 18 13  6 19 20 16  8 12  3 17 21  5
 2 13  8 15 16 12 10 14  1  6  3 18 21 20  0  5 17 11  7  9  4 19
 1  2 18  5  8  0 17 15 16 21 11  3  9  6  4  7 10 14 12 13 19 20
 6 21  9 12 17  7 14 16  0  1  2 19 20 15 10 11  3 18 13  4  5  8
11 10 15  8  5  4 13 18  3 19 20  1  2 14  7 17 12  9 21  6  0 16
21  9 12 17  7 14 16  0  6 20 19  2  1 18 13  4  5  8 15 10 11  3
 9 12 17  7 14 16  0  6 21  2  1 20 19 11  3 18 13  4  5  8 15 10
 7 20 19 10 13  6 12  5 15 11  9 21  4  3 17  8 18 16  0 14  2  1
20 19 11  4  0  9  8 10 17  3 21  6  5  1 18 12 15 13 14 16  7  2
19  3  5 16 21 15 11 12 20 18  6  0  8  2  1 13  9 10  4  7 14 17
18  8 14  6 10  3  9 20 19 13  0 16 15 12  2  1  4 21 11  5 17  7
15  7  0 11 18 21 20 19 13  4 16 14 10 17  9  2  1  5  6  3  8 12
17 16  3 13  6 20 19  4 10  5 14  7 11  9 12 21  2  1  8  0 18 15
14 18  4  0 20 19  5 11 12  8  7 17  3 10 21  9  6  2  1 15 16 13
13  5 16 20 19  8  3  9  7 15 17 12 18  4 11  6 21  0  2  1 10 14
 8 14 20 19 15 18 21 17  4 10 12  9 13  7  5  3  0  6 16  2  1 11

mate #2
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
 5  6  1  2 11 13  4 21 14 12 15 10 17 16  8  0  7  3 19 20  9 18
16  4 21  1  2 10 18 13  9 17  8 15  7  5  6 14 11 19 20 12  3  0
12  0 13  9  1  2 15  3 18  7  5  8 14 21 16 10 19 20 17 11  6  4
 3 17  6 18 12  1  2  8 11 14  4  5 16  0 15 19 20  7 10 21 13  9
10 11  7 21  3 17  1  2  5 16 13  4  0  8 19 20 14 15  9 18 12  6
 4 15 10 14  9 11  7  1  2  0 18 13  6 19 20 16  8 12  3 17 21  5
 2 13  8 15 16 12 10 14  1  6  3 18 21 20  0  5 17 11  7  9  4 19
 1  2 18  5  8  0 17 15 16 21 11  3  9  6  4  7 10 14 12 13 19 20
 6 21  9 12 17  7 14 16  0  1  2 20 19 15 10 11  3 18 13  4  5  8
11 10 15  8  5  4 13 18  3 20 19  1  2 14  7 17 12  9 21  6  0 16
21  9 12 17  7 14 16  0  6 19 20  2  1 18 13  4  5  8 15 10 11  3
 9 12 17  7 14 16  0  6 21  2  1 19 20 11  3 18 13  4  5  8 15 10
 7 20 19 10 13  6 12  5 15 11  9 21  4  3 17  8 18 16  0 14  2  1
20 19 11  4  0  9  8 10 17  3 21  6  5  1 18 12 15 13 14 16  7  2
19  3  5 16 21 15 11 12 20 18  6  0  8  2  1 13  9 10  4  7 14 17
18  8 14  6 10  3  9 20 19 13  0 16 15 12  2  1  4 21 11  5 17  7
15  7  0 11 18 21 20 19 13  4 16 14 10 17  9  2  1  5  6  3  8 12
17 16  3 13  6 20 19  4 10  5 14  7 11  9 12 21  2  1  8  0 18 15
14 18  4  0 20 19  5 11 12  8  7 17  3 10 21  9  6  2  1 15 16 13
13  5 16 20 19  8  3  9  7 15 17 12 18  4 11  6 21  0  2  1 10 14
 8 14 20 19 15 18 21 17  4 10 12  9 13  7  5  3  0  6 16  2  1 11
. . . . . . 

mate #71
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
16  6  1  2 11 13  4 21 14 12  7 10 17  5  8  0 15  3 19 20  9 18
 5  0 21  1  2 10 18 13  9 17 14  7 15 16  6  8 11 19 20 12  3  4
12  4  6  9  1  2  7  3 18 15  5 14  8 21 16 10 19 20 17 11 13  0
 3 17 13 21 12  1  2 14 11  8  4  5 16  0  7 19 20 15 10 18  6  9
10 11 15 18  9 17  1  2  5 16 13  4  0 14 19 20  8  7  3 21 12  6
 4  7 10  8  3 12 15  1  2  0 18 13  6 19 20 16 14 11  9 17 21  5
 2 13 14  7 16 11 17  8  1  6  3 18 21 20  0  5 10 12 15  9  4 19
 1  2 18  5 14  0 10 15 16 21 11  3  9  6  4  7 17  8 12 13 19 20
 6 21  9 12 17 15  8 16  0 19 20  1  2  7 10 11  3 18 13  4  5 14
11 10  7 14  5  4 13 18  3  1  2 19 20  8 15 17 12  9 21  6  0 16
21  9 12 17 15  8 16  0  6  2  1 20 19 18 13  4  5 14  7 10 11  3
 9 12 17 15  8 16  0  6 21 20 19  2  1 11  3 18 13  4  5 14  7 10
15 20 19 10 13  6 14 17  7 11  9 21  4  3  5 12 18 16  0  8  2  1
20 19 11  4  0  7 12 10 17  3 21  6  5  1 18 14  9 13  8 16 15  2
19  3  5 16 10  9 11 12 20 18  6  0 14  2  1 13  7 21  4 15  8 17
18 14  8 11 21  3  9 20 19 13  0 16  7 12  2  1  4 10  6  5 17 15
 7 15  3  6 18 21 20 19 13  4 16  8 10 17  9  2  1  5 11  0 14 12
17 18  0 13  6 20 19  4 10  5  8 15 11  9 12 21  2  1 14  3 16  7
13 16  4  0 20 19  5 11 12 14 15 17  3 10 21  9  6  2  1  7 18  8
 8  5 16 20 19 14  3  9  4  7 17 12 18 15 11  6 21  0  2  1 10 13
14  8 20 19  7 18 21  5 15 10 12  9 13  4 17  3  0  6 16  2  1 11

mate #72
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
16  6  1  2 11 13  4 21 14 12  7 10 17  5  8  0 15  3 19 20  9 18
 5  0 21  1  2 10 18 13  9 17 14  7 15 16  6  8 11 19 20 12  3  4
12  4  6  9  1  2  7  3 18 15  5 14  8 21 16 10 19 20 17 11 13  0
 3 17 13 21 12  1  2 14 11  8  4  5 16  0  7 19 20 15 10 18  6  9
10 11 15 18  9 17  1  2  5 16 13  4  0 14 19 20  8  7  3 21 12  6
 4  7 10  8  3 12 15  1  2  0 18 13  6 19 20 16 14 11  9 17 21  5
 2 13 14  7 16 11 17  8  1  6  3 18 21 20  0  5 10 12 15  9  4 19
 1  2 18  5 14  0 10 15 16 21 11  3  9  6  4  7 17  8 12 13 19 20
 6 21  9 12 17 15  8 16  0 19 20  2  1  7 10 11  3 18 13  4  5 14
11 10  7 14  5  4 13 18  3  2  1 19 20  8 15 17 12  9 21  6  0 16
21  9 12 17 15  8 16  0  6  1  2 20 19 18 13  4  5 14  7 10 11  3
 9 12 17 15  8 16  0  6 21 20 19  1  2 11  3 18 13  4  5 14  7 10
15 20 19 10 13  6 14 17  7 11  9 21  4  3  5 12 18 16  0  8  2  1
20 19 11  4  0  7 12 10 17  3 21  6  5  1 18 14  9 13  8 16 15  2
19  3  5 16 10  9 11 12 20 18  6  0 14  2  1 13  7 21  4 15  8 17
18 14  8 11 21  3  9 20 19 13  0 16  7 12  2  1  4 10  6  5 17 15
 7 15  3  6 18 21 20 19 13  4 16  8 10 17  9  2  1  5 11  0 14 12
17 18  0 13  6 20 19  4 10  5  8 15 11  9 12 21  2  1 14  3 16  7
13 16  4  0 20 19  5 11 12 14 15 17  3 10 21  9  6  2  1  7 18  8
 8  5 16 20 19 14  3  9  4  7 17 12 18 15 11  6 21  0  2  1 10 13
14  8 20 19  7 18 21  5 15 10 12  9 13  4 17  3  0  6 16  2  1 11

Итак, оценка для порядка 22 сильно улучшена, в три раза
a(22) >= 72.
Интересно, сработает ли для этой порции ОДЛК 22-го порядка метод Пелегрино-Ланселотти.

И ещё ждём результат для порядка 18, этот набор всё обрабатывается.
ID: 2286 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2287 - Posted: 6 Jun 2021, 14:05:11 UTC
Last modified: 6 Jun 2021, 20:25:50 UTC

Ой! Ай!
Офигенный результат для порядка 20, смотрите выше исходный квадрат.
Это я обработала только 48*48=2304 вариантов; Harry прислал мне эти варианты.
Вот что получилось

Order? 20

Enter the name of the squares file: inp
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file inp-orthCounts.txt
..output file inp-orthNos.txt
squares 18240 total orthogonal pairs 7743744
Maximum pairs for square 1: 1128
There are 9023 other squares with this maximum number of pairs.
..output file inp-1orths.txt
Pairs for square 1: 1128

elapsed time 0:06:31

Фантастика!
Образовано 7743744 ортогональных пар.
Найдено 9024 ДЛК, имеющих 1128 ОДЛК!

Показываю основной ДЛК одной из 1128-к и пару ортогоналек

DLK
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17
 3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7
10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5
11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4
 9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6
16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13
19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12
17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3
 6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1
 7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0
 5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2
12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11
14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9
15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8
13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10

mate #1
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17
12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11
15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8
13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10
14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3
 7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0
 5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2
 6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1
16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12
17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13
 8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7
11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4
 9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6
10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5

mate #2
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17
12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11
15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4 11 10  9  8
13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10
14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5 10 11  8  9
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3
 7  6  5  4 11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0
 5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2
 6  7  4  5 10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1
16 17 18 19  0  1  2  3  4  5  6  7  8  9 11 10 12 13 14 15
19 18 17 16  3  2  1  0  7  6  5  4 10 11  9  8 15 14 13 12
17 16 19 18  1  0  3  2  5  4  7  6  9  8 10 11 13 12 15 14
18 19 16 17  2  3  0  1  6  7  4  5 11 10  8  9 14 15 12 13
 8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7
11 10  9  8 15 14 13 12 19 18 17 16  3  2  1  0  7  6  5  4
 9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6
10 11  8  9 14 15 12 13 18 19 16 17  2  3  0  1  6  7  4  5

Не знаю, справится ли черепашка с набором из 48*48*48=110592 вариантов.
Сейчас гляну на этот набор. Скорее всего, не справится.

Всё верно, алгоритм работает!
Как я и предполагала, для показанного ДЛК 20-го порядка вариантов будет астрономическое количество.
Обработать их все можно разве что на суперкомпьютере.

Пока оценка для порядка 20 такая
a(20) >= 1128.
ID: 2287 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2288 - Posted: 6 Jun 2021, 14:12:04 UTC

Посмотрите на счётчик ортогональных пар (фрагмент)

                orthogonal
      square       pairs
      ------    ----------

           1         1128
           2          576
           3          576
           4         1128
           5         1128
           6          576
           7          576
           8         1128
           9         1128
          10          576

          11          576
          12         1128
          13         1128
          14          576
          15          576
          16         1128
          17         1128
          18          576
          19          576
          20         1128

          21         1128
          22          576
          23          576
          24         1128
          25         1128
          26          576
          27          576
          28         1128
          29         1128
          30          576

          31          576
          32         1128
          33         1128
          34          576
          35          576
          36         1128
          37         1128
          38          576
          39          576
          40         1128

          41         1128
          42          576
          43          576
          44         1128
          45         1128
          46          576
          47          576
          48         1128
          49         1128
          50          576

          51          576
          52         1128
          53         1128
          54          576
          55          576
          56         1128
          57         1128
          58          576
          59          576
          60         1128

          61         1128
          62          576
          63          576
          64         1128
          65         1128
          66          576
          67          576
          68         1128
          69         1128
          70          576

          71          576
          72         1128
          73         1128
          74          576
          75          576
          76         1128
          77         1128
          78          576
          79          576
          80         1128
. . . . . . . . .

И так для всех ДЛК набора, а ДЛК в наборе 18240.
ID: 2288 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2289 - Posted: 6 Jun 2021, 14:42:47 UTC
Last modified: 6 Jun 2021, 20:27:54 UTC

Черепашка попытается

Order? 20

Enter the name of the squares file: inp
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file inp-orthCounts.txt
..output file inp-orthNos.txt
    .. increasing LS store to     100,000
    .. increasing LS store to     200,000
    .. increasing LS store to     400,000
squares 221184

Это я ещё сделала облегчённый вариант (программа Rotate с параметром 7, только транспонированный вариант для каждого ДЛК).
А если делать полный набор, он будет в 4 раза больше.

Работать это будет очень долго, не знаю, уложимся ли до отбоя. Вряд ли.

Да, до отбоя черепашка не уложилась, будет работать ночью.
Хорошо, если программа вырулит ещё за сутки.
ID: 2289 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2290 - Posted: 7 Jun 2021, 1:15:19 UTC
Last modified: 7 Jun 2021, 1:20:52 UTC

Всем доброе утро!
Черепашка героически трудится.

Вот для сравнения обработка набора ДЛК 26-го порядка на компьютере Harry

Order? 26
 
Enter the name of the squares file: 26aAllCenter4ToNFR
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file 26aAllCenter4ToNFR-orthCounts.txt
..output file 26aAllCenter4ToNFR-orthNos.txt
    .. increasing LS store to     100,000
    .. increasing LS store to     200,000
    .. increasing LS store to     400,000
squares 286656 total orthogonal pairs 3545856
Maximum pairs for square 913: 48
There are 8831 other squares with this maximum number of pairs.
..output file 26aAllCenter4ToNFR-913orths.txt
Pairs for square 913: 48
 
elapsed time 11:32:42

И набор ДЛК побольше (286656), и порядок ДЛК побольше (26); обработка выполнялась 11,5 часов.
Сколько же черепашке придётся работать?
Программа запущена вчера в 17:30 по московскому времени.
ID: 2290 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2291 - Posted: 7 Jun 2021, 3:24:32 UTC
Last modified: 7 Jun 2021, 3:36:22 UTC

Черепашку постигла неудача :(
Программа отработала, но результата нет

Order? 20

Enter the name of the squares file: inp
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file inp-orthCounts.txt
..output file inp-orthNos.txt
    .. increasing LS store to     100,000
    .. increasing LS store to     200,000
    .. increasing LS store to     400,000
squares 221184 total orthogonal pairs -1007874560

Error writing file: No space left on device

elapsed time 12:27:32

Как я понимаю, все ортогональные пары не смогли записаться на диск.
Обидно!
Максимальная группа ОДЛК, наверное, большая тут, но я её не получила.

PS. Непонятно, о каком файле идёт речь. На диск ортогональные пары вроде и не записываются, нет выходного файла со всеми ортогональными парами.
Не смогла записаться таблица ортогональных пар?
ID: 2291 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2292 - Posted: 7 Jun 2021, 4:18:39 UTC

Для порядка 16 у меня очень маленькая нижняя граница
a(16) >= 13.
Можно увеличить её данным алгоритмом.
Приготовила аналогичный исходный ДЛК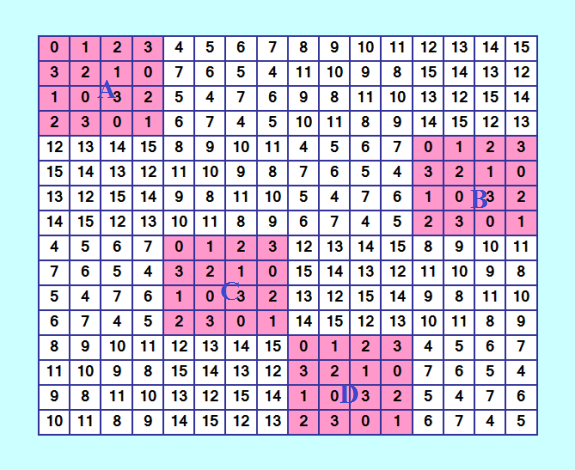



Этот ДЛК построен методом составных квадратов и является SODLS.
Всё совершенно аналогично порядку 20, только вариантов здесь будет поменьше.
Однако всё равно много.
Только для выделенных подквадратов 4х4 будет 2*48*48*48 вариантов.
Но ведь варьировать можно и другие подквадраты 4х4.
Так что, обо всех вариантах здесь можно не думать, суперкомпьютера у меня нет и ВЦ тоже только в мечтах.
Даже 2*48*48*48 не берусь обработать, после такой неудачи с ДЛК порядка 20.
Могу обработать только 2*48*48=4608 вариантов.

Попрошу Harry сделать мне эти варианты.
ID: 2292 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2293 - Posted: 7 Jun 2021, 5:03:13 UTC
Last modified: 7 Jun 2021, 12:36:33 UTC

Запустила метод Пелегрино-Ланселотти для порядка 66 на базе найденной 72-ки 22-го порядка.
Ортогональные пары строятся. Интересно, что получится в итоге. 72-ка вряд ли получится, что-нибудь поменьше.

Построение ортогональных пар подходит к финишу.
Сейчас будем смотреть, что получилось в наборе ДЛК 66-го порядка.

Вот что получилось

Order? 66

Enter the name of the squares file: INP1
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file INP1-orthCounts.txt
..output file INP1-orthNos.txt
squares 600 total orthogonal pairs 576
Maximum pairs for square 73: 24
There are 23 other squares with this maximum number of pairs.
..output file INP1-73orths.txt
Pairs for square 73: 24

Только 24-ки, но их 24 штуки!

Показываю основной ДЛК одной из 24-ок

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65
2 42 5 19 8 22 17 6 7 18 9 16 10 14 1 4 11 3 21 15 12 13 24 20 27 41 30 0 39 28 29 40 31 38 32 36 23 26 33 25 65 37 56 35 46 64 49 63 52 44 61 50 51 62 53 60 54 58 45 48 55 47 43 59 34 57
7 19 37 17 21 2 20 11 6 3 18 4 9 5 22 16 8 12 1 10 13 14 29 41 15 39 65 24 42 33 28 25 40 26 31 27 0 38 30 34 23 54 35 36 51 63 59 61 43 46 64 55 50 47 62 48 53 49 44 60 52 56 45 32 57 58
6 7 21 23 11 12 19 15 16 8 3 22 18 20 4 2 10 5 9 13 14 17 28 29 65 1 33 34 41 37 38 30 25 0 40 42 26 24 32 27 53 35 36 39 50 51 43 45 55 56 63 59 60 52 47 44 62 64 48 46 54 49 31 57 58 61
4 6 7 12 27 16 10 21 1 2 8 20 3 22 19 9 17 18 13 14 11 15 26 28 29 34 5 38 32 65 23 24 30 42 25 0 41 31 39 62 35 36 33 37 48 50 51 56 49 60 54 43 45 46 52 64 47 44 63 53 61 40 57 58 55 59
5 22 6 7 10 39 4 9 12 19 2 15 8 21 18 11 3 13 14 16 1 20 27 0 28 29 32 17 26 31 34 41 24 37 30 65 40 33 47 35 36 38 23 42 49 44 50 51 54 61 48 53 56 63 46 59 52 43 62 55 25 57 58 60 45 64
10 17 20 6 7 9 33 22 18 21 19 1 2 3 16 8 13 14 4 5 15 12 32 39 42 28 29 31 11 0 40 65 41 23 24 25 38 52 35 36 26 27 37 34 54 61 64 50 51 53 55 44 62 43 63 45 46 47 60 30 57 58 48 49 59 56
3 9 11 15 6 7 18 38 20 12 21 5 19 4 2 13 14 22 17 1 10 8 25 31 33 37 28 29 40 16 42 34 65 27 41 26 46 35 36 0 39 23 32 30 47 53 55 59 50 51 62 60 64 56 43 49 63 48 24 57 58 44 61 45 54 52
15 8 18 16 1 6 7 3 26 10 12 17 21 19 13 14 20 11 5 9 2 22 37 30 40 38 23 28 29 25 4 32 34 39 65 63 35 36 42 33 27 31 24 0 59 52 62 60 45 50 51 47 48 54 56 61 43 41 57 58 64 55 49 53 46 44
16 4 22 20 15 1 5 17 11 29 6 14 13 10 12 21 19 2 8 3 18 9 38 26 0 42 37 23 27 39 33 7 28 36 57 32 34 65 41 24 30 25 40 31 60 48 44 64 59 45 49 61 55 51 50 58 35 54 56 43 63 46 52 47 62 53
18 3 8 2 19 21 12 10 9 13 36 6 7 11 17 5 1 15 20 22 4 16 40 25 30 24 41 65 34 32 31 35 14 50 29 33 39 27 23 37 42 0 26 38 62 47 52 46 63 43 56 54 53 57 58 28 51 55 61 49 45 59 64 44 48 60
9 18 3 8 2 19 21 12 10 6 7 35 14 17 5 1 15 20 22 4 16 11 31 40 25 30 24 41 65 34 32 28 51 13 36 39 27 23 37 42 0 26 38 33 53 62 47 52 46 63 43 56 54 50 29 57 58 61 49 45 59 64 44 48 60 55
1 5 17 11 16 4 22 20 15 14 13 7 28 9 10 12 21 19 2 8 3 18 23 27 39 33 38 26 0 42 37 58 35 29 6 31 32 34 65 41 24 30 25 40 45 49 61 55 60 48 44 64 59 36 57 51 50 53 54 56 43 63 46 52 47 62
8 15 16 9 3 18 14 13 17 11 5 2 4 34 7 6 22 21 10 20 19 1 30 37 38 31 25 40 36 35 61 33 27 24 26 12 29 28 0 65 32 42 41 23 52 59 60 53 47 62 58 57 39 55 49 46 48 56 51 50 44 43 54 64 63 45
20 11 10 18 9 14 13 5 3 17 1 8 16 15 65 7 6 4 19 12 22 2 42 33 32 40 31 36 35 49 25 39 23 30 38 37 21 29 28 26 41 34 0 24 64 55 54 62 53 58 57 27 47 61 45 52 60 59 43 51 50 48 63 56 44 46
17 12 9 10 14 13 1 18 22 5 15 3 11 8 20 41 7 6 16 2 21 4 39 34 31 32 36 35 45 40 0 27 37 25 33 30 42 19 29 28 38 24 65 26 61 56 53 54 58 57 23 62 44 49 59 47 55 52 64 63 51 50 60 46 43 48
21 10 12 14 13 15 9 4 5 1 20 18 17 16 3 22 24 7 6 11 8 19 65 32 34 36 35 59 31 26 27 23 42 40 39 38 25 0 2 29 28 33 30 41 43 54 56 58 57 37 53 48 49 45 64 62 61 60 47 44 46 51 50 55 52 63
12 21 14 13 20 10 16 1 19 15 22 9 5 2 11 18 4 30 7 6 17 3 34 65 36 35 64 32 38 23 41 37 0 31 27 24 33 40 26 8 29 28 39 25 56 43 58 57 42 54 60 45 63 59 44 53 49 46 55 62 48 52 51 50 61 47
19 14 13 22 12 11 15 2 21 20 4 10 1 18 8 17 9 16 25 7 6 5 41 36 35 44 34 33 37 24 65 42 26 32 23 40 30 39 31 38 3 29 28 27 63 58 57 0 56 55 59 46 43 64 48 54 45 62 52 61 53 60 47 51 50 49
14 13 4 21 17 20 8 19 2 22 16 12 15 1 9 3 5 10 11 40 7 6 36 35 48 65 39 42 30 41 24 0 38 34 37 23 31 25 27 32 33 18 29 28 58 57 26 43 61 64 52 63 46 44 60 56 59 45 53 47 49 54 55 62 51 50
13 16 19 5 22 3 2 8 14 4 11 21 20 6 15 10 18 1 12 17 31 7 35 60 41 27 0 25 24 30 36 26 33 65 42 28 37 32 40 23 34 39 9 29 57 38 63 49 44 47 46 52 58 48 55 43 64 50 59 54 62 45 56 61 53 51
11 2 1 4 18 8 3 14 13 16 17 19 22 7 6 20 12 9 15 21 5 32 55 24 23 26 40 30 25 36 35 38 39 41 0 29 28 42 34 31 37 65 27 10 33 46 45 48 62 52 47 58 57 60 61 63 44 51 50 64 56 53 59 43 49 54
44 58 50 54 49 59 46 55 45 61 57 52 64 47 63 51 48 56 53 18 62 60 11 14 6 8 20 4 10 1 22 15 13 12 16 21 9 7 17 3 2 43 34 5 38 25 42 32 36 29 24 37 41 28 33 31 40 65 0 39 35 30 26 23 19 27
50 62 59 43 45 44 56 46 55 53 61 48 57 63 58 49 52 8 60 51 64 47 6 19 4 18 22 11 3 10 1 2 15 17 13 9 14 20 12 54 5 7 16 65 42 34 29 23 41 38 30 24 37 26 28 35 33 0 25 36 31 32 27 39 40 21
55 43 51 56 5 50 62 52 46 54 53 49 61 59 44 48 45 64 58 57 47 63 1 18 7 3 60 6 19 12 10 8 2 20 15 4 11 17 22 40 14 13 21 9 37 23 39 30 27 42 34 31 24 32 26 36 28 29 38 35 41 16 25 33 65 0
46 55 60 58 52 64 43 51 48 45 54 44 53 62 49 50 57 59 61 47 9 56 10 1 5 14 12 16 23 7 17 22 8 11 2 19 20 6 13 4 15 21 63 3 24 37 27 25 31 40 18 39 35 41 32 38 26 34 36 42 33 29 28 65 0 30
49 46 55 64 59 17 57 60 58 50 45 62 54 44 43 61 56 53 47 63 52 51 20 10 1 16 4 48 13 27 14 6 22 19 8 11 18 15 3 2 21 9 12 7 36 24 37 40 29 35 33 5 25 42 41 34 32 38 23 28 30 26 65 0 31 39
59 44 46 1 57 56 49 61 64 43 50 51 45 60 53 52 54 47 63 48 58 62 4 38 10 55 13 3 20 15 16 18 6 7 22 5 2 12 8 21 9 17 14 19 29 11 24 37 33 30 36 28 40 23 42 39 41 27 26 31 32 65 0 35 25 34
57 56 62 46 55 61 52 44 53 60 43 58 6 54 48 45 47 63 49 59 51 64 33 3 19 10 1 15 12 11 2 5 18 14 50 8 17 22 21 9 20 4 7 16 13 30 34 24 37 28 31 38 26 27 23 25 42 32 35 41 65 0 36 29 39 40
54 61 52 51 46 55 53 48 62 64 60 59 43 49 50 47 63 44 3 58 57 45 8 15 12 7 10 37 2 17 19 16 5 4 18 20 6 21 9 11 56 14 13 22 32 28 31 39 24 1 26 35 34 40 27 29 23 36 42 65 0 38 30 25 33 41
51 45 53 48 58 46 55 54 49 57 64 56 60 43 21 63 62 52 59 61 50 44 7 22 26 17 14 10 1 8 20 13 16 3 5 18 47 9 19 12 4 15 6 11 39 41 2 35 25 24 37 32 36 33 40 30 27 23 65 0 34 31 29 28 42 38
48 20 44 62 51 58 59 56 52 55 46 63 47 57 64 60 43 50 45 54 53 61 17 49 11 19 7 14 4 3 12 1 10 9 21 13 16 5 18 6 22 32 2 15 35 36 38 34 39 25 29 30 31 37 24 0 65 33 40 27 23 42 41 8 26 28
53 54 45 50 43 60 64 57 61 47 63 46 55 12 56 59 58 51 62 44 49 48 2 8 22 6 18 5 16 13 15 21 9 10 1 52 3 4 25 7 19 11 20 17 26 32 41 42 23 27 40 33 28 65 0 24 37 31 30 29 14 39 34 38 36 35
61 53 54 45 50 43 60 16 57 46 55 47 63 56 59 58 51 62 44 49 48 52 15 2 8 22 42 18 5 64 13 10 1 21 9 3 4 14 7 19 11 20 17 12 28 26 32 41 6 23 27 40 33 24 37 65 0 30 29 25 39 34 38 36 35 31
58 59 56 52 48 49 11 62 51 63 47 55 46 61 57 64 60 43 50 45 54 53 14 4 3 12 17 20 44 19 39 9 21 1 10 15 13 16 5 18 6 22 8 2 25 29 30 31 35 36 38 34 7 0 65 37 24 28 33 40 27 23 42 41 32 26
22 51 48 61 54 53 63 47 56 52 59 50 49 64 55 46 44 60 57 62 43 58 45 7 17 15 8 2 9 21 3 12 29 6 20 16 1 10 11 5 13 19 18 14 41 39 35 28 32 26 0 65 30 31 4 42 36 40 37 24 38 27 33 34 23 25
62 52 57 53 61 63 47 59 54 56 14 45 48 51 60 55 46 49 43 64 44 50 19 12 13 2 15 9 21 4 8 3 58 22 35 7 5 1 10 20 18 16 11 6 34 31 33 26 28 0 65 29 32 30 25 41 17 39 27 37 24 36 23 40 38 42
56 64 15 57 63 47 58 53 44 59 51 54 52 45 62 43 55 46 48 50 60 49 3 16 61 13 9 21 14 2 11 4 7 8 12 41 19 18 1 10 17 6 5 20 30 40 28 33 0 65 25 26 38 29 39 32 31 22 34 23 37 24 35 42 27 36
60 57 64 63 47 51 61 49 4 58 62 53 56 48 54 44 50 55 46 52 45 43 5 13 16 0 21 7 15 20 59 14 19 2 3 17 8 11 6 1 10 12 22 18 27 33 40 9 65 39 28 36 29 25 34 26 30 35 32 38 42 37 24 31 41 23
64 60 63 47 62 57 48 58 43 7 44 61 59 50 52 53 49 45 55 46 56 54 16 5 9 21 19 13 17 14 18 51 11 28 4 6 12 2 20 22 1 10 3 8 40 27 0 65 34 33 35 25 23 39 38 15 29 42 31 26 36 41 37 24 30 32
43 63 47 44 64 52 51 50 60 62 49 13 58 53 45 56 61 48 54 55 46 59 18 9 21 11 16 12 7 6 5 19 20 57 14 2 22 30 15 17 8 1 10 4 23 0 65 38 40 31 39 42 27 34 36 33 25 26 41 3 28 35 32 37 24 29
63 47 49 60 56 62 45 43 50 44 48 64 51 58 61 54 59 57 52 53 55 10 9 21 20 5 3 19 22 18 6 11 17 16 7 14 15 8 4 13 31 2 1 46 0 65 36 27 30 34 41 23 42 38 35 40 39 25 28 32 29 33 12 26 37 24
47 48 43 59 44 54 50 45 63 49 52 60 62 46 51 57 2 58 64 56 61 55 21 17 18 4 11 8 6 22 9 36 12 5 19 10 7 13 53 14 16 3 15 1 65 35 23 29 38 32 42 41 0 20 31 27 34 24 39 33 26 25 40 30 28 37
52 50 58 49 53 45 54 63 47 48 56 43 44 55 46 19 64 61 51 60 59 57 12 6 14 20 2 22 8 9 21 17 3 18 11 1 24 62 16 15 7 5 4 13 31 42 25 36 26 41 32 0 65 35 30 23 38 37 10 34 40 28 39 27 29 33
23 33 65 24 37 38 35 36 41 25 40 0 31 28 29 39 42 26 30 34 27 46 13 44 47 53 61 64 57 58 62 56 43 45 63 50 51 48 49 59 54 52 60 32 55 9 14 12 7 6 17 20 16 19 21 18 22 15 4 2 5 1 8 3 11 10
65 27 38 34 41 23 26 35 36 30 25 42 40 29 33 37 0 24 32 39 63 28 47 11 64 52 62 55 59 57 58 54 56 49 43 51 44 61 45 53 46 48 31 50 14 60 6 3 16 13 1 17 20 8 19 5 21 4 9 7 18 12 10 2 22 15
36 34 39 26 32 65 27 0 35 24 30 37 25 38 23 42 41 31 33 43 28 29 58 52 2 59 46 47 60 45 57 53 54 61 56 64 55 49 62 63 44 40 50 51 20 3 48 1 10 14 11 18 17 12 8 7 19 6 13 5 16 22 9 21 15 4
35 36 32 33 0 31 34 39 42 41 24 23 30 27 37 65 40 38 56 28 29 26 57 58 46 9 45 63 52 48 49 62 53 55 54 60 61 47 43 64 25 50 51 59 17 20 10 44 18 22 3 2 5 16 12 13 8 11 7 14 21 6 19 15 4 1
37 35 36 31 38 42 40 32 33 65 41 27 24 23 34 25 26 54 28 29 0 39 61 57 58 63 6 49 43 46 44 47 62 60 53 55 52 56 59 30 50 51 45 48 7 17 20 22 64 5 21 10 9 14 16 11 12 13 3 19 1 8 15 4 18 2
38 23 35 36 40 26 37 25 31 34 65 39 41 32 30 0 53 28 29 42 33 27 64 55 57 58 43 1 61 56 63 52 47 48 62 46 54 45 24 50 51 49 44 60 6 13 17 20 21 59 7 19 22 3 14 2 16 10 8 18 12 15 4 5 9 11
40 26 27 35 36 25 0 23 30 32 34 33 65 24 42 62 28 29 37 38 39 31 43 59 60 57 58 56 18 55 54 46 52 44 47 53 49 41 50 51 61 64 48 63 21 1 11 17 20 19 45 13 8 10 3 9 14 12 5 16 15 4 7 6 2 22
24 25 0 39 35 36 30 42 27 31 32 38 34 37 47 28 29 23 26 33 40 41 53 56 45 48 57 58 54 5 60 63 46 64 52 61 65 50 51 55 59 44 43 62 12 19 18 2 17 20 8 49 11 22 10 6 3 7 14 15 4 13 1 9 21 16
39 41 30 42 33 35 36 24 37 40 31 26 32 52 28 29 27 0 38 25 65 23 48 62 54 49 44 57 58 53 7 43 63 59 46 34 50 51 60 45 64 56 47 55 2 16 8 5 9 17 20 12 61 21 22 1 10 3 15 4 11 18 6 19 14 13
42 37 23 27 39 33 38 26 0 36 35 29 50 40 31 32 34 65 41 24 30 25 49 61 55 60 48 44 64 59 45 20 57 51 28 43 63 46 52 47 62 53 54 56 5 7 13 11 2 9 6 1 18 58 17 4 15 21 22 10 3 14 16 12 8 19
30 24 41 65 34 32 31 40 25 28 29 57 36 0 26 38 33 39 27 23 37 42 54 53 62 47 52 46 63 43 56 50 4 35 58 45 59 64 44 48 60 55 61 49 8 12 16 14 3 10 22 21 19 15 51 17 20 18 1 6 9 2 11 13 7 5
25 30 24 41 65 34 32 31 40 35 58 28 29 26 38 33 39 27 23 37 42 0 56 54 53 62 47 52 46 63 43 57 36 15 51 59 64 44 48 60 55 61 49 45 19 8 12 16 14 3 10 22 21 17 20 50 4 1 6 9 2 11 13 7 5 18
33 38 26 0 42 37 23 27 39 51 28 36 35 25 40 31 32 34 65 41 24 30 44 64 59 45 49 61 55 60 48 29 50 58 17 56 43 63 46 52 47 62 53 54 9 6 1 18 5 7 13 11 2 4 15 20 57 19 21 22 10 3 14 16 12 8
41 39 42 25 24 30 29 28 59 0 38 65 37 31 36 35 23 32 40 27 34 33 62 48 49 56 53 54 51 50 26 45 64 47 61 22 58 57 55 46 43 60 52 44 16 2 5 19 12 8 4 15 1 18 6 14 7 63 20 17 13 10 21 11 3 9
27 0 40 30 25 29 28 64 24 26 33 41 42 39 32 36 35 37 34 31 23 65 60 45 43 54 56 51 50 38 53 59 44 62 49 48 10 58 57 61 52 63 55 47 11 18 21 8 19 4 15 6 12 1 9 16 5 2 46 20 17 7 3 22 13 14
26 31 25 40 29 28 44 30 23 38 39 24 0 41 27 34 36 35 42 65 32 37 59 63 56 43 51 50 33 54 55 64 48 53 45 62 60 3 58 57 49 47 46 61 1 22 19 21 4 15 9 8 13 6 2 12 18 16 11 52 20 17 5 14 10 7
32 40 31 29 28 48 25 37 38 33 27 30 26 42 24 23 65 36 35 0 41 34 46 43 63 51 50 39 56 61 64 44 60 54 59 49 53 55 14 58 57 45 62 52 10 21 22 4 15 2 19 7 6 9 11 8 1 5 12 13 47 20 17 18 16 3
31 32 29 28 60 40 42 33 34 39 23 25 38 65 0 30 37 41 36 35 26 24 63 46 51 50 27 43 49 44 52 48 55 56 64 47 45 54 61 16 58 57 59 53 22 10 4 15 11 21 5 9 3 2 13 19 6 14 18 8 7 62 20 17 1 12
34 29 28 55 31 0 39 65 32 27 37 40 33 30 41 26 25 42 24 36 35 38 52 51 50 23 63 45 48 47 46 60 61 43 44 54 62 59 56 49 12 58 57 64 3 4 15 13 22 18 2 14 10 11 7 21 9 8 16 1 19 5 53 20 17 6
29 28 61 32 26 27 41 34 65 23 42 31 39 33 25 24 38 40 0 30 36 35 51 50 37 46 59 60 62 52 47 55 49 63 48 44 56 53 64 43 45 8 58 57 4 15 7 10 1 11 16 3 14 13 5 22 2 9 19 12 6 21 18 54 20 17
28 49 34 38 23 24 65 41 29 37 0 32 27 35 39 40 30 33 31 26 25 36 50 42 52 64 55 53 47 62 51 61 45 46 60 57 48 43 54 44 63 59 19 58 15 5 3 6 13 12 14 16 4 7 18 10 11 17 2 21 8 9 22 1 56 20
45 65 33 37 30 41 24 29 28 42 26 34 23 36 35 27 31 25 39 32 38 40 0 47 44 61 54 62 53 51 50 49 59 52 55 58 57 60 63 56 48 46 64 21 18 14 9 7 8 16 12 4 15 5 1 3 13 20 17 11 22 19 2 10 6 43

Итак, оценка для порядка 66 немного улучшилась
a(66) >= 24.
ID: 2293 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2295 - Posted: 7 Jun 2021, 13:16:44 UTC
Last modified: 7 Jun 2021, 13:23:31 UTC

Harry прислал мне варианты для исходного ДЛК 16-го порядка. Спасибо!
Я обработала 2*48*48=4608 вариантов.

Кстати, Harry пишет, что его предположение о количестве вариантов углового подквадрата 4х4 оказалось ошибочным, он тоже может иметь 48 различных вариантов.

Вот что у меня получилось для 4608 вариантов

Order? 16

Enter the name of the squares file: INP1
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file INP1-orthCounts.txt
..output file INP1-orthNos.txt
squares 27646 total orthogonal pairs 8623873
Maximum pairs for square 1: 1151
There are 2301 other squares with this maximum number of pairs.
..output file INP1-1orths.txt
Pairs for square 1: 1151

elapsed time 0:09:21

Отличный результат!
Образовано 8623873 ортогональных пар.
Найдено 2302 ДЛК, имеющих 1151 ОДЛК!

Показываю основной ДЛК одной из 1151-ек и несколько ортогоналек

DLK
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
 2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13
 3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
 8  9 10 11 12 13 14 15  0  1  2  3  4  5  6  7
10 11  8  9 14 15 12 13  2  3  0  1  6  7  4  5
11 10  9  8 15 14 13 12  3  2  1  0  7  6  5  4
 9  8 11 10 13 12 15 14  1  0  3  2  5  4  7  6
12 13 14 15  8  9 10 11  4  5  6  7  0  1  2  3
14 15 12 13 10 11  8  9  6  7  4  5  2  3  0  1
15 14 13 12 11 10  9  8  7  6  5  4  3  2  1  0
13 12 15 14  9  8 11 10  5  4  7  6  1  0  3  2
 4  5  6  7  0  1  2  3 12 13 14 15  8  9 10 11
 6  7  4  5  2  3  0  1 14 15 12 13 10 11  8  9
 7  6  5  4  3  2  1  0 15 14 13 12 11 10  9  8
 5  4  7  6  1  0  3  2 13 12 15 14  9  8 11 10

mate #1
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
 3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
 2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13
12 13 14 15  8  9 10 11  4  5  6  7  0  1  2  3
15 14 13 12 11 10  9  8  7  6  5  4  3  2  1  0
13 12 15 14  9  8 11 10  5  4  7  6  1  0  3  2
14 15 12 13 10 11  8  9  6  7  4  5  2  3  0  1
 4  5  6  7  0  1  2  3 12 13 14 15  8  9 10 11
 7  6  5  4  3  2  1  0 15 14 13 12 11 10  9  8
 5  4  7  6  1  0  3  2 13 12 15 14  9  8 11 10
 6  7  4  5  2  3  0  1 14 15 12 13 10 11  8  9
 8  9 10 11 12 13 14 15  0  1  2  3  4  5  6  7
11 10  9  8 15 14 13 12  3  2  1  0  7  6  5  4
 9  8 11 10 13 12 15 14  1  0  3  2  5  4  7  6
10 11  8  9 14 15 12 13  2  3  0  1  6  7  4  5

mate #2
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
 3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
 2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13
12 13 14 15  8  9 10 11  4  5  6  7  0  1  2  3
15 14 13 12 11 10  9  8  7  6  5  4  3  2  1  0
13 12 15 14  9  8 11 10  5  4  7  6  1  0  3  2
14 15 12 13 10 11  8  9  6  7  4  5  2  3  0  1
 4  5  6  7  0  1  2  3 12 13 15 14  8  9 10 11
 7  6  5  4  3  2  1  0 14 15 13 12 11 10  9  8
 5  4  7  6  1  0  3  2 13 12 14 15  9  8 11 10
 6  7  4  5  2  3  0  1 15 14 12 13 10 11  8  9
 8  9 10 11 12 13 14 15  0  1  2  3  4  5  6  7
11 10  9  8 15 14 13 12  3  2  1  0  7  6  5  4
 9  8 11 10 13 12 15 14  1  0  3  2  5  4  7  6
10 11  8  9 14 15 12 13  2  3  0  1  6  7  4  5
. . . . . . 

mate #1150
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
 3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
 2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13
12 13 14 15 11 10  9  8  4  5  6  7  0  1  2  3
15 14 13 12  8  9 10 11  7  6  5  4  3  2  1  0
13 12 15 14 10 11  8  9  5  4  7  6  1  0  3  2
14 15 12 13  9  8 11 10  6  7  4  5  2  3  0  1
 4  5  6  7  0  1  2  3 15 14 12 13  8  9 10 11
 7  6  5  4  3  2  1  0 13 12 14 15 11 10  9  8
 5  4  7  6  1  0  3  2 14 15 13 12  9  8 11 10
 6  7  4  5  2  3  0  1 12 13 15 14 10 11  8  9
 8  9 10 11 12 13 14 15  0  1  2  3  4  5  6  7
11 10  9  8 15 14 13 12  3  2  1  0  7  6  5  4
 9  8 11 10 13 12 15 14  1  0  3  2  5  4  7  6
10 11  8  9 14 15 12 13  2  3  0  1  6  7  4  5

mate #1151
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
 3  2  1  0  7  6  5  4 11 10  9  8 15 14 13 12
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
 2  3  0  1  6  7  4  5 10 11  8  9 14 15 12 13
12 13 14 15 11 10  9  8  4  5  6  7  0  1  2  3
15 14 13 12  8  9 10 11  7  6  5  4  3  2  1  0
13 12 15 14 10 11  8  9  5  4  7  6  1  0  3  2
14 15 12 13  9  8 11 10  6  7  4  5  2  3  0  1
 4  5  6  7  0  1  2  3 15 14 13 12  8  9 10 11
 7  6  5  4  3  2  1  0 12 13 14 15 11 10  9  8
 5  4  7  6  1  0  3  2 14 15 12 13  9  8 11 10
 6  7  4  5  2  3  0  1 13 12 15 14 10 11  8  9
 8  9 10 11 12 13 14 15  0  1  2  3  4  5  6  7
11 10  9  8 15 14 13 12  3  2  1  0  7  6  5  4
 9  8 11 10 13 12 15 14  1  0  3  2  5  4  7  6
10 11  8  9 14 15 12 13  2  3  0  1  6  7  4  5

Итак. оценка для порядка 16 сильно улучшена
a(16) >= 1151.
И может быть ещё сильно улучшена данным алгоритмом.

Интересные свойства у ОДЛК 1151-ки 16-го порядка

Order? 16

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt

Counts
------
      1152 diagonal Latin
         1 weakly pandiagonal
         2 double axial symmetric
        48 center symmetric
      1152 nfr
         1 orthogonal pair
      1152 self-orthogonal
        31 axial parity 1-way
         1 symmetric parity
ID: 2295 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
ProfileNatalia Makarova
Project scientist
Avatar

Send message
Joined: 22 Oct 17
Posts: 3083
Credit: 0
RAC: 0
Message 2296 - Posted: 7 Jun 2021, 14:02:18 UTC
Last modified: 7 Jun 2021, 14:03:31 UTC

О-о-о!
У Harry завершилась обработка набора ДЛК 18-го порядка

Order? 18
 
Enter the name of the squares file: 18aAllCenter4ToNFR
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file 18aAllCenter4ToNFR-orthCounts.txt
..output file 18aAllCenter4ToNFR-orthNos.txt
    .. increasing LS store to     100,000
    .. increasing LS store to     200,000
    .. increasing LS store to     400,000
    .. increasing LS store to     800,000
    .. increasing LS store to   1,600,000
squares 960000 total orthogonal pairs 12828672
Maximum pairs for square 220273: 96
There are 2303 other squares with this maximum number of pairs.
..output file 18aAllCenter4ToNFR-220273orths.txt
Pairs for square 220273: 96
 
elapsed time 58:11:27

Грандиозно!
Обратите внимание на время.
Образовано 12828672 ортогональных пар.
Найдено 2304 ДЛК, имеющих 96 ОДЛК!

Показываю основной ДЛК одной из 96-ок и несколько ортогоналек

DLK
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
 6  7 16  8 17 14  5 10 15 11  4 12 13  9  3  2  1  0
 5  6 10  2 15  1  9  4  3  0 14 13 11 17  8 16  7 12
11  5  6  4  8  3 16 14 17  7  9  0  1 15  2 10 12 13
 2  0  5  6 14 15 17  9  1 10 11 16  3  8  4 12 13  7
 1  8  7  5  6  9  3 11 16  4  0 17 15 14 12 13 10  2
17 16 15 10  5  6 11  0  2 14  7  3  9 12 13  4  8  1
 4 14  9 11  0  7 10  6  5 13 12 15  8  2 16  1 17  3
 3 17  1 16  2  8 15 12 13  5  6  9 14  4 10  7  0 11
 8 15  3 17  1 16  2  5  6 12 13 10  7  0 11  9 14  4
 9 11  0  7 10  4 14 13 12  6  5  1 17  3 15  8  2 16
16 10 11  1 13 12  7  3 14  8 15  2  6  5  0 17  4  9
 7  9 17 13 12  0  1 15  4  2  8 14 16  6  5 11  3 10
14  3 13 12 11 17  0  8 10 16  2  7  4  1  6  5  9 15
15 13 12  9  3 11  4  2  7  1 16  8  0 10 17  6  5 14
13 12 14 15  9 10  8 16  0 17  1  4  2 11  7  3  6  5
12  4  8 14  7  2 13  1 11  3 17  5 10 16  9  0 15  6
10  2  4  0 16 13 12 17  9 15  3  6  5  7  1 14 11  8

mate #1
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
 5 12  1  2  0  9 11 13  6 14  3 17 10  8 15 16  7  4
 4 11 17  1  2 12 14 10  5  8  0  3  6 15 16 13  9  7
 8  9  4  7  1  2 17  3 11  6 12  5 15 16 10 14 13  0
 7  6 14  9 13  1  2  0  4  5 17 15 16  3  8 10 12 11
 2 13  5  8 14 10  1 12  9 11  7 16  0  6  3 17  4 15
 1  2 10 11  6  8  3 17 14  4 13 12  5  0  7  9 15 16
12 17  7 13 10  3  0  1  2 15 16  8 14  9  4 11  5  6
 9 14  8  6  5 11  4 15 16  1  2 13  7 17 12  0  3 10
10  3  0 12 17  7 13 16 15  2  1  9  4 11  5  6  8 14
17  7 13 10  3  0 12  2  1 16 15 14  9  4 11  5  6  8
 3 16 15  0 11  6  8 14 10 17  5  4 13 12  9  7  2  1
16 15  3  5  8 14 10  9 13 12  6  1 11  7  0  4 17  2
15 10  6 14  9 13 16  4  7  0  8  2  1  5 17  3 11 12
13  8  9  4  7 16 15 11 17  3 14  0  2  1  6 12 10  5
14  4 11 17 16 15  7  5 12 10  9  6  3  2  1  8  0 13
11  5 12 16 15 17  9  6  0 13  4  7  8 10  2  1 14  3
 6  0 16 15 12  4  5  8  3  7 11 10 17 14 13  2  1  9

mate #2
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
 5 12  1  2  0  9 11 13  6 14  3 17 10  8 15 16  7  4
 4 11 17  1  2 12 14 10  5  8  0  3  6 15 16 13  9  7
 8  9  4  7  1  2 17  3 11  6 12  5 15 16 10 14 13  0
 7  6 14  9 13  1  2  0  4  5 17 15 16  3  8 10 12 11
 2 13  5  8 14 10  1 12  9 11  7 16  0  6  3 17  4 15
 1  2 10 11  6  8  3 17 14  4 13 12  5  0  7  9 15 16
12 17  7 13 10  3  0  1  2 16 15  8 14  9  4 11  5  6
 9 14  8  6  5 11  4 16 15  1  2 13  7 17 12  0  3 10
10  3  0 12 17  7 13 15 16  2  1  9  4 11  5  6  8 14
17  7 13 10  3  0 12  2  1 15 16 14  9  4 11  5  6  8
 3 16 15  0 11  6  8 14 10 17  5  4 13 12  9  7  2  1
16 15  3  5  8 14 10  9 13 12  6  1 11  7  0  4 17  2
15 10  6 14  9 13 16  4  7  0  8  2  1  5 17  3 11 12
13  8  9  4  7 16 15 11 17  3 14  0  2  1  6 12 10  5
14  4 11 17 16 15  7  5 12 10  9  6  3  2  1  8  0 13
11  5 12 16 15 17  9  6  0 13  4  7  8 10  2  1 14  3
 6  0 16 15 12  4  5  8  3  7 11 10 17 14 13  2  1  9
. . . . . . 

mate #95
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
11 13  1  2  0  9  8 12  6 14  3 10 17  5 15 16  7  4
 6  4 17  1  2 13 14 10 11  5  0  7  8 15 16 12  9  3
 5 11  9  7  1  2 17  3  4  8 13  6 15 16 10 14  0 12
 7  8  4 14 12  1  2  0  9  6 17 15 16  3  5 13 10 11
 2 12  6  9  5 10  1 13 14 11  7 16  0  8 17  3  4 15
 1  2 10 11 14  8  3 17  5  4 12 13  6  7  0  9 15 16
13 17  7 12 10  3  0 15 16  1  2  5 14  9  4 11  6  8
 9 14  5  8  6 11  4  1  2 15 16 12  7 17 13  0  3 10
10  3  0 13 17  7 12  2  1 16 15  9  4 11  6  8  5 14
17  7 12 10  3  0 13 16 15  2  1 14  9  4 11  6  8  5
 3 16 15  0 11  6  5 14 10 17  8  4 13 12  9  7  2  1
16 15  3  6  8 14 10  9 12 13  5  1 11  0  7  4 17  2
15 10  8  5  9 12 16  4  7  0 14  2  1  6  3 17 11 13
12  5 14  4  7 16 15 11 17  3  9  0  2  1  8 10 13  6
14  9 11 17 16 15  7  6 13 10  4  8  3  2  1  5 12  0
 4  6 13 16 15 17  9  8  0 12 11  3  5 10  2  1 14  7
 8  0 16 15 13  4 11  5  3  7  6 17 10 14 12  2  1  9

mate #96
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
11 13  1  2  0  9  8 12  6 14  3 10 17  5 15 16  7  4
 6  4 17  1  2 13 14 10 11  5  0  7  8 15 16 12  9  3
 5 11  9  7  1  2 17  3  4  8 13  6 15 16 10 14  0 12
 7  8  4 14 12  1  2  0  9  6 17 15 16  3  5 13 10 11
 2 12  6  9  5 10  1 13 14 11  7 16  0  8 17  3  4 15
 1  2 10 11 14  8  3 17  5  4 12 13  6  7  0  9 15 16
13 17  7 12 10  3  0 15 16  2  1  5 14  9  4 11  6  8
 9 14  5  8  6 11  4  2  1 15 16 12  7 17 13  0  3 10
10  3  0 13 17  7 12  1  2 16 15  9  4 11  6  8  5 14
17  7 12 10  3  0 13 16 15  1  2 14  9  4 11  6  8  5
 3 16 15  0 11  6  5 14 10 17  8  4 13 12  9  7  2  1
16 15  3  6  8 14 10  9 12 13  5  1 11  0  7  4 17  2
15 10  8  5  9 12 16  4  7  0 14  2  1  6  3 17 11 13
12  5 14  4  7 16 15 11 17  3  9  0  2  1  8 10 13  6
14  9 11 17 16 15  7  6 13 10  4  8  3  2  1  5 12  0
 4  6 13 16 15 17  9  8  0 12 11  3  5 10  2  1 14  7
 8  0 16 15 13  4 11  5  3  7  6 17 10 14 12  2  1  9

Итак, оценка для порядка 18 сильно улучшена
a(18) >= 96.

Теперь надо попробовать метод Пелегрино-Ланселотти для порядка 54 на базе 96-ки 18-го порядка.
ID: 2296 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Previous · 1 · 2 · 3 · 4 · 5 . . . 11 · Next

Message boards : Science : Алгоритм получения двушек для порядков n=4k+2

©2024 ©2024 Progger & Stefano Tognon (ice00) & Reese