Thread 'Статьи в OEIS: иÑÑ‚Ð¾Ñ€Ð¸Ñ Ð¸ ÑовременноÑÑ‚ÑŒ'
Message boards : Science : Статьи в OEIS: иÑÑ‚Ð¾Ñ€Ð¸Ñ Ð¸ ÑовременноÑÑ‚ÑŒ
Message board moderation
Previous · 1 · 2 · 3 · 4 · 5 · 6 · 7 . . . 23 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
И проÑто поÑмотрите на черновик обÑуждаемой Ñтатьи OEIS LINKS Ðа каждый чих ÑÑылка! По каждой ÑÑылке одно Ñообщение! Ðвтор - единÑтвенный и неповторимый! У Ð¼ÐµÐ½Ñ Ð±Ñ‹Ð»Ð¸ ÑÑылки на большие темы, которые (ÑÑылки) удалÑлиÑÑŒ редактором, потому что в темах "обÑуждение между вами и вами". Слава Богу, мне больше не надо давать никаких ÑÑылок в OEIS. СчаÑтлива безмерно! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата И вот тут результаты Итак, моё Ñдро БД КФ ОДЛК 11-го порÑдка выложено 18 ÑÐ½Ð²Ð°Ñ€Ñ 2021 г. Оно Ñодержит 109025 КФ ОДЛК. Беру Ñто Ñдро, выбраÑываю шеÑÑ‚ÑŒ топовых ДЛК (потому что они обÑчитываютÑÑ Ð½Ð° ОДЛК довольно долго) и обÑчитываю вÑе оÑтавшиеÑÑ Ð”Ð›Ðš программой Белышева ortogon_u. Программа ÑправлÑетÑÑ Ñ Ñтим за 50 минут на моём тихоходе. Показываю полученный Ñпектр вмеÑте Ñ Ð”Ð›Ðš (количеÑтво ОДЛК Ñледует за DLK в круглых Ñкобках) [DLK(1):1] 0 2 3 4 5 6 7 8 9 A 1 5 1 0 A 6 7 8 3 4 2 9 A 6 2 0 7 8 9 1 3 5 4 2 7 8 3 9 0 A 4 5 1 6 3 A 9 8 4 1 0 5 6 7 2 7 4 A 1 8 5 2 9 0 6 3 8 3 4 5 A 9 6 2 1 0 7 4 9 5 6 0 A 1 7 2 3 8 6 5 7 9 1 2 3 A 8 4 0 1 8 6 7 2 3 4 0 A 9 5 9 0 1 2 3 4 5 6 7 8 A [DLK(2):86] 0 2 3 4 6 7 8 9 A 5 1 4 1 6 2 7 8 9 A 5 0 3 A 9 2 5 0 6 7 1 3 4 8 8 0 1 3 A 9 5 4 2 6 7 1 8 9 7 4 A 2 0 6 3 5 6 3 A 8 9 5 1 2 0 7 4 5 7 4 A 8 0 6 3 1 2 9 3 4 8 6 5 1 0 7 9 A 2 2 6 7 9 3 4 A 5 8 1 0 7 A 5 0 1 2 3 8 4 9 6 9 5 0 1 2 3 4 6 7 8 A [DLK(3):954] 0 2 3 7 5 9 4 6 A 8 1 7 1 4 A 3 2 8 5 9 0 6 9 5 2 1 8 6 0 A 3 7 4 5 A 6 3 7 8 9 2 4 1 0 A 0 8 9 4 3 7 1 5 6 2 2 4 0 6 1 5 3 8 7 A 9 4 7 5 8 9 A 6 0 1 2 3 6 8 9 4 A 1 2 7 0 3 5 3 9 A 2 6 0 1 4 8 5 7 1 6 7 5 0 4 A 3 2 9 8 8 3 1 0 2 7 5 9 6 4 A [DLK(4):2178] 0 2 3 A 6 7 4 8 9 5 1 3 1 4 2 A 9 8 5 7 0 6 7 5 2 9 1 8 0 A 3 6 4 A 4 6 3 8 1 9 2 5 7 0 6 0 8 5 4 A 7 1 2 3 9 9 A 7 8 3 5 1 6 0 4 2 2 7 5 1 9 4 6 0 A 8 3 1 8 9 4 0 3 2 7 6 A 5 5 9 A 0 2 6 3 4 8 1 7 4 6 0 7 5 2 A 3 1 9 8 8 3 1 6 7 0 5 9 4 2 A [DLK(5):3292] 0 2 4 7 8 3 9 6 5 A 1 6 1 9 8 7 2 3 A 4 0 5 1 7 2 A 0 6 8 5 3 4 9 4 A 6 3 5 9 0 2 7 1 8 A 8 3 6 4 0 7 1 9 5 2 7 9 8 1 A 5 4 3 6 2 0 3 5 1 2 9 A 6 8 0 7 4 9 3 0 4 2 1 5 7 A 8 6 2 0 A 5 6 4 1 9 8 3 7 5 6 7 0 1 8 A 4 2 9 3 8 4 5 9 3 7 2 0 1 6 A [DLK(6):4488] 0 2 4 9 6 8 7 5 A 3 1 A 1 3 0 8 7 5 9 4 2 6 7 9 2 4 1 6 8 0 3 A 5 2 6 8 3 0 A 1 4 9 5 7 1 3 A 7 4 9 0 8 5 6 2 6 A 9 8 7 5 3 2 1 0 4 8 4 5 2 A 1 6 3 0 7 9 3 5 1 6 9 0 A 7 2 4 8 5 0 7 A 2 4 9 6 8 1 3 4 8 6 1 5 3 2 A 7 9 0 9 7 0 5 3 2 4 1 6 8 A [DLK(7):5855] 0 2 5 7 3 4 8 6 9 A 1 6 1 4 8 9 0 A 5 7 2 3 8 A 2 9 7 1 5 0 3 4 6 5 9 A 3 6 8 2 4 1 7 0 1 5 8 2 4 3 0 9 A 6 7 2 7 6 0 1 5 9 A 4 3 8 3 4 0 1 A 7 6 8 2 5 9 A 3 9 6 8 2 4 7 0 1 5 4 6 7 A 5 9 3 1 8 0 2 7 8 3 5 0 A 1 2 6 9 4 9 0 1 4 2 6 7 3 5 8 A [DLK(8):6400] 0 2 5 7 8 9 3 A 4 6 1 7 1 3 5 6 8 9 0 A 2 4 A 6 2 4 5 7 1 9 3 0 8 5 9 A 3 0 6 8 4 1 7 2 1 5 8 9 4 A 0 2 6 3 7 4 0 1 2 3 5 7 8 9 A 6 3 7 4 8 A 0 6 1 2 5 9 8 3 9 6 2 4 A 7 0 1 5 2 A 7 1 9 3 5 6 8 4 0 6 8 0 A 1 2 4 5 7 9 3 9 4 6 0 7 1 2 3 5 8 A [DLK(9):4778] 0 2 4 9 7 8 3 5 6 A 1 6 1 8 7 3 2 9 A 5 0 4 9 7 2 A 5 6 4 0 3 1 8 1 5 6 3 A 4 0 2 7 8 9 3 8 0 6 4 9 7 1 A 2 5 4 A 7 0 8 5 1 6 9 3 2 5 3 1 8 9 A 6 4 2 7 0 A 9 3 4 2 1 8 7 0 5 6 2 4 A 1 0 3 5 9 8 6 7 7 6 5 2 1 0 A 8 4 9 3 8 0 9 5 6 7 2 3 1 4 A [DLK(10):92252] 0 3 8 9 5 7 A 2 4 6 1 5 1 4 7 8 6 3 0 A 2 9 7 5 2 0 6 A 1 9 3 8 4 A 6 5 3 1 9 8 4 7 0 2 2 9 A 5 4 8 0 6 1 3 7 4 0 1 2 3 5 7 8 9 A 6 3 7 9 4 A 2 6 5 0 1 8 8 A 3 6 2 1 9 7 5 4 0 6 2 7 1 9 0 4 A 8 5 3 1 8 0 A 7 4 2 3 6 9 5 9 4 6 8 0 3 5 1 2 7 A [DLK(11):115512] 0 7 8 4 3 6 9 2 A 5 1 4 1 6 7 0 A 3 9 5 2 8 1 0 2 A 6 9 8 5 3 7 4 A 2 1 3 9 8 5 4 6 0 7 8 9 3 2 4 7 0 A 1 6 5 7 6 A 9 8 5 2 1 0 4 3 5 4 9 0 A 3 6 8 7 1 2 3 A 4 6 5 2 1 7 9 8 0 6 3 7 5 2 1 4 0 8 A 9 2 8 5 1 7 0 A 3 4 9 6 9 5 0 8 1 4 7 6 2 3 A [DLK(12):73511] 0 2 A 7 5 9 3 8 4 6 1 5 1 3 9 6 8 7 0 A 2 4 A 5 2 4 8 7 1 9 3 0 6 7 9 5 3 0 6 8 4 1 A 2 1 6 8 5 4 A 0 2 9 3 7 2 3 4 0 1 5 9 A 6 7 8 3 7 1 8 A 0 6 5 2 4 9 8 0 9 6 2 4 A 7 5 1 3 4 A 7 1 9 3 2 6 8 5 0 6 8 0 A 3 2 4 1 7 9 5 9 4 6 2 7 1 5 3 0 8 A [DLK(13):4230] 0 2 4 8 9 A 7 3 5 6 1 8 1 3 0 7 9 4 5 A 2 6 6 7 2 4 1 8 5 9 3 A 0 2 A 6 3 0 7 8 4 9 1 5 1 3 9 A 4 6 0 8 2 5 7 7 6 A 9 8 5 2 1 0 4 3 3 5 8 2 A 4 6 0 1 7 9 5 9 1 6 2 3 A 7 4 0 8 A 0 7 1 5 2 9 6 8 3 4 4 8 0 5 6 1 3 A 7 9 2 9 4 5 7 3 0 1 2 6 8 A [DLK(14):6310] 0 2 5 7 8 4 3 A 9 6 1 7 1 3 5 6 0 9 8 A 2 4 A 6 2 4 5 1 7 9 3 0 8 5 9 A 3 0 2 8 4 1 7 6 1 5 8 9 4 3 0 2 6 A 7 8 7 6 A 9 5 1 0 4 3 2 3 0 4 8 A 7 6 1 2 5 9 4 3 9 6 2 8 A 7 0 1 5 2 A 7 1 3 9 5 6 8 4 0 6 8 0 2 1 A 4 5 7 9 3 9 4 1 0 7 6 2 3 5 8 A [DLK(16):6062] 0 2 5 7 8 4 3 6 9 A 1 3 1 4 8 9 0 A 5 7 2 6 8 6 2 A 5 7 4 1 3 0 9 A 7 9 3 1 2 8 4 0 6 5 6 5 8 2 4 1 0 9 A 7 3 2 9 6 0 3 5 7 A 4 1 8 7 3 0 1 A 9 6 8 2 5 4 5 4 A 6 2 8 9 7 1 3 0 1 A 7 9 6 3 5 0 8 4 2 4 8 3 5 0 A 1 2 6 9 7 9 0 1 4 7 6 2 3 5 8 A [DLK(17):90347] 0 3 8 2 7 9 A 5 4 6 1 6 1 4 7 3 8 5 0 A 2 9 4 A 2 0 6 7 1 9 3 8 5 A 0 9 3 1 6 8 4 7 5 2 2 9 1 8 4 A 0 6 5 3 7 7 6 A 9 8 5 2 1 0 4 3 3 7 5 4 A 0 6 2 9 1 8 8 5 3 6 2 4 9 7 1 A 0 5 2 7 1 9 3 4 A 8 0 6 1 8 0 A 5 2 7 3 6 9 4 9 4 6 5 0 1 3 8 2 7 A [DLK(18):90559] 0 3 8 4 2 9 7 A 5 6 1 3 1 4 7 9 8 A 5 0 2 6 1 A 2 9 6 7 5 0 3 4 8 A 7 0 3 1 6 2 4 9 8 5 8 5 6 2 4 A 0 9 7 1 3 6 0 9 8 7 5 3 2 1 A 4 7 9 3 1 A 0 6 8 4 5 2 5 2 1 6 8 4 9 7 A 3 0 2 6 7 A 5 3 4 1 8 0 9 4 8 A 5 0 2 1 3 6 9 7 9 4 5 0 3 1 8 6 2 7 A [DLK(20):45141] 0 2 5 8 6 9 4 A 7 3 1 A 1 3 5 7 8 9 6 4 2 0 6 9 2 4 5 7 A 0 3 1 8 5 A 8 3 0 6 1 4 2 7 9 1 5 9 7 4 A 0 3 6 8 2 4 0 1 2 3 5 7 8 9 A 6 9 7 4 1 8 2 6 5 A 0 3 8 3 0 9 A 1 2 7 5 6 4 2 4 A 6 9 0 3 1 8 5 7 3 6 7 A 1 4 8 2 0 9 5 7 8 6 0 2 3 5 9 1 4 A [DLK(21):95720] 0 3 9 A 8 4 7 5 2 6 1 7 1 4 8 9 0 5 3 A 2 6 8 6 2 0 7 1 4 9 3 A 5 6 7 A 3 1 2 8 4 9 5 0 2 A 6 9 4 3 0 8 5 1 7 1 2 3 4 0 5 A 6 7 8 9 3 9 5 2 A 7 6 1 4 0 8 A 5 1 6 2 8 9 7 0 3 4 5 0 7 1 6 9 3 A 8 4 2 4 8 0 7 5 A 1 2 6 9 3 9 4 8 5 3 6 2 0 1 7 A [DLK(28):92639] 0 3 8 A 7 9 2 6 5 4 1 3 1 A 7 0 8 9 5 4 2 6 1 0 2 9 5 7 4 A 3 6 8 A 7 0 3 2 6 1 4 9 8 5 7 9 3 1 4 A 0 8 6 5 2 6 A 9 8 3 5 7 2 1 0 4 8 5 4 2 A 0 6 9 7 1 3 5 2 1 6 9 4 8 7 A 3 0 2 4 7 0 6 3 5 1 8 A 9 4 8 6 5 1 2 A 3 0 9 7 9 6 5 4 8 1 3 0 2 7 A [DLK(32):3346] 0 2 4 7 8 6 3 9 5 A 1 7 1 3 0 6 A 8 5 9 2 4 A 6 2 4 1 9 5 8 3 0 7 2 9 A 3 0 8 7 4 1 6 5 1 7 8 9 4 3 0 2 A 5 6 8 3 6 A 9 5 1 0 4 7 2 4 5 0 8 A 7 6 1 2 3 9 5 4 9 6 3 2 A 7 0 1 8 3 A 7 2 5 1 9 6 8 4 0 6 8 1 5 2 0 4 A 7 9 3 9 0 5 1 7 4 2 3 6 8 A [DLK(33):6082] 0 2 5 7 8 4 3 9 6 A 1 7 1 3 5 6 0 8 A 9 2 4 A 6 2 4 5 1 9 8 3 0 7 5 9 A 3 0 2 7 4 1 6 8 1 5 8 9 4 3 0 2 A 7 6 8 7 6 A 9 5 1 0 4 3 2 4 3 0 8 A 7 6 1 2 5 9 2 4 9 6 3 8 A 7 0 1 5 3 A 7 2 1 9 5 6 8 4 0 6 8 1 0 2 A 4 5 7 9 3 9 0 4 1 7 6 2 3 5 8 A [DLK(34):47381] 0 2 5 9 7 4 8 3 6 A 1 6 1 3 5 8 0 4 A 9 2 7 7 A 2 4 5 1 9 8 3 6 0 5 6 9 3 0 2 7 4 A 1 8 1 5 A 8 4 3 0 9 2 7 6 8 7 6 A 9 5 1 0 4 3 2 4 3 8 1 A 7 6 2 0 5 9 2 9 0 6 3 8 A 7 1 4 5 A 4 7 2 1 9 5 6 8 0 3 3 8 1 0 6 A 2 5 7 9 4 9 0 4 7 2 6 3 1 5 8 A [DLK(35):4545] 0 2 4 9 7 6 8 3 5 A 1 6 1 3 0 8 A 4 5 9 2 7 7 A 2 4 1 9 5 8 3 6 0 2 6 9 3 0 8 7 4 A 1 5 1 3 A 8 4 7 0 9 2 5 6 8 7 6 A 9 5 1 0 4 3 2 4 5 8 1 A 3 6 2 0 7 9 5 9 0 6 3 2 A 7 1 4 8 A 4 7 2 5 1 9 6 8 0 3 3 8 1 5 6 0 2 A 7 9 4 9 0 5 7 2 4 3 1 6 8 A [DLK(36):3310] 0 2 4 7 8 6 3 9 5 A 1 7 1 3 0 6 A 8 5 9 2 4 A 6 2 4 1 9 5 8 3 0 7 2 9 A 3 0 8 7 4 1 6 5 1 3 8 9 4 7 0 2 A 5 6 8 7 6 A 9 5 1 0 4 3 2 4 5 0 8 A 3 6 1 2 7 9 5 4 9 6 3 2 A 7 0 1 8 3 A 7 2 5 1 9 6 8 4 0 6 8 1 5 2 0 4 A 7 9 3 9 0 5 1 7 4 2 3 6 8 A [DLK(37):101743] 0 4 6 9 3 7 5 A 2 8 1 4 1 0 A 8 6 9 3 7 2 5 7 0 2 1 9 A 4 6 3 5 8 8 6 1 3 2 9 A 4 5 7 0 3 7 A 2 4 8 0 5 6 1 9 6 A 9 8 7 5 3 2 1 0 4 1 9 4 5 A 2 6 8 0 3 7 A 3 5 6 0 1 8 7 9 4 2 2 5 7 4 6 0 1 9 8 A 3 5 8 3 7 1 4 2 0 A 9 6 9 2 8 0 5 3 7 1 4 6 A [DLK(38):113806] 0 7 3 5 6 8 9 2 A 4 1 A 1 6 4 5 7 3 9 0 2 8 5 9 2 A 0 6 8 1 3 7 4 1 5 8 3 9 A 2 4 6 0 7 8 2 5 7 4 9 0 A 1 6 3 4 0 1 2 3 5 7 8 9 A 6 7 4 9 0 A 1 6 3 5 8 2 3 A 4 6 8 0 1 7 2 5 9 6 3 7 9 2 4 A 0 8 1 5 2 8 A 1 7 3 5 6 4 9 0 9 6 0 8 1 2 4 5 7 3 A [DLK(47):94498] 0 3 9 7 5 2 8 6 4 A 1 5 1 4 8 6 3 A 0 9 2 7 A 5 2 0 7 4 1 8 3 6 9 6 9 5 3 1 0 7 4 A 8 2 2 A 8 5 4 1 0 9 7 3 6 7 6 A 9 8 5 2 1 0 4 3 4 7 3 1 A 9 6 5 2 0 8 8 2 0 6 3 A 9 7 5 1 4 1 4 7 2 9 6 3 A 8 5 0 3 8 1 A 0 7 4 2 6 9 5 9 0 6 4 2 8 5 3 1 7 A [DLK(127):90826] 0 3 8 4 7 A 2 5 9 6 1 6 1 4 7 0 9 5 8 A 2 3 1 A 2 0 6 8 7 9 3 4 5 A 2 9 3 1 7 8 4 0 5 6 2 9 3 8 4 6 0 1 5 A 7 8 7 6 A 9 5 1 0 4 3 2 3 0 5 9 A 4 6 2 7 1 8 4 5 A 6 2 3 9 7 1 8 0 5 6 7 1 3 2 4 A 8 0 9 7 8 0 2 5 1 A 3 6 9 4 9 4 1 5 8 0 3 6 2 7 A И дальше Ñледуют шеÑÑ‚ÑŒ топовых ДЛК, которые показаны выше; они в Ñвоё Ð²Ñ€ÐµÐ¼Ñ Ð±Ñ‹Ð»Ð¸ обÑчитаны на ОДЛК. Итак, полученный по моей чаÑтичной БД КФ ОДЛК 11-гbr /> 8 5 4 2 A 0 6 9 7 1 3 5 2 1 6 9 4 8 7 A 3 0 2 4 7 0 6 3 5 1 8 A 9 4 8 6 5 1 2 A 3 0 9 7 9 6 5 4 8 1 3 0 2 7 A [DLK(32):3346] 0 2 4 7 8 6 3 9 5 A 1 7 1 3 0 6 A 8 5 9 2 4 A 6 2 4 1 9 5 8 3 0 7 2 9 A 3 0 8 7 4 1 6 5 1 7 8 9 4 3 0 2 A 5 6 8 3 6 A 9 5 1 0 4 7 2 4 5 0 8 A 7 6 1 2 3 9 5 4 9 6 3 2 A 7 0 1 8 3 A 7 2 5 1 9 6 8 4 0 6 8 1 5 2 0 4 A 7 9 3 9 0 5 1 7 4 2 3 6 8 A [DLK(33):6082] 0 2 5 7 8 4 3 9 6 A 1 7 1 3 5 6 0 8 A 9 2 4 A 6 2 4 5 1 9 8 3 0 7 5 9 A 3 0 2 7 4 1 6 8 1 5 8 9 4 3 0 2 A 7 6 8 7 6 A 9 5 1 0 4 3 2 4 3 0 8 A 7 6 1 2 5 9 2 4 9 6 3 8 A 7 0 1 5 3 A 7 2 1 9 5 6 8 4 0 6 8 1 0 2 A 4 5 7 9 3 9 0 4 1 7 6 2 3 5 8 A [DLK(34):47381] 0 2 5 9 7 4 8 3 6 A 1 6 1 3 5 8 0 4 A 9 2 7 7 A 2 4 5 1 9 8 3 6 0 5 6 9 3 0 2 7 4 A 1 8 1 5 A 8 4 3 0 9 2 7 6 8 7 6 A 9 5 1 0 4 3 2 4 3 8 1 A 7 6 2 0 5 9 2 9 0 6 3 8 A 7 1 4 5 A 4 7 2 1 9 5 6 8 0 3 3 8 1 0 6 A 2 5 7 9 4 9 0 4 7 2 6 3 1 5 8 A [DLK(35):4545] 0 2 4 9 7 6 8 3 5 A 1 6 1 3 0 8 A 4 5 9 2 7 7 A 2 4 1 9 5 8 3 6 0 2 6 9 3 0 8 7 4 A 1 5 1 3 A 8 4 7 0 9 2 5 6 8 7 6 A 9 5 1 0 4 3 2 4 5 8 1 A 3 6 2 0 7 9 5 9 0 6 3 2 A 7 1 4 8 A 4 7 2 5 1 9 6 8 0 3 3 8 1 5 6 0 2 A 7 9 4 9 0 5 7 2 4 3 1 6 8 A [DLK(36):3310] 0 2 4 7 8 6 3 9 5 A 1 7 1 3 0 6 A 8 5 9 2 4 A 6 2 4 1 9 5 8 3 0 7 2 9 A 3 0 8 7 4 1 6 5 1 3 8 9 4 7 0 2 A 5 6 8 7 6 A 9 5 1 0 4 3 2 4 5 0 8 A 3 6 1 2 7 9 5 4 9 6 3 2 A 7 0 1 8 3 A 7 2 5 1 9 6 8 4 0 6 8 1 5 2 0 4 A 7 9 3 9 0 5 1 7 4 2 3 6 8 A [DLK(37):101743] 0 4 6 9 3 7 5 A 2 8 1 4 1 0 A 8 6 9 3 7 2 5 7 0 2 1 9 A 4 6 3 5 8 8 6 1 3 2 9 A 4 5 7 0 3 7 A 2 4 8 0 5 6 1 9 6 A 9 8 7 5 3 2 1 0 4 1 9 4 5 A 2 6 8 0 3 7 A 3 5 6 0 1 8 7 9 4 2 2 5 7 4 6 0 1 9 8 A 3 5 8 3 7 1 4 2 0 A 9 6 9 2 8 0 5 3 7 1 4 6 A [DLK(38):113806] 0 7 3 5 6 8 9 2 A 4 1 A 1 6 4 5 7 3 9 0 2 8 5 9 2 A 0 6 8 1 3 7 4 1 5 8 3 9 A 2 4 6 0 7 8 2 5 7 4 9 0 A 1 6 3 4 0 1 2 3 5 7 8 9 A 6 7 4 9 0 A 1 6 3 5 8 2 3 A 4 6 8 0 1 7 2 5 9 6 3 7 9 2 4 A 0 8 1 5 2 8 A 1 7 3 5 6 4 9 0 9 6 0 8 1 2 4 5 7 3 A [DLK(47):94498] 0 3 9 7 5 2 8 6 4 A 1 5 1 4 8 6 3 A 0 9 2 7 A 5 2 0 7 4 1 8 3 6 9 6 9 5 3 1 0 7 4 A 8 2 2 A 8 5 4 1 0 9 7 3 6 7 6 A 9 8 5 2 1 0 4 3 4 7 3 1 A 9 6 5 2 0 8 8 2 0 6 3 A 9 7 5 1 4 1 4 7 2 9 6 3 A 8 5 0 3 8 1 A 0 7 4 2 6 9 5 9 0 6 4 2 8 5 3 1 7 A [DLK(127):90826] 0 3 8 4 7 A 2 5 9 6 1 6 1 4 7 0 9 5 8 A 2 3 1 A 2 0 6 8 7 9 3 4 5 A 2 9 3 1 7 8 4 0 5 6 2 9 3 8 4 6 0 1 5 A 7 8 7 6 A 9 5 1 0 4 3 2 3 0 5 9 A 4 6 2 7 1 8 4 5 A 6 2 3 9 7 1 8 0 5 6 7 1 3 2 4 A 8 0 9 7 8 0 2 5 1 A 3 6 9 4 9 4 1 5 8 0 3 6 2 7 A [/code] И дальше Ñледуют шеÑÑ‚ÑŒ топовых ДЛК, которые показаны выше; они в Ñвоё Ð²Ñ€ÐµÐ¼Ñ Ð±Ñ‹Ð»Ð¸ обÑчитаны на ОДЛК. Итак, полученный по моей чаÑтичной БД КФ ОДЛК 11-го порÑдка Ñпектр [code]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 28, 32, 33, 34, 35, 36, 37, 38, 47, 127, 18530, 19139, 24593, 26914, 30198, 32462}[/code] Сравните Ñо Ñпектром гоÑподина Ватутина {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 28, 32, 33, 34, 35, 36, 37, 38, 47, 127, 18530, 19139, 24593, 26914, 30198, 32462} Ð’Ñ‹ видите разницу в Ñтих двух Ñпектрах? Я не вижу, они абÑолютно одинаковые. Ðу хоть бы одно новое значение было добавлено в Ñпектр Ватутина! Результаты откровенно Ñкопированы и приÑвоены. Обычное дело Ð´Ð»Ñ Ð³Ð¾Ñподина Ватутина. Сообщать о плагиате в OEIS, конечно, не буду. Я Ñто уже проходила. Тогда речь шла о результатах Harry White, которые также были Ñодраны гоÑподином Ватутиным. Мне админиÑтратор OEIS ответил, что Ð´Ð»Ñ OEIS понÑÑ‚Ð¸Ñ "плагиат" не ÑущеÑтвует: кто опубликовал результаты, тот и автор. ПоÑле чего забанил Ð¼ÐµÐ½Ñ Ð½Ð° год. ГоÑподин Ватутин Ñодрал результаты (и опубликовал их в OEIS Ñо Ñвоим авторÑтвом) у Белышева, у Francis Gaspalou, у Harry White, у Ðткина (пандиагональные латинÑкие квадраты). И ещё еÑÑ‚ÑŒ навернÑка много чего Ñ Ð½Ðµ видела, Ñпециально не Ñлежу за Ñтим. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата из ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=109&postid=1298 23 ÑÐ½Ð²Ð°Ñ€Ñ Ñ‚. г. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ñмотрю, Ñколько КФ ОДЛК у Ð¼ÐµÐ½Ñ Ð² БД 12-го порÑдка. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð² Ñдре БД КФ ОДЛК 12-го порÑдка мы имеем примерно 2 миллиарда КФ ОДЛК, может быть, даже и 3 миллиарда. Ð’Ñе они опубликованы. Большой вклад в БД КФ ОДЛК 12-го порÑдка Ñделали мои замечательные помощники, они обÑчитывали ДЛК. Ðу, Ñпектр (чаÑтичный) по ОДЛК 12-го порÑдка можно хороший ÑоÑтавить, ежели поÑтаратьÑÑ. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð²Ð·Ñла Ñамую малюÑенькую чаÑÑ‚ÑŒ БД и запуÑтила в программе Белышева ortogon_u. Конечно, ДЛК 12-го порÑдка бывают очень разные: одни обÑчитываютÑÑ Ð·Ð° неÑколько минут, а другие - за неÑколько недель. Ру гоÑподина Ватутина один интереÑный ДЛК 12-го порÑдка уже два меÑÑца обÑчитываетÑÑ Ð½Ð° ОДЛК в BOINC-проекте. Я уже отмечала, что ДЛК порÑдка 12 имеют проÑто фееричеÑкий Ñффект по ОДЛК. У одного ДЛК может быть более миллиарда ОДЛК. Я нашла один такой ДЛК, помощник назвал его квадрозавром, о нём много напиÑано. Ðу, жду, как отÑтрелÑетÑÑ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð° Белышева, пока пыхтит Проверка ДЛК12 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 6460 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 2124 Соквадратов: 230 Ð’Ñ€ÐµÐ¼Ñ Ð² Ñек: 1905 144 21 1 3 Ð’ Ñтом наборе вÑего 6460 КФ ОДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Пока программа Белышева пыхтит, Ñобрала примеры ДЛК 12-го порÑдка вмеÑте Ñ ÐºÐ¾Ð»Ð¸Ñ‡ÐµÑтвом ОДЛК в теме https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=109 БольшинÑтво из них обÑчитывал помощник Mynx. 57 квадратиков наÑобирала. Ðу, ещё включу Ñтих двух квадрозавров (их обÑчитал другой помощник) [DLK(724775546):1] 0 2 4 6 3 9 7 8 5 10 11 1 6 1 7 5 2 8 3 11 9 4 0 10 9 4 2 8 10 0 1 6 11 3 5 7 7 0 9 3 11 1 8 10 2 5 4 6 8 7 1 11 4 6 10 5 0 2 9 3 11 3 10 0 7 5 4 9 6 1 8 2 1 9 0 10 5 7 6 3 4 11 2 8 2 5 11 1 6 4 0 7 10 8 3 9 5 10 3 9 1 11 2 0 8 7 6 4 3 6 8 2 0 10 11 4 1 9 7 5 4 11 5 7 8 2 9 1 3 6 10 0 10 8 6 4 9 3 5 2 7 0 1 11 [DLK(1764493860):1] 0 10 4 6 2 8 9 3 7 5 11 1 11 1 7 5 9 3 2 8 4 6 0 10 4 6 2 8 1 11 10 0 9 3 7 5 7 5 9 3 10 0 1 11 2 8 4 6 3 9 0 10 4 6 7 5 11 1 8 2 8 2 11 1 7 5 4 6 0 10 3 9 2 8 1 11 5 7 6 4 10 0 9 3 9 3 10 0 6 4 5 7 1 11 2 8 5 7 3 9 0 10 11 1 8 2 6 4 6 4 8 2 11 1 0 10 3 9 5 7 1 11 5 7 3 9 8 2 6 4 10 0 10 0 6 4 8 2 3 9 5 7 1 11 Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð½Ð°Ñ€Ð¸Ñую вам Ñпектр :) Программу Ñортировки мне Ñделал форумчанин на форуме Math Help Planet; она Ñортирует по убыванию, то еÑÑ‚ÑŒ в Ñамом начале Ñпектра будут два квадрозавра. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Готово! ÐариÑовала Ñпектр :) [DLK(1764493860):1] 0 10 4 6 2 8 9 3 7 5 11 1 11 1 7 5 9 3 2 8 4 6 0 10 4 6 2 8 1 11 10 0 9 3 7 5 7 5 9 3 10 0 1 11 2 8 4 6 3 9 0 10 4 6 7 5 11 1 8 2 8 2 11 1 7 5 4 6 0 10 3 9 2 8 1 11 5 7 6 4 10 0 9 3 9 3 10 0 6 4 5 7 1 11 2 8 5 7 3 9 0 10 11 1 8 2 6 4 6 4 8 2 11 1 0 10 3 9 5 7 1 11 5 7 3 9 8 2 6 4 10 0 10 0 6 4 8 2 3 9 5 7 1 11 [DLK(724775546):1] 0 2 4 6 3 9 7 8 5 10 11 1 6 1 7 5 2 8 3 11 9 4 0 10 9 4 2 8 10 0 1 6 11 3 5 7 7 0 9 3 11 1 8 10 2 5 4 6 8 7 1 11 4 6 10 5 0 2 9 3 11 3 10 0 7 5 4 9 6 1 8 2 1 9 0 10 5 7 6 3 4 11 2 8 2 5 11 1 6 4 0 7 10 8 3 9 5 10 3 9 1 11 2 0 8 7 6 4 3 6 8 2 0 10 11 4 1 9 7 5 4 11 5 7 8 2 9 1 3 6 10 0 10 8 6 4 9 3 5 2 7 0 1 11 [DLK(3326729):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 5 7 3 9 8 2 4 6 0 A 5 7 2 8 0 A B 1 9 3 4 6 4 6 9 3 B 1 0 A 2 8 7 5 2 8 1 B 4 6 7 5 A 0 9 3 9 3 A 0 7 5 4 6 1 B 8 2 3 9 0 A 5 7 6 4 B 1 2 8 8 2 B 1 6 4 5 7 0 A 3 9 6 4 3 9 1 B A 0 8 2 5 7 7 5 8 2 A 0 1 B 3 9 6 4 1 B 7 5 9 3 2 8 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(1566818):1] 0 A 4 5 2 8 9 3 7 6 B 1 B 1 7 6 9 3 2 8 4 5 0 A 4 6 2 8 0 A B 1 9 3 7 5 7 5 9 3 B 1 0 A 2 8 4 6 9 3 0 A 4 6 7 5 B 1 2 8 2 8 B 1 7 5 4 6 0 A 9 3 8 2 1 B 5 7 6 4 A 0 3 9 3 9 A 0 6 4 5 7 1 B 8 2 5 7 3 9 1 B A 0 8 2 6 4 6 4 8 2 A 0 1 B 3 9 5 7 1 B 6 7 3 9 8 2 5 4 A 0 A 0 5 4 8 2 3 9 6 7 1 B [DLK(1534214):1] 0 A 4 5 2 8 9 3 7 6 B 1 B 1 7 6 9 3 2 8 4 5 0 A 6 4 2 8 0 A B 1 9 3 5 7 5 7 9 3 B 1 0 A 2 8 6 4 2 8 A 0 4 6 7 5 1 B 9 3 9 3 1 B 7 5 4 6 A 0 2 8 3 9 B 1 5 7 6 4 0 A 8 2 8 2 0 A 6 4 5 7 B 1 3 9 7 5 3 9 1 B A 0 8 2 4 6 4 6 8 2 A 0 1 B 3 9 7 5 1 B 6 7 3 9 8 2 5 4 A 0 A 0 5 4 8 2 3 9 6 7 1 B [DLK(1243865):1] 0 A 4 6 2 8 3 9 5 7 B 1 B 1 5 7 3 9 2 8 6 4 0 A 4 6 2 8 1 B A 0 9 3 7 5 7 5 9 3 A 0 1 B 2 8 6 4 9 3 0 A 4 6 7 5 B 1 2 8 2 8 B 1 7 5 4 6 0 A 3 9 8 2 1 B 5 7 6 4 A 0 9 3 3 9 A 0 6 4 5 7 1 B 8 2 5 7 3 9 0 A B 1 8 2 4 6 6 4 8 2 B 1 0 A 3 9 5 7 1 B 7 5 9 3 8 2 4 6 A 0 A 0 6 4 8 2 9 3 7 5 1 B [DLK(1230431):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 2 8 4 6 0 A 4 6 2 8 1 B A 0 9 3 7 5 7 5 9 3 A 0 1 B 2 8 4 6 3 9 0 A 4 6 7 5 B 1 8 2 8 2 B 1 7 5 4 6 0 A 3 9 2 8 1 B 5 7 6 4 A 0 9 3 9 3 A 0 6 4 5 7 1 B 2 8 5 7 3 9 0 A B 1 8 2 6 4 6 4 8 2 B 1 0 A 3 9 5 7 1 B 5 7 9 3 8 2 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(1225216):1] 0 A 4 6 2 8 3 9 5 7 B 1 B 1 5 7 3 9 2 8 6 4 0 A 5 7 2 8 0 A B 1 9 3 6 4 4 6 9 3 B 1 0 A 2 8 5 7 8 2 B 1 4 6 7 5 0 A 3 9 3 9 0 A 7 5 4 6 B 1 2 8 9 3 A 0 5 7 6 4 1 B 8 2 2 8 1 B 6 4 5 7 A 0 9 3 6 4 3 9 1 B A 0 8 2 7 5 7 5 8 2 A 0 1 B 3 9 4 6 1 B 7 5 9 3 8 2 4 6 A 0 A 0 6 4 8 2 9 3 7 5 1 B [DLK(1068592):1] 0 A 4 6 2 8 9 3 7 5 B 1 B 1 7 5 9 3 2 8 4 6 0 A 4 6 2 8 0 A B 1 9 3 7 5 7 5 9 3 B 1 0 A 2 8 4 6 2 8 B 1 4 6 7 5 0 A 9 3 9 3 0 A 7 5 4 6 B 1 2 8 3 9 A 0 5 7 6 4 1 B 8 2 8 2 1 B 6 4 5 7 A 0 3 9 5 7 3 9 1 B A 0 8 2 6 4 6 4 8 2 A 0 1 B 3 9 5 7 1 B 5 7 3 9 8 2 6 4 A 0 A 0 6 4 8 2 3 9 5 7 1 B [DLK(1013437):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 2 8 4 6 0 A 4 6 2 8 A 0 1 B 9 3 7 5 7 5 9 3 1 B A 0 2 8 4 6 8 2 0 A 4 6 7 5 B 1 3 9 3 9 B 1 7 5 4 6 0 A 8 2 9 3 1 B 5 7 6 4 A 0 2 8 2 8 A 0 6 4 5 7 1 B 9 3 5 7 3 9 B 1 0 A 8 2 6 4 6 4 8 2 0 A B 1 3 9 5 7 1 B 5 7 9 3 8 2 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(842966):1] 0 A 4 5 2 8 9 3 7 6 B 1 B 1 7 6 9 3 2 8 4 5 0 A 4 6 2 8 1 B A 0 9 3 7 5 7 5 9 3 A 0 1 B 2 8 4 6 3 9 0 A 4 6 7 5 B 1 8 2 8 2 B 1 7 5 4 6 0 A 3 9 2 8 1 B 5 7 6 4 A 0 9 3 9 3 A 0 6 4 5 7 1 B 2 8 6 7 3 9 0 A B 1 8 2 5 4 5 4 8 2 B 1 0 A 3 9 6 7 1 B 5 7 3 9 8 2 6 4 A 0 A 0 6 4 8 2 3 9 5 7 1 B [DLK(839153):1] 0 A 4 6 2 8 3 9 5 7 B 1 B 1 5 7 3 9 2 8 6 4 0 A 5 7 2 8 0 A B 1 9 3 6 4 4 6 9 3 1 B 0 A 2 8 5 7 8 2 B 1 4 6 7 5 0 A 3 9 3 9 0 A 7 5 4 6 1 B 2 8 9 3 A 0 5 7 6 4 B 1 8 2 2 8 1 B 6 4 5 7 A 0 9 3 6 4 3 9 B 1 A 0 8 2 7 5 7 5 8 2 A 0 1 B 3 9 4 6 1 B 7 5 9 3 8 2 4 6 A 0 A 0 6 4 8 2 9 3 7 5 1 B [DLK(812536):1] 0 8 4 6 2 A 9 3 7 5 B 1 B 1 7 5 9 3 2 8 4 6 0 A 4 6 2 A 8 0 1 B 9 3 7 5 7 5 9 3 1 B A 0 2 8 4 6 A 2 0 8 4 6 7 5 B 1 3 9 3 9 B 1 7 5 4 6 0 A 8 2 9 3 1 B 5 7 6 4 A 0 2 8 2 A 8 0 6 4 5 7 1 B 9 3 5 7 3 9 B 1 0 A 8 2 6 4 6 4 A 2 0 8 B 1 3 9 5 7 1 B 5 7 3 9 8 2 6 4 A 0 8 0 6 4 A 2 3 9 5 7 1 B [DLK(771790):1] 0 A 4 5 2 8 9 3 7 6 B 1 B 1 7 6 9 3 2 8 4 5 0 A 4 5 2 8 B 1 0 A 9 3 7 6 7 6 9 3 0 A B 1 2 8 4 5 9 3 0 A 4 6 7 5 B 1 2 8 2 8 B 1 7 5 4 6 0 A 9 3 8 2 1 B 5 7 6 4 A 0 3 9 3 9 A 0 6 4 5 7 1 B 8 2 5 7 3 9 A 0 1 B 8 2 6 4 6 4 8 2 1 B A 0 3 9 5 7 1 B 5 7 3 9 8 2 6 4 A 0 A 0 6 4 8 2 3 9 5 7 1 B [DLK(747762):1] 0 A 4 6 2 8 3 9 5 7 B 1 B 1 5 7 3 9 2 8 6 4 0 A 4 6 2 8 1 B A 0 9 3 7 5 7 5 9 3 0 A 1 B 2 8 6 4 9 3 A 0 4 6 7 5 B 1 2 8 2 8 B 1 7 5 4 6 0 A 3 9 8 2 1 B 5 7 6 4 A 0 9 3 3 9 0 A 6 4 5 7 1 B 8 2 5 7 3 9 A 0 B 1 8 2 4 6 6 4 8 2 B 1 0 A 3 9 5 7 1 B 7 5 9 3 8 2 4 6 A 0 A 0 6 4 8 2 9 3 7 5 1 B [DLK(702675):1] 0 A 4 6 2 8 3 9 5 7 B 1 B 1 5 7 3 9 8 2 6 4 0 A 4 6 2 8 1 B 0 A 9 3 5 7 5 7 9 3 0 A B 1 2 8 6 4 3 9 0 A 4 6 7 5 1 B 2 8 2 8 B 1 7 5 4 6 0 A 3 9 8 2 1 B 5 7 6 4 A 0 9 3 9 3 A 0 6 4 5 7 B 1 8 2 7 5 3 9 A 0 1 B 8 2 4 6 6 4 8 2 B 1 A 0 3 9 7 5 1 B 7 5 9 3 2 8 4 6 A 0 A 0 6 4 8 2 9 3 7 5 1 B [DLK(688489):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 8 2 4 6 0 A 4 6 2 8 0 A B 1 9 3 7 5 7 5 9 3 B 1 0 A 2 8 4 6 2 8 A 0 4 6 7 5 1 B 9 3 9 3 1 B 7 5 4 6 A 0 8 2 3 9 B 1 5 7 6 4 0 A 2 8 8 2 0 A 6 4 5 7 B 1 3 9 5 7 3 9 1 B A 0 8 2 6 4 6 4 8 2 A 0 1 B 3 9 5 7 1 B 5 7 9 3 2 8 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(674177):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 8 2 4 6 0 A 5 7 2 8 A 0 1 B 9 3 6 4 6 4 9 3 1 B A 0 2 8 5 7 2 8 B 1 4 6 7 5 0 A 3 9 3 9 0 A 7 5 4 6 B 1 8 2 9 3 A 0 5 7 6 4 1 B 2 8 8 2 1 B 6 4 5 7 A 0 9 3 4 6 3 9 B 1 0 A 8 2 7 5 7 5 8 2 0 A B 1 3 9 4 6 1 B 5 7 9 3 2 8 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(670762):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 8 2 4 6 0 A 5 7 2 8 1 B A 0 9 3 6 4 6 4 9 3 A 0 1 B 2 8 5 7 3 9 B 1 4 6 7 5 0 A 8 2 2 8 0 A 7 5 4 6 B 1 3 9 8 2 A 0 5 7 6 4 1 B 9 3 9 3 1 B 6 4 5 7 A 0 2 8 4 6 3 9 0 A B 1 8 2 7 5 7 5 8 2 B 1 0 A 3 9 4 6 1 B 5 7 9 3 2 8 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(660443):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 8 2 4 6 0 A 4 6 2 8 0 A B 1 9 3 7 5 7 5 9 3 B 1 0 A 2 8 4 6 8 2 A 0 4 6 7 5 1 B 9 3 9 3 1 B 7 5 4 6 A 0 2 8 3 9 B 1 5 7 6 4 0 A 8 2 2 8 0 A 6 4 5 7 B 1 3 9 5 7 3 9 1 B A 0 8 2 6 4 6 4 8 2 A 0 1 B 3 9 5 7 1 B 5 7 9 3 2 8 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(641726):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 8 2 4 6 0 A 5 7 2 8 1 B A 0 9 3 6 4 6 4 9 3 A 0 1 B 2 8 5 7 3 9 B 1 4 6 7 5 0 A 2 8 8 2 0 A 7 5 4 6 B 1 3 9 2 8 A 0 5 7 6 4 1 B 9 3 9 3 1 B 6 4 5 7 A 0 8 2 4 6 3 9 0 A B 1 8 2 7 5 7 5 8 2 B 1 0 A 3 9 4 6 1 B 5 7 9 3 2 8 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(640449):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 8 2 4 6 0 A 5 7 2 8 A 0 1 B 9 3 6 4 6 4 9 3 1 B A 0 2 8 5 7 8 2 B 1 4 6 7 5 0 A 3 9 3 9 0 A 7 5 4 6 B 1 2 8 9 3 A 0 5 7 6 4 1 B 8 2 2 8 1 B 6 4 5 7 A 0 9 3 4 6 3 9 B 1 0 A 8 2 7 5 7 5 8 2 0 A B 1 3 9 4 6 1 B 5 7 9 3 2 8 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(415944):1] 0 A 4 5 2 8 9 3 7 6 B 1 B 1 7 6 9 3 2 8 4 5 0 A 4 5 2 8 1 B A 0 9 3 7 6 7 6 9 3 A 0 1 B 2 8 4 5 3 9 0 A 4 6 7 5 B 1 8 2 8 2 B 1 7 5 4 6 0 A 3 9 2 8 1 B 5 7 6 4 A 0 9 3 9 3 A 0 6 4 5 7 1 B 2 8 5 7 3 9 0 A B 1 8 2 6 4 6 4 8 2 B 1 0 A 3 9 5 7 1 B 6 7 3 9 8 2 5 4 A 0 A 0 5 4 8 2 3 9 6 7 1 B [DLK(406894):1] 0 A 4 5 2 8 9 3 7 6 B 1 B 1 7 6 9 3 2 8 4 5 0 A 4 5 2 8 B 1 0 A 9 3 7 6 7 6 9 3 0 A B 1 2 8 4 5 9 3 0 A 4 6 7 5 B 1 2 8 2 8 B 1 7 5 4 6 0 A 9 3 8 2 1 B 5 7 6 4 A 0 3 9 3 9 A 0 6 4 5 7 1 B 8 2 5 7 3 9 A 0 1 B 8 2 6 4 6 4 8 2 1 B A 0 3 9 5 7 1 B 6 7 3 9 8 2 5 4 A 0 A 0 5 4 8 2 3 9 6 7 1 B [DLK(277340):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 2 8 4 6 0 A 4 6 2 8 1 B A 0 9 3 7 5 7 5 9 3 A 0 1 B 2 8 4 6 3 9 0 A 4 6 7 5 B 1 8 2 8 2 B 1 7 5 4 6 0 A 9 3 2 8 1 B 5 7 6 4 A 0 3 9 9 3 A 0 6 4 5 7 1 B 2 8 5 7 3 9 0 A B 1 8 2 6 4 6 4 8 2 B 1 0 A 3 9 5 7 1 B 5 7 9 3 8 2 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(246191):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 2 8 4 6 0 A 6 4 2 8 0 A B 1 9 3 5 7 5 7 9 3 B 1 0 A 2 8 6 4 2 8 0 A 4 6 7 5 B 1 9 3 9 3 B 1 7 5 4 6 0 A 8 2 3 9 1 B 5 7 6 4 A 0 2 8 8 2 A 0 6 4 5 7 1 B 3 9 7 5 3 9 1 B A 0 8 2 4 6 4 6 8 2 A 0 1 B 3 9 7 5 1 B 5 7 9 3 8 2 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(240546):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 2 8 4 6 0 A 4 6 2 8 0 A B 1 9 3 7 5 7 5 9 3 B 1 0 A 2 8 4 6 2 8 A 0 4 6 7 5 1 B 9 3 9 3 1 B 7 5 4 6 A 0 8 2 3 9 B 1 5 7 6 4 0 A 2 8 8 2 0 A 6 4 5 7 B 1 3 9 5 7 3 9 1 B A 0 8 2 6 4 6 4 8 2 A 0 1 B 3 9 5 7 1 B 5 7 9 3 8 2 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(235897):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 2 8 4 6 0 A 4 6 2 8 B 1 0 A 9 3 7 5 7 5 9 3 0 A B 1 2 8 4 6 3 9 0 A 4 6 7 5 B 1 2 8 2 8 B 1 7 5 4 6 0 A 9 3 8 2 1 B 5 7 6 4 A 0 3 9 9 3 A 0 6 4 5 7 1 B 8 2 5 7 3 9 A 0 1 B 8 2 6 4 6 4 8 2 1 B A 0 3 9 5 7 1 B 5 7 9 3 8 2 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(231093):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 2 8 4 6 0 A 6 4 2 8 0 A B 1 9 3 5 7 5 7 9 3 B 1 0 A 2 8 6 4 2 8 A 0 4 6 7 5 1 B 3 9 9 3 1 B 7 5 4 6 A 0 2 8 3 9 B 1 5 7 6 4 0 A 8 2 8 2 0 A 6 4 5 7 B 1 9 3 7 5 3 9 1 B A 0 8 2 4 6 4 6 8 2 A 0 1 B 3 9 7 5 1 B 5 7 9 3 8 2 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(224391):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 2 8 4 6 0 A 4 6 2 8 A 0 1 B 9 3 7 5 7 5 9 3 1 B A 0 2 8 4 6 8 2 0 A 4 6 7 5 B 1 3 9 9 3 B 1 7 5 4 6 0 A 8 2 3 9 1 B 5 7 6 4 A 0 2 8 2 8 A 0 6 4 5 7 1 B 9 3 5 7 3 9 B 1 0 A 8 2 6 4 6 4 8 2 0 A B 1 3 9 5 7 1 B 5 7 9 3 8 2 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(179815):1] 0 8 4 6 2 A 9 3 7 5 B 1 B 1 7 5 9 3 2 8 4 6 0 A 6 4 2 A 0 8 B 1 9 3 5 7 5 7 9 3 B 1 0 A 2 8 6 4 2 A 8 0 4 6 7 5 1 B 9 3 9 3 1 B 7 5 4 6 A 0 2 8 3 9 B 1 5 7 6 4 0 A 8 2 A 2 0 8 6 4 5 7 B 1 3 9 7 5 3 9 1 B A 0 8 2 4 6 4 6 A 2 8 0 1 B 3 9 7 5 1 B 5 7 3 9 8 2 6 4 A 0 8 0 6 4 A 2 3 9 5 7 1 B [DLK(69812):1] 0 A 4 6 2 8 9 3 7 5 B 1 B 1 5 7 9 3 2 8 6 4 0 A 4 6 2 8 0 A B 1 9 3 7 5 7 5 9 3 B 1 0 A 2 8 4 6 9 3 0 A 4 6 7 5 B 1 2 8 2 8 B 1 7 5 4 6 0 A 9 3 8 2 1 B 5 7 6 4 A 0 3 9 3 9 A 0 6 4 5 7 1 B 8 2 5 7 3 9 1 B A 0 8 2 6 4 6 4 8 2 A 0 1 B 3 9 5 7 1 B 7 5 3 9 8 2 4 6 A 0 A 0 6 4 8 2 3 9 5 7 1 B [DLK(68679):1] 0 A 4 6 2 8 9 3 7 5 B 1 B 1 5 7 3 9 8 2 6 4 0 A 4 7 2 8 0 A B 1 9 3 6 5 7 4 9 3 B 1 0 A 2 8 5 6 8 3 1 B 4 6 7 5 A 0 2 9 3 8 0 A 7 5 4 6 B 1 9 2 9 2 A 0 5 7 6 4 1 B 3 8 2 9 B 1 6 4 5 7 0 A 8 3 5 6 3 9 1 B A 0 8 2 7 4 6 5 8 2 A 0 1 B 3 9 4 7 1 B 7 5 9 3 2 8 4 6 A 0 A 0 6 4 8 2 3 9 5 7 1 B [DLK(28230):1201770] 0 2 4 A 7 8 9 6 B 5 3 1 4 1 3 7 9 B A 8 6 2 0 5 7 0 2 4 8 A B 9 5 3 1 6 9 5 0 3 B 6 7 A 2 1 4 8 B 9 7 1 4 3 2 5 0 6 8 A 2 6 B 8 0 5 4 1 9 A 7 3 8 4 1 2 A 7 6 B 3 0 5 9 1 3 5 B 6 9 8 7 A 4 2 0 3 7 A 9 1 4 5 0 8 B 6 2 5 A 8 6 2 0 1 3 7 9 B 4 6 B 9 5 3 1 0 2 4 8 A 7 A 8 6 0 5 2 3 4 1 7 9 B [DLK(14818):1] 0 2 4 A 7 8 9 6 B 5 3 1 7 1 3 5 9 A B 8 4 2 0 6 4 A 2 6 8 1 0 9 7 3 B 5 8 7 1 3 B 4 5 A 2 0 6 9 B 3 7 1 4 9 8 5 0 6 2 A 9 6 0 2 A 5 4 B 3 1 7 8 3 4 A 8 0 7 6 1 9 B 5 2 1 9 5 B 6 3 2 7 A 4 8 0 2 5 B 9 1 6 7 0 8 A 4 3 6 0 8 4 2 B A 3 5 9 1 7 5 B 9 7 3 0 1 2 6 8 A 4 A 8 6 0 5 2 3 4 1 7 9 B [DLK(12253):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 8 2 4 6 0 A 5 7 2 8 B 1 0 A 9 3 6 4 6 4 9 3 0 A B 1 2 8 5 7 3 8 B 1 4 6 7 5 0 A 9 2 8 3 0 A 7 5 4 6 B 1 2 9 2 9 A 0 5 7 6 4 1 B 8 3 9 2 1 B 6 4 5 7 A 0 3 8 4 6 3 9 A 0 1 B 8 2 7 5 7 5 8 2 1 B A 0 3 9 4 6 1 B 5 7 9 3 2 8 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(10357):1] 0 A 4 6 2 8 9 3 7 5 B 1 B 1 5 7 3 9 8 2 6 4 0 A 4 7 2 8 0 A B 1 9 3 6 5 7 4 9 3 1 B A 0 2 8 5 6 8 3 0 B 4 6 7 5 A 1 2 9 3 8 A 0 7 5 4 6 1 B 9 2 9 2 1 A 5 7 6 4 B 0 3 8 2 9 B 1 6 4 5 7 0 A 8 3 5 6 3 9 B 1 0 A 8 2 7 4 6 5 8 2 A 0 1 B 3 9 4 7 1 B 7 5 9 3 2 8 4 6 A 0 A 0 6 4 8 2 3 9 5 7 1 B [DLK(10129):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 8 2 4 6 0 A 5 7 2 8 1 B A 0 9 3 6 4 6 4 9 3 A 0 1 B 2 8 5 7 8 3 B 1 4 6 7 5 0 A 2 9 3 8 0 A 7 5 4 6 B 1 9 2 9 2 A 0 5 7 6 4 1 B 3 8 2 9 1 B 6 4 5 7 A 0 8 3 4 6 3 9 0 A B 1 8 2 7 5 7 5 8 2 B 1 0 A 3 9 4 6 1 B 5 7 9 3 2 8 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(8335):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 2 8 4 6 0 A 6 4 2 8 0 A B 1 9 3 5 7 5 7 9 3 B 1 A 0 2 8 6 4 2 8 1 A 4 6 7 5 B 0 9 3 3 9 A 1 7 5 4 6 0 B 2 8 9 3 0 B 5 7 6 4 A 1 8 2 8 2 B 0 6 4 5 7 1 A 3 9 7 5 3 9 1 B 0 A 8 2 4 6 4 6 8 2 A 0 1 B 3 9 7 5 1 B 5 7 9 3 8 2 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(7729):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 2 8 4 6 0 A 4 6 2 8 0 B A 1 9 3 7 5 7 5 9 3 B 0 1 A 2 8 4 6 8 2 0 A 4 6 7 5 1 B 3 9 9 3 B 1 7 5 4 6 0 A 8 2 3 9 1 B 5 7 6 4 A 0 2 8 2 8 A 0 6 4 5 7 B 1 9 3 5 7 3 9 1 A B 0 8 2 6 4 6 4 8 2 A 1 0 B 3 9 5 7 1 B 5 7 9 3 8 2 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(6168):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 8 2 6 4 0 A 5 6 2 8 0 A B 1 9 3 7 4 6 5 9 3 1 B 0 A 2 8 4 7 8 2 0 A 4 6 7 5 1 B 9 3 9 3 1 B 7 5 4 6 0 A 8 2 3 9 B 1 5 7 6 4 A 0 2 8 2 8 A 0 6 4 5 7 B 1 3 9 4 7 3 9 B 1 A 0 8 2 6 5 7 4 8 2 A 0 1 B 3 9 5 6 1 B 5 7 9 3 2 8 4 6 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(5380):1] 0 A 4 6 2 8 3 9 5 7 B 1 B 1 5 7 3 9 8 2 6 4 0 A 5 7 2 8 A 0 1 B 9 3 4 6 4 6 9 3 1 B A 0 2 8 5 7 9 2 B 1 4 6 7 5 0 A 3 8 2 9 0 A 7 5 4 6 B 1 8 3 8 3 A 0 5 7 6 4 1 B 2 9 3 8 1 B 6 4 5 7 A 0 9 2 6 4 3 9 B 1 0 A 8 2 7 5 7 5 8 2 0 A B 1 3 9 6 4 1 B 7 5 9 3 2 8 4 6 A 0 A 0 6 4 8 2 9 3 7 5 1 B [DLK(4945):1] 0 A 4 6 2 8 3 9 7 5 B 1 B 1 7 5 3 9 2 8 4 6 0 A 4 6 2 8 B 1 0 A 9 3 7 5 7 5 9 3 0 A B 1 2 8 4 6 2 8 0 A 4 6 7 5 B 1 3 9 9 3 B 1 7 5 4 6 0 A 2 8 3 9 1 B 5 7 6 4 A 0 8 2 8 2 A 0 6 4 5 7 1 B 9 3 5 7 3 9 A 0 1 B 8 2 6 4 6 4 8 2 1 B A 0 3 9 5 7 1 B 5 7 9 3 8 2 6 4 A 0 A 0 6 4 8 2 9 3 5 7 1 B [DLK(2229):16191] 0 2 4 A 7 9 8 6 B 5 3 1 2 1 A 5 8 6 7 9 4 B 0 3 B 6 2 4 9 1 0 8 5 3 7 A 7 A 5 3 0 8 9 1 2 4 B 6 3 7 9 1 4 A B 5 0 8 6 2 6 3 1 8 B 5 4 A 9 0 2 7 4 9 B 2 1 7 6 0 3 A 8 5 9 5 3 B 6 0 1 7 A 2 4 8 5 0 7 9 A 2 3 B 8 6 1 4 1 4 8 6 3 B A 2 7 9 5 0 8 B 0 7 2 4 5 3 6 1 A 9 A 8 6 0 5 3 2 4 1 7 9 B [DLK(1305):1006179] 0 2 4 6 8 B A 9 7 5 3 1 B 1 7 8 3 4 5 2 9 6 0 A 8 A 2 5 7 0 1 6 4 3 B 9 6 5 1 3 B 8 9 A 2 0 4 7 7 9 0 B 4 3 2 5 A 1 8 6 3 6 9 A 0 5 4 1 B 8 7 2 9 4 3 0 A 7 6 B 1 2 5 8 5 3 A 1 6 9 8 7 0 B 2 4 4 7 B 9 1 2 3 0 8 A 6 5 2 0 8 7 5 A B 4 6 9 1 3 1 B 5 2 9 6 7 8 3 4 A 0 A 8 6 4 2 1 0 3 5 7 9 B [DLK(792):1008488] 0 2 4 6 8 B A 9 7 5 3 1 B 1 9 7 5 2 3 4 6 8 0 A 7 5 2 8 B 0 1 A 9 3 4 6 6 9 1 3 A 4 5 B 2 0 8 7 8 A 7 1 4 3 2 5 0 6 B 9 3 6 0 A 9 5 4 8 B 1 7 2 9 4 A 0 3 7 6 2 1 B 5 8 2 0 5 B 6 9 8 7 A 4 1 3 4 3 B 9 0 6 7 1 8 A 2 5 5 7 8 2 1 A B 0 3 9 6 4 1 B 3 5 7 8 9 6 4 2 A 0 A 8 6 4 2 1 0 3 5 7 9 B [DLK(563):1007877] 0 2 4 6 8 B A 9 7 5 3 1 B 1 9 7 5 2 3 4 6 8 0 A 6 4 2 8 B 0 1 A 9 3 5 7 7 9 1 3 A 4 5 B 2 0 8 6 8 A 7 1 4 3 2 5 0 6 B 9 3 7 0 A 9 5 4 8 B 1 6 2 9 5 A 0 3 7 6 2 1 B 4 8 2 0 5 B 6 9 8 7 A 4 1 3 5 3 B 9 0 6 7 1 8 A 2 4 4 6 8 2 1 A B 0 3 9 7 5 1 B 3 5 7 8 9 6 4 2 A 0 A 8 6 4 2 1 0 3 5 7 9 B [DLK(538):15172] 0 2 4 A 7 8 9 6 B 5 3 1 8 1 B 6 2 4 5 3 7 A 0 9 4 0 2 7 A 9 8 B 6 3 1 5 B 5 7 3 9 1 0 8 2 6 4 A 7 3 9 B 4 0 1 5 A 8 2 6 3 6 A 8 1 5 4 0 9 B 7 2 9 4 0 2 B 7 6 A 3 1 5 8 5 9 3 1 6 A B 7 0 2 8 4 1 7 5 9 3 B A 2 8 4 6 0 6 A 8 5 0 3 2 1 4 9 B 7 2 B 1 4 8 6 7 9 5 0 A 3 A 8 6 0 5 2 3 4 1 7 9 B [DLK(481):15710] 0 2 4 A 7 8 9 6 B 5 3 1 9 1 B 5 3 6 7 2 4 A 0 8 7 0 2 4 8 B A 9 5 3 1 6 1 7 5 3 B 9 8 A 2 4 6 0 8 6 A 2 4 0 1 5 3 B 7 9 6 3 9 B 0 5 4 1 A 8 2 7 4 9 3 1 A 7 6 B 0 2 8 5 2 4 0 8 6 A B 7 9 1 5 3 B 5 7 9 1 3 2 0 8 6 4 A 5 A 8 6 2 1 0 3 7 9 B 4 3 B 1 7 9 4 5 8 6 0 A 2 A 8 6 0 5 2 3 4 1 7 9 B [DLK(465):18420] 0 2 4 A 7 9 8 6 B 5 3 1 3 1 A 5 8 6 7 9 4 B 0 2 1 7 2 4 9 A B 8 5 3 6 0 7 0 5 3 B 8 9 A 2 4 1 6 6 3 9 B 4 1 0 5 A 8 2 7 2 6 B 8 0 5 4 1 9 A 7 3 8 4 1 2 A 7 6 B 3 0 5 9 4 9 3 1 6 B A 7 0 2 8 5 5 A 7 9 1 2 3 0 8 6 B 4 B 5 8 6 3 0 1 2 7 9 4 A 9 B 0 7 2 4 5 3 6 1 A 8 A 8 6 0 5 3 2 4 1 7 9 B [DLK(395):18885] 0 2 4 A 7 9 8 6 B 5 3 1 9 1 B 4 2 6 7 3 5 A 0 8 1 6 2 5 B 8 9 A 4 3 7 0 6 0 5 3 9 B A 8 2 4 1 7 2 7 A 8 4 0 1 5 9 B 6 3 7 3 9 1 A 5 4 B 0 8 2 6 5 9 3 B 0 7 6 1 A 2 8 4 8 5 0 2 6 A B 7 3 1 4 9 4 A 7 9 3 1 0 2 8 6 B 5 B 4 8 7 1 2 3 0 6 9 5 A 3 B 1 6 8 4 5 9 7 0 A 2 A 8 6 0 5 3 2 4 1 7 9 B [DLK(364):1007513] 0 2 4 6 8 B A 9 7 5 3 1 B 1 9 5 7 2 3 6 4 8 0 A 6 4 2 8 B 0 1 A 9 3 5 7 5 9 1 3 A 6 7 B 2 0 8 4 8 A 7 1 4 3 2 5 0 6 B 9 3 7 0 A 9 5 4 8 B 1 6 2 9 5 A 0 3 7 6 2 1 B 4 8 2 0 5 B 6 9 8 7 A 4 1 3 7 3 B 9 0 4 5 1 8 A 2 6 4 6 8 2 1 A B 0 3 9 7 5 1 B 3 7 5 8 9 4 6 2 A 0 A 8 6 4 2 1 0 3 5 7 9 B [DLK(353):14819] 0 2 4 A 7 8 9 6 B 5 3 1 8 1 A 6 2 4 5 3 7 B 0 9 B 4 2 7 0 9 8 1 6 3 5 A 4 0 7 3 9 B A 8 2 6 1 5 7 9 3 B 4 0 1 5 A 2 8 6 9 7 B 2 1 5 4 0 3 A 6 8 3 5 1 8 B 7 6 A 9 0 4 2 5 3 9 1 6 A B 7 0 8 2 4 6 A 5 9 3 1 0 2 8 4 B 7 1 6 8 5 A 3 2 B 4 9 7 0 2 B 0 4 8 6 7 9 5 1 A 3 A 8 6 0 5 2 3 4 1 7 9 B [DLK(194):19280] 0 2 4 A 7 9 8 6 B 5 3 1 9 1 B 7 2 4 5 3 6 A 0 8 B 7 2 4 9 0 1 8 5 3 6 A 6 0 5 3 B 8 9 A 2 4 1 7 7 9 3 1 4 B A 5 0 2 8 6 2 6 0 8 A 5 4 B 9 1 7 3 8 4 A 2 0 7 6 1 3 B 5 9 5 3 9 B 6 1 0 7 A 8 2 4 4 A 7 9 1 2 3 0 8 6 B 5 1 5 8 6 3 A B 2 7 9 4 0 3 B 1 5 8 6 7 9 4 0 A 2 A 8 6 0 5 3 2 4 1 7 9 B [DLK(58):1] 0 2 3 4 8 B 9 6 A 7 5 1 3 1 7 6 A 4 B 8 9 5 0 2 1 0 2 5 9 8 A B 4 3 7 6 8 9 B 3 7 6 1 0 2 A 4 5 7 3 A B 4 9 8 5 1 2 6 0 2 A 0 8 1 5 4 9 B 6 3 7 4 8 5 0 2 7 6 A 3 B 1 9 B 5 9 A 6 3 2 7 0 1 8 4 6 7 1 9 B A 5 4 8 0 2 3 5 4 8 7 0 1 3 2 6 9 B A 9 B 6 2 3 0 7 1 5 4 A 8 A 6 4 1 5 2 0 3 7 8 9 B [DLK(48):1008440] 0 2 4 6 8 B A 9 7 5 3 1 B 1 9 7 5 2 3 4 6 8 0 A 6 5 2 8 B 0 1 A 9 3 4 7 7 9 1 3 A 4 5 B 2 0 8 6 8 A 7 1 4 3 2 5 0 6 B 9 3 7 0 A 9 5 4 8 B 1 6 2 9 4 A 0 3 7 6 2 1 B 5 8 2 0 5 B 6 9 8 7 A 4 1 3 4 3 B 9 0 6 7 1 8 A 2 5 5 6 8 2 1 A B 0 3 9 7 4 1 B 3 5 7 8 9 6 4 2 A 0 A 8 6 4 2 1 0 3 5 7 9 B [DLK(34):1009280] 0 2 4 6 8 B A 9 7 5 3 1 B 1 9 7 5 3 2 4 6 8 0 A 7 5 2 1 9 A B 8 0 3 4 6 9 6 1 3 B 4 5 A 2 0 7 8 6 0 A 2 4 8 9 5 3 B 1 7 3 8 7 0 A 5 4 B 1 6 9 2 8 3 5 A 0 7 6 1 B 4 2 9 4 A 0 8 6 2 3 7 9 1 B 5 2 4 B 9 1 6 7 0 8 A 5 3 5 7 8 B 2 0 1 3 A 9 6 4 1 B 3 5 7 9 8 6 4 2 A 0 A 9 6 4 3 1 0 2 5 7 8 B [DLK(29):1007484] 0 2 4 6 8 B A 9 7 5 3 1 B 1 9 5 7 2 3 4 6 8 0 A 6 4 2 8 B 0 1 A 9 3 5 7 5 9 1 3 A 4 7 B 2 0 8 6 8 A 7 1 4 3 2 5 0 6 B 9 3 7 0 A 9 5 4 8 B 1 6 2 9 5 A 0 3 7 6 2 1 B 4 8 2 0 5 B 6 9 8 7 A 4 1 3 7 3 B 9 0 6 5 1 8 A 2 4 4 6 8 2 1 A B 0 3 9 7 5 1 B 3 7 5 8 9 6 4 2 A 0 A 8 6 4 2 1 0 3 5 7 9 B [DLK(1):1] 0 2 3 4 9 8 7 6 B A 5 1 3 1 7 6 8 9 5 A 4 B 0 2 1 9 2 5 7 A 8 B 0 3 6 4 5 4 A 3 B 0 9 8 2 6 1 7 6 7 B A 4 1 0 5 9 2 8 3 B 0 6 8 2 5 4 1 A 7 3 9 2 8 4 1 A 7 6 9 3 5 B 0 8 3 9 2 6 B A 7 1 0 4 5 4 A 5 9 3 2 B 0 8 1 7 6 7 5 8 B 0 3 1 4 6 9 2 A 9 B 0 7 1 6 2 3 5 4 A 8 A 6 1 0 5 4 3 2 7 8 9 B Ой, в конце однушечка :) прелеÑÑ‚ÑŒ. Программа Белышева закончит проверку, добавлю к Ñтому Ñпектру новые значениÑ. Спектр Ð´Ð»Ñ ÐžÐ”Ð›Ðš к ДЛК 12-го порÑдка впечатлÑет. От однушки до 1764493860 ОДЛК! Вполне возможно, что Ñто не предел. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð Ñто тот же Ñамый Ñпектр без ДЛК [DLK(1764493860):1] [DLK(724775546):1] [DLK(3326729):1] [DLK(1566818):1] [DLK(1534214):1] [DLK(1243865):1] [DLK(1230431):1] [DLK(1225216):1] [DLK(1068592):1] [DLK(1013437):1] [DLK(842966):1] [DLK(839153):1] [DLK(812536):1] [DLK(771790):1] [DLK(747762):1] [DLK(702675):1] [DLK(688489):1] [DLK(674177):1] [DLK(670762):1] [DLK(660443):1] [DLK(641726):1] [DLK(640449):1] [DLK(415944):1] [DLK(406894):1] [DLK(277340):1] [DLK(246191):1] [DLK(240546):1] [DLK(235897):1] [DLK(231093):1] [DLK(224391):1] [DLK(179815):1] [DLK(69812):1] [DLK(68679):1] [DLK(28230):1201770] [DLK(14818):1] [DLK(12253):1] [DLK(10357):1] [DLK(10129):1] [DLK(8335):1] [DLK(7729):1] [DLK(6168):1] [DLK(5380):1] [DLK(4945):1] [DLK(2229):16191] [DLK(1305):1006179] [DLK(792):1008488] [DLK(563):1007877] [DLK(538):15172] [DLK(481):15710] [DLK(465):18420] [DLK(395):18885] [DLK(364):1007513] [DLK(353):14819] [DLK(194):19280] [DLK(58):1] [DLK(48):1008440] [DLK(34):1009280] [DLK(29):1007484] [DLK(1):1] Ðапомню: количеÑтво ОДЛК указано в круглых Ñкобках Ñразу за DLK. Так наглÑднее. Можно и так напиÑать {1, 29, 34, 48, 58, 194, 353, 364, 395, 465, 481, 538, 563, 792, 1305, ..., 724775546, 1764493860}ПовторÑющихÑÑ ÐºÐ¾Ð»Ð¸Ñ‡ÐµÑтв ОДЛК в Ñтой чаÑти Ñпектра нет. ПредÑтавьте, какой огромный будет Ñпектр, еÑли обÑчитать вÑе КФ ОДЛК, имеющиеÑÑ Ð½Ð° данный момент в нашей БД. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Я начала обÑчитывать ДЛК 11-го порÑдка на ОДЛК год назад. Ðапример, Ñтот ДЛК из полной ÑиÑтемы MOLS  был обÑчитан 7 Ð¸ÑŽÐ½Ñ Ð¿Ñ€Ð¾ÑˆÐ»Ð¾Ð³Ð¾ года. Дублирую Ñообщение https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=5695 Протокол работы программы Белышева ortogon_u |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Рпрограмма вÑÑ‘ работает! Проверка ДЛК12 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 6460 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 2430 Соквадратов: 125 Ð’Ñ€ÐµÐ¼Ñ Ð² Ñек: 17135 133 1 17 6 1 ЕÑли повторений количеÑтв ОДЛК будет мало, более 6000 значений даÑÑ‚ Ñтот набор ДЛК в Ñпектр. Ðу, что такое 6000 значений! Похоже, в Ñпектре ОДЛК Ð´Ð»Ñ Ð”Ð›Ðš 12-го порÑдка будут миллионы значений. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Программе Белышева попалÑÑ "Ñ‚Ñжёлый" ДЛК Проверка ДЛК12 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 6460 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 5504 Соквадратов: 47142 Ð’Ñ€ÐµÐ¼Ñ Ð² Ñек: 43245 304 126 11 4 2 Прервала программу, потому что Ñтот ДЛК будет долго обÑчитыватьÑÑ. Буду Ñмотреть на полученный Ñпектр. ОбÑчитано 2367 КФ ОДЛК из 6460, меньше половины. Программа работала 12 чаÑов. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Спектр получилÑÑ Ð¾Ð±Ð°Ð»Ð´ÐµÐ½Ð½Ñ‹Ð¹! Показываю начало и конец (Ñпектр начинаетÑÑ Ñ Ñамого большого количеÑтва ОДЛК в проверенном наборе и далее по убыванию) [DLK(21022):172970] [DLK(3597):100512] [DLK(3568):95673] [DLK(2786):128058] [DLK(2761):425942] [DLK(2686):315560] [DLK(2305):114283] [DLK(2260):170710] [DLK(2148):240127] [DLK(1919):415793] [DLK(1915):151109] [DLK(1748):273797] [DLK(1733):354347] [DLK(1700):405114] [DLK(1699):299102] [DLK(1675):440743] [DLK(1659):262498] [DLK(1658):307159] [DLK(1572):226137] [DLK(1531):343351] [DLK(1505):321877] [DLK(1500):337176] [DLK(1474):394451] [DLK(1463):369396] [DLK(1439):444258] [DLK(1438):140630] [DLK(1428):380991] [DLK(1387):326904] [DLK(1377):461826] [DLK(1374):257187] [DLK(1358):456927] [DLK(1337):193992] [DLK(1328):166225] [DLK(1321):479110] [DLK(1309):162706] [DLK(1294):134818] [DLK(1294):320583] [DLK(1270):305889] [DLK(1261):169449] [DLK(1257):283013] [DLK(1252):421808] [DLK(1242):292194] [DLK(1227):202177] [DLK(1221):364201] [DLK(1199):161507] [DLK(1192):235800] [DLK(1186):328291] [DLK(1182):123230] [DLK(1179):261319] [DLK(1166):278230] [DLK(1164):195485] [DLK(1164):481051] [DLK(1159):269371] [DLK(1156):233662] [DLK(1146):455781] [DLK(1134):165091] [DLK(1126):131452] [DLK(1120):329518] [DLK(1114):124412] [DLK(1104):205964] [DLK(1097):460729] [DLK(1086):217196] [DLK(1071):366869] [DLK(1065):310257] [DLK(1056):338676] [DLK(1053):154251] [DLK(1049):379942] [DLK(1044):356625] [DLK(1042):333996] [DLK(1040):133397] [DLK(1039):390789] [DLK(1037):153024] [DLK(1034):349717] [DLK(1030):436585] [DLK(1029):402260] [DLK(1026):324262] [DLK(1024):287773] [DLK(1023):358340] [DLK(1002):215954] [DLK(1000):246569] [DLK(996):228726] [DLK(996):238494] [DLK(989):412899] [DLK(983):433144] [DLK(978):212459] [DLK(974):363227] [DLK(965):284639] [DLK(960):335122] [DLK(960):389829] [DLK(959):267003] [DLK(957):294917] [DLK(955):242275] [DLK(946):448044] [DLK(937):309320] [DLK(937):391997] [DLK(933):121822] [DLK(933):227709] [DLK(932):396306] [DLK(931):351639] [DLK(929):281018] . . . . . . [DLK(161):112336] [DLK(159):39093] [DLK(158):41882] [DLK(157):9741] [DLK(155):8378] первый разрыв Ñпектра [DLK(152):20013] [DLK(151):52242] [DLK(150):169299] [DLK(149):39258] [DLK(148):3396] [DLK(147):25906] [DLK(146):111650] [DLK(145):94790] [DLK(144):52752] [DLK(143):108166] [DLK(142):11655] [DLK(141):44218] [DLK(140):18466] [DLK(139):90437] [DLK(138):47231] [DLK(137):2703] [DLK(136):376922] [DLK(135):81009] [DLK(134):25772] [DLK(133):15622] [DLK(132):2878] [DLK(131):22359] [DLK(130):14813] [DLK(129):74853] [DLK(128):36317] [DLK(127):26318] [DLK(126):89013] [DLK(125):50339] [DLK(124):3208] [DLK(123):24084] [DLK(122):26445] [DLK(121):42191] [DLK(120):18847] [DLK(119):84176] [DLK(118):43447] [DLK(117):20392] [DLK(116):156048] [DLK(115):11540] [DLK(114):29699] [DLK(113):111159] [DLK(112):7416] [DLK(111):48703] [DLK(110):8533] [DLK(109):32183] [DLK(108):10323] [DLK(107):25624] [DLK(106):19566] [DLK(105):85054] [DLK(104):63206] [DLK(103):18967] [DLK(102):3106] [DLK(101):8097] [DLK(100):37641] [DLK(99):1996] [DLK(98):31695] [DLK(97):79897] [DLK(96):3010] [DLK(95):26160] [DLK(94):3544] [DLK(93):38237] [DLK(92):13074] [DLK(91):6117] [DLK(90):10575] [DLK(89):17394] [DLK(88):53705] [DLK(87):764] [DLK(86):7915] [DLK(85):2618] [DLK(84):37748] [DLK(83):17118] [DLK(82):64037] [DLK(81):8911] [DLK(80):10665] [DLK(79):190] [DLK(78):5818] [DLK(77):687] [DLK(76):5223] [DLK(75):2112] [DLK(74):6247] [DLK(73):10148] [DLK(72):4842] [DLK(71):616] [DLK(70):3853] [DLK(69):24015] [DLK(68):3697] [DLK(67):851] [DLK(66):486] [DLK(65):1759] [DLK(64):552] [DLK(63):5948] [DLK(62):14987] [DLK(61):346] [DLK(60):5302] [DLK(59):2441] [DLK(58):1508] [DLK(57):1617] [DLK(56):2287] [DLK(55):1704] [DLK(54):11265] [DLK(53):137] [DLK(52):4244] [DLK(51):1041] [DLK(50):1181] [DLK(49):1292] [DLK(48):2393] [DLK(47):2240] [DLK(46):91] [DLK(45):301] [DLK(44):6695] [DLK(43):1432] [DLK(42):5126] [DLK(41):1350] [DLK(40):7868] [DLK(39):948] [DLK(38):6568] [DLK(37):3765] [DLK(36):1092] [DLK(35):11019] [DLK(34):2840] [DLK(33):1475] [DLK(32):269] [DLK(31):5032] [DLK(30):918] [DLK(29):4743] [DLK(28):6538] [DLK(27):6443] [DLK(26):1] [DLK(25):5923] [DLK(24):4710] [DLK(23):4592] [DLK(22):7394] [DLK(21):27] [DLK(20):1021] [DLK(19):5896] [DLK(18):7097] [DLK(17):2095] [DLK(16):4228] [DLK(15):75] [DLK(14):24488] [DLK(13):9506] [DLK(12):10540] [DLK(11):4645] [DLK(10):106445] [DLK(9):1341] [DLK(8):3388] [DLK(7):7861] [DLK(6):7193] [DLK(5):7220] [DLK(4):2874] [DLK(3):5168] [DLK(2):987] [DLK(1):74] От 1 до 152 Ñпектр непрерывный, поÑле 152 первое пропущенное значение. Однако не факт, что тут дейÑтвительно Ñпектр разрываетÑÑ, потому что проверена Ð¼Ð¸Ð·ÐµÑ€Ð½Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ КФ ОДЛК. Ðебольшие количеÑтва ОДЛК повторÑÑŽÑ‚ÑÑ (Ñ ÑƒÐ´Ð°Ð»Ð¸Ð»Ð° повторы), в верхушке Ñпектра повторÑющихÑÑ ÐºÐ¾Ð»Ð¸Ñ‡ÐµÑтв очень мало (не удалила их). Первое повторенное количеÑтво в верхушке Ñпектра, кажетÑÑ, 1294 (на беглый взглÑд). |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата Спектр Ð´Ð»Ñ ÐžÐ”Ð›Ðš к ДЛК 12-го порÑдка впечатлÑет. От однушки до 1764493860 ОДЛК! РазумеетÑÑ, веÑÑŒ имеющийÑÑ Ñпектр по ÑущеÑтвующей чаÑти БД КФ ОДЛК можно ÑоÑтавить - дело техники. ИнтереÑнее задача: увеличить текущее макÑимальное значение Ñпектра. СущеÑтвует ли другой квадрозавр Ñ ÐºÐ¾Ð»Ð¸Ñ‡ÐµÑтвом ОДЛК больше 1764493860? Ðекоторые гоÑпода не верÑÑ‚ и в квадрозавра, имеющего 1764493860 ОДЛК. Ðапример, цитирую диÑкуÑÑию в OEIS Thu Apr 29 08:36 Eduard I. Vatutin: As far as I know, the calculation of the ODLS number for the DLS of order of 12 was carried out by separate parts (subtasks). Natalia, can you guarantee that there are no repeating ODLSs in the separate parts? This requires the use of a number of special algorithmic techniques. Otherwise, the estimate 1764493860 is significantly overestimated. Fri Apr 30 07:40 Joerg Arndt: If 1764493860 is too big than the inequality a(12) >= 1764493860 could be plain wrong! Sat May 01 10:08 Andrew Howroyd: Personally, I don't see the problem here. Natalia is only claiming a count on a single given square. a(12) >= 6640729. Since there is a 534MB dump of the Latin squares, Eduardo can easily verify in a few minutes if he is so inclined (it seems easier than arguing it would take weeks to perform his own independent and full counts). The only number that might be slightly suspect is the a(12) >= 1764493860, but that is clearly qualified with a might be wrong. https://oeis.org/history?seq=A287695&start=30 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Объединила две полученные чаÑти Ñпектра и показываю верхнюю чаÑÑ‚ÑŒ Ñпектра до количеÑтва ОДЛК равного 501 [DLK(1764493860):1] [DLK(724775546):1] [DLK(3326729):1] [DLK(1566818):1] [DLK(1534214):1] [DLK(1243865):1] [DLK(1230431):1] [DLK(1225216):1] [DLK(1068592):1] [DLK(1013437):1] [DLK(842966):1] [DLK(839153):1] [DLK(812536):1] [DLK(771790):1] [DLK(747762):1] [DLK(702675):1] [DLK(688489):1] [DLK(674177):1] [DLK(670762):1] [DLK(660443):1] [DLK(641726):1] [DLK(640449):1] [DLK(415944):1] [DLK(406894):1] [DLK(277340):1] [DLK(246191):1] [DLK(240546):1] [DLK(235897):1] [DLK(231093):1] [DLK(224391):1] [DLK(179815):1] [DLK(69812):1] [DLK(68679):1] [DLK(28230):1201770] [DLK(21022):172970] [DLK(14818):1] [DLK(12253):1] [DLK(10357):1] [DLK(10129):1] [DLK(8335):1] [DLK(7729):1] [DLK(6168):1] [DLK(5380):1] [DLK(4945):1] [DLK(3597):100512] [DLK(3568):95673] [DLK(2786):128058] [DLK(2761):425942] [DLK(2686):315560] [DLK(2305):114283] [DLK(2260):170710] [DLK(2229):16191] [DLK(2148):240127] [DLK(1919):415793] [DLK(1915):151109] [DLK(1748):273797] [DLK(1733):354347] [DLK(1700):405114] [DLK(1699):299102] [DLK(1675):440743] [DLK(1659):262498] [DLK(1658):307159] [DLK(1572):226137] [DLK(1531):343351] [DLK(1505):321877] [DLK(1500):337176] [DLK(1474):394451] [DLK(1463):369396] [DLK(1439):444258] [DLK(1438):140630] [DLK(1428):380991] [DLK(1387):326904] [DLK(1377):461826] [DLK(1374):257187] [DLK(1358):456927] [DLK(1337):193992] [DLK(1328):166225] [DLK(1321):479110] [DLK(1309):162706] [DLK(1305):1006179] [DLK(1294):134818] [DLK(1294):320583] [DLK(1270):305889] [DLK(1261):169449] [DLK(1257):283013] [DLK(1252):421808] [DLK(1242):292194] [DLK(1227):202177] [DLK(1221):364201] [DLK(1199):161507] [DLK(1192):235800] [DLK(1186):328291] [DLK(1182):123230] [DLK(1179):261319] [DLK(1166):278230] [DLK(1164):195485] [DLK(1164):481051] [DLK(1159):269371] [DLK(1156):233662] [DLK(1146):455781] [DLK(1134):165091] [DLK(1126):131452] [DLK(1120):329518] [DLK(1114):124412] [DLK(1104):205964] [DLK(1097):460729] [DLK(1086):217196] [DLK(1071):366869] [DLK(1065):310257] [DLK(1056):338676] [DLK(1053):154251] [DLK(1049):379942] [DLK(1044):356625] [DLK(1042):333996] [DLK(1040):133397] [DLK(1039):390789] [DLK(1037):153024] [DLK(1034):349717] [DLK(1030):436585] [DLK(1029):402260] [DLK(1026):324262] [DLK(1024):287773] [DLK(1023):358340] [DLK(1002):215954] [DLK(1000):246569] [DLK(996):228726] [DLK(996):238494] [DLK(989):412899] [DLK(983):433144] [DLK(978):212459] [DLK(974):363227] [DLK(965):284639] [DLK(960):335122] [DLK(960):389829] [DLK(959):267003] [DLK(957):294917] [DLK(955):242275] [DLK(946):448044] [DLK(937):309320] [DLK(937):391997] [DLK(933):121822] [DLK(933):227709] [DLK(932):396306] [DLK(931):351639] [DLK(929):281018] [DLK(923):145438] [DLK(923):331377] [DLK(915):382689] [DLK(912):290359] [DLK(907):365962] [DLK(897):214029] [DLK(893):476914] [DLK(891):378055] [DLK(890):146361] [DLK(889):420366] [DLK(888):392934] [DLK(877):295874] [DLK(877):473114] [DLK(870):236992] [DLK(869):383782] [DLK(852):164095] [DLK(851):272885] [DLK(849):138551] [DLK(849):247765] [DLK(849):304474] [DLK(848):442418] [DLK(847):137423] [DLK(843):167662] [DLK(843):265959] [DLK(842):116588] [DLK(833):203404] [DLK(833):476002] [DLK(832):437671] [DLK(831):253553] [DLK(824):251285] [DLK(822):243892] [DLK(822):434956] [DLK(820):400669] [DLK(819):132578] [DLK(816):341733] [DLK(815):230657] [DLK(811):464835] [DLK(810):119925] [DLK(810):372222] [DLK(809):231472] [DLK(808):160633] [DLK(808):223227] [DLK(807):254384] [DLK(803):244714] [DLK(796):198606] [DLK(795):434161] [DLK(792):1008488] [DLK(791):454255] [DLK(790):336082] [DLK(786):385996] [DLK(786):417763] [DLK(784):117430] [DLK(783):224035] [DLK(778):414405] [DLK(776):279396] [DLK(771):401489] [DLK(769):319357] [DLK(769):345602] [DLK(768):296751] [DLK(768):470016] [DLK(767):342584] [DLK(764):142547] [DLK(758):352923] [DLK(755):204540] [DLK(755):386782] [DLK(754):458285] [DLK(749):430629] [DLK(747):211032] [DLK(744):13736] [DLK(743):159728] [DLK(738):69432] [DLK(738):368658] [DLK(736):136647] [DLK(735):455046] [DLK(734):449412] [DLK(733):157052] [DLK(731):35079] [DLK(731):407663] [DLK(730):438922] [DLK(726):208230] [DLK(725):447319] [DLK(722):408636] [DLK(721):149046] [DLK(721):260078] [DLK(721):314218] [DLK(719):218282] [DLK(718):225419] [DLK(718):377337] [DLK(714):346490] [DLK(713):470784] [DLK(712):301289] [DLK(708):147316] [DLK(705):125761] [DLK(704):330638] [DLK(704):475298] [DLK(703):139400] [DLK(700):302376] [DLK(699):280319] [DLK(698):463203] [DLK(696):477807] [DLK(694):268677] [DLK(692):474573] [DLK(691):419675] [DLK(689):197917] [DLK(687):118632] [DLK(687):361381] [DLK(684):196649] [DLK(681):373653] [DLK(680):211779] [DLK(678):258628] [DLK(678):411751] [DLK(673):367940] [DLK(669):143360] [DLK(669):205295] [DLK(668):293436] [DLK(667):451338] [DLK(666):353681] [DLK(663):399396] [DLK(662):243230] [DLK(662):277368] [DLK(661):376214] [DLK(660):28867] [DLK(659):374478] [DLK(658):267962] [DLK(656):298208] [DLK(654):255694] [DLK(653):387537] [DLK(648):67937] [DLK(647):303310] [DLK(642):357669] [DLK(642):452977] [DLK(637):156415] [DLK(636):286973] [DLK(636):453619] [DLK(634):435778] [DLK(631):398711] [DLK(629):121193] [DLK(629):393822] [DLK(629):407034] [DLK(626):425316] [DLK(625):411126] [DLK(622):385374] [DLK(621):314939] [DLK(620):209437] [DLK(618):221516] [DLK(618):249173] [DLK(617):245952] [DLK(616):220848] [DLK(615):464013] [DLK(614):379328] [DLK(611):429180] [DLK(610):415183] [DLK(608):130844] [DLK(608):471994] [DLK(607):362620] [DLK(606):119319] [DLK(604):237890] [DLK(604):312990] [DLK(602):424714] [DLK(599):289166] [DLK(597):155354] [DLK(595):419080] [DLK(595):446272] [DLK(595):468866] [DLK(594):289765] [DLK(592):213437] [DLK(591):201065] [DLK(591):207639] [DLK(590):239537] [DLK(589):388752] [DLK(587):157785] [DLK(587):220261] [DLK(586):403739] [DLK(584):197333] [DLK(584):450463] [DLK(583):384791] [DLK(582):473991] [DLK(580):158372] [DLK(578):222649] [DLK(578):360540] [DLK(575):311322] [DLK(575):445697] [DLK(574):144864] [DLK(574):148472] [DLK(571):270999] [DLK(571):439652] [DLK(568):150314] [DLK(568):375137] [DLK(567):233095] [DLK(566):199988] [DLK(566):285604] [DLK(566):305323] [DLK(563):1007877] [DLK(562):126466] [DLK(562):340616] [DLK(559):248614] [DLK(557):252996] [DLK(556):323382] [DLK(555):341178] [DLK(555):469461] [DLK(553):73786] [DLK(553):259306] [DLK(553):421255] [DLK(553):443705] [DLK(552):362068] [DLK(551):467971] [DLK(550):294104] [DLK(547):21325] [DLK(547):149767] [DLK(547):312373] [DLK(545):356080] [DLK(543):397238] [DLK(540):199402] [DLK(540):365422] [DLK(540):460189] [DLK(538):15172] [DLK(537):28330] [DLK(533):432171] [DLK(531):418549] [DLK(531):478579] [DLK(530):340066] [DLK(529):265405] [DLK(529):452448] [DLK(528):219273] [DLK(527):140103] [DLK(527):360013] [DLK(526):224893] [DLK(520):127028] [DLK(520):260799] [DLK(519):72753] [DLK(517):413888] [DLK(514):73272] [DLK(514):74339] [DLK(514):409563] [DLK(513):325740] [DLK(512):472602] [DLK(511):200554] [DLK(510):127548] [DLK(509):375705] [DLK(508):371316] [DLK(507):35810] [DLK(504):136112] [DLK(503):308817] [DLK(503):373150] [DLK(501):15755] ПовторÑющиеÑÑ ÐºÐ¾Ð»Ð¸Ñ‡ÐµÑтва не удалÑла здеÑÑŒ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ждём Ñпектр количеÑтв ОДЛК Ð´Ð»Ñ Ð”Ð›Ðš 12-го порÑдка гоÑподина Ватутина. У него ДЛК 12-го порÑдка обÑчитываютÑÑ Ð½Ð° ОДЛК в BOINC-проекте. ЕÑтеÑтвенно, Ñто должно дать уже Ñпектр из неÑкольких Ñ‚Ñ‹ÑÑч значений. Как уже Ñказано, такой Ñпектр можно получить и по имеющейÑÑ Ð² моём проекте чаÑтичной БД КФ ОДЛК 12-го порÑдка, но Ð´Ð»Ñ Ñтого нужна Ð¼Ð¾Ñ‰Ð½Ð°Ñ Ñ‚ÐµÑ…Ð½Ð¸ÐºÐ° и времÑ. Ðе Ñчитаю Ñту задачу интереÑной, чтобы тратить на неё реÑурÑÑ‹. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата из ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=138&postid=2605 И далее о Ñпектре ОДЛК цитирую недавнее Ñообщение гоÑподина Ватутина Обратим внимание на: СпиÑок образуемых ими комбинаторных Ñтруктур доÑтупен онлайн: http://evatutin.narod.ru/evatutin_ls_all_structs_rus.pdf Уверена на вÑе Ñто, что вÑе "комбинаторные Ñтруктуры" предÑтавлены Ватутиным, как найденные им и только им, и нет ни одной ÑÑылки на авторов, например, первой найденной тройки, первой найденной деÑÑтки, первой (и единÑтвенной на данный момент!) Ñемёрки. ПоÑтому раÑÑкажу о Ñпектре ОДЛК 10-го порÑдка подробно Ñ ÑƒÐºÐ°Ð·Ð°Ð½Ð¸ÐµÐ¼ ÑÑылок и авторов. Итак, мы имеем на данный момент Ñледующий Ñпектр ОДЛК Ð´Ð»Ñ Ð”Ð›Ðš 10-го порÑдка {1, 2, 3, 4, 5, 6, 7, 8, 10}. Я предпочитаю не включать в Ñпектр значение ноль. ÐŸÐµÑ€Ð²Ð°Ñ Ð¾Ð´Ð½ÑƒÑˆÐºÐ° и ещё две ортогональные пары ДЛК 10-го порÑдка были найдены в 1992 г. Смотрите Ñтатью "Brown et al. "Completion of the Spectrum of Orthogonal Diagonal Latin Squares". Lecture notes in pure and applied mathematics 139 (1992), 43-49." Ð Ñто иллюÑÑ‚Ñ€Ð°Ñ†Ð¸Ñ Ð¿ÐµÑ€Ð²Ñ‹Ñ… ортогональных пар ДЛК 10-го порÑдка из указанной Ñтатьи  Однушка поÑледнÑÑ (ÑÑ‡Ð¸Ñ‚Ð°Ñ Ñверху). Рпервые две ортогональные пары - Ñто двушка, ÐºÐ¾Ñ‚Ð¾Ñ€Ð°Ñ Ð¿Ð¾Ð·Ð¶Ðµ была доÑтроена до четвёрки Олегом Заикиным. Следовательно, Ñто Ð¿ÐµÑ€Ð²Ð°Ñ Ñ‡ÐµÑ‚Ð²Ñ‘Ñ€ÐºÐ°, авторы Браун Ñ ÐºÐ¾Ð¼Ð¿Ð°Ð½Ð¸ÐµÐ¹ & Олег Заикин. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Кто нашёл первую двушку, Ñ Ð½Ðµ знаю. Двушек найдено очень много. ЗдеÑÑŒ http://mathhelpplanet.com/viewtopic.php?p=274618#p274618 раÑÑказано, как Ñ Ð½Ð°ÑˆÐ»Ð° Ñвою первую двушку. Ðто был поиÑк Ñлучайной генерацией! Вот Ñта двушка 0 1 2 3 4 5 6 7 8 9 6 9 0 1 2 4 8 3 5 7 7 4 8 9 3 6 5 2 1 0 4 8 1 5 9 7 3 0 6 2 2 7 3 0 6 8 1 9 4 5 9 5 4 8 0 3 2 6 7 1 8 2 6 4 1 0 7 5 9 3 5 3 7 2 8 9 4 1 0 6 3 6 9 7 5 1 0 4 2 8 1 0 5 6 7 2 9 8 3 4 sq1 0 1 2 3 4 5 6 7 8 9 6 9 0 1 8 4 2 3 5 7 7 4 8 9 3 6 5 2 1 0 4 8 1 5 9 7 3 0 6 2 2 7 3 0 6 8 1 9 4 5 9 5 4 2 0 3 8 6 7 1 8 2 6 4 1 0 7 5 9 3 5 3 7 8 2 9 4 1 0 6 3 6 9 7 5 1 0 4 2 8 1 0 5 6 7 2 9 8 3 4 sq2 Square: 0 1 2 3 4 5 6 7 8 9 8 6 7 4 1 3 5 9 0 2 9 5 3 8 2 0 1 6 7 4 2 7 8 9 0 6 4 5 1 3 7 4 0 6 5 2 3 1 9 8 3 2 6 1 8 7 9 4 5 0 4 0 9 7 6 1 8 3 2 5 6 8 1 5 9 4 0 2 3 7 1 3 5 0 7 9 2 8 4 6 5 9 4 2 3 8 7 0 6 1 ОДЛК предÑтавлены в формате программы С. БелÑева; в то Ð²Ñ€ÐµÐ¼Ñ Ñтой программой и выполнÑлÑÑ Ð¿Ð¾Ð¸Ñк ортогональных диагональных Ñоквадратов. ИллюÑтрацию покажу  ПовторюÑÑŒ: Ñто Ð¼Ð¾Ñ Ð¿ÐµÑ€Ð²Ð°Ñ Ð´Ð²ÑƒÑˆÐºÐ°, но, вполне возможно, не приоритетнаÑ. Может быть, Ð¿ÐµÑ€Ð²Ð°Ñ Ð´Ð²ÑƒÑˆÐºÐ° была найдена ранее. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
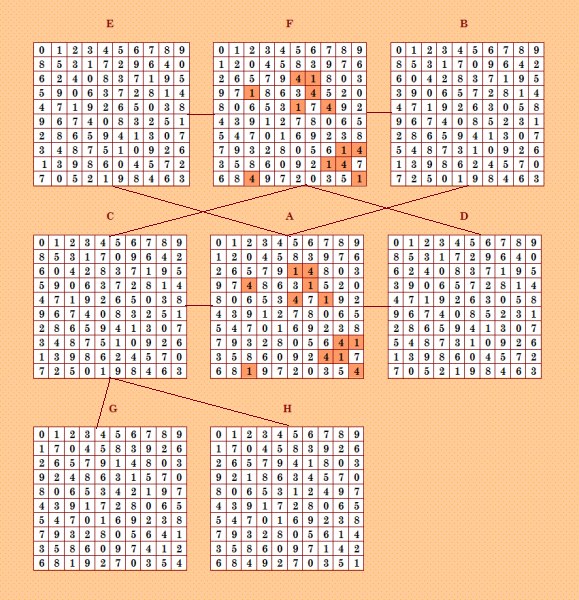
То, что гоÑподин Ватутин называет "комбинаторные Ñтруктуры", Ñ Ð½Ð°Ð·Ñ‹Ð²Ð°ÑŽ конфигурации. Смотрите тему "Различные группы пар ОДЛК10" https://boinc.progger.info/odlk/forum_thread.php?id=46#1024 Двушки дают интереÑные конфигурации. Ðапример: двушка Ñ Ð°Ð¿Ð¿ÐµÐ½Ð´Ð¸ÐºÑом  ФактичеÑки здеÑÑŒ две двушки и ÐºÐ°Ð¶Ð´Ð°Ñ Ð¸Ð· них Ñ Ð°Ð¿Ð¿ÐµÐ½Ð´Ð¸ÐºÑом :) двушки-близнÑшки 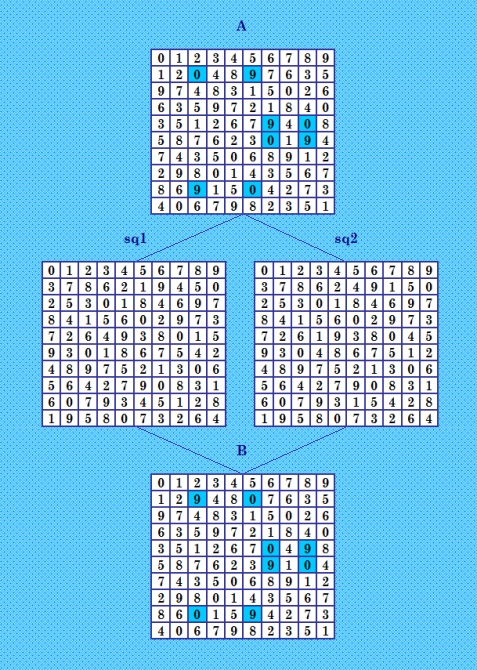 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
О первой тройке, найденной ÐлекÑеем Белышевым (приоритетнаÑ!) Ñмотрите Ñообщение https://boinc.progger.info/odlk/forum_thread.php?id=42&postid=868 Показываю иллюÑтрацию  Ðвтором первой тройки ОДЛК 10-го порÑдка отныне и навÑегда ÑвлÑетÑÑ ÐлекÑей Белышев, даже еÑли гоÑподин Ватутин забыл Ñто указать в Ñвоём ÑпиÑке комбинаторных Ñтруктур (наверное, забыл). Тройки тоже дают интереÑные конфигурации. Ðапример, тройки-близнÑшки  О вÑех тройках в нашей БД КФ ОДЛК 10-го порÑдка Ñмотрите тему "Группы из трёх пар ОДЛК" https://boinc.progger.info/odlk/forum_thread.php?id=42 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Об авторах первой четвёрки уже напиÑано выше. Одна из найденных мной четвёрок - на раннем Ñтапе ручного проекта 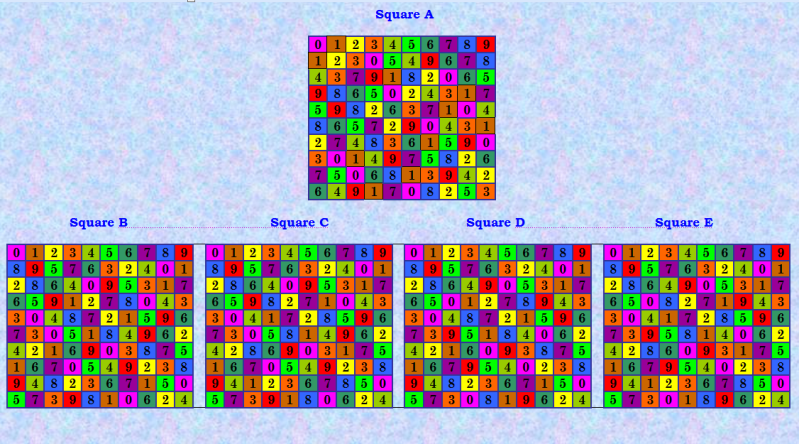 О вÑех четвёрках в нашей БД КФ ОДЛК 10-го порÑдка Ñмотрите тему "Группы из четырёх ортогональных пар ДЛК" https://boinc.progger.info/odlk/forum_thread.php?id=40 Четвёрки порождают Ñамые разнообразные конфигурации. Пример Вот ÐºÐ¾Ð½Ñ„Ð¸Ð³ÑƒÑ€Ð°Ñ†Ð¸Ñ Ð¸Ð· 8 уникальных ОДЛК; четвёрку, порождающую данную конфигурацию, нашёл Demis, Ð¿Ð¾Ð¼Ð¾Ð³Ð°Ñ Ð¼Ð½Ðµ выполнÑÑ‚ÑŒ ÑкÑперимент Ñ Ð¿ÑевдоаÑÑоциативными ДЛК https://boinc.progger.info/odlk/forum_thread.php?id=46&postid=2311 Продолжение Ñледует... |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
О нашей первой пÑтёрке (не приоритетнаÑ) цитирую Ñообщение https://boinc.progger.info/odlk/forum_thread.php?id=90&postid=2346 ПÑтёрку нашёл Demis в ÑкÑперименте по поиÑку решений Ñ Ñимметрией (4,31,31). Ð’ нашей БД КФ ОДЛК 10-го порÑдка на данный момент имеетÑÑ Ð²Ñго три пÑтёрки. Смотрите тему "Группы из пÑти пар ОДЛК" https://boinc.progger.info/odlk/forum_thread.php?id=90 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
О первых шёÑтёрках в нашей БД КФ ОДЛК 10-го порÑдка дублирую Ñообщение от 21 Ð¸ÑŽÐ½Ñ 2018 г. https://boinc.progger.info/odlk/forum_thread.php?id=71&postid=1795 Первые группы из шеÑти пар ортогональных ДЛК (кратко называемые "шеÑтёрки") были найдены более двух лет назад в нашем Ñ Ð‘ÐµÐ»Ñ‹ÑˆÐµÐ²Ñ‹Ð¼ ÑкÑперименте Ñ ÑемейÑтвом ЛК блочной Ñтруктуры â„–1. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese