Thread 'Статьи в OEIS: иÑÑ‚Ð¾Ñ€Ð¸Ñ Ð¸ ÑовременноÑÑ‚ÑŒ'
Message boards : Science : Статьи в OEIS: иÑÑ‚Ð¾Ñ€Ð¸Ñ Ð¸ ÑовременноÑÑ‚ÑŒ
Message board moderation
Previous · 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 . . . 23 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Покажу две иллюÑтрации, демонÑтрирующие два вида конфигураций, порождаемых шеÑтёрками. Обе Ñти группы ОДЛК найдены мной в ÑкÑперименте Ñ Ð¿ÑевдоаÑÑоциативными ДЛК. Первый вид конфигурации - ÑÐ¸Ð¼Ð¼ÐµÑ‚Ñ€Ð¸Ñ‡Ð½Ð°Ñ ÑˆÐµÑтёрка 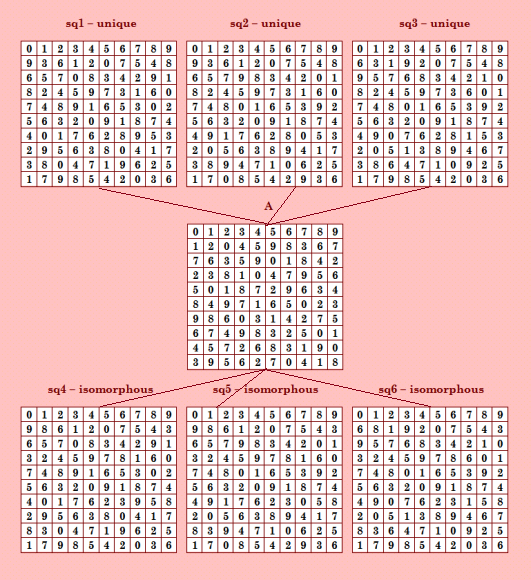 Второй вид конфигурации - не ÑÐ¸Ð¼Ð¼ÐµÑ‚Ñ€Ð¸Ñ‡Ð½Ð°Ñ Ð¿Ð¾Ð»Ð½Ð¾Ð²ÐµÑÐ½Ð°Ñ ÑˆÐµÑтёрка 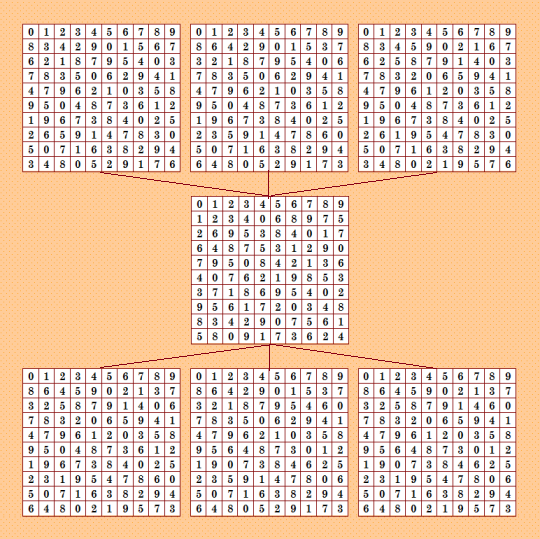 О других шеÑтёрках в нашей БД КФ ОДЛК 10-го порÑдка Ñмотрите тему "Группы из шеÑти пар ортогональных ДЛК" https://boinc.progger.info/odlk/forum_thread.php?id=71 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ртеперь о приоритете на шеÑтёрку. Сообщение на форуме boinc.ru давно кануло в лету. Ðо! К ÑчаÑтью, оно ÑохранилоÑÑŒ в моей фундаментальной теме "Ортогональные латинÑкие квадраты 10-го порÑдка" на форуме Math Help Planet. Тема Ñта тоже давно закрыта, но, Ñлава Богу, пока живаÑ. Ð’ Ñтом Ñообщении от 29 Ñ„ÐµÐ²Ñ€Ð°Ð»Ñ 2016 г. http://mathhelpplanet.com/viewtopic.php?p=262095#p262095 Ñ Ð¸ процитировала Ñообщение Ñ Ñ„Ð¾Ñ€ÑƒÐ¼Ð° boinc.ru Ðа форуме boinc.ru выложили результат Ðвтор ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ Alexone. Ркто нашёл шеÑтёрку, о которой ÑообщаетÑÑ, Ñ Ð½Ðµ знаю. Думаю, что Alexone принимал в Ñтом учаÑтие. Ðо Ð¿ÐµÑ€Ð²Ð°Ñ ÑˆÐµÑтёрка показана! Далее Ñледовало Ñообщение Белышева от 15 марта 2016 г. http://mathhelpplanet.com/viewtopic.php?p=263776#p263776 Выкладываю архив 944 КФ ДЛК изоморфных (как ЛК) латинÑкому квадрату Паркера/Wanless/Брауна. Ð’ Ñтом ÑкÑперименте Белышевым найдены две шеÑтёрки. И только поÑле Ñтого был наш ÑовмеÑтный Ñ Ð‘ÐµÐ»Ñ‹ÑˆÐµÐ²Ñ‹Ð¼ ÑкÑперимент, в котором найдены шеÑÑ‚ÑŒ шеÑтёрок. Об Ñтом ÑкÑперименте Ñказано выше. Ð’ Ñти шеÑÑ‚ÑŒ шеÑтёрок входит и ÑÐ°Ð¼Ð°Ñ Ð¿ÐµÑ€Ð²Ð°Ñ ÑˆÐµÑтёрка и две шеÑтёрки, найденные в ÑкÑперименте Белышева. Вот такие приоритеты. PS. Замечу, что именно в указанном ÑкÑперименте Белышев нашёл первую тройку, но в цитируемом Ñообщении о ней не Ñказано. Белышев её проÑто потерÑл, а Ñ Ð½Ð°ÑˆÐ»Ð° :) Ещё отмечу: поÑмотрела ÑÐµÐ¹Ñ‡Ð°Ñ Ð°Ñ€Ñ…Ð¸Ð², выложенный Белышевым https://disk.yandex.ru/d/eXghlY-yqC2Dh Скачан 10 раз. Очень мало! ГоÑпода! Ðто иÑторичеÑкие решениÑ, найденные 5 лет назад в первом крупном ÑкÑперименте Белышева. Скачайте вÑе! ПуÑÑ‚ÑŒ будет как можно больше копий. Ðто необходимо Ñохранить. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
О Ñемёрке дублирую Ñообщение https://boinc.progger.info/odlk/forum_thread.php?id=136&postid=4550 Ðаша Ð¿ÐµÑ€Ð²Ð°Ñ Ð¸ пока единÑÑ‚Ð²ÐµÐ½Ð½Ð°Ñ Ñемёрка была найдена мной в ручном ÑкÑперименте Ñ Ð¿ÑевдоаÑÑоциативными ДЛК (PADLS) 15 Ð°Ð¿Ñ€ÐµÐ»Ñ 2018 г. Смотрите Ñообщение https://boinc.progger.info/odlk/forum_thread.php?id=1&postid=1741#1741 Так Ñемёрка выдаётÑÑ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð¾Ð¹ БелÑева от оÑновного ДЛК в первом формате 0 1 2 3 4 5 6 7 8 9 3 9 6 1 5 4 2 8 0 7 8 0 5 9 2 6 7 3 1 4 7 4 1 8 6 2 5 9 3 0 1 5 4 0 7 8 3 2 9 6 9 6 8 2 1 3 4 0 7 5 2 7 3 4 0 9 1 6 5 8 5 3 7 6 9 0 8 4 2 1 4 2 0 7 8 1 9 5 6 3 6 8 9 5 3 7 0 1 4 2 sq1 0 1 2 3 4 5 6 7 8 9 3 9 6 1 5 4 2 8 0 7 8 0 5 2 9 6 7 3 1 4 7 4 1 8 6 9 5 2 3 0 1 5 4 0 7 8 3 9 2 6 2 6 8 9 1 3 4 0 7 5 9 7 3 4 2 0 1 6 5 8 5 3 7 6 0 2 8 4 9 1 4 2 9 7 8 1 0 5 6 3 6 8 0 5 3 7 9 1 4 2 sq2 0 1 2 3 4 5 6 7 8 9 3 9 6 1 5 4 2 8 0 7 8 0 5 2 9 6 7 3 1 4 7 4 1 8 6 9 5 2 3 0 1 5 4 0 7 8 3 9 6 2 6 2 8 9 1 3 4 0 7 5 9 7 3 4 2 0 1 6 5 8 5 3 7 6 0 2 8 4 9 1 4 6 9 7 8 1 0 5 2 3 2 8 0 5 3 7 9 1 4 6 sq3 0 1 2 3 4 5 6 7 8 9 3 9 6 1 5 4 2 8 0 7 8 0 5 9 2 6 7 3 1 4 7 4 1 8 6 2 5 9 3 0 1 5 4 0 7 8 3 2 9 6 9 6 8 2 1 3 4 0 7 5 2 7 3 4 9 0 1 6 5 8 5 3 7 6 0 9 8 4 2 1 4 2 9 7 8 1 0 5 6 3 6 8 0 5 3 7 9 1 4 2 sq4 0 1 2 3 4 5 6 7 8 9 3 9 6 1 5 4 2 8 0 7 8 6 5 2 0 9 7 3 1 4 7 4 1 8 9 0 5 2 3 6 1 5 4 9 7 8 3 6 2 0 2 0 8 6 1 3 4 9 7 5 9 7 3 4 2 6 1 0 5 8 5 3 7 0 6 2 8 4 9 1 4 2 9 7 8 1 0 5 6 3 6 8 0 5 3 7 9 1 4 2 sq5 0 1 2 3 4 5 6 7 8 9 3 9 6 1 5 4 2 8 0 7 8 6 5 9 0 2 7 3 1 4 7 4 1 8 2 0 5 9 3 6 1 5 4 2 7 8 3 6 9 0 9 0 8 6 1 3 4 2 7 5 2 7 3 4 9 6 1 0 5 8 5 3 7 0 6 9 8 4 2 1 4 2 9 7 8 1 0 5 6 3 6 8 0 5 3 7 9 1 4 2 sq6 0 1 2 3 4 5 6 7 8 9 3 9 6 7 5 4 1 8 0 2 8 6 5 9 0 7 2 3 1 4 2 4 1 8 7 0 5 9 3 6 4 5 7 2 1 8 3 6 9 0 9 0 8 6 2 3 7 1 4 5 7 2 3 1 9 6 4 0 5 8 5 3 4 0 6 9 8 2 7 1 1 7 9 4 8 2 0 5 6 3 6 8 0 5 3 1 9 4 2 7 sq7 Square: 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 7 9 5 6 8 3 9 4 0 7 1 5 8 2 6 9 0 3 1 8 4 7 6 5 2 5 8 9 7 6 2 0 1 4 3 7 5 6 8 0 9 2 4 3 1 6 4 7 5 1 3 8 2 9 0 2 6 1 9 5 8 4 3 0 7 8 3 5 2 9 6 1 0 7 4 4 7 8 6 2 0 3 9 1 5 Семёрка полновеÑнаÑ, порождает конфигурацию из 8 уникальных ОДЛК. ПоÑмотрим на конфигурацию, полученную от оÑновного ДЛК во втором формате программой Белышева  ЧудеÑные узорчатые ортогональные Ñоквадраты! Только ортогональный Ñоквадрат mate #7 не узорчатый. Как бы на оÑновании такой чудеÑной узорчатоÑти ортогональных Ñоквадратов поиÑкать новые Ñемёрочки? Что-то они очень плохо у Ð½Ð°Ñ Ð½Ð°Ñ…Ð¾Ð´ÑÑ‚ÑÑ, вот вÑего одна нашлаÑÑŒ на многомиллионную БД. РдевÑтки так и вообще нет ни одной. Ðу, не может быть, что её (девÑтки) вообще не ÑущеÑтвует. Такое у Ð¼ÐµÐ½Ñ Ð¿Ñ€ÐµÐ´Ñ‡ÑƒÐ²Ñтвие :) не научное! ___________________ конец дублируемого ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ Ð¡ÐµÐ¼Ñ‘Ñ€ÐºÐ° до Ñих пор единÑÑ‚Ð²ÐµÐ½Ð½Ð°Ñ Ð² нашей БД. ÐаÑколько мне извеÑтно, не только в нашей. Может быть, пропуÑтила ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ Ð¾ других Ñемёрках в альтернативной БД. Ðо Ð¿Ð¾ÐºÐ°Ð·Ð°Ð½Ð½Ð°Ñ Ð¿ÐµÑ€Ð²Ð°Ñ Ñемёрка была найдена мной, тут моё авторÑтво беÑÑпорно. Продолжение Ñледует... |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата Сообщение на форуме boinc.ru давно кануло в лету. Ðе вÑÑ‘ кануло в лету! Demis приÑлал ÑÑылку https://web.archive.org/web/20161222153334/http://forum.boinc.ru/default.aspx?g=posts&t=1872#post79208 Да, Ñто начало той Ñамой темы на форуме boinc.ru. Очень интереÑно поÑмотреть, как вÑÑ‘ начиналоÑÑŒ. Однако в архиве ÑохранилиÑÑŒ только три первые Ñтраницы темы. Ð¡Ð¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ Ð¾ найденной шеÑтёрке там нет. Оно было позже - на четвёртой или пÑтой Ñтранице. Плохо ÑохранÑет вебархив темы. Ð’ теме 69 Ñтраниц. Сохранено только три. Ð’Ñе оÑтальные Ñтраницы потерÑны, как Ñ Ð¿Ð¾Ð½Ð¸Ð¼Ð°ÑŽ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Так, перехожу к воÑьмёркам. Тема "Ортогональные латинÑкие квадраты 10-го порÑдка" очень большаÑ, а Ñтранички на форуме Math Help Planet малюÑенькие. ИÑкать трудно, но вот нашла Ñообщение от 9 марта 2016 г. http://mathhelpplanet.com/viewtopic.php?p=263172#p263172 Показываю Ñкриншот Ñтого ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ (цитировать тему нельзÑ, потому что она закрыта) 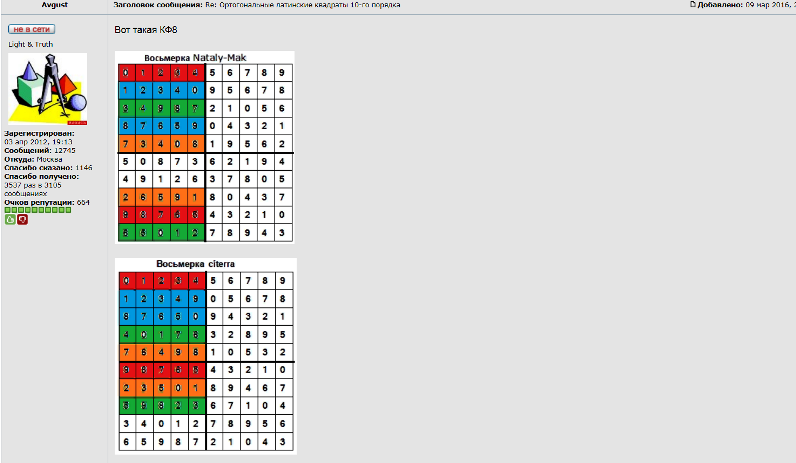 ЗдеÑÑŒ показана Ð¿Ñ€Ð¸Ð¾Ñ€Ð¸Ñ‚ÐµÑ‚Ð½Ð°Ñ Ð²Ð¾Ñьмёрка, Ð½Ð°Ð¹Ð´ÐµÐ½Ð½Ð°Ñ citerra (нижнÑÑ). Сразу же вÑлед за ним Ñ Ð¿Ð¾Ð²Ñ‚Ð¾Ñ€Ð¸Ð»Ð° ÑкÑперимент по поиÑку воÑьмёрок и нашла ÑущеÑтвенно новую воÑьмёрку (не изоморфную). Ðто была Ð²Ñ‚Ð¾Ñ€Ð°Ñ Ð²Ð¾Ñьмёрка. Ðа иллюÑтрации Avgust изобразил Ñти две первые воÑьмёрки. Ðа Ñкриншоте видна дата - 9 марта 2016 г. Читайте далее о воÑьмёрках, найденных в нашем Ñ Ð‘ÐµÐ»Ñ‹ÑˆÐµÐ²Ñ‹Ð¼ ÑкÑперименте. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Дублирую Ñообщение https://boinc.progger.info/odlk/forum_thread.php?id=72&postid=1801 Первые группы из воÑьми пар ортогональных ДЛК (кратко называемые "воÑьмёрка") были найдены в нашем Ñ Ð‘ÐµÐ»Ñ‹ÑˆÐµÐ²Ñ‹Ð¼ ÑкÑперименте Ñ ÑемейÑтвом ЛК блочной Ñтруктуры â„–1. Их было вÑего две, вот они (КФ оÑновного ДЛК в первом формате) 0 1 2 3 4 5 6 7 8 9 1 2 3 4 0 9 5 6 7 8 3 4 9 8 7 2 1 0 5 6 8 7 6 5 9 0 4 3 2 1 7 3 4 0 8 1 9 5 6 2 5 0 8 7 3 6 2 1 9 4 4 9 1 2 6 3 7 8 0 5 2 6 5 9 1 8 0 4 3 7 9 8 7 6 5 4 3 2 1 0 6 5 0 1 2 7 8 9 4 3 0 1 2 3 4 5 6 7 8 9 1 2 3 4 9 0 5 6 7 8 8 7 6 5 0 9 4 3 2 1 4 0 1 7 6 3 2 8 9 5 7 6 4 9 8 1 0 5 3 2 9 8 7 6 5 4 3 2 1 0 2 3 5 0 1 8 9 4 6 7 5 9 8 2 3 6 7 1 0 4 3 4 0 1 2 7 8 9 5 6 6 5 9 8 7 2 1 0 4 3 ОÑновные ДЛК Ñтих воÑьмёрок Ñимметричны по Гергели/Брауну. Более того, они ÑвлÑÑŽÑ‚ÑÑ "браунами". КФ оÑновных ДЛК Ñтих воÑьмёрок во втором формате принадлежат линейке â„– 6. ВоÑьмёрки Ñти не полновеÑные, ÐºÐ°Ð¶Ð´Ð°Ñ Ð´Ð°Ñ‘Ñ‚ только 5 уникальных КФ ОДЛК. То еÑÑ‚ÑŒ Ñреди ортогональных Ñоквадратов каждой воÑьмёрки еÑÑ‚ÑŒ 4 не уникальных ДЛК. Вот такие были наши первые воÑьмёрки. О двух Ñледующих воÑьмёрках далее. _________________________________________ конец дублируемого ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ Ð¡Ñ€Ð°Ð²Ð½Ð¸Ñ‚Ðµ в первыми Ð´Ð²ÑƒÐ¼Ñ Ð²Ð¾Ñьмёрками, показанными в предыдущем поÑте. Ðто те же Ñамые воÑьмёрки. Ð’ Ñообщении не утверждаетÑÑ, что Ñти воÑьмёрки были найдены впервые. Да, они были найдены в нашем Ñ Ð‘ÐµÐ»Ñ‹ÑˆÐµÐ²Ñ‹Ð¼ ÑкÑперименте, но к моменту нашего ÑкÑперимента уже были извеÑтны. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитирую Ñообщение https://boinc.progger.info/odlk/forum_thread.php?id=72&postid=1803 5 Ð°Ð¿Ñ€ÐµÐ»Ñ Ñ. г. мной была найдена пÑÑ‚Ð°Ñ Ð²Ð¾Ñьмёрка, в ÑкÑперименте Ñ Ð¿ÑевдоаÑÑоциативными ДЛК. ЗдеÑÑŒ тоже не утверждаетÑÑ, что Ð´Ð°Ð½Ð½Ð°Ñ Ð²Ð¾Ñьмёрка была найдена впервые. Может быть, Ñто не так. Ðто Ð¿ÐµÑ€Ð²Ð°Ñ Ð²Ð¾Ñьмёрка в нашей БД, ÐºÐ¾Ñ‚Ð¾Ñ€Ð°Ñ Ð¿Ð¾Ñ€Ð¾Ð¶Ð´Ð°ÐµÑ‚ 9 уникальных ОДЛК (то еÑÑ‚ÑŒ полновеÑнаÑ). О вÑех других воÑьмёрках в нашей БД Ñмотрите тему "Группы из воÑьми пар ортогональных ДЛК" https://boinc.progger.info/odlk/forum_thread.php?id=72 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
О деÑÑтках Ñмотрите тему "Группы из деÑÑти ортогональных пар ДЛК" https://boinc.progger.info/odlk/forum_thread.php?id=113 Ðе буду много цитировать. Ðапишу главное. Сообщение о найденной мной первой деÑÑтке https://boinc.progger.info/odlk/forum_thread.php?id=1&postid=1742#1742 Ðто авторÑÐºÐ°Ñ Ð´ÐµÑÑтка, что отмечено в OEIS https://oeis.org/A287695 то еÑÑ‚ÑŒ был найден первый ДЛК 10-го порÑдка, который имеет 10 ортогональных ДЛК. Результат в OEIS добавил гоÑподин Ватутин (Ñ Ð² то Ð²Ñ€ÐµÐ¼Ñ Ð±Ñ‹Ð»Ð° заблокирована в OEIS). Цитирую a(10) >= 10 (Updated). - Eduard I. Vatutin, Apr 27 2018 Однако редактор попроÑил гоÑподина Ватутина указать ÑÑылку на Ñтот результат, что он и Ñделал. Цитирую Natalia Makarova, Diagonal Latin square with 10 orthogonal squares КонфигурациÑ, Ð¿Ð¾Ñ€Ð¾Ð¶Ð´Ð°ÐµÐ¼Ð°Ñ Ð½Ð°Ð¹Ð´ÐµÐ½Ð½Ð¾Ð¹ мной деÑÑткой 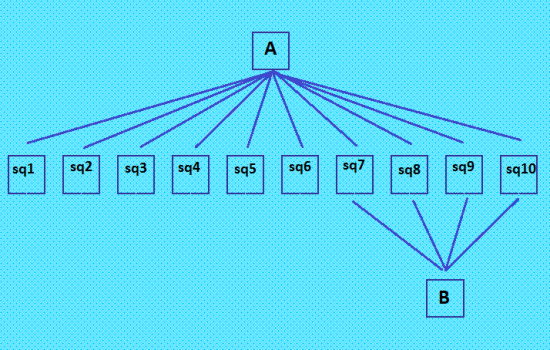 Читала Ñ Ð´Ð°Ð²Ð½Ð¾ какую-то Ñтатью гоÑподина Ватутина (Ñ Ñоавторами) о "ÑпиÑке комбинаторных Ñтруктур" Ð´Ð»Ñ ÐžÐ”Ð›Ðš 10-го порÑдка. ÐŸÐ¾ÐºÐ°Ð·Ð°Ð½Ð½Ð°Ñ ÐºÐ¾Ð½Ñ„Ð¸Ð³ÑƒÑ€Ð°Ñ†Ð¸Ñ, Ð¿Ð¾Ñ€Ð¾Ð¶Ð´Ð°ÐµÐ¼Ð°Ñ Ð¿ÐµÑ€Ð²Ð¾Ð¹ деÑÑткой, в Ñтатье, конечно, приведена, но никаких ÑÑылок и ÑƒÐºÐ°Ð·Ð°Ð½Ð¸Ñ Ð°Ð²Ñ‚Ð¾Ñ€Ð° нет. Рведь автор гоÑподину Ватутину хорошо извеÑтен! Сам вноÑил результат в OEIS. Ðу, и не только Ñта конфигурациÑ. Там много конфигураций, Ð´Ð»Ñ Ñ‚Ð¾Ð¹ же Ñемёрки, к примеру. Рона тоже найдена мной. Ðо вÑе Ñти конфигурации нашёл и "перенашёл" гоÑподин Ватутин, и теперь он единÑтвенный автор вÑех конфигураций. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðедавно помощник Mynx приÑлал результаты от пÑти новых ДЛК 12-го порÑдка. Ðто интереÑные результаты, они добавлÑÑŽÑ‚ÑÑ Ð² верхнюю чаÑÑ‚ÑŒ Ñпектра количеÑтв ОДЛК Ð´Ð»Ñ Ð”Ð›Ðš 12-го порÑдка. Показываю верхнюю чаÑÑ‚ÑŒ Ñпектра Ñ Ð´Ð¾Ð±Ð°Ð²Ð»ÐµÐ½Ð½Ñ‹Ð¼Ð¸ значениÑми, они выделены краÑным [DLK(1764493860):1] [DLK(724775546):1] [DLK(3326729):1] [DLK(2631797):1] [DLK(1566818):1] [DLK(1534214):1] [DLK(1262133):1] [DLK(1243865):1] [DLK(1230431):1] [DLK(1225216):1] [DLK(1211559):1] [DLK(1130710):1] [DLK(1068592):1] [DLK(1059810):1] [DLK(1013437):1] [DLK(842966):1] [DLK(839153):1] [DLK(812536):1] [DLK(771790):1] [DLK(747762):1] [DLK(702675):1] [DLK(688489):1] [DLK(674177):1] [DLK(670762):1] [DLK(660443):1] [DLK(641726):1] [DLK(640449):1] . . . . . . Результаты выложены. Смотрите тему "ODLS of order n>10" https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=109 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ЧаÑÑ‚ÑŒ БД КФ ОДЛК 10-го порÑдка, Ð¿Ð¾Ð»ÑƒÑ‡ÐµÐ½Ð½Ð°Ñ Ð² ручном проекте, Ñодержит на данный момент 263396 КФ ОДЛК. ПропуÑтила Ñту чаÑÑ‚ÑŒ БД через программу Белышева ortogon_u. Показываю начало и конец выходного файла output.txt [DLK(2):1] 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 0 1 5 6 4 3 8 9 7 3 6 7 8 2 9 1 0 5 4 8 5 4 7 9 2 0 6 1 3 5 4 8 9 0 7 2 1 3 6 9 8 3 6 7 0 4 5 2 1 6 9 5 0 1 8 7 3 4 2 7 3 9 2 5 1 8 4 6 0 4 7 6 1 8 3 9 2 0 5 [DLK(1):3] 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 0 1 5 6 4 9 8 3 7 9 4 7 6 5 8 0 3 1 2 8 9 6 1 7 3 4 0 2 5 5 3 8 7 1 9 2 6 0 4 7 5 3 2 9 0 8 1 4 6 6 8 5 0 2 7 3 4 9 1 3 6 4 9 8 1 7 2 5 0 4 7 9 8 0 2 1 5 6 3 [DLK(1):4] 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 0 1 5 9 4 7 8 6 3 6 4 8 9 7 3 1 5 2 0 9 7 4 6 8 2 0 1 3 5 5 8 9 1 6 7 4 3 0 2 7 9 6 0 5 8 3 2 4 1 3 6 5 8 0 1 2 4 9 7 8 3 7 2 1 0 9 6 5 4 4 5 3 7 2 9 8 0 1 6 [DLK(1):5] 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 0 1 5 9 8 7 4 6 3 4 3 5 6 7 9 1 8 2 0 9 7 4 2 8 3 0 1 5 6 5 4 3 9 2 7 8 6 0 1 7 8 6 0 1 2 9 3 4 5 3 6 8 1 0 4 2 5 9 7 8 5 9 7 6 1 4 0 3 2 6 9 7 8 5 0 3 2 1 4 [DLK(1):6] 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 0 3 1 5 8 4 6 9 7 8 4 6 7 0 9 3 5 2 1 9 8 5 2 6 0 7 3 1 4 5 7 4 9 2 1 8 0 3 6 6 3 7 8 1 2 9 4 5 0 7 6 1 5 9 4 2 8 0 3 3 5 9 6 8 7 0 1 4 2 4 9 8 0 7 3 1 2 6 5 [DLK(1):7] 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 0 3 1 5 8 7 6 9 4 6 3 7 8 9 2 0 4 5 1 4 8 5 9 7 1 2 0 3 6 5 9 6 7 2 4 1 8 0 3 7 6 1 5 8 0 9 3 4 2 9 5 8 6 0 3 4 1 2 7 8 4 9 2 1 7 3 5 6 0 3 7 4 0 6 9 8 2 1 5 [DLK(1):8] 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 0 3 1 5 8 9 6 4 7 8 4 9 5 7 2 1 0 3 6 6 3 7 9 8 4 0 2 1 5 4 7 5 6 0 9 8 3 2 1 9 8 6 2 1 3 7 4 5 0 5 6 8 7 2 0 4 1 9 3 7 5 4 0 9 1 3 8 6 2 3 9 1 8 6 7 2 5 0 4 [DLK(2):9] 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 0 3 1 6 4 8 5 9 7 3 7 1 6 2 9 4 8 5 0 5 8 6 7 9 2 0 4 3 1 7 6 5 9 1 8 2 3 0 4 8 4 9 0 5 3 7 2 1 6 4 5 8 2 0 7 9 1 6 3 9 3 7 5 8 0 1 6 4 2 6 9 4 8 7 1 3 0 2 5 [DLK(2):11] 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 0 3 1 6 4 8 5 9 7 5 7 6 8 9 2 1 4 3 0 6 9 7 5 1 8 3 0 4 2 8 5 9 6 0 7 4 2 1 3 7 4 1 2 5 3 9 8 0 6 9 3 4 7 8 1 0 6 2 5 4 6 8 9 2 0 7 3 5 1 3 8 5 0 7 9 2 1 6 4 [DLK(2):13] 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 0 3 1 6 4 8 5 9 7 5 8 7 6 9 2 4 0 3 1 7 6 5 9 8 1 2 3 0 4 4 5 9 8 0 7 1 2 6 3 8 7 6 2 5 3 9 4 1 0 3 4 8 0 2 9 7 1 5 6 9 3 1 5 7 8 0 6 4 2 6 9 4 7 1 0 3 8 2 5 [DLK(2):15] 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 6 5 9 7 8 2 0 3 1 6 4 8 5 9 7 7 6 1 9 5 3 2 8 0 4 8 4 5 2 7 0 9 3 1 6 9 5 4 7 1 8 0 6 2 3 3 8 7 6 2 9 4 0 5 1 6 7 8 5 9 2 3 1 4 0 5 3 9 0 8 7 1 4 6 2 4 9 6 8 0 1 7 2 3 5 . . . . . . [DLK(1):284848] 0 1 2 3 4 5 6 7 8 9 2 3 0 7 6 9 8 4 5 1 6 4 1 9 2 8 3 0 7 5 7 0 5 8 1 3 2 6 9 4 9 7 8 0 5 6 4 1 2 3 8 2 9 5 7 4 0 3 1 6 4 9 6 1 3 2 7 5 0 8 5 6 4 2 8 7 1 9 3 0 1 8 3 4 9 0 5 2 6 7 3 5 7 6 0 1 9 8 4 2 [DLK(2):284849] 0 1 2 3 4 5 6 7 8 9 2 3 0 7 8 9 5 1 4 6 9 2 8 6 5 1 4 0 7 3 4 8 7 1 9 0 2 3 6 5 7 5 4 0 6 3 9 2 1 8 8 6 3 9 1 2 0 4 5 7 1 4 5 8 3 6 7 9 0 2 3 9 6 4 0 7 8 5 2 1 6 7 1 5 2 4 3 8 9 0 5 0 9 2 7 8 1 6 3 4 [DLK(4):284851] 0 1 2 3 4 5 6 7 8 9 2 3 0 7 8 9 5 6 4 1 5 4 6 0 3 1 9 8 7 2 8 9 3 5 6 4 2 0 1 7 9 6 8 2 1 3 7 4 5 0 4 5 9 8 0 7 1 2 6 3 7 0 4 1 2 6 8 3 9 5 1 2 5 6 7 0 4 9 3 8 3 7 1 4 9 8 0 5 2 6 6 8 7 9 5 2 3 1 0 4 [DLK(2):284855] 0 1 2 3 4 5 6 7 8 9 2 3 0 8 1 9 4 5 7 6 6 5 4 7 9 1 8 2 0 3 8 6 3 1 0 2 5 4 9 7 7 2 8 9 5 0 3 6 4 1 9 0 7 4 8 6 1 3 5 2 4 9 5 6 2 8 7 1 3 0 5 8 1 2 3 7 0 9 6 4 1 4 6 0 7 3 9 8 2 5 3 7 9 5 6 4 2 0 1 8 [DLK(2):284857] 0 1 2 3 4 5 6 7 8 9 2 3 0 8 7 9 5 4 6 1 3 4 9 7 0 6 1 8 5 2 8 9 6 1 3 4 2 5 7 0 7 2 5 4 6 3 9 0 1 8 6 0 8 5 1 7 4 9 2 3 5 7 4 0 2 1 8 3 9 6 1 6 7 9 5 8 0 2 3 4 9 5 1 2 8 0 3 6 4 7 4 8 3 6 9 2 7 1 0 5 [DLK(1):284859] 0 1 2 3 4 5 6 7 8 9 2 3 0 9 1 8 4 5 6 7 5 9 4 1 3 6 7 8 2 0 9 2 6 5 0 3 1 4 7 8 7 6 9 4 8 0 5 3 1 2 6 4 1 8 2 7 9 0 5 3 8 0 5 7 6 1 2 9 3 4 1 7 3 0 9 2 8 6 4 5 3 5 8 2 7 4 0 1 9 6 4 8 7 6 5 9 3 2 0 1 [DLK(2):284860] 0 1 2 3 4 5 6 7 8 9 2 3 1 4 0 6 9 8 5 7 3 6 5 8 1 7 2 0 9 4 6 7 0 9 2 8 3 5 4 1 5 4 9 7 8 2 1 3 0 6 8 9 4 5 7 1 0 6 2 3 9 0 8 1 6 4 7 2 3 5 1 2 6 0 9 3 5 4 7 8 7 8 3 2 5 9 4 1 6 0 4 5 7 6 3 0 8 9 1 2 Ð Ñто Ñпектр Ð´Ð»Ñ Ð´Ð°Ð½Ð½Ð¾Ð¹ чаÑти БД Ñ ÑƒÐºÐ°Ð·Ð°Ð½Ð¸ÐµÐ¼ количеÑтва групп ОДЛК [DLK(10):58674] - 2 [DLK(8):64407] - 7 [DLK(7):23007] - 1 [DLK(6):116023] - 5 [DLK(5):175630] - 3 [DLK(4):165] - 301 [DLK(3):1158] - 90 [DLK(2):1] - 20277 [DLK(1):3] - 242711 Как видим, в оÑновном в БД КФ ОДЛК 10-го порÑдка имеютÑÑ Ð¾Ð´Ð½ÑƒÑˆÐºÐ¸ и двушки (Ñто не только в БД ручного проекта). Среди групп выше двушки больше вÑего вÑтречаетÑÑ Ñ‡ÐµÑ‚Ð²Ñ‘Ñ€Ð¾Ðº. Ð’Ñех оÑтальных групп ОДЛК очень мало. Отмечу, что в БД ручного проекта предÑтавлен веÑÑŒ извеÑтный на данный момент Ñпектр. Ð’ БД, полученной в трёх BOINC-проектах (ОДЛК, ODLK1 и TBEG), нет деÑÑток, Ñемёрки и пÑтёрок. Ð’Ñе Ñти группы найдены в ручном проекте. Почему так получилоÑÑŒ? Я много пиÑала об Ñтом. Ð’ BOINC-проектах ОДЛК и ODLK1 работает алгоритм грубой Ñилы. Ðти BOINC-проекты оказалиÑÑŒ не ÑпоÑобными к динамичеÑкому развитию: к обновлению алгоритмов и запуÑку более Ñффективных Приложений. Ð’ BOINC-проекте TBEG пыталиÑÑŒ запуÑтить более Ñффективный алгоритм, но надолго запала не хватило. Увы! Подпроект по поиÑку ОДЛК 10-го порÑдка в проекте TBEG давно оÑтановлен. Ð’ заключение: Ñто Ñпектр в нашей общей БД (три указанных выше BOINC-проекта и мой ручной проект) < [code][DLK(10)] - 2 [DLK(8)] - 11 [DLK(7)] - 1 [DLK(6)] - 11 [DLK(5)] - 3 [DLK(4)] - 564 [DLK(3)] - 134 [DLK(2)] - не поÑчитаны [DLK(1)] - не поÑчитаны[/code] Сколько двушек, не могу Ñказать. Однушек - неÑколько миллионов. Точно никто не Ñчитал. Общей БД вÑех проектов нет. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Продолжу о Ñпектрах. Что мы знаем о Ñпектре количеÑтв ОДЛК Ð´Ð»Ñ Ð”Ð›Ðš 13-го порÑдка? Похоже, пока ничего не знаем. ÐижнÑÑ Ñ‡Ð°ÑÑ‚ÑŒ Ñпектра - однушки. Ðу, Ñто пожалуйÑта. Вот SODLS 13-го порÑдка 0 2 3 4 5 6 7 8 11 10 12 9 1 3 1 6 5 12 7 8 10 9 11 2 0 4 1 7 2 8 0 11 9 12 10 6 3 4 5 5 10 12 3 6 9 1 11 4 2 8 7 0 2 9 7 12 4 3 10 0 5 1 11 8 6 9 11 8 7 10 5 0 4 3 12 1 6 2 4 0 5 9 11 10 6 2 1 3 7 12 8 10 6 11 0 9 8 12 7 2 5 4 1 3 6 4 1 11 7 12 2 9 8 0 5 3 10 12 5 4 10 8 1 11 3 6 9 0 2 7 7 8 9 6 2 0 3 1 12 4 10 5 11 8 12 10 1 3 2 4 5 0 7 6 11 9 11 3 0 2 1 4 5 6 7 8 9 10 12 Однушка гарантирована. Может быть, у Ñтого ДЛК еÑÑ‚ÑŒ и ещё ОДЛК, но главное, что точно еÑÑ‚ÑŒ один ОДЛК - его транÑпонированный вариант. Ð’ Ñообщении https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=130&postid=1732 предÑтавлены 6 топовых ДЛК 13-го порÑдка по Д-транÑверÑалÑм, ни один из них не обÑчитан на ОДЛК. Ðто первый топовый ДЛК 13-го порÑдка из указанного ÑообщениÑ. 1. 131106 Д-транÑверÑалей из полной ÑиÑтемы MOLS 0 3 8 12 2 6 9 10 4 5 11 7 1 7 1 4 6 11 0 8 5 3 12 9 2 10 5 9 2 1 6 10 7 4 11 3 0 12 8 10 11 7 3 12 1 0 8 2 4 6 5 9 9 12 10 2 4 11 1 0 5 7 3 8 6 12 8 11 10 0 5 2 3 9 1 7 6 4 1 2 0 4 5 3 6 9 7 8 12 10 11 8 6 5 11 3 9 10 7 12 2 1 4 0 6 4 9 5 7 12 11 1 8 10 2 0 3 3 7 6 8 10 4 12 11 0 9 5 1 2 4 0 12 9 1 8 5 2 6 11 10 3 7 2 10 3 0 9 7 4 12 1 6 8 11 5 11 5 1 7 8 2 3 6 10 0 4 9 12 Tomas Brada начинал обÑчитывать Ñтот ДЛК на ОДЛК, но полноÑтью не обÑчитал. Вот что он наÑчитал EUELx2zmrdPHyTGkGJhedf1cuDmJzqhw6hUme293TPB (13, 131106, >>248703) отÑюда https://boinc.tbrada.eu/forum_thread.php?id=3104&postid=4133 Таким образом, у Ð½Ð°Ñ Ð½ÐµÑ‚ пока ничего в Ñпектре количеÑтв ОДЛК Ð´Ð»Ñ Ð”Ð›Ðš 13-го порÑдка, кроме однушки. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Программа Белышева ortogon_u охотно Ñчитает Ñтот квадратик :) Проверка ДЛК13 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 1 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 131106 Соквадратов: 31 Ð’Ñ€ÐµÐ¼Ñ Ð² Ñек: 55 9114 4149 1561 504 133 39 6 9114 чаÑтей. Многовато. Ортогональки поÑвлÑÑŽÑ‚ÑÑ ÑˆÑƒÑтро, только запуÑтила, уже 31 ОДЛК найден. Можно иÑпользовать программу поиÑка по чаÑÑ‚Ñм Tomas Brada. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ЗапуÑкаю первую чаÑÑ‚ÑŒ в программе Tomas Brada C:\Users\Дом\Downloads\libr>ortogonbw.exe E1QZUHrrX59ZeMFL996pDWjJTW5Ug3FkY3XwbGd6 1 1>out2.txt init_trans(13) used 575 nodes num_dtrans: 131106 init_disjoint(13) used 170 heads and 1704548 nodes L(0) c(85) 1 / 9114 L(1) c(73) X / 4149 ИнтереÑно, как долго будет ÑчитатьÑÑ Ð¿ÐµÑ€Ð²Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ. Думаю, что долго, Ð´Ð»Ñ Ñ‡ÐµÑ€ÐµÐ¿Ð°ÑˆÐºÐ¸ нереально даже одну чаÑÑ‚ÑŒ полноÑтью поÑчитать. Рортогональки уже побежали, 80 штук уже еÑÑ‚ÑŒ # in: E1QZUHrrX59ZeMFL996pDWjJTW5Ug3FkY3XwbGd6 1 # num_dtrans: 131106 EGPgH3g14opP71RZbvR8YhewYyuodSbDRDajfA EtjtMKwRUFGAhKWGUbKM8197z2iRJrnTvr1Ure6 EUbFRa7zhfQzp2rex9kZaqW2iuZ6bDXnhTVZNC EoMnitsTz2dUZRG7gCeUL8WFy3Wqc7U7fuB636 ETHXTuwzESCQHkd6hKsfxN4mFfhB3XVzM7LeXZ EFNTQZhTX6uA8rTHGBUb9UzijvLUH2vS7wwEJ96 ELcKCmeiRo5NTWniRNaai2AfGtR2KS5JduCEsmF EaTHXApcyE2eEaJsaiVP2dgx8mwzFh1jUbq4wBB EJKyA98snCxZbN3u8KGSMWV4iPzBoL1wEZSEax3 EU8LTiMWdQzU8vdnFgYK4ZKp4d4M8MwWZTjsn6k E2s1mikt5tCHpNFBqkPGqC9vW7Cx41BnXNF3va8 EvH82kD8V4gBe39z2dDrWrhvDq3YgTz7C1FqT5W3 E4fvw7XwtZhdzPte1ZdoMUKhu7seYaTxXFtNks22 EhXam15S9HQonVguoGNeJ6jXM8PQL8enhJWCvH Ev5VHwwmn9xxxTVmTPUAeDNYHU43k5hT9LmvHp5 EnZY28ZTadT1bQyytVFm2Ca1b3WdVPjUJcAJ8BR EAFKdcMS9J9drrKg5NQd41wRFLnYqYFiagt4QZ2 EtgeToq3QgGF7JYat2Y6faV4FZsZUYeWkjDYkm5 . . . . . . EMLyuLqbhEwEmVawaPHovfxBTinjZP5RtsmMz2w2 EzkE9y8JgPRbc2tzez443MyEXG96jHhuK7gXw9S EbL7bbsMbHHuaTbLF4Z3VvrVZnacp4uDpHV4Ri4 EQqMt3eGNbqRKZRrCtcXYGz2TfZP6MuGiTbk1gR EzQM8XALXdRf1sYvQcFFQxUZBrSAAikCsJYbA2 EDpU9mbx9uCvmsE27kfGLVDVZK42adPekqUscM3 EV9GeFpHxzLrVHNwkfZ9jbPSN4wBUuVD3kkbhz2 Em27EFFBTADuXoF3ZXWH9TyTT44dXcgocwkxvj EbyDnnJ5tQLMMjErXKpEy2jHhb1CsvddLqhCt2 EYMPy9CK7YQ2NQT7ZNWbRJv1RvyKXJYJgQpdGRE Eq2Biz3jzb8z59GYL5fcuMr9darZPyV8w2QrNg СчитаетÑÑ Ñ…Ð¾Ñ€Ð¾ÑˆÐ¾. Уже 522 ОДЛК. Однако прерываю. Ðто уже Ñчитал Tomas Brada. ОбÑчитать полноÑтью Ñтот ДЛК трудно, надо иметь мощную технику и много времени. Пока Ñ Ñ‚ÑƒÑ‚ пиÑала, уже 580 ОДЛК нашлёпалоÑÑŒ :) Прервала. Ртеперь взÑла первый из найденных ОДЛК и пробую его обÑчитать, Ð´Ð»Ñ Ð½Ð°Ñ‡Ð°Ð»Ð° - Ð¿ÐµÑ€Ð²Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ C:\Users\Дом\Downloads\libr>ortogonbw.exe EGPgH3g14opP71RZbvR8YhewYyuodSbDRDajfA 1 1>>out2.txt init_trans(13) used 575 nodes num_dtrans: 9748 init_disjoint(13) used 170 heads and 126894 nodes L(0) c(85) 1 / 684 L(1) c(104) X / 273 Ð’ Ñтом ДЛК вÑего 9748 Д-транÑверÑалей. 684 чаÑти. ИнтереÑно, как Ñтот квадратик будет ÑчитатьÑÑ. Он, конечно, полегче первого топового. Опа! ÐŸÐµÑ€Ð²Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ уже отÑтрелÑлаÑÑŒ C:\Users\Дом\Downloads\libr>ortogonbw.exe EGPgH3g14opP71RZbvR8YhewYyuodSbDRDajfA 1 1>>out2.txt init_trans(13) used 575 nodes num_dtrans: 9748 init_disjoint(13) used 170 heads and 126894 nodes L(0) c(85) 1 / 684 L(1) c(104) X / 273 C:\Users\Дом\Downloads\libr>pause Ð”Ð»Ñ Ð¿Ñ€Ð¾Ð´Ð¾Ð»Ð¶ÐµÐ½Ð¸Ñ Ð½Ð°Ð¶Ð¼Ð¸Ñ‚Ðµ любую клавишу . . . Отлично! ОДЛК не найдены в Ñтой чаÑти. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð·Ð°Ð¿ÑƒÑ‰Ñƒ Ñледующие чаÑти. ЗапуÑтила 15 чаÑтей. ЕÑли у Ñтого ДЛК нет других ОДЛК, значит, Ñто Ñ‚Ð¾Ñ‡Ð½Ð°Ñ Ð¾Ð´Ð½ÑƒÑˆÐºÐ°. ЕÑли ещё другие еÑÑ‚ÑŒ - тоже хорошо. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Проверила 30 чаÑтей Ñтого ДЛК. Ðи одного ДЛК не нашла. Ðадумала найти Ñреди имеющихÑÑ ÐžÐ”Ð›Ðš (к первому топовому ДЛК) ДЛК Ñ Ð¼Ð¸Ð½Ð¸Ð¼Ð°Ð»ÑŒÐ½Ñ‹Ð¼ количеÑтвом Д-транÑверÑалей. Ðашла ДЛК Ñ 9570 Д-транÑверÑалей. Ðачала его проверÑÑ‚ÑŒ. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÑетÑÑ . . . . . C:\Users\Дом\Downloads\libr>ortogonbw.exe EjPJ4EAAYThzXNPZSjAFkES3LPL76WtYsDWhAqG 112 1>>output.txt init_trans(13) used 575 nodes num_dtrans: 9570 init_disjoint(13) used 170 heads and 124580 nodes L(0) c(129) 112 / 677 L(1) c(85) X / 267 C:\Users\Дом\Downloads\libr>ortogonbw.exe EjPJ4EAAYThzXNPZSjAFkES3LPL76WtYsDWhAqG 113 1>>output.txt init_trans(13) used 575 nodes num_dtrans: 9570 init_disjoint(13) used 170 heads and 124580 nodes L(0) c(129) 113 / 677 L(1) c(136) X / 268 C:\Users\Дом\Downloads\libr>ortogonbw.exe EjPJ4EAAYThzXNPZSjAFkES3LPL76WtYsDWhAqG 114 1>>output.txt init_trans(13) used 575 nodes num_dtrans: 9570 init_disjoint(13) used 170 heads and 124580 nodes L(0) c(129) 114 / 677 L(1) c(28) X / 263 ОДЛК тоже пока не найдены. Такое подозрение, что вÑе Ñти ОДЛК к первому топовому ДЛК однушки, то еÑÑ‚ÑŒ они имеют ровно один ортогональный диагональный Ñоквадрат - первый топовый ДЛК. ПоÑмотрим. ЗдеÑÑŒ проверить реально полноÑтью вÑе чаÑти. ЕÑли будет чиÑÑ‚Ð°Ñ Ð¾Ð´Ð½ÑƒÑˆÐºÐ°, очень хорошо. Ðачало Ñпектра будет положено. ЕÑли будет найдена Ð´Ñ€ÑƒÐ³Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° ОДЛК, тоже хорошо. ИнтереÑно пощупать Ñтот процеÑÑ Ð²Ð¶Ð¸Ð²ÑƒÑŽ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Проверка близитÑÑ Ðº финишу. ОДЛК пока не найдены. Покажу, что Ñ Ð¸Ð¼ÐµÑŽ в виду под чиÑтой однушкой, на примере ДЛК 11-го порÑдка. Вот Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° Ð 0 1 2 3 4 5 6 7 8 9 10 6 10 7 5 1 3 8 2 9 0 4 10 8 1 7 0 6 3 4 2 5 9 9 6 8 2 5 7 10 3 4 1 0 7 2 9 10 3 8 1 5 0 4 6 1 9 0 8 6 4 2 10 5 3 7 2 4 5 0 7 10 9 8 3 6 1 5 7 4 9 8 1 0 6 10 2 3 3 0 6 4 9 2 5 1 7 10 8 4 5 3 6 10 9 7 0 1 8 2 8 3 10 1 2 0 4 9 6 7 5 Ð’ 0 1 2 3 4 5 6 7 8 9 10 5 4 1 10 6 9 7 0 3 2 8 6 9 5 8 3 10 0 2 4 1 7 10 7 6 9 8 3 2 5 1 0 4 4 3 0 1 10 2 8 6 7 5 9 2 5 8 4 1 7 10 3 9 6 0 8 6 7 5 9 0 1 10 2 4 3 3 2 10 6 0 4 9 8 5 7 1 7 10 3 0 2 1 4 9 6 8 5 9 0 4 2 7 8 5 1 10 3 6 1 8 9 7 5 6 3 4 0 10 2 Квадрат Римеет один ортогональный диагональный Ñоквадрат (Ð’); квадрат Ð’ имеет один ортогональный диагональный Ñоквадрат (Ð). Других ОДЛК Ñти ДЛК не имеют. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðга, попалÑÑ, голубчик # in: EjPJ4EAAYThzXNPZSjAFkES3LPL76WtYsDWhAqG 604 # num_dtrans: 9570 E1QZUHrrX59ZeMFL996pDWjJTW5Ug3FkY3XwbGd6 Ð’ 604-й чаÑти! И ещё один! # in: EjPJ4EAAYThzXNPZSjAFkES3LPL76WtYsDWhAqG 628 # num_dtrans: 9570 ENVQFySJ95mjgRU27Pu6M3EYvpAACi3EkmzmrEo3 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Обработка завершена. Пощупали процеÑÑ Ð²Ð¶Ð¸Ð²ÑƒÑŽ. Ð”Ð»Ñ "лёгких" ДЛК 13-го порÑдка (то еÑÑ‚ÑŒ - Ñ Ð½ÐµÐ±Ð¾Ð»ÑŒÑˆÐ¸Ð¼ количеÑтвом Д-транÑверÑалей) обработку реально выполнить даже на моём ПК. Итак, Ñто иÑходный ДЛК 13-го порÑдка EjPJ4EAAYThzXNPZSjAFkES3LPL76WtYsDWhAqG Ñто два его ОДЛК E1QZUHrrX59ZeMFL996pDWjJTW5Ug3FkY3XwbGd6 ENVQFySJ95mjgRU27Pu6M3EYvpAACi3EkmzmrEo3 Один из ОДЛК - первый топовый ДЛК. Таким образом, найдена двушка от иÑходного ДЛК, но двушка Ñ Ð¿Ñ€ÐµÐ¾Ð³Ñ€Ð¾Ð¼Ð½Ñ‹Ð¼ аппендикÑом, который проиÑходит от первого топового ДЛК. Может быть, и от второго ОДЛК тоже проиÑходит аппендикÑ, Ñто можно проверить. Ð’ любом Ñлучае, двушка найдена. Думаю, что однушки (чиÑтые и прочие) Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 13 тоже еÑÑ‚ÑŒ. Таким образом, о Ñпектре количеÑтв ОДЛК Ð´Ð»Ñ Ð”Ð›Ðš 13-го порÑдка пока знаем Ñледующее: {1, 2, . . . , X} где Ð¥ >> 248703, то еÑÑ‚ÑŒ много больше 248703. Сколько в Ñпектре значений, каково текущее макÑимальное значение в Ñпектре - ничего Ñтого пока нет. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðу вот, наконец, и интереÑный ДЛК 12-го порÑдка обÑчитан в BOINC-проекте ГераÑим. Дублирую Ñообщение гоÑподина Ватутина ÐкÑперимент по подÑчету ОДЛК Ð´Ð»Ñ Ð¸Ð½Ñ‚ÐµÑ€ÐµÑного ДЛК порÑдка 12 завершен. По его итогам можно Ñказать, что ДЛК отÑюда https://boinc.ru/forum/topic/proekt-gerasimhome/?part=102#postid-4436 Можно поздравить гоÑподина Ватутина Ñ Ð»Ð¸Ñ‡Ð½Ñ‹Ð¼ рекордом. Ðто позволÑет добавить еще одно значение в ÑоответÑтвующий Ñпектр ОДЛК Можно также добавить ещё одно значение в Ñпектры по транÑверÑалÑм Ð´Ð»Ñ Ð”Ð›Ðš 12-го порÑдка. Ðу, Ñто гоÑподин Ватутин, наверное, уже давно Ñделал. Ð’ моём ÑпиÑке ДЛК 12-го порÑдка по Д-транÑверÑалÑм новое значение Ñпектра (от квадрата гоÑподина Ватутина) добавлÑетÑÑ Ð¼ÐµÐ¶Ð´Ñƒ Ñтими ДЛК 24618 0 7 3 10 8 6 11 9 5 2 4 1 10 1 4 5 7 8 3 2 11 6 0 9 8 10 2 7 0 4 9 11 1 3 6 5 11 2 10 3 9 1 0 8 4 7 5 6 6 0 9 8 4 3 1 5 7 11 2 10 9 3 7 2 11 5 8 0 6 10 1 4 1 11 8 9 5 10 6 4 2 0 7 3 3 6 5 4 2 9 10 7 0 1 11 8 2 4 1 6 3 11 7 10 8 5 9 0 4 8 11 0 6 2 5 1 10 9 3 7 5 9 0 11 1 7 4 6 3 8 10 2 7 5 6 1 10 0 2 3 9 4 8 11 24676 0 1 2 3 4 5 6 7 8 9 10 11 8 7 6 9 2 3 4 10 11 5 1 0 3 2 10 11 7 8 1 6 9 0 4 5 5 4 7 8 1 0 10 2 3 11 6 9 7 0 3 6 5 2 9 8 10 4 11 1 11 10 4 5 6 9 2 1 0 3 7 8 2 5 8 10 0 7 11 3 6 1 9 4 9 6 1 0 10 11 7 4 5 8 2 3 10 8 9 4 3 6 5 11 1 2 0 7 1 11 5 2 9 4 3 0 7 6 8 10 4 9 0 7 11 1 8 5 2 10 3 6 6 3 11 1 8 10 0 9 4 7 5 2 Смотрите Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=138&postid=2547 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё раз цитирую Ñообщение гоÑподина Ватутина ...обработка более Ñ‚Ñжелых квадратов в перÑпективе должна позволить найти ДЛК порÑдка 12 Ñ ÐµÑ‰Ðµ бОльшим чиÑлом ОДЛК, будем иÑкать... Уже позволила :) Ðтот первый топовый ДЛК 12-го порÑдка по Д-транÑверÑалÑм 28496 Д-транÑверÑалей 0 10 4 6 2 8 9 3 7 5 11 1 11 1 7 5 9 3 2 8 4 6 0 10 4 6 2 8 1 11 10 0 9 3 7 5 7 5 9 3 10 0 1 11 2 8 4 6 3 9 0 10 4 6 7 5 11 1 8 2 8 2 11 1 7 5 4 6 0 10 3 9 2 8 1 11 5 7 6 4 10 0 9 3 9 3 10 0 6 4 5 7 1 11 2 8 5 7 3 9 0 10 11 1 8 2 6 4 6 4 8 2 11 1 0 10 3 9 5 7 1 11 5 7 3 9 8 2 6 4 10 0 10 0 6 4 8 2 3 9 5 7 1 11 имеет 1764493860 ОДЛК. У Ñтого ДЛК текущий макÑимум по Д-транÑверÑалÑм, а также текущий макÑимум по ОДЛК. Я раÑÑматривала бы такой Ñценарий поиÑка: надо найти ДЛК Ñ Ð±ÐžÐ»ÑŒÑˆÐ¸Ð¼ количеÑтвом Д-транÑверÑалей. Возможно, такой ДЛК даÑÑ‚ и бОльшее количеÑтво ОДЛК. PS. Показанный первый топовый ДЛК ÑвлÑетÑÑ Ð”Ð›Ðš клаÑÑичеÑкой блочной Ñтруктуры, а также ÑвлÑетÑÑ "брауном" по Ñтрокам и по Ñтолбцам. Утилита Harry White GetType1 отмечает Ñледующие ÑвойÑтва у Ñтого ДЛК Order? 12
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_7.txt
Counts
------
1 diagonal Latin
1 associative
1 double axial symmetric
1 natural \diagonal
1 axial parity 1-wayДважды Ñимметричный по Гергели/Брауну (Ð³Ð¾Ñ€Ð¸Ð·Ð¾Ð½Ñ‚Ð°Ð»ÑŒÐ½Ð°Ñ Ð¸ Ð²ÐµÑ€Ñ‚Ð¸ÐºÐ°Ð»ÑŒÐ½Ð°Ñ Ð¾ÑÐµÐ²Ð°Ñ ÑимметриÑ), ещё аÑÑоциативный. Очень гармоничный ДЛК! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
A307164 https://oeis.org/A307164 A307164 Maximum number of intercalates in a diagonal Latin square of order n. AUTHOR Eduard I. Vatutin, Mar 27 2019 ИнтеркалÑÑ‚Ñ‹ - Ñто другое название блоков 2Ñ…2. Ð’ Ñтой поÑледовательноÑти Ð¼ÐµÐ½Ñ Ð·Ð°Ð¸Ð½Ñ‚ÐµÑ€ÐµÑовал ДЛК 12-го порÑдка, цитирую a(12) >= 188 Ðашла Ñтот ДЛК в приложении к поÑледовательноÑти https://oeis.org/A307164/a307164.txt Цитирую n=12, a(12)>=188 Ð”Ð»Ñ ÑравнениÑ: в Ñтом первом топовом ДЛК по Д-транÑверÑалÑм (а также по количеÑтву ОДЛК) 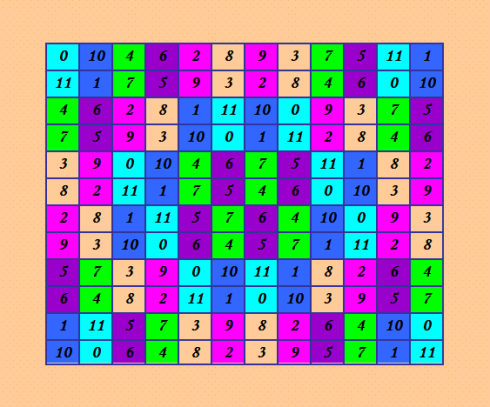 вÑего 72 блока, как утверждает программа Harry White. Ðа иллюÑтрации видим 36 раÑкрашенных блоков. ÐŸÐ»ÑŽÑ ÐµÑÑ‚ÑŒ ещё 36 блоков. ПоÑмотрите, например, на Ñту иллюÑтрацию 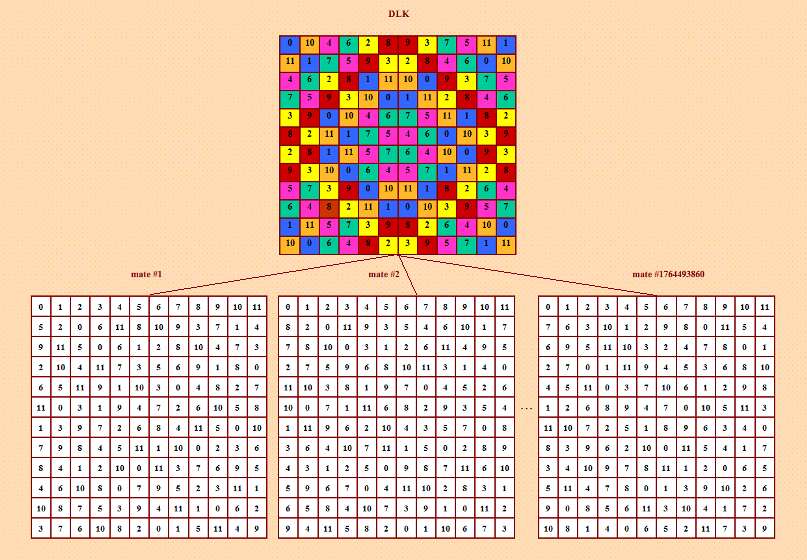 ЗдеÑÑŒ показаны раÑкраÑкой другие 36 блоков. (Вообще-то, Ñ ÑомневаюÑÑŒ, что в Ñтом ДЛК вÑего 72 блока; может быть, Harry White проÑто оÑтановилÑÑ Ð½Ð° 72 блоках Ð´Ð»Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ñ‹ поворота блоков, которую он делал по моей проÑьбе.) Однако чемпион по интеркалÑтвм (блокам) веÑьма Ñкромно выглÑдит по Д-транÑверÑалÑм и по ОДЛК. Он Ñодержит вÑего 4512 Д-транÑверÑалей. ОбÑчитала Ñтот ДЛК на ОДЛК; обÑчиталÑÑ Ð±Ñ‹Ñтро, потому что Д-транÑверÑалей мало. Ðайдено только 5186 ОДЛК. Подумала: что бы такое ещё извлечь из Ñтого ДЛК? ВзÑла его ортогональки и запуÑтила на обÑчёт по ОДЛК. Ð’Ñе они обÑчитываютÑÑ Ð±Ñ‹Ñтро, так как Ñодержат мало Д-транÑверÑалей. Ðе Ñтала обÑчитывать вÑе 5186 ДЛК, обÑчитала 2657 ДЛК. Показываю верхнюю чаÑÑ‚ÑŒ полученного Ñпектра по ОДЛК, до Ð·Ð½Ð°Ñ‡ÐµÐ½Ð¸Ñ 501, дубликаты значений не удалÑла [DLK(6933):218469] [DLK(3804):225402] [DLK(3328):299593] [DLK(2815):6417] [DLK(2733):21754] [DLK(2711):16593] [DLK(2597):197888] [DLK(2225):205321] [DLK(2050):46101] [DLK(2005):10110] [DLK(1799):37531] [DLK(1785):13551] [DLK(1738):187547] [DLK(1714):104024] [DLK(1704):39330] [DLK(1638):149202] [DLK(1638):289939] [DLK(1633):168729] [DLK(1554):111478] [DLK(1531):42794] [DLK(1479):207752] [DLK(1423):91164] [DLK(1394):142829] [DLK(1373):209318] [DLK(1364):51325] [DLK(1364):107221] [DLK(1281):123462] [DLK(1279):119289] [DLK(1273):93408] [DLK(1237):102787] [DLK(1229):129239] [DLK(1225):19304] [DLK(1225):20529] [DLK(1222):193755] [DLK(1192):287348] [DLK(1163):155369] [DLK(1150):152455] [DLK(1140):238817] [DLK(1137):159293] [DLK(1098):12453] [DLK(1082):52689] [DLK(1065):147089] [DLK(1063):235906] [DLK(1059):189782] [DLK(1044):84034] [DLK(1037):230857] [DLK(1026):34883] [DLK(1026):56895] [DLK(1016):217453] [DLK(1016):229206] [DLK(1015):79] [DLK(969):61455] [DLK(966):59534] [DLK(956):127654] [DLK(937):131723] [DLK(931):164081] [DLK(922):307544] [DLK(902):86448] [DLK(888):44325] [DLK(888):45213] [DLK(880):246883] [DLK(879):251675] [DLK(874):176132] [DLK(872):192858] [DLK(866):76902] [DLK(861):232107] [DLK(856):203042] [DLK(853):132660] [DLK(847):264359] [DLK(844):36447] [DLK(839):173547] [DLK(839):195659] [DLK(837):108585] [DLK(830):178107] [DLK(825):232968] [DLK(820):95283] [DLK(818):165630] [DLK(817):76055] [DLK(816):4594] [DLK(814):181786] [DLK(811):1094] [DLK(808):24954] [DLK(805):234463] [DLK(796):170362] [DLK(793):80478] [DLK(786):158507] [DLK(785):153796] [DLK(775):69548] [DLK(771):274419] [DLK(767):114747] [DLK(765):73601] [DLK(746):72739] [DLK(741):273590] [DLK(740):270803] [DLK(735):125806] [DLK(731):277920] [DLK(725):172273] [DLK(724):244714] [DLK(723):81296] [DLK(723):145190] [DLK(721):74366] [DLK(717):63768] [DLK(714):303470] [DLK(710):265704] [DLK(709):72011] [DLK(708):85740] [DLK(705):179987] [DLK(705):183664] [DLK(703):282873] [DLK(702):255744] [DLK(702):306842] [DLK(700):62462] [DLK(700):190921] [DLK(698):78429] [DLK(693):98206] [DLK(682):167426] [DLK(681):70420] [DLK(681):99469] [DLK(680):54092] [DLK(678):60777] [DLK(675):134469] [DLK(672):106267] [DLK(670):233793] [DLK(670):281796] [DLK(669):192164] [DLK(667):126541] [DLK(666):75161] [DLK(666):275548] [DLK(665):100292] [DLK(661):25762] [DLK(653):298257] [DLK(652):87646] [DLK(648):280878] [DLK(647):247763] [DLK(643):259530] [DLK(640):68384] [DLK(639):96144] [DLK(635):230222] [DLK(633):130468] [DLK(631):77768] [DLK(629):182600] [DLK(628):118258] [DLK(624):50574] [DLK(624):276936] [DLK(622):131101] [DLK(621):168108] [DLK(620):288608] [DLK(619):151778] [DLK(617):113866] [DLK(617):161580] [DLK(616):101509] [DLK(614):215508] [DLK(610):181161] [DLK(609):89517] [DLK(607):90413] [DLK(607):286741] [DLK(603):144353] [DLK(603):286138] [DLK(602):200667] [DLK(601):94682] [DLK(601):253881] [DLK(597):258913] [DLK(596):298953] [DLK(595):210819] [DLK(590):165012] [DLK(590):270213] [DLK(589):297179] [DLK(588):212401] [DLK(585):236969] [DLK(578):83015] [DLK(574):204747] [DLK(572):292500] [DLK(571):254917] [DLK(570):262336] [DLK(570):284437] [DLK(569):257349] [DLK(569):267081] [DLK(568):280291] [DLK(567):163514] [DLK(566):260704] [DLK(565):202398] [DLK(557):65335] [DLK(543):110935] [DLK(543):142243] [DLK(537):305848] [DLK(535):289350] [DLK(529):105738] [DLK(529):113337] [DLK(524):148154] [DLK(524):148678] [DLK(522):133637] [DLK(522):261553] [DLK(513):267650] [DLK(507):69024] [DLK(506):50068] [DLK(504):138091] [DLK(503):166923] [DLK(501):115514] . . . . . . Сюда можно добавить ещё значение 5186. Вот такой вариант Ñпектра получен от чемпиона по интеркалÑтам. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese