Выполнила нормализацию и удаление дубликатов, получила 13 пандиагональных ДЛК

 0  1  2  3  4  5  6  7  8  9 10 11 12
 2  3  0  1  7 10 11  9  6 12  8  4  5
 1  5  6 12 11  9  7 10  4  3  0  2  8
 9  7 11  5 10 12  8  1  0  2  4  3  6
11  6  9  8  2  4  0 12  3  1  5 10  7
10 12  3  4  0  8  2  5 11  6  7  1  9
 8  4 10  2  3  1  9  6  7  5 11 12  0
12  0  1  7  5  6  3 11  9 10  2  8  4
 3 11  5  6  1  7 10  4 12  8  9  0  2
 5  2  7 11  9  0 12  8 10  4  3  6  1
 6  9  8 10 12 11  4  0  2  7  1  5  3
 4 10 12  9  8  2  5  3  1  0  6  7 11
 7  8  4  0  6  3  1  2  5 11 12  9 10

 0  1  2  3  4  5  6  7  8  9 10 11 12
 2 12  0  6  9 10  8  5 11  7  3  4  1
 4  5 11 10  8  6  9  3  2 12  1  7  0
 6 10  4  9 11  7  0 12  1  3  2  5  8
 5  8  7  1  3 12 11  2  0  4  9  6 10
11  2  3 12  7  1  4 10  5  6  0  8  9
 3  9  1  2  0  8  5  6  4 10 11 12  7
12  0  6  4  5  2 10  8  9  1  7  3 11
10  4  5  0  6  9  3 11  7  8 12  1  2
 1  6 10  8 12 11  7  9  3  2  5  0  4
 8  7  9 11 10  3 12  1  6  0  4  2  5
 9 11  8  7  1  4  2  0 12  5  6 10  3
 7  3 12  5  2  0  1  4 10 11  8  9  6

 0  1  2  3  4  5  6  7  8  9 10 11 12
 2 12  5  1 10 11  8  9  6  7  0  3  4
 3 10  9  6  8  1  7 11 12  5  4  2  0
 7  6  8 10  9 12  2  0  4 11  3  5  1
 5  9  7 11  3  0  4 12  2  1  8 10  6
11  4 12  0  7  2  3  5  9 10  6  1  8
12  0 11  4  5  6  1 10  3  8  9  7  2
 4  2  3  8  1 10  5  6  7  0 11 12  9
10  5  1  2  6  8  9  4 11 12  7  0  3
 1  3 10  9 12  7 11  8  0  4  2  6  5
 6  8  0  7 11  9 12  2  1  3  5  4 10
 9  7  6 12  0  4 10  3  5  2  1  8 11
 8 11  4  5  2  3  0  1 10  6 12  9  7

 0  1  2  3  4  5  6  7  8  9 10 11 12
 3  6  7  5  2  8  4  0  1 11 12  9 10
 7  5  3  6  0 12  9 11  4 10  1  2  8
 6  8  4 10  9 11  0 12  2  5  3  7  1
11  0  9  8 12 10  1  6  3  7  2  5  4
 9  4 11  1  7  2  3 10  5  6  8 12  0
12 10  5  2  3  1  7  8  9  4  0  6 11
 1  2 12  7  5  6 11  4  0  8  9 10  3
10  3  6  0  8  4  5  9 11 12  7  1  2
 5  9  8  4  6  0 12  2 10  1 11  3  7
 8  7  0  9 11  3 10  1 12  2  5  4  6
 4 11  1 12 10  9  2  3  7  0  6  8  5
 2 12 10 11  1  7  8  5  6  3  4  0  9

 0  1  2  3  4  5  6  7  8  9 10 11 12
 3 12  8  9  6  7  4  5 11  1  2  0 10
 7  4  6 12  5  9 10  3  2  0 11  1  8
 6  8  7 10  0 11  2  9  1  3 12  5  4
 5  9  1 11  2 10  0 12  6  8  4  3  7
10 11  5  0  1  3  7  8  4 12  6  9  2
 9  2  3  4 12  8  1  6  7  5  0 10 11
 1  6 12  8  3  4  5 11  9 10  7  2  0
12  0  4  6  7  2  9 10  5 11  1  8  3
 8  7 10  5  9  6 11  2  0  4  3 12  1
11  5  9  7 10  0 12  1  3  2  8  4  6
 4 10 11  2  8  1  3  0 12  6  9  7  5
 2  3  0  1 11 12  8  4 10  7  5  6  9

 0  1  2  3  4  5  6  7  8  9 10 11 12
 5  3  0  6  2 11 12  9 10  7  8  1  4
 1  4 11 10  7  9  2  8 12  0  6  5  3
 2  8  7  9 11 10  0  3  1  5 12  4  6
 7  6 10  8 12  4  1  5  0  3  2  9 11
 9 12  5  0  1  8  3  4  6 10 11  7  2
 3  0  1 12  5  6  7  2 11  4  9 10  8
10  5  3  4  9  2 11  6  7  8  1 12  0
 4 11  6  2  3  7  9 10  5 12  0  8  1
 6  2  4 11 10  0  8 12  9  1  5  3  7
11  7  9  1  8 12 10  0  3  2  4  6  5
12 10  8  7  0  1  5 11  4  6  3  2  9
 8  9 12  5  6  3  4  1  2 11  7  0 10

 0  1  2  3  4  5  6  7  8  9 10 11 12
 5  6  4  1  7  3 12  0 10 11  8  9  2
 4  2  5 12 11  8 10  3  9  0  1  7  6
 7  3  9  8 10 12 11  1  4  2  6  0  5
12  8  7 11  9  0  5  2  6  1  4  3 10
 3 10  0  6  1  2  9  4  5  7 11 12  8
 9  4  1  2  0  6  7  8  3 12  5 10 11
 1 11  6  4  5 10  3 12  7  8  9  2  0
 2  5 12  7  3  4  8 10 11  6  0  1  9
 8  7  3  5 12 11  1  9  0 10  2  6  4
 6 12  8 10  2  9  0 11  1  4  3  5  7
10  0 11  9  8  1  2  6 12  5  7  4  3
11  9 10  0  6  7  4  5  2  3 12  8  1

 0  1  2  3  4  5  6  7  8  9 10 11 12
 6  3  4  1  2  8 11 12 10  7  0  9  5
 9  2  6  7  0 12 10  8 11  5  4  1  3
 7 10  8 12  6 11  0  9  2  1  3  5  4
 8 12  7 10  9  3  5  1  0  4  2  6 11
10 11  0  4  5  1  9  3  6 12  7  8  2
 1  9  5 11  3  4  2 10  7  8  6 12  0
 5  0  1  2  8  6  7  4 12 10 11  3  9
 3  4 12  6  7  2  8 11  5  0  9 10  1
 2  6  3  8 12 10  1  0  9 11  5  4  7
 4  7 10  9 11  0 12  5  1  3  8  2  6
12  5 11  0 10  9  3  6  4  2  1  7  8
11  8  9  5  1  7  4  2  3  6 12  0 10

 0  1  2  3  4  5  6  7  8  9 10 11 12
 6  7  4  5  2  3  9 12  0 11  8  1 10
 4 10  3  7  8  1  0 11  9 12  6  5  2
 5  8 11  9  0  7 12  1 10  3  2  4  6
12  9  0  8 11 10  4  6  2  1  5  3  7
 3 11 12  1  5  6  2 10  4  7  0  8  9
 1  2 10  6 12  4  5  3 11  8  9  7  0
10  6  1  2  3  9  7  8  5  0 11 12  4
 2  4  5  0  7  8  3  9 12  6  1 10 11
 8  3  7  4  9  0 11  2  1 10 12  6  5
 7  5  8 11 10 12  1  0  6  2  4  9  3
 9  0  6 12  1 11 10  4  7  5  3  2  8
11 12  9 10  6  2  8  5  3  4  7  0  1

 0  1  2  3  4  5  6  7  8  9 10 11 12
11  4  0  9 10  7  8  5  6 12  2  3  1
 9  8  5  7  0  6 10 11  4  3  1 12  2
 5  7  9  8 11  1 12  3 10  2  4  0  6
 8  6 10  2 12  3 11  1  0  7  9  5  4
 3 11 12  6  1  2  4  8  9  5  0  7 10
12 10  3  4  5  0  9  2  7  8  6  1 11
 1  2  7  0  9  4  5  6 12 10 11  8  3
 4  0  1  5  7  8  3 10 11  6 12  2  9
 2  9  8 11  6 10  7 12  3  1  5  4  0
 7 12  6 10  8 11  1  0  2  4  3  9  5
 6  5 11 12  3  9  2  4  1  0  7 10  8
10  3  4  1  2 12  0  9  5 11  8  6  7

 0  1  2  3  4  5  6  7  8  9 10 11 12
11  4  7  8  6  3  9  5  1  2 12  0 10
 9  8  6  4  7  1  0 10 12  5 11  2  3
 2  7  9  5 11 10 12  1  0  3  6  4  8
 5 12  1 10  9  0 11  2  7  4  8  3  6
 1 10  5 12  2  8  3  4 11  6  7  9  0
12  0 11  6  3  4  2  8  9 10  5  1  7
 4  2  3  0  8  6  7 12  5  1  9 10 11
 3 11  4  7  1  9  5  6 10 12  0  8  2
 8  6 10  9  5  7  1  0  3 11  2 12  4
 7  9  8  1 10 12  4 11  2  0  3  6  5
 6  5 12  2  0 11 10  3  4  8  1  7  9
10  3  0 11 12  2  8  9  6  7  4  5  1

 0  1  2  3  4  5  6  7  8  9 10 11 12
11  7  8  5  6  3  4 10  0  1 12  9  2
 3  5 11  4  8  9  2  1 12 10  0  7  6
 7  6  9 12 10  1  8  0  2 11  4  3  5
 8  0 10  1  9 12 11  5  7  3  2  6  4
10  4 12  0  2  6  7  3 11  5  8  1  9
 1  2  3 11  7  0  5  6  4 12  9 10  8
 5 11  7  2  3  4 10  8  9  6  1 12  0
12  3  5  6  1  8  9  4 10  0  7  2 11
 6  9  4  8  5 10  1 12  3  2 11  0  7
 4  8  6  9 12 11  0  2  1  7  3  5 10
 9 10  1  7  0  2 12 11  5  8  6  4  3
 2 12  0 10 11  7  3  9  6  4  5  8  1

 0  1  2  3  4  5  6  7  8  9 10 11 12
11 12  5  8  9  7  4 10  6  2  3  0  1
 4 10  9  7  5  8  2  1 11  0  6 12  3
 9  3  8 10  6 12 11  0  2  1  4  7  5
 7  6  0  2 11 10  1 12  3  8  5  9  4
 1  2 11  6  0  3  9  4  5 12  7  8 10
 8  0  1 12  7  4  5  3  9 10 11  6  2
12  5  3  4  1  9  7  8  0  6  2 10 11
 3  4 12  5  8  2 10  6  7 11  0  1  9
 5  9  7 11 10  6  8  2  1  4 12  3  0
 6  8 10  9  2 11  0  5 12  3  1  4  7
10  7  6  0  3  1 12 11  4  5  9  2  8
 2 11  4  1 12  0  3  9 10  7  8  5  6

Проверяю эти ДЛК утилитой Harry White

Order? 13

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
        13 diagonal Latin
        13 pandiagonal
         1 center symmetric
        13 nfr

Итак, это нормализованные полуциклические пандиагональные ДЛК в указанном выше смысле?
Будем считать, что да. Их получилось 13 у меня.
Всего не хватает мне 208 полуциклических пандиагональных ДЛК.
208 делится на 13. Значит, надо найти ещё 15 подобных наборов по 13 квадратов.
Как их найти?

Кстати, исходный квадрат (из статьи) в полученном наборе из 13 нормализованных полуциклических пандиагональных квадратов, конечно, есть

 0  1  2  3  4  5  6  7  8  9 10 11 12
 5  3  0  6  2 11 12  9 10  7  8  1  4
 1  4 11 10  7  9  2  8 12  0  6  5  3
 2  8  7  9 11 10  0  3  1  5 12  4  6
 7  6 10  8 12  4  1  5  0  3  2  9 11
 9 12  5  0  1  8  3  4  6 10 11  7  2
 3  0  1 12  5  6  7  2 11  4  9 10  8
10  5  3  4  9  2 11  6  7  8  1 12  0
 4 11  6  2  3  7  9 10  5 12  0  8  1
 6  2  4 11 10  0  8 12  9  1  5  3  7
11  7  9  1  8 12 10  0  3  2  4  6  5
12 10  8  7  0  1  5 11  4  6  3  2  9
 8  9 12  5  6  3  4  1  2 11  7  0 10

Возьмите исходный квадрат и нормализуйте его, получите показанный квадрат.
В этом квадрате, как и во всех квадратах полученного набора из 13 квадратов, вообще никакой цикличности не видно - ни в каких смыслах. Можно подумать, что он не циклический пандиагональный.

В общем, странная такая цикличность придумана - в направлении (1,4).
Главное: непонятно, какие ещё подобные направления могут быть.
И для направления (1,4) приведённый квадрат, возможно, не единственный.
Если устроить полный перебор, может быть, ещё подобные пандиагональные ДЛК найдутся.

Ещё раз показываю исходный квадрат в том виде, как он приведён в статье

0 B 1 7 5 9 3 A 4 8 6 C 2 
9 7 0 3 1 C 2 8 6 A 4 B 5 
B 5 C 6 A 8 1 4 2 0 3 9 7 
1 4 A 8 C 6 0 7 B 9 2 5 3 
A 3 6 4 2 5 B 9 0 7 1 8 C 
8 2 9 0 B 4 7 5 3 6 C A 1 
7 0 B 2 9 3 A 1 C 5 8 6 4 
6 9 7 5 8 1 C 3 A 4 B 2 0 
5 C 3 1 7 A 8 6 9 2 0 4 B 
3 1 5 C 6 0 4 2 8 B 9 7 A 
C A 8 B 4 2 6 0 7 1 5 3 9 
2 6 4 A 0 B 9 C 5 3 7 1 8 
4 8 2 9 3 7 5 B 1 C A 0 6

Господа, сколько времени понадобится вам, чтобы у видеть в этом квадрате цикличность в направлении (1,4)?
Я вчера смотрела на этот квадрат непрерывно в течение 10 минут. Наконец, дошло :)

У меня отличная новость!
Вчера отправила Harry White паттерн для идеальных ДЛК 19-го порядка и попросила его быстренько найти все квадраты по этому паттерну.
Сейчас получила результат. Быстро!
Harry выполнил программу для порядков 17 и 19

.. writing squares to file 17UDLS.txt
16
32
48
64
80
96
112
128
144
160
176
number of DLS 180

elapsed time 0:00:12
---------------------------------------------------
.. writing squares to file 19UDLS.txt
16
32
48
64
80
96
112
128
144
160
176
192
208
224
240
256
272
288
304
320
336
352
368
384
400
416
432
448
464
480
496
512
528
544
number of DLS 544

Для порядка 17 я сама писала программу и тоже нашла 180 ДЛК по паттерну.
Для порядка 19 Harry нашёл 544 идеальных ДЛК по соответствующему паттерну.
Он также выполнил программу для порядков 23 и 25.

Спасибо, Harry!
Сейчас я займусь этими идеальными квадратиками, покручу их на торе.

Покажу три первых идеальных ДЛК 19-го порядка из присланных Harry

11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10
13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12
16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0
 9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8
14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13
12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
 7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6
 5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4
10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9
18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2
 6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5
 8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7

11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10
13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12
17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2
18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3
 9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8
 5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13
10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9
15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
 7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0
16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1
 6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5
 8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7

11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10
13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12
17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0
12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3
 9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8
14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
 5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4
10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9
15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
 7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6
18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1
 6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5
 8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7

Итак, жутко интересно, что дадут эти квадратики, покрутившись на торе.

А свойства у этих квадратиков обалденные!

Order? 19

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
       544 diagonal Latin
       544 associative
       544 pandiagonal
        16 cyclic 4-way
       528 semi-cyclic
       544 ultramagic
         1 orthogonal pair
        16 self-orthogonal
       544 symmetric parity

16 циклических пандиагональных (комплект!), остальные 528 полуциклические пандиагональные с цикличностью в строках.

Квадратики на торе благополучно покрутились, ни один не свалился с тора :)
Вот что получилось после нормализации всех полученных ДЛК и удаления дубликатов

Order? 19

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt

Counts
------
     10048 diagonal Latin
     10048 pandiagonal
        16 cyclic 4-way
     10032 semi-cyclic
       544 center symmetric
     10048 nfr
         1 orthogonal pair
        16 self-orthogonal

16 циклических пандиагональных и 10032 полуциклических пандиагональных ДЛК с цикличностью в строках.
Отличная порция! Хотя, конечно, это не все полуциклические пандиагональные ДЛК 19-го порядка.
Я эту порцию сейчас ещё размножу и получу 10032*4=40128 нормализованных полуциклических пандиагональных ДЛК с цикличностью в строках, в столбцах и в диагоналях обоих направлений.
Уже солидная порция по сравнению с той, что я получила раньше.
Итак, моя схема преобразований
1) поворот на 90 градусов первой порции ДЛК;
2) преобразование "строки диагонали" для первой порции ДЛК (с цикличностью в строках);
3) преобразование "строки диагонали" для второй порции ДЛК (с цикличностью в столбцах).

Выбросила из набора 16 циклических пандиагональных ДЛК.
Получила отличный набор из 10032 нормализованных полуциклических пандиагональных ДЛК 19-го порядка с цикличностью в строках

Order? 19

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt

Counts
------
     10032 diagonal Latin
     10032 pandiagonal
     10032 semi-cyclic
       528 center symmetric
     10032 nfr
         1 orthogonal pair

Покажу первые два ДЛК из этого набора

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3
 6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5
 8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7
12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11
14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13
16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
 7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2
10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9
17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
 5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0
 9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8
11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10
13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12
15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3
 6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5
 8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7
13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12
11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10
17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0
 5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4
 9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8
18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2
 7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6
12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11
10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9
16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13

Всё чудесно! Алгоритм работает.
Дальше - размножение этой порции ДЛК по показанной выше схеме.

Поворот на 90 градусов выполнила, полученные ДЛК нормализовала; получила 10032 нормализованных полуциклических пандиагональных ДЛК 19-го порядка с цикличностью в столбцах.
Покажу два ДЛК из этой порции

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
11 12 13  7 17 15 10  2 16 14 18  6  0  1  3  9  5  8  4
 6  0  1  2  8  9 18 13  5  3  4 10 11 12  7 14 15 16 17
10 11 12 13 16 14  4  1 15  7 17 18  6  0  2  3  9  5  8
18  6  0  1  5  3 17 12  9  2  8  4 10 11 13  7 14 15 16
 4 10 11 12 15  7  8  0 14 13 16 17 18  6  1  2  3  9  5
17 18  6  0  9  2 16 11  3  1  5  8  4 10 12 13  7 14 15
 8  4 10 11 14 13  5  6  7 12 15 16 17 18  0  1  2  3  9
16 17 18  6  3  1 15 10  2  0  9  5  8  4 11 12 13  7 14
 5  8  4 10  7 12  9 18 13 11 14 15 16 17  6  0  1  2  3
15 16 17 18  2  0 14  4  1  6  3  9  5  8 10 11 12 13  7
 9  5  8  4 13 11  3 17 12 10  7 14 15 16 18  6  0  1  2
14 15 16 17  1  6  7  8  0 18  2  3  9  5  4 10 11 12 13
 3  9  5  8 12 10  2 16 11  4 13  7 14 15 17 18  6  0  1
 7 14 15 16  0 18 13  5  6 17  1  2  3  9  8  4 10 11 12
 2  3  9  5 11  4  1 15 10  8 12 13  7 14 16 17 18  6  0
13  7 14 15  6 17 12  9 18 16  0  1  2  3  5  8  4 10 11
 1  2  3  9 10  8  0 14  4  5 11 12 13  7 15 16 17 18  6
12 13  7 14 18 16 11  3 17 15  6  0  1  2  9  5  8  4 10

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
10 11 12 13 14 16 18  2 15 17  1  6  3  0  7  4  8  5  9
 1  6  3  0  7  8  9 12  4  5 11 18 13 10  2 14 15 16 17
11 18 13 10  2 15 17  3 14 16  6  9  0  1 12  7  4  8  5
 6  9  0  1 12  4  5 13  7  8 18 17 10 11  3  2 14 15 16
18 17 10 11  3 14 16  0  2 15  9  5  1  6 13 12  7  4  8
 9  5  1  6 13  7  8 10 12  4 17 16 11 18  0  3  2 14 15
17 16 11 18  0  2 15  1  3 14  5  8  6  9 10 13 12  7  4
 5  8  6  9 10 12  4 11 13  7 16 15 18 17  1  0  3  2 14
16 15 18 17  1  3 14  6  0  2  8  4  9  5 11 10 13 12  7
 8  4  9  5 11 13  7 18 10 12 15 14 17 16  6  1  0  3  2
15 14 17 16  6  0  2  9  1  3  4  7  5  8 18 11 10 13 12
 4  7  5  8 18 10 12 17 11 13 14  2 16 15  9  6  1  0  3
14  2 16 15  9  1  3  5  6  0  7 12  8  4 17 18 11 10 13
 7 12  8  4 17 11 13 16 18 10  2  3 15 14  5  9  6  1  0
 2  3 15 14  5  6  0  8  9  1 12 13  4  7 16 17 18 11 10
12 13  4  7 16 18 10 15 17 11  3  0 14  2  8  5  9  6  1
 3  0 14  2  8  9  1  4  5  6 13 10  7 12 15 16 17 18 11
13 10  7 12 15 17 11 14 16 18  0  1  2  3  4  8  5  9  6

Дальше применю преобразование "строки-диагонали" к обеим порциям.
Матрица этого преобразования показана в сообщении
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=132&postid=1813

К первой порции преобразоание "строки-диагонали" применила, нормализовала полученные ДЛК и получила 10032 нормализованных полуциклических пандиагональных ДЛК 19-го порядка с цикличностью в диагоналях параллельных главной.

Покажу первые два ДЛК из этой порции

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
 8 17 16  1 12  2  3  4  5  6  7  9 14 18 11 10 13  0 15
13  6 15  0 16 18  1 12  2  3  4  5  7 10  8 14  9 11 17
15 11  4 13 17  0  8 16 18  1 12  2  3  5  9  6 10  7 14
10 13 14  2 11 15 17  6  0  8 16 18  1 12  3  7  4  9  5
 3  9 11 10  1 14 13 15  4 17  6  0  8 16 18 12  5  2  7
 5 12  7 14  9 16 10 11 13  2 15  4 17  6  0  8 18  3  1
16  3 18  5 10  7  0  9 14 11  1 13  2 15  4 17  6  8 12
18  0 12  8  3  9  5 17  7 10 14 16 11  1 13  2 15  4  6
 4  8 17 18  6 12  7  3 15  5  9 10  0 14 16 11  1 13  2
 1  2  6 15  8  4 18  5 12 13  3  7  9 17 10  0 14 16 11
14 16  1  4 13  6  2  8  3 18 11 12  5  7 15  9 17 10  0
17 10  0 16  2 11  4  1  6 12  8 14 18  3  5 13  7 15  9
 7 15  9 17  0  1 14  2 16  4 18  6 10  8 12  3 11  5 13
11  5 13  7 15 17 16 10  1  0  2  8  4  9  6 18 12 14  3
12 14  3 11  5 13 15  0  9 16 17  1  6  2  7  4  8 18 10
 9 18 10 12 14  3 11 13 17  7  0 15 16  4  1  5  2  6  8
 6  7  8  9 18 10 12 14 11 15  5 17 13  0  2 16  3  1  4
 2  4  5  6  7  8  9 18 10 14 13  3 15 11 17  1  0 12 16

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
 2 17 10  8  9  0  1 18 14 16 12  6  7  5 11  3 13  4 15
13  8 15  6 16 12 17 10  2  3  4  5 18 14  1  7  9 11  0
17 11 16 13 18  4  5 15  6  8  9  0  1  2  3 10 14 12  7
14 15  7  4 11  2  0  1 13 18 16 12 17 10  8  9  6  3  5
 1  3 13 14  0  7  8 17 10 11  2  4  5 15  6 16 12 18  9
12 10  9 11  3 17 14 16 15  6  7  8  0  1 13 18  4  5  2
 8  5  6 12  7  9 15  3  4 13 18 14 16 17 10 11  2  0  1
10 16  1 18  5 14 12 13  9  0 11  2  3  4 15  6  7  8 17
15  6  4 10  2  1  3  5 11 12 17  7  8  9  0 13 18 14 16
 4 13 18  0  6  8 10  9  1  7  5 15 14 16 12 17 11  2  3
 9  0 11  2 17 18 16  6 12 10 14  1 13  3  4  5 15  7  8
16 12 17  7  8 15  2  4 18  5  6  3 10 11  9  0  1 13 14
 3  4  5 15 14 16 13  8  0  2  1 18  9  6  7 12 17 10 11
 7  9  0  1 13  3  4 11 16 17  8 10  2 12 18 14  5 15  6
18 14 12 17 10 11  9  0  7  4 15 16  6  8  5  2  3  1 13
11  2  3  5 15  6  7 12 17 14  0 13  4 18 16  1  8  9 10
 6  7  8  9  1 13 18 14  5 15  3 17 11  0  2  4 10 16 12
 5 18 14 16 12 10 11  2  3  1 13  9 15  7 17  8  0  6  4

Проверка этой порции программой GetCyclic

Order? 19

Enter the name of the squares file: inp
Count only? y
Get cyclic for, (1 rows, 2 columns, 3 \diagonals, 4 /diagonals)? 3
Get squares with cyclic:  \diagonals
Exact match? y
Number of squares: 10032 number matched 10032

Отлично! Все 10032 квадратика с цикличностью в диагоналях параллельных главной.

Ну, и ещё ко второй порции применю преобразование "строки-диагонали".

Готово!
Показываю два ДЛК из этой порции - нормализованные полуциклические пандиагональные с цикличностью в диагоналях параллельных побочной

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
 4  9  6 11 14 13 10 18 16 17 12  2  1 15  3  0  5  7  8
16 13 12 15  1 17  7  0  5  2  9  4  3  6  8 14 10 18 11
 1  2  3  4  5 10  8 14  9 16 11  6 13 18 15 17  7 12  0
 9  6 11 14 17 18 15 16  0 12 13  1  7  3  5 10  2  8  4
13 12 15  5  7  3  0  8  2  1  4 10  6 14 17  9 18 11 16
 2  3 14 10  6  8 18  9  4 11 17 13 15  5 16  7 12  0  1
 6 15 17 13 18  7 16 11 12  5  1  3 14  0 10  2  8  4  9
 3  5  1  7 10  0 12  2 14  4  6 15  8 17  9 18 11 16 13
14  4 10 17  8  2  9 15 11 13  3 18  5 16  7 12  0  1  6
11 17  5 18  9 16  3 12  1  6  7 14  0 10  2  8  4 13 15
 5 14  7 16  0  6  2  4 13 10 15  8 17  9 18 11  1  3 12
15 10  0  8 13  9 11  1 17  3 18  5 16  7 12  4  6  2 14
17  8 18  1 16 12  4  5  6  7 14  0 10  2 11 13  9 15  3
18  7  4  0  2 11 14 13 10 15  8 17  9 12  1 16  3  6  5
10 11  8  9 12 15  1 17  3 18  5 16  2  4  0  6 13 14  7
12 18 16  2  3  4  5  6  7 14  0  9 11  8 13  1 15 10 17
 7  0  9  6 11 14 13 10 15  8 16 12 18  1  4  3 17  5  2
 8 16 13 12 15  1 17  3 18  0  2  7  4 11  6  5 14  9 10

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
 3 16 13  6  7 11 17 15  0  5 18  9  4  8  1 10 14 12  2
10  4 11 17 18 14  1  2  7 12  0  6 15  3  5  8  9 16 13
 6 18 14 12  8  3 16 17  9  2 11  1 13  7 15  0 10  4  5
12  8  9 15 13 10 14  0 16 18  3  4 17  1  2  5  6  7 11
15  0  1  4  5  8  2 10 12 13  6 14  3 16  7 11 17 18  9
 2  3  6  7 15 16  5  9  4 11  8 13 10 17 18 14 12  0  1
13 11 17  1 10  7  0  6 18 15  4  5 14 12  8  9  2  3 16
18 14  3  5 17  2 11 12  1  6  7  8  9 15  0 16 13 10  4
 8 13  7 14 16 18  9  3 11 17 15  0  1  2 10  4  5  6 12
 4 17  8 10 12  0 13 18 14  1  2  3 16  5  6  7 11  9 15
14 15  5  9  2  4 12  8  3 16 13 10  7 11 17 18  0  1  6
 1  7  0 16  6  9 15 13 10  4  5 17 18 14 12  2  3 11  8
17  2 10 11  0  1  4  5  6  7 14 12  8  9 16 13 18 15  3
16  5 18  2  3  6  7 11 17  8  9 15  0 10  4 12  1 13 14
 7 12 16 13 11 17 18 14 15  0  1  2  5  6  9  3  4  8 10
 9 10  4 18 14 12  8  1  2  3 16  7 11  0 13  6 15  5 17
 5  6 12  8  9 15  3 16 13 10 17 18  2  4 11  1  7 14  0
11  9 15  0  1 13 10  4  5 14 12 16  6 18  3 17  8  2  7

Проверка этой порции программой Get Cyclic

Order? 19

Enter the name of the squares file: inp
Count only? y
Get cyclic for, (1 rows, 2 columns, 3 \diagonals, 4 /diagonals)? 4
Get squares with cyclic:  /diagonals
Exact match? y
Number of squares: 10032 number matched 10032

Всё превосходно!

Итак, я получила 10032*4=40128 нормализованных полуциклических пандиагональных ДЛК 19-го порядка с цикличностью в строках, в столбцах и в диагоналях обоих направлений.
Конечно, это не все такие пандиагональные ДЛК.
К тому же, у меня нет полуциклических пандиагональных ДЛК со странной, на мой взгляд, цикличностью в направлении (1,4).

А сейчас посмотрим, как циклические и полуциклические пандиагональные ДЛК 19-го порядка вступают между собой в отношение ортогональности.
Ну, циклические-то хорошо вступают: они все друг другу ортогональны.
Так что, в данном наборе есть клика размера 16.

Итак, к порции 40128 полуциклических ДЛК добавляю 16 циклических ДЛК, получаю порцию 40144 ДЛК.

Проверяю...
Готово!

Order? 19

Enter the name of the squares file: a
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file a-orthCounts.txt
..output file a-orthNos.txt
squares 40144 total orthogonal pairs 33408
Maximum pairs for square 1: 471
There are 7 other squares with this maximum number of pairs.
..output file a-1orths.txt
Pairs for square 1: 471

elapsed time 0:23:31

33408 ортогонгальных пар!
Максимальная группа ОДЛК от квдарата 1 (и ещё от 7 квадратов): 471 ОДЛК!
Трам-там-там!!!
Оценка для порядка 19 улучшена
a(19) >= 471.

Первые 16 ДЛК в наборе циклические пандиагональные.
Смотрим счётчик ортогональных пар (фрагмент)

                orthogonal
      square       pairs
      ------    ----------

           1          471
           2          471
           3           15
           4           15
           5          471
           6           15
           7           15
           8          471
           9          471
          10           15

          11           15
          12          471
          13           15
          14           15
          15          471
          16          471
          17            1
          18            1
          19            1
          20            1
. . . . . . . . 
         231            1
         232            2
         233            1
         234            9
         235            1
         236            2
         237            2
         238            1
         239            2
         240            9
. . . . . 

Очень хорошо вступают в отношение ортогональности циклические пандиагональные ДЛК (они самые первые в таблице), а среди полуциклических уже двушки, девятки, может, дальше ещё что-то есть.

Показываю основной ДЛК 471-ки, он нам хорошо известен - циклический пандиагональный из полной системы MOLS

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3
 6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5
 8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7
10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9
12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11
14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13
16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2
 5  6  7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4
 7  8  9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6
 9 10 11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8
11 12 13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10
13 14 15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12
15 16 17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
17 18  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16

И ещё 7 циклических пандиагональных ДЛК 19-го порядка тоже имеют 471 ОДЛК.

К тому же, показанный ДЛК рекордный по количеству Д-трансверсалей на данный момент.
Цитата из сообщения
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=130&postid=1758

О первом топовом ДЛК 19-го порядка дублирую сообщение
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=122&postid=1412

n=19
11254190082 Д-трансверсалей
ДЛК из полной системы MOLS

Вычисление количества Д-трансверсалей программой Tomas Brada

C:\Users\Дом\Downloads\libr>ortogonb.exe -c LNPBNdjGWMGj8q6LJcFJQDE9d3bfxZxELHin
jkmjZp9FAqyy8P8Byyzks9rAa4GSffr4GSWyqqvwagd8aKGotS6KZZhYQ1KhesT4XnarJWF83MvkwohS
EvKg3  1>out.txt
init_trans(19) used 1181 nodes
dance_mt: using 2 threads for 19 rows in column 1
l(1) 19 / 19

Помню, что затрачено на вычисления 4,5 часа.
В программе Tomas Brada используется многопоточный режим. Ну, у меня всего-то 2 потока.

Результат

num_dtrans: 11254190082

Осталось иллюстрацию показать. Сейчас найду её у себя в компьютере.

ДЛК этот я построила вручную методом циклического сдвига.
Он является пандиагональным циклическим ДЛК.

Вот он какой красивый



Раскраской показана пандиагональность квадрата.

Ну как, господа, вы разглядели цикличность в этом пандиагональном ДЛК 13-го порядка?

   0 11  1  7  5  9  3 10  4  8  6 12  2
   9  7  0  3  1 12  2  8  6 10  4 11  5
  11  5 12  6 10  8  1  4  2  0  3  9  7
   1  4 10  8 12  6  0  7 11  9  2  5  3
  10  3  6  4  2  5 11  9  0  7  1  8 12
   8  2  9  0 11  4  7  5  3  6 12 10  1
   7  0 11  2  9  3 10  1 12  5  8  6  4
   6  9  7  5  8  1 12  3 10  4 11  2  0
   5 12  3  1  7 10  8  6  9  2  0  4 11
   3  1  5 12  6  0  4  2  8 11  9  7 10
  12 10  8 11  4  2  6  0  7  1  5  3  9
   2  6  4 10  0 11  9 12  5  3  7  1  8
   4  8  2  9  3  7  5 11  1 12 10  0  6

Сейчас покажу иллюстрацию и расскажу про эту цикличность в направлении (1,4).

Иллю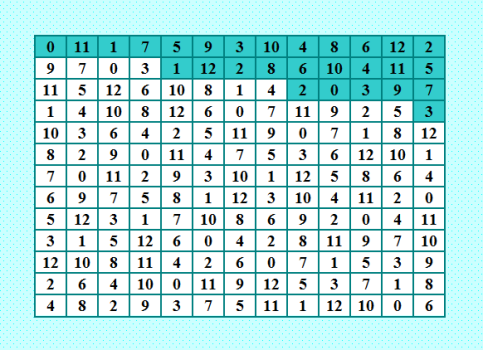страция



Раскраской показана цикличность в четырёх первых строках (сверху).
Числа в каждой следующей строке сдвигаются относительно предыдущей строки на 4 ячейки вправо. При этом все числа увеличиваются на 1 (по модулю 13).
Вот и вся цикличность.

Тэк-с, на торе я этот квадратик прокатила; это дало мне 13 полуциклических пандиагональных ДЛК в направлении (1,4).
Ну, я так думаю :)
Если неправильно думаю, эксперты поправят.
Что бы такое ещё с этим квадратиком сделать?
Преобразование "строки-диагонали" тут ничего не даст.
Есть ещё одна идейка, надо опробовать.

А у вас есть идеи, господа?

Выложила на Яндекс.Диск 40128 нормализованных полуциклических пандиагональных ДЛК 19-го порядка
https://disk.yandex.ru/d/fa7EgybCtiH2xA
7,1 МБ, текстовый файл сжат.

Подчеркну: это не все полуциклические пандиагональные ДЛК 19-го порядка.

А сейчас посмотрю порцию идеальных ДЛК 23-го порядка специального вида, которые прислал мне Harry White.
Этими ДЛК я ещё не занималась.
Известны 20 циклических пандиагональных ДЛК из полной системы MOLS данного порядка.

Полная система MOLS 23-го порядка показана в сообщении
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117&postid=1208

7456 идеальных ДЛК 23-го порядка по паттерну построила программа Harry.
Проверила их утилитой GetType1

Order? 23

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt

Counts
------
      7456 diagonal Latin
      7456 associative
      7456 pandiagonal
        20 cyclic 4-way
      7436 semi-cyclic
      7456 ultramagic
         1 orthogonal pair
        20 self-orthogonal
      7456 symmetric parity

Великолепные квадратики!
20 циклических ДЛК и 7436 получциклических с цикличностью в строках.

Теперь надо покрутить эти квадратики на торе.

Ой, бублик тор надо очень большой для этой порции ДЛК :)

Пока покрутила 1000 ДЛК. Получено 529000 пандиагональных ДЛК. Хорошо, что нормализация даёт много дубликатов, в результате осталось 22934 нормализованных пандиагональных ДЛК.
Утилита GetType1 сообщает об этих ДЛК

Order? 23

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt

Counts
------
     22934 diagonal Latin
     22934 pandiagonal
         3 cyclic 4-way
     22931 semi-cyclic
      1000 center symmetric
     22934 nfr
         3 self-orthogonal

Пока всё замечательно.
Завтра продолжу крутить квадратики на торе.

Покажу один нормализованный полуциклический пандиагональный ДЛК 23-го порядка с цикличностью в строках из полученной порции

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22  0  1
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22  0  1  2  3
 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22  0
 8  9 10 11 12 13 14 15 16 17 18 19 20 21 22  0  1  2  3  4  5  6  7
11 12 13 14 15 16 17 18 19 20 21 22  0  1  2  3  4  5  6  7  8  9 10
18 19 20 21 22  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
15 16 17 18 19 20 21 22  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14
17 18 19 20 21 22  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
19 20 21 22  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18
 9 10 11 12 13 14 15 16 17 18 19 20 21 22  0  1  2  3  4  5  6  7  8
 6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22  0  1  2  3  4  5
 3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22  0  1  2
20 21 22  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22  0  1  2  3  4  5  6
 5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22  0  1  2  3  4
21 22  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
14 15 16 17 18 19 20 21 22  0  1  2  3  4  5  6  7  8  9 10 11 12 13
12 13 14 15 16 17 18 19 20 21 22  0  1  2  3  4  5  6  7  8  9 10 11
22  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21
16 17 18 19 20 21 22  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
13 14 15 16 17 18 19 20 21 22  0  1  2  3  4  5  6  7  8  9 10 11 12
10 11 12 13 14 15 16 17 18 19 20 21 22  0  1  2  3  4  5  6  7  8  9

Уф! Замучилась черепашка с этими большими квадратами - катать их на торе :)
Итак, порция из 7456 идеальных ДЛК 23-го порядка крутилась на торе.
После нормализации и удаления дубликатов получилось 171048 пандиагональных ДЛК.
Проверяю утилитой Harry White свойства этих пандиагональных ДЛК

Order? 23

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
    171048 diagonal Latin
    171048 pandiagonal
        20 cyclic 4-way
    171028 semi-cyclic
      7456 center symmetric
    171048 nfr
         1 orthogonal pair
        20 self-orthogonal

Отлично! 20 циклических и 171028 получциклических пандиагональных ДЛК.
Сейчас удалю циклические и получу порцию из 171028 нормализованных полуциклических пандиагональных ДЛК 23-го порядка с цикличностью в строках.

Ну, а дальше размножение по моей схеме, которое даст 4*171028=684112 нормализованных полуциклических пандиагональных ДЛК 23-го порядка с цикличностью в строках, в столбцах и в диагоналях обоих направлений (в каждой порции из 171028 ДЛК цикличность в одном из перечисленных направлений).

На ортогональные пары предварительно проверю полученную порцию из 171048 пандиагональных ДЛК, она содержит и циклические и полуциклические пандиагональные ДЛК.
После размножения порция будет очень большая и проверить её на ортогональные пары будет сложно (по времени).

Запустила проверку на ортогональные пары.
Жду...

Программа всё работает.
Справится ли? Квадраты большие и порция большая.

Кажется, программа GerOrthogonal не справляется с этим набором пандиагональных ДЛК 23-го порядка

Order? 23

Enter the name of the squares file: perenos_part1
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file perenos_part1-orthCounts.txt
..output file perenos_part1-orthNos.txt
    .. increasing LS store to     100,000
    .. increasing LS store to     200,000
squares 171048

Ну, пусть ещё немного поработает.

Пока программа проверки на ортогональные пары работает, удалила из порции циклические ДЛК и получила порцию из 171028 нормализованных полуциклических пандиагональных ДЛК 23-го порядка с цикличностью в строках.
Проверила программой GetType1

Order? 23

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt

Counts
------
    171028 diagonal Latin
    171028 pandiagonal
    171028 semi-cyclic
      7436 center symmetric
    171028 nfr
         1 orthogonal pair

Всё отлично.

Сделать поворот этой порции ДЛК на 90 градусов я могу, а вот применить преобразование "строки-диагонали" пока не могу, потому что у меня нет матрицы этого преобразования для порядка 23.
Не думала, что дойду до этого порядка и заказала форумчанину на форуме Math Help Planet сделать матрицы только для порядков 17 и 19.
А сочинять эту матрицу вручную очень долго.

Поворот на 90 градусов выполнила; получила 171028 нормализованных полуциклических пандиагональных ДЛК 23-го порядка с цикличностью в столбцах.
Показываю два ДЛК

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
 2  3  4  5  6  7 10 16 20 19 22 21 15  9  0 18 12 13 14  8  1 17 11
 4  5  6  7 10 16 22 12  1  8 11 17 18 19  2 14 15  9  0 20  3 13 21
 6  7 10 16 22 12 11 15  3 20 21 13 14  8  4  0 18 19  2  1  5  9 17
10 16 22 12 11 15 21 18  5  1 17  9  0 20  6  2 14  8  4  3  7 19 13
22 12 11 15 21 18 17 14  7  3 13 19  2  1 10  4  0 20  6  5 16  8  9
11 15 21 18 17 14 13  0 16  5  9  8  4  3 22  6  2  1 10  7 12 20 19
21 18 17 14 13  0  9  2 12  7 19 20  6  5 11 10  4  3 22 16 15  1  8
17 14 13  0  9  2 19  4 15 16  8  1 10  7 21 22  6  5 11 12 18  3 20
13  0  9  2 19  4  8  6 18 12 20  3 22 16 17 11 10  7 21 15 14  5  1
 9  2 19  4  8  6 20 10 14 15  1  5 11 12 13 21 22 16 17 18  0  7  3
19  4  8  6 20 10  1 22  0 18  3  7 21 15  9 17 11 12 13 14  2 16  5
 8  6 20 10  1 22  3 11  2 14  5 16 17 18 19 13 21 15  9  0  4 12  7
20 10  1 22  3 11  5 21  4  0  7 12 13 14  8  9 17 18 19  2  6 15 16
 1 22  3 11  5 21  7 17  6  2 16 15  9  0 20 19 13 14  8  4 10 18 12
 3 11  5 21  7 17 16 13 10  4 12 18 19  2  1  8  9  0 20  6 22 14 15
 5 21  7 17 16 13 12  9 22  6 15 14  8  4  3 20 19  2  1 10 11  0 18
 7 17 16 13 12  9 15 19 11 10 18  0 20  6  5  1  8  4  3 22 21  2 14
16 13 12  9 15 19 18  8 21 22 14  2  1 10  7  3 20  6  5 11 17  4  0
12  9 15 19 18  8 14 20 17 11  0  4  3 22 16  5  1 10  7 21 13  6  2
15 19 18  8 14 20  0  1 13 21  2  6  5 11 12  7  3 22 16 17  9 10  4
18  8 14 20  0  1  2  3  9 17  4 10  7 21 15 16  5 11 12 13 19 22  6
14 20  0  1  2  3  4  5 19 13  6 22 16 17 18 12  7 21 15  9  8 11 10

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
 2  3  4  5  6  9 15 19 18 21 20 14  8 22 17 11 12 13  7  0 16 10  1
 4  5  6  9 15 21 11  0  7 10 16 17 18  1 13 14  8 22 19  2 12 20  3
 6  9 15 21 11 10 14  2 19 20 12 13  7  3 22 17 18  1  0  4  8 16  5
15 21 11 10 14 20 17  4  0 16  8 22 19  5  1 13  7  3  2  6 18 12  9
11 10 14 20 17 16 13  6  2 12 18  1  0  9  3 22 19  5  4 15  7  8 21
14 20 17 16 13 12 22 15  4  8  7  3  2 21  5  1  0  9  6 11 19 18 10
17 16 13 12 22  8  1 11  6 18 19  5  4 10  9  3  2 21 15 14  0  7 20
13 12 22  8  1 18  3 14 15  7  0  9  6 20 21  5  4 10 11 17  2 19 16
22  8  1 18  3  7  5 17 11 19  2 21 15 16 10  9  6 20 14 13  4  0 12
 1 18  3  7  5 19  9 13 14  0  4 10 11 12 20 21 15 16 17 22  6  2  8
 3  7  5 19  9  0 21 22 17  2  6 20 14  8 16 10 11 12 13  1 15  4 18
 5 19  9  0 21  2 10  1 13  4 15 16 17 18 12 20 14  8 22  3 11  6  7
 9  0 21  2 10  4 20  3 22  6 11 12 13  7  8 16 17 18  1  5 14 15 19
21  2 10  4 20  6 16  5  1 15 14  8 22 19 18 12 13  7  3  9 17 11  0
10  4 20  6 16 15 12  9  3 11 17 18  1  0  7  8 22 19  5 21 13 14  2
20  6 16 15 12 11  8 21  5 14 13  7  3  2 19 18  1  0  9 10 22 17  4
16 15 12 11  8 14 18 10  9 17 22 19  5  4  0  7  3  2 21 20  1 13  6
12 11  8 14 18 17  7 20 21 13  1  0  9  6  2 19  5  4 10 16  3 22 15
 8 14 18 17  7 13 19 16 10 22  3  2 21 15  4  0  9  6 20 12  5  1 11
18 17  7 13 19 22  0 12 20  1  5  4 10 11  6  2 21 15 16  8  9  3 14
 7 13 19 22  0  1  2  8 16  3  9  6 20 14 15  4 10 11 12 18 21  5 17
19 22  0  1  2  3  4 18 12  5 21 15 16 17 11  6 20 14  8  7 10  9 13

Всё чётко.
Чтобы удостовериться, проверяю полученную порцию программой GetCyclic

Order? 23

Enter the name of the squares file: inp
Count only? y
Get cyclic for, (1 rows, 2 columns, 3 \diagonals, 4 /diagonals)? 2
Get squares with cyclic:  columns
Exact match? y
Number of squares: 171028 number matched 171028

Всё верно, все 171028 ДЛК с цикличностью в столбцах.

В общем, с порядком 23 всё ясно, все нужные порции полуциклических пандиагональных ДЛК получаются.
Осталось применить преобразование "строки-диагонали", но дело за матрицей преобразования.

Некоторая часть полуциклических пандиагональных ДЛК 23-го порядка получена.