Thread 'Maximum number of normalized ODLS from one DLS'
Message boards : Science : Maximum number of normalized ODLS from one DLS
Message board moderation
Previous · 1 . . . 5 · 6 · 7 · 8 · 9 · 10 · 11 . . . 14 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата PS. Программа GetOrthogonal Ñообщает, что макÑимальное количеÑтво ОДЛК от одного ДЛК равно 14. Похоже, глаза мне пока не врут :) Делаю финт, рекомендованный Harry: перемещаю квадрат 1 в конец маÑÑива ДЛК. ПроверÑÑŽ теперь на ортогональные пары программой GetOrthogonal Order? 56 Enter the name of the squares file: out ..output file outPairs.txt ..output file outPairNos.txt squares 22 Total orthogonal pairs 151 Maximum pairs for LS 22: 15 This is the only LS with this maximum number of pairs. ..output file outMaxPairs.txt Теперь программа Ñообщает, что макÑимальное количеÑтво ОДЛК у квадрата 22 и оно равно 15. Квадрат 22 ÑÐµÐ¹Ñ‡Ð°Ñ - Ñто бывший квадрат 1. Таким образом, квадрат 1 имеет-таки 15 ортогональных ДЛК. Почему программа не заметила Ñтого, когда квадрат 1 ÑтоÑл на Ñвоём меÑте? Ðу, оценка a(56) >= 15 не актуальна, как Ñ ÑƒÐ¶Ðµ отметила выше. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Итак, квадрат 1, который показан в Ñообщении https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=133&postid=2065 как DLK, имеет 15 ортогональных ДЛК. Ð’ Ñтой 15-ке находитÑÑ Ð¸ группа MODLS, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· 4-Ñ… взаимно ортогональных ДЛК 56-го порÑдка [1, 2, 8, 12] ÐÑ…, покрутить что ли квадратики? :) Ð¥Ð¾Ñ‚Ñ Ð½Ð¸Ñ‡ÐµÐ³Ð¾ нового не ожидаетÑÑ. Рвдруг... |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Покрутила 22 квадратика 56-го порÑдка программой Rotate; получила 176 ДЛК, нормализовала их и проверила программой Harry на дубликаты. Программа Ñообщает Order? 56 Enter the name of the squares file: inp total allocated 0,100,122,048 bytes .. reading square numbers as unsigned shorts Sort: 1 ascending or 2 descending? 1 .. sorting squares .. writing squares to file inpSortedA.txt Number of squares 176 minus 152 duplicates: 24. .. freeing squares Очень интереÑно: добавилоÑÑŒ два новеньких квадратика. Дадут ли они новые ортогональные пары? Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÑŽ. Программа GetOrthogonal Ñообщает Order? 56 Enter the name of the squares file: inp1 ..output file inp1Pairs.txt ..output file inp1PairNos.txt squares 24 Total orthogonal pairs 180 Maximum pairs for LS 21: 15 There are 3 other LS with this maximum number of pairs. ..output file inp1MaxPairs.txt ДобавилиÑÑŒ новые ортогональные пары. МакÑимальное количеÑтво ОДЛК от одного ДЛК здеÑÑŒ показываетÑÑ 15. ПоÑмотрим на таблицу ортогональных пар 5: 2 3 4 6: 1 3 4 7: 1 2 4 8: 1 2 3 9: 2 3 4 6 7 8 10: 1 3 4 5 7 8 11: 1 2 4 5 6 8 12: 1 2 3 5 6 7 13: 2 3 4 6 7 8 10 11 12 14: 1 3 4 5 7 8 9 11 12 15: 1 2 4 5 6 8 9 10 12 16: 1 2 3 5 6 7 9 10 11 17: 2 3 4 6 7 8 10 11 12 14 15 16 18: 1 3 4 5 7 8 9 11 12 13 15 16 19: 1 2 4 5 6 8 9 10 12 13 14 16 20: 1 2 3 5 6 7 9 10 11 13 14 15 21: 2 3 4 6 7 8 10 11 12 14 15 16 18 19 20 22: 1 3 4 5 7 8 9 11 12 13 15 16 17 19 20 23: 1 2 4 5 6 8 9 10 12 13 14 16 17 18 20 24: 1 2 3 5 6 7 9 10 11 13 14 15 17 18 19 Да, визуально Ñ Ð½Ðµ вижу ОДЛК больше 15 от одного ДЛК. Выкладываю Ñту 15-ку 56-го порÑдка прÑмо в том виде, Ñ ÐºÐ°ÐºÐ¾Ð¼ её выдала программа GetOrthogonal https://disk.yandex.ru/d/IQ2icCHSBMoo4Q ЯндекÑ.ДиÑк, 147 КБ, текÑтовый файл не Ñжат. Первый квадрат - оÑновной ДЛК 15-ки, далее Ñледуют 15 ортогональных ДЛК. ИнтереÑно: ОДЛК Ñтой 15-ки образуют 75 ортогональных пар Enter the name of the squares file: inp ..output file inpPairs.txt ..output file inpPairNos_1.txt squares 16 orthogonal pairs 75 Таблица ортогональных пар 2: 1 3: 1 4: 1 5: 1 3 4 6: 1 2 4 7: 1 2 3 8: 1 3 4 6 7 9: 1 2 4 5 7 10: 1 2 3 5 6 11: 1 3 4 6 7 9 10 12: 1 2 4 5 7 8 10 13: 1 2 3 5 6 8 9 14: 1 3 4 6 7 9 10 12 13 15: 1 2 4 5 7 8 10 11 13 16: 1 2 3 5 6 8 9 11 12 Ð¢Ð°ÐºÐ°Ñ Ð²Ð¾Ñ‚ 15-ка 56-го порÑдка - очень ÑимпатичнаÑ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Рна картинке ещё Ñимпатичнее :) С детÑтва люблю риÑовать, Ñ…Ð¾Ñ‚Ñ Ñ…ÑƒÐ´Ð¾Ð¶Ð½Ð¸Ðº из Ð¼ÐµÐ½Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»ÑÑ Ð½Ð¸ÐºÑƒÐ´Ñ‹ÑˆÐ½Ñ‹Ð¹. Ðо наглÑдноÑÑ‚ÑŒ мне нравитÑÑ Ð²Ð¾ вÑех ÑлучаÑÑ…. РиÑует программа SageMath. Код sage: d = {2: [1],
3: [1],
4: [1],
5: [1,3,4],
6: [1,2,4],
7: [1,2,3],
8: [1,3,4,6,7],
9: [1,2,4,5,7],
10: [1,2,3,5,6],
11: [1,3,4,6,7,9,10],
12: [1,2,4,5,7,8,10],
13: [1,2,3,5,6,8,9],
14: [1,3,4,6,7,9,10,12,13],
15: [1,2,4,5,7,8,10,11,13],
16: [1,2,3,5,6,8,9,11,12]}
sage: g = Graph (d)
sage: g.show ()
sage: g.cliques_maximum ()Картинка 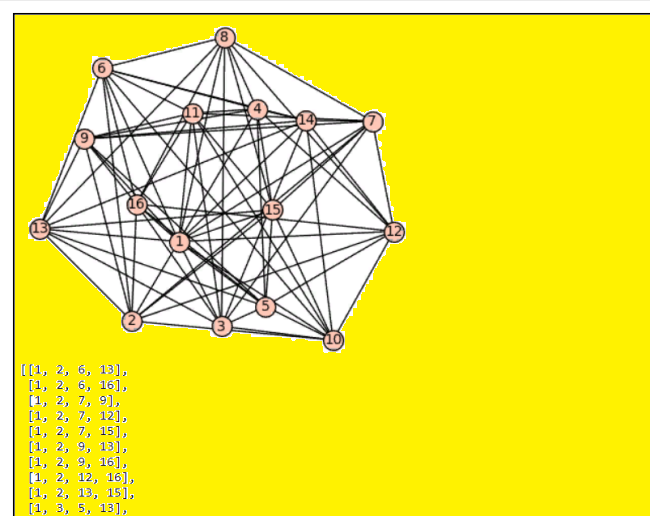 Ð’ Ñтой группе ортогональных пар поменьше, поÑтому граф более прозрачный, лучше раÑÑматриваютÑÑ Ð²Ñе рёбра. МакÑимальные клики по-прежнему размера 4. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
При проверке ÑвойÑтв 22 ДЛК 56-го порÑдка вижу . . . . . 11 ... diagonal Latin, weakly pandiagonal, center symmetric, nfr, self-orthogonal diagonal Latin, weakly pandiagonal, center symmetric, nfr, self-orthogonal diagonal Latin, weakly pandiagonal, center symmetric, nfr, orthogonal pair, self-orthogonal diagonal Latin, weakly pandiagonal, center symmetric, nfr, self-orthogonal diagonal Latin, weakly pandiagonal, center symmetric, nfr, self-orthogonal diagonal Latin, center symmetric, nfr, orthogonal pair, self-orthogonal diagonal Latin, center symmetric, nfr, self-orthogonal diagonal Latin, center symmetric, nfr, self-orthogonal diagonal Latin, center symmetric, nfr, orthogonal pair, self-orthogonal diagonal Latin, center symmetric, nfr, self-orthogonal . . . . . . Очень интереÑÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° ДЛК diagonal Latin, weakly pandiagonal, center symmetric, nfr, self-orthogonal diagonal Latin, weakly pandiagonal, center symmetric, nfr, orthogonal pair, self-orthogonal Ðти ДЛК образуют ортогональную пару, они центрально-Ñимметричные и Ñлабо пандиагональные, оба ÑвлÑÑŽÑ‚ÑÑ SODLS и DSODLS. ПревратÑÑ‚ÑÑ Ð»Ð¸ они в идеальные (аÑÑоциативные и Ñлабо пандиагональные) при превращении в СРДЛК? Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÑŽ. Ð’ аÑÑоциативные Ñти ДЛК превратилиÑÑŒ, но... иÑчезла ÑÐ»Ð°Ð±Ð°Ñ Ð¿Ð°Ð½Ð´Ð¸Ð°Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð¾ÑÑ‚ÑŒ Order? 56
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_5.txt
Counts
------
2 diagonal Latin
2 associative
2 natural \diagonal
1 orthogonal pair
2 self-orthogonalЖаль! Ортогональных идеальных ДЛК 56-го порÑдка не получилоÑÑŒ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Смотрим ещё раз на поÑледовательноÑÑ‚ÑŒ OEIS https://oeis.org/A287695 Maximum number of normalized diagonal Latin squares that can be orthogonal to the same diagonal Latin square of order n. Ð’ опубликованной верÑии еÑÑ‚ÑŒ такие оценки: a(11) >= 32462. - Eduard I. Vatutin from T. Brada, Mar 11 2021 Я добавила ещё неÑколько оценок, но Ñто пока виÑит в черновике: COMMENTS a(21) >= 1, a(22) >= 1, a(23) >= 19, a(24) >= 824, a(25) >= 21, a(26) >= 1, a(27) >= 23, a(28) >= 1, a(29) >= 25, a(30) >= 1. - Natalia Makarova, Alex Chernov, May 10 2021 Оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 28 уже улучшена: a(28) >= 3. Также улучшена оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдков 14, 18 и 20. Ðадо Ñобрать вÑе полученные в теме оценки в одно меÑто, чтобы не иÑкать их по вÑей теме. Завтра Ñ ÑƒÑ‚Ñ€ÐµÑ‡ÐºÐ° займуÑÑŒ Ñтим. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Рдальше хочу попробовать метод Пелегрино-ЛанÑелотти Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 42. Базовые ортогоналные пары ДЛК 14-го порÑдка буду брать от ДЛК, поÑтроенного методом Гергели. Одна Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° ДЛК 42-го порÑдка была поÑтроена в показанном ранее примере; Ð±Ð°Ð·Ð¾Ð²Ð°Ñ Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° ДЛК 14-го порÑдка взÑта от ДЛК Гергели. ÐеизвеÑтно, будут ли хорошо другие ортогональные пары ÑтроитьÑÑ, метод Пелегрино-ЛанÑелотти капризный: базовые ортогональные пары ДЛК порÑдка k не вÑегда дают ортогональную пару ДЛК порÑдка 3k. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðашла пример поÑÑ‚Ñ€Ð¾ÐµÐ½Ð¸Ñ Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð¾Ð¹ пары ДЛК 42-го порÑдка методом Пелегрино-ЛанÑелотти Цитата ПорÑдок 42 проблемный Ð´Ð»Ñ Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ñ‹Ñ… пар ДЛК, а Ð´Ð»Ñ Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ñ‹Ñ… пар ЛК - нет, так как 42=3*14. Смотрите Ñообщение https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=5812 И в Ñледующем Ñообщении показана поÑÑ‚Ñ€Ð¾ÐµÐ½Ð½Ð°Ñ Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° ДЛК 42-го порÑдка. Ðу, теперь, как говоритÑÑ, дело техники. У ДЛК Гергели уйма ортогональных ДЛК, то еÑÑ‚ÑŒ ортогональных пар имеетÑÑ Ð²Ð°Ð³Ð¾Ð½ и Ð¼Ð°Ð»ÐµÐ½ÑŒÐºÐ°Ñ Ñ‚ÐµÐ»ÐµÐ¶ÐºÐ°. ЗапуÑкаем поÑтроение ортогональных пар и Ñмотрим, как они будут ÑтроитьÑÑ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Квадрат Гергели поÑтроен мной в Ñтатье http://www.natalimak1.narod.ru/dlk.htm (Ñмотрите риÑ. 16) Очень хороший квадрат! Д-транÑверÑалей Ñодержит 364252, ОДЛК имеет много (при Ñтом Ñреди ОДЛК почти нет изоморфных). Вот ещё иллюÑÑ‚Ñ€Ð°Ñ†Ð¸Ñ Ñтого Ñимпатичного квадратика  ЗдеÑÑŒ и выше в цитате ДЛК показан в том виде, как он был поÑтроен в Ñтатье. Покажу и иллюÑтрацию Ñтого ДЛК в нормализованном виде 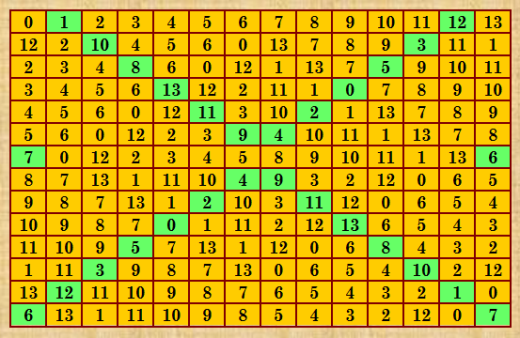 Ð”Ð»Ñ ÑкÑперимента возьму не нормализованный вариант, потому что Ñ Ð½Ð¸Ð¼ уже одна Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° поÑтроена. Так и продолжу. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Собрала результаты (нижнÑÑ Ð³Ñ€Ð°Ð½Ð¸Ñ†Ð° Ð´Ð»Ñ Ð¼Ð°ÐºÑимального количеÑтва нормализованных ОДЛК от одного ДЛК порÑдка n) a(10) >= 10 a(11) >= 32462 a(12) >= 3855983322 a(13) >= 248703 a(14) >= 307662 a(15) >= 3 a(16) >= 1658880 a(17) >= 2453352 a(18) >= 96 a(19) >= 1383 a(20) >= 995328 a(21) >= 995328 a(22) >= 432000 a(23) >= 525 a(24) >= 345600 a(25) >= 345600 a(26) >= 48 a(27) >= 345600 a(28) >= 663552 a(29) >= 663552 a(30) >= 40320 a(31) >= 58 a(32) >= 10000 a(33) >= 20000 a(34) >= 20000 a(35) >= 1875 a(36) >= 10000 a(37) >= 10000 a(38) >= 20000 a(39) >= 2344 a(40) >= 10000 a(41) >= 20000 a(42) >= 10000 a(43) >= 39 a(44) >= 32462 a(45) >= 1000000 a(46) >= 10000 a(47) >= 43 a(48) >= 3855983322 a(49) >= 10000 a(50) >= 15000 a(51) >= 1000000 a(52) >= 248703 a(53) >= 10000 a(54) >= 1560 a(55) >= 32462 a(56) >= 307662 a(57) >= 5760 a(58) >= 10000 a(59) >= 55 a(60) >= 3855983322 a(61) >= 10000 a(62) >= 1728 a(63) >= 10000 a(64) >= 1658880 a(65) >= 248703 a(66) >= 10000 a(67) >= 63 a(68) >= 2453352 a(69) >= 2926 a(70) >= 307662 a(71) >= 10000 a(72) >= 8000 a(73) >= 8000 a(74) >= 10000 a(75) >= 960 a(76) >= 1383 a(77) >= 32462 a(78) >= 10000 a(79) >= 75 a(80) >= 1658880 a(81) >= 10000 a(82) >= 10000 a(83) >= 79 a(84) >= 995328 a(85) >= 2453352 a(86) >= 85 a(87) >= 120 a(88) >= 432000 a(89) >= 85 a(90) >= 96 a(91) >= 248703 a(92) >= 525 a(93) >= 361 a(94) >= 328 a(95) >= 1383 a(96) >= 345600 a(97) >= 93 a(98) >= 307662 a(99) >= 32462 a(100) >= 345600 КраÑным цветом выделены улучшенные оценки Ð´Ð»Ñ ÑƒÐ¶Ðµ опубликованных в Ñтатье OEIS. Результаты получены мной и Harry White. Ðекоторые результаты получены Ñ Ð¸Ñпользованием программы ÐлекÑÐµÑ Ð§ÐµÑ€Ð½Ð¾Ð²Ð°. Смотрите данную тему и тему https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=136 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата из ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=133&postid=2061 ÐžÑ‚Ð»Ð¸Ñ‡Ð½Ð°Ñ Ð½Ð¾Ð²Ð¾ÑÑ‚ÑŒ! Выложила Ñтот интереÑный результат https://disk.yandex.ru/d/XWv7ttV2vQpzBA ЯндекÑ.ДиÑк, текÑтовый файл Ñжат, 137 КБ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ртем временем мы перешли на третью Ñтраницу. Страницу 2 Ñкопировала, ÑÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ð»Ð¾Ð¶Ñƒ на ЯндекÑ.ДиÑк. Готово! https://disk.yandex.ru/d/dIK60e4RoZNyQQ формат html, 723 КБ. ÐšÐ¾Ð¿Ð¸Ñ Ñтраницы 1 тут https://disk.yandex.ru/d/ozQ84tVSEQbmRQ |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ВозвращаюÑÑŒ к ÑкÑперименту Ñ ÐºÐ²Ð°Ð´Ñ€Ð°Ñ‚Ð¾Ð¼ Гергели и методом Пелегрино-ЛанÑелотти. Мой помощник немного обÑчитывал ДЛК Гергели (в ÑкÑперименте Ñ Ð¿Ð¾Ð¸Ñком Ñдра БД КФ ОДЛК 14-го порÑдка). Ðапример, Ñ€ÐµÑˆÐµÐ½Ð¸Ñ Ð¸Ð· 7600-й чаÑти # in: FZ6P2fxvxqsd3GrUPmTuqQRE6BCU383vKyutP7TR7G8whx 7600 # num_dtrans: 364252 FWyFRZFi89xuHKFEQbR73cgYVZpsZFGmPmNqjGZRhQB6SEn FXVgh9QmXbegd1Lo7evjknAoSr5S9YrajsbLz37hCfZpUhN FHUpTVdWNvcskJbnsnQiyMgZcYAnYRDwLyQosTmJnVmUvAX3 F2SDYHJyzbbFg6jPihMBsXxR9edNSY5RoviaLebqEnzaL1G FihmDbM84vUH7JM6Qv4o3f8Z7rUv3g4VrYKkKpzAWpt5g7E F6y2KfiaEfsXsfXkE1oEtfXDHYhpb2fGXX7SnfFY1Rv3K2J F77LbegT9BQJ52k9BFGVtpi7YRHbUcdGNwkLBNGfEtcHdK8 FFiiP9nFfn8TC1RjcTBPtYCqrgwLDdVhf6P3ncydQ3vZJkQ Fmr23x6tzv2BfcBjH3TPZZ6zzRjvVFaEDxkxyfKZwG66oLA FWLuNtDPsrJMG1XRVCULGFg4hwS5vLbdGoV8a1cuMBLVC8M6 Fv2FuouiMn42GWMgBy226w3azkYUsUNJKSkY1pS6WBkDAD6 Fq9xz3cc6a6AXdv3h7Gefz1XakFUMefQqewV2TtGRwTqjd3 FhNwnjfugWqABoc2nWE4eKMFTBMYHvyCrEbd5DpmDf7iFNU5 FifTCQLSETAUFcCR4EQwnzxhUB3AsHNbbeMhnhhGA3hRsPY Fw4r1ryDARRfa6fXhkryDys5RWnZLK6N89xyagJXTeShFRi6 FENJ76R5hLL6gHyPHpZTCq4KPEC3h8oL7mEWFiEYA5dEZn2 FuXWhbeULZtFPfgzjhKvr19ZScNoLMNcvf826TEBWoBytdP3 Fw1DSH5xKMGpjb1FUhZvz4gaEL5gY5UKULDkovv8AAhbt555 F4qV5ScoTw5cVNQmTfH76hEN8w3oLmsAijo3ckdj9ysC5qFg FfjNHYJpqDy9SPuJucuSa3aaiGUEHk1TqAPrHkmPjgZVuNw FAXqkzaJZ9NUMgdmssKBarzVq9eTE6EZjc6Meq1P4DkKSvT2 FMHN1MTYdfzmxwNBK19u7bHgqjub3VktcYRxDS4wrqwzUshe F7P6atgMb4Xg3U9kKgPUWcYTrtAoM2Bpo3cKR8ZiZkJJfyBK F77h5h2NMZsE1dsJUom5uCvNWnJSdBQ4eYiDYhNiN71M8gR FJqembpe5C5xyYMTdR5yEBFRYqiRiM4qFoV7ttM4titdJMq6 FwQQmEEEC8pETwo9JEvRKxmMwtmFPhS39PgcARn8uAWqmSD FFNH7ncW6JpeVCLe1NUu2tUXnDsQKXCsq4e1Tv96gpDsikj2 FXR4yjokcWHchy3eknzneaEadhQXqnbaUvvhTUavjhumGxq5 FZzunrXTk8M53ZcwBYg9UthSUqEXQ4Yrg9cuNGRRQvHyDXcE Fhk1trGkos1wzRQdPbpoNSd6jPd4psm6S9pu5fiNny7o8U6 FRLohV9D9oZ2XiXpmVqRSoM19A5cDa6VDAmvjde3e4YyYUR FcyrmBMAGcuL3gohkRXMab6ZD8Yij6FeA5LHKxL7jqThsx6 F9Bcg2SKajQ1wX3RYVfWwZJ2Yha76GckCanQ3q4Z6ev1EQB FMV4x5CzAtUu82FKZUiLpvtVHcYwTsJDP1QEDji4tLVJZpV2 . . . . . . Теперь надо попробовать Ñтроить ортогональные пары 42-го порÑдка на базе Ñтих ортогональных пар 14-го порÑдка. Будут ли ÑтроитьÑÑ? Как много? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ортогональные пары 42-го порÑдка методом Пелегрино-ЛанÑелотти ÑтроÑÑ‚ÑÑ Ð½Ð° базе ортогональных пар ДЛК 14-го порÑдка, полученных от ДЛК Гергели. Однако... в группе полученных ОДЛК нет ни одной двушки! Ð’Ñе однушки. Проверила две порции. ÐŸÐµÑ€Ð²Ð°Ñ Ð¿Ð¾Ñ€Ñ†Ð¸Ñ Ð´Ð°Ð»Ð° 442 нормализованных различных ОДЛК, Ð²Ñ‚Ð¾Ñ€Ð°Ñ Ð¿Ð¾Ñ€Ñ†Ð¸Ñ - 384. Ð’Ñего 826 ОДЛК, и вÑе только однушки! Продолжать поÑтроение ортогональных пар на базе ортогональных пар от ДЛК Гергели не буду. Попробую другой ДЛК 14-го порÑдка, например, Ñтот топовый по Д-транÑверÑалÑм 0 2 4 6 12 11 7 9 13 10 8 5 3 1 12 1 3 11 8 7 5 4 9 6 13 2 0 10 10 0 2 13 6 9 4 5 7 8 11 3 1 12 7 11 8 3 5 0 12 10 1 4 2 6 13 9 9 13 6 2 4 1 10 12 0 5 3 8 11 7 6 12 1 7 13 5 3 2 4 11 9 0 10 8 4 9 11 1 2 12 6 8 10 3 0 13 7 5 1 3 5 8 10 13 9 7 11 12 6 4 2 0 2 5 7 10 0 6 13 11 8 1 12 9 4 3 13 8 10 5 7 3 1 0 2 9 4 12 6 11 3 4 9 12 1 8 11 13 6 0 10 7 5 2 5 7 13 0 3 10 8 6 12 2 1 11 9 4 8 10 0 9 11 4 2 3 5 13 7 1 12 6 11 6 12 4 9 2 0 1 3 7 5 10 8 13 ДЛК немного обÑчитывалÑÑ Ð¿Ð¾Ð¼Ð¾Ñ‰Ð½Ð¸ÐºÐ¾Ð¼. Ðти результаты и попробую ÑейчаÑ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Попробовала, тот же Ñамый результат. Ортогональные пары ÑтроÑÑ‚ÑÑ Ñ…Ð¾Ñ€Ð¾ÑˆÐ¾, получила 741 различных нормализованных ОДЛК, проверÑÑŽ группу на ортогональные пары, только однушки. Да, что-то не работает Ñтот алгоритм Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 42. ОÑтанавливаю ÑкÑперимент. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПорÑдок 64 интереÑный. Ð”Ð»Ñ Ñтого порÑдка ÑущеÑтвует Ð¿Ð¾Ð»Ð½Ð°Ñ ÑиÑтема MOLS, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· 63 взаимно ортогональных ЛК, 62 из которых ÑвлÑÑŽÑ‚ÑÑ Ð”Ð›Ðš и образуют группу MODLS. Таким образом, одна оценка уже готова: a(64) >= 61. ИнтереÑно было поÑмотреть, как работает метод ÑоÑтавных квадратов: 64=8*8. ПоÑмотрела :) ПоÑтроила вÑе возможные ортогональные пары, получила 34 различных нормализованных ОДЛК. Проверка Ñтой группы ОДЛК программой GetOrthogonal даёт Order? 64 Enter the name of the squares file: INP1 ..output file INP1Pairs.txt ..output file INP1PairNos.txt squares 34 Total orthogonal pairs 401 Maximum pairs for LS 31: 24 There are 3 other LS with this maximum number of pairs. ..output file INP1MaxPairs.txt ЗдеÑÑŒ макÑимальное количеÑтво ОДЛК от одного ДЛК показываетÑÑ 24. Смотрим таблицу ортогональных пар 2: 1 3: 1 4: 1 5: 1 6: 1 7: 3 4 5 6 8: 2 4 5 6 9: 2 3 5 6 10: 2 3 4 6 11: 1 3 4 5 6 8 9 10 12: 1 2 4 5 6 7 9 10 13: 1 2 3 5 6 7 8 10 14: 1 2 3 4 6 7 8 9 15: 1 2 3 4 5 7 8 9 10 16: 1 3 4 5 6 8 9 10 12 13 14 15 17: 1 2 4 5 6 7 9 10 11 13 14 15 18: 1 2 3 5 6 7 8 10 11 12 14 15 19: 1 2 3 4 6 7 8 9 11 12 13 15 20: 1 2 3 4 5 7 8 9 10 11 12 13 14 21: 1 3 4 5 6 8 9 10 12 13 14 15 17 18 19 20 22: 1 2 4 5 6 7 9 10 11 13 14 15 16 18 19 20 23: 1 2 3 5 6 7 8 10 11 12 14 15 16 17 19 20 24: 1 2 3 4 6 7 8 9 11 12 13 15 16 17 18 20 25: 1 2 3 4 5 7 8 9 10 11 12 13 14 16 17 18 19 26: 1 3 4 5 6 8 9 10 12 13 14 15 17 18 19 20 22 23 24 25 27: 1 2 4 5 6 7 9 10 11 13 14 15 16 18 19 20 21 23 24 25 28: 1 2 3 5 6 7 8 10 11 12 14 15 16 17 19 20 21 22 24 25 29: 1 2 3 4 6 7 8 9 11 12 13 15 16 17 18 20 21 22 23 25 30: 1 2 3 4 5 7 8 9 10 11 12 13 14 16 17 18 19 21 22 23 24 31: 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 32: 2 3 4 5 6 7 8 9 10 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 33: 2 3 4 5 6 7 8 9 10 11 12 13 14 15 21 22 23 24 25 26 27 28 29 30 34: 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 26 27 28 29 30 Ð’ таблице ортогональных пар видим, что квадрату 1 ортогональны 25 ДЛК. ÐÐ½Ð°Ð»Ð¾Ð³Ð¸Ñ‡Ð½Ð°Ñ ÑÐ¸Ñ‚ÑƒÐ°Ñ†Ð¸Ñ ÑƒÐ¶Ðµ вÑтречалаÑÑŒ при поÑтроении ортогональных пар ДЛК 56-го порÑдка методом ÑоÑтавных квадратов. Программа почему-то не видит вÑе ортогональные ДЛК квадрата 1. Ðу и конечно, тут должна быть клика размера 6 - по теории. ЕÑли не ошиблаÑÑŒ в поÑтроении ортогональных пар, должна быть Ñ‚Ð°ÐºÐ°Ñ ÐºÐ»Ð¸ÐºÐ°. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ð¿Ñ‹Ñ‚Ð°ÑŽÑÑŒ поÑтроить Ñтот граф в программе SageMath. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’ÑÑ‘ превоÑходно! Программа SageMath риÑует граф и выдаёт клики размера 6. Код sage: d = {2: [1],
3: [1],
4: [1],
5: [1],
6: [1],
7: [3,4,5,6],
8: [2,4,5,6],
9: [2,3,5,6],
10: [2,3,4,6],
11: [1,3,4,5,6,8,9,10],
12: [1,2,4,5,6,7,9,10],
13: [1,2,3,5,6,7,8,10],
14: [1,2,3,4,6,7,8,9],
15: [1,2,3,4,5,7,8,9,10],
16: [1,3,4,5,6,8,9,10,12,13,14,15],
17: [1,2,4,5,6,7,9,10,11,13,14,15],
18: [1,2,3,5,6,7,8,10,11,12,14,15],
19: [1,2,3,4,6,7,8,9,11,12,13,15],
20: [1,2,3,4,5,7,8,9,10,11,12,13,14],
21: [1,3,4,5,6,8,9,10,12,13,14,15,17,18,19,20],
22: [1,2,4,5,6,7,9,10,11,13,14,15,16,18,19,20],
23: [1,2,3,5,6,7,8,10,11,12,14,15,16,17,19,20],
24: [1,2,3,4,6,7,8,9,11,12,13,15,16,17,18,20],
25: [1,2,3,4,5,7,8,9,10,11,12,13,14,16,17,18,19],
26: [1,3,4,5,6,8,9,10,12,13,14,15,17,18,19,20,22,23,24,25],
27: [1,2,4,5,6,7,9,10,11,13,14,15,16,18,19,20,21,23,24,25],
28: [1,2,3,5,6,7,8,10,11,12,14,15,16,17,19,20,21,22,24,25],
29: [1,2,3,4,6,7,8,9,11,12,13,15,16,17,18,20,21,22,23,25],
30: [1,2,3,4,5,7,8,9,10,11,12,13,14,16,17,18,19,21,22,23,24],
31: [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30],
32: [2,3,4,5,6,7,8,9,10,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30],
33: [2,3,4,5,6,7,8,9,10,11,12,13,14,15,21,22,23,24,25,26,27,28,29,30],
34: [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,26,27,28,29,30],}
sage: g = Graph (d)
sage: g.show ()
sage: g.cliques_maximum ()Результат 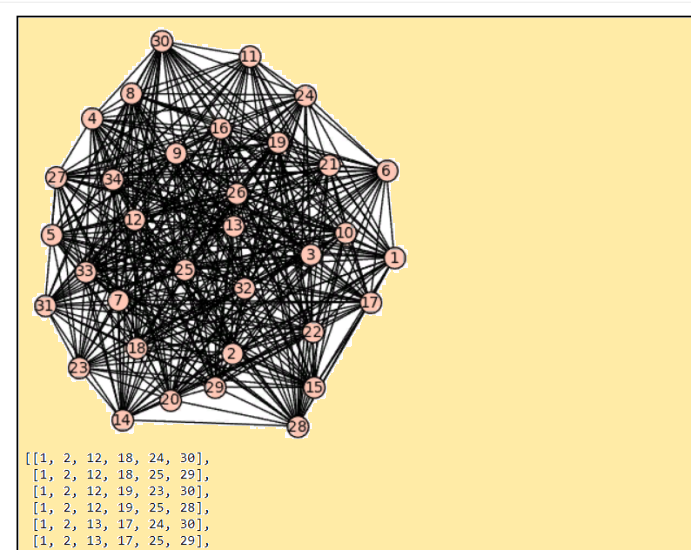 Лепота! Практика подтверждает теорию: ОДЛК 64-го порÑдка, поÑтроенные методом ÑоÑтавных квадратов (на базе ортогональных ДЛК 8-го порÑдка), образуют клику размера 6, то еÑÑ‚ÑŒ группу MODLS, ÑоÑтоÑщую из 6 взаимно ортогональных ДЛК. PS. ÐžÑ‚Ð»Ð¸Ñ‡Ð½Ð°Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð° SageMath, очень проÑта в пользовании, быÑтро работает, хорошо ÑправлÑетÑÑ Ñ Ð¸Ð·Ð¾Ð±Ñ€Ð°Ð¶ÐµÐ½Ð¸ÐµÐ¼ графов. СпаÑибо ÑоздателÑм! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðто был проÑто ÑкÑперимент по методу ÑоÑтавных квадратов. Как уже отмечено выше, ДЛК 64-го порÑдка образуют группу MODLS, ÑоÑтоÑщую из 62 взаимно ортогональных ДЛК. Полную ÑиÑтему MOLS данного порÑдка можно попробовать ÑоÑтавить в программе SageMath. Кому интереÑно, попробуйте. Ру Ð¼ÐµÐ½Ñ Ñ‚Ð°ÐºÐ¾Ð¹ интереÑный вопроÑ: даÑÑ‚ ли метод ÑоÑтавных квадратов группу ОДЛК 64-го порÑдка, в которой у ДЛК имеетÑÑ 824 ортогональных ДЛК? По теории должен дать. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€Ð¸Ð¼. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Да! Ðто получилоÑÑŒ! Метод ÑоÑтавных квадратов Ñтабильно работает. Вот проверка полученной группы ОДЛК 64-го порÑдка программой GetOrthogonal Order? 64 Enter the name of the squares file: INP1 ..output file INP1Pairs.txt ..output file INP1PairNos.txt squares 825 Total orthogonal pairs 824 Maximum pairs for LS 2: 1 There are 823 other LS with this maximum number of pairs. Ðу, "Maximum pairs for LS 2: 1" неверно, опÑÑ‚ÑŒ программа не видит ортогональные ДЛК квадрата 1. Смотрим таблицу ортогональных пар (чаÑтично показываю, очень длиннаÑ) 2: 1 3: 1 4: 1 5: 1 6: 1 7: 1 8: 1 9: 1 10: 1 11: 1 12: 1 13: 1 14: 1 15: 1 16: 1 17: 1 18: 1 19: 1 20: 1 21: 1 22: 1 23: 1 24: 1 25: 1 26: 1 27: 1 . . . . 800: 1 801: 1 802: 1 803: 1 804: 1 805: 1 806: 1 807: 1 808: 1 809: 1 810: 1 811: 1 812: 1 813: 1 814: 1 815: 1 816: 1 817: 1 818: 1 819: 1 820: 1 821: 1 822: 1 823: 1 824: 1 825: 1 Квадрату 1 ортогональны 824 ДЛК. Показываю квадрат 1 - оÑновной ДЛК Ñтой замечательной 824-ки 64-го порÑдка 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 22 23 20 21 18 19 16 17 30 31 28 29 26 27 24 25 38 39 36 37 34 35 32 33 46 47 44 45 42 43 40 41 54 55 52 53 50 51 48 49 62 63 60 61 58 59 56 57 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 19 18 17 16 23 22 21 20 27 26 25 24 31 30 29 28 35 34 33 32 39 38 37 36 43 42 41 40 47 46 45 44 51 50 49 48 55 54 53 52 59 58 57 56 63 62 61 60 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 21 20 23 22 17 16 19 18 29 28 31 30 25 24 27 26 37 36 39 38 33 32 35 34 45 44 47 46 41 40 43 42 53 52 55 54 49 48 51 50 61 60 63 62 57 56 59 58 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 17 16 19 18 21 20 23 22 25 24 27 26 29 28 31 30 33 32 35 34 37 36 39 38 41 40 43 42 45 44 47 46 49 48 51 50 53 52 55 54 57 56 59 58 61 60 63 62 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 23 22 21 20 19 18 17 16 31 30 29 28 27 26 25 24 39 38 37 36 35 34 33 32 47 46 45 44 43 42 41 40 55 54 53 52 51 50 49 48 63 62 61 60 59 58 57 56 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 18 19 16 17 22 23 20 21 26 27 24 25 30 31 28 29 34 35 32 33 38 39 36 37 42 43 40 41 46 47 44 45 50 51 48 49 54 55 52 53 58 59 56 57 62 63 60 61 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 20 21 22 23 16 17 18 19 28 29 30 31 24 25 26 27 36 37 38 39 32 33 34 35 44 45 46 47 40 41 42 43 52 53 54 55 48 49 50 51 60 61 62 63 56 57 58 59 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 22 23 20 21 18 19 16 17 30 31 28 29 26 27 24 25 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 54 55 52 53 50 51 48 49 62 63 60 61 58 59 56 57 38 39 36 37 34 35 32 33 46 47 44 45 42 43 40 41 19 18 17 16 23 22 21 20 27 26 25 24 31 30 29 28 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 51 50 49 48 55 54 53 52 59 58 57 56 63 62 61 60 35 34 33 32 39 38 37 36 43 42 41 40 47 46 45 44 21 20 23 22 17 16 19 18 29 28 31 30 25 24 27 26 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 53 52 55 54 49 48 51 50 61 60 63 62 57 56 59 58 37 36 39 38 33 32 35 34 45 44 47 46 41 40 43 42 17 16 19 18 21 20 23 22 25 24 27 26 29 28 31 30 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 49 48 51 50 53 52 55 54 57 56 59 58 61 60 63 62 33 32 35 34 37 36 39 38 41 40 43 42 45 44 47 46 23 22 21 20 19 18 17 16 31 30 29 28 27 26 25 24 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 55 54 53 52 51 50 49 48 63 62 61 60 59 58 57 56 39 38 37 36 35 34 33 32 47 46 45 44 43 42 41 40 18 19 16 17 22 23 20 21 26 27 24 25 30 31 28 29 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 50 51 48 49 54 55 52 53 58 59 56 57 62 63 60 61 34 35 32 33 38 39 36 37 42 43 40 41 46 47 44 45 20 21 22 23 16 17 18 19 28 29 30 31 24 25 26 27 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 52 53 54 55 48 49 50 51 60 61 62 63 56 57 58 59 36 37 38 39 32 33 34 35 44 45 46 47 40 41 42 43 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 38 39 36 37 34 35 32 33 46 47 44 45 42 43 40 41 54 55 52 53 50 51 48 49 62 63 60 61 58 59 56 57 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 22 23 20 21 18 19 16 17 30 31 28 29 26 27 24 25 35 34 33 32 39 38 37 36 43 42 41 40 47 46 45 44 51 50 49 48 55 54 53 52 59 58 57 56 63 62 61 60 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 19 18 17 16 23 22 21 20 27 26 25 24 31 30 29 28 37 36 39 38 33 32 35 34 45 44 47 46 41 40 43 42 53 52 55 54 49 48 51 50 61 60 63 62 57 56 59 58 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 21 20 23 22 17 16 19 18 29 28 31 30 25 24 27 26 33 32 35 34 37 36 39 38 41 40 43 42 45 44 47 46 49 48 51 50 53 52 55 54 57 56 59 58 61 60 63 62 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 17 16 19 18 21 20 23 22 25 24 27 26 29 28 31 30 39 38 37 36 35 34 33 32 47 46 45 44 43 42 41 40 55 54 53 52 51 50 49 48 63 62 61 60 59 58 57 56 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 23 22 21 20 19 18 17 16 31 30 29 28 27 26 25 24 34 35 32 33 38 39 36 37 42 43 40 41 46 47 44 45 50 51 48 49 54 55 52 53 58 59 56 57 62 63 60 61 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 18 19 16 17 22 23 20 21 26 27 24 25 30 31 28 29 36 37 38 39 32 33 34 35 44 45 46 47 40 41 42 43 52 53 54 55 48 49 50 51 60 61 62 63 56 57 58 59 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 20 21 22 23 16 17 18 19 28 29 30 31 24 25 26 27 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 54 55 52 53 50 51 48 49 62 63 60 61 58 59 56 57 38 39 36 37 34 35 32 33 46 47 44 45 42 43 40 41 22 23 20 21 18 19 16 17 30 31 28 29 26 27 24 25 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 51 50 49 48 55 54 53 52 59 58 57 56 63 62 61 60 35 34 33 32 39 38 37 36 43 42 41 40 47 46 45 44 19 18 17 16 23 22 21 20 27 26 25 24 31 30 29 28 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 53 52 55 54 49 48 51 50 61 60 63 62 57 56 59 58 37 36 39 38 33 32 35 34 45 44 47 46 41 40 43 42 21 20 23 22 17 16 19 18 29 28 31 30 25 24 27 26 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 49 48 51 50 53 52 55 54 57 56 59 58 61 60 63 62 33 32 35 34 37 36 39 38 41 40 43 42 45 44 47 46 17 16 19 18 21 20 23 22 25 24 27 26 29 28 31 30 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 55 54 53 52 51 50 49 48 63 62 61 60 59 58 57 56 39 38 37 36 35 34 33 32 47 46 45 44 43 42 41 40 23 22 21 20 19 18 17 16 31 30 29 28 27 26 25 24 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 50 51 48 49 54 55 52 53 58 59 56 57 62 63 60 61 34 35 32 33 38 39 36 37 42 43 40 41 46 47 44 45 18 19 16 17 22 23 20 21 26 27 24 25 30 31 28 29 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 52 53 54 55 48 49 50 51 60 61 62 63 56 57 58 59 36 37 38 39 32 33 34 35 44 45 46 47 40 41 42 43 20 21 22 23 16 17 18 19 28 29 30 31 24 25 26 27 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 40 41 42 43 44 45 46 47 32 33 34 35 36 37 38 39 56 57 58 59 60 61 62 63 48 49 50 51 52 53 54 55 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 24 25 26 27 28 29 30 31 16 17 18 19 20 21 22 23 46 47 44 45 42 43 40 41 38 39 36 37 34 35 32 33 62 63 60 61 58 59 56 57 54 55 52 53 50 51 48 49 14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1 30 31 28 29 26 27 24 25 22 23 20 21 18 19 16 17 43 42 41 40 47 46 45 44 35 34 33 32 39 38 37 36 59 58 57 56 63 62 61 60 51 50 49 48 55 54 53 52 11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4 27 26 25 24 31 30 29 28 19 18 17 16 23 22 21 20 45 44 47 46 41 40 43 42 37 36 39 38 33 32 35 34 61 60 63 62 57 56 59 58 53 52 55 54 49 48 51 50 13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2 29 28 31 30 25 24 27 26 21 20 23 22 17 16 19 18 41 40 43 42 45 44 47 46 33 32 35 34 37 36 39 38 57 56 59 58 61 60 63 62 49 48 51 50 53 52 55 54 9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6 25 24 27 26 29 28 31 30 17 16 19 18 21 20 23 22 47 46 45 44 43 42 41 40 39 38 37 36 35 34 33 32 63 62 61 60 59 58 57 56 55 54 53 52 51 50 49 48 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 42 43 40 41 46 47 44 45 34 35 32 33 38 39 36 37 58 59 56 57 62 63 60 61 50 51 48 49 54 55 52 53 10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5 26 27 24 25 30 31 28 29 18 19 16 17 22 23 20 21 44 45 46 47 40 41 42 43 36 37 38 39 32 33 34 35 60 61 62 63 56 57 58 59 52 53 54 55 48 49 50 51 12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3 28 29 30 31 24 25 26 27 20 21 22 23 16 17 18 19 56 57 58 59 60 61 62 63 48 49 50 51 52 53 54 55 40 41 42 43 44 45 46 47 32 33 34 35 36 37 38 39 24 25 26 27 28 29 30 31 16 17 18 19 20 21 22 23 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 62 63 60 61 58 59 56 57 54 55 52 53 50 51 48 49 46 47 44 45 42 43 40 41 38 39 36 37 34 35 32 33 30 31 28 29 26 27 24 25 22 23 20 21 18 19 16 17 14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1 59 58 57 56 63 62 61 60 51 50 49 48 55 54 53 52 43 42 41 40 47 46 45 44 35 34 33 32 39 38 37 36 27 26 25 24 31 30 29 28 19 18 17 16 23 22 21 20 11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4 61 60 63 62 57 56 59 58 53 52 55 54 49 48 51 50 45 44 47 46 41 40 43 42 37 36 39 38 33 32 35 34 29 28 31 30 25 24 27 26 21 20 23 22 17 16 19 18 13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2 57 56 59 58 61 60 63 62 49 48 51 50 53 52 55 54 41 40 43 42 45 44 47 46 33 32 35 34 37 36 39 38 25 24 27 26 29 28 31 30 17 16 19 18 21 20 23 22 9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6 63 62 61 60 59 58 57 56 55 54 53 52 51 50 49 48 47 46 45 44 43 42 41 40 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 58 59 56 57 62 63 60 61 50 51 48 49 54 55 52 53 42 43 40 41 46 47 44 45 34 35 32 33 38 39 36 37 26 27 24 25 30 31 28 29 18 19 16 17 22 23 20 21 10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5 60 61 62 63 56 57 58 59 52 53 54 55 48 49 50 51 44 45 46 47 40 41 42 43 36 37 38 39 32 33 34 35 28 29 30 31 24 25 26 27 20 21 22 23 16 17 18 19 12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 24 25 26 27 28 29 30 31 16 17 18 19 20 21 22 23 40 41 42 43 44 45 46 47 32 33 34 35 36 37 38 39 56 57 58 59 60 61 62 63 48 49 50 51 52 53 54 55 14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1 30 31 28 29 26 27 24 25 22 23 20 21 18 19 16 17 46 47 44 45 42 43 40 41 38 39 36 37 34 35 32 33 62 63 60 61 58 59 56 57 54 55 52 53 50 51 48 49 11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4 27 26 25 24 31 30 29 28 19 18 17 16 23 22 21 20 43 42 41 40 47 46 45 44 35 34 33 32 39 38 37 36 59 58 57 56 63 62 61 60 51 50 49 48 55 54 53 52 13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2 29 28 31 30 25 24 27 26 21 20 23 22 17 16 19 18 45 44 47 46 41 40 43 42 37 36 39 38 33 32 35 34 61 60 63 62 57 56 59 58 53 52 55 54 49 48 51 50 9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6 25 24 27 26 29 28 31 30 17 16 19 18 21 20 23 22 41 40 43 42 45 44 47 46 33 32 35 34 37 36 39 38 57 56 59 58 61 60 63 62 49 48 51 50 53 52 55 54 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 47 46 45 44 43 42 41 40 39 38 37 36 35 34 33 32 63 62 61 60 59 58 57 56 55 54 53 52 51 50 49 48 10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5 26 27 24 25 30 31 28 29 18 19 16 17 22 23 20 21 42 43 40 41 46 47 44 45 34 35 32 33 38 39 36 37 58 59 56 57 62 63 60 61 50 51 48 49 54 55 52 53 12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3 28 29 30 31 24 25 26 27 20 21 22 23 16 17 18 19 44 45 46 47 40 41 42 43 36 37 38 39 32 33 34 35 60 61 62 63 56 57 58 59 52 53 54 55 48 49 50 51 24 25 26 27 28 29 30 31 16 17 18 19 20 21 22 23 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 56 57 58 59 60 61 62 63 48 49 50 51 52 53 54 55 40 41 42 43 44 45 46 47 32 33 34 35 36 37 38 39 30 31 28 29 26 27 24 25 22 23 20 21 18 19 16 17 14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1 62 63 60 61 58 59 56 57 54 55 52 53 50 51 48 49 46 47 44 45 42 43 40 41 38 39 36 37 34 35 32 33 27 26 25 24 31 30 29 28 19 18 17 16 23 22 21 20 11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4 59 58 57 56 63 62 61 60 51 50 49 48 55 54 53 52 43 42 41 40 47 46 45 44 35 34 33 32 39 38 37 36 29 28 31 30 25 24 27 26 21 20 23 22 17 16 19 18 13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2 61 60 63 62 57 56 59 58 53 52 55 54 49 48 51 50 45 44 47 46 41 40 43 42 37 36 39 38 33 32 35 34 25 24 27 26 29 28 31 30 17 16 19 18 21 20 23 22 9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6 57 56 59 58 61 60 63 62 49 48 51 50 53 52 55 54 41 40 43 42 45 44 47 46 33 32 35 34 37 36 39 38 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 63 62 61 60 59 58 57 56 55 54 53 52 51 50 49 48 47 46 45 44 43 42 41 40 39 38 37 36 35 34 33 32 26 27 24 25 30 31 28 29 18 19 16 17 22 23 20 21 10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5 58 59 56 57 62 63 60 61 50 51 48 49 54 55 52 53 42 43 40 41 46 47 44 45 34 35 32 33 38 39 36 37 28 29 30 31 24 25 26 27 20 21 22 23 16 17 18 19 12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3 60 61 62 63 56 57 58 59 52 53 54 55 48 49 50 51 44 45 46 47 40 41 42 43 36 37 38 39 32 33 34 35 Итак, Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 64 получена оценка a(64) >= 824. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’ Ñообщении https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117&postid=1118 показана Ð¿Ð¾Ð»Ð½Ð°Ñ ÑиÑтема MOLS 16-го порÑдка, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· 15 взаимно ортогональных ЛК, 14 из которых ÑвлÑÑŽÑ‚ÑÑ Ð”Ð›Ðš и образуют группу MODLS. Попробовала метод Пелегрино-ЛанÑелотти Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 48 на базе ортогональных пар ДЛК 16-го порÑдка из полной ÑиÑтемы MOLS. ПрекраÑно работает! ПоÑтроилиÑÑŒ вÑе ортогональные пары! ПоÑтроила группу ОДЛК 48-го порÑдка, проверÑÑŽ программой GetOrthogonal (Harry White приÑлал ÑÐµÐ³Ð¾Ð´Ð½Ñ Ð½Ð¾Ð²ÑƒÑŽ верÑию Ñтой программы!) Order? 48 Enter the name of the squares file: inp Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file inp-orthCounts.txt ..output file inp-orthNos.txt squares 26 total orthogonal pairs 157 Maximum pairs for square 1: 13 There is 1 other square with this maximum number of pairs. ..output file inp-1orths.txt Pairs for square 1: 13 ÐžÑ‚Ð»Ð¸Ñ‡Ð½Ð°Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð°! СпаÑибо, Harry! Ð’ группе ОДЛК 48-го порÑдка имеем макÑимальное количеÑтво ОДЛК от одного ДЛК равное 13 - точно так же, как в иÑходной группе MODLS 16-го порÑдка. Показываю квадрат 1, который имеет 13 ОДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 2 19 16 1 6 7 4 5 10 11 8 9 14 15 12 13 18 3 0 17 22 23 20 21 26 27 24 25 30 47 44 29 34 35 32 33 38 39 36 37 42 43 40 41 46 31 28 45 4 5 22 7 16 1 2 3 12 13 14 15 8 9 10 11 20 21 6 23 0 17 18 19 28 29 30 47 24 41 26 27 36 37 38 39 32 33 34 35 44 45 46 31 40 25 42 43 6 7 4 21 2 3 16 1 14 15 12 13 10 11 8 9 22 23 20 5 18 19 0 17 30 47 28 29 42 27 24 25 38 39 36 37 34 35 32 33 46 31 44 45 26 43 40 41 8 9 10 11 28 13 14 15 16 1 2 3 4 5 6 7 24 25 26 27 12 29 30 47 0 17 18 35 20 21 22 23 40 41 42 43 44 45 46 31 32 33 34 19 36 37 38 39 10 11 8 9 14 47 12 13 2 3 16 1 6 7 4 5 26 27 24 25 30 15 28 29 18 19 32 17 22 23 20 21 42 43 40 41 46 31 44 45 34 35 0 33 38 39 36 37 12 13 14 15 8 9 26 11 4 5 6 7 16 1 2 3 28 29 30 47 24 25 10 27 20 37 22 23 0 17 18 19 44 45 46 31 40 41 42 43 36 21 38 39 32 33 34 35 14 15 12 13 10 11 8 25 6 7 4 5 2 3 16 1 30 47 28 29 26 27 24 9 38 23 20 21 18 19 0 17 46 31 44 45 42 43 40 41 22 39 36 37 34 35 32 33 3 2 1 16 7 6 5 4 27 10 9 8 15 14 13 12 19 18 17 0 23 22 21 36 11 26 25 24 47 30 29 28 35 34 33 32 39 38 37 20 43 42 41 40 31 46 45 44 1 16 3 2 5 4 7 6 9 24 11 10 13 12 15 14 17 0 19 18 21 20 39 22 25 8 27 26 29 28 47 30 33 32 35 34 37 36 23 38 41 40 43 42 45 44 31 46 7 6 5 4 3 2 1 16 15 14 29 12 11 10 9 8 23 22 21 20 19 34 17 0 47 30 13 28 27 26 25 24 39 38 37 36 35 18 33 32 31 46 45 44 43 42 41 40 5 4 7 6 1 16 3 2 13 12 15 30 9 8 11 10 21 20 23 22 33 0 19 18 29 28 47 14 25 24 27 26 37 36 39 38 17 32 35 34 45 44 31 46 41 40 43 42 11 10 9 8 15 14 13 12 3 2 1 16 23 6 5 4 27 26 25 40 47 30 29 28 19 18 17 0 7 22 21 20 43 42 41 24 31 46 45 44 35 34 33 32 39 38 37 36 9 8 11 10 13 12 15 14 1 16 3 2 5 20 7 6 25 24 43 26 29 28 47 30 17 0 19 18 21 4 23 22 41 40 27 42 45 44 31 46 33 32 35 34 37 36 39 38 15 14 13 12 11 10 9 8 7 6 5 4 3 2 17 16 47 46 29 28 27 26 25 24 23 22 21 20 19 18 1 0 31 30 45 44 43 42 41 40 39 38 37 36 35 34 33 32 13 12 15 14 9 8 11 10 5 4 7 6 1 16 3 18 45 28 47 30 25 24 27 26 21 20 23 22 17 0 19 2 29 44 31 46 41 40 43 42 37 36 39 38 33 32 35 34 18 40 0 17 22 23 20 21 26 27 24 25 30 47 28 29 41 19 11 42 45 44 31 46 33 32 35 34 37 36 39 38 9 8 43 10 13 12 15 14 1 16 3 2 5 4 7 6 43 17 18 19 20 21 22 23 24 25 26 27 28 29 30 47 0 42 41 8 31 46 45 44 35 34 33 32 39 38 37 36 11 10 9 40 15 14 13 12 3 2 1 16 7 6 5 4 22 23 20 46 18 19 0 17 30 47 28 29 26 27 24 25 13 44 31 21 41 40 43 42 37 36 39 38 33 32 35 34 45 12 15 14 9 8 11 10 5 4 7 6 1 16 3 2 20 21 45 23 0 17 18 19 28 29 30 47 24 25 26 27 31 14 22 44 43 42 41 40 39 38 37 36 35 34 33 32 15 46 13 12 11 10 9 8 7 6 5 4 3 2 1 16 26 27 24 25 30 36 28 29 18 19 0 17 22 23 20 21 33 32 35 34 37 47 7 38 41 40 43 42 45 44 31 46 1 16 3 2 5 4 39 6 9 8 11 10 13 12 15 14 24 25 26 27 39 29 30 47 0 17 18 19 20 21 22 23 35 34 33 32 28 38 37 4 43 42 41 40 31 46 45 44 3 2 1 16 7 6 5 36 11 10 9 8 15 14 13 12 30 47 28 29 26 27 24 34 22 23 20 21 18 19 0 17 37 36 39 38 1 32 35 25 45 44 31 46 41 40 43 42 5 4 7 6 33 16 3 2 13 12 15 14 9 8 11 10 28 29 30 47 24 25 33 27 20 21 22 23 0 17 18 19 39 38 37 36 35 2 26 32 31 46 45 44 43 42 41 40 7 6 5 4 3 34 1 16 15 14 13 12 11 10 9 8 17 0 19 18 21 20 23 22 25 35 27 26 29 28 47 30 42 43 40 41 46 31 44 45 34 24 16 33 38 39 36 37 10 11 8 9 14 15 12 13 2 3 32 1 6 7 4 5 19 18 17 0 23 22 21 20 32 26 25 24 47 30 29 28 40 41 42 43 44 45 46 31 27 33 34 3 36 37 38 39 8 9 10 11 12 13 14 15 16 1 2 35 4 5 6 7 21 20 23 22 17 0 19 18 29 28 47 37 25 24 27 26 46 31 44 45 42 43 40 41 6 39 36 30 34 35 32 33 14 15 12 13 10 11 8 9 38 7 4 5 2 3 16 1 23 22 21 20 19 18 17 0 47 30 38 28 27 26 25 24 44 45 46 31 40 41 42 43 36 5 29 39 32 33 34 35 12 13 14 15 8 9 10 11 4 37 6 7 16 1 2 3 25 24 27 26 29 28 47 30 17 0 19 18 21 31 23 22 34 35 32 33 38 39 36 37 42 43 40 41 46 20 12 45 2 3 16 1 6 7 4 5 10 11 8 9 14 15 44 13 27 26 25 24 47 30 29 28 19 18 17 0 44 22 21 20 32 33 34 35 36 37 38 39 40 41 42 43 23 45 46 15 16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 31 29 28 47 30 25 24 27 26 21 20 23 22 17 0 19 41 38 39 36 37 34 35 32 33 46 31 44 45 10 43 40 18 6 7 4 5 2 3 16 1 14 15 12 13 42 11 8 9 47 30 29 28 27 26 25 24 23 22 21 20 19 18 42 0 36 37 38 39 32 33 34 35 44 45 46 31 40 9 17 43 4 5 6 7 16 1 2 3 12 13 14 15 8 41 10 11 38 39 36 37 34 35 32 33 46 31 44 45 42 43 40 2 29 12 15 14 9 8 11 10 5 4 7 6 1 16 3 41 13 28 47 30 25 24 27 26 21 20 23 22 17 0 19 18 36 37 38 39 32 33 34 35 44 45 46 31 40 41 1 43 15 30 13 12 11 10 9 8 7 6 5 4 3 2 42 16 47 14 29 28 27 26 25 24 23 22 21 20 19 18 17 0 34 35 32 33 38 39 36 37 42 43 40 41 46 4 44 45 9 8 27 10 13 12 15 14 1 16 3 2 5 31 7 6 25 24 11 26 29 28 47 30 17 0 19 18 21 20 23 22 32 33 34 35 36 37 38 39 40 41 42 43 7 45 46 31 11 10 9 24 15 14 13 12 3 2 1 16 44 6 5 4 27 26 25 8 47 30 29 28 19 18 17 0 23 22 21 20 46 31 44 45 42 43 40 41 38 39 36 14 34 35 32 33 5 4 7 6 17 16 3 2 13 12 15 37 9 8 11 10 21 20 23 22 1 0 19 18 29 28 47 30 25 24 27 26 44 45 46 31 40 41 42 43 36 37 13 39 32 33 34 35 7 6 5 4 3 18 1 16 15 14 38 12 11 10 9 8 23 22 21 20 19 2 17 0 47 30 29 28 27 26 25 24 42 43 40 41 46 31 44 45 34 8 32 33 38 39 36 37 1 16 3 2 5 4 23 6 9 35 11 10 13 12 15 14 17 0 19 18 21 20 7 22 25 24 27 26 29 28 47 30 40 41 42 43 44 45 46 31 11 33 34 35 36 37 38 39 3 2 1 16 7 6 5 20 32 10 9 8 15 14 13 12 19 18 17 0 23 22 21 4 27 26 25 24 47 30 29 28 37 36 39 38 33 32 35 9 45 44 31 46 41 40 43 42 14 15 12 13 10 11 8 34 22 7 4 5 2 3 16 1 30 47 28 29 26 27 24 25 6 23 20 21 18 19 0 17 39 38 37 36 35 34 10 32 31 46 45 44 43 42 41 40 12 13 14 15 8 9 33 11 4 21 6 7 16 1 2 3 28 29 30 47 24 25 26 27 20 5 22 23 0 17 18 19 33 32 35 34 37 15 39 38 41 40 43 42 45 44 31 46 10 11 8 9 14 36 12 13 2 3 0 1 6 7 4 5 26 27 24 25 30 47 28 29 18 19 16 17 22 23 20 21 35 34 33 32 12 38 37 36 43 42 41 40 31 46 45 44 8 9 10 11 39 13 14 15 16 1 2 19 4 5 6 7 24 25 26 27 28 29 30 47 0 17 18 3 20 21 22 23 45 44 31 5 41 40 43 42 37 36 39 38 33 32 35 34 6 7 4 46 2 3 16 1 14 15 12 13 26 11 8 9 22 23 20 21 18 19 0 17 30 47 28 29 10 27 24 25 31 46 6 44 43 42 41 40 39 38 37 36 35 34 33 32 4 5 45 7 16 1 2 3 12 13 14 15 8 25 10 11 20 21 22 23 0 17 18 19 28 29 30 47 24 9 26 27 41 3 43 42 45 44 31 46 33 32 35 34 37 36 39 38 2 40 16 1 6 7 4 5 10 11 8 9 14 15 28 13 18 19 0 17 22 23 20 21 26 27 24 25 30 47 12 29 16 42 41 40 31 46 45 44 35 34 33 32 39 38 37 36 43 1 2 3 4 5 6 7 8 9 10 11 12 13 14 47 0 17 18 19 20 21 22 23 24 25 26 27 28 29 30 15 Таблица ортогональных пар в новой верÑии программы выводитÑÑ Ð½ÐµÑколько иначе: длкаждого ДЛК выводитÑÑ Ð¿Ð¾Ð»Ð½Ñ‹Ð¹ ÑпиÑок его ортогональных Ñоквадратов. Ð”Ð»Ñ Ð¿Ð¾ÐºÐ°Ð·Ð°Ð½Ð½Ð¾Ð¹ группы ОДЛК 48-го порÑдка таблица ортогональных пар [code]1: [3,5,7,9,11,13,15,17,19,21,23,25,26], 2: [5,7,9,11,13,15,17,19,21,23,25,26], 3: [1,4,6,8,10,12,14,16,18,20,22,24], 4: [3,7,9,11,13,15,17,19,21,23,25,26], 5: [1,2,6,8,10,12,14,16,18,20,22,24], 6: [3,5,9,11,13,15,17,19,21,23,25,26], 7: [1,2,4,8,10,12,14,16,18,20,22,24], 8: [3,5,7,11,13,15,17,19,21,23,25,26], 9: [1,2,4,6,10,12,14,16,18,20,22,24], 10: [3,5,7,9,13,15,17,19,21,23,25,26], 11: [1,2,4,6,8,12,14,16,18,20,22,24], 12: [3,5,7,9,11,15,17,19,21,23,25,26], 13: [1,2,4,6,8,10,14,16,18,20,22,24], 14: [3,5,7,9,11,13,17,19,21,23,25,26], 15: [1,2,4,6,8,10,12,16,18,20,22,24], 16: [3,5,7,9,11,13,15,19,21,23,25,26], 17: [1,2,4,6,8,10,12,14,18,20,22,24], 18: [3,5,7,9,11,13,15,17,21,23,25,26], 19: [1,2,4,6,8,10,12,14,16,20,22,24], 20: [3,5,7,9,11,13,15,17,19,23,25,26], 21: [1,2,4,6,8,10,12,14,16,18,22,24], 22: [3,5,7,9,11,13,15,17,19,21,25,26], 23: [1,2,4,6,8,10,12,14,16,18,20,24], 24: [3,5,7,9,11,13,15,17,19,21,23,26], 25: [1,2,4,6,8,10,12,14,16,18,20,22], 26: [1,2,4,6,8,10,12,14,16,18,20,22,24][/code] ИнтереÑно: еÑÑ‚ÑŒ две 13-ки - от квадрата 1 и от квадрата 26. Программа SageMath риÑует Ñту группу ОДЛК 48-го порÑдка так  Очень ÑÐ¸Ð¼Ð¿Ð°Ñ‚Ð¸Ñ‡Ð½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° ОДЛК! |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese