Ссылки на новую версию программы GetOrthogonal от Harry White

New http://budshaw.ca/Download.html#getorthogonal
and http://budshaw.ca/Download.html#getorthogonal64

Замечательный инструмент!
Ещё раз спасибо, Harry.

Вот уже и опробовала программу на новой группе ОДЛК.
Смотрите предыдущее сообщение.
Очень хорошо работает.

Да, ещё в новой программе есть счётчик ОДЛК для каждого ДЛК

               orthogonal
      square       pairs
      ------    ----------

           1           13
           2           12
           3           12
           4           12
           5           12
           6           12
           7           12
           8           12
           9           12
          10           12

          11           12
          12           12
          13           12
          14           12
          15           12
          16           12
          17           12
          18           12
          19           12
          20           12

          21           12
          22           12
          23           12
          24           12
          25           12
          26           13

Любопытно, два ДЛК имеют 13 ОДЛК, а все остальные ДЛК имеют 12 ОДЛК.

Ну, 13-ка для порядка 48 не актуальна, хотя группа ОДЛК интересна сама по себе, как полученная методом Пелегрино-Ланселотти.
В моей таблице вы видите такую оценку для порядка 48
a(48) >= 6640729 (1764493860)

Это по группе ОДЛК 12-го порядка, на основе метода составных квадратов: 48=4*12.

В сообщении
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=133&postid=2012
показана двушечка 20-го порядка, найденная от красивого ДЛК, построенного мной очень давно.

Проверила, сработает ли для этой двушечки метод Пелегрино-Ланселотти.
Сработал! Обе ортогональные пары 60-го порядка построились.
Потом ещё покрутила полученные ОДЛК 60-го порядка программой Rotate.
В результате получила замечательную группу ОДЛК 60-го порядка из 24 ОДЛК.
Проверка этой группы ОДЛК программой GetOrthogonal

Order? 60

Enter the name of the squares file: inp
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file inp-orthCounts_1.txt
..output file inp-orthNos_1.txt
squares 24 total orthogonal pairs 16
Maximum pairs for square 1: 2
There are 7 other squares with this maximum number of pairs.
..output file inp-1orths_1.txt
Pairs for square 1: 2

Класс!
ОДЛК образуют 16 ортогональных пар, двушки есть, аж 8 штук.
Смотрим таблицу ортогональных пар

1:  21 22
2:  23 24
3:  15
4:  14
5:  14
6:  15
7:  13
8:  16
9:  13
10:  16
11:  17 18
12:  19 20
13:  7 9
14:  4 5
15:  3 6
16:  8 10
17:  11
18:  11
19:  12
20:  12
21:  1
22:  1
23:  2
24:  2

Великолепный граф для порядка 60, сейчас я его нарисую :)

Итак, метод Пелегрино-Ланселотти работает для порядков k = 8, 10, 12, 16, 20 (получаются ортогональные пары порядка 3k).
Почему-то не получилось для порядка 14. Может быть, исходные ДЛК 14-го порядка плохие, нет в них нужных трансверсалей.

Ну, двушка для порядка 60, конечно, не актуальна.
В моей таблице вы видите такую оценку для порядка 60
a(60) >= 6640729 (1764493860)

Это по ДЛК 12-го порядка, на основе метода составных квадратов: 60=5*12.

Вот - золотое ожерелье 60-й пробы :)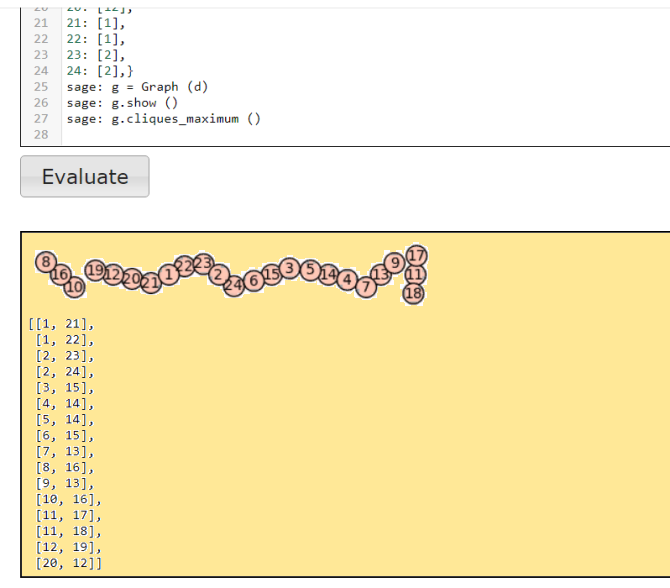



Не забывайте, это ОДЛК 60-го порядка.
Очаровательные квадратики, двушечки!
Первая двушечка
1: 21, 22
выдана программой GetOrthogonal.
Вот она

DLK
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59
10 20 12 13 14 15 16 17 18 19 59  1  2  3  4  5  6  7  8  9 30  0 32 33 34 35 36 37 38 39 48 21 22 23 24 25 26 27 28 29 50 51 52 53 54 55 56 57 58 31 40 41 42 43 44 45 46 47 11 49
 7  6 24 19  1 59 13 12 14 15 17 16  8  9 11 10  3  2  4  5 27 26 38 39 21 20 33 32 34 35 37 36 28 29  0 30 23 22 42 25 47 46 58 31 41 40 53 52 54 55 57 56 48 49 51 50 43 18 44 45
17 16  8 35 11 10  3  2  4  5  7  6 18 19  1 59 13 12 14 15 37 36 28 29  0 30 23 22 24 25 27 26 38 39 21 20 33 32 34 53 57 56 48 49 51 50 43 42 44 45 47 46 58 31 41 40  9 52 54 55
 3  2  5  4 34 17  8  9 10 11 13 12 15 14  6  7 18 19 59  1 23 22 25 24 36 37 28 29 30  0 33 32 35 47 26 27 38 39 20 21 43 42 45 44 56 57 48 49 50 51 53 52 55 54 46 16 58 31 40 41
13 12 15 14  6 25 18 19 59  1  3  2  5  4 16 17  8  9 10 11 33 32 35 34 26 27 38 39 20 21 23 22 56 24 36 37 28 29 30  0 53 52 55 54 46 47 58 31 40 41 43 42 45 44  7 57 48 49 50 51
19 18 11 10 13 12 23 15 16 17  9  8  1 59  3  2  4  5  6  7 39 38  0 30 33 32 34 35 36 37 29 28 21 20 40 22 24 25 26 27 31 58 51 50 53 52 54 55 56 57 49 48 41 14 43 42 44 45 46 47
 9  8  1 59  3  2  4 32  6  7 19 18 11 10 13 12 14 15 16 17 29 28 21 20 23 22 24 25 26 27 39 38  0 30 33 51 34 35 36 37 49 48 41 40 43 42 44 45 46 47 31 58  5 50 53 52 54 55 56 57
15 14 16 17  8  9 11 10 33 13  5  4  6  7 18 19  1 59  2  3 35 34 36 37 28 29  0 30 32 44 25 24 26 27 38 39 21 20 22 23 55 54 56 57 48 49 51 50 52 53 45 12 46 47 58 31 41 40 42 43
 5  4  6  7 18 19  1 59  2 22 15 14 16 17  8  9 11 10 12 13 25 24 26 27 38 39 21 20 55 23 35 34 36 37 28 29  0 30 32 33 45 44 46 47 58 31 41 40 42 43  3 54 56 57 48 49 51 50 52 53
11 10 13 12 15 14 17 16 19 18 27 59  3  2  5  4  7  6  9  8  0 30 33 32 35 34 37 36 39 38 21 20 23 22 25 24 58 26 29 28 51 50 53 52 55 54 57 56 31  1 41 40 43 42 45 44 47 46 49 48
 1 59  3  2  5  4  7  6  9  8 11 36 13 12 15 14 17 16 19 18 21 20 23 22 25 24 27 26 29 28  0 30 33 32 35 34 37 49 39 38 41 40 43 42 45 44 47 46 10 48 51 50 53 52 55 54 57 56 31 58
16 17  9  8 10 11  2  3  5  4  6  7 30 18 59  1 12 13 15 14 36 37 29 28 43  0 22 23 25 24 26 27 39 38 20 21 32 33 35 34 56 57 49 48 50 51 42 19 45 44 46 47 31 58 40 41 52 53 55 54
 6  7 19 18 59  1 12 13 15 14 16 17  9 21 10 11  2  3  5  4 26 27 39 38 20 52 32 33 35 34 36 37 29 28 30  0 22 23 25 24 46 47 31 58 40 41  8 53 55 54 56 57 49 48 50 51 42 43 45 44
12 13 14 15  7  6 19 18  1 59  2  3  4  5 39 16  9  8 11 10 32 33 34 35 27 26 46 38 21 20 22 23 24 25 37 36 29 28  0 30 52 53 54 55 47 17 31 58 41 40 42 43 44 45 57 56 49 48 51 50
 2  3  4  5 17 16  9  8 11 10 12 13 14 15  7 28 19 18  1 59 22 23 24 25 37 36 29 57  0 30 32 33 34 35 27 26 39 38 21 20 42 43 44 45  6 56 49 48 51 50 52 53 54 55 47 46 31 58 41 40
 8  9 59  1  2  3  5  4  7  6 18 19 10 11 12 13 29 14 17 16 28 41 20 21 22 23 25 24 27 26 38 39 30  0 32 33 35 34 37 36 48 49 40 15 42 43 45 44 47 46 58 31 50 51 52 53 55 54 57 56
18 19 10 11 12 13 15 14 17 16  8  9 59  1  2  3  5 38  7  6 50 39 30  0 32 33 35 34 37 36 28 29 20 21 22 23 25 24 27 26 58 31  4 51 52 53 55 54 57 56 48 49 40 41 42 43 45 44 47 46
 4  5  7  6 19 18 59  1  3  2 14 15 17 16  9  8 10 11 26 12 24 25 27 45 39 38 20 21 23 22 34 35 37 36 29 28 30  0 33 32 44 13 47 46 31 58 40 41 43 42 54 55 57 56 49 48 50 51 53 52
14 15 17 16  9  8 10 11 13 12  4  5  7  6 19 18 59  1  3 37 34 35 54 36 29 28 30  0 33 32 24 25 27 26 39 38 20 21 23 22  2 55 57 56 49 48 50 51 53 52 44 45 47 46 31 58 40 41 43 42
59 27 37 22 38 32 28 25 21 35 36 20 33 26 23 29 34 39 24 50 48 52 55 40 42 56 45 58 57 41 43  0 51 44 47 53 49 54 14 46 30 15 18 19 12 13 17 16 11 10  4  5  8  9  2  3  7  6  1 31
36 11 33 26 23 29 34 39 24 30  0 27 37 22 38 32 28 25 41 35 43 31 51 44 47 53 49 54 50 46 20 52 55 40 42 56 45 58 57  5  4 21  8  9  2  3  7  6  1 59 14 15 18 19 12 13 17 16 48 10
25 28 18 30 27  0 26 33 23 29 39 34 21 35 20 36 22 40 38 32 58 45 50 46 52 48 44 51 47 53 54 49 57 41 31 43  1 55 24 56 16 17 37 59 15 14  9  8  2  3  6  7 11 10  5  4 19 42 12 13
39 34 21  9 20 36 22 37 38 32 25 28 24 30 27  0 51 33 23 29 54 49 57 41 31 43 40 55 42 56 58 45 50 46 52 48 44 10 47 35  6  7 11 26  5  4 19 18 12 13 16 17  1 59 15 14 53  8  2  3
22 37 32 38 16 39 21 35 36 20 26 33 29 23 28 45 24 30  0 27 40 55 56 42 49 54 57 41 43 31 44 51 53 34  7 58 50 46 48 52 19 18 13 12 25  6 11 10  4  5  9  8  3  2 17 47  1 59 14 15
26 33 29 23 28  7 24 30  0 27 22 37 32 38 54 39 21 35 36 20 44 51 53 47 45 58 50 46 48 52 40 55 25 42 49 16 57 41 43 31  9  8  3  2 17 34  1 59 14 15 19 18 13 12 56  6 11 10  4  5
30 24 20 36 26 33 14 29 34 39 35 21 27 52 22 37 38 32 28 25 46 50 31 43 44 51 47 53 49 54 41 57  2 48 23 55 42 56 45 58 59  1  5  4  9  8  0  3  7  6 10 11 15 40 19 18 12 13 17 16
35 21 27  0 22 37 38  5 28 25 30 24 43 36 26 33 23 29 34 39 41 57 52 48 40 55 42 56 45 58 46 50 31 13 44 32 47 53 49 54 10 11 15 14 19 18 12 20 17 16 59  1 51  4  9  8  2  3  7  6
29 23 34 39 21 35 20 36 12 26 32 56 28 25 24 30 27  0 37 22 53 47 49 54 57 41 31 43 51 33  8 42 45 58 50 46 52 48 55 40  3  2  7  6 11 10  5  4 38  9 13 44 17 16  1 59 15 14 18 19
32 38 28 25 24 30 27  0 37  3 47 23 34 39 21 35 20 36 33 26 56 42 45 58 50 46 52 48 22 40 53 19 49 54 57 41 31 43 51 44 13 12 17 16  1 59 15 14 18 29 55  2  7  6 11 10  5  4  8  9
20 36 26 33 29 23 39 34 30 46  1  0 22 37 32 38 25 28 35 21 31 43 44 51 53 47 54 49 15 50 52 48 40 55 56 42 27 45 41 57  5  4  9  8  3  2  6  7 59 58 24 14 19 18 13 12 16 17 10 11
27  0 22 37 32 38 25 28 57 21 20 10 26 33 29 23 39 34 30 24 52 48 40 55 56 42 58 45 41  4 31 43 44 51 53 47 54 36 46 50 15 14 19 18 13 12 16 17 49 11  5 35  9  8  3  2  6  7 59  1
34 39 35 21 36 20 37 55 32 38 28 25 19 24  0 27 33 26 29 23 49 54 41 57 30 31 59 40 56 42 45 58 46 50 48 52 51 44 53 47  7  6 10 11  4  5 18 43 13 12 17 16 22  1 14 15  8  9  3  2
28 25 30 24  0 27 44 26 29 23 34 39 35  8 36 20 37 22 32 38 45 58 46 50 48 21 51 11 53 47 49 54 41 57 43 31 55 40 56 42 17 16 59  1 14 15 52  9  3  2  7  6 10 33  4  5 18 19 13 12
33 26 23 29 25 58 30 24 27  0 37 22 38 32 17 34 35 21 20 36 51 44 47 53  6 45 39 50 52 48 55 40 42 56 54 49 41 57 31 43  8  9  2  3 16 46 59  1 15 14 18 19 12 13 28  7 10 11  5  4
37 22 38 32 49 34 35 21 20 36 33 26 23 29 25  6 30 24 27  0 55 40 42 56 54 17 41 28 31 43 51 44 47 53 58 45 46 50 52 48 18 19 12 13 57  7 10 11  5  4  8  9  2  3 16 39 59  1 15 14
21 35  0 48 37 22 32 38 25 28 24 30 36 20 33 26 15 23 39 34 57 29  3 52 55 40 56 42 58 45 50 46 43 31 51 44 53 47 54 49 11 10 14 41 18 19 13 12 16 17  1 59  4  5  8  9 27  2  6  7
24 30 31 20 33 26 29 23 39 34 21 35  0 27 37 22 32  4 25 28 38 46 43 12 51 44 53 47 54 49 57 41 48 52 55 40 56 42 58 45  1 59 50  5  8  9  3  2  6  7 11 10 14 15 18 19 13 36 16 17
38 42 25 28 30 24  0 27 22 37 23 29 39 34 35 21 36 20 13 33  9 56 58 26 46 50 48 52 40 55 47 53 54 49 41 57 43 31 44 51 12 45 16 17 59  1 14 15 19 18  2  3  6  7 10 11  4  5 32  8
53 29 39 34 35 21 36 20 26 33 38 32 25 28 30 24  0 27 22  2 47 18 37 49 41 57 43 31 44 51 42 56 58 45 46 50 48 52 40 55 54  3  6  7 10 11  4  5  9  8 12 13 16 17 59  1 14 15 19 23
52 48 40 55 56 42 58 45 41 57 31 43 44 51 53 47 54 49 46 30  3  2 59  1  9  8  7  6  4  5 13 12 10 11 19 18 17 16 50 15 14 24 23 29 36 20 39 34 33 26 35 21 38 32  0 27 25 28 37 22
31 43 44 51 53 47 54 49 46 50 52 48 40 55 56 42 58 45 21 57 13 12 10 11 19 18 17 16 14 15  3  2 59  1  9  8  7  6  4 41 35  5 38 32  0 27 25 28 37 22 30 24 23 29 36 20 39 34 33 26
45 58 46 50 48 52 51 44 53 47 49 54 41 57 43 31 55 37 56 42  6  7 14 15  2  3 11 10 19 18 16 17  4  5 12 13 40 59  9  8 34 39  1 22 24 30 32 38  0 27 28 25 33 26 21 35 29 23 36 20
49 54 41 57 43 31 55 40 56 42 45 58 46 50 48 52 26 44 53 47 16 17  4  5 12 13  1 59  9  8  6  7 14 15  2  3 11 51 19 18 28 25 33 10 21 35 29 23 36 20 34 39 37 22 24 30 32 38  0 27
55 40 42 56 54 49 41 57 31 43 51 44 47 53 58 25 46 50 52 48  1 59  8  9 17 16  4  5 13 12 11 10 18 19 45  6 14 15  3  2 29 23 20 36  7 28 33 26 35 21 32 38 27  0 39 34 37 22 30 24
51 44 47 53 58 45 46 50 52 48 55 40 42 56 34 49 41 57 31 43 11 10 18 19  7  6 14 15  3  2  1 59  8  9 17 54  4  5 13 12 32 38 27  0 39 16 37 22 30 24 29 23 20 36 25 28 33 26 35 21
50 46 43 31 51 44 53 47 54 49 57 41 48  0 55 40 56 42 58 45 15 14 12 13 11 10 19 18 17 16  5  4 52  3  1 59  9  8  7  6 22 37 21 35 32 38  2 27 25 28 26 33 24 30 29 23 36 20 39 34
57 41 48 52 55 40 56 42 58 45 50 46 20 31 51 44 53 47 54 49  5  4  2  3  1 59  9  8  7  6 15 14 12 43 11 10 19 18 17 16 26 33 24 30 29 23 36 13 39 34 22 37 21 35 32 38  0 27 25 28
47 53 54 49 41 57 43 31 44 51 42 38 58 45 46 50 48 52 40 55 18 19 17 16  4  5 12 13 10 11 56  9  7  6 14 15  2  3 59  1 27  0 25 28 33 26 21 35  8 32 20 36 39 34 37 22 24 30 23 29
42 56 58 45 46 50 48 52 40 55 29 53 54 49 41 57 43 31 44 51  8  9  7  6 14 15  2  3 59  1 18 47 17 16  4  5 12 13 10 11 20 36 39 34 37 22 24 30 23 19 27  0 25 28 33 26 21 35 38 32
43 31 51 44 47 53 49 54 50 24 48 52 55 40 42 56 45 58 57 41 12 13 11 10 18 19 16 17 46 14  2  3  1 59  8  9  6  7  5  4 21 35 32 38 27  0 28 25 22 37 15 30 29 23 20 36 34 39 26 33
48 52 55 40 42 56 45 58 35 41 43 31 51 44 47 53 49 54 50 46  2  3  1 59  8  9  6  7  5 57 12 13 11 10 18 19 16 17 15 14 24 30 29 23 20 36 34 39 26 33 21  4 32 38 27  0 28 25 22 37
54 49 57 41 31 43 40 22 42 56 58 45 50 46 52 48 44 51 47 53 17 16  5  4 13 12 55  1  8  9  7  6 15 14  3  2 10 11 18 19 25 28 26 33 35 21 23 29 20 36 39 34 59 37 30 24 38 32 27  0
58 45 50 46 52 48 33 51 47 53 54 49 57 41 31 43 40 55 42 56  7  6 15 14  3  2 10 44 18 19 17 16  5  4 13 12 59  1  8  9 39 34 22 37 30 24 38 32 27  0 25 28 26 11 35 21 23 29 20 36
44 51 53 47 45 28 50 46 48 52 40 55 56 42 49 54 57 41 43 31 10 11 19 18 58  7 15 14  2  3 59  1  9  8 16 17  5  4 12 13 38 32  0 27 34 39 22 37 24 30 23 29 36 20  6 25 26 33 21 35
40 55 56 42 39 54 57 41 43 31 44 51 53 47 45 58 50 46 48 52 59  1  9  8 16 49  5  4 12 13 10 11 19 18  6  7 15 14  2  3 23 29 36 20 28 25 26 33 21 35 38 32  0 27 34 17 22 37 24 30
41 57 52 27 40 55 42 56 45 58 46 50 31 43 44 51 47 53 49 54  4  5 48  2 59  1  8  9  6  7 14 15 13 12 10 11 18 19 16 17 33 26 30 24 23 29 20 36 34 39 37 22 35 21 38 32  3  0 28 25
46 50 36 43 44 51 47 53 49 54 41 57 52 48 40 55 42 56 45 58 14 15 13 31 10 11 18 19 16 17  4  5  3  2 59  1  8  9  6  7 37 22 35 21 38 32 27  0 28 25 33 26 30 24 23 29 20 12 34 39
56 32 45 58 50 46 52 48 55 40 53 47 49 54 57 41 31 43 51 44 42  8  6  7 15 14  3  2  1 59 19 18 16 17  5  4 13 12 11 10 36 20 34 39 22 37 30 24 29 23  0 27 28 25 26 33 35 21  9 38
23 47 49 54 57 41 31 43 51 44 56 42 45 58 50 46 52 48 55 40 19 53 16 17  5  4 13 12 11 10  9  8  6  7 15 14  3  2  1 59  0 27 28 25 26 33 35 21 32 38 36 20 34 39 22 37 30 24 29 18

mate #1
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59
11 49 13 12 15 14 17 16 19 18  1 31  3  2  5  4  7  6  9  8 59 30 33 32 35 34 37 36 39 38 10 20 23 22 25 24 27 26 29 28 51 50 53 52 55 54 57 56  0 58 41 40 43 42 45 44 47 46 21 48
15 14 40  7  8  9 11 10  3  2  5  4 16 17 18 19  1 31 13 12 35 34 26 27 28 29 59 30 23 22 25 24 36 37 38 39 21 20  6 32 55 54 46 47 48 49 51 50 43 42 45 44 56 57 58  0 41 33 53 52
 4  5 17 50 19 18 31  1 12 13 14 15  7  6  9  8 10 11  2  3 24 25 37 36 39 38 20 21 32 33 34 35 27 26 29 28 30 59 22 16 44 45 57 56  0 58 40 41 52 53 54 55 47 46 49 48 23 51 42 43
 8  9 11 10 53  3 14 15  7  6 18 19  1 31 12 13  4  5 17 16 28 29 59 30 22 23 34 35 27 26 38 39 21  2 32 33 24 25 37 36 48 49 51 50 42 43 54 55 47 46 58  0 41 40 52 20 44 45 57 56
19 18 31  1 13 43  5  4 16 17  9  8 10 11  3  2 15 14  6  7 39 38 20 21 33 32 25 24 36 37 29 28 12 59 23 22 35 34 26 27  0 58 40 41 53 52 45 44 56 57 49 48 50 51 30 42 55 54 46 47
 2  3 15 14 16 17 44  8  1 31 12 13  5  4  6  7 19 18 11 10 22 23 35 34 36 37 29 28 21 20 32 33 25 24  9 27 39 38 59 30 42 43 55 54 56 57 49 48 41 40 52 53 45 26 46 47  0 58 51 50
13 12  4  5  7  6 18 54 10 11  3  2 14 15 17 16  8  9 31  1 33 32 24 25 27 26 38 39 30 59 23 22 34 35 37 19 28 29 20 21 53 52 44 45 47 46 58  0 50 51 43 42 36 55 57 56 48 49 40 41
17 16 18 19 10 11 12 13 46  4  7  6  8  9 31  1  2  3 15 14 37 36 38 39 30 59 32 33 25  5 27 26 28 29 20 21 22 23 35 34 57 56 58  0 50 51 52 53 45 44 47 24 48 49 40 41 42 43 55 54
 6  7  9  8  1 31  3  2 14 56 16 17 19 18 11 10 13 12  4  5 26 27 29 28 21 20 23 22 15 35 36 37 39 38 59 30 33 32 24 25 46 47 49 48 41 40 43 42 54 55 34 57  0 58 51 50 53 52 44 45
 1 31  3  2  5  4  7  6  9  8 48 10 13 12 15 14 17 16 19 18 21 20 23 22 25 24 27 26 29 28 59 30 33 32 35 34 11 36 39 38 41 40 43 42 45 44 47 46 49 37 51 50 53 52 55 54 57 56  0 58
10 11 12 13 14 15 16 17 18 19 31 58  2  3  4  5  6  7  8  9 30 59 32 33 34 35 36 37 38 39 20 21 22 23 24 25 26  1 28 29 50 51 52 53 54 55 56 57 27  0 40 41 42 43 44 45 46 47 48 49
14 15  7  6  9  8 10 11  2  3  4  5 51 16 19 18 31  1 12 13 34 35 27 26 17 28 30 59 22 23 24 25 37 36 39 38 20 21 32 33 54 55 47 46 49 48 50 29 42 43 44 45 57 56  0 58 40 41 52 53
 5  4 16 17 18 19  1 31 13 12 15 14  6 41  8  9 11 10  3  2 25 24 36 37 38  7 21 20 33 32 35 34 26 27 28 29 59 30 23 22 45 44 56 57 58  0 39 40 53 52 55 54 46 47 48 49 51 50 43 42
 9  8 10 11  3  2 15 14  6  7 19 18 31  1 42 12  5  4 16 17 29 28 30 59 23 22 13 34 26 27 39 38 20 21 33 32 25 24 36 37 49 48 50 51 43 35 55 54 46 47  0 58 40 41 53 52 45 44 56 57
18 19  1 31 12 13  4  5 17 16  8  9 11 10  2 52 14 15  7  6 38 39 21 20 32 33 24  3 37 36 28 29 59 30 22 23 34 35 27 26 58  0 41 40 25 53 44 45 57 56 48 49 51 50 42 43 54 55 47 46
 3  2 14 15 17 16  8  9 31  1 13 12  4  5  7  6 55 19 10 11 23 18 34 35 37 36 28 29 20 21 33 32 24 25 27 26 38 39 30 59 43 42 54 22 57 56 48 49 40 41 53 52 44 45 47 46 58  0 50 51
12 13  5  4  6  7 19 18 11 10  2  3 15 14 16 17  9 45  1 31  8 33 25 24 26 27 39 38 59 30 22 23 35 34 36 37 29 28 21 20 52 53 32 44 46 47  0 58 51 50 42 43 55 54 56 57 49 48 41 40
16 17 19 18 11 10 13 12  4  5  6  7  9  8  1 31  3  2 57 15 36 37 39 14 59 30 33 32 24 25 26 27 29 28 21 20 23 22 34 35 56 38  0 58 51 50 53 52 44 45 46 47 49 48 41 40 43 42 54 55
 7  6  8  9 31  1  2  3 15 14 17 16 18 19 10 11 12 13  5 47 27 26  4 29 20 21 22 23 35 34 37 36 38 39 30 59 32 33 25 24 28 46 48 49 40 41 42 43 55 54 57 56 58  0 50 51 52 53 45 44
31 58 53 52 47 46 40 41 45 44 49 48 43 42 57 56 50 51 55 33  2 10 18 16  5  3  9  1  4 17 12 59  8  6 15 13 19 11 54  7 14 39 35 30 26 32 24 28 37 21 23 29 25 20 36 22 34 38 27  0
48 10 42 43 56 57 51 50 54 55 58  0 52 53 46 47 41 40 23 45 31 12  6  8 13 15 11 19  7 14 21  2 16 18  3  5  1  9 17 44 29  4 20 25 22 36 38 34 59 27 39 33 30 35 32 26 28 24 49 37
56 57  6 41 45 44 48 49 52 53 46 47 50 51 55 54 58 24 42 43 13 15  9  1  4 17 31 12 16 18  3  5 19 11 14  7  0  2 33  8 22 36 10 28 37 21 29 23 30 35 32 26 34 38 27 59 39 40 20 25
47 46 51 16 54 55  0 58 43 42 57 56 41 40 44 45 34 48 53 52  5  3 11 19  7 14  2 10  8  6 15 13  1  9 17  4 12 49 18 23 26 32 38 31 59 27 33 39 25 20 36 22 28 24 21 37 50 29 35 30
45 44 48 49  2 52 57 56 41 40 55 54 58  0 43 35 47 46 51 50  4 17 31 12 18 16 15 13  1  9 14  7 10 20 42  6  5  3 11 19 37 21 29 23  8 30 36 22 28 24 27 59 39 33 25 53 26 32 38 34
54 55  0 58 42 12 46 47 50 51 44 45 49 48 25 53 56 57 40 41  7 14  2 10  6  8  3  5 19 11 17  4 30 31 16 52 13 15  9  1 59 27 33 39 20 18 32 26 34 38 21 37 23 29 43 35 22 36 24 28
53 52 56 57 50 51  9 45 58  0 43 42 46 21 40 41 54 55 48 49 18 16 13 15 19 11 17  4 10  2  8  6 47  5 26  1  7 14 31 12 35 30 22 36 34 38  3 37 39 33 25 20 32 44 24 28 59 27 29 23
42 43 47 46 41 40 55 19 49 48 52 53 59 56 51 50 45 44  0 58  6  8  5  3  1  9 14  7 12 31 16 18 15 57 11 36  4 17  2 10 20 25 26 32 28 24 27 13 23 29 30 35 54 22 38 34 37 21 33 39
51 50 55 54 49 48 43 42  5 47 41 32 45 44  0 58 53 52 56 57 11 19 14  7 12 31  8  6  3 24 40  9  4 17  2 10 18 16 13 15 38 34 27 59 23 29 25 20  1 26 28 46 37 21 33 39 35 30 22 36
40 41 44 45 58  0 52 53 57 15 22 51 54 55 48 49 42 43 47 46  9  1 17  4 10  2 16 18 34 13 19 50  7 14 31 12  6  8  5  3 24 28 21 37 39 33 30 35 36 11 56 38 59 27 29 23 20 25 26 32
58  0 52 53 46 47 41 40 44 29 11 49 42 43 56 57 51 50 54 55 10  2 16 18  3  5  1  9 45  4 31 12  6  8 13 15 37 19  7 14 39 33 30 35 32 26 28 24 21 48 17 23 20 25 22 36 38 34 59 27
49 48 43 42 57 56 50 51 39 54  0  1 53 52 47 46 40 41 45 44 12 31  8  6 15 13 19 11 14 55  2 10 18 16  5  3  9 27  4 17 23 29 25 20 36 22 34 38 58 59 33  7 35 30 26 32 24 28 37 21
57 56 41 40 44 45 49 38 53 52 47 46 17 50 54 55  0 58 43 42 15 13  1  9 29  4 48 31 18 16  5  3 11 19  7 14  2 10  8  6 36 22 28 24 21 37 23 51 35 30 26 32 12 34 59 27 33 39 25 20
46 47 50 51 55 54 28  0 42 43 56 57 40  7 45 44 48 49 52 53  3  5 19 11 14 39 10 58  6  8 13 15  9  1  4 17 31 12 16 18 32 26 34 38 27 59 41 33 20 25 22 36 24  2 37 21 29 23 30 35
44 45 49 48 52 20 56 57 40 41 54 55  0 58 13 43 46 47 50 51 17  4 12 31 53 18 35 15  9  1  7 14  2 10  6  8  3  5 19 11 21 37 23 29 30 42 22 36 24 28 59 27 33 39 16 25 32 26 34 38
55 54 58  0 30 42 47 46 51 50 45 44 48 49 53  3 57 56 41 40 14  7 10  2  8 43  5 25 11 19  4 17 31 12 18 16 15 13  1  9 27 59 39 33 52 20 26 32 38 34 37 21 29 23 35  6 36 22 28 24
52 53 57 27 51 50 45 44  0 58 42 43 47 46 41 40 18 54 49 48 16 22 56 13 11 19  4 17  2 10  6  8  5  3  1  9 14  7 12 31 30 35 36 55 38 34 37 21 33 39 20 25 26 32 28 24 15 59 23 29
43 42 37 47 40 41 54 55 48 49 53 52 56 57 50 51 44  8 58  0 32  6  3 46  9  1  7 14 31 12 18 16 13 15 19 11 17  4 10  2 25 20 45 26 24 28 59 27 29 23 35 30 22 36 34 38 21  5 39 33
50 36 54 55 48 49 42 43 47 46 40 41 44 45 58  0 52 53 14 56 51 11  7 38 31 12  6  8  5  3  9  1 17  4 10  2 16 18 15 13 34 57 59 27 29 23 20 25 26 32 24 28 21 37 39 33 30 35 19 22
26 40 45 44  0 58 53 52 56 57 51 50 55 54 49 48 43 42 46  4  1 41 28 17  2 10 18 16 13 15 11 19 14  7 12 31  8  6  3  5 47 24 37 21 33 39 35 30 22 36 38 34 27 59 23 29 25 20 32  9
24 28 20 25 21 37 32 26 29 23 34 38 30 35 59 27 22 36 39 54 58  0 52 53 46 47 41 40 44 45 48 49 42 43 56 57 51 50 14 55 33  7  8  6  9  1 10  2  5  3  4 17 18 16 19 11 31 12 15 13
38 34 35 30 27 59 36 22 33 39 28 24 25 20 37 21 26 32 44 29 49 48 43 42 57 56 50 51 55 54  0 58 53 52 47 46 40 41 45  4 17 23 16 18 11 19 12 31 13 15  7 14  6  8  1  9  2 10  3  5
27 59 32 26 29 23 38 34 25 20 37 21 22 36 39 33 28  0 35 30 57 56 41 40 44 45 49 48 53 52 47 46 51 50 54 55 10 58 43 42 11 19 24  2  5  3 17  4  6  8  1  9 31 12 15 13  7 14 16 18
21 37 36 22 33 39 24 28 30 35 59 27 26 32 23 29 49 38 20 25 46 47 50 51 55 54 58  0 42 43 56 57 40 41 45 44 48 31 52 53  9  1 12 34 13 15 14  7 18 16 19 11  2 10  3  5  4 17  8  6
29 23 38 34 20 25 59 27 26 32 39 33 28 24 30 42 21 37 36 22 44 45 49 48 52 53 56 57 40 41 54 55  0 58  8 43 46 47 50 51  5  3 17  4 35  6 19 11  2 10 15 13  7 14 18 16  9  1 12 31
33 39 24 28 35 30 37 21 22 36 23 29 34 38 52 20 27 59 32 26 55 54 58  0 43 42 47 46 51 50 45 44 48 49 53 18 57 56 41 40 13 15 14  7 16 25  1  9 31 12  3  5  4 17  6  8 11 19 10  2
20 25 27 59 22 36 23 29 28 24 30 35 37 47 32 26 33 39 38 34 52 53 57 56 51 50 45 44  0 58 42 43  3 46 41 40 55 54 49 48  8  6 11 19 31 12 21  5  7 14 18 16  1  9 10  2 13 15 17  4
35 30 21 37 26 32 39 33 34 38 25 20 57 27 36 22 29 23 24 28 43 42 46 47 40 41 54 55 48 49 53 52 56 13 50 51 44 45 58  0 16 18  9  1  2 10 15 59  4 17  6  8 19 11 12 31  5  3 14  7
36 22 39 33 34 38 30 35 37 21 26 40 29 23 24 28 20 25 27 59 50 51 54 55 48 49 42 43 47 46  1 41 44 45 58  0 52 53 57 56 12 31 15 13  4 17 18 16 32  9  2 10  5  3 14  7  8  6 11 19
32 26 23 29 28 24 25 20 59 27 50 36 33 39 38 34 35 30 21 37 41 40 45 44  0 58 53 52 56 57 51 11 55 54 49 48 43 42 46 47 10  2  3  5  7 14  6  8 19 22 31 12 13 15 17  4 16 18  9  1
28 24 25 20 37 21 26 32 23 45 38 34 35 30 27 59 36 22 33 39  0 58 53 52 47 46 40 41 17 44 49 48 43 42 57 56 50 51 55 54  7 14  6  8  1  9  2 10  3  5 29  4 16 18 11 19 12 31 13 15
34 38 30 35 59 27 22 36 55 33 24 28 20 25 21 37 32 26 29 23 48 49 42 43 56 57 51 50 54  7 58  0 52 53 46 47 41 40 44 45  4 17 18 16 19 11 31 12 15 13 14 39  8  6  9  1 10  2  5  3
59 27 26 32 23 29 34 48 20 25 21 37 36 22 33 39 24 28 30 35 56 57 40 41 45 44 12 49 52 53 46 47 50 51 55 54 58  0 42 43 19 11  2 10  3  5  4 17  8  6  9  1 38 31 13 15 14  7 18 16
37 21 22 36 39 33 58 24 35 30 27 59 32 26 29 23 38 34 25 20 47 46 51 50 54 55  0  2 43 42 57 56 41 40 44 45 49 48 53 52  1  9 31 12 15 13  7 14 16 18 11 19 10 28  5  3 17  4  6  8
23 29 34 38 25 53 27 59 32 26 33 39 24 28 35 30 37 21 22 36 45 44 48 49 16 52 57 56 41 40 55 54 58  0 43 42 47 46 51 50  3  5  4 17  6  8 11 19 10  2 13 15 14  7 20 18  1  9 31 12
39 33 28 24 43 35 21 37 36 22 29 23 38 34 20 25 59 27 26 32 54 55  0 58 42  6 46 47 50 51 44 45 49 48 52 53 56 57 40 41 15 13  7 14 18 16  9  1 12 31  5  3 17  4  8 30 19 11  2 10
25 20 59 56 36 22 29 23 24 28 35 30 21 37 26 32 39 33 34 38 53 52 15 57 50 51 44 45 58  0 43 42 46 47 40 41 54 55 48 49  6  8 19 11 12 31  5  3 14  7 16 18  9  1  2 10 27 13  4 17
30 35 46 21 32 26 33 39 38 34 20 25 27 59 22 36 23 29 28 24 42 43 47  5 41 40 55 54 49 48 52 53 57 56 51 50 45 44  0 58 18 16  1  9 10  2 13 15 17  4  8  6 11 19 31 12  3 37  7 14
22 51 33 39 38 34 35 30 21 37 32 26 23 29 28 24 25 20 59 27 19 50 55 54 49 48 43 42 46 47 41 40 45 44  0 58 53 52 56 57 31 12 13 15 17  4 16 18  9  1 10  2  3  5  7 14  6  8 36 11
41 32 29 23 24 28 20 25 27 59 36 22 39 33 34 38 30 35 37 21 40  9 44 45 58  0 52 53 57 56 50 51 54 55 48 49 42 43 47 46  2 10  5  3 14  7  8  6 11 19 12 31 15 13  4 17 18 16  1 26

mate #2
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59
11 49 13 12 15 14 17 16 19 18  1 31  3  2  5  4  7  6  9  8 59 30 33 32 35 34 37 36 39 38 10 20 23 22 25 24 27 26 29 28 51 50 53 52 55 54 57 56  0 58 41 40 43 42 45 44 47 46 21 48
15 14 41 16  9  8 10 11 12 13  5  4  7  6 19 18 31  1  2  3 35 34 37 36 29 28 30 59 32 33 25 24 27 26 39 38 20 21 17 23 55 54 57 56 49 48 50 51 52 53 45 44 47 46  0 58 40 22 42 43
 4  5  6 51 18 19  1 31  3  2 14 15 16 17  8  9 11 10 13 12 24 25 26 27 38 39 21 20 23 22 34 35 36 37 28 29 59 30 33  7 44 45 46 47 58  0 41 40 43 42 54 55 56 57 48 49 32 50 53 52
18 19 11 10 43 13  5  4 16 17  8  9  1 31  2  3 15 14  6  7 38 39 59 30 32 33 25 24 36 37 28 29 21 12 22 23 35 34 26 27 58  0 51 50 52 53 45 44 56 57 48 49 41 40 42 20 55 54 46 47
 9  8 31  1  3 53 14 15  7  6 19 18 10 11 13 12  4  5 17 16 29 28 20 21 23 22 34 35 27 26 39 38  2 59 33 32 24 25 37 36 49 48 40 41 43 42 54 55 47 46  0 58 50 51 30 52 44 45 57 56
13 12  5  4 16 17 54 18 10 11  3  2 15 14  6  7  9  8 31  1 33 32 25 24 36 37 39 38 30 59 23 22 35 34 19 27 29 28 20 21 53 52 45 44 56 57  0 58 50 51 43 42 55 26 46 47 49 48 40 41
 2  3 14 15  7  6  8 44  1 31 12 13  4  5 17 16 18 19 11 10 22 23 34 35 27 26 28 29 21 20 32 33 24 25 37  9 38 39 59 30 42 43 54 55 47 46 48 49 41 40 52 53 36 45 57 56 58  0 51 50
16 17 19 18  1 31 12 13 47 15  6  7  9  8 11 10  2  3  4  5 36 37 39 38 21 20 32 33 34 14 26 27 29 28 59 30 22 23 24 25 56 57  0 58 41 40 52 53 54 55 46 35 49 48 51 50 42 43 44 45
 7  6  8  9 10 11  3  2  5 57 17 16 18 19 31  1 13 12 15 14 27 26 28 29 30 59 23 22  4 24 37 36 38 39 20 21 33 32 35 34 47 46 48 49 50 51 43 42 45 44 25 56 58  0 40 41 53 52 55 54
 1 31  3  2  5  4  7  6  9  8 48 10 13 12 15 14 17 16 19 18 21 20 23 22 25 24 27 26 29 28 59 30 33 32 35 34 11 36 39 38 41 40 43 42 45 44 47 46 49 37 51 50 53 52 55 54 57 56  0 58
10 11 12 13 14 15 16 17 18 19 31 58  2  3  4  5  6  7  8  9 30 59 32 33 34 35 36 37 38 39 20 21 22 23 24 25 26  1 28 29 50 51 52 53 54 55 56 57 27  0 40 41 42 43 44 45 46 47 48 49
14 15 16 17  8  9 11 10 13 12  4  5 50  7 18 19  1 31  3  2 34 35 36 37  6 29 59 30 33 32 24 25 26 27 38 39 21 20 23 22 54 55 56 57 48 49 51 28 53 52 44 45 46 47 58  0 41 40 43 42
 5  4  7  6 19 18 31  1  2  3 15 14 17 40  9  8 10 11 12 13 25 24 27 26 39 16 20 21 22 23 35 34 37 36 29 28 30 59 32 33 45 44 47 46  0 58 38 41 42 43 55 54 57 56 49 48 50 51 52 53
19 18 10 11 13 12  4  5 17 16  9  8 31  1 52  2 14 15  7  6 39 38 30 59 33 32  3 25 37 36 29 28 20 21 23 22 34 35 27 26  0 58 50 51 53 24 44 45 57 56 49 48 40 41 43 42 54 55 47 46
 8  9  1 31  2  3 15 14  6  7 18 19 11 10 12 42  5  4 16 17 28 29 21 20 22 23 35 13 26 27 38 39 59 30 32 33 25 24 36 37 48 49 41 40 34 43 55 54 46 47 58  0 51 50 52 53 45 44 56 57
12 13  4  5 17 16 18 19 11 10  2  3 14 15  7  6 45  9  1 31 32  8 24 25 37 36 38 39 59 30 22 23 34 35 27 26 28 29 21 20 52 53 44 33 57 56 58  0 51 50 42 43 54 55 47 46 48 49 41 40
 3  2 15 14  6  7  9  8 31  1 13 12  5  4 16 17 19 55 10 11 18 22 35 34 26 27 29 28 20 21 33 32 25 24 36 37 39 38 30 59 43 42 23 54 46 47 49 48 40 41 53 52 45 44 56 57  0 58 50 51
17 16 18 19 31  1 13 12 15 14  7  6  8  9 10 11  3  2 56  4 37 36 38  5 20 21 33 32 35 34 27 26 28 29 30 59 23 22 25 24 57 39 58  0 40 41 53 52 55 54 47 46 48 49 50 51 43 42 45 44
 6  7  9  8 11 10  2  3  4  5 16 17 19 18  1 31 12 13 14 46 26 27 15 28 59 30 22 23 24 25 36 37 39 38 21 20 32 33 34 35 29 47 49 48 51 50 42 43 44 45 56 57  0 58 41 40 52 53 54 55
31 58 53 52 57 56 50 51 45 44 49 48 43 42 47 46 40 41 55 38 12 10 17 18  3  4 19  1  6 15  2 59  7  8 13 14  9 11 54  5 16 22 34 20 36 33 29 35 37 21 28 32 24 30 26 23 39 25 27  0
48 10 42 43 46 47 41 40 54 55 58  0 52 53 56 57 51 50 28 45 31  2  8  7 14 13 11  9  5 16 21 12 18 17  4  3  1 19 15 44 32  6 30 24 23 26 25 39 59 27 22 38 20 34 33 36 35 29 49 37
46 47 17 40 44 45 49 48 43 42 56 57 51 50 54 55  0 25 53 52 14 13 11  9 15  6  2 31  7  8  4  3  1 19  5 16 58 10 22 18 23 26 12 39 21 37 28 32 24 30 33 36 35 29 59 27 38 41 34 20
57 56 50  7 55 54 58  0 52 53 47 46 40 41 45 44 35 49 42 43  3  4 19  1 16  5 10 12 18 17 13 14  9 11  6 15 31 48  8 32 36 33 29  2 27 59 22 38 20 34 26 23 39 25 37 21 51 28 30 24
55 54 48 49 12 42 56 57 40 41 45 44 58  0 53 24 46 47 50 51 16  5 31  2  7  8  4  3  9 11  6 15 10 20 52 18 14 13 19  1 27 59 32 28 17 30 33 36 39 25 37 21 22 38 34 43 23 26 29 35
44 45  0 58 52  2 47 46 51 50 54 55 49 48 34 43 57 56 41 40 15  6 12 10 18 17 13 14  1 19  5 16 30 31  8 42  3  4 11  9 21 37 38 22 20  7 26 23 35 29 59 27 28 32 53 24 36 33 25 39
42 43 56 57 40 41 19 55 49 48 52 53 46 59 50 51 44 45  0 58  8  7  4  3  9 11  5 16  2 31 18 17 47 13 26  1 15  6 12 10 30 24 33 36 39 25 14 27 28 32 20 34 23 54 29 35 21 37 38 22
53 52 47 46 51 50 45  9 58  0 43 42 21 56 41 40 55 54 48 49 17 18 13 14  1 19  6 15 10 12  7  8  3 57 11 36 16  5 31  2 34 20 26 23 35 29 37  4 22 38 24 30 44 33 25 39 27 59 32 28
40 41 54 55 58  0 43 42 14 46 50 26 44 45 48 49 53 52 57 56  9 11  5 16 10 12  7  8 13 35 51  1 15  6 31  2 17 18  3  4 39 25 59 27 22 38 24 30 19 23 29 47 21 37 32 28 34 20 36 33
51 50 45 44 49 48 52 53 56  4 36 40 55 54  0 58 42 43 46 47  1 19  6 15  2 31 18 17 25  3 11 41 16  5 12 10  8  7 14 13 35 29 37 21 28 32 20 34 33  9 57 39 27 59 38 22 30 24 23 26
58  0 52 53 56 57 51 50 44 32 11 49 42 43 46 47 41 40 54 55 10 12 18 17  4  3  1 19 45  6 31  2  8  7 14 13 37  9  5 16 22 38 20 34 33 36 35 29 21 48 15 28 30 24 23 26 25 39 59 27
49 48 43 42 47 46 40 41 22 54  0  1 53 52 57 56 50 51 45 44  2 31  7  8 13 14  9 11 16 55 12 10 17 18  3  4 19 27  6 15 28 32 24 30 26 23 39 25 58 59 38  5 34 20 36 33 29 35 37 21
47 46 40 41 45 44 48 29 42 43 57 56  6 51 55 54 58  0 52 53 13 14  9 11 28 15 49  2  8  7  3  4 19  1 16  5 10 12 18 17 26 23 39 25 37 21 32 50 30 24 36 33 31 35 27 59 22 38 20 34
56 57 51 50 54 55 39 58 53 52 46 47 41 16 44 45 49 48 43 42  4  3  1 19  5 38 12  0 17 18 14 13 11  9 15  6  2 31  7  8 33 36 35 29 59 27 40 22 34 20 23 26 25 10 21 37 28 32 24 30
54 55 49 48 42 20 57 56 41 40 44 45  0 58  3 53 47 46 51 50  5 16  2 31 43  7 24  4 11  9 15  6 12 10 18 17 13 14  1 19 59 27 28 32 30 52 36 33 25 39 21 37 38 22  8 34 26 23 35 29
45 44 58  0 30 52 46 47 50 51 55 54 48 49 43 13 56 57 40 41  6 15 10 12 17 53 14 34 19  1 16  5 31  2  7  8  4  3  9 11 37 21 22 38 42 20 23 26 29 35 27 59 32 28 24 18 33 36 39 25
43 42 57 37 41 40 55 54 48 49 53 52 47 46 51 50  8 44 58  0  7 33 56  4 11  9 16  5 31  2 17 18 13 14  1 19  6 15 10 12 24 30 36 45 25 39 27 59 32 28 34 20 26 23 35 29  3 21 22 38
52 53 27 47 50 51 44 45  0 58 42 43 56 57 40 41 54 18 49 48 23 17 14 46 19  1 15  6 12 10  8  7  4  3  9 11  5 16  2 31 20 34 55 26 29 35 21 37 38 22 30 24 33 36 39 25 59 13 28 32
41 33 55 54  0 58 42 43 46 47 51 50 45 44 49 48 52 53  5 57 40  9 16 39 12 10  8  7 14 13  1 19  6 15  2 31 18 17  4  3 25 56 27 59 38 22 30 24 23 26 35 29 37 21 28 32 20 34 11 36
23 51 44 45 48 49 53 52 57 56 40 41 54 55 58  0 43 42 47 15 19 50 29  6 31  2 17 18  3  4  9 11  5 16 10 12  7  8 13 14 46 35 21 37 32 28 34 20 36 33 39 25 59 27 22 38 24 30 26  1
39 25 30 24 21 37 23 26 32 28 29 35 20 34 59 27 33 36 22 54 58  0 52 53 56 57 51 50 44 45 48 49 42 43 46 47 41 40 16 55 38  5  7  8  9 11 31  2  3  4  6 15 17 18 19  1 10 12 13 14
35 29 34 20 27 59 36 33 38 22 25 39 24 30 37 21 26 23 44 32 49 48 43 42 47 46 40 41 55 54  0 58 53 52 57 56 50 51 45  6 15 28 18 17  1 19 12 10 14 13  5 16  8  7 11  9  2 31  4  3
27 59 36 33 28 32 29 35 20 34 37 21 26 23 38 22 39 58 30 24 47 46 40 41 45 44 48 49 42 43 57 56 50 51 55 54 12  0 52 53  1 19 25 10  4  3  6 15 17 18 11  9  2 31 14 13 16  5  7  8
21 37 23 26 22 38 25 39 24 30 59 27 33 36 32 28 48 29 34 20 56 57 51 50 54 55  0 58 53 52 46 47 41 40 44 45 49  2 43 42  9 11 31 35 13 14  5 16  8  7 19  1 10 12  3  4 15  6 18 17
22 38 35 29 20 34 37 21 33 36 32 28 25 39 30 52 27 59 23 26 54 55 49 48 42 43 57 56 41 40 44 45  0 58 17 53 47 46 51 50 13 14 15  6 24 18 11  9 10 12  3  4  5 16  7  8  1 19 31  2
28 32 39 25 24 30 59 27 26 23 38 22 29 35 42 20 21 37 36 33 45 44 58  0 53 52 46 47 50 51 55 54 48 49 43  7 56 57 40 41  4  3 16  5  8 34 19  1  2 31 14 13  6 15 18 17  9 11 12 10
34 20 37 21 33 36 38 22 29 35 24 30 27 47 23 26 28 32 39 25 43 42 57 56 41 40 55 54 48 49 53 52 14 46 51 50 45 44 58  0 18 17 11  9 10 12 59 13  6 15  8  7  1 19 31  2  4  3 16  5
30 24 59 27 26 23 32 28 25 39 20 34 57 37 36 33 22 38 35 29 52 53 46 47 50 51 44 45  0 58 42 43 56  4 40 41 54 55 49 48  7  8 19  1  2 31  3 21  5 16 17 18  9 11 12 10 13 14 15  6
33 36 38 22 25 39 20 34 59 27 23 51 28 32 35 29 30 24 21 37 41 40 55 54  0 58 42 43 46 47 19 50 45 44 49 48 52 53 56 57 10 12 14 13  5 16 17 18 26  1 31  2  4  3 15  6  7  8  9 11
26 23 32 28 29 35 24 30 37 21 41 33 22 38 39 25 34 20 27 59 50 51 44 45 48 49 53 52 57 56 40  9 54 55 58  0 43 42 47 46  2 31  3  4  6 15  8  7 11 36 12 10 13 14 16  5 18 17  1 19
25 39 24 30 37 21 26 23 28 45 35 29 34 20 27 59 36 33 38 22  0 58 53 52 57 56 50 51 15 44 49 48 43 42 47 46 40 41 55 54  5 16  8  7 11  9  2 31  4  3 32  6 18 17  1 19 12 10 14 13
29 35 20 34 59 27 33 36 55 38 39 25 30 24 21 37 23 26 32 28 48 49 42 43 46 47 41 40 54  5 58  0 52 53 56 57 51 50 44 45  6 15 17 18 19  1 10 12 13 14 16 22  7  8  9 11 31  2  3  4
59 27 33 36 32 28 35 49 34 20 21 37 23 26 22 38 25 39 24 30 46 47 41 40 44 45 31 48 43 42 56 57 51 50 54 55  0 58 53 52 19  1 10 12  3  4 15  6 18 17  9 11 29  2 13 14  5 16  8  7
37 21 26 23 38 22  0 25 30 24 27 59 36 33 28 32 29 35 20 34 57 56 50 51 55 54 58 10 52 53 47 46 40 41 45 44 48 49 42 43 11  9  2 31 14 13 16  5  7  8  1 19 12 39  4  3  6 15 17 18
38 22 29 35 34 43 21 37 36 33 28 32 39 25 24 30 59 27 26 23 55 54 48 49  8 42 56 57 40 41 45 44 58  0 53 52 46 47 50 51 14 13  6 15 18 17  9 11 12 10  4  3 16  5 20  7 19  1  2 31
32 28 25 39 53 24 27 59 23 26 22 38 35 29 20 34 37 21 33 36 44 45  0 58 52 18 47 46 51 50 54 55 49 48 42 43 57 56 41 40  3  4  5 16  7  8  1 19 31  2 13 14 15  6 17 30 11  9 10 12
20 34 21 56 36 33 22 38 35 29 30 24 59 27 26 23 32 28 25 39 42 43  3 57 40 41 54 55 49 48 52 53 46 47 50 51 44 45  0 58 17 18  9 11 12 10 13 14 15  6  7  8 19  1  2 31 37  4  5 16
24 30 46 59 23 26 28 32 39 25 34 20 37 21 33 36 38 22 29 35 53 52 47 13 51 50 45 44 58  0 43 42 57 56 41 40 55 54 48 49  8  7  1 19 31  2  4  3 16  5 18 17 11  9 10 12 14 27  6 15
36 40 22 38 39 25 34 20 27 59 26 23 32 28 29 35 24 30 37 21 11 41 54 55 58  0 43 42 47 46 50 51 44 45 48 49 53 52 57 56 12 10 13 14 16  5 18 17  1 19  2 31  3  4  6 15  8  7 33  9
50 26 28 32 35 29 30 24 21 37 33 36 38 22 25 39 20 34 59 27 51  1 45 44 49 48 52 53 56 57 41 40 55 54  0 58 42 43 46 47 31  2  4  3 15  6  7  8  9 11 10 12 14 13  5 16 17 18 19 23

О проверке текущей БД КФ ОДЛК 9-го порядка в нашем ручном проекте напишу тут.
Опробовала новую программу Harry White GetOrthogonal.
Посмотрела, как программа справится с большим набором ОДЛК. Справилась отлично!

Итак, беру нашу БД КФ ОДЛК 9-го порядка, которая содержит на данный момент 68669 КФ ОДЛК.
Замечу, что это не сильно меньше, чем полная БД КФ ОДЛК данного порядка, найденная в BOINC-проектах (75307 КФ ОДЛК там получено).

Пропускаю все КФ ОДЛК через программу Белышева ortogon_u.
Получаю много-много mates.
"Хвост" выходного файла

. . . . . 
[DLK(1):283367]
0 8 7 6 3 4 5 2 1
7 1 3 4 5 2 8 0 6
4 7 2 1 0 6 3 8 5
6 0 8 3 2 7 1 5 4
5 3 6 7 4 8 2 1 0
1 2 0 8 6 5 7 4 3
8 4 5 2 1 0 6 3 7
3 6 4 5 8 1 0 7 2
2 5 1 0 7 3 4 6 8

[DLK(1):283368]
0 8 7 6 3 4 5 2 1
7 1 3 4 5 2 8 0 6
6 0 2 7 8 1 3 4 5
4 5 8 3 1 7 2 6 0
5 3 1 2 4 6 0 8 7
3 4 6 8 0 5 7 1 2
1 2 5 0 7 8 6 3 4
8 6 4 5 2 0 1 7 3
2 7 0 1 6 3 4 5 8

[DLK(1):283369]
0 8 7 6 3 4 5 2 1
7 1 3 4 5 2 8 0 6
8 5 2 1 0 6 3 4 7
6 0 8 3 2 7 4 1 5
5 3 1 7 4 8 0 6 2
1 2 4 8 6 5 7 3 0
3 7 5 2 1 0 6 8 4
4 6 0 5 8 1 2 7 3
2 4 6 0 7 3 1 5 8

"Товарищей" имеем 283369. Ну, их надо нормализовать и удалить дубликаты. В результате "товарищей" станет меньше.
Объединив всех нормализованных "товарищей" с исходными ДЛК БД, получила группу ОДЛК в количестве 180402 штук.
Солидная группа! Программа GetOrthogonal пыхтела над проверкой зтой группы 2,5 часа.
Вот результат проверки

Order? 9

Enter the name of the squares file: INP1
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file INP1-orthCounts.txt
..output file INP1-orthNos.txt
    .. increasing LS store to     100,000
    .. increasing LS store to     200,000
squares 180402 total orthogonal pairs 285407
Maximum pairs for square 14597: 614
This is the only square with this maximum number of pairs.
..output file INP1-14597orths.txt
Pairs for square 14597: 614

elapsed time 2:30:22

Очень интересно!
Во-первых, данная группа ОДЛК образует 285407 ортогональных пар.
Во-вторых, максимальную группу ОДЛК от одного ДЛК программа обнаружила только одну, она происходит от квадрата 14597, программа выводит эту максимальную группу ОДЛК.
В-третьих, интересно изучить таблицу ортогональных пар, она сейчас очень удобная для исследования.
Показываю фрагмент таблицы ортогональных пар

. . . . . . 
170:  97035
171:  172470 172471 172510 172511
172:  147283
173:  150788
174:  103398 103479
175:  103399 103480
176:  103456 103459 103464 103467 103472 103475 107086 107087 107090 107091
 107094 107095
177:  103375 103378 103383 103386 103391 103394 103456 103459 103464 103467
 103472 103475 107072 107073 107076 107077 107086 107087 107090 107091
 107094 107095 122148 122149 122152 122153 122158 122159 122162 122163
 127491 127492 127493 127502 127503 127505 154912 154915 154920 154923
 154928 154931 155008 155011 155016 155019 155024 155027 171461 171464
 171465 171474 171478 171479
178:  103374 103379 103382 103387 103390 103395 103455 103460 103463 103468
 103471 103476 107071 107074 107075 107078 107085 107088 107089 107092
 107093 107096 122147 122150 122151 122154 122157 122160 122161 122164
 154911 154916 154919 154924 154927 154932 155007 155012 155015 155020
 155023 155028 171462 171463 171466 171475 171477 171480
179:  107077
180:  103375 103378 103383 103386 103391 103394 103456 103459 103464 103467
 103472 103475 107072 107073 107076 107077 107086 107087 107090 107091
 107094 107095 122148 122149 122152 122153 122158 122159 122162 122163
 154912 154915 154920 154923 154928 154931 155008 155011 155016 155019
 155024 155027 171464 171465 171478 171479
. . . . . .

Наконец, программа выводит счётчик ортогональных пар для всех ДЛК группы, это тоже очень удобно.

В общем, изучаем, господа, БД КФ ОДЛК 9-го порядка.
В моём ручном проекте пока БД КФ ОДЛК 9-го порядка не полная.
О текущем состоянии данного проекта смотрите тему
https://boinc.progger.info/odlk/forum_thread.php?id=44

Господин Ватутин объявил о получении полной БД КФ ОДЛК 9-го порядка в двух BOINC-проектах.
И что мешает проверить всю БД на максимальную клику?
Я выдвинула гипотезу в OEIS, что максимальная группа MODLS 9-го порядка содержит 6 взаимно ортогональных ДЛК.
Вообще-то, сначала это была не гипотеза, а утверждение.
Но Ватутин сказал, что говорить о максимальной клике 9-го порядка преждевременно, пока нет полной БД и нельзя это проверить полным перебором.
Теперь полная БД уже давно есть.
Что мешает проверить???

Смотрю в счётчик ортогональных пар.
Вот стайка 20-к

        199           20
         200           20

         201           20
         202           20
         203           20
         204           20
         205           20
         206           20
         207           20
         208           20

Вот тут много солидных групп подряд

        260          196

         261           10
         262            2
         263          188
         264          204
         265            4
         266            4
         267          220
         268           10
         269           10
         270            2

         271          196
         272          190
         273            9
         274            9
         275            5
         276            5
         277           22
         278           20
         279           20
         280           22

         281            8
         282            2
         283           16
         284           16
         285            4
         286            2
         287           14
         288           14
         289           12
         290           12

Ну, и так далее.
Надо посмотреть, не нашлись ли группы ОДЛК, которые раньше отсутствовали.

Удивительно! Отсутствующих раньше групп ОДЛК и сейчас нет.

Это начало группы из 614 ОДЛК к квадрату 14597, выданной программой GetOrthogonal

0 2 5 4 7 3 8 6 1
5 1 6 7 8 2 4 0 3
8 4 2 5 6 0 3 1 7
6 8 0 3 2 7 1 5 4
1 0 3 8 4 6 7 2 5
4 7 1 6 3 5 2 8 0
7 3 8 0 5 1 6 4 2
3 5 4 2 1 8 0 7 6
2 6 7 1 0 4 5 3 8

0 1 2 3 4 5 6 7 8
3 7 4 8 5 2 1 6 0
2 4 8 7 6 1 3 0 5
8 3 5 4 7 0 2 1 6
6 8 1 0 2 3 7 5 4
5 2 3 1 8 6 0 4 7
1 6 7 2 0 4 5 8 3
7 5 0 6 1 8 4 3 2
4 0 6 5 3 7 8 2 1

0 1 2 3 4 5 6 7 8
4 2 1 6 3 8 7 5 0
5 0 3 1 8 6 2 4 7
3 7 8 4 5 1 0 6 2
1 4 7 8 6 2 3 0 5
8 5 6 0 1 7 4 2 3
2 8 4 7 0 3 5 1 6
6 3 5 2 7 0 1 8 4
7 6 0 5 2 4 8 3 1

0 1 2 3 4 5 6 7 8
4 2 1 6 3 8 7 5 0
5 0 3 1 8 6 2 4 7
3 8 7 4 5 1 0 6 2
1 4 8 7 6 2 3 0 5
8 5 6 0 1 7 4 2 3
2 7 4 8 0 3 5 1 6
6 3 5 2 7 0 1 8 4
7 6 0 5 2 4 8 3 1

0 1 2 3 4 5 6 7 8
4 3 8 2 1 6 0 5 7
7 8 5 0 6 4 1 2 3
1 5 7 6 8 0 4 3 2
6 2 0 8 7 3 5 4 1
5 7 1 4 2 8 3 0 6
8 4 3 1 5 7 2 6 0
3 6 4 7 0 2 8 1 5
2 0 6 5 3 1 7 8 4
. . . . . . 

Первый ДЛК - это основной ДЛК, то есть квадрат 14597.
Да, всё точно. Этот тот самый ДЛК!
Смотрите на иллюстрации этот ДЛК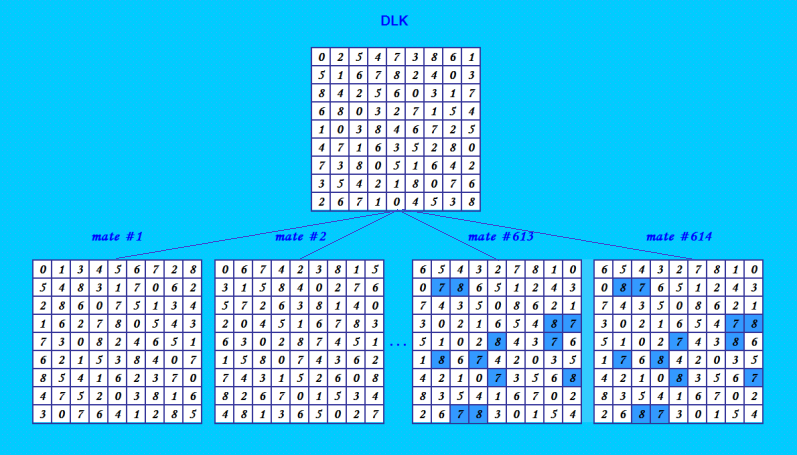



Только на иллюстрации ортогональки не нормализованные, а программа GetOrthogonal выводит нормализованные ортогональки, потому что она такие получила на входе.

В сообщении
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=133&postid=2013
показана двушка 18-го порядка, полученная от ДЛК, построенного мной очень давно.

Тэк-с, а для двушки 18-го порядка я, кажется, метод Пелегрино-Ланселотти не пробовала.
Сейчас попробую.

У-р-р-р-а-а-а!
Получилось! Двушечка 54-го порядка найдена, и не одна.

Order? 54

Enter the name of the squares file: inp
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file inp-orthCounts_2.txt
..output file inp-orthNos_2.txt
squares 24 total orthogonal pairs 16
Maximum pairs for square 5: 2
There are 7 other squares with this maximum number of pairs.
..output file inp-5orths.txt
Pairs for square 5: 2

Смотрим таблицу ортогональных пар

1:  18
2:  18
3:  9
4:  9
5:  16 17
6:  7 8
7:  6
8:  6
9:  3 4
10:  24
11:  24
12:  19 20
13:  23
14:  23
15:  21 22
16:  5
17:  5
18:  1 2
19:  12
20:  12
21:  15
22:  15
23:  13 14
24:  10 11

Двушек 8 штук.
Наверное, тоже получится ожерелье, только 54-й пробы :)
Сейчас нарисую :)

Да, главное забыла: получили улучшение оценки для порядка 54
a(54) >= 2.
Сейчас в таблице исправлю.

И двушечку 54-го порядка покажу, которую вывела программа GetOrthogohal; это одна из 8 двушек, имеющихся в данной группе ОДЛК

DLK
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
6 29 12 2 3 4 5 1 10 8 16 13 14 15 17 7 18 9 24 11 30 20 21 22 23 19 28 26 34 31 32 33 53 25 36 27 42 47 48 38 39 40 41 37 46 44 52 49 50 51 35 43 0 45
14 9 24 13 2 3 4 12 16 10 7 15 17 18 1 11 8 5 32 27 6 31 20 21 22 30 34 28 25 33 53 0 19 47 26 23 50 45 42 49 38 39 40 48 52 46 43 51 35 36 37 29 44 41
17 15 8 27 14 2 3 13 7 16 1 18 11 12 6 10 5 4 53 33 26 9 32 20 21 31 25 34 19 0 29 30 42 28 23 22 35 51 44 45 50 38 39 49 43 52 37 36 47 48 24 46 41 40
11 18 17 10 26 15 2 14 1 7 12 6 13 9 16 5 4 3 29 0 53 28 8 33 20 32 19 25 30 24 31 45 34 23 22 21 47 36 35 46 44 51 38 50 37 43 48 42 49 27 52 41 40 39
9 6 11 18 16 28 17 15 12 1 13 14 8 7 5 4 3 2 27 24 29 0 34 10 53 33 30 19 31 32 44 25 23 22 21 20 45 42 47 36 52 46 35 51 48 37 49 50 26 43 41 40 39 38
15 8 9 6 11 7 34 17 13 12 14 10 1 5 4 3 2 18 33 26 27 24 29 25 16 53 31 30 32 46 19 23 22 21 20 0 51 44 45 42 47 43 52 35 49 48 50 28 37 41 40 39 38 36
1 12 13 14 15 17 18 22 5 2 3 7 16 10 8 9 6 11 19 30 31 32 33 53 0 4 23 20 39 25 34 28 26 27 24 29 37 48 49 50 51 35 36 40 41 38 21 43 52 46 44 45 42 47
8 10 16 7 1 12 13 2 21 4 5 9 6 11 18 17 15 14 26 28 34 25 19 30 31 20 3 40 23 27 24 29 0 53 33 32 44 46 52 43 37 48 49 38 39 22 41 45 42 47 36 35 51 50
12 13 14 15 17 18 11 3 2 23 4 1 7 16 10 8 9 6 30 31 32 33 53 0 29 21 38 5 22 19 25 34 28 26 27 24 48 49 50 51 35 36 47 39 20 41 40 37 43 52 46 44 45 42
10 16 7 1 12 13 14 5 4 3 20 8 9 6 11 18 17 15 28 34 25 19 30 31 32 41 22 21 2 26 27 24 29 0 53 33 46 52 43 37 48 49 50 23 40 39 38 44 45 42 47 36 35 51
7 2 3 4 5 11 15 16 9 6 8 53 18 1 12 13 14 10 25 20 21 22 23 29 51 34 27 24 26 17 0 19 30 31 32 28 43 38 39 40 41 47 33 52 45 42 44 35 36 37 48 49 50 46
2 3 4 5 18 14 8 10 6 11 9 16 33 17 7 1 12 13 20 21 22 23 0 50 26 28 24 29 27 34 15 53 25 19 30 31 38 39 40 41 36 32 44 46 42 47 45 52 51 35 43 37 48 49
3 4 5 17 13 9 12 8 11 18 6 2 10 32 15 16 7 1 21 22 23 53 49 27 30 26 29 0 24 20 28 14 33 34 25 19 39 40 41 35 31 45 48 44 47 36 42 38 46 50 51 52 43 37
4 5 15 12 6 1 7 9 18 17 11 3 2 8 31 14 10 16 22 23 33 48 24 19 25 27 0 53 29 21 20 26 13 32 28 34 40 41 51 30 42 37 43 45 36 35 47 39 38 44 49 50 46 52
5 14 1 11 7 16 10 6 17 15 18 4 3 2 9 30 13 8 23 32 37 29 25 34 28 24 53 33 0 22 21 20 27 12 31 26 41 50 19 47 43 52 46 42 35 51 36 40 39 38 45 48 49 44
13 7 18 16 10 8 9 11 15 14 17 5 4 3 2 6 19 12 31 43 0 34 28 26 27 29 33 32 53 23 22 21 20 24 1 30 49 25 36 52 46 44 45 47 51 50 35 41 40 39 38 42 37 48
16 17 10 8 9 6 1 18 14 13 15 12 5 4 3 2 11 25 52 53 28 26 27 24 19 0 32 31 33 30 23 22 21 20 29 7 34 35 46 44 45 42 37 36 50 49 51 48 41 40 39 38 47 43
42 49 41 40 39 38 16 43 52 45 46 47 48 51 50 36 37 35 8 15 5 4 3 2 44 12 1 10 7 9 14 18 24 6 13 11 20 27 33 31 53 34 29 0 28 25 19 22 32 21 17 30 26 23
44 47 48 41 40 39 38 49 46 52 37 51 50 36 35 12 42 45 16 9 14 5 31 3 2 15 7 1 13 18 17 6 11 43 8 10 29 22 32 33 4 53 34 27 19 28 26 21 24 30 23 0 20 25
50 45 44 51 41 40 39 48 37 46 43 36 35 42 49 47 1 38 17 25 16 18 5 4 3 14 13 7 12 6 11 8 15 9 52 2 24 10 29 21 33 31 53 32 26 19 0 30 23 20 27 22 28 34
35 36 52 45 50 41 40 51 43 37 49 42 47 14 44 46 38 39 11 6 1 10 17 5 4 18 12 13 15 8 9 48 16 7 2 53 23 30 28 25 24 33 31 21 0 26 27 20 22 32 29 19 34 3
47 42 35 46 52 36 41 50 49 43 48 44 51 45 13 38 39 40 9 8 11 7 1 6 33 17 15 12 14 16 18 10 37 2 3 4 22 20 23 19 28 30 5 24 27 0 32 29 21 25 26 34 53 31
45 44 47 42 37 46 35 36 48 49 51 17 52 43 38 39 40 41 10 16 9 8 13 7 11 6 14 15 21 50 1 12 2 3 4 5 25 29 22 20 26 19 23 30 32 27 18 24 28 0 34 53 31 33
36 52 45 44 47 43 37 35 51 48 50 46 15 38 39 40 41 42 6 1 10 16 9 12 13 23 18 14 17 7 49 2 3 4 5 8 30 28 25 29 22 0 26 11 21 32 24 19 27 34 53 31 33 20
49 48 51 50 36 35 42 39 38 5 40 43 37 46 52 45 44 47 15 14 18 17 6 11 8 3 2 41 4 12 26 7 1 10 16 9 27 32 21 24 30 23 20 53 34 33 31 0 13 19 28 25 29 22
52 46 37 43 49 48 51 41 40 39 2 45 44 47 42 35 36 50 1 7 13 12 15 32 18 5 4 3 38 10 16 9 8 11 6 17 28 19 26 0 27 14 21 33 31 53 34 25 29 22 20 23 30 24
48 51 50 36 35 42 47 4 41 38 39 49 43 37 46 52 45 44 14 18 17 30 11 8 9 40 5 2 3 15 12 13 7 1 10 16 32 21 24 6 23 20 22 31 33 34 53 27 0 26 19 28 25 29
46 37 43 49 48 51 50 38 3 40 41 52 45 44 47 42 35 36 7 13 12 15 14 18 17 2 39 4 5 28 10 16 9 8 11 6 19 26 0 27 32 21 24 34 53 31 33 1 25 29 22 20 23 30
43 41 40 39 38 47 36 37 45 44 52 35 42 49 48 51 50 7 12 5 4 3 2 9 6 13 10 16 1 11 8 27 14 18 17 46 0 33 31 53 34 22 30 26 25 29 28 23 20 15 32 21 24 19
41 40 39 38 8 50 52 46 44 47 45 37 36 35 43 49 48 51 5 4 3 2 42 17 1 7 16 22 10 13 6 11 12 15 14 18 33 31 53 34 20 24 28 19 29 9 25 26 30 23 0 27 32 21
40 39 38 35 51 10 48 52 47 42 44 41 46 50 36 37 43 49 4 3 2 11 18 45 14 1 9 8 16 5 7 17 6 13 0 15 31 53 34 23 21 25 32 28 22 20 29 33 19 24 30 26 12 27
39 38 6 48 44 49 43 45 42 35 47 40 41 52 51 50 46 37 3 2 36 14 16 15 12 10 20 11 9 4 5 1 18 17 7 13 53 34 30 32 29 27 0 25 8 23 22 31 33 28 21 24 19 26
38 50 49 9 43 37 46 44 35 36 42 39 40 41 45 48 51 52 34 17 15 47 12 13 7 16 11 6 8 3 4 5 10 14 18 1 2 24 27 22 0 26 19 29 23 30 20 53 31 33 25 32 21 28
18 43 42 37 46 52 45 47 36 50 35 38 39 40 41 44 49 48 51 12 8 13 7 1 10 9 6 17 11 2 3 4 5 29 15 14 21 0 20 26 19 28 25 22 30 24 23 34 53 31 33 16 27 32
37 11 46 52 45 44 49 42 50 51 36 48 38 39 40 41 47 43 13 35 19 1 10 16 15 8 17 18 6 14 2 3 4 5 9 12 26 23 7 28 25 29 27 20 24 21 30 32 34 53 31 33 22 0
19 24 21 20 23 22 31 29 33 32 53 30 27 26 28 34 0 46 2 36 39 38 41 40 37 35 49 48 50 43 47 42 45 44 51 25 52 12 18 8 11 9 7 3 4 6 14 10 16 17 15 13 5 1
31 30 27 21 20 23 22 24 53 33 0 26 28 34 25 29 52 32 37 10 47 39 38 41 40 36 50 49 51 42 45 44 46 35 19 48 7 43 16 18 8 11 9 12 14 4 5 17 15 13 1 3 2 6
28 32 31 26 21 20 23 27 0 53 29 34 25 19 24 43 33 22 45 48 7 42 39 38 41 47 51 50 35 44 46 52 36 30 49 40 15 6 37 17 18 8 11 16 5 14 3 13 1 2 12 10 4 9
25 34 33 32 28 21 20 26 29 0 24 19 30 27 37 53 22 23 46 44 49 6 45 39 38 42 35 51 36 52 43 47 31 50 40 41 1 13 4 48 15 18 8 17 3 5 12 2 10 16 7 14 9 11
30 19 25 53 33 34 21 28 24 29 27 31 26 48 0 22 23 20 43 52 46 50 4 44 39 45 36 35 47 37 42 32 51 40 41 38 10 2 1 14 49 13 18 15 12 3 16 7 17 6 5 9 11 8
32 31 30 19 0 53 25 34 27 24 26 28 49 29 22 23 20 21 48 37 43 52 51 14 46 44 47 36 42 45 33 35 40 41 38 39 6 7 10 2 5 50 1 13 16 12 17 15 4 3 9 11 8 18
34 33 32 31 30 29 0 25 26 27 28 50 24 22 23 20 21 19 44 49 48 37 43 35 5 46 42 47 45 53 36 40 41 38 39 52 13 4 6 7 10 3 51 1 17 16 15 14 12 9 11 8 18 2
24 27 26 28 34 25 19 23 22 21 38 29 0 53 33 32 31 30 36 47 42 45 44 46 52 11 40 39 20 35 51 50 49 48 37 43 12 16 17 15 13 1 2 41 9 18 8 3 5 14 4 6 7 10
33 53 0 29 24 27 26 21 20 41 22 32 31 30 19 25 34 28 49 50 51 35 36 47 42 39 8 23 40 48 37 43 52 46 44 45 4 14 5 3 12 16 17 18 38 11 9 6 7 10 2 1 13 15
27 26 28 34 25 19 30 20 39 22 23 24 29 0 53 33 32 31 47 42 45 44 46 52 43 38 21 9 41 36 35 51 50 49 48 37 16 17 15 13 1 2 10 8 18 40 11 12 3 5 14 4 6 7
53 0 29 24 27 26 28 40 23 20 21 33 32 31 30 19 25 34 50 51 35 36 47 42 45 22 41 38 18 49 48 37 43 52 46 44 14 5 3 12 16 17 15 9 11 8 39 4 6 7 10 2 1 13
29 21 20 23 22 30 44 0 32 31 33 25 19 24 27 26 28 53 35 39 38 41 40 43 34 51 48 37 49 1 52 36 47 42 45 50 3 18 8 11 9 10 13 5 6 7 4 46 2 12 16 17 15 14
21 20 23 22 19 45 33 53 31 30 32 0 34 25 29 24 27 26 39 38 41 40 52 28 49 50 37 43 48 51 13 46 35 36 47 42 18 8 11 9 2 15 4 14 7 10 6 5 44 1 3 12 16 17
20 23 22 25 42 32 27 33 30 19 31 21 53 28 34 0 29 24 38 41 40 46 26 48 47 49 43 52 37 39 50 15 44 51 35 36 8 11 9 1 17 6 16 4 10 2 7 18 14 45 13 5 3 12
23 22 34 47 31 24 29 32 19 25 30 20 21 33 26 28 53 0 41 40 44 27 37 36 35 48 52 46 43 38 39 49 17 45 50 51 11 9 13 16 7 12 3 6 2 1 10 8 18 4 42 15 14 5
22 28 36 30 29 0 53 31 25 34 19 23 20 21 32 27 26 33 40 45 24 43 35 51 50 37 46 44 52 41 38 39 48 16 42 49 9 15 12 10 3 5 14 7 1 13 2 11 8 18 6 47 17 4
26 35 19 0 53 33 32 30 34 28 25 22 23 20 21 31 24 27 42 29 52 51 50 49 48 43 44 45 46 40 41 38 39 37 12 47 17 3 2 5 14 4 6 10 13 15 1 9 11 8 18 7 36 16
51 25 53 33 32 31 24 19 28 26 34 27 22 23 20 21 30 29 0 46 50 49 48 37 36 52 45 42 44 47 40 41 38 39 43 3 5 1 14 4 6 7 12 2 15 17 13 16 9 11 8 18 10 35

mate #1
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
10 22 5 6 18 1 9 17 16 7 8 12 13 14 15 2 11 3 28 4 23 24 0 19 27 53 34 25 26 30 31 32 33 20 47 21 46 40 41 42 36 37 45 35 52 43 44 48 49 50 51 38 29 39
12 8 19 9 3 4 5 11 2 17 16 13 14 15 6 10 18 7 30 26 1 27 21 22 23 29 20 53 34 31 32 33 24 46 0 25 48 44 37 45 39 40 41 47 38 35 52 49 50 51 42 28 36 43
13 12 16 23 7 18 1 10 6 11 2 14 15 3 8 4 17 9 31 30 34 5 25 0 19 28 24 29 20 32 33 21 44 22 53 27 49 48 52 41 43 36 37 46 42 47 38 50 51 39 26 40 35 45
14 13 12 2 27 17 4 8 3 10 6 15 18 16 1 11 7 5 32 31 30 20 9 53 22 26 21 28 24 33 0 52 19 29 25 23 50 49 48 38 45 35 40 44 39 46 42 51 36 34 37 47 43 41
15 14 13 12 6 25 11 16 18 8 3 4 2 5 10 17 9 1 33 32 31 30 24 7 29 34 0 26 21 22 38 23 28 53 27 19 51 50 49 48 42 43 47 52 36 44 39 40 20 41 46 35 45 37
1 15 14 13 12 3 53 2 4 16 18 6 9 8 11 7 5 10 19 33 32 31 30 21 17 20 22 34 0 42 27 26 29 25 23 28 37 51 50 49 48 39 35 38 40 52 36 24 45 44 47 43 41 46
7 17 11 10 8 16 2 30 14 15 13 9 5 1 4 18 3 6 25 53 29 28 26 34 20 12 32 33 49 27 23 19 22 0 21 24 43 35 47 46 44 52 38 48 50 51 31 45 41 37 40 36 39 42
5 9 7 17 11 10 8 13 33 14 12 1 4 18 3 6 2 16 23 27 25 53 29 28 26 31 15 50 30 19 22 0 21 24 20 34 41 45 43 35 47 46 44 49 51 32 48 37 40 36 39 42 38 52
9 7 17 11 10 8 16 14 12 31 15 5 1 4 18 3 6 2 27 25 53 29 28 26 34 32 48 13 33 23 19 22 0 21 24 20 45 43 35 47 46 44 52 50 30 49 51 41 37 40 36 39 42 38
11 10 8 16 2 6 3 15 13 12 32 17 7 9 5 1 4 18 29 28 26 34 20 24 21 51 31 30 14 53 25 27 23 19 22 0 47 46 44 52 38 42 39 33 49 48 50 35 43 45 41 37 40 36
4 16 6 18 1 2 7 9 10 5 11 21 17 12 13 14 15 8 22 34 24 0 19 20 43 27 28 23 29 3 53 30 31 32 33 26 40 52 42 36 37 38 25 45 46 41 47 39 35 48 49 50 51 44
8 2 3 4 16 9 10 5 11 1 17 18 24 7 12 13 14 15 26 20 21 22 34 45 28 23 29 19 53 0 6 25 30 31 32 33 44 38 39 40 52 27 46 41 47 37 35 36 42 43 48 49 50 51
16 6 18 8 5 11 15 1 17 4 7 10 3 20 9 12 13 14 34 24 0 26 41 29 33 19 53 22 25 28 21 2 27 30 31 32 52 42 36 44 23 47 51 37 35 40 43 46 39 38 45 48 49 50
2 3 10 1 17 15 14 4 7 18 9 8 11 6 34 5 12 13 20 21 28 37 53 33 32 22 25 0 27 26 29 24 16 23 30 31 38 39 46 19 35 51 50 40 43 36 45 44 47 42 52 41 48 49
6 11 4 7 15 14 13 18 9 3 5 16 10 17 2 26 1 12 24 29 40 25 33 32 31 0 27 21 23 34 28 53 20 8 19 30 42 47 22 43 51 50 49 36 45 39 41 52 46 35 38 44 37 48
17 18 9 15 14 13 12 3 5 6 1 2 8 11 7 16 28 4 53 36 27 33 32 31 30 21 23 24 19 20 26 29 25 34 10 22 35 0 45 51 50 49 48 39 41 42 37 38 44 47 43 52 46 40
3 5 15 14 13 12 18 6 1 2 4 7 16 10 17 9 8 29 39 23 33 32 31 30 0 24 19 20 22 25 34 28 53 27 26 11 21 41 51 50 49 48 36 42 37 38 40 43 52 46 35 45 44 47
28 34 26 20 21 22 39 23 29 24 19 25 32 33 30 31 27 0 41 50 51 49 43 38 53 48 36 35 45 37 52 47 2 40 46 42 7 14 15 13 11 3 4 12 1 10 17 9 6 8 44 5 16 18
19 21 22 53 28 34 24 0 27 23 29 32 33 30 31 51 25 20 45 43 38 39 7 50 35 42 46 48 36 52 47 44 40 26 37 49 17 11 3 4 41 14 10 18 16 12 1 6 8 2 5 15 9 13
32 29 34 24 20 21 22 25 26 0 27 33 30 31 53 19 41 23 52 1 50 35 49 43 38 37 51 42 46 47 44 40 39 45 28 48 6 36 14 10 13 11 3 9 15 18 16 8 2 5 4 17 7 12
33 32 27 22 23 28 34 19 53 25 26 30 31 49 29 21 0 24 47 52 46 38 48 41 50 45 39 37 51 44 40 20 36 43 42 10 8 6 16 3 12 7 14 17 4 9 15 2 5 13 1 11 18 35
30 33 32 26 24 0 21 29 20 19 53 31 28 27 50 25 23 22 44 47 52 51 35 42 11 36 49 45 39 40 41 46 34 37 48 38 2 8 6 15 10 18 43 1 13 17 4 5 7 16 14 9 12 3
31 30 33 32 53 23 25 27 28 29 20 43 26 22 19 0 24 34 40 44 47 52 39 48 37 46 41 36 13 21 51 38 45 42 35 50 5 2 8 6 4 12 9 16 7 1 49 11 15 3 17 18 10 14
34 31 30 33 32 20 0 26 21 27 28 53 35 29 25 23 22 19 50 40 44 47 52 49 42 15 43 46 41 39 24 36 37 48 38 45 14 5 2 8 6 13 18 51 11 16 7 4 10 1 9 12 3 17
23 0 25 19 29 27 26 32 30 40 33 24 22 34 21 28 20 53 48 42 37 45 36 46 51 52 44 31 47 35 3 50 43 41 49 39 12 18 9 17 1 16 15 6 2 5 8 10 38 14 11 7 13 4
22 24 23 0 25 19 29 33 31 30 52 34 21 28 20 53 26 27 38 35 48 42 37 17 36 47 40 44 32 50 43 41 49 39 51 46 3 10 12 18 9 45 1 8 5 2 6 14 11 7 13 4 15 16
24 23 0 25 19 29 27 44 32 33 31 22 34 21 28 20 53 26 35 48 42 9 45 36 46 30 52 47 40 38 50 43 41 49 39 51 10 12 18 37 17 1 16 2 6 8 5 3 14 11 7 13 4 15
25 19 29 27 26 53 20 31 47 32 30 0 23 24 22 34 21 28 37 45 36 46 51 39 49 40 33 52 44 18 48 35 38 50 43 41 9 17 1 16 15 4 13 5 8 6 2 42 12 10 3 14 11 7
21 27 53 28 34 26 23 24 19 22 25 20 0 32 33 30 31 36 43 46 39 41 50 51 48 35 45 38 37 49 42 6 47 44 40 29 11 16 4 7 14 15 12 10 17 3 9 13 18 52 8 2 5 1
29 26 20 21 46 24 19 22 25 34 0 28 53 23 32 33 30 31 36 51 49 43 27 35 45 38 37 14 42 41 39 48 52 47 44 40 1 15 13 11 16 10 17 3 9 50 18 7 4 12 6 8 2 5
27 53 28 29 22 37 31 34 0 21 23 19 20 26 24 32 33 30 46 39 41 36 38 25 40 50 42 43 48 45 49 51 35 52 8 44 16 4 7 1 3 9 5 14 18 11 12 17 13 15 10 6 47 2
26 20 45 34 0 31 30 21 23 28 24 29 25 53 27 22 32 33 51 49 19 50 42 40 44 43 12 41 35 36 37 39 46 38 52 47 15 13 17 14 18 5 2 11 48 7 10 1 9 4 16 3 6 8
53 25 21 48 31 30 33 28 24 20 22 27 19 0 26 29 34 32 4 37 43 23 40 44 47 41 35 49 38 46 45 42 51 36 50 52 39 9 11 12 5 2 8 7 10 13 3 16 17 18 15 1 14 6
42 28 24 31 30 33 32 20 22 53 34 26 29 25 23 27 19 21 0 41 35 40 44 47 52 49 38 39 50 51 36 37 48 16 45 43 18 7 10 5 2 8 6 13 3 4 14 15 1 9 12 46 17 11
20 38 31 30 33 32 28 53 34 26 21 23 27 19 0 24 29 25 49 22 5 44 47 52 41 39 50 51 43 48 46 45 42 35 36 37 13 3 40 2 8 6 7 4 14 15 11 12 16 17 18 10 1 9
38 48 35 42 45 46 43 39 50 37 51 41 47 52 40 44 49 11 21 5 6 18 1 9 3 17 16 7 8 10 15 14 13 12 2 36 4 22 34 24 0 19 20 27 28 23 29 53 33 32 31 30 26 25
51 45 46 43 38 48 37 36 49 39 50 47 52 40 44 35 10 42 8 0 9 3 4 5 7 11 2 17 16 15 14 13 12 6 41 18 29 1 19 20 21 22 23 25 26 27 28 33 32 31 30 34 53 24
47 50 48 37 42 45 46 41 35 36 49 52 40 44 43 8 38 39 15 16 22 7 18 1 9 10 6 11 2 14 13 12 3 51 4 17 33 28 5 23 24 0 19 53 34 25 26 32 31 30 20 29 21 27
52 47 49 46 39 38 48 51 43 41 35 40 44 42 16 45 36 37 14 15 2 19 17 4 5 8 3 10 6 13 12 18 50 1 11 7 32 33 26 9 27 21 22 29 20 53 34 31 30 24 28 0 25 23
40 52 47 35 37 36 45 50 42 51 43 44 38 2 48 41 39 46 13 14 15 6 23 11 1 16 18 8 3 12 4 49 5 10 17 9 31 32 33 34 7 25 0 28 24 29 20 30 21 26 22 53 27 19
44 40 52 47 43 39 41 49 38 50 42 45 6 46 51 36 37 48 12 13 14 15 3 27 10 2 4 16 18 1 35 9 8 11 7 5 30 31 32 33 20 17 53 26 21 28 24 0 34 19 29 25 23 22
48 44 40 52 47 42 36 35 45 49 38 3 37 50 41 39 46 51 5 12 13 14 15 18 25 6 1 2 4 43 7 16 10 17 9 8 22 30 31 32 33 24 11 34 0 26 21 20 23 28 53 27 19 29
39 36 41 51 50 49 35 47 40 44 14 37 46 48 45 38 42 43 17 11 10 8 16 2 6 33 13 12 52 7 9 5 1 4 18 3 27 25 53 29 28 26 34 15 31 30 32 23 19 22 0 21 24 20
46 37 39 36 41 51 50 52 44 13 47 48 45 38 42 43 35 49 9 7 17 11 10 8 16 14 30 40 15 5 1 4 18 3 6 2 19 23 27 25 53 29 28 32 12 31 33 22 0 21 24 20 34 26
37 39 36 41 51 50 49 40 15 52 44 46 48 45 38 42 43 35 7 17 11 10 8 16 2 13 47 32 12 9 5 1 4 18 3 6 23 27 25 53 29 28 26 31 33 14 30 19 22 0 21 24 20 34
41 51 50 49 35 43 42 12 52 47 40 36 39 37 46 48 45 38 10 8 16 2 6 3 18 44 14 15 31 11 17 7 9 5 1 4 53 29 28 26 34 20 24 30 32 33 13 25 27 23 19 22 0 21
45 49 43 38 48 35 17 37 51 46 41 42 36 47 52 40 44 50 1 2 3 4 5 6 39 7 8 9 10 24 11 15 14 13 12 16 0 26 20 21 22 34 27 23 29 19 53 18 25 33 32 31 30 28
50 35 42 45 49 7 51 46 41 48 36 38 43 39 47 52 40 44 16 6 18 1 2 37 8 9 10 5 11 4 20 17 15 14 13 12 28 34 24 0 26 23 29 19 53 22 25 21 3 27 33 32 31 30
49 43 38 50 9 41 44 48 36 45 39 51 42 35 37 47 52 40 2 3 4 16 46 10 12 5 11 1 17 8 18 34 7 15 14 13 26 20 21 28 19 53 30 22 25 0 27 29 24 6 23 33 32 31
35 42 51 5 36 44 40 45 39 38 37 50 41 43 49 46 47 52 6 18 8 48 11 12 13 1 17 4 7 16 10 3 26 9 15 14 34 24 29 22 25 30 31 0 27 21 23 28 53 20 2 19 33 32
43 41 1 39 44 40 52 38 37 42 46 49 51 36 35 50 48 47 3 10 45 17 12 13 14 4 7 18 9 2 8 11 6 28 5 15 20 53 0 27 30 31 32 21 23 24 19 26 29 25 34 16 22 33
36 4 37 44 40 52 47 42 46 43 48 35 50 41 39 49 51 45 11 38 7 12 13 14 15 18 9 3 5 6 16 10 17 2 29 1 25 21 23 30 31 32 33 24 19 20 22 34 28 53 27 26 8 0
18 46 44 40 52 47 38 43 48 35 45 39 49 51 36 37 50 41 42 9 12 13 14 15 4 3 5 6 1 17 2 8 11 7 16 53 24 19 30 31 32 33 21 20 22 34 0 27 26 29 25 23 28 10

mate #2
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
10 22 5 6 18 1 9 17 16 7 8 12 13 14 15 2 11 3 28 4 23 24 0 19 27 53 34 25 26 30 31 32 33 20 47 21 46 40 41 42 36 37 45 35 52 43 44 48 49 50 51 38 29 39
12 8 19 9 3 4 5 11 2 17 16 13 14 15 6 10 18 7 30 26 1 27 21 22 23 29 20 53 34 31 32 33 24 46 0 25 48 44 37 45 39 40 41 47 38 35 52 49 50 51 42 28 36 43
13 12 16 23 7 18 1 10 6 11 2 14 15 3 8 4 17 9 31 30 34 5 25 0 19 28 24 29 20 32 33 21 44 22 53 27 49 48 52 41 43 36 37 46 42 47 38 50 51 39 26 40 35 45
14 13 12 2 27 17 4 8 3 10 6 15 18 16 1 11 7 5 32 31 30 20 9 53 22 26 21 28 24 33 0 52 19 29 25 23 50 49 48 38 45 35 40 44 39 46 42 51 36 34 37 47 43 41
15 14 13 12 6 25 11 16 18 8 3 4 2 5 10 17 9 1 33 32 31 30 24 7 29 34 0 26 21 22 38 23 28 53 27 19 51 50 49 48 42 43 47 52 36 44 39 40 20 41 46 35 45 37
1 15 14 13 12 3 53 2 4 16 18 6 9 8 11 7 5 10 19 33 32 31 30 21 17 20 22 34 0 42 27 26 29 25 23 28 37 51 50 49 48 39 35 38 40 52 36 24 45 44 47 43 41 46
7 17 11 10 8 16 2 31 12 15 14 9 5 1 4 18 3 6 25 53 29 28 26 34 20 13 30 33 50 27 23 19 22 0 21 24 43 35 47 46 44 52 38 49 48 51 32 45 41 37 40 36 39 42
5 9 7 17 11 10 8 14 33 12 13 1 4 18 3 6 2 16 23 27 25 53 29 28 26 32 15 48 31 19 22 0 21 24 20 34 41 45 43 35 47 46 44 50 51 30 49 37 40 36 39 42 38 52
9 7 17 11 10 8 16 12 13 32 15 5 1 4 18 3 6 2 27 25 53 29 28 26 34 30 49 14 33 23 19 22 0 21 24 20 45 43 35 47 46 44 52 48 31 50 51 41 37 40 36 39 42 38
11 10 8 16 2 6 3 15 14 13 30 17 7 9 5 1 4 18 29 28 26 34 20 24 21 51 32 31 12 53 25 27 23 19 22 0 47 46 44 52 38 42 39 33 50 49 48 35 43 45 41 37 40 36
4 16 6 18 1 2 7 9 10 5 11 21 17 12 13 14 15 8 22 34 24 0 19 20 43 27 28 23 29 3 53 30 31 32 33 26 40 52 42 36 37 38 25 45 46 41 47 39 35 48 49 50 51 44
8 2 3 4 16 9 10 5 11 1 17 18 24 7 12 13 14 15 26 20 21 22 34 45 28 23 29 19 53 0 6 25 30 31 32 33 44 38 39 40 52 27 46 41 47 37 35 36 42 43 48 49 50 51
16 6 18 8 5 11 15 1 17 4 7 10 3 20 9 12 13 14 34 24 0 26 41 29 33 19 53 22 25 28 21 2 27 30 31 32 52 42 36 44 23 47 51 37 35 40 43 46 39 38 45 48 49 50
2 3 10 1 17 15 14 4 7 18 9 8 11 6 34 5 12 13 20 21 28 37 53 33 32 22 25 0 27 26 29 24 16 23 30 31 38 39 46 19 35 51 50 40 43 36 45 44 47 42 52 41 48 49
6 11 4 7 15 14 13 18 9 3 5 16 10 17 2 26 1 12 24 29 40 25 33 32 31 0 27 21 23 34 28 53 20 8 19 30 42 47 22 43 51 50 49 36 45 39 41 52 46 35 38 44 37 48
17 18 9 15 14 13 12 3 5 6 1 2 8 11 7 16 28 4 53 36 27 33 32 31 30 21 23 24 19 20 26 29 25 34 10 22 35 0 45 51 50 49 48 39 41 42 37 38 44 47 43 52 46 40
3 5 15 14 13 12 18 6 1 2 4 7 16 10 17 9 8 29 39 23 33 32 31 30 0 24 19 20 22 25 34 28 53 27 26 11 21 41 51 50 49 48 36 42 37 38 40 43 52 46 35 45 44 47
28 34 26 20 21 22 39 23 29 24 19 25 31 30 33 32 27 0 41 48 51 50 43 38 53 49 36 35 45 37 52 47 2 40 46 42 7 12 15 14 11 3 4 13 1 10 17 9 6 8 44 5 16 18
19 21 22 53 28 34 24 0 27 23 29 31 30 33 32 51 25 20 45 43 38 39 7 48 35 42 46 49 36 52 47 44 40 26 37 50 17 11 3 4 41 12 10 18 16 13 1 6 8 2 5 15 9 14
31 29 34 24 20 21 22 25 26 0 27 30 33 32 53 19 41 23 52 1 48 35 50 43 38 37 51 42 46 47 44 40 39 45 28 49 6 36 12 10 14 11 3 9 15 18 16 8 2 5 4 17 7 13
30 31 27 22 23 28 34 19 53 25 26 33 32 50 29 21 0 24 47 52 46 38 49 41 48 45 39 37 51 44 40 20 36 43 42 10 8 6 16 3 13 7 12 17 4 9 15 2 5 14 1 11 18 35
33 30 31 26 24 0 21 29 20 19 53 32 28 27 48 25 23 22 44 47 52 51 35 42 11 36 50 45 39 40 41 46 34 37 49 38 2 8 6 15 10 18 43 1 14 17 4 5 7 16 12 9 13 3
32 33 30 31 53 23 25 27 28 29 20 43 26 22 19 0 24 34 40 44 47 52 39 49 37 46 41 36 14 21 51 38 45 42 35 48 5 2 8 6 4 13 9 16 7 1 50 11 15 3 17 18 10 12
34 32 33 30 31 20 0 26 21 27 28 53 35 29 25 23 22 19 48 40 44 47 52 50 42 15 43 46 41 39 24 36 37 49 38 45 12 5 2 8 6 14 18 51 11 16 7 4 10 1 9 13 3 17
23 0 25 19 29 27 26 30 31 40 33 24 22 34 21 28 20 53 49 42 37 45 36 46 51 47 52 32 44 35 3 48 43 41 50 39 13 18 9 17 1 16 15 8 6 5 2 10 38 12 11 7 14 4
22 24 23 0 25 19 29 33 32 31 47 34 21 28 20 53 26 27 38 35 49 42 37 17 36 44 40 52 30 48 43 41 50 39 51 46 3 10 13 18 9 45 1 2 5 6 8 12 11 7 14 4 15 16
24 23 0 25 19 29 27 52 30 33 32 22 34 21 28 20 53 26 35 49 42 9 45 36 46 31 47 44 40 38 48 43 41 50 39 51 10 13 18 37 17 1 16 6 8 2 5 3 12 11 7 14 4 15
25 19 29 27 26 53 20 32 44 30 31 0 23 24 22 34 21 28 37 45 36 46 51 39 50 40 33 47 52 18 49 35 38 48 43 41 9 17 1 16 15 4 14 5 2 8 6 42 13 10 3 12 11 7
21 27 53 28 34 26 23 24 19 22 25 20 0 31 30 33 32 36 43 46 39 41 48 51 49 35 45 38 37 50 42 6 47 44 40 29 11 16 4 7 12 15 13 10 17 3 9 14 18 52 8 2 5 1
29 26 20 21 46 24 19 22 25 34 0 28 53 23 31 30 33 32 36 51 50 43 27 35 45 38 37 12 42 41 39 49 52 47 44 40 1 15 14 11 16 10 17 3 9 48 18 7 4 13 6 8 2 5
27 53 28 29 22 37 32 34 0 21 23 19 20 26 24 31 30 33 46 39 41 36 38 25 40 48 42 43 49 45 50 51 35 52 8 44 16 4 7 1 3 9 5 12 18 11 13 17 14 15 10 6 47 2
26 20 45 34 0 32 33 21 23 28 24 29 25 53 27 22 31 30 51 50 19 48 42 40 44 43 13 41 35 36 37 39 46 38 52 47 15 14 17 12 18 5 2 11 49 7 10 1 9 4 16 3 6 8
53 25 21 49 32 33 30 28 24 20 22 27 19 0 26 29 34 31 4 37 43 23 40 44 47 41 35 50 38 46 45 42 51 36 48 52 39 9 11 13 5 2 8 7 10 14 3 16 17 18 15 1 12 6
42 28 24 32 33 30 31 20 22 53 34 26 29 25 23 27 19 21 0 41 35 40 44 47 52 50 38 39 48 51 36 37 49 16 45 43 18 7 10 5 2 8 6 14 3 4 12 15 1 9 13 46 17 11
20 38 32 33 30 31 28 53 34 26 21 23 27 19 0 24 29 25 50 22 5 44 47 52 41 39 48 51 43 49 46 45 42 35 36 37 14 3 40 2 8 6 7 4 12 15 11 13 16 17 18 10 1 9
38 49 35 42 45 46 43 39 48 37 51 41 40 44 47 52 50 11 21 5 6 18 1 9 3 17 16 7 8 10 14 15 12 13 2 36 4 22 34 24 0 19 20 27 28 23 29 53 32 33 30 31 26 25
51 45 46 43 38 49 37 36 50 39 48 40 44 47 52 35 10 42 8 0 9 3 4 5 7 11 2 17 16 14 15 12 13 6 41 18 29 1 19 20 21 22 23 25 26 27 28 32 33 30 31 34 53 24
40 48 49 37 42 45 46 41 35 36 50 44 47 52 43 8 38 39 14 16 22 7 18 1 9 10 6 11 2 15 12 13 3 51 4 17 32 28 5 23 24 0 19 53 34 25 26 33 30 31 20 29 21 27
44 40 50 46 39 38 49 51 43 41 35 47 52 42 16 45 36 37 15 14 2 19 17 4 5 8 3 10 6 12 13 18 48 1 11 7 33 32 26 9 27 21 22 29 20 53 34 30 31 24 28 0 25 23
47 44 40 35 37 36 45 48 42 51 43 52 38 2 49 41 39 46 12 15 14 6 23 11 1 16 18 8 3 13 4 50 5 10 17 9 30 33 32 34 7 25 0 28 24 29 20 31 21 26 22 53 27 19
52 47 44 40 43 39 41 50 38 48 42 45 6 46 51 36 37 49 13 12 15 14 3 27 10 2 4 16 18 1 35 9 8 11 7 5 31 30 33 32 20 17 53 26 21 28 24 0 34 19 29 25 23 22
49 52 47 44 40 42 36 35 45 50 38 3 37 48 41 39 46 51 5 13 12 15 14 18 25 6 1 2 4 43 7 16 10 17 9 8 22 31 30 33 32 24 11 34 0 26 21 20 23 28 53 27 19 29
39 36 41 51 48 50 35 44 40 52 12 37 46 49 45 38 42 43 17 11 10 8 16 2 6 33 14 13 47 7 9 5 1 4 18 3 27 25 53 29 28 26 34 15 32 31 30 23 19 22 0 21 24 20
46 37 39 36 41 51 48 47 52 14 44 49 45 38 42 43 35 50 9 7 17 11 10 8 16 12 31 40 15 5 1 4 18 3 6 2 19 23 27 25 53 29 28 30 13 32 33 22 0 21 24 20 34 26
37 39 36 41 51 48 50 40 15 47 52 46 49 45 38 42 43 35 7 17 11 10 8 16 2 14 44 30 13 9 5 1 4 18 3 6 23 27 25 53 29 28 26 32 33 12 31 19 22 0 21 24 20 34
41 51 48 50 35 43 42 13 47 44 40 36 39 37 46 49 45 38 10 8 16 2 6 3 18 52 12 15 32 11 17 7 9 5 1 4 53 29 28 26 34 20 24 31 30 33 14 25 27 23 19 22 0 21
45 50 43 38 49 35 17 37 51 46 41 42 36 40 44 47 52 48 1 2 3 4 5 6 39 7 8 9 10 24 11 14 15 12 13 16 0 26 20 21 22 34 27 23 29 19 53 18 25 32 33 30 31 28
48 35 42 45 50 7 51 46 41 49 36 38 43 39 40 44 47 52 16 6 18 1 2 37 8 9 10 5 11 4 20 17 14 15 12 13 28 34 24 0 26 23 29 19 53 22 25 21 3 27 32 33 30 31
50 43 38 48 9 41 52 49 36 45 39 51 42 35 37 40 44 47 2 3 4 16 46 10 13 5 11 1 17 8 18 34 7 14 15 12 26 20 21 28 19 53 31 22 25 0 27 29 24 6 23 32 33 30
35 42 51 5 36 52 47 45 39 38 37 48 41 43 50 46 40 44 6 18 8 49 11 13 12 1 17 4 7 16 10 3 26 9 14 15 34 24 29 22 25 31 30 0 27 21 23 28 53 20 2 19 32 33
43 41 1 39 52 47 44 38 37 42 46 50 51 36 35 48 49 40 3 10 45 17 13 12 15 4 7 18 9 2 8 11 6 28 5 14 20 53 0 27 31 30 33 21 23 24 19 26 29 25 34 16 22 32
36 4 37 52 47 44 40 42 46 43 49 35 48 41 39 50 51 45 11 38 7 13 12 15 14 18 9 3 5 6 16 10 17 2 29 1 25 21 23 31 30 33 32 24 19 20 22 34 28 53 27 26 8 0
18 46 52 47 44 40 38 43 49 35 45 39 50 51 36 37 48 41 42 9 13 12 15 14 4 3 5 6 1 17 2 8 11 7 16 53 24 19 31 30 33 32 21 20 22 34 0 27 26 29 25 23 28 10

Золотое ожерелье 54-й пробы :)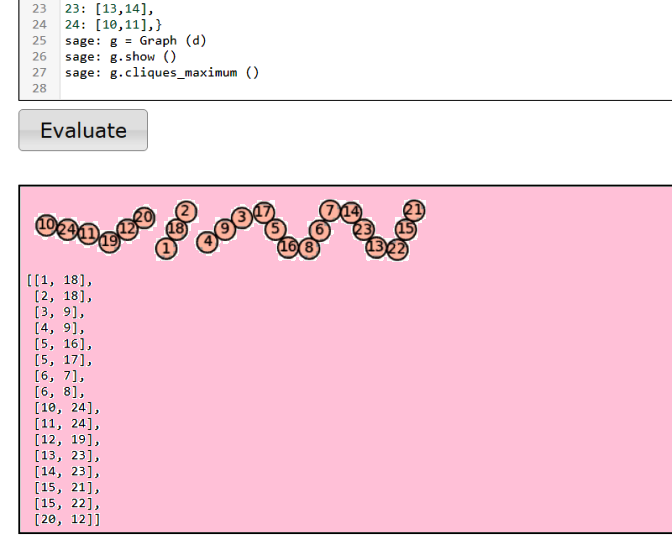



Нарисовано в программе SageMath.

Так, осталось заставить метод Пелегрино-Ланселотти построить ортогональные пары ДЛК 42-го порядка на базе ортогональных пар ДЛК 14-го порядка. Где раздобыть хорошие ортогональные пары ДЛК 14-го порядка, чтобы метод для них работал?

Нашла в программе SageMath известную группу MOLS 66-го порядка, состоящую из 5 взаимно ортогональных ЛК.
ДЛК в этой группе нет.

От одной ортогональной пары ДЛК 22-го порядка удалось построить ортогональную пару ДЛК 66-го порядка методом Пелегрино-Ланселотти.
Если бы ортогональных пар было побольше и от одного ДЛК, можно было бы применить этот метод.

Пока для порядка 66 оценка минимальная
a(66) >= 1.

Добавила в свою таблицу очевидные оценки до порядка 75 включительно.

Кажется, я понимаю, почему с ОДЛК 42-го порядка от ДЛК Гергели 14-го порядка ничего не получается методом Пелегрино-Ланселотти.
Да, ОДЛК у этого ДЛК много, но... все его "товарищи" между собой не "товарищи" :)
То есть все эти ОДЛК не вступают друг с другом в отношение ортогональности.
Сейчас проверила несколько порций ОДЛК от ДЛК Гергели. Только однушки!
И ортогональные пары 42-го порядка соответственно не дают групп ОДЛК выше однушки, хотя они и строятся в достаточно большом количестве.
Свойство наследуется от исходных ДЛК.
Возможно, моя версия ошибочна, но другого объяснения пока не вижу.

Для порядка 72 оценку я сделала по группе ОДЛК 8-го порядка, на основе метода составных квадратов.
Интересно посмотреть группу ОДЛК, построенную методом составных квадратов, но на базе других ортогональных пар порядков 8 и 9 (из групп MODLS). Должна получиться группа MODLS 72-го порядка.
Метод Пелегрино-Ланселотти тоже интересно попробовать на базе ортогональных пар ДЛК 24-го порядка.

Цитирую

Выложила этот красивый результат
https://disk.yandex.ru/d/jJ2O7xB4yyIJQw
Яндекс.Диск, 155 КБ (текстовый файл сжат).

Эти 824 ОДЛК 24-го порядка от одного ДЛК получены методом Пелегрино-Ланселоти на базе 824-х ОДЛК 8-го порядка от одного ДЛК.
Следующий шаг выполнится: от порядка n=24 к порядку n=72?
Завтра мы с черепашкой попробуем.

Метод Пелегрино-Ланселотти для порядка 72 попробовала.
Первые 5 ортогональных пар построились быстро, на шестой ортогональной паре программа впала в глубокую задумчивость.
Подозреваю, что выполняется поиск нужных трансверсалей, а проверка всех трансверсалей в ДЛК 24-го порядка дело очень сложное.
В общем, прервала программу.
Проверила построенные ортогональные пары 72-го порядка

Order? 72

Enter the name of the squares file: inp
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file inp-orthCounts_4.txt
..output file inp-orthNos_4.txt
squares 10 total orthogonal pairs 5
Maximum pairs for square 1: 1
There are 9 other squares with this maximum number of pairs.
..output file inp-1orths_4.txt
Pairs for square 1: 1

Да, все 5 ортогональных пар получились, но... двушек пока нет. Может быть, появятся, если построить все 824 ортогональные пары.

Сейчас буду пробовать метод составных квадратов на базе ортогональных пар ДЛК порядков 8 и 9 из групп MODLS.
Надеюсь получить этим методом группу MODLS 72-го порядка, состоящую из 6 взаимно ортогональных ДЛК.

Полные системы MOLS порядков 7 и 8 уже показаны в этой теме.
Покажу полную систему MOLS 9-го порядка



Эта система тоже построена коллегой М. Алексеевым в матпакете Maple в те далёкие времена. когда я только начинала заниматься латинскими квадратами.
Полная система MOLS 9-го порядка содержит группу MODLS, состоящую из 6 взаимно ортогональных ДЛК.
Я нашла статью, в которой приведены все возможные (различные) полные системы MOLS 9-го порядка.
Проверила все эти полные системы MOLS и не нашла ни в одной из них группу MODLS из более 6 ДЛК.
На основании этого сделала вывод, что группа MODLS 9-го порядка не может содержать больше 6 взаимно ортогональных ДЛК.
Но этот вывод не принят господином Ватутиным, как я уже писала выше.
Он считает, что это утверждение не доказано и доказывать его надо полным перебором.
Флаг вам в руки, господин Ватутин!
Полная БД КФ ОДЛК 9-го порядка у вас есть. Организуйте полный перебор и найдите клику размера 7.
Клики размера 8 точно не может быть, так как тогда существовала бы полная система MOLS, состоящая только из ДЛК. Но такой полной системы MOLS нет в указанной статье со всеми полными системами MOLS 9-го порядка.
Впрочем, в этой статье нет и полной системы MOLS, содержащей 7 взаимно ортогональных ДЛК.
Но это почему-то не принимается в качестве доказательства.

Итак, перед вами, господа, открытая проблема.
Моя гипотеза, приведённая в статье OEIS, должна быть доказана или опровергнута.
Цитирую

Conjecture: a(9) = 6. - Natalia Makarova, Dec 24 2020

Я считаю, что гипотеза уже доказана.
Для опровержения - контрпример в студию!!

В методе составных квадратов всё гораздо проще.
Построила все возможные ортогональные пары ДЛК 72-го порядка на базе ортогональных пар ДЛК порядков 8 и 9 из групп MODLS.
Проверка полученной группы ОДЛК 72-го порядка программой GetOrthogonal

Order? 72

Enter the name of the squares file: inp
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file inp-orthCounts_4.txt
..output file inp-orthNos_4.txt
squares 34 total orthogonal pairs 401
Maximum pairs for square 1: 25
There is 1 other square with this maximum number of pairs.
..output file inp-1orths_4.txt
Pairs for square 1: 25

Замечательно!
Смотрим таблицу ортогональных пар

1:  6 7 8 9 10 11 12 13 14 15
 16 17 18 19 20 21 22 23 24 25
 26 27 28 29 30
2:  7 8 9 10 12 13 14 15 17 18
 19 20 22 23 24 25 27 28 29 30
 31 32 33 34
3:  6 8 9 10 11 13 14 15 16 18
 19 20 21 23 24 25 26 28 29 30
 31 32 33 34
4:  6 7 9 10 11 12 14 15 16 17
 19 20 21 22 24 25 26 27 29 30
 31 32 33 34
5:  6 7 8 10 11 12 13 15 16 17
 18 20 21 22 23 25 26 27 28 30
 31 32 33 34
6:  1 3 4 5 12 13 14 15 17 18
 19 20 22 23 24 25 27 28 29 30
 32 33 34
7:  1 2 4 5 11 13 14 15 16 18
 19 20 21 23 24 25 26 28 29 30
 32 33 34
8:  1 2 3 5 11 12 14 15 16 17
 19 20 21 22 24 25 26 27 29 30
 32 33 34
9:  1 2 3 4 11 12 13 15 16 17
 18 20 21 22 23 25 26 27 28 30
 32 33 34
10:  1 2 3 4 5 11 12 13 14 16
 17 18 19 21 22 23 24 26 27 28
 29 32 33 34
11:  1 3 4 5 7 8 9 10 17 18
 19 20 22 23 24 25 27 28 29 30
 31 33 34
12:  1 2 4 5 6 8 9 10 16 18
 19 20 21 23 24 25 26 28 29 30
 31 33 34
13:  1 2 3 5 6 7 9 10 16 17
 19 20 21 22 24 25 26 27 29 30
 31 33 34
14:  1 2 3 4 6 7 8 10 16 17
 18 20 21 22 23 25 26 27 28 30
 31 33 34
15:  1 2 3 4 5 6 7 8 9 16
 17 18 19 21 22 23 24 26 27 28
 29 31 33 34
16:  1 3 4 5 7 8 9 10 12 13
 14 15 22 23 24 25 27 28 29 30
 31 32 34
17:  1 2 4 5 6 8 9 10 11 13
 14 15 21 23 24 25 26 28 29 30
 31 32 34
18:  1 2 3 5 6 7 9 10 11 12
 14 15 21 22 24 25 26 27 29 30
 31 32 34
19:  1 2 3 4 6 7 8 10 11 12
 13 15 21 22 23 25 26 27 28 30
 31 32 34
20:  1 2 3 4 5 6 7 8 9 11
 12 13 14 21 22 23 24 26 27 28
 29 31 32 34
21:  1 3 4 5 7 8 9 10 12 13
 14 15 17 18 19 20 27 28 29 30
 31 32 33
22:  1 2 4 5 6 8 9 10 11 13
 14 15 16 18 19 20 26 28 29 30
 31 32 33
23:  1 2 3 5 6 7 9 10 11 12
 14 15 16 17 19 20 26 27 29 30
 31 32 33
24:  1 2 3 4 6 7 8 10 11 12
 13 15 16 17 18 20 26 27 28 30
 31 32 33
25:  1 2 3 4 5 6 7 8 9 11
 12 13 14 16 17 18 19 26 27 28
 29 31 32 33
26:  1 3 4 5 7 8 9 10 12 13
 14 15 17 18 19 20 22 23 24 25
 31 32 33 34
27:  1 2 4 5 6 8 9 10 11 13
 14 15 16 18 19 20 21 23 24 25
 31 32 33 34
28:  1 2 3 5 6 7 9 10 11 12
 14 15 16 17 19 20 21 22 24 25
 31 32 33 34
29:  1 2 3 4 6 7 8 10 11 12
 13 15 16 17 18 20 21 22 23 25
 31 32 33 34
30:  1 2 3 4 5 6 7 8 9 11
 12 13 14 16 17 18 19 21 22 23
 24 31 32 33 34
31:  2 3 4 5 11 12 13 14 15 16
 17 18 19 20 21 22 23 24 25 26
 27 28 29 30
32:  2 3 4 5 6 7 8 9 10 16
 17 18 19 20 21 22 23 24 25 26
 27 28 29 30
33:  2 3 4 5 6 7 8 9 10 11
 12 13 14 15 21 22 23 24 25 26
 27 28 29 30
34:  2 3 4 5 6 7 8 9 10 11
 12 13 14 15 16 17 18 19 20 26
 27 28 29 30

И счётчик ортогональных пар

                orthogonal
      square       pairs
      ------    ----------

           1           25
           2           24
           3           24
           4           24
           5           24
           6           23
           7           23
           8           23
           9           23
          10           24

          11           23
          12           23
          13           23
          14           23
          15           24
          16           23
          17           23
          18           23
          19           23
          20           24

          21           23
          22           23
          23           23
          24           23
          25           24
          26           24
          27           24
          28           24
          29           24
          30           25

          31           24
          32           24
          33           24
          34           24

Два ДЛК в группе имеют 25 ОДЛК (максимальное количество).

Осталось найти клику размера 6.
Сейчас попробую это сделать в программе SageMath.

Нарисовала



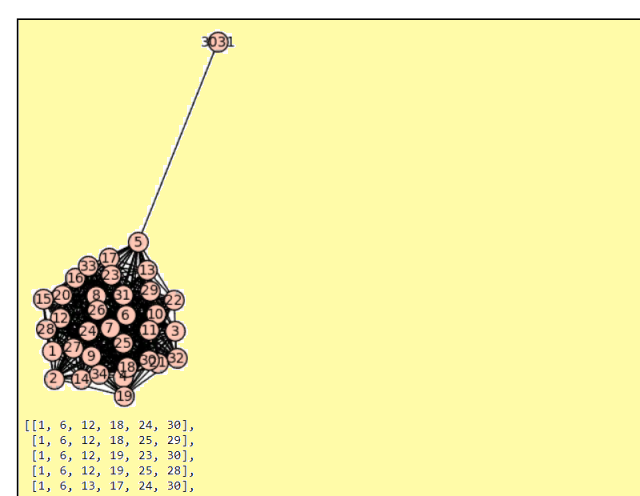Воздушный шар повис на двух узлах :)
Непонятно, почему эти два узла вынесены.

Клики размера 6 есть и их много.

Метод составных квадратов на базе 824-х ортогональных пар ДЛК 8-го порядка от одного ДЛК и какой-нибудь ортогональной пары ДЛК 9-го порядка тоже очень просто применить.
В результате получатся 824 ортогональные пары ДЛК 72-го порядка от одного ДЛК
То есть получаем оценку
a(72) >= 824.