Эта конфигурация из максимального количества ОДЛК от одного ДЛК 9-го порядка, найденная мной, тоже не полная



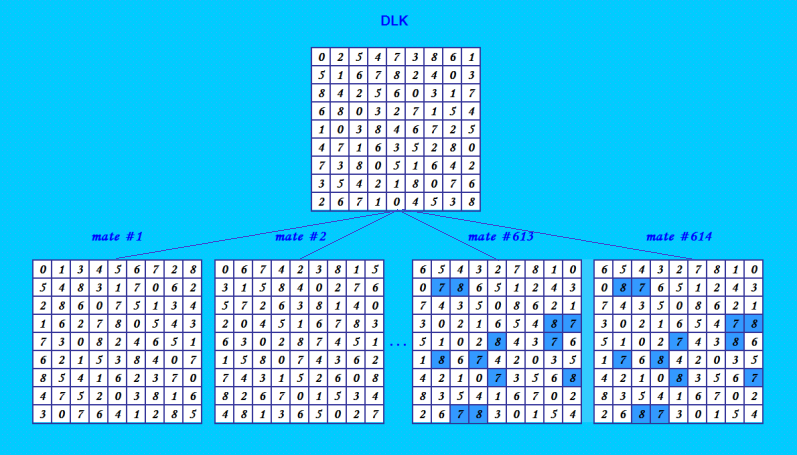Здесь эффект снежного кома очень сильный.
Нашла все ОДЛК второго уровня, объединила их с ОДЛК первого уровня, нормализовала все ОДЛК (включая основной ДЛК конфигурации) и отбросила дубликаты.
Получила 712 нормализованных различных ОДЛК.
Проверка программой GetOrthogonal показывает

Order? 9

Enter the name of the squares file: a
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file a-orthCounts.txt
..output file a-orthNos.txt
squares 712 total orthogonal pairs 5522
Maximum pairs for square 68: 614
This is the only square with this maximum number of pairs.
..output file a-68orths.txt
Pairs for square 68: 614

Таким образом, на первом и втором уровнях получено 5522 ортогональные пары.
Третий уровень наверняка тоже будет, но не буду его смотреть.

Замечание: в конфигурации рассматриваются нормализованные различные ОДЛК, среди которых могут быть изоморфные.
Например, среди 614 ОДЛК первого уровня в показанной выше максимальной конфигурации ОДЛК 9-го порядка имеется только 166 уникальных

Order? 9
Format, (1: first row or 2: \diagonal)? 2
File name? inp
.. writing DLS to file output9CF2_4.txt
number of DLS 614 CFs 166

В максимальных конфигурациях ОДЛК рассматриваются все нормализованные различные ОДЛК; изоморфные ОДЛК не исключаются из конфигурации.
Так предложено автором статьи OEIS
https://oeis.org/A287695
Maximum number of normalized diagonal Latin squares that can be orthogonal to the same diagonal Latin square of order n.

По поводу последнего замечания посмотрим классику.

Цитата из сообщения https://boinc.progger.info/odlk/forum_thread.php?id=40&postid=742

Начнём с самого первого - исторического - вида четвёрок.
1. Четвёрки, происходящие от "браунов".

Первая, классическая, четвёрка такого вида была опубликована в 1992 г. в статье
“Completion of the Spectrum of Orthogonal Diagonal Latin Squares” (J. W. Brown и другие).
Фактически была опубликована только двушка, смотрите две первые (сверху) ортогональные пары на иллюстрации



В 2016 г. О. Заикин нашёл ещё две пары ортогональных ДЛК в этой группе, и двушка превратилась в четвёрку. Смотрите
Pairs of diagonal orthogonal Latin squares of order 10 based on the turn square from Brown et al, 1992.
http://sat.isa.ru/pdsat/additional_solutions.php
Интересный момент в том, что два найденных Заикиным ортогональных диагональных соквадрата оказались изоморфными двум известным ортогональным диагональным соквадратам.

Мне до сих пор остаётся непонятно: то ли авторы этого классического примера Браун и Ко не нашли ещё два ОДЛК в найденной ими двушке, то ли они просто отбросили их как изоморфные.
Последний вариант тоже вполне возможен.
И если так, тогда максимальные конфигурации надо рассматривать только с уникальными ОДЛК.
Мне этот вариант больше нравится.

PS. Таким образом, первая четвёрка 10-го порядка была найдена либо Брауном с компанией в 1992 г., либо О. Заикиным в 2016 г.
Во всяком случае, Браун с компанией нашли основной ДЛК этой четвёрки.
Сейчас в нашей БД КФ ОДЛК 10-го порядка имеется 564 четвёрки.

И очень интересный факт о группе ОДЛК 10-го порядка, найденной Брауном и Ко.

Цитата из сообщения
https://boinc.progger.info/odlk/forum_thread.php?id=116&postid=3541

А знаете ли вы?
Очень интересный факт!
5 ОДЛК, найденные Брауном и компанией (один из 6 ОДЛК повторяется), дают в Замыкании (обработка скриптом Белышева zamyk.bat) 470 уникальных КФ ОДЛК!

Найдено марьяжных КФ:
count[1] = 321
count[2] = 116
count[3] = 1
count[4] = 30
count[6] = 2
Всего: 470
Найдено соквадратов: 688
КФ соквадратов: 470

в том числе тройка, 30 четвёрок (!) и две шестёрки.

Вот какие результаты были получены ещё в 1992 году!
Авторы результатов об этом, наверное, и не догадывались :)
У них не было замечательного скрипта Белышева.

Выполнила маленький эксперимент со вторым уровнем ОДЛК от квадрозавра.
Взяла 570 ОДЛК первого уровня, нашла к ним все ОДЛК программой Белышева ortogon_u, объединила ОДЛК обоих уровней, нормализовала все ОДЛК, включая самого квадрозавра, удалила дубликаты.
Получилось 581 нормализованных различных ОДЛК, включая самого квадрозавра.
Проверяю эту группу ОДЛК программой Harry White GetOrthogonal

Order? 12

Enter the name of the squares file: a
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file a-orthCounts.txt
..output file a-orthNos.txt
squares 581 total orthogonal pairs 592
Maximum pairs for square 577: 570
This is the only square with this maximum number of pairs.
..output file a-577orths.txt
Pairs for square 577: 570

Всего получено 592 ортогональные пары, то есть второй уровень добавил 22 новые ортогональные пары.

Из таблицы ортогональных пар: на втором уровне десятка появилась

. . . . . 
570:  577
571:  32 92 232 298 346 354 451 537 541 545

572:  399
573:  119
574:  417
575:  285 436
576:  186 322
. . . . . 

В последовательности OEIS
https://oeis.org/A287695
изменилось название

A287695 Maximum number of diagonal Latin squares with the first row in ascending order that can be orthogonal to a given diagonal Latin square of order n.

Редактор посчитал, что "diagonal Latin squares with the first row in ascending order" лучше, чем "normalized diagonal Latin squares".
Он написал

Fri May 28 18:41
Andrew Howroyd: Changed to 'with the first row in ascending order' for consistency of terminology with your other sequences.

На мой непросвещённый взгляд, термин "нормализованные ДЛК" является общепринятым.
И если уже приводить в соответствие с терминологией в других последовательностях, то надо было изменить в других последовательностях, а не в этой.
Но редактору, конечно, виднее.

На мой вопрос редакторы ничего не ответили.

Fri May 21 09:43 Natalia Makarova: I am stopping research on this topic for now. My results are published here https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=133&postid=2080 Is it worth making an a-file with examples of DLS?

Таким образом, понятно, что a-file со всеми результатами и с примерами ДЛК в OEIS не нужен.
У них там диск лопнет от моих квадратов :)
Кстати, a-file в статье есть от автора статьи господина Ватутина
https://oeis.org/A287695/a287695_2.txt
но эти данные явно устарели.

Цитирую результаты, имеющиеся в опубликованной версии статьи

a(12) >= 655, a(13) >= 9, a(14) >= 1, a(15) >= 3, a(16) >= 13, a(17) >= 13, a(18) >= 1, a(19) >= 15, a(20) >= 1.
a(12) >= 6640729, a(13) >= 248703, a(14) >= 295309, a(17) >= 421. The result for a(12) was calculated by a volunteer. Found a new lower bound a(12) >= 1764493860. An independent confirmation of this result is required. - Natalia Makarova, Tomáš Brada, Apr 29 2021
a(14) >= 307662, a(18) >= 2, a(20) >= 2, a(21) >= 1, a(22) >= 1, a(23) >= 19, a(24) >= 824, a(25) >= 21, a(26) >= 1, a(27) >= 23, a(28) >= 3, a(29) >= 25, a(30) >= 1. - Natalia Makarova, Alex Chernov, Harry White, May 21 2021

Смотрим результаты для порядков n = 12 - 30 в моей таблице

a(12) >= 724775546 (1764493860)
a(13) >= 248703
a(14) >= 307662
a(15) >= 3
a(16) >= 1658880
a(17) >= 2453352
a(18) >= 96
a(19) >= 1383
a(20) >= 995328
a(21) >= 995328
a(22) >= 432000
a(23) >= 525
a(24) >= 345600
a(25) >= 345600
a(26) >= 48
a(27) >= 345600
a(28) >= 663552
a(29) >= 663552
a(30) >= 24

Пометила красным результаты, которые уже успела улучшить, занимаясь исследованием полуциклических пандиагональных ДЛК.

PS. А файл со всеми результатами и с примерами ДЛК я соберу на досуге и выложу его на Яндекс.Диск.
Яндекс.Диск не лопнет :)
Иметь в одном файле все ДЛК с максимальной группой ОДЛК очень важно.
Тема большая, и найти в ней все эти ДЛК трудно.

В теме «Алгоритм получения двушек для порядков n=4k+2»
строятся двушки (и не только!) для порядков проблемной серии n=4k+2.
Это даёт улучшение оценок для ДЛК порядков данной серии.
Новые оценки добавляю в мою таблицу.

Особенно порадовал результат для порядка 18 (24 ОДЛК от одного ДЛК) и на его основе результат для порядка 54, тоже 24-ка (хорошо работает метод Пелегрино-Ланселотти).

Для порядка 22 пока получена только троечка.
Но, возможно, Harry White напишет новую программу для порядков 22, 26 и т. д.

Сейчас уже получена 24-ка для порядка 22.
Смотрите сообщение
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=136&postid=2270

Думаю, что и для порядков 26 и 30 24-ки будут получены точно так же.

Это второй топовый ДЛК 12-го порядка по Д-трансверсалям

26164 Д-трансверсалей

 0  2  4  6  3  9  7  8  5 10 11  1
 6  1  7  5  2  8  3 11  9  4  0 10
 9  4  2  8 10  0  1  6 11  3  5  7
 7  0  9  3 11  1  8 10  2  5  4  6
 8  7  1 11  4  6 10  5  0  2  9  3
11  3 10  0  7  5  4  9  6  1  8  2
 1  9  0 10  5  7  6  3  4 11  2  8
 2  5 11  1  6  4  0  7 10  8  3  9
 5 10  3  9  1 11  2  0  8  7  6  4
 3  6  8  2  0 10 11  4  1  9  7  5
 4 11  5  7  8  2  9  1  3  6 10  0
10  8  6  4  9  3  5  2  7  0  1 11

Иллюстрация



Раскраской показана классическая блочная структура ДЛК.
Это квадрозавр №2 :) младший брат первого квадрозавра.
Симпатичный квадратик!

Свойства, выданные утилитой Harry White GetType1

Order? 12

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         1 diagonal Latin
         1 axial symmetric
         1 natural \diagonal
         1 axial parity 1-way

Отмечена осевая симметрия по Гергели/Брауну (горизонтальная).

Продолжение следует...

Итак, младший брат квадрозавра (смотрите предыдущий пост) обсчитан помощником!
Результат прекрасный для младшего брата
724 775 546 ОДЛК.

Ещё раз отработала программа Tomas Brada - поиск ОДЛК по частям. Замечательная программа!
Всё пространство поиска для данного ДЛК было разбито программой на 2107 частей.
Помощник прислал данные по частям, сколько ОДЛК найдено в каждой части; покажу фрагмент

1	328365
2	352095
3	339652
4	359215
5	327790
6	323619
7	418821
8	426100
9	336552
10	413849
. . . . . . 
2092	392212
2093	342088
2094	334055
2095	375906
2096	350476
2097	384690
2098	346868
2099	342873
2100	414752
2101	415779
2102	365182
2103	402278
2104	403355
2105	378135
2106	374315
2107	348125
	724775546

Первый столбец - номер части, второй столбец - количество ОДЛК в части.
Последняя строка - общее количество ОДЛК.
Конечно, ОДЛК мы не канонизировали, потому что для такого большого количества ОДЛК канонизация будет выполняться слишком долго.
Зато помощник нормализовал все полученные ОДЛК и проверил их на дубликаты.
Дубликатов нет и не могло быть!
В нескольких частях была проверена подлинность ОДЛК, то есть что эти квадраты действительно ортогональны исходному ДЛК.
Хотя программа Tomas Brada уже опробована десятки раз и никаких ошибок за ней не замечено, но лишняя проверка всегда полезна.
Подлинность ОДЛК проверялась программой Harry White GetOrthogonal.
Помощник прислал мне протоколы работы этой программы.
Например, протокол проверки первой части

Order? 12

Enter the name of the squares file: out1
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file out1-orthCounts.txt
..output file out1-orthNos.txt
    .. increasing LS store to     100,000
    .. increasing LS store to     200,000
    .. increasing LS store to     400,000
squares 328366 total orthogonal pairs 328365
Maximum pairs for square 328366: 328365
This is the only square with this maximum number of pairs.
..output file out1-328366orths.txt
Pairs for square 328366: 328365

elapsed time 1:58:28

Всё правильно: все 328365 ДЛК ортогональны исходному ДЛК, который в наборе стоит последним (328366-й).

Таким образом, результат превосходный и полностью проверенный.
Позже выложу все ОДЛК от этого квадрозаврика.

Время обсчёта квадрозаврика и мощности ─
цитирую

С 24 мая начался расчет. Вчера закончился. Значит, ушло две недели без одного дня. С постобработкой (удаление первых двух строк, нормализация, поиск дубликатов, нарезка на файлы 2 и 4 ГБ) - ровно две недели.
Мощности: ~210 ядер, ~3 ГГц
Всю постобработку делал на ноутбуке параллельно расчету по мере поступления результатов: 16 ядер, 4 ГГц (правда здесь и 4 ядер бы хватило).

Высший пилотаж! Восхищаюсь!
Огромная благодарность помощнику!

Выкладываю ссылки на результаты от квадрозавра №2

1: https://disk.yandex.ru/d/fgyv8TFUJaK1cQ
2: https://disk.yandex.ru/d/n5EWkK7hQQkk-g
3: https://disk.yandex.ru/d/qe60v36ISe-Kjg
4: https://disk.yandex.ru/d/ekeEKtU8u7TPrg
5: https://disk.yandex.ru/d/SqtJDe7rHK3DoA
6: https://disk.yandex.ru/d/5OymHktJg1EpCg
7: https://disk.yandex.ru/d/q-Y3TXTwT0P92A
8: https://disk.yandex.ru/d/BBwiF_vaUFENuQ
9: https://disk.yandex.ru/d/ZFddtUpSzmwKHw

Цитирую письмо помощника

Все 2107 частей сгруппированы в архивы по этим ссылкам. Каждый архив размером ~2 ГБ (из-за ограничений Яндекса), кроме последнего 9-го. Он ~1 ГБ. Каждый архив самостоятелен, не является частью большого многотомного архива.

ОДЛК выложены в кодах по системе Tomas Brada (так они выводятся программой поиска ОДЛК).
Декодирование выполняет его программа dlkconv.
Эта программа выложена тут
https://disk.yandex.ru/d/TI1t3PTYqwE_rA

Для конвертирования кодов в обычный числовой формат запишите в файл a.txt коды квадратов и выполните командную строку

dlkconv es <a.txt s >out.txt

Оригинал программы выложен автором в сообщении
https://boinc.tbrada.eu/forum_thread.php?id=3104&postid=4132

Попутно отмечу, что помощник выполнил полную проверку нормализованных ОДЛК на дубликаты для первого квадрозавра (результат 1764493860 ОДЛК).
Дубликатов не обнаружено, как и должно быть по логике программы поиска ОДЛК.

Напомню: на данный момент есть две нижние границы для ДЛК 12-го порядка
a(12) >= 6640729 (1764493860)

Обе они внесены в OEIS, но вторая (максимальная) граница не утверждена и требует независимого подтверждения.
А не утверждена она совершенно напрасно! Ибо результат этот абсолютно правильный.

Нижняя граница 6640729 получена от другого ДЛК, который не был обсчитан полностью, только небольшая часть.
Прогноз для этого ДЛК около 400 миллионов ОДЛК.

Теперь мы имеем ещё одну нижнюю границу
a(12) >= 724775546.

Сейчас Harry White получил группу ОДЛК от одного ДЛК 16-го порядка, содержащую 1658880 ОДЛК
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=136&postid=2338

Итак, уже появились миллионы в максимальной группе.
Очевидно, что это далеко не максимум для порядка 16. Вполне могут появиться и миллиарды ОДЛК в максимальной группе.

Надеюсь, теперь такого результата a(12) >= 1764493860 никто не испугается :)
Когда я ввела этот результат в OEIS, все весьма удивились, начиная от автора статьи и кончая редакторами.
Цитирую

a(12) >= 6640729, a(13) >= 248703, a(14) >= 295309, a(17) >= 421. The result for a(12) was calculated by a volunteer. Found a new lower bound a(12) >= 1764493860. An independent confirmation of this result is required. - Natalia Makarova, Tomáš Brada, Apr 29 2021

Это было 29 апреля т. г.
Первый огромный результат, качественный скачок для максимальных групп ОДЛК от одного ДЛК.

Автор статьи господин Ватутин написал

Thu Apr 29 08:36 Eduard I. Vatutin: As far as I know, the calculation of the ODLS number for the DLS of order of 12 was carried out by separate parts (subtasks). Natalia, can you guarantee that there are no repeating ODLSs in the separate parts? This requires the use of a number of special algorithmic techniques. Otherwise, the estimate 1764493860 is significantly overestimated.

https://oeis.org/history?seq=A287695&start=30

Особенно мне понравилось: "This requires the use of a number of special algorithmic techniques." :)
То есть проверка ОДЛК на различность "требует использования ряда специальных алгоритмических приемов" (в переводе Google).
Никаких особых алгоритмических приёмов для проверки ОДЛК на различность не требуется.
Мой помощник нормализовал все ОДЛК в этой максимальной группе и проверил их на дубликаты.
Вот и все алгоритмические приёмы!
Разумеется, дубликатов не обнаружено. Их и не могло быть по логике программы поиска ОДЛК (автор Tomas Brada).
Позже господин Ватутин развил теорию, доказывающую, что при данном алгоритме поиска ОДЛК дубликатов быть не может.
Я выше цитировала эту теорию.

Ещё оригинальнее написал редактор OEIS

Fri Apr 30 07:40 Joerg Arndt: If 1764493860 is too big than the inequality a(12) >= 1764493860 could be plain wrong!

Слишком большой результат, значит, он неправильный :)
Возможно, теперь редактор изменит своё мнение.

Под таким давлением мне пришлось изменить оценку на такую a(12) >= 6640729.
И такой результат тоже вызвал у господина Ватутина сомнения в отсутствии повторяющихся ОДЛК.
К счастью, этот результат поддержал другой редактор

Sat May 01 10:08
Andrew Howroyd: Personally, I don't see the problem here. Natalia is only claiming a count on a single given square. a(12) >= 6640729. Since there is a 534MB dump of the Latin squares, Eduardo can easily verify in a few minutes if he is so inclined (it seems easier than arguing it would take weeks to perform his own independent and full counts). The only number that might be slightly suspect is the a(12) >= 1764493860, but that is clearly qualified with a might be wrong.

Результат утверждён.
Однако этот результат - не полная максимальная группа ОДЛК от одного ДЛК, так как данный ДЛК не был полностью обсчитан, только маленькая часть.
Мы с помощником недавно повторили эксперимент со вторым топовым ДЛК 12-го порядка и получили новую оценку
a(12) >= 724775546.
Смотрите сообщение
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=133&postid=2298

Надеюсь, что эта оценка будет утверждена. Пока не вводила её в OEIS.
Мы с Harry работаем с этой проблемой. Появляются новые оценки для других порядков.
Смотрите тему
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=136

Ещё раз покажу все три результата, полученные для ДЛК 12-го порядка, вместе с ДЛК (в порядке возрастания оценок).

1. 24901 Д-трансверсалей

 0  8  3  6  5 11 10  4  9  2  7  1
10  1  9 11  8  2  7  3  4  6  0  5
 1  7  2  9 10  4  5 11  6  3  8  0
 8 10 11  3  0  9  1  6  2  4  5  7
 6  3  1 10  4  7 11  8  5  0  2  9
 3 11  7  1  6  5  9 10  0  8  4  2
 2  4  8  0  9 10  6  5  1  7 11  3
 9  2  0  5 11  8  4  7 10  1  3  6
11  9  5  7  3  0  2  1  8 10  6  4
 5  0  6  4  7  3  8  2 11  9  1 10
 7  5  4  2  1  6  0  9  3 11 10  8
 4  6 10  8  2  1  3  0  7  5  9 11

Иллю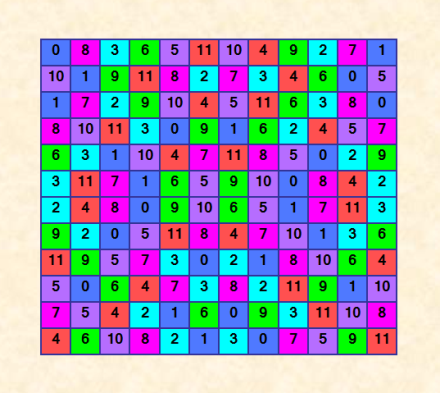страция



Результат
a(12) >= 6640729

2. 26164 Д-трансверсалей

 0  2  4  6  3  9  7  8  5 10 11  1
 6  1  7  5  2  8  3 11  9  4  0 10
 9  4  2  8 10  0  1  6 11  3  5  7
 7  0  9  3 11  1  8 10  2  5  4  6
 8  7  1 11  4  6 10  5  0  2  9  3
11  3 10  0  7  5  4  9  6  1  8  2
 1  9  0 10  5  7  6  3  4 11  2  8
 2  5 11  1  6  4  0  7 10  8  3  9
 5 10  3  9  1 11  2  0  8  7  6  4
 3  6  8  2  0 10 11  4  1  9  7  5
 4 11  5  7  8  2  9  1  3  6 10  0
10  8  6  4  9  3  5  2  7  0  1 11

Иллюстрация



Результат
a(12) >= 724775546

3. 28496 Д-трансверсалей

 0 10  4  6  2  8  9  3  7  5 11  1
11  1  7  5  9  3  2  8  4  6  0 10
 4  6  2  8  1 11 10  0  9  3  7  5
 7  5  9  3 10  0  1 11  2  8  4  6
 3  9  0 10  4  6  7  5 11  1  8  2
 8  2 11  1  7  5  4  6  0 10  3  9
 2  8  1 11  5  7  6  4 10  0  9  3
 9  3 10  0  6  4  5  7  1 11  2  8
 5  7  3  9  0 10 11  1  8  2  6  4
 6  4  8  2 11  1  0 10  3  9  5  7
 1 11  5  7  3  9  8  2  6  4 10  0
10  0  6  4  8  2  3  9  5  7  1 11

Иллю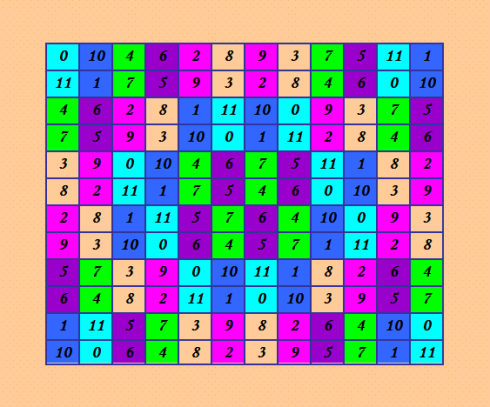страция



Результат
a(12) >= 1764493860

Все результаты опубликованы. Смотрите ссылки в данной теме.

Покажу ещё раз иллюстрацию: последняя максимальная группа (от квадрозавра), рекордная на данный момент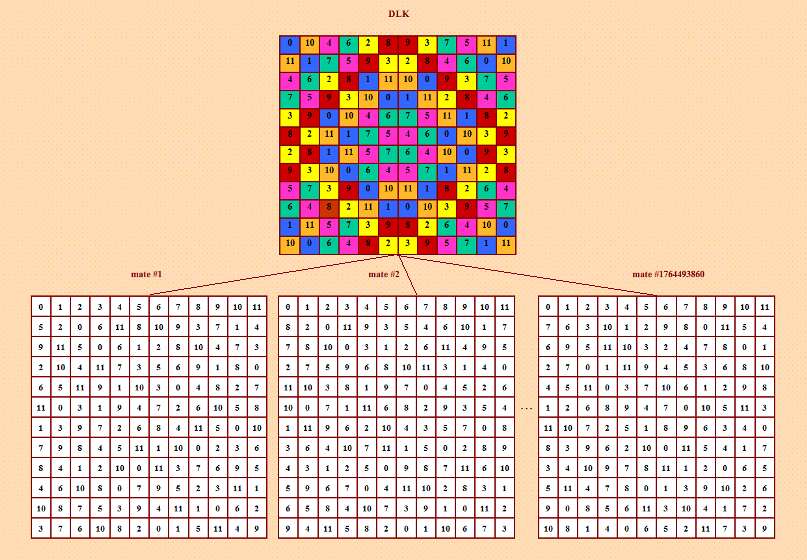



Квадрозавр на этой иллюстрации по-другому раскрашен, тоже показана классическая блочная структура, но с другими блоками.

Заархивировала тему и выложила архив на Яндекс.Диск
https://disk.yandex.ru/d/WonLI9-SbWn_-g
В архиве три файла в формате html, соответствующие трём страницам темы.
207 КБ.

Смотрите связанную тему
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=136
которая тоже заархивирована.

Дублирую сообщение
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=138&postid=3056

Повторю цитату из сообщения господина Ватутина

В ходе анализа первых результатов диагонализации ДЛК порядка 12 с рекордным на данный момент числом диагональных трансверсалей, равным 28496, был найден ДЛК с 30192 диагональными трансверсалями, что позволяет усилить ограничение с a(12)>=28496 до a(12)>=30192 в ряду https://oeis.org/A287648

Ссылка:
https://boinc.ru/forum/topic/proekt-gerasimhome/?part=104#postid-4533

Новый квадрозавр найден, но не опубликован.
Посмотрела в статье OEIS, там этого результата тоже нет.
Новый квадрозавр засекречен :)
Ну, какой секрет, вот он, черепашка его нашла :)

30192 Д-трансверсали

 0 10  4  5  2  9  3  8  6  7 11  1
11  1  5  4  8  3  9  2  7  6  0 10
 5  6  2  8  0  1 10 11  9  3  4  7
 7  4  9  3  1  0 11 10  2  8  6  5
 2  3 11  0  4  6  7  5 10  1  8  9
 3  2  1 10  7  5  4  6  0 11  9  8
 8  9  0 11  5  7  6  4  1 10  2  3
 9  8 10  1  6  4  5  7 11  0  3  2
 6  5  3  9 10 11  0  1  8  2  7  4
 4  7  8  2 11 10  1  0  3  9  5  6
 1 11  6  7  9  2  8  3  4  5 10  0
10  0  7  6  3  8  2  9  5  4  1 11

Никаких свойств в новом квадрозавре утилита Harry White не обнаружила

Order? 12

Enter the name of the squares file: a
.. writing type information to file aTypeDetail.txt

Counts
------
         1 diagonal Latin
         1 natural \diagonal

В новом квадрозавре количество общих трансверсалей такое же, как в предыдущем квадрозавре

order? 12
Type of transversals, 1 all or 2 diagonal? 1
File name? b
.. writing counts to file 12Transversals_1.txt
square 1 max transversals 198144

_______________________________________
конец дублируемого 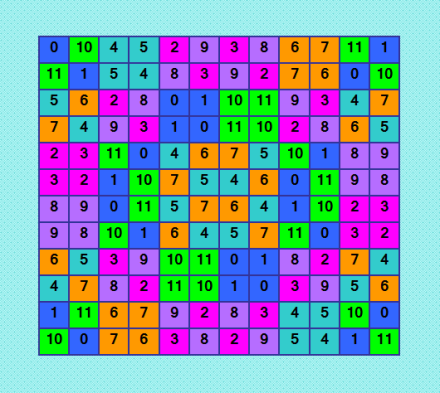сообщения

Иллюстрация


Очень красивый новый квадрозавр.
Я начала искать его в этой теме (9 мая т. г.)
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=134
И начинала с известного преобразования - поворота блоков (интеркалятов).
Потом подключила несколько других преобразований: перестановку строк/столбцов, преобразование циклических блоков, преобразование других нестандартных блоков.
И вот, наконец-то, я его нашла!

Сообщение господина Ватутина об этом квадрозавре написано 18 августа т. г.
Но... смотрите, какая интересная интрига :)
Сообщение о квадрозавре есть, но сам квадрозавр в нём не опубликован.
Вопрос: почему не опубликован? Каждый может ответить на этот вопрос самостоятельно.
Не был внесён этот ДЛК и в OEIS, сразу, как был найден.
А теперь внимание!
27 сентября я опубликовала найденный мной новый квадрозавр (смотрите дублируемое сообщение).
И! 27 сентября господин Ватутин вносит результат в OEIS!
Жутко испугался за свой приоритет :)

Разумеется, я искала новый квадрозавр для того, чтобы получить новый результат по ОДЛК от одного ДЛК 12-го порядка.
И конечно же, мы с помощником начали обсчёт нового квадрозавра на ОДЛК.
Обсчёт стартовал 1 октября т. г.
Помощник пишет, что в каждой части нового квадрозавра примерно в два раза больше ОДЛК, чем было от прежнего квадрозавра.
Отсюда можно сделать прогноз, что и общее количество ОДЛК от нового квадрозавра примерно в два раза больше, а это более 3 миллиардов.
К тому же, частей в новом квадрозавре больше, 2180, а в прежнем было 2048.
Ну, прогноз, конечно, очень приблизительный. Посчитаем, увидим, сколько ОДЛК даёт новый квадрозавр.
Очень интересно!

Напомню: предыдущий квадрозавр (28496 Д-трансверсалей) имеет 1764493860 ОДЛК.

К обсчёту нового квадрозавра подключился Mynx.
Смотрите сообщение
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=138&postid=3089

Помощник сообщает

Сейчас посчитано чуть больше 400 частей.
....
Время от времени попадаются части, которые считаются и трое, и даже четверо суток; на выходе у них получаются, конечно, гигантские файлы, под 100 ГБ.

Интересная статистика от Mynx

В 19 частях всего 36 663 439 ОДЛК (в среднем 1 929 655 ОДЛК на одну часть)
Минимальное количество ОДЛК в посчитанной части: 1,257,849 ОДЛК (часть 2014)
Максимальное — 4,988,520 ОДЛК (часть 2000).

Супер!

Вот ортогональки от нового квадрозавра (из 2001-й части, в этой части 1697979 ОДЛК)

# in: DfunSxMmH9rgDoppyRs2sEPwdrPS6m4 2001
# num_dtrans: 30192
DxA7o4etb9Pbmk5FKZpNya3Wk3ECBjy
DsTaBetZxo2GQSUh1gyqWLdnqsHqW97
DJiwLdq8wbzYKA3h13kCrJyXXgWz9z3
DA7uqXbbasDkAi6xSp585jEYRTKaUVC
DKQFvgHstg6SpshJ5zQx1uRFnHNRmD12
DQFQkXaeX4QLXHBmoRZb8LuakEihrx3
DKEUz5BLDx2XxkBwiwbhYVMH5sdk3C5
DzXDKxsj5j8p3scLcdsTn6ZRcEXDVFw
DTVewkoJeSp5XgWtWPRm1dU5j2e9XD62
Dpr9wDJxya5k6t9wyvy2GjG8xQy2pYz
D8dYma8jPkivZa7iSKjhePn4NVuL7kL
DfzLiFWBhUhtVAUzv7aLX64vGXN8bn3
DjXCU8cRRe5tGgwAe6eUpRqAirbNHp2
DrrbxY7H49q9jCjtpqv9FARteezQPk
Da53URWiMPoXotifGimVVxYarqaQtE2
DtEP7CyDWYWFjjeSCovMgTCWEZ2HHy8
DCUoyyTmsLUeyRtnt1hkHD8FVwsHD4E
DFJ5Wjj4SXAPVGNVHjfhe8SoK2MBGG8
Doanuv5oQXngoUkytj1Vdr2VRLdpzQ2
DDe54VztLn6Ys3Ptt62JiMUWhB3Pwv2
DSgnWUf6KnhCwHAp8eoMXAzMNGtEksB
DNbAriyUV5gY4nN5FriYg8W2Zas2ja2
DbfvDBnnz3tDnJztxNzF5scfhPAzk8c
Dv8AhXWEXh4zVgAVfqH7bajyJ3Rbh1S
DxvZ2a9YQSaj6Hwp3hyT9qhWyZTJUhx
DZ6iNbdFXhYnqRG4yMJ9hgafJM1kT7k2
D3w3ZSvVyLLjTW8KHxB2hTPLomtCJy2
DNXTRzPdH6tx35zBAgZj4pTqM56GfK
. . . . . 
DhiqLiK8swxZjiKnoQxqGFPFB7sgzrBH
DohDCohfrzNrLtCxcP79Q9Sisf6gbaP
D3cs8by2m3GUwkwYQGPpEdmfNLLGkY1B
Dvud8vUwsAWgLMdvfSFRFHA7CLf2DRdZ
DihA62eEE9eZ3mgf6x6q6e7pnMWynhE2
DA5gWS1gJAuCYfWtQ5URPbKi64eAWZd3
Djbr1DzghPKrpcfCFxvcUFTH9rSpjACJ
DPk9eXsgaoQDDpiHXSvN4pFcJ4K1arg4
D9mjSbBMtxBQAQEh1uExDSedMRzWjJr
D6LeNh4w168KaVNMKZeq6ADUuSMHMZJ
DthuenqC33e5WQSqBLrhrGQArXvPd8C2
DD69NCsxHixs7x1JhpqcU7gWAiRExqBG
DEDRu43KDiQPYY4WvxcpFgAU57LkFN8A2
DDJobFdeyobWM8fWHTemGtVnRi6mdzWV3
Dta6fZxvAMMtbEpc1NfGvuRr4DadKbm
DoDGrfaGH7Z3oxPysUAT87wecBvQBQB
DvGQporKw5xp7p9XECtVufriBhmLJdzc
DNz9G69sfpGKcj9oNqQKn9BYyhkC4re
Dadj4RVmFcbCzWHVf61x5gD2QsYzUtB
DGLD6CcPqcLkRnfPjioHGqbt8CUz9aK
D76Hqo1j4Fv4zJMJ17pzDphepcpLk52T
DJVK89qwHS5evhWhBy1XP1Q4N6yCRqX
DTaL8WEmRGdHejofTtCw8mMJ5DwW2K2
DjuASwWaWFbwYpw76yPL5hBad8RYYJKF

Хорошая техника у помощников.
Черепашка немножко завидует :) Она тоже хочет обсчитывать квадрозавр, но ей не по силам.
Мы с черепашкой от души желаем нашим замечательным помощникам постоянного электричества и стабильной работы компьютеров.
Большое спасибо им!

После завершения проекта "БД КФ ОДЛК 9-го порядка" XAVER подключился к обсчёту нового квадрозавра на ОДЛК.
Такая дружная команда из трёх человек трудится в этом эксперименте :) Замечательные у меня помощники!

Пришли первые результаты от XAVER, пока выделила ему 100 частей (1900 - 1999).
Посмотрим, как у него пойдут вычисления.
Покажу несколько первых и последних ОДЛК в 1900-й части

# in: DfunSxMmH9rgDoppyRs2sEPwdrPS6m4 1900
# num_dtrans: 30192
DdJCFV9qFRTmjgbA45aD87gatqJJFHC
DH6ZQ4ZACEZWemfJQV6f4UWM7KEk81r3
DhNig9jmAWH1eHMqaheioafaQD6NTb4
DK6fTZBn2P4TBdLEA4PRowAkLUmzcg
DfSNHkV8aQoNoJTTHRRTEVsH5MT8WHX
Dexvf6eebUqJ7jXw8wfugfAYnTQsvs2
DNKSrgGEy73DW9jLexxSiYAvmXpdeY2
Do7UvuKTAyyX8fUw6zHTfTKvhtftkUM
DHkReVmc9B7sVrXZa7rGm1SVn3Gr3Bg5
DTCtwP1ep2jLgcuXUurUHercW5LMKi2
DA7dCnzZTVA14sRsSxTB1texAcdY83
D7yde5GWMQJq7ECsfPdPa1S2KGLpCZ
DxN7Zxh6M9YDPWBpZm1h8Cg9HMi8R8
. . . . . . . . 
DSMUaEMuD79BAM5a3CuubTgUWxU8tp
DoCNqqoH5nku6ej8Searo7yiH6vVbK3
DGpoxEMrhELtC73zA38oWbbk3RVZMg
DMvq5uLZQ27c2rRpzDrpZ54RUYrzdVv
DRVtaWCWkEDaCETvALxLJWyRf1ZrrKr
DoCYdq2NRRDNFPkAyfZfa7UUkKJsyc9
DHNfKvPRfZuD5TQfzkS9F8b1joVQUSx
D4HLFhMa2fJELAy59ruTbaYnHmFxFCd2
DbcM6bsgbPPUkZgMAJvUtTDTG77hM6
D5prVp5LnPJjqe8QoG1tkrcbF7xJvn7
DumXHCh2dWc5J8J28ehizpPQVKek2HC
DoxbXm18E6xiW6iP2MXzR4nRupdJtZD
Dn27fZ7okak3eWYozjhRjoYtB1uHMnM
Dm1TMUZnuFQsMbQJuSe37jQUFVNSE2a2
DoPAhnTPaYJBqWLMUaV64wHTvDKGuCX
DzXzTjYUTYK8RKGHzzaBUXF3VArEb1R

В этой части содержится 2182361 ОДЛК.

А между тем обещанного в начале октября результата от нового квадрозавра (я так предполагаю, что в Герасиме обсчитывается новый квадрозавр) не получилось.
У Герасима были технические проблемы.

Цитирую сообщение господина Ватутина

Обработка текущего многострадального, но интересного ДЛК порядка 12 на предмет подсчета числа ОДЛК подходит к концу, на данный момент остались невыданными около 60 тыс. WU'шек, они будут разобраны приблизительно к вечеру, дальше пойдут хвосты.

Ссылка:
https://boinc.ru/forum/topic/proekt-gerasimhome/?part=117#postid-4835

И ещё (думаю, это о том же обсчёте нового квадрозавра на ОДЛК)

Благодаря соревнованию досчет последней партии WU'шек оперативно завершился, пошли хвосты, но... Сегодня обнаружил еще 6 WU'шек с битыми входными файлами :(. Файлы поправил вручную, перезалил на сервер для повторного расчета. Сколько еще таких будет, хз...

Ссылка:
https://boinc.ru/forum/topic/proekt-gerasimhome/?part=118#postid-4849

Напомню: этот обсчёт был запущен в BOINC-проекте Gerasim@Home 26 августа т. г.
Наш эксперимент по обсчёту нового квадрозавра на ОДЛК стартовал 1 октября т. г. Новый квадрозавр был найден мной 27 сентября т. г.
У нас не BOINC-проект, а трое моих замечательных помощников работают в этом эксперименте.
Прогноз по времени от главного помощника (он выполняет бОльшую часть работы) - примерно полтора месяца, прогноз по количеству ОДЛК - более трёх миллиардов.
Если всё будет хорошо (без непредвиденных препятствий), мы ожидаем результат во второй половине ноября т. г.

PS. Из более миллиона вушек найти все битые... Да-а-а-а, задача не хилая.
И где гарантия, что они все будут найдены?

XAVER прислал результаты ещё из пяти обсчитанных частей.
Работает стабильно. Живые ОДЛК идут. Отлично!
Всего у XAVER пока посчитано 10 частей (1900 - 1909).