Thread 'Статьи в OEIS: иÑÑ‚Ð¾Ñ€Ð¸Ñ Ð¸ ÑовременноÑÑ‚ÑŒ'
Message boards : Science : Статьи в OEIS: иÑÑ‚Ð¾Ñ€Ð¸Ñ Ð¸ ÑовременноÑÑ‚ÑŒ
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
A001438 https://oeis.org/A001438 Maximal number of mutually orthogonal Latin squares (or MOLS) of order n. AUTHOR N. J. A. Sloane К Ñожалению, дата ÑÐ¾Ð·Ð´Ð°Ð½Ð¸Ñ Ñтатьи не указана. Ðо ÑÑƒÐ´Ñ Ð¿Ð¾ номеру поÑледовательноÑти ÑÑ‚Ð°Ñ‚ÑŒÑ Ñоздана очень давно. Ðто иÑториÑ. Да, над Ñозданием групп MOLS математики работают давно и уÑпешно. ЕдинÑтвенный крепкий орешек - группа MOLS 10-го порÑдка. Ðе найдена даже группа MOLS данного порÑдка, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· трёх взаимно ортогональных ЛК. Однако доказано, что группа MOLS данного порÑдка из 9 ЛК не ÑущеÑтвует. ИзвеÑтно, цитирую a(n) <= n-1 for all n>1. - Tom Edgar, Apr 27 2015 Таким образом, Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 10 имеем такую оценку 2 <= a(10) <= 8 Ð’ Ñтатье напиÑано, цитирую Parker and others conjecture that a(10) = 2. Может быть, Ñта гипотеза верна, но пока её и не доказали, и не опровергли. СвÑзанные Ñтатьи: A287695, A328873. Ðто уже ÑовременноÑÑ‚ÑŒ. Смотрите об Ñтих ÑтатьÑÑ… далее. Я добавила бы в Ñту Ñтатью 1) ÑÑылку на таблицу групп MOLS https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117&postid=1189 Ð Ñто Ñама таблица 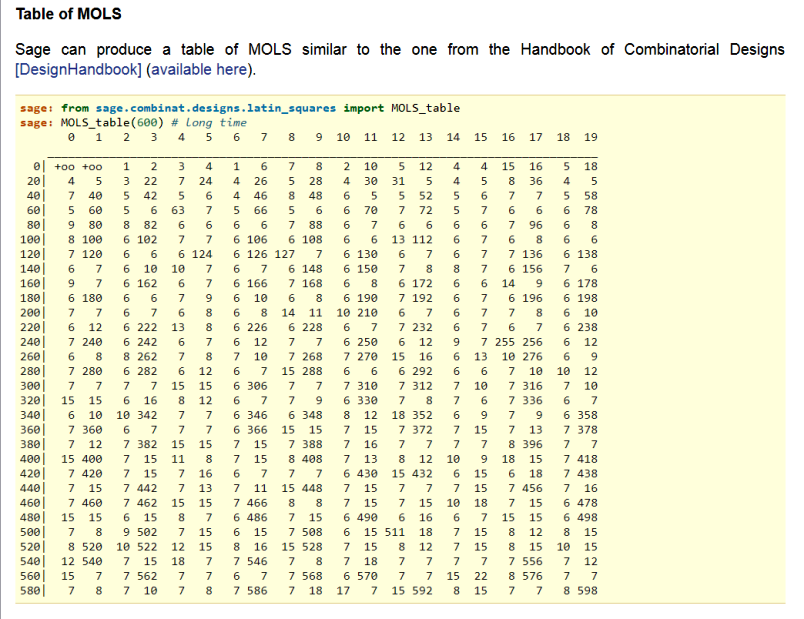 2) ÑÑылку на тему "Complete MOLS systems" https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117 3) Пример группы MOLS 12-го порÑдка, ÑоÑтоÑщей из четырёх ДЛК и одного ЛК. Ðто очень краÑÐ¸Ð²Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð°, Ð½Ð°Ð¹Ð´ÐµÐ½Ð½Ð°Ñ Ð¼Ð½Ð¾Ð¹.  Смотрите опиÑание ÑÐ¾Ð·Ð´Ð°Ð½Ð¸Ñ Ñтой группы в теме "MOLS and MODLS of order 12" https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=120 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
A287695 https://oeis.org/A287695 Maximum number of diagonal Latin squares with the first row in ascending order that can be orthogonal to a given diagonal Latin square of order n. 1, 0, 0, 1, 1, 0, 3, 824, 614 AUTHOR Eduard I. Vatutin, May 30 2017 Ð’ Ñту поÑледовательноÑÑ‚ÑŒ у Ð¼ÐµÐ½Ñ ÐµÑÑ‚ÑŒ много новых результатов. Смотрите темы: 1. "Maximum number of normalized ODLS from one DLS" https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=133 2. "Ðлгоритм Ð¿Ð¾Ð»ÑƒÑ‡ÐµÐ½Ð¸Ñ Ð´Ð²ÑƒÑˆÐµÐº Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдков n=4k+2" https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=136 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
A328873 https://oeis.org/A328873 Maximal size of a set of pairwise mutually orthogonal diagonal Latin squares of order n. 1, 0, 0, 2, 2, 1, 4, 6, 6 AUTHOR Eduard I. Vatutin, Oct 29 2019 Ð’ Ñтой Ñтатье еÑÑ‚ÑŒ ÑÐ»ÐµÐ´ÑƒÑŽÑ‰Ð°Ñ Ð³Ð¸Ð¿Ð¾Ñ‚ÐµÐ·Ð°: Conjecture: a(9) = 6. - Natalia Makarova, Dec 24 2020 ÐžÑ‚ÐºÑ€Ñ‹Ñ‚Ð°Ñ Ð¿Ñ€Ð¾Ð±Ð»ÐµÐ¼Ð°. Я где-то пиÑала об Ñтом подробно. Считаю, что гипотеза доказана. Однако моё доказательÑтво в OEIS не принÑто, потому что автор Ñтатьи Ñчитает его неверным. Он напиÑал, что Ñто надо доказывать полным перебором. За чем дело Ñтало??? ÐŸÐ¾Ð»Ð½Ð°Ñ Ð‘Ð” КФ ОДЛК 9-го порÑдка найдена в двух BOINC-проектах в начале Ñ‚. г. 75307 КФ ОДЛК не так уж и много. Доказывайте, гоÑподин Ватутин! Ðедавно Ñ Ð½Ð°ÑˆÐ»Ð° оригинальную группу MODLS 12-го порÑдка, ÑоÑтоÑщую из четырёх взаимно ортогональных ДЛК.  Смотрите тему "MOLS and MODLS of order 12" https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=120 Сразу же добавила Ñту оценку в Ñтатью, цитирую COMMENTS a(12) >= 4. - Natalia Makarova, May 30 2021 Добавление до Ñих пор не утверждено. О группах MODLS 9-го порÑдка Ñмотрите тему "Группы MODLS порÑдка 9" https://boinc.progger.info/odlk/forum_thread.php?id=171#6591 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
A330391 https://oeis.org/A330391 Number of main classes of diagonal Latin squares of order n with at least one orthogonal diagonal mate. 1, 0, 0, 1, 1, 0, 5, 1105, 75307 AUTHOR Eduard I. Vatutin, Feb 25 2020 РздеÑÑŒ о базах данных, тех Ñамых БД КФ ОДЛК, которые мы ищем. Тут еÑÑ‚ÑŒ иÑториÑ, ÐºÐ¾Ñ‚Ð¾Ñ€Ð°Ñ ÑохранилаÑÑŒ в правках https://oeis.org/history?seq=A330391&start=10 1 ноÑÐ±Ñ€Ñ Ð¿Ñ€Ð¾ÑˆÐ»Ð¾Ð³Ð¾ года Ñ Ð´Ð¾Ð±Ð°Ð²Ð¸Ð»Ð° оценку Ð´Ð»Ñ Ð‘Ð” КФ ОДЛК 9-го порÑдка. Мой ручной проект по поиÑку БД КФ ОДЛК 9-го порÑдка был запущен 10 авгуÑта прошлого года, о чём было объÑвлено здеÑÑŒ https://boinc.progger.info/odlk/forum_thread.php?id=165&postid=6220 К 1 ноÑÐ±Ñ€Ñ Ð¿Ñ€Ð¾ÑˆÐ»Ð¾Ð³Ð¾ года наша БД Ñодержала 53844 КФ ОДЛК, и была внеÑена в OEIS Ñта оценка: a(9) > 53844. ÐŸÑ€ÐµÐ´Ð²Ð°Ñ€Ð¸Ñ‚ÐµÐ»ÑŒÐ½Ð°Ñ Ð‘Ð”, ÑÐ¾Ð´ÐµÑ€Ð¶Ð°Ñ‰Ð°Ñ ÑƒÐ¶Ðµ больше данного количеÑтва КФ ОДЛК (56171), была опубликована немного позже. Смотрите Ñообщение https://boinc.progger.info/odlk/forum_thread.php?id=174&postid=6882 Ðта оценка была удалена в марте Ñ‚. г., когда автор Ñтатьи вноÑил данные о полной БД КФ ОДЛК, найденной в двух BOINC-проектах, поиÑк в которых был запущен 10 ÑентÑÐ±Ñ€Ñ Ð¿Ñ€Ð¾ÑˆÐ»Ð¾Ð³Ð¾ года, то еÑÑ‚ÑŒ через меÑÑц поÑле Ñтарта моего ручного проекта. Вообще-то, можно было и не удалÑÑ‚ÑŒ. Оценка вполне Ð¿Ñ€Ð°Ð²Ð¸Ð»ÑŒÐ½Ð°Ñ Ð¸ внеÑена была именно в тот момент, когда Ñто количеÑтво КФ ОДЛК было найдено. И было найдено уже более половины вÑей БД! Ðа данный момент наша БД КФ ОДЛК 9-го порÑдка Ñодержит 70815 КФ ОДЛК. Мы продолжаем Ñтот ручной проект. Смотрите тему "БД КФ ОДЛК 9-го порÑдка" https://boinc.progger.info/odlk/forum_thread.php?id=44 Я добавила бы в Ñту Ñтатью оценку: a(10) >15000000 Ñо ÑÑылкой на тему "DB CF ODLS of order 10" https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=114 БольшинÑтво результатов BOINC-проектов ОДЛК и ODLK1, которые занимаютÑÑ Ð¿Ð¾Ð¸Ñком БД КФ ОДЛК 10-го порÑдка, опубликованы. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
A338620 https://oeis.org/A338620 Number of pandiagonal Latin squares of order 2n+1 with the first row in ascending order. 1, 0, 2, 4, 0, 8, 12386, 0 AUTHOR Eduard I. Vatutin, Nov 04 2020 Ðту Ñтатью Ð½ÐµÐ»ÑŒÐ·Ñ Ð½Ð°Ð·Ð²Ð°Ñ‚ÑŒ Ñтатьёй. Содраны количеÑтва квадратов из извеÑтной Ñтатьи. Ðикаких ÑобÑтвенных результатов автор не предÑтавил. Ðа мой Ð²Ð¾Ð¿Ñ€Ð¾Ñ "как получить обозначенные квадраты" он ответил, что можно их получить алгоритмом грубой Ñилы. Была Ð±ÑƒÑ€Ð½Ð°Ñ Ð´Ð¸ÑкуÑÑÐ¸Ñ Ñ Ñ€ÐµÐ´Ð°ÐºÑ‚Ð¾Ñ€Ð¾Ð¼ по поводу Ñтой Ñтатьи. Приведу поÑледний комментарий редактора Fri Apr 09 09:43 Andrew Howroyd: Your links are not of general interest. The one I removed is a rant - who wants to read your every passing thought? - you even include a running commentary on the history of this sequence as it is being made!!!?? What you publish on your own web site is your business, but at oeis we do have quality standards and a review process. Your claim that these links contain original studies is irrelevant, dubious and certainly incorrect. You are in no position to claim something is original when you have not so much as looked at the existing links attached to this page. Your claim is also nebulous in that you do not provide a clear example of a new previously unknown fact or theorem that is not covered by any existing research. So far I have seen nothing worth publishing. I am also not in favor of restoring the old link that you so thoughtfully removed, but will leave that decision to others. Again it is incoherent garbage. I see no reason to pollute the two perfectly good references this sequence has with your 3rd rate and basically worthless musings. By the way, the Atkin paper is remarkable - they computed this sequence in 1982 on a machine with 2MB of Ram and surely a 1000 times slower than any computer today. Now to the example Latin square: it is rather an example for those Latin squares counted by A071607. This sequence already has a good example that clearly clarifies what this sequence is about - your example would not improve clarity - it is not even a good example for a semi-cyclic square, since it doesn't illustrate the general case. Again there is a good illustration of a semi-cyclic square in the references. I do not understand your complaint. I spent over 2 hours of my time to reproduce the 348 squares and find the A071607 sequence and quickly look through the references to see if I could understand where the difference came from and offer you suggestions. It is not my fault that you have nothing to add to this sequence at this time. I wish you luck with your complaint to administration - when a little crocodile bites your toes it is beyond foolish to run to the mother. https://oeis.org/history?seq=A338620&start=10 Я перевела (то еÑÑ‚ÑŒ прочитала) Ñтот комментарий пару дней назад и немного комментировала здеÑÑŒ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=135&postid=2385 Мои иÑÑÐ»ÐµÐ´Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¾ полуцикличеÑких (и не только) пандиагональных ДЛК Ñмотрите в темах 1. Experiment (pandiagonal DLS of order 13) https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=128 2. Semi-cyclic pandiagonal DLS of prime order n>11 https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=132 3. Semi-cyclic pandiagonal DLS of order 17 https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=135 СÑылки на Ñти темы редактор удалÑет, так как не видит в темах ничего интереÑного и доÑтойного публикации. Позже редактор Andrew Howroyd Ñоздал поÑледовательноÑÑ‚ÑŒ, поÑвÑщённую полуцикличеÑким пандиагональным ЛК. Далее раÑÑкажу об Ñтой поÑледовательноÑти. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
A343867 https://oeis.org/A343867 Number of semicyclic pandiagonal Latin squares of order 2*n+1 with the first row in ascending order. 0, 0, 0, 0, 0, 0, 1560, 0, 34000, 175104, 0, 22417824 AUTHOR Andrew Howroyd, May 08 2021 Я предÑтавила в Ñту Ñтатью полные комплекты нормализованных полуцикличеÑких пандиагональных ДЛК порÑдков 13 и 17. Ðти комплекты принÑÑ‚Ñ‹, однако ÑÑылка на Ñтатью "Semi-cyclic pandiagonal DLS of order 17" удалена. ÐÑ€Ð³ÑƒÐ¼ÐµÐ½Ñ‚Ð°Ñ†Ð¸Ñ Ð¾Ñ‡ÐµÐ½ÑŒ Ð¾Ñ€Ð¸Ð³Ð¸Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Thu Jun 03 12:54 Andrew Howroyd: I don't think the discussion between you and yourself is of interest - removed. https://oeis.org/history?seq=A343867 Цитирую Natalia Makarova, 1560 semi-cyclic Latin squares of order 13 ЗдеÑÑŒ, конечно, пропущено важное Ñлово "pandiagonal". Ðто вот почему. Мои первоначальные Ð½Ð°Ð·Ð²Ð°Ð½Ð¸Ñ Ñ€ÐµÐ´Ð°ÐºÑ‚Ð¾Ñ€ отредактировал вообще до Ñмехотворно коротких: "1560 squares of order 13" и "34000 square of order 17". Какие квадраты??? Я подумала, что Ð½Ð°Ð·Ð²Ð°Ð½Ð¸Ñ Ñлишком длинные, но вÑÑ‘-таки отредактировала Ñнова и добавила, что Ñто не чёрт знает какие квадраты, а "semi-cyclic Latin squares". |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
A339999 https://oeis.org/A339999 СÑылка недейÑтвительна. ПоÑледовательноÑÑ‚ÑŒ удалена! ПытаÑÑÑŒ разобратьÑÑ Ð² цикличеÑких, полуцикличеÑких и не цикличеÑких пандиагональных ДЛК, Ñ Ñоздала Ñту поÑледовательноÑÑ‚ÑŒ. Она была о главных клаÑÑах пандиагональных ДЛК. Я понимала главные клаÑÑÑ‹ пандиагональных ДЛК в нашей трактовке, то еÑÑ‚ÑŒ по количеÑтву каноничеÑких форм (КФ). Вполне допуÑкаю, что Ñта Ð¸Ð½Ñ‚ÐµÑ€Ð¿Ñ€ÐµÑ‚Ð°Ñ†Ð¸Ñ Ð² применении к пандиагональным ДЛК невернаÑ. Ðо! УдалÑÑ‚ÑŒ поÑледовательноÑÑ‚ÑŒ без ÑƒÐ²ÐµÐ´Ð¾Ð¼Ð»ÐµÐ½Ð¸Ñ Ð°Ð²Ñ‚Ð¾Ñ€Ð° - Ñто нормально? И Ñколько же моих поÑледовательноÑтей удалено? ДеÑÑÑ‚ÑŒ? Двадцать? Ðаверное, в правилах Ñнциклопедии OEIS так и напиÑано, что админиÑÑ‚Ñ€Ð°Ñ†Ð¸Ñ Ð¸Ð¼ÐµÐµÑ‚ право удалить любую поÑледовательноÑÑ‚ÑŒ без ÑƒÐ²ÐµÐ´Ð¾Ð¼Ð»ÐµÐ½Ð¸Ñ Ð°Ð²Ñ‚Ð¾Ñ€Ð° и объÑÑÐ½ÐµÐ½Ð¸Ñ Ð¿Ñ€Ð¸Ñ‡Ð¸Ð½. Правила Ñнциклопедии, чеÑтно Ñкажу, не читала. Однако, где здравый Ñмыл??? Человек Ñоздал поÑледовательноÑÑ‚ÑŒ, пытаетÑÑ Ð¿Ð¾Ð½ÑÑ‚ÑŒ тему, разобратьÑÑ, затрачивает времÑ. Через некоторое Ð²Ñ€ÐµÐ¼Ñ Ð¿Ñ€Ð¸Ñ…Ð¾Ð´Ð¸Ñ‚ и... видит, что его поÑледовательноÑти уже давно нет. Сначала даже не поверила в Ñтот абÑурд, подумала, что Ñ Ð½Ð° бумажке неправильно запиÑала номер поÑледовательноÑти. Ðо вот пиÑьмо, полученное мной 21 ÑÐ½Ð²Ð°Ñ€Ñ Ñ‚. г. Dear Natalia Makarova: Ðикакой ошибки нет, поÑледовательноÑÑ‚ÑŒ A339999 была Ñоздана и опубликована. Ð ÑÐµÐ¹Ñ‡Ð°Ñ ÐµÑ‘ нет. Что-то Ñ Ð½Ðµ ÑовÑем понимаю: Ñто так и должно быть? ИнтереÑÐ½Ð°Ñ Ð¿Ð¾Ð»Ð¸Ñ‚Ð¸ÐºÐ°, однако, в Ñнциклопедии. Ð’ÑÑ‘ больше ÑклонÑÑŽÑÑŒ к мыÑли, что Ñ Ð² Ñтом бардаке Ñ Ð½Ð°Ð·Ð²Ð°Ð½Ð¸ÐµÐ¼ "ÐÐ½Ñ†Ð¸ÐºÐ»Ð¾Ð¿ÐµÐ´Ð¸Ñ OEIS" не учаÑтник. Как напиÑал редактор (Ñм. комментарий выше) I wish you luck with your complaint to administration - when a little crocodile bites your toes it is beyond foolish to run to the mother. То еÑÑ‚ÑŒ, читайте так: жаловатьÑÑ Ð±ÐµÑполезно. И не буду. Уже понÑла, что беÑполезно. Редакторы - крокодилы. ÐдминиÑтратор помалкивает в Ñ‚Ñ€Ñпочку. По-хорошему, еÑли поÑледовательноÑÑ‚ÑŒ признана неверной, она должна быть проÑто заблокирована Ð´Ð»Ñ Ð¿ÑƒÐ±Ð»Ð¸Ñ‡Ð½Ð¾Ð³Ð¾ чтениÑ, но ни в коем Ñлучае не удалена. И, разумеетÑÑ, автора необходимо поÑтавить в извеÑтноÑÑ‚ÑŒ, почему его поÑледовательноÑÑ‚ÑŒ признана неверной и заблокирована. Ðаверное, у Ð¼ÐµÐ½Ñ Ð´Ñ€ÐµÐ¼ÑƒÑ‡Ð¸Ðµ предÑÑ‚Ð°Ð²Ð»ÐµÐ½Ð¸Ñ Ð¾ нормальной Ñтике в научном ÑообщеÑтве. По-Ñовременному вÑÑ‘ гораздо проще: удалили и вÑе дела. Рвдруг окажетÑÑ, что Ð¼Ð¾Ñ Ð¸Ð½Ñ‚ÐµÑ€Ð¿Ñ€ÐµÑ‚Ð°Ñ†Ð¸Ñ ÐºÐ°Ðº раз правильнаÑ, а тот, кто удалил поÑледовательноÑÑ‚ÑŒ, ошибаетÑÑ. И где потом иÑкать Ñту мою интерпретацию, еÑли поÑледовательноÑÑ‚ÑŒ начиÑто удалена? Очевидно, что Ñто в корне Ð½ÐµÐ¿Ñ€Ð°Ð²Ð¸Ð»ÑŒÐ½Ð°Ñ Ð¿Ð¾Ð»Ð¸Ñ‚Ð¸ÐºÐ°. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата A328873 Ух! ПоÑмотрела внимательно на Ñту поÑледовательноÑÑ‚ÑŒ 1, 0, 0, 2, 2, 1, 4, 6, 6 И что Ñ Ð²Ð¸Ð¶Ñƒ! a(9) = 6 !!! Смотрю иÑторию правок. Mon Feb 15 08:46 Eduard I. Vatutin: Brute force based search of cliques shows that there are 1164 cliques with cardinality 3, 11 cliques with cardinality 4 and 71 cliques with cardinality 6. Cliques with cardinality >6 does not exist, so a(9)=6. Makarova's proof is not really such because it is based on considering only small part of the cliques. https://oeis.org/history?seq=A328873&start=10 Перевод в Google ПоиÑк клик методом грубой Ñилы показывает, что ÑущеÑтвует 1164 клик Ñ Ð¼Ð¾Ñ‰Ð½Ð¾Ñтью 3, 11 клик Ñ Ð¼Ð¾Ñ‰Ð½Ð¾Ñтью 4 и 71 клик Ñ Ð¼Ð¾Ñ‰Ð½Ð¾Ñтью 6. Клик Ñ Ð¼Ð¾Ñ‰Ð½Ð¾Ñтью> 6 не ÑущеÑтвует, поÑтому a (9) = 6. ДоказательÑтво Макаровой на Ñамом деле не так, потому что оно оÑновано на раÑÑмотрении лишь небольшой чаÑти клик. Так значит Ð¼Ð¾Ñ Ð³Ð¸Ð¿Ð¾Ñ‚ÐµÐ·Ð° доказана ещё раз! И ещё один абÑурд в OEIS: почему Ñ Ð½Ðµ уведомлена об Ñтом? Ðи автор Ñтатьи, ни редакторы не Ñочли нужным Ñообщить мне о том, что Ð¼Ð¾Ñ Ð³Ð¸Ð¿Ð¾Ñ‚ÐµÐ·Ð° доказана ещё раз (другим ÑпоÑобом) и мой результат a(9) = 6 подтверждён. Я учаÑтник, Ñделавший вклад в Ñту Ñтатью, выдвинувший данную гипотезу, ÐºÐ¾Ñ‚Ð¾Ñ€Ð°Ñ Ð²Ð¾Ð¾Ð±Ñ‰Ðµ-то первоначально не была гипотезой. Был внеÑён результат a(9) = 6. И Ñ Ð±Ñ‹Ð»Ð° абÑолютно уверена в Ñвоём доказательÑтве. Ðо гоÑподин Ватутин поÑчитал, что моё доказательÑтво неверное, и результат перенеÑли в ÑÑ‚Ð°Ñ‚ÑƒÑ Ð³Ð¸Ð¿Ð¾Ñ‚ÐµÐ·Ñ‹. Теперь результат подтверждён, однако гоÑподин Ватутин забыл мне об Ñтом Ñообщить. Ркогда Ñ Ñ€ÐµÐ·ÑƒÐ»ÑŒÑ‚Ð°Ñ‚ опубликовала в OEIS, он приÑлал неÑколько пиÑем, ÑƒÐ±ÐµÐ¶Ð´Ð°Ñ Ð¼ÐµÐ½Ñ Ð² том, что моё доказательÑтво неверное. Да, и вот Ñто ДоказательÑтво Макаровой на Ñамом деле не так, потому что оно оÑновано на раÑÑмотрении лишь небольшой чаÑти клик. Моё доказательÑтво оÑновано на раÑÑмотрении вÑех полных ÑиÑтем MOLS, опубликованных в Ñтатье, ÑÑылку на которую Ñ ÑƒÐºÐ°Ð·Ð°Ð»Ð° в OEIS. Ðто вÑе полные ÑиÑтемы MOLS 9-го порÑдка, и ни одна из них не Ñодержит группу MODLS из более 6 ДЛК. Приведу пару цитат из диÑкуÑÑии Thu Dec 24 07:28 Natalia Makarova: 1. I am confident in the correctness of my proof that a (9) = 6. 2. I would like to see the opinion of Max Alekseyev, who wrote that a (9) > = 6. 3. If my opponents claim that a (9) = 6 is not proven, I propose to formulate this statement as my hypothesis. We will wait for the hypothesis to be refuted by a counterexample. No counterexample has been found at this time. The proof that a (9) = 7 is also not shown. https://oeis.org/history?seq=A328873&start=30 Fri Jan 08 04:24 Natalia Makarova: @E. I. Vatutin you have a complete set of orthogonal Diagonal Latin squares of order 9. Find a clique of size larger than 6. https://oeis.org/history?seq=A328873&start=20 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
И продолжение цитаты из моего ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=138&postid=2404 Ðедавно Ñ Ð½Ð°ÑˆÐ»Ð° оригинальную группу MODLS 12-го порÑдка, ÑоÑтоÑщую из четырёх взаимно ортогональных ДЛК. Ðе поÑтому ли редакторы не кажут ноÑа в Ñту поÑледовательноÑÑ‚ÑŒ? Что-то очень Ñтранно. Ð¢Ñ€ÐµÑ‚ÑŒÑ Ð½ÐµÐ´ÐµÐ»Ñ Ð¸Ð´Ñ‘Ñ‚, в поÑледовательноÑти ни одного ÐºÐ¾Ð¼Ð¼ÐµÐ½Ñ‚Ð°Ñ€Ð¸Ñ Ð¾Ñ‚ редакторов. Зато гоÑподин Ватутин откомментировал by Eduard I. Vatutin at Sun Jun 13 06:36:46 EDT 2021 Он добавил найденную мной группу MODLS 12-го порÑдка в Ñвой "подтверждающий ÑпиÑок" - Proving list (best known examples). Подтверждайте, гоÑподин Ватутин, ваша учаÑÑ‚ÑŒ Ñ‚Ð°ÐºÐ°Ñ â€“ подтверждать и перенаходить методом грубой Ñилы (в гриде). Впрочем, результат ещё не утверждён редактором OEIS. За фигом его подтверждать в "подтверждающем ÑпиÑке"? Он, может, неправильный. Или не понравитÑÑ Ð»ÐµÐ²Ð¾Ð¹ пÑтке редактора :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вот думаю: Ñтоит ли прокомментировать Ñто в диÑкуÑÑии OEIS? Ðаверное, не Ñтоит. Бардак от Ñтого меньше не Ñтанет. И редакторы - крокодилы никуда не денутÑÑ. Так и будут куÑать за пÑтки. И маме жаловатьÑÑ Ð½Ðµ велÑÑ‚ :) Лучше вÑего уйти, чтобы не куÑали. Любопытно вÑÑ‘-таки, что же будет Ñ Ð¼Ð¾Ð¸Ð¼ добавлением. Так и будет виÑеть в черновике? И в "подтверждающем ÑпиÑке" гоÑподина Ватутина :) Мне его Ð¿Ð¾Ð´Ñ‚Ð²ÐµÑ€Ð¶Ð´ÐµÐ½Ð¸Ñ Ð½Ð¸Ñколько не нужны. Я в Ñвоих результатах уверена без его подтверждений. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПопыталаÑÑŒ разобратьÑÑ Ñ Ð³Ð»Ð°Ð²Ð½Ñ‹Ð¼Ð¸ клаÑÑами пандиагональных ДЛК (печально ÑƒÐ´Ð°Ð»Ñ‘Ð½Ð½Ð°Ñ Ð¼Ð¾Ñ Ð¿Ð¾ÑледовательноÑÑ‚ÑŒ Ð339999). Два автора Ñоздают Ñвои поÑледовательноÑти по Ñтому вопроÑу, при Ñтом чёрт ногу Ñломит в Ñтих поÑледоваетльноÑÑ‚ÑÑ…, потому что у одного автора одна трактовка, у другого автора Ð´Ñ€ÑƒÐ³Ð°Ñ Ñ‚Ñ€Ð°ÐºÑ‚Ð¾Ð²ÐºÐ°. И вÑÑ‘ Ñто перемешано в одном флаконе. И получилаÑÑŒ Ð¿Ð¾Ð»Ð½Ð°Ñ Ñ‡ÑƒÑˆÑŒ! Я помню хорошо поÑледовательноÑÑ‚ÑŒ, Ñозданную гоÑподином Ватутиным, и даже помню, что он ÑÑылалÑÑ Ð² ней на мою поÑледовательноÑÑ‚ÑŒ Ð339999 ныне И трактовка гоÑподина Ватутина Ñ‚Ð°ÐºÐ°Ñ Ð¶Ðµ, как была в моей поÑледовательноÑти, то еÑÑ‚ÑŒ количеÑтво главных клаÑÑов цикличеÑких пандиагональных ДЛК определÑлоÑÑŒ через количеÑтво каноничеÑких форм (КФ). И Ñто Ð¿Ñ€Ð°Ð²Ð¸Ð»ÑŒÐ½Ð°Ñ Ñ‚Ñ€Ð°ÐºÑ‚Ð¾Ð²ÐºÐ°! Ðо гоÑподин Andrew Howroyd через некоторое Ð²Ñ€ÐµÐ¼Ñ Ñоздаёт Ñвою поÑледоваетльноÑÑ‚ÑŒ Ñо Ñвоей трактовкой, ÐºÐ¾Ñ‚Ð¾Ñ€Ð°Ñ Ð¾Ñ‚Ð»Ð¸Ñ‡Ð°ÐµÑ‚ÑÑ Ð¾Ñ‚ трактовки гоÑподина Ватутина. И Ñовершенно непонÑтно, зачем он Ñто делает! Ðу, и попутно удалÑетÑÑ Ð¼Ð¾Ñ Ð¿Ð¾ÑледовательноÑÑ‚ÑŒ Ð339999, причём мне об Ñтом не ÑообщаетÑÑ. Однако Ð¼Ð¾Ñ Ð¿Ð¾ÑледовательноÑÑ‚ÑŒ была Ñоздана раньше обеих указанных поÑледовательноÑтей двух хороших гоÑподинов, и она могла заменить обе Ñти поÑледовательноÑти. И её не надо было удалÑÑ‚ÑŒ, а не Ñледовало Ñоздавать вот Ñти две поÑледовательноÑти, в которых вÑÑ‘ до Ð±ÐµÐ·Ð¾Ð±Ñ€Ð°Ð·Ð¸Ñ Ð¿ÐµÑ€ÐµÐ¼ÐµÑˆÐ°Ð»Ð¸ и Ñпутали. Показываю Ñти поÑледовательноÑти. A341585 https://oeis.org/A341585 Number of main classes of cyclic diagonal Latin squares of order 2n+1. 1, 0, 1, 1, 0, 2, 3, 0, 4, 4, 0, 5, 1, 0, 7, 7, 0, 1, 9, 0, 10, 10, 0, 11, 1, 0, 13, 2, 0, 14, 15, 0, 3, 16, 0, 17, 18, 0, 4, 19, 0, 20, 4, 0, 22, 5, 0, 4, 24, 0, 25, 25, 0, 26, 27, 0, 28, 5, 0, 7, 2, 0, 1, 31, 0, 32, 8, 0, 34, 34, 0, 10, 7, 0, 37, 37, 0, 7, 39, 0, 10 AUTHOR Eduard I. Vatutin, Feb 15 2021 Цитирую From Andrew Howroyd, May 01 2021: (Start) И ещё цитирую EXAMPLE For n=0 there is only 1 Latin square of order 1, so a(0)=1. For n=2 there is one main class with canonical form (CF) of cyclic diagonal Latin squares of order 2n+1=5: 0 1 2 3 4 2 3 4 0 1 4 0 1 2 3 1 2 3 4 0 3 4 0 1 2 so a(2)=1. For n=3 there is one main class of order 7 with CF: 0 1 2 3 4 5 6 2 3 4 5 6 0 1 4 5 6 0 1 2 3 6 0 1 2 3 4 5 1 2 3 4 5 6 0 3 4 5 6 0 1 2 5 6 0 1 2 3 4 so a(3)=1. Ð’ примерах хорошо видно, что автор Ñтатьи показывает главные клаÑÑÑ‹ через количеÑтво каноничеÑких форм (КФ). Ðо тут вÑтавлÑет комментарий гоÑподин Andrew Howroyd. Цитирую a(12) = 1. There are A123565(25) = 10 cyclic diagonal Latin squares whose first row is in ascending order. The 10 row permutations constructed by selecting every k-th row cyclically where k is one of 1, 4, 6, 9, 11, 14, 16, 19, 21, 24 (numbers congruent to 1 or -1 modulo 5) transforms each of these between each other so there is only a single class. - Andrew Howroyd, May 02 2021 Итак, цикличеÑкие пандиагональные ДЛК 25-го порÑдка по трактовке гоÑподина Andrew Howroyd имеют вÑего один клаÑÑ. Я не знаю, Ñколько главных клаÑÑов имеют цикличеÑкие пандиагональны ДЛК 25-го порÑдка по трактовке гоÑподина Ватутина (то еÑÑ‚ÑŒ по количеÑтву каноничеÑких форм), так как не имею возможноÑти найти каноничеÑкие формы Ñтих 10 ДЛК (не имею канонизатора Ð´Ð»Ñ Ð”Ð›Ðš 25-го порÑдка). Ðо что-то Ñильно ÑомневаюÑÑŒ, что Ñто будет вÑего один клаÑÑ, то еÑÑ‚ÑŒ Ñреди 10 цикличеÑких пандиагональных ДЛК 25-го порÑдка еÑÑ‚ÑŒ вÑего один уникальный ДЛК (одна КФ). Ðо в поÑледовательноÑти, да, Ñтоит a(12)=1. Запомним Ñтот результат. A343866 https://oeis.org/A343866 Number of inequivalent cyclic diagonal Latin squares of order 2n+1 up to rotations, reflections and permutation of symbols. 1, 0, 1, 1, 0, 2, 3, 0, 4, 4, 0, 5, 3, 0, 7, 7, 0, 2, 9, 0, 10, 10, 0, 11, 7, 0, 13, 4, 0, 14, 15, 0, 6, 16, 0, 17, 18, 0, 8, 19, 0, 20, 8, 0, 22, 10, 0, 8, 24, 0, 25, 25, 0, 26, 27, 0, 28, 10, 0, 14, 22, 0, 13, 31, 0, 32, 16, 0, 34, 34, 0, 20, 14, 0, 37, 37, 0, 14, 39, 0, 20 AUTHOR Andrew Howroyd, May 02 2021 Цитирую EXAMPLE a(12) = 3 since there are A123565(25) = 10 cyclic diagonal Latin squares whose first row is in ascending order. Each of these is uniquely defined by the step between rows and form 5 pairs by horizontal or vertical reflection (negating the step between rows). Up to exchanging rows with columns there are 3 distinct classes, so a(12) = 3. И что же мы видим! Мы видим, что те же Ñамые 10 цикличеÑких пандиагональных ДЛК 25-го порÑдка имеют три клаÑÑа! Так Ñколько же на Ñамом деле главных клаÑÑов имеют цикличеÑкие пандиагональные ДЛК 25-го порÑдка??? Один или три??? Что-то ÑовÑем запуталиÑÑŒ гоÑпода!!! Отмечу, что в поÑледовательноÑти гоÑподина Andrew Howroyd нет Ð½Ð°Ð·Ð²Ð°Ð½Ð¸Ñ "главные клаÑÑÑ‹", как в поÑледовательноÑти гоÑподина Ватутина. Смотрите название поÑледовательноÑти гоÑподина Andrew Howroyd Number of inequivalent cyclic diagonal Latin squares of order 2n+1 up to rotations, reflections and permutation of symbols. То еÑÑ‚ÑŒ Ñто не ÑовÑем то, что гоÑподин Ватутин называет "главные клаÑÑÑ‹". Ðо зачем тогда гоÑподин Andrew Howroyd влез Ñ Ñтими Ñвоими "клаÑÑами ÑквивалентноÑти" в поÑледовательноÑÑ‚ÑŒ гоÑподина Ватутина, а которой раÑÑматриваютÑÑ "main classes of cyclic diagonal Latin squares of order 2n+1"? Ð’ результате получилаÑÑŒ Ð¶ÑƒÑ‚ÐºÐ°Ñ Ð¿ÑƒÑ‚Ð°Ð½Ð¸Ñ†Ð°. И ещё раз обратите внимание на комментарий, который приводитÑÑ Ð² поÑледоваетельноÑти гоÑподина Ватутина гоÑподином Andrew Howroyd a(12) = 1. There are A123565(25) = 10 cyclic diagonal Latin squares whose first row is in ascending order. The 10 row permutations constructed by selecting every k-th row cyclically where k is one of 1, 4, 6, 9, 11, 14, 16, 19, 21, 24 (numbers congruent to 1 or -1 modulo 5) transforms each of these between each other so there is only a single class. - Andrew Howroyd, May 02 2021 Перевела в Google a (12) = 1. ИмеетÑÑ A123565 (25) = 10 цикличеÑких диагональных латинÑких квадратов, Ð¿ÐµÑ€Ð²Ð°Ñ Ñтрока которых находитÑÑ Ð² порÑдке возраÑтаниÑ. 10 переÑтановок Ñтрок, поÑтроенные цикличеÑким выбором каждой k-й Ñтроки, где k - одно из 1, 4, 6, 9, 11, 14, 16, 19, 21, 24 (чиÑла, Ñравнимые Ñ 1 или -1 по модулю 5), преобразуют каждую из них между Ñобой, поÑтому ÑущеÑтвует только один клаÑÑ. ÐбÑолютно не понимаю, что за Ð¿Ñ€ÐµÐ¾Ð±Ñ€Ð°Ð·Ð¾Ð²Ð°Ð½Ð¸Ñ Ñ‚ÑƒÑ‚ опиÑываютÑÑ, и как они приводÑÑ‚ к одному клаÑÑу. Речь идёт о каких-то 10 переÑтановках Ñтрок. Ðо Ñильно ÑомневаюÑÑŒ, что опиÑываетÑÑ Ð¿Ñ€Ð¾Ñ†ÐµÑÑ Ð¿Ð¾Ð¸Ñка каноничеÑких форм Ñтих 10 пандиагональных ДЛК 25-го порÑдка. Ð’Ñ‹ что-то понÑли, гоÑпода, из вÑего Ñтого? Я ничего не понÑла :( ЕÑли вы хоть-что то понÑли, раÑÑкажите. пожалуйÑта. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё цитирую из поÑледовательноÑти гоÑподина Ватутина FORMULA То еÑÑ‚ÑŒ Ð´Ð»Ñ Ð¿Ñ€Ð¾ÑÑ‚Ñ‹Ñ… n количеÑтво главных клаÑÑов (по Ватутину) Ñовпадает Ñ ÐºÐ¾Ð»Ð¸Ñ‡ÐµÑтвом клаÑÑов ÑквивалентноÑти (по Andrew Howroyd). Ð Ð´Ð»Ñ ÑоÑтавных n не Ñовпадает. Ðапример, Ð´Ð»Ñ n=25 количеÑтво главных клаÑÑов равно 1, а количеÑтво клаÑÑов ÑквивалентноÑти равно 3. Ещё раз подчеркну: у Ð¼ÐµÐ½Ñ Ð±Ð¾Ð»ÑŒÑˆÐ¸Ðµ ÑÐ¾Ð¼Ð½ÐµÐ½Ð¸Ñ Ð² том, что количеÑтво главных клаÑÑов (по Ватутину), то еÑÑ‚ÑŒ количеÑтво КФ, Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка n=25 поÑчитано правильно. Смотрите в предыдущем поÑте, как Andrew Howroyd Ñто вычиÑлÑл, и получил один клаÑÑ. Какие-то 10 переÑтановок Ñтрок. Разве так находÑÑ‚ÑÑ ÐºÐ°Ð½Ð¾Ð½Ð¸Ñ‡ÐµÑкие формы (КФ)? Более того, Ñ ÑомневаюÑÑŒ, что и Ð´Ð»Ñ Ð¿Ñ€Ð¾ÑÑ‚Ñ‹Ñ… n Ð¿Ñ€Ð¸Ð²ÐµÐ´Ñ‘Ð½Ð½Ð°Ñ Ñ„Ð¾Ñ€Ð¼ÑƒÐ»Ð° верна. Главные клаÑÑÑ‹ (по Ватутину) и клаÑÑÑ‹ ÑквивалентноÑти (по Andrew Howroyd) далеко не одно и то же. ПоÑтому и Ð´Ð»Ñ Ð¿Ñ€Ð¾ÑÑ‚Ñ‹Ñ… порÑдков количеÑтва Ñтих разных клаÑÑов врÑд ли Ñовпадают. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата из моего ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117&postid=1180 ПоÑтроила методом цикличеÑкого Ñдвига 20 ЛК 25-го порÑдка (4 ЛК не получилиÑÑŒ). Ðти ДЛК Ñ Ð¿Ð¾Ñтроила вручную методом цикличеÑкого Ñдвига. Ð’ цитате показан один из цикличеÑких пандиагональных ДЛК 25-го порÑдка. ПоÑкольку главных клаÑÑов ДЛК 25-го порÑдка еÑÑ‚ÑŒ вÑего один (как утверждаетÑÑ Ð² поÑледовательноÑти OEIS), показанный ДЛК можно Ñчитать предÑтавителем Ñтого единÑтвенного клаÑÑа. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Проверка показанного цикличеÑкого пандиагонального ДЛК 25-го порÑдка утилитой Harry White GetType1 Order? 25
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
1 diagonal Latin
1 pandiagonal
1 cyclic 4-way
1 center symmetric
1 nfr
1 self-orthogonalÐ’ÑÑ‘ замечательно в Ñтом квадратике! Он пандиагональный, цикличеÑкий в 4-Ñ… направлениÑÑ… (cyclic 4-way), центрально-Ñимметричный (center symmetric), нормализованный (nfr) и ÑвлÑетÑÑ SODLS (self-orthogonal). Вполне пригоден предÑтавлÑÑ‚ÑŒ главный клаÑÑ Ð²Ñех 10 цикличеÑких пандиагональных ДЛК порÑдка 25. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ñмотрю, Ñохранила ли Ñ Ð²Ñе 10 цикличеÑких пандиагональных ДЛК 25-го порÑдка. ЕÑли Ñохранила, покажу. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Сделала показанный пандиагональный цикличеÑкий ДЛК 25-го порÑдка идеальным, Ð´Ð»Ñ Ñтого превратила его в СРДЛК (то еÑÑ‚ÑŒ Ñ Ð½Ð¾Ñ€Ð¼Ð°Ð»Ð¸Ð·Ð¾Ð²Ð°Ð½Ð½Ð¾Ð¹ главной диагональю). Показываю Ñтот ДЛК 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 13 12 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 15 14 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 17 16 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 19 18 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 21 20 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 23 22 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 24 СвойÑтва Order? 25
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_7.txt
Counts
------
1 diagonal Latin
1 associative
1 pandiagonal
1 cyclic 4-way
1 ultramagic
1 natural \diagonal
1 self-orthogonal
1 symmetric parityКакой квадратик! ВоÑторг! Ðо единÑтвенный ли главный клаÑÑ Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 25??? Терзает Ð¼ÐµÐ½Ñ Ñтот вопроÑ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Показываю 10 нормализованных цикличеÑких пандиагональных ДЛК 25-го порÑдка, поÑтроенных методом цикличеÑкого Ñдвига 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 219 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 9 10 11 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 6 7 8 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2 3 4 5 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1 2[/code] СвойÑтва [code]Order? 25 Enter the name of the squares file: inp .. writing type information to file inpTypeDetail_6.txt Counts ------ 10 diagonal Latin 10 pandiagonal 10 cyclic 4-way 10 center symmetric 10 nfr 9 orthogonal pair 10 self-orthogonal[/code] ГоÑпода! Суперзадача! Канонизировать Ñти 10 ДЛК. Кто может? Ðеужели только одна КФ??? Ðеужели??? Ð¡ÐµÐ¹Ñ‡Ð°Ñ Harry White отправлю нижайшую проÑьбу. Может быть, он решит Ñту задачу. ÐлекÑей Белышев мог бы решить. Дорогой ÐлекÑей! Где вы? Помогите, пожалуйÑта. Тут Ñ‚Ð°ÐºÐ°Ñ Ñупер-задача! :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðижайшую проÑьбу Harry отправила. Рпока разберёмÑÑ Ñ Ð³Ð»Ð°Ð²Ð½Ñ‹Ð¼Ð¸ клаÑÑами Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдков 5, 7, 11, 13, 17, 19. Ещё раз цитирую Ñтатью гоÑподина Ватутина EXAMPLE For n=0 there is only 1 Latin square of order 1, so a(0)=1. Ðто примеры Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдков 5 и 7. Тут вÑÑ‘ верно. Ð’Ñего нормализованных цикличеÑких пандиагональных ДЛК 5-го порÑдка два 0 1 2 3 4 2 3 4 0 1 4 0 1 2 3 1 2 3 4 0 3 4 0 1 2 0 1 2 3 4 3 4 0 1 2 1 2 3 4 0 4 0 1 2 3 2 3 4 0 1 КФ одна. Ð’Ñего нормализованных цикличеÑких пандиагональных ДЛК 7-го порÑдка четыре 0 1 2 3 4 5 6 2 3 4 5 6 0 1 4 5 6 0 1 2 3 6 0 1 2 3 4 5 1 2 3 4 5 6 0 3 4 5 6 0 1 2 5 6 0 1 2 3 4 0 1 2 3 4 5 6 3 4 5 6 0 1 2 6 0 1 2 3 4 5 2 3 4 5 6 0 1 5 6 0 1 2 3 4 1 2 3 4 5 6 0 4 5 6 0 1 2 3 0 1 2 3 4 5 6 4 5 6 0 1 2 3 1 2 3 4 5 6 0 5 6 0 1 2 3 4 2 3 4 5 6 0 1 6 0 1 2 3 4 5 3 4 5 6 0 1 2 0 1 2 3 4 5 6 5 6 0 1 2 3 4 3 4 5 6 0 1 2 1 2 3 4 5 6 0 6 0 1 2 3 4 5 4 5 6 0 1 2 3 2 3 4 5 6 0 1 КФ одна. Продолжение Ñледует... |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
РпоÑмотрите-ка моё Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=110&postid=1022 Ðто Ñообщение напиÑано 31 Ð´ÐµÐºÐ°Ð±Ñ€Ñ Ð¿Ñ€Ð¾ÑˆÐ»Ð¾Ð³Ð¾ года. Рв Ñнваре Ñ‚. г. Ñ Ñоздала поÑледовательноÑÑ‚ÑŒ Ð339999 именно по данному вопроÑу (главные клаÑÑÑ‹ пандиагональных ДЛК), ÐºÐ¾Ñ‚Ð¾Ñ€Ð°Ñ ÐºÐ¾Ð¼Ñƒ-то не понравилаÑÑŒ и была удалена. Дублирую Ñообщение Как уже отмечено выше, пандиагональные ЛК ÑвлÑÑŽÑ‚ÑÑ Ð”Ð›Ðš. Ð’ Ñтом Ñообщении вÑÑ‘ раÑÑмотрено Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдков 5, 7, 11. Далее Ñ Ñ€Ð°ÑÑмотрела и цикличеÑкие пандиагональные ДЛК Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 13. Ð’ поÑледовательноÑти OEIS Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 11 имеетÑÑ Ñледующий член a(5) = 2. Ð’ÑÑ‘ верно, два главных клаÑÑа. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’ Ñообщении https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=110&postid=1023 показаны 10 нормализованных цикличеÑких пандиагональных ДЛК 13-го порÑдка. Канонизирую Ñти ДЛК и получаю три КФ Order? 13 Format, (1: first row or 2: \diagonal)? 1 File name? a .. writing DLS to file output13CF1.txt number of DLS 10 CFs 3 Ð’ÑÑ‘ верно и Ð´Ð»Ñ Ñледующего члена поÑледовательноÑти OEIS a(6) = 3. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Идём дальше. Ð’ Ñообщении https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117&postid=1119 показана Ð¿Ð¾Ð»Ð½Ð°Ñ ÑиÑтема MOLS 17-го порÑдка, ÐºÐ¾Ñ‚Ð¾Ñ€Ð°Ñ Ñодержит 14 цикличеÑких пандиагональных ДЛК. Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 17 канонизатор Harry White не работает, поÑтому буду канонизировать канонизатором Tomas Brada. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese