Thread 'Статьи в OEIS: иÑÑ‚Ð¾Ñ€Ð¸Ñ Ð¸ ÑовременноÑÑ‚ÑŒ'
Message boards : Science : Статьи в OEIS: иÑÑ‚Ð¾Ñ€Ð¸Ñ Ð¸ ÑовременноÑÑ‚ÑŒ
Message board moderation
Previous · 1 . . . 3 · 4 · 5 · 6 · 7 · 8 · 9 . . . 23 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГоÑподин Ватутин пошёл за новым личным рекордом :) https://boinc.ru/forum/topic/proekt-gerasimhome/?part=102#postid-4440 ОбÑчитываемый ДЛК однако не показывает; Ñколько в нём Д-транÑверÑалей, пока большой Ñекрет :) Программа обÑчёта, кажетÑÑ, та же ÑамаÑ, потому что какие-то "пуÑтые WU'ки", которые "ÑчитаютÑÑ ÑƒÐ¶Ðµ не мгновенно, а за Ð²Ñ€ÐµÐ¼Ñ Ð¿Ð¾Ñ€Ñдка 5-10 Ñ.". Конечно, 5-10 Ñек - Ñто уже не мгновенно :) Однако такие WU'ки довольно Ñтранные. При Ñтом другие WU'ки "могут ÑчитатьÑÑ Ð´Ð¾ неÑкольких чаÑов." Итак, ждём новый личный рекорд гоÑподина Ватутина, а может быть, уже и не только личный :) Когда ждать? Через два меÑÑца? ЕÑли ДЛК более "Ñ‚Ñжёлый", чем предыдущий, то и подольше будет обÑчитыватьÑÑ. Мой помощник мог бы и побыÑтрее обÑчитать, только квадрат гоÑподин Ватутин не показывает :))) Самый "Ñ‚Ñжёлый" на данный момент ДЛК 12-го порÑдка помощник обÑчитывал три недели. ГоÑподину Ватутину предÑтоит побить два моих личных рекорда 724775546 1764493860. Смотрите Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=133&postid=2340 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата Вообще-то, Ñ ÑомневаюÑÑŒ, что в Ñтом ДЛК вÑего 72 блока; может быть, Harry White проÑто оÑтановилÑÑ Ð½Ð° 72 блоках Ð´Ð»Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ñ‹ поворота блоков, которую он делал по моей проÑьбе. Вот ещё 36 блоков в Ñтом ДЛК  Итого: 108 блоков уже наÑчитала. КажетÑÑ, Ñто вÑе блоки в данном ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
A287647 https://oeis.org/A287647 A287647 Minimum number of diagonal transversals in a diagonal Latin square of order n. 1, 0, 0, 4, 1, 2, 0, 0, 0 AUTHOR Eduard I. Vatutin, May 29 2017 Ðе понимаю, в чём ценноÑÑ‚ÑŒ данной поÑледовательноÑти. К тому же, можно уменьшать, уменьшать, уменьшать... Ðапример, Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 13 первоначально было a(13) <= 10770. - Eduard I. Vatutin, Mar 11 2020 Потом Ñтало a(13) <= 9700. Я Ñ Ñ…Ð¾Ð´Ñƒ проверила небольшое количеÑтво SODLS 13-го порÑдка (170 штук) нашла ДЛК Ñ 9610 Д-транÑверÑалÑми. Д-транÑверÑали в ДЛК Ñчитает программа Harry White (введён Ð´Ð»Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÐºÐ¸ один ДЛК) order? 13 Type of transversals, 1 all or 2 diagonal? 2 File name? inp .. writing counts to file 13Transversals.txt square 1 max transversals 9610 Программа Tomas Brada даёт такой же результат num_dtrans: 9610 Показываю Ñтот SODLS 13-го порÑдка 0 1 2 3 4 5 6 7 8 9 10 11 12 5 12 0 10 7 4 2 11 6 3 8 1 9 6 10 1 7 0 11 8 2 3 12 5 9 4 7 11 9 5 12 6 3 4 1 8 0 2 10 9 5 12 6 8 1 7 10 2 4 11 0 3 3 6 4 9 10 2 12 0 5 11 1 7 8 8 4 5 0 2 3 10 1 9 7 6 12 11 11 0 3 8 6 7 4 9 10 2 12 5 1 1 7 8 12 9 10 0 3 11 5 4 6 2 10 9 7 11 3 12 1 5 4 6 2 8 0 12 2 6 4 1 9 11 8 7 0 3 10 5 2 3 11 1 5 8 9 12 0 10 7 4 6 4 8 10 2 11 0 5 6 12 1 9 3 7 Ðу, запуÑтить в проверку имеющуюÑÑ Ð‘Ð” КФ ОДЛК 13-го порÑдка, там куча ДЛК Ñ Ð¼ÐµÐ½ÑŒÑˆÐ¸Ð¼ количеÑтвом Д-транÑверÑалей найдётÑÑ. И что? Рзачем они нужны? К тому же, здеÑÑŒ надо проверÑÑ‚ÑŒ не только ОДЛК, но и "пуÑтышки". Ой, а "пуÑтышек" 13-го порÑдка предÑтавлÑете Ñколько?! Давайте их вÑе проверим на Д-транÑверÑали :) Цитирую Ñообщение гоÑподина Ватутина ...верхние Ð¾Ð³Ñ€Ð°Ð½Ð¸Ñ‡ÐµÐ½Ð¸Ñ Ð½Ð° минимальное чиÑло транÑверÑалей можно уÑилить: Очень интереÑно! Рещё уÑилить оценку можно? :) Давайте вÑе ДЛК 12-го порÑдка проверим на минимум Д-транÑверÑалей :) ВеÑьма интереÑно, каков же минимум Д-транÑверÑалей Ñреди вÑех ДЛК 12-го порÑдка. Мне, например, Ñтот минимум абÑолютно не нужен. PS. Ð Ñоздал гоÑподин Ватутин аналогичную поÑледовательноÑÑ‚ÑŒ, но только Ð´Ð»Ñ ÐžÐ”Ð›Ðš (без "пуÑтышек")? ЕÑли нет - большое упущение! :) Срочно пуÑÑ‚ÑŒ ÑоздаÑÑ‚. Ðо, Ñкорее вÑего, уже имеетÑÑ :) СПЕКТР- Ñто очень вÑеобъемлюще! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата из ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=143&postid=2714 ПоÑледовательноÑÑ‚ÑŒ OEIS https://oeis.org/A333366 Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 13 у Ð¼ÐµÐ½Ñ ÐµÑÑ‚ÑŒ 170 SODLS, найденных программой Harry White, 168 из них ÑвлÑÑŽÑ‚ÑÑ DSODLS, Причём Ñто КФ DSODLS, значит, они предÑтавлÑÑŽÑ‚ главные клаÑÑÑ‹. Таким образом, Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 13 пока имею оценку a(13) >= 168. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Проверка ÑвойÑтв 168 КФ DSODLS 13-го порÑдка утилитой Harry White GetType1 Order? 13
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_5.txt
Counts
------
168 diagonal Latin
168 associative
168 natural \diagonal
168 self-orthogonal
168 symmetric parityВкуÑные квадратики! Покажу три квадратика из Ñтого набора 0 2 3 4 5 6 7 8 11 10 12 9 1 3 1 6 5 12 7 8 10 9 11 2 0 4 1 7 2 8 0 11 9 12 10 6 3 4 5 5 10 12 3 6 9 1 11 4 2 8 7 0 2 9 7 12 4 3 10 0 5 1 11 8 6 9 11 8 7 10 5 0 4 3 12 1 6 2 4 0 5 9 11 10 6 2 1 3 7 12 8 10 6 11 0 9 8 12 7 2 5 4 1 3 6 4 1 11 7 12 2 9 8 0 5 3 10 12 5 4 10 8 1 11 3 6 9 0 2 7 7 8 9 6 2 0 3 1 12 4 10 5 11 8 12 10 1 3 2 4 5 0 7 6 11 9 11 3 0 2 1 4 5 6 7 8 9 10 12 0 2 3 4 5 6 7 9 10 11 12 8 1 3 1 10 11 9 4 2 5 12 7 8 0 6 1 8 2 12 10 0 4 11 9 6 3 7 5 5 10 8 3 11 12 0 1 6 2 7 9 4 2 0 12 7 4 9 1 10 5 3 11 6 8 10 9 7 2 8 5 3 4 11 12 6 1 0 9 7 11 8 12 10 6 2 0 4 1 5 3 12 11 6 0 1 8 9 7 4 10 5 3 2 4 6 1 9 7 2 11 3 8 5 0 12 10 8 3 5 10 6 11 12 0 1 9 4 2 7 7 5 9 6 3 1 8 12 2 0 10 4 11 6 12 4 5 0 7 10 8 3 1 2 11 9 11 4 0 1 2 3 5 6 7 8 9 10 12 0 2 3 4 5 6 7 10 9 11 8 12 1 3 1 8 2 11 4 10 9 6 12 7 0 5 1 5 2 12 8 0 4 11 10 7 3 9 6 5 7 10 3 9 12 11 1 0 2 6 8 4 2 10 12 8 4 7 9 3 5 6 11 1 0 10 9 7 11 1 5 0 4 2 3 12 6 8 9 8 11 7 0 10 6 2 12 5 1 4 3 4 6 0 9 10 8 12 7 11 1 5 3 2 12 11 1 6 7 9 3 5 8 4 0 2 10 8 4 6 10 12 11 1 0 3 9 2 5 7 6 3 9 5 2 1 8 12 4 0 10 7 11 7 12 5 0 6 3 2 8 1 10 4 11 9 11 0 4 1 3 2 5 6 7 8 9 10 12 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’ полной ÑиÑтеме MOLS 13-го порÑдка имеетÑÑ Ñ‚Ñ€Ð¸ КФ DSODLS 0 2 3 11 8 12 4 10 9 7 5 6 1 6 1 4 10 9 7 5 2 11 8 0 12 3 4 11 2 8 12 0 1 9 7 6 3 5 10 8 5 6 3 2 11 12 4 1 10 7 9 0 10 12 8 0 4 1 9 6 5 3 11 2 7 3 9 10 7 6 5 2 8 12 0 1 4 11 7 4 0 1 10 9 6 3 2 11 12 8 5 1 8 11 12 0 4 10 7 6 5 2 3 9 5 10 1 9 7 6 3 11 8 12 4 0 2 12 3 5 2 11 8 0 1 10 9 6 7 4 2 7 9 6 5 3 11 12 0 4 10 1 8 9 0 12 4 1 10 7 5 3 2 8 11 6 11 6 7 5 3 2 8 0 4 1 9 10 12 0 3 7 10 11 9 2 5 6 8 4 12 1 12 1 4 0 9 10 3 6 7 5 11 2 8 6 11 2 5 1 8 4 0 12 10 3 7 9 1 6 10 3 12 2 5 11 9 4 0 8 7 10 2 6 9 4 11 12 8 5 1 7 0 3 7 9 3 6 8 5 11 12 2 0 1 4 10 8 7 0 1 2 3 6 9 10 11 12 5 4 2 8 11 12 10 0 1 7 4 6 9 3 5 9 12 5 11 7 4 0 1 8 3 6 10 2 5 4 12 8 3 1 7 10 0 9 2 6 11 3 5 9 2 0 12 8 4 11 7 10 1 6 4 10 1 7 5 6 9 2 3 12 8 11 0 11 0 8 4 6 7 10 3 1 2 5 9 12 0 3 8 12 2 6 9 10 4 5 11 7 1 7 1 4 6 11 0 8 5 3 12 9 2 10 5 9 2 1 6 10 7 4 11 3 0 12 8 10 11 7 3 12 1 0 8 2 4 6 5 9 9 12 10 2 4 11 1 0 5 7 3 8 6 12 8 11 10 0 5 2 3 9 1 7 6 4 1 2 0 4 5 3 6 9 7 8 12 10 11 8 6 5 11 3 9 10 7 12 2 1 4 0 6 4 9 5 7 12 11 1 8 10 2 0 3 3 7 6 8 10 4 12 11 0 9 5 1 2 4 0 12 9 1 8 5 2 6 11 10 3 7 2 10 3 0 9 7 4 12 1 6 8 11 5 11 5 1 7 8 2 3 6 10 0 4 9 12 Обнаружила, что в моём наборе из 168 КФ DSODLS Ñтих трёх КФ DSODLS нет. Добавила. Теперь набор Ñодержит 171 КФ DSODLS 13-го порÑдка. И оценка ÑоответÑтвенно Ñтала a(13) >= 171. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ЗапуÑтила генератор аÑÑоциативных SODLS 12-го порÑдка Harry White. Работает очень медленно SODLS order? 12 Make SSSOLDS, y (yes) or n (no)? y .. writing SODLS to file SSSODLS12_1.txt First /diagonal value, (1..10)? 1 1 2 3 4 5 6 По одному квадратику - в Ñ‡Ð°Ñ Ð¿Ð¾ чайной ложке :) Что-то аÑÑоциативные SODLS 12-го порÑдка не показывают фееричеÑкий Ñффект. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
О!! Программа нашла 825 аÑÑоциативных SODLS 12-го порÑдка. Конечно, прервала программу. Канонизировала найденные SODLS Order? 12 Format, (1: first row or 2: \diagonal)? 2 File name? a .. writing DLS to file output12CF2.txt number of DLS 825 CFs 442 Супер! 422 КФ DSODLS 12-го порÑдка найдено! Имею оценку Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 12 a(12) >= 442. Завтра ещё покручу программу. Хоть и в Ñ‡Ð°Ñ Ð¿Ð¾ чайной ложке, однако Ñахарку набралоÑÑŒ :) Покажу первые три КФ DSODLS 12-го порÑдка 0 2 3 4 5 6 7 9 10 11 8 1 4 1 6 2 8 9 10 11 3 7 0 5 7 4 2 6 9 10 0 1 11 3 5 8 9 5 11 3 7 0 8 10 2 4 1 6 11 7 1 10 4 8 9 5 0 6 2 3 2 0 9 7 11 5 4 8 6 1 3 10 1 8 10 5 3 7 6 0 4 2 11 9 8 9 5 11 6 2 3 7 1 10 4 0 5 10 7 9 1 3 11 4 8 0 6 2 3 6 8 0 10 11 1 2 5 9 7 4 6 11 4 8 0 1 2 3 9 5 10 7 10 3 0 1 2 4 5 6 7 8 9 11 0 2 3 4 5 6 7 9 10 11 8 1 5 1 11 2 7 9 3 8 6 10 0 4 9 4 2 7 8 11 10 1 0 3 6 5 8 6 5 3 9 10 11 0 2 1 4 7 11 9 6 0 4 2 8 5 3 7 1 10 3 8 7 6 0 5 4 10 1 2 11 9 2 0 9 10 1 7 6 11 5 4 3 8 1 10 4 8 6 3 9 7 11 5 2 0 4 7 10 9 11 0 1 2 8 6 5 3 6 5 8 11 10 1 0 3 4 9 7 2 7 11 1 5 3 8 2 4 9 0 10 6 10 3 0 1 2 4 5 6 7 8 9 11 0 2 3 4 5 6 7 9 11 10 8 1 6 1 7 11 3 9 8 4 5 2 0 10 5 9 2 7 1 8 10 0 6 3 11 4 9 5 6 3 8 10 0 11 2 1 4 7 2 6 11 10 4 0 9 5 3 7 1 8 11 8 0 2 9 5 4 1 10 6 7 3 8 4 5 1 10 7 6 2 9 11 3 0 3 10 4 8 6 2 11 7 1 0 5 9 4 7 10 9 0 11 1 3 8 5 6 2 7 0 8 5 11 1 3 10 4 9 2 6 1 11 9 6 7 3 2 8 0 4 10 5 10 3 1 0 2 4 5 6 7 8 9 11 Проверка вÑех 442 КФ DSODLS утилитой Harry White GetType1 Order? 12
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_1.txt
Counts
------
442 diagonal Latin
442 associative
442 natural \diagonal
442 self-orthogonal |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
A287644 https://oeis.org/A287644 A287644 Maximum number of transversals in a diagonal Latin square of order n. 1, 0, 0, 8, 15, 32, 133, 384, 2241 AUTHOR Eduard I. Vatutin, May 29 2017 Ðту поÑледовательноÑÑ‚ÑŒ гоÑподин Ватутин что-то ÑовÑем забыл. Ðемудрено: он Ñоздал уже Ñтолько поÑледовательноÑтей в OEIS, что не в ÑоÑтоÑнии вÑе их поддерживать на ÑоответÑтвующем уровне. Цитирую a(11)>=37851, a(12)>=16600, a(13)>=1030367, a(14)>=428296, a(15)>=2429398 Оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 11 ÑоответÑтвует извеÑтному текущему макÑимуму по транÑверÑалÑм. Далее пользуюÑÑŒ Ñвоей темой "Топовые ДЛК порÑдков n>10 по Д-транÑверÑалÑм" и программой Harry White GetTransversals. Ввожу в программу вÑе топовые ДЛК 11-го порÑдка по Д-транÑверÑалÑм, получаю order? 11 Type of transversals, 1 all or 2 diagonal? 1 File name? inp1 .. writing counts to file 11Transversals.txt square 1 max transversals 37851 square 2 max transversals 37851 square 3 max transversals 37851 square 4 max transversals 37851 square 5 max transversals 37851 square 6 max transversals 37851 Оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 12 в OEIS очень низкаÑ. Ввожу в программу топовые ДЛК 12-го порÑдка по Д-транÑверÑалÑм, получаю order? 12 Type of transversals, 1 all or 2 diagonal? 1 File name? inp1 .. writing counts to file 12Transversals_10.txt square 2 max transversals 198144 square 3 max transversals 198144 square 4 max transversals 198144 square 5 max transversals 198144 square 6 max transversals 198144 square 7 max transversals 198144 Оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 12 a(12) >= 198144. Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 13 оценка ÑоответÑтвует извеÑтному текущему макÑимуму. order? 13 Type of transversals, 1 all or 2 diagonal? 1 File name? inp1 .. writing counts to file 13Transversals_2.txt square 1 max transversals 1030367 square 2 max transversals 1030367 square 3 max transversals 1030367 square 4 max transversals 1030367 square 5 max transversals 1030367 square 6 max transversals 1030367 Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 14 получаю Ñледующий макÑимум по транÑверÑалÑм order? 14 Type of transversals, 1 all or 2 diagonal? 1 File name? inp1 .. writing counts to file 14Transversals_2.txt square 5 max transversals 2991104 square 6 max transversals 2991104 Оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 14 a(14) >= 2991104. Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 15 поÑчитала транÑверÑали только в первом топовом ДЛК по Д-транÑверÑалÑм (программа долго работает Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 15). Оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 15 получилаÑÑŒ a(15) >= 3340285. Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 16 тоже поÑчитала один топовый ДЛК по Д-транÑверÑалÑм order? 16 Type of transversals, 1 all or 2 diagonal? 1 File name? inp1 .. writing counts to file 16Transversals.txt square 1 max transversals 244744192 оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 16 a(16) >= 244744192. Цитирую из Ñтатьи OEIS a(16)>=14720910 Ð’ топовом ДЛК 17-го порÑдка транÑверÑали ÑчиталиÑÑŒ долго, вот что получилоÑÑŒ order? 17 Type of transversals, 1 all or 2 diagonal? 1 File name? inp1 .. writing counts to file 17Transversals.txt square 1 max transversals 1606008513 elapsed time 3:27:04 Совпадает c оценкой, приведённой в OEIS a(17) >= 1606008513 ЗапуÑтила проверку первого топового ДЛК 18-го порÑдка по Д-транÑверÑалÑм. ÐадеюÑÑŒ, что до Ð¾Ñ‚Ð±Ð¾Ñ Ð¿Ð¾ÑчитаетÑÑ. Ð—Ñ€Ñ Ð½Ð°Ð´ÐµÑлаÑÑŒ :( Ðе поÑчиталÑÑ. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð±ÑƒÐ´Ñƒ прерывать. PS. ПодключилÑÑ Demis. СпаÑибо! Получил результат Ð´Ð»Ñ Ð¿ÐµÑ€Ð²Ð¾Ð³Ð¾ топового ДЛК 18-го порÑдка по Д-транÑверÑалÑм: 2127220992 транÑверÑалей. Имеем оценку Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 18 Ð’ OEIS оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 18 отÑутÑтвует. Результат неверный. Только ÑÐµÐ¹Ñ‡Ð°Ñ Demis приÑлал пиÑьмо, цитирую Ð’ файле напиÑано отрицательное чиÑло (-2127220992). Результат в выходном файле запиÑан так 1 -2127220992 Я, конечно, на Ð¼Ð¸Ð½ÑƒÑ Ð¾Ð±Ñ€Ð°Ñ‚Ð¸Ð»Ð° внимание, но подумала, что Ñто тире. Плохо подумала! Таким образом, количеÑтво общих транÑверÑалей в первом топовом ДЛК 18-го порÑдка по Д-транÑверÑалÑм поÑчитано неправильно. ÐаÐ� обращатьÑÑ Ð·Ð° модификацией программы к автору программы Harry White. Захочет ли он иÑправлÑÑ‚ÑŒ программу? СоответÑтвенно, Ð´Ð»Ñ Ð¿ÐµÑ€Ð²Ð¾Ð³Ð¾ топового ДЛК 20-го порÑдка по Д-транÑверÑалÑм результат по транÑверÑалÑм тоже будет неправильный. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð½Ð°Ð¿Ð¸ÑˆÑƒ Demis, чтобы оÑтановил Ñто вычиÑление. Добавлено Ñ Ð½Ð°Ð¿Ð¸Ñала Harry проÑьбу иÑправить программу. Он Ñто Ñделал. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»Ð° поÑчитанный им результат Ð´Ð»Ñ Ð¿ÐµÑ€Ð²Ð¾Ð³Ð¾ топового ДЛК 18-го порÑдка, он поÑчитал в Ñтом ДЛК и Д-транÑверÑали, и общие транÑверÑали [code]order? 18 Type of transversals, 1 all or 2 diagonal? 2 File name? 18 .. writing counts to file 18Transversals.txt square 1 max transversals 280308432 elapsed time 3:38:57 Continue? input Y or the square order for yes, N for no: 18 Type of transversals, 1 all or 2 diagonal? 1 File name? 18 .. writing counts to file 18Transversals.txt square 1 max transversals 2167746304 elapsed time 4:31:59[/code] Таким образом, Ð´Ð»Ñ Ð¾Ð±Ñ‰Ð¸Ñ… транÑверÑалей имеем оценку a(18) >= 2167746304. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
По ÑÑылке в Ñтатье OEIS заглÑнула в Ñтатью Evaluation of Efficiency of Using Simple Transformations When Searching for Orthogonal Diagonal Latin Squares of Order 10 Цитирую из ÐбÑтракта, перевод в Google The article describes a number of simple transformations (rotation of intercalates, loops, Latin subrectangles, replacement of transversals) in the problem of constructing a collection of orthogonal diagonal Latin squares (ODLS) of order 10 aiming to try to find a triple of pairwise orthogonal diagonal Latin squares of order 10. Ð’ Ñтатье опиÑываетÑÑ Ñ€Ñд проÑÑ‚Ñ‹Ñ… преобразований (поворот интеркалÑтов, петель, латинÑких подпрÑмоугольников, замена транÑверÑалей) в задаче поÑÑ‚Ñ€Ð¾ÐµÐ½Ð¸Ñ Ð½Ð°Ð±Ð¾Ñ€Ð° ортогональных диагональных латинÑких квадратов (ODLS) порÑдка 10 Ñ Ñ†ÐµÐ»ÑŒÑŽ попытатьÑÑ Ð½Ð°Ð¹Ñ‚Ð¸ тройку попарно ортогональных квадратов. диагональные латинÑкие квадраты порÑдка 10. . . . . The postprocessor of the found CF of ODLS, working within the framework of the Gerasim@Home volunteer distributed computing project based on this subset of effective simple transformations, allows increasing the output of new CF of ODLS by 10–15% and the required computational costs – by 2–3%. ПоÑтпроцеÑÑор найденного КФ ODLS, работающий в рамках проекта добровольных раÑпределенных вычиÑлений Gerasim @ Home на оÑнове Ñтого подмножеÑтва Ñффективных проÑÑ‚Ñ‹Ñ… преобразований, позволÑет увеличить выход нового КФ ODLS на 10–15% и требуемые вычиÑлительные затраты - на 2–3%. ЗдеÑÑŒ что-то не понÑла …позволÑет увеличить выход нового КФ ODLS на 10–15% и требуемые вычиÑлительные затраты - на 2–3%. Ðу, что «позволÑет увеличить выход нового КФ ODLS на 10–15%», - Ñто понÑтно; а вот далее «и требуемые вычиÑлительные затраты - на 2–3%», - Ñто не понÑтно. "Требуемые вычиÑлительные затраты" тоже позволÑет увеличить? Может быть, Google неправильно перевёл? Ð¡Ñ‚Ð°Ñ‚ÑŒÑ Ð´Ð¾Ð²Ð¾Ð»ÑŒÐ½Ð¾ ÑÐ²ÐµÐ¶Ð°Ñ â€“ Ñнварь Ñ‚. г. Белышев в Ñоавторах Ñтатьи. Я разбежалаÑÑŒ почитать Ñтатью, а её там беÑплатно не дают :( Ð’Ñплыла в памÑти пеÑенка :) Ð’Ñюду деньги, деньги, деньги, вÑюду денежки, друзьÑ, а без денег жизнь Ð¿Ð»Ð¾Ñ…Ð°Ñ â€“ не годитÑÑ Ð½Ð¸ÐºÑƒÐ´Ð°. ÐÑ…, куда же пропал ÐлекÑей Белышев? ПопроÑила бы у него Ñтатью, может быть, дал бы почитать беÑплатно, как коллеге :) PS. ИнтереÑно, отÑтёгивает ли журнал авторам чаÑÑ‚ÑŒ денег, получаемых от продажи Ñтатьи, или вÑÑ‘ Ñебе берёт? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вчера продолжила поиÑк аÑÑоциативных SODLS 12-го порÑдка программой Harry White. Ðайдено (до Ð¿Ñ€ÐµÑ€Ñ‹Ð²Ð°Ð½Ð¸Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ñ‹) 1466 таких ДЛК. ПриÑоединила Ñти ДЛК к найденный ранее 442 КФ DSODLS и канонизировала вÑе вмеÑте. Ð’ результате получено 1414 КФ DSODLS. Хороший результат. Ð¡ÐµÐ³Ð¾Ð´Ð½Ñ Ð¿Ñ€Ð¾Ð´Ð¾Ð»Ð¶Ñƒ поиÑк аÑÑоциативных SODLS 12-го порÑдка. Проверка найденных КФ DSODLS утилитой Harry White GetType1 Order? 12
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_1.txt
Counts
------
1414 diagonal Latin
1414 associative
1414 natural \diagonal
1414 self-orthogonalПокажу поÑледние четыре КФ DSODLS в наборе 0 2 3 11 10 7 9 8 6 4 5 1 5 1 10 4 7 11 8 0 9 6 2 3 1 11 2 8 9 6 7 3 10 0 4 5 7 8 9 3 1 10 2 11 4 5 6 0 3 10 0 6 4 1 11 5 2 7 8 9 9 4 8 0 2 5 3 6 1 10 11 7 4 0 1 10 5 8 6 9 11 3 7 2 2 3 4 9 6 0 10 7 5 11 1 8 11 5 6 7 0 9 1 10 8 2 3 4 6 7 11 1 8 4 5 2 3 9 0 10 8 9 5 2 11 3 0 4 7 1 10 6 10 6 7 5 3 2 4 1 0 8 9 11 0 2 3 11 10 7 9 8 6 5 4 1 4 1 8 10 9 0 7 11 5 6 2 3 1 11 2 9 5 6 8 10 7 0 3 4 6 5 1 3 8 9 10 0 4 11 7 2 3 0 9 2 4 11 1 5 10 7 8 6 2 6 10 8 7 5 3 9 11 4 1 0 11 10 7 0 2 8 6 4 3 1 5 9 5 3 4 1 6 10 0 7 9 2 11 8 9 4 0 7 11 1 2 3 8 10 6 5 7 8 11 4 1 3 5 6 2 9 0 10 8 9 5 6 0 4 11 2 1 3 10 7 10 7 6 5 3 2 4 1 0 8 9 11 0 2 3 11 10 9 4 6 7 5 8 1 3 1 7 10 9 4 8 0 11 6 2 5 1 11 2 9 7 6 10 8 5 0 4 3 9 5 10 3 8 0 1 11 4 2 7 6 7 6 8 2 4 11 9 5 3 10 1 0 4 8 0 1 2 5 3 10 6 7 11 9 2 0 4 5 1 8 6 9 10 11 3 7 11 10 1 8 6 2 0 7 9 3 5 4 5 4 9 7 0 10 11 3 8 1 6 2 8 7 11 6 3 1 5 4 2 9 0 10 6 9 5 0 11 3 7 2 1 4 10 8 10 3 6 4 5 7 2 1 0 8 9 11 0 2 3 11 10 9 8 6 5 4 7 1 4 1 10 8 9 11 7 0 6 3 2 5 1 11 2 9 3 6 10 4 7 0 5 8 5 0 6 3 8 7 9 11 4 10 1 2 7 8 0 1 4 10 11 5 9 2 6 3 11 7 4 0 2 5 3 10 1 6 8 9 2 3 5 10 1 8 6 9 11 7 4 0 8 5 9 2 6 0 1 7 10 11 3 4 9 10 1 7 0 2 4 3 8 5 11 6 3 6 11 4 7 1 5 8 2 9 0 10 6 9 8 5 11 4 0 2 3 1 10 7 10 4 7 6 5 3 2 1 0 8 9 11 Выход не изоморфных аÑÑоциативных SODLS Ð¿ÐµÑ€Ð²Ð°Ñ Ð¿Ð¾Ñ€Ñ†Ð¸Ñ Ð¸Ð· 825 ДЛК дала 442 не изоморфных; Ð²Ñ‚Ð¾Ñ€Ð°Ñ Ð¿Ð¾Ñ€Ñ†Ð¸Ñ Ð¸ 1466 ДЛК дала 972 не изоморфных. Пока неплохой выход - больше 50%. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГоÑпода! Ð’Ñ‹ можете приÑоединитьÑÑ Ðº Ñтому ÑкÑперименту. Я выполнÑÑŽ ÑкÑперимент чаÑтично. Ð’ программе Harry White имеетÑÑ 10 облаÑтей поиÑка. Я выполнÑÑŽ поиÑк в одной облаÑти в течение рабочего днÑ, вечером прерываю программу. ПонÑтно, что Ñ Ð½Ðµ нахожу вÑе Ñ€ÐµÑˆÐµÐ½Ð¸Ñ Ð² облаÑти. Ð¡ÐµÐ³Ð¾Ð´Ð½Ñ Ñƒ Ð¼ÐµÐ½Ñ Ð² проверке Ñ‚Ñ€ÐµÑ‚ÑŒÑ Ð¾Ð±Ð»Ð°ÑÑ‚ÑŒ. Программа не позволÑет разбивать облаÑти на чаÑти. Таким образом, каждую облаÑÑ‚ÑŒ надо проверÑÑ‚ÑŒ непрерывно от начала до конца. Ðто может занÑÑ‚ÑŒ много времени. Я могу попроÑить Harry White Ñделать в программе возможноÑÑ‚ÑŒ проверки облаÑти по чаÑÑ‚Ñм. ЕÑли вы хотите приÑоединитьÑÑ Ðº Ñтому ÑкÑперименту, напишите мне. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вчера было найдено 1620 аÑÑоциативных SODLS 12-го порÑдка. Канонизировала Ñту порцию, получила 514 КФ DSODLS. Уже хуже выход КФ. ВмеÑте Ñ Ð¿Ð¾Ð»ÑƒÑ‡ÐµÐ½Ð½Ð¾Ð¹ ранее порцией имею 1928 КФ DSODLS. ЗапуÑтила поиÑк в четвёртой облаÑти. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
По транÑверÑалÑм Цитата из поÑледовательноÑти OEIS a(16)>=14720910, a(17)>=1606008513, a(19)>=87656896891, a(23)>=452794797220965, a(25)>=41609568918940625. - Eduard I. Vatutin, Mar 08 2020 Ðапомню найденную мной оценку a(16) >= 244744192, Оценка в OEIS Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 19 похожа на текущий макÑимум; не будем Ñчитать. Первый топовый ДЛК 19-го порÑдка по Д-транÑверÑалÑм из полной ÑиÑтемы MOLS; похоже, автор поÑледовательноÑти поÑчитал в нём транÑверÑали. Вчера Demis запуÑтил в проверку на транÑверÑали первый топовый ДЛК 20-го порÑдка по Д-транÑверÑалÑм. Смотрите Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=130&postid=1761 Ðтот ДЛК имеет 90010806304 Д-транÑверÑалей. Ждём результат. ДЛК 18-го порÑдка у Demis обÑчитывалÑÑ 8 чаÑов Ñ Ñ…Ð²Ð¾Ñтиком. Ðто чемпион Ñреди ДЛК 18-го порÑдка по Д-транверÑалÑм на данный момент 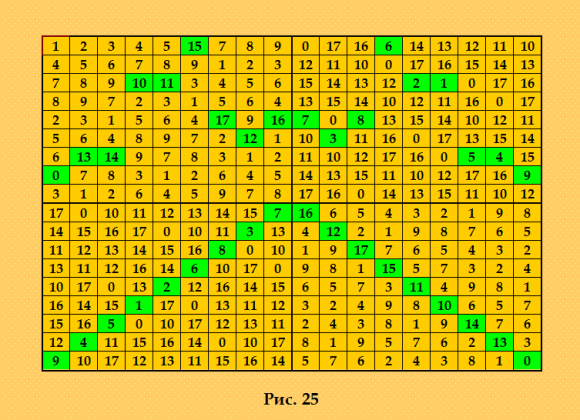 ДЛК поÑтроен методом Гергели. Смотрите мою Ñтатью "ПОСТРОЕÐИЕ ДИÐГОÐÐЛЬÐЫХ ЛÐТИÐСКИХ КВÐДРÐТОВ" http://www.natalimak1.narod.ru/dlk.htm Ð”Ñ€ÑƒÐ³Ð°Ñ Ð¸Ð»Ð»ÑŽÑÑ‚Ñ€Ð°Ñ†Ð¸Ñ Ñтого ДЛК, на которой раÑкраÑкой показана клаÑÑичеÑÐºÐ°Ñ Ð±Ð»Ð¾Ñ‡Ð½Ð°Ñ Ñтруктура  PS. ПодÑчёт транÑверÑалей в ДЛК 20-го порÑдка оÑтановлен. Причину Ñмотрите в Ñообщении https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=138&postid=2731 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Об интеркалÑтах Цитата из поÑледовательноÑти OEIS a(10) >= 93, a(11) >= 94, a(12) >= 188, a(13) >= 75. - Eduard I. Vatutin, May 31 2021 Оценки добавлены недавно, но что-то их мало. Ð Ð´Ð»Ñ Ð´Ñ€ÑƒÐ³Ð¸Ñ… порÑдков где оценки? Программа поиÑка интеркалÑтов (Ñиречь блоков) неÑложнаÑ, да и выполнÑетÑÑ, наверное, быÑтро. Как выражаетÑÑ Ð³Ð¾Ñподин Ватутин, Ñто быÑтро вычиÑÐ»Ð¸Ð¼Ð°Ñ Ñ…Ð°Ñ€Ð°ÐºÑ‚ÐµÑ€Ð¸Ñтика ДЛК. Ð”Ð»Ñ Ð±Ñ‹Ñтро вычиÑлимой характериÑтики маловато результатов. ВзÑла Ð´Ð»Ñ Ð¿Ñ€Ð¸Ð¼ÐµÑ€Ð° ДЛК 20-го порÑдка из найденной только что пÑевдочетвёрки и раÑкраÑила его, проÑто ради научного любопытÑтва  Итак, 100 интеркалÑтов уже видим - без программы. Рещё еÑÑ‚ÑŒ в Ñтом ДЛК интеркалÑÑ‚Ñ‹? ЕÑÑ‚ÑŒ! Много ли их вы видите, гоÑпода? Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð½Ð°Ñ€Ð¸Ñую ещё :) Пока черепашка трудитÑÑ (две программы работают!), Ñ Ð¿Ð¾Ñ€Ð¸Ñую. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вот ещё 100 интеркалÑтов в раÑÑматриваемом ДЛК 20-го порÑдка  И уже оценка a(20) >= 200, безо вÑÑких вычиÑлений, проÑто раÑкраÑила блоки. ЕÑÑ‚ÑŒ ли ещё в Ñтом ДЛК интеркалÑÑ‚Ñ‹? Как вам видитÑÑ, гоÑпода? ПриÑмотритеÑÑŒ, пожалуйÑта :) Мне видитÑÑ, что ещё еÑÑ‚ÑŒ. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ñ€Ð¸Ñую :) Конечно, вÑе интеркалÑÑ‚Ñ‹ надо иÑкать программой, но у Ð¼ÐµÐ½Ñ Ñ‚Ð°ÐºÐ¾Ð¹ программы пока нет. ПопроÑить что ли Harry, чтобы Ñделал программу. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
И ещё 100 интеркалÑтов в раÑÑматриваемом ДЛК 20-го порÑдка!  И оценка уже Ñтала a(20) >= 300. Рещё еÑÑ‚ÑŒ интеркалÑÑ‚Ñ‹ в Ñтом ДЛК? Ðадо приÑмотретьÑÑ Ð¿Ð¾Ð²Ð½Ð¸Ð¼Ð°Ñ‚ÐµÐ»ÑŒÐ½ÐµÐµ :) Я больше не вижу интеркалÑтов. Конечно, Ñта вручную Ð¿Ð¾Ð»ÑƒÑ‡ÐµÐ½Ð½Ð°Ñ Ð¾Ñ†ÐµÐ½ÐºÐ°, Ñкорее вÑего, будет улучшена. Дело техники и, прежде вÑего, хорошей программы. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’ Ñтом чемпионе по Д-транÑверÑалÑм (на данный момент) тоже Ñ Ñ…Ð¾Ð´Ñƒ визуально наÑчитываетÑÑ 300 интеркалÑтов. Ðа иллюÑтрации вы видите 100 раÑкрашенных интеркалÑтов  Ð’ данный момент Demis Ñчитает в Ñтом ДЛК общие транÑверÑали. PS. ПодÑчёт транÑверÑалей в Ñтом ДЛК оÑтановлен. Причину Ñмотрите в Ñообщении https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=138&postid=2731 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПоиÑк КФ DSODLS 12-го порÑдка идёт уÑпешно. Вчера в четвёртой облаÑти было найдено программой Harry White 1240 аÑÑоциативных SODLS (до Ð¿Ñ€ÐµÑ€Ñ‹Ð²Ð°Ð½Ð¸Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ñ‹). Они дали 1224 КФ DSODLS. Отличный выход! Теперь у Ð¼ÐµÐ½Ñ Ð¾Ð±Ñ‰Ð¸Ð¹ итог: 3152 КФ DSODLS 12-го порÑдка. Проверка ÑвойÑтв Order? 12
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_2.txt
Counts
------
3152 diagonal Latin
3152 associative
3152 natural \diagonal
3152 self-orthogonal
1 axial parity 1-wayОчень Ñимпатичные квадратики! ЗапуÑтила поиÑк в пÑтой облаÑти. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Снова об интеркалÑтах Цитата из поÑледовательноÑти OEIS a(10) >= 93, a(11) >= 94, a(12) >= 188, a(13) >= 75. - Eduard I. Vatutin, May 31 2021 Ð’ прикреплённом к поÑледовательноÑти а-файле https://oeis.org/A307164/a307164.txt нашла ДЛК 10-го порÑдка, имеющий макÑимальное количеÑтво интеркалÑтов (на данный момент) n=10, a(10)>=93 Ðапомню, что Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 10 Белышев Ñделал программу поиÑка интеркалÑтов в ЛК, interkalyator.exe. Он выкладывал её на форуме boinc.ru Ð´Ð»Ñ Ð¾Ð±Ñ‰ÐµÐ³Ð¾ пользованиÑ. ИнтереÑно: в файле readme.txt (к программе) Белышев привёл определение интеркалÑта из какой-то англоÑзычной Ñтатьи Brendan McKay: "An intercalate is a 2x2 Latin subsquare; that is, two rows and two columns whose intersection includes only two symbols". И ещё интереÑно из того же файла, цитирую Общее чиÑло интеркалÑтов ÑвлÑетÑÑ Ð¸Ð½Ð²Ð°Ñ€Ð¸Ð°Ð½Ñ‚Ð¾Ð¼ изоморфизма ЛК, но их раÑпределение по типам может отличатьÑÑ Ð´Ð»Ñ Ñ€Ð°Ð·Ð½Ñ‹Ñ… Ñрезов. Протокол работы программы Белышева interkalyator.exe Ð´Ð»Ñ Ð¿Ð»ÐºÐ°Ð·Ð°Ð½Ð½Ð¾Ð³Ð¾ ДЛК, чемпиона по интеркалÑтам на данный момент Программа поиÑка интеркалÑтов в ЛК10: 0 8 6 5 7 1 2 9 4 3 9 1 7 4 6 8 3 0 5 2 4 3 2 9 5 0 1 8 6 7 1 9 4 3 2 6 7 5 0 8 5 2 3 0 4 9 8 1 7 6 3 7 8 1 0 5 9 6 2 4 8 0 5 2 3 7 6 4 9 1 2 6 1 8 9 4 0 7 3 5 7 4 9 6 1 3 5 2 8 0 6 5 0 7 8 2 4 3 1 9 Ðайдено: 93 Ð”Ð»Ñ Ð²Ñ‹Ñ…Ð¾Ð´Ð° нажмите любую клавишу . . . Ð’ÑÑ‘ верно, программа нашла в Ñтом ДЛК 93 интеркалÑта. Теперь, думаю, вÑÑ‘ Ñовершенно понÑтно Ñ Ð¸Ð½Ñ‚ÐµÐºÐ°Ð»Ñтами. Ðадо бы программу Ñделать Ð´Ð»Ñ Ð¿Ð¾Ð¸Ñка интекалÑтов в ДЛК порÑдков n>10. Я вчера вручную проверила вÑе интеркалÑÑ‚Ñ‹ в показанном ДЛК, нашла вÑе 93 интеркалÑта. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾ÐºÐ°Ð¶Ñƒ небольшую иллюÑтрацию, и поиÑк интеркалÑтов будет ÑовÑем понÑтен. Да, и интереÑен вывод Ñамих интеркалÑтов программой Белышева (показываю один Ñрез) Ñрез #1
0 1 2 3 4 5 6 7 8 9
1 0 3 6 9 4 2 8 7 5
2 3 0 4 1 6 8 9 5 7
3 6 9 0 8 7 1 5 4 2
4 8 7 2 5 9 3 6 1 0
5 7 8 9 6 2 4 3 0 1
6 2 5 1 7 8 0 4 9 3
7 5 4 8 2 1 9 0 3 6
8 9 6 7 3 0 5 1 2 4
9 4 1 5 0 3 7 2 6 8
{1,6} = 2 : (0,3,1,6) (1,6,0,3)
{2,3} = 2 : (5,9,5,7) (7,8,4,8)
{4,8} = 2 : (0,3,4,8) (1,6,5,7)
{5,9} = 2 : (5,9,0,3) (7,8,1,6)
{0,1} = 5 : (0,1,0,1) (2,9,2,4) (3,6,3,6) (4,5,8,9) (7,8,5,7)
{0,2} = 5 : (0,2,0,2) (1,6,1,6) (3,4,3,9) (5,8,5,8) (7,9,4,7)
{0,3} = 5 : (0,3,0,3) (1,2,1,2) (4,6,6,9) (5,7,7,8) (8,9,4,5)
{0,6} = 5 : (0,6,0,6) (1,3,1,3) (2,8,2,5) (4,7,7,9) (5,9,4,8)
{0,7} = 5 : (0,7,0,7) (1,5,1,8) (2,4,2,9) (3,8,3,5) (6,9,4,6)
{1,5} = 5 : (0,7,1,5) (1,5,0,9) (2,4,4,8) (3,8,6,7) (6,9,2,3)
{1,8} = 5 : (0,4,1,8) (1,8,0,7) (2,3,4,6) (5,9,2,9) (6,7,3,5)
{2,4} = 5 : (0,7,2,4) (1,5,5,6) (2,4,0,3) (3,8,8,9) (6,9,1,7)
{2,9} = 5 : (0,3,2,9) (1,7,4,6) (2,9,0,7) (4,5,3,5) (6,8,1,8)
{3,5} = 5 : (0,9,3,5) (1,6,2,9) (2,7,1,8) (3,5,0,7) (4,8,4,6)
{3,8} = 5 : (0,7,3,8) (1,5,2,7) (2,4,1,6) (3,8,0,4) (6,9,5,9)
{4,6} = 5 : (0,5,4,6) (1,2,3,5) (3,9,1,8) (4,6,0,7) (7,8,2,9)
{4,7} = 5 : (0,6,4,7) (1,3,5,8) (2,8,3,9) (4,7,0,2) (5,9,1,6)
{5,7} = 5 : (0,3,5,7) (1,2,8,9) (4,6,2,4) (5,7,0,1) (8,9,3,6)
{6,9} = 5 : (0,7,6,9) (1,5,3,4) (2,4,5,7) (3,8,1,2) (6,9,0,8)
{7,8} = 5 : (0,1,7,8) (2,9,6,9) (3,6,4,5) (4,5,1,2) (7,8,0,3)
{7,9} = 5 : (0,2,7,9) (1,6,4,8) (3,4,2,5) (5,8,1,3) (7,9,0,6)ЗапиÑÑŒ {1,6} означает тип интеркалÑта. Ðапомню: мы называем интеркалÑÑ‚Ñ‹ также блоками. Вот блок - интеркалÑÑ‚ 1 6 6 1 или повернутый на 90 градуÑов 6 1 1 6 Ðто один и тот же тип интеркалÑта. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese