Thread 'Статьи в OEIS: иÑÑ‚Ð¾Ñ€Ð¸Ñ Ð¸ ÑовременноÑÑ‚ÑŒ'
Message boards : Science : Статьи в OEIS: иÑÑ‚Ð¾Ñ€Ð¸Ñ Ð¸ ÑовременноÑÑ‚ÑŒ
Message board moderation
Previous · 1 . . . 13 · 14 · 15 · 16 · 17 · 18 · 19 . . . 23 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вот как поворачиваютÑÑ Ð±Ð»Ð¾ÐºÐ¸ в Ñтом малыше новой программой Harry White .. writing DLS to file 12DLS.txt Break into how many runs? 1 Combos 7819 DLS 7819 elapsed time 0:00:00 Blocks 22 intersections 56 ÐŸÐ¾Ñ€Ñ†Ð¸Ñ Ð”Ð›Ðš маленькаÑ. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ñ‡ÐµÑ€ÐµÐ¿Ð°ÑˆÐºÐ° проверит её на Д-транÑверÑали. Готово! Ðайдено 42 новых Ñлемента Ñпектра. Теперь наш Ñпектр Ñодержит 14991 Ñлементов. Минимум и макÑимум без изменений. КоÑффициент плотноÑти Ñпектра на данный момент K = 0,532. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПереÑтановка Ñтрок и Ñтолбцов в ДЛК Ñ 324 Д-транÑверÑалÑми дала 23 новых Ñлемента, Ñреди который еÑÑ‚ÑŒ новый минимальный Ñлемент. Ура! Min = 300. Показываю новое начало нашего Ñпектра (нижнÑÑ Ñ‡Ð°ÑÑ‚ÑŒ) 300 304 324 328 332 346 348 352 356 358 368 370 378 386 388 392 394 396 404 410 412 432 434 456 458 468 474 496 508 520 528 588 600 604 652 663 666 671 674 677 679 683 684 689 691 692 695 698 702 704 705 706 711 714 715 716 718 726 727 731 732 736 741 742 745 746 748 753 754 759 760 762 763 764 765 766 768 769 771 772 776 778 779 780 781 782 783 784 785 786 787 788 790 791 792 793 794 795 796 797 798 800 801 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833 834 835 836 838 839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 861 862 864 865 866 867 868 870 871 872 873 874 875 876 877 878 879 880 881 882 883 884 885 886 887 888 889 890 891 892 893 894 895 896 897 898 899 900 901 902 903 904 905 906 907 908 909 910 911 912 913 914 916 917 918 920 921 922 923 924 925 926 927 928 929 930 931 932 933 934 935 936 937 938 939 940 941 942 943 944 945 946 947 949 950 951 952 953 954 955 956 957 958 959 960 961 962 963 964 965 966 967 968 969 970 971 972 973 974 975 976 977 978 979 980 981 982 983 984 985 986 987 988 989 990 991 992 993 994 995 996 997 998 999 1000 ... ÐÐ¾Ð²Ð°Ñ ÑˆÐ¸Ñ€Ð¸Ð½Ð° Ñпектра - 28197. ÐÐ¾Ð²Ð°Ñ Ð¼Ð¾Ñ‰Ð½Ð¾ÑÑ‚ÑŒ Ñпектра - 15014. КоÑффициент плотноÑти Ñпектра не изменилÑÑ. Ðаш новый малыш 300 Д-транÑверÑалей 0 2 4 5 7 9 3 8 6 10 11 1 11 1 10 6 3 8 7 9 5 4 0 2 4 6 2 8 0 10 11 1 9 3 7 5 6 4 9 3 10 0 1 11 2 8 5 7 8 3 7 11 4 6 2 5 0 1 9 10 9 10 1 0 2 5 4 6 11 7 8 3 2 0 11 10 9 7 6 4 1 5 3 8 1 8 0 4 6 3 5 7 10 11 2 9 7 5 3 9 11 1 0 10 8 2 4 6 5 7 8 2 1 11 10 0 3 9 6 4 3 11 5 1 8 4 9 2 7 6 10 0 10 9 6 7 5 2 8 3 4 0 1 11 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Поворот блоков в поÑледнем малыше (300 Д-транÑверÑалей) новой программой Harry White дал 28 новых Ñлементов Ñпектра. Теперь наш Ñпектр Ñодержит 15042 Ñлемента. Чуть раÑширилаÑÑŒ в одну Ñторону Ð½ÐµÐ¿Ñ€ÐµÑ€Ñ‹Ð²Ð½Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ Ñпектра в начале, была Ñ 1360 по 9720, Ñтала Ñ 1340 по 9720. Минимум и макÑимум не изменилиÑÑŒ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё одна Ð¿Ð¾Ñ€Ñ†Ð¸Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€Ð¸Ð»Ð°ÑÑŒ у Demis. ÐŸÐ¾Ñ€Ñ†Ð¸Ñ Ð¿Ð¾Ð»ÑƒÑ‡ÐµÐ½Ð° поворотом блоков в Ñтом ДЛК 370 Д-транÑверÑалей 0 2 4 6 5 8 9 3 7 10 11 1 3 1 7 10 9 4 5 8 11 6 0 2 4 6 2 8 0 10 11 1 9 3 7 5 7 5 9 3 11 1 0 10 2 8 4 6 9 3 10 0 4 6 7 5 1 11 2 8 2 0 1 11 8 5 4 6 10 7 9 3 8 10 11 1 2 7 6 4 0 5 3 9 11 9 0 5 6 3 2 7 4 1 8 10 5 7 3 9 1 11 10 0 8 2 6 4 6 4 8 2 10 0 1 11 3 9 5 7 1 11 5 7 3 9 8 2 6 4 10 0 10 8 6 4 7 2 3 9 5 0 1 11 Ðайдено 2500 Ñлементов Ñпектра в промежутке [711, 6125], в том чиÑле 5 новых. Теперь наш Ñпектр Ñодержит 15047 Ñлементов. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
У Demis порции ДЛК закончилиÑÑŒ :) ШуÑтро он проверÑет. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð±ÑƒÐ´Ñƒ генерировать новые порции Ð´Ð»Ñ Ð½ÐµÐ³Ð¾. Рпотом буду вручную риÑовать неÑтандартные блоки в нашем новом малыше Ñ 300 Д-транÑверÑалÑми, чтобы его иÑпортить, то еÑÑ‚ÑŒ получить меньшее количеÑтво Д-транÑверÑалей. ÐœÐ¸Ð½Ð¸Ð¼Ð¸Ð·Ð°Ñ†Ð¸Ñ Ñпектра Д-транÑверÑалей Ð´Ð»Ñ Ð”Ð›Ðš 12-го порÑдка у Ð¼ÐµÐ½Ñ Ð¿Ñ€Ð¾Ð´Ð²Ð¸Ð³Ð°ÐµÑ‚ÑÑ, Ñ…Ð¾Ñ‚Ñ Ð¸ не так быÑтро, как хотелоÑÑŒ бы. Ðу, вот нужна программа поворота (точнее: переворота) неÑтандартных блоков в ДЛК. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ñ Ð¸Ñ‰Ñƒ такие блоки визуально и переворачиваю их вручную. ПонÑтно, что Ñтот ручной поиÑк много не даÑÑ‚. Пример неÑтандартного блока Ñ ÐµÐ³Ð¾ переворачиванием 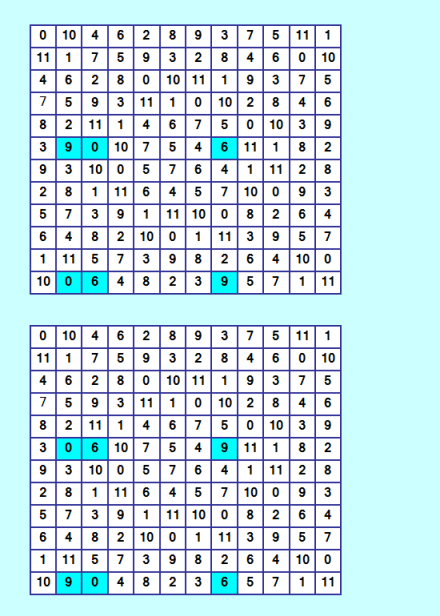 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðашла в ДЛК Ñ 300 Д-транÑверÑалÑми визуально неÑколько неÑтандартных блоков, преобразовала ДЛК Ñ Ð¿Ð¾Ð¼Ð¾Ñ‰ÑŒÑŽ Ð¿ÐµÑ€ÐµÐ²Ñ‘Ñ€Ñ‚Ñ‹Ð²Ð°Ð½Ð¸Ñ Ñтих блоков, получила 16 новых ДЛК, которые дали Ñледующие количеÑтва Д-транÑверÑалей 1 318
2 280
3 298
4 272
5 262
6 316
7 286
8 204
9 280
10 328
11 1430
12 1580
13 1413
14 1626
15 1658
16 1670Ура, ура, ура! ЕÑÑ‚ÑŒ новый минимум! Ðто 204 Д-транÑверÑали. Супер! ТÑк-Ñ, ÑÐµÐ¹Ñ‡Ð°Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÑŽ Ñти Ð·Ð½Ð°Ñ‡ÐµÐ½Ð¸Ñ Ð½Ð° добавление в Ñпектр. 8 новых Ñлементов добавилоÑÑŒ в Ñпектр. Теперь наш Ñпектр Ñодержит 15055 Ñлементов. Ширина Ñпектра чуть-чуть увеличилаÑÑŒ, Ñтала 28293. КоÑффициент плотноÑти Ñпектра не изменилÑÑ. Показываю новое начало Ñпектра (нижнÑÑ Ñ‡Ð°ÑÑ‚ÑŒ) 204 262 272 280 286 298 300 304 316 318 324 328 332 346 348 352 356 358 368 370 378 386 388 392 394 396 404 410 412 432 434 456 458 468 474 496 508 520 528 588 594 600 604 607 616 646 652 658 660 661 663 665 666 671 674 676 677 679 681 683 684 685 689 691 692 695 698 700 702 703 704 705 706 711 714 715 716 718 721 726 727 730 731 732 733 736 740 741 742 745 746 748 753 754 758 759 760 761 762 763 764 765 766 768 769 771 772 774 776 778 779 780 781 782 783 784 785 786 787 788 790 791 792 793 794 795 796 797 798 800 801 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833 834 835 836 838 839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 861 862 864 865 866 867 868 870 871 872 873 874 875 876 877 878 879 880 881 882 883 884 885 886 887 888 889 890 891 892 893 894 895 896 897 898 899 900 901 902 903 904 905 906 907 908 909 910 911 912 913 914 915 916 917 918 919 920 921 922 923 924 925 926 927 928 929 930 931 932 933 934 935 936 937 938 939 940 941 942 943 944 945 946 947 949 950 951 952 953 954 955 956 957 958 959 960 961 962 963 964 965 966 967 968 969 970 971 972 973 974 975 976 977 978 979 980 981 982 983 984 985 986 987 988 989 990 991 992 993 994 995 996 997 998 999 1000 ... Ð Ñто наш новый малыш - антиквадрозаврик 204 Д-транÑверÑали 0 10 4 5 2 9 3 8 6 7 11 1 8 1 7 11 3 6 2 9 5 4 0 10 4 6 2 8 0 10 11 1 9 3 7 5 6 4 9 3 10 0 1 11 2 8 5 7 11 3 10 6 4 8 7 5 0 1 9 2 9 2 1 0 7 5 4 6 11 10 8 3 2 9 11 10 5 7 6 4 1 0 3 8 1 8 0 4 6 3 5 7 10 11 2 9 7 5 3 9 11 1 0 10 8 2 4 6 5 7 8 2 1 11 10 0 3 9 6 4 3 11 5 1 8 4 9 2 7 6 10 0 10 0 6 7 9 2 8 3 4 5 1 11 Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¼Ñ‹ Ñ Ð½Ð¸Ð¼ разберёмÑÑ :) Повернём блоки (интеркалÑÑ‚Ñ‹), переÑтавим Ñтроки/Ñтолбцы, а потом будем портить Ñ Ð¿Ð¾Ð¼Ð¾Ñ‰ÑŒÑŽ неÑтандартных блоков. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Поворот блоков в новом малыше (Ð¼Ð°Ð»ÐµÐ½ÑŒÐºÐ°Ñ Ð¿Ð¾Ñ€Ñ†Ð¸Ñ Ð”Ð›Ðš) дал 6 новых Ñлементов Ñпектра. Demis отправила порцию ДЛК побольше Ð´Ð»Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÐºÐ¸. ПереÑтановка Ñтрок и Ñтолбцов дала 17 новых Ñлементов Ñпектра. Теперь наш Ñпектр Ñодержит 15078 Ñлементов. Показываю новое начало Ñпектра (нижнÑÑ Ñ‡Ð°ÑÑ‚ÑŒ) 204 220 256 262 272 280 284 286 298 300 304 314 316 318 324 328 332 338 346 348 352 356 358 368 370 378 386 388 390 392 394 396 404 406 410 412 422 432 434 438 450 452 456 458 468 474 484 496 500 508 520 528 532 557 569 588 589 594 600 602 604 607 616 646 650 652 658 660 661 663 665 666 671 672 674 676 677 679 681 683 684 685 689 691 692 695 698 700 702 703 704 705 706 711 714 715 716 718 721 726 727 730 731 732 733 736 740 741 742 745 746 748 753 754 758 759 760 761 762 763 764 765 766 768 769 771 772 774 776 778 779 780 781 782 783 784 785 786 787 788 790 791 792 793 794 795 796 797 798 800 801 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833 834 835 836 838 839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 861 862 863 864 865 866 867 868 869 870 871 872 873 874 875 876 877 878 879 880 881 882 883 884 885 886 887 888 889 890 891 892 893 894 895 896 897 898 899 900 901 902 903 904 905 906 907 908 909 910 911 912 913 914 915 916 917 918 919 920 921 922 923 924 925 926 927 928 929 930 931 932 933 934 935 936 937 938 939 940 941 942 943 944 945 946 947 948 949 950 951 952 953 954 955 956 957 958 959 960 961 962 963 964 965 966 967 968 969 970 971 972 973 974 975 976 977 978 979 980 981 982 983 984 985 986 987 988 989 990 991 992 993 994 995 996 997 998 999 1000 ... Очень хорошо идёт уплотнение Ñтой чаÑти Ñпектра. Ðу что, пойду риÑовать неÑтандартные блоки в малыше. ÐвоÑÑŒ, ещё удаÑÑ‚ÑÑ Ð¼Ð¸Ð½Ð¸Ð¼Ð¸Ð·Ð¸Ñ€Ð¾Ð²Ð°Ñ‚ÑŒ Ñпектр. Пока Min = 204. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Блоки нариÑовала, получила 34 варианта ДЛК, вот какие количеÑтва Д-транÑверÑалей в них оказалиÑÑŒ 1 280
2 560
3 280
4 1208
5 280
6 1224
7 1895
8 1238
9 1630
10 1251
11 1509
12 2280
13 1909
14 1248
15 1396
16 1598
17 268
18 288
19 268
20 1639
21 1440
22 1603
23 1422
24 1674
25 266
26 284
27 262
28 2301
29 2281
30 2273
31 2660
32 1662
33 1634
34 1396
Увы, иÑпортить не удалоÑÑŒ, наоборот удалоÑÑŒ только улучшить. КÑтати, надо попробовать Ñтот метод Ð´Ð»Ñ Ð¼Ð°ÐºÑимизации Ñпектра, ведь вот же получаетÑÑ ÑƒÐ²ÐµÐ»Ð¸Ñ‡ÐµÐ½Ð¸Ðµ количеÑтва Д-транÑверÑалей в результате таких преобразований неÑтандартных блоков. Ðадо в квадрозаврах Ñтот метод попробовать. Ðо, конечно, нужна программа, вручную много не найдёшь неÑтандартных блоков и не преобразуешь их вÑе в разных комбинациÑÑ…. Однако, найдено 4 новых Ñлемента Ñпектра. Теперь наш Ñпектр Ñодержит 15082 Ñлемента. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Поиграла Ñ ÐºÐ²Ð°Ð´Ñ€Ð¾Ð·Ð°Ð²Ñ€Ð¾Ð¼ (28496 Д-транÑверÑалей)  Ðа иллюÑтрации показаны раÑкрашенные неÑтандартные блоки, найденные визуально. ИнтереÑен зелёный блок, такой вÑего один мне вÑтретилÑÑ. Ðтот блок переÑекаетÑÑ Ñ Ñиреневым блоком, то еÑÑ‚ÑŒ Ñти два блока не ÑвлÑÑŽÑ‚ÑÑ Ð½ÐµÐ·Ð°Ð²Ð¸Ñимыми. Диагонали раÑкрашены краÑным цветом Ð´Ð»Ñ Ñ‚Ð¾Ð³Ð¾, чтобы Ñлементы блоков не попадали на диагонали. С помощью Ð¿Ñ€ÐµÐ¾Ð±Ñ€Ð°Ð·Ð¾Ð²Ð°Ð½Ð¸Ñ Ñтих неÑтандартных блоков получила 45 новых ДЛК. Однако макÑимизациÑ, увы, не получилаÑÑŒ, удалоÑÑŒ только иÑпортить ДЛК, то еÑÑ‚ÑŒ уменьшить в нём количеÑтво Д-транÑверÑалей. Показываю результаты по Д-транÑверÑалÑм в Ñтих 45 ДЛК 1 10782
2 9828
3 9625
4 11344
5 9594
6 9664
7 9878
8 10722
9 9848
10 12695
11 9446
12 9489
13 9809
14 9724
15 10418
16 12700
17 10387
18 9713
19 9793
20 9628
21 9714
22 9332
23 9716
24 9552
25 9628
26 9351
27 9344
28 9892
29 9639
30 10522
31 4380
32 4343
33 4256
34 4388
35 4675
36 4799
37 4621
38 4579
39 4368
40 4424
41 4243
42 4267
43 4402
44 4415
45 9760Ð—Ð½Ð°Ñ‡ÐµÐ½Ð¸Ñ Ð² промежутке [4243, 12700]. Ðайдено три новых Ñлемента Ñпектра. Теперь наш Ñпектр Ñодержит 15085 Ñлементов. КоÑффициент плотноÑти Ñпектра на данный момент: К=0,533. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё поигралаÑÑŒ Ñ Ð”Ð›Ðš, имеющим 204 Д-транÑверÑали. ОпÑÑ‚ÑŒ риÑовала неÑтандартные блоки. Получила 20 новых ДЛК. ÐœÐ¸Ð½Ð¸Ð¼Ð¸Ð·Ð°Ñ†Ð¸Ñ Ð¾Ð¿ÑÑ‚ÑŒ не получилаÑÑŒ. Рпотом переÑтавила Ñтроки и Ñтолбцы в Ñтих 20 ДЛК. Ðто дало 11 новых Ñлементов Ñектра. Теперь наш Ñпектр Ñодержит 15096 Ñлементов. Ðемного раÑширилаÑÑŒ Ð½ÐµÐ¿Ñ€ÐµÑ€Ñ‹Ð²Ð½Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ Ñпектра: была Ñ 1340 по 9720, Ñтала Ñ 1316 по 9720. Показываю фрагмент Ñтой непрерывной чаÑти Ñпектра ... 1316 1317 1318 1319 1320 1321 1322 1323 1324 1325 1326 1327 1328 1329 1330 1331 1332 1333 1334 1335 1336 1337 1338 1339 1340 1341 1342 1343 1344 1345 1346 1347 1348 1349 1350 1351 1352 1353 1354 1355 1356 1357 1358 1359 1360 1361 1362 1363 1364 1365 1366 1367 1368 1369 1370 1371 1372 1373 1374 1375 1376 1377 1378 1379 1380 1381 1382 1383 1384 1385 1386 1387 1388 1389 1390 1391 1392 1393 1394 1395 1396 1397 1398 1399 1400 1401 1402 1403 1404 1405 1406 1407 1408 1409 1410 1411 1412 1413 1414 1415 1416 1417 1418 1419 1420 1421 1422 1423 1424 1425 1426 1427 1428 1429 1430 1431 1432 1433 1434 1435 1436 1437 1438 1439 1440 1441 1442 1443 1444 1445 1446 1447 1448 1449 1450 1451 1452 1453 1454 1455 1456 1457 1458 1459 1460 1461 1462 1463 1464 1465 1466 1467 1468 1469 1470 1471 1472 1473 1474 1475 1476 1477 1478 1479 1480 1481 1482 1483 1484 1485 1486 1487 1488 1489 1490 1491 1492 1493 1494 1495 1496 1497 1498 1499 1500 ... МощноÑÑ‚ÑŒ Ñтой непрерывной чаÑти Ñпектра (а также её ширина) равна 8405. Отлично! 8405 Ñлементов Ñпектра идут подрÑд, без пропуÑков. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Прибыли результаты подÑчёта Д-транÑверÑалей в больших порциÑÑ… ДЛК от Demis. Хорошо пополнилÑÑ Ð½Ð°Ñˆ Ñпектр, найдено 224 новых Ñлемента. Теперь наш Ñпектр Ñодержит 15320 Ñлементов. Минимум и макÑимум не изменилиÑÑŒ, Ñледовательно, произошло очень хорошее уплотнение Ñпектра. КоÑффициент плотноÑти Ñпектра на данный момент: К=0,541. Показываю нижнюю чаÑÑ‚ÑŒ Ñпектра в промежутке [204, 1000] 204 220 256 262 266 268 272 280 284 286 288 298 300 304 314 316 318 324 328 332 338 346 348 352 356 358 368 370 378 386 388 390 392 394 396 404 406 410 412 422 425 432 434 438 445 450 452 453 456 458 460 466 468 474 484 496 497 500 504 508 520 523 527 528 531 532 541 554 557 560 562 568 569 570 572 575 579 584 585 587 588 589 590 593 594 599 600 601 602 604 607 615 616 618 620 621 622 624 626 632 634 636 638 640 643 646 647 650 652 654 657 658 659 660 661 662 663 664 665 666 670 671 672 674 675 676 677 679 681 682 683 684 685 686 687 689 690 691 692 695 696 697 698 699 700 702 703 704 705 706 707 708 710 711 712 713 714 715 716 717 718 719 720 721 722 723 724 725 726 727 728 729 730 731 732 733 734 735 736 737 738 739 740 741 742 743 744 745 746 747 748 749 750 751 752 753 754 755 756 757 758 759 760 761 762 763 764 765 766 767 768 769 770 771 772 773 774 775 776 777 778 779 780 781 782 783 784 785 786 787 788 789 790 791 792 793 794 795 796 797 798 799 800 801 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833 834 835 836 837 838 839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 861 862 863 864 865 866 867 868 869 870 871 872 873 874 875 876 877 878 879 880 881 882 883 884 885 886 887 888 889 890 891 892 893 894 895 896 897 898 899 900 901 902 903 904 905 906 907 908 909 910 911 912 913 914 915 916 917 918 919 920 921 922 923 924 925 926 927 928 929 930 931 932 933 934 935 936 937 938 939 940 941 942 943 944 945 946 947 948 949 950 951 952 953 954 955 956 957 958 959 960 961 962 963 964 965 966 967 968 969 970 971 972 973 974 975 976 977 978 979 980 981 982 983 984 985 986 987 988 989 990 991 992 993 994 995 996 997 998 999 1000 ... ЗдеÑÑŒ пока много пропуÑков. СовÑем чуточку раÑширилаÑÑŒ Ð½ÐµÐ¿Ñ€ÐµÑ€Ñ‹Ð²Ð½Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ Ñпектра, вÑего добавилоÑÑŒ два Ñлемента, было Ñ 1316 по 9720, Ñтало Ñ 1314 по 9720. ÐÐ°Ñ‡Ð°Ð»ÑŒÐ½Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ Ñпектра от ÑущеÑтвующего минимального Ñлемента 204 до Ñлемента 1314 пока Ñ Ð¿Ñ€Ð¾Ð¿ÑƒÑками, а дальше идёт Ð±Ð¾Ð»ÑŒÑˆÐ°Ñ Ð½ÐµÐ¿Ñ€ÐµÑ€Ñ‹Ð²Ð½Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ Ñпектра - до Ñлемента 9720 включительно. И дальше Ñнова пропуÑки. Таким образом, ещё очень долго надо а) иÑкать новые минимум и макÑимум; б) уплотнÑÑ‚ÑŒ Ñпектр до полной непрерывноÑти или (еÑли Ð¿Ð¾Ð»Ð½Ð°Ñ Ð½ÐµÐ¿Ñ€ÐµÑ€Ñ‹Ð²Ð½Ð¾ÑÑ‚ÑŒ невозможна) до макÑимального Ð·Ð½Ð°Ñ‡ÐµÐ½Ð¸Ñ ÐºÐ¾Ñффициента плотноÑти Ñпектра, то еÑÑ‚ÑŒ до макÑимально возможной непрерывноÑти. Задача трудно решаемаÑ, дело техники и времени. Конечно, ещё можно реализовать новые Ñпециальные алгоритмы, например, Ñделать программу преобразований ДЛК Ñ Ð¿Ñ€Ð¸Ð¼ÐµÐ½ÐµÐ½Ð¸ÐµÐ¼ неÑтандартных блоков. Ðто даÑÑ‚, Ñ Ð´ÑƒÐ¼Ð°ÑŽ, отличное пополнение Ñпектра. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё раз вручную пориÑовала неÑтандартные блоки, на Ñтот раз в Ñтом ДЛК Ñ 18808 Д-транÑверÑалÑми 0 10 4 6 2 8 3 9 7 5 11 1 11 1 7 5 3 9 8 2 4 6 0 10 6 4 2 8 0 10 11 1 9 3 5 7 5 7 9 3 11 1 0 10 2 8 6 4 2 8 0 10 4 6 7 5 11 1 9 3 9 3 11 1 7 5 4 6 0 10 2 8 3 9 1 11 5 7 6 4 10 0 8 2 8 2 10 0 6 4 5 7 1 11 3 9 7 5 3 9 1 11 10 0 8 2 4 6 4 6 8 2 10 0 1 11 3 9 7 5 1 11 5 7 9 3 2 8 6 4 10 0 10 0 6 4 8 2 9 3 5 7 1 11 Получила 34 новых ДЛК, поÑчитала в них Д-транÑверÑали, вот что наÑчиталоÑÑŒ 1 7146
2 6611
3 3190
4 5310
5 9208
6 3686
7 3580
8 3234
9 3190
10 3401
11 5623
12 3871
13 2890
14 2274
15 3153
16 2555
17 2108
18 2619
19 2108
20 2357
21 2213
22 2115
23 2143
24 2021
25 2638
26 2428
27 2304
28 2067
29 2262
30 2026
31 2113
32 2146
33 2208
34 2334Ð’ÑÑ‘ только иÑпортилоÑÑŒ, причём очень Ñильно иÑпортилоÑÑŒ, значений Ñ€Ñдом Ñ 18808 не получилоÑÑŒ. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ñмотрю, еÑÑ‚ÑŒ ли тут новые Ñлементы Ñпектра. Увы! Ðовые Ñлементы Ñпектра не найдены. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ð¿Ñ€Ð¾Ð±ÑƒÑŽ Ñ Ñтими 34 ДЛК поколдовать, может, что-то найдётÑÑ Ð½Ð¾Ð²Ð¾Ðµ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Прибыли новые результаты от Demis. Отличные результаты! Ðайдено 378 новых Ñлементов Ñпектра. Теперь наш Ñпектр Ñодержит 15698 Ñлементов. Минимум и макÑимум не изменилиÑÑŒ. ПонÑтно, что произошло очень хорошее уплотнение Ñпектра. КоÑффициент плотноÑти Ñпектра К=0,555. Ðемного раÑширилаÑÑŒ Ð½ÐµÐ¿Ñ€ÐµÑ€Ñ‹Ð²Ð½Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ Ñпектра, была Ñ 1314 по 9720, Ñтала Ñ 1302 по 9720 ... 1302 1303 1304 1305 1306 1307 1308 1309 1310 1311 1312 1313 1314 1315 1316 1317 1318 1319 1320 1321 1322 1323 1324 1325 1326 1327 1328 1329 1330 1331 1332 1333 1334 1335 1336 1337 1338 1339 1340 1341 1342 1343 1344 1345 1346 1347 1348 1349 1350 1351 1352 1353 1354 1355 1356 1357 1358 1359 1360 1361 1362 1363 1364 1365 1366 1367 1368 1369 1370 1371 1372 1373 1374 1375 1376 1377 1378 1379 1380 1381 1382 1383 1384 1385 1386 1387 1388 1389 1390 1391 1392 1393 1394 1395 1396 1397 1398 1399 1400 . . . . . 9601 9602 9603 9604 9605 9606 9607 9608 9609 9610 9611 9612 9613 9614 9615 9616 9617 9618 9619 9620 9621 9622 9623 9624 9625 9626 9627 9628 9629 9630 9631 9632 9633 9634 9635 9636 9637 9638 9639 9640 9641 9642 9643 9644 9645 9646 9647 9648 9649 9650 9651 9652 9653 9654 9655 9656 9657 9658 9659 9660 9661 9662 9663 9664 9665 9666 9667 9668 9669 9670 9671 9672 9673 9674 9675 9676 9677 9678 9679 9680 9681 9682 9683 9684 9685 9686 9687 9688 9689 9690 9691 9692 9693 9694 9695 9696 9697 9698 9699 9700 9701 9702 9703 9704 9705 9706 9707 9708 9709 9710 9711 9712 9713 9714 9715 9716 9717 9718 9719 9720 ... ÐžÑ‚Ð»Ð¸Ñ‡Ð½Ð°Ñ Ð½ÐµÐ¿Ñ€ÐµÑ€Ñ‹Ð²Ð½Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ, мощноÑÑ‚ÑŒ (и ширина) Ñтой непрерывной чаÑти равна 8419. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё Ð½ÐµÐ±Ð¾Ð»ÑŒÑˆÐ°Ñ Ð¿Ð¾Ñ€Ñ†Ð¸Ñ Ñ€ÐµÑˆÐµÐ½Ð¸Ð¹ прибыла от Demis. Ðайдено 32 новых Ñлемента Ñпектра. Теперь наш Ñпектр Ñодержит 15730 Ñлементов. Минимум и макÑимум не изменилиÑÑŒ. РаÑÑˆÐ¸Ñ€ÐµÐ½Ð¸Ñ Ñпектра нет, зато еÑÑ‚ÑŒ уплотнение Ñпектра. КоÑффициент плотноÑти Ñпектра К=0,556. Ð’ непрерывной чаÑти Ñпектра раÑÑˆÐ¸Ñ€ÐµÐ½Ð¸Ñ Ð½Ðµ произошло. Ðо еÑÑ‚ÑŒ интереÑный момент: Ñ 1302 по 9720 Ñпектр непрерывный, Ñлемент 9721 отÑутÑтвует, а Ñ 9722 по 10102 Ñпектр Ñнова непрерывный. И опÑÑ‚ÑŒ нет нечётного Ñлемента Ñпектра! Вот граничный ДЛК Ñ 9720 Д-транÑверÑалÑми 0 3 6 8 11 4 7 2 10 5 9 1 3 1 10 7 9 2 5 11 4 8 0 6 7 10 2 9 5 1 0 6 11 3 8 4 4 6 1 3 7 11 9 8 2 0 5 10 10 8 3 2 4 0 11 5 9 1 6 7 1 0 8 10 2 5 4 9 7 6 11 3 2 11 7 4 3 8 6 0 5 10 1 9 6 5 0 1 10 9 2 7 3 11 4 8 11 9 5 6 1 7 10 3 8 4 2 0 5 4 11 0 8 6 3 10 1 9 7 2 8 7 9 11 6 3 1 4 0 2 10 5 9 2 4 5 0 10 8 1 6 7 3 11 Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ð¿Ñ€Ð¾Ð±ÑƒÑŽ переÑтавить в нём Ñтроки и Ñтолбцы. Может быть, удаÑÑ‚ÑÑ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ñ‚ÑŒ Ñлемент 9721. Ðет, не удалоÑÑŒ получить Ñлемент 9721. Вот какие нашлиÑÑŒ Ñлементы Ñпектра 9626 9632 9661 9672 9679 9702 9706 9720 9736 9745 9758 9778 9842 9867 9896 9897 9932 9958 9959 9965 9975 9976 9995 10003 10010 10016 10017 10020 10021 10022 10029 10033 10037 10042 10044 10059 10060 10063 10068 10070 10073 10074 10077 10080 10097 10098 10099 10107 10112 10120 10127 10130 10132 10135 10143 10145 10149 10152 10153 10158 10160 10162 10163 10164 10182 10183 10186 10191 10194 10196 10198 10201 10206 10208 10209 10210 10219 10228 10229 10232 10233 10238 10241 10242 10244 10247 10248 10254 10260 10268 10271 10272 10274 10276 10279 10280 10284 10296 10299 10300 10302 10308 10315 10317 10319 10327 10333 10338 10350 10351 10352 10356 10360 10363 10364 10365 10369 10370 10371 10373 10375 10379 10386 10388 10395 10398 10401 10405 10412 10421 10422 10427 10428 10460 10475 10476 10481 10489 10519 10549 10553 10554 10565 10581 10585 10608 10625 10628 10679 10703 10707 10719 10722 10726 10733 10740 10741 10743 10746 10862 10926 Вокруг и около :) Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÑŽ, нет ли тут новых Ñлементов Ñпектра. Ого! ЗдеÑÑŒ 24 новых Ñлемента Ñпектра! Здорово! Теперь наш Ñпектр Ñодержит 15754 Ñлемента. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Второй граничный квадрат (Ñправа) Ñ 9722 Д-транÑверÑалÑми 0 2 11 9 5 8 4 3 6 10 7 1 3 1 8 10 0 7 11 6 9 5 2 4 9 11 2 0 6 1 7 10 4 3 5 8 10 8 1 3 9 4 2 5 0 6 11 7 11 9 0 2 4 3 5 8 7 1 6 10 1 10 3 8 2 5 9 4 11 7 0 6 2 0 9 11 7 10 6 1 5 8 4 3 8 3 10 1 11 6 0 7 2 4 9 5 4 6 5 7 1 11 10 0 8 2 3 9 5 7 4 6 10 0 1 11 3 9 8 2 7 5 6 4 8 9 3 2 1 11 10 0 6 4 7 5 3 2 8 9 10 0 1 11 Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð² Ñтом ДЛК переÑтавлю Ñтроки и Ñтолбцы. Готово! Ðлемент 9721 не найден. Зато найдено 15 новых Ñлементов Ñпектра. Теперь наш Ñпектр Ñодержит 15769 Ñлементов. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё выполнила небольшой ÑкÑперимент: взÑла Ñ€Ñдом Ñ Ð¾Ñ‚ÑутÑтвующим Ñлементом 9721 неÑколько Ñлементов Ñлева и Ñправа. ПереÑтавила Ñтроки и Ñтолбцы в ÑоответÑтвующих Ñтим Ñлементам квадратах. Ðлемент 9721 опÑÑ‚ÑŒ не найден. Зато найдено 74 новых Ñлемента Ñпектра. Теперь наш Ñпектр Ñодержит 15843 Ñлемента. Минимум и макÑимум без изменений. Однако... Ñлемент 9721 очень редкий, никак не находитÑÑ. Ð¡Ð»ÐµÐ´ÑƒÑŽÑ‰Ð°Ñ Ð·Ð° Ñтим Ñлементом Ð½ÐµÐ¿Ñ€ÐµÑ€Ñ‹Ð²Ð½Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ Ñпектра немного раÑширилаÑÑŒ, была Ñ 9722 по 10102, Ñтала Ñ 9722 по 10356. Показываю ... 10349 10350 10351 10352 10353 10354 10355 10356 10358 10359 10360 10361 10362 10363 10364 10365 10366 10367 10368 10369 10370 10371 10372 10373 10374 10375 10376 10377 10378 10379 10380 10381 10382 10383 10384 10385 10386 10387 10388 10389 10390 10391 10392 10393 10394 10395 10396 10397 10398 10399 10400 10401 10402 10403 10404 10405 10406 10407 10408 10409 10410 10411 10412 10413 10414 10415 10416 10417 10418 10419 10420 10421 10422 10423 10424 10425 10426 10427 10428 10429 10430 10431 10432 10433 10434 10435 10436 10437 10438 10439 10440 10441 10442 10443 10444 10445 10446 10447 10448 10449 10451 10452 10453 10454 10455 10456 10457 10458 10459 10460 10462 10463 10464 10465 10466 10467 10468 10469 10470 10471 10472 10473 10474 10475 10476 10477 10478 10480 10481 10482 10483 10484 10485 10486 10487 10488 10489 10490 10492 10494 10495 10496 10497 10498 10500 10501 10502 10504 10505 10506 10508 10512 10514 10515 10516 10517 10518 10519 10520 10522 10523 10524 10526 10527 10528 10529 10530 10531 10532 10534 10536 10538 10539 10540 10541 10542 ... ПоÑле Ñлемента 10356 отÑутÑтвует Ñлемент 10357 (опÑÑ‚ÑŒ нечётный!) и далее Ð½ÐµÐ±Ð¾Ð»ÑŒÑˆÐ°Ñ Ð½ÐµÐ¿Ñ€ÐµÑ€Ñ‹Ð²Ð½Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ Ñпектра по 10449. Рвот тут отÑутÑтвует чётный Ñлемент 10450. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПоÑмотрела Ñвои темы об узорчатых ДЛК. Ðашла вот такие интереÑные неÑтандартные блоки  отÑюда https://boinc.progger.info/odlk/forum_thread.php?id=137&postid=4585 Обнаружила, что гоÑподином Ватутиным Ñоздана поÑледовательноÑÑ‚ÑŒ OEIS https://oeis.org/A307166 о таких блоках. Он называет их циклами. Ðадо поиÑкать такие блоки в ДЛК 12-го порÑдка; конечно, они должны быть. (Визуально иÑкать Ñложно, нужна программа.) Может быть, Ð¿Ñ€ÐµÐ¾Ð±Ñ€Ð°Ð·Ð¾Ð²Ð°Ð½Ð¸Ñ Ñ‚Ð°ÐºÐ¸Ñ… блоков дадут что-то новое в количеÑтвах Д-транÑверÑалей в ДЛК 12-го порÑдка. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
С ходу нашла такие неÑтандартные блоки в квадрозавре (28496 Д-транÑверÑалей) 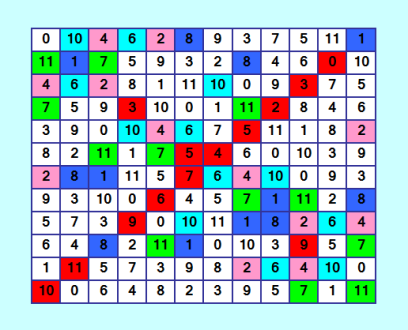 Ðти неÑтандартные блоки Ñ Ð½Ð°Ð·Ð¾Ð²Ñƒ цикличеÑкими блоками. Ðа иллюÑтрации диагонали ДЛК изначально были окрашены в краÑный цвет, чтобы видеть, как блоки "наезжают" на диагонали. Ð’ показанных блоках "наезжают" они удачно: диагональноÑÑ‚ÑŒ квадрата не нарушаетÑÑ Ð¿Ñ€Ð¸ преобразовании блока. Показаны только незавиÑимые блоки, то еÑÑ‚ÑŒ такие, которые друг на друга не "наезжают" или не переÑекаютÑÑ. ÐезавиÑимые блоки можно преобразовывать в любой момент - незавиÑимо от того, преобразованы или нет другие блоки. Ðу, как преобразовывать цикличеÑкие блоки, думаю, понÑтно. ЦикличеÑкий блок ÑоÑтоит из двух различных чиÑел, которые бегают по Ñтрокам/Ñтолбцам. Визуально иÑкать цикличеÑкие блоки легко, но вот получить вÑе возможные Ð¿Ñ€ÐµÐ¾Ð±Ñ€Ð°Ð·Ð¾Ð²Ð°Ð½Ð¸Ñ Ð²Ñех незавиÑимых и завиÑимых блоков - Ñложно. Ещё надо отÑлеживать, чтобы не нарушалаÑÑŒ диагональноÑÑ‚ÑŒ квадрата. Так вот: преобразование цикличеÑкого блока ÑоÑтоит во взаимной замене ÑоÑтавлÑющих его Ñлементов. Ðапример, в зелёном блоке надо заменить Ñлемент 7 на 11, а Ñлемент 11 на 7. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ð¿Ñ€Ð¾Ð±ÑƒÑŽ преобразовать показанные на иллюÑтрации в предыдущем поÑте цикличеÑкие блоки и поÑчитаю Д-транÑверÑали в полученных ДЛК. Сделала неÑколько преобразований, конечно, не вÑе. Получила 7 новых ДЛК, вот какие в них количеÑтва Д-транÑверÑалей 1 10924
2 8542
3 6984
4 2738
5 10940
6 4330
7 3300ТÑк-Ñ, квадрозавр Ñильно иÑпортилÑÑ Ð² ÑмыÑле количеÑтва Д-транÑверÑалей. Теперь надо Ñделать такие же Ð¿Ñ€ÐµÐ¾Ð±Ñ€Ð°Ð·Ð¾Ð²Ð°Ð½Ð¸Ñ Ð² малыше - антиквадрозаврике (204 Д-транÑверÑали). ЕÑли он тоже иÑпортитÑÑ, будет очень хорошо :) Ðо вот он-то может и не иÑпортитьÑÑ! Ðо надо попробовать переÑтавить Ñтроки и Ñтолбцы в полученных ДЛК. Ðто чаÑто даёт новые Ñлементы Ñпектра. Выполнила переÑтановку Ñтрок и Ñтолбцов в полученных 7 ДЛК. Ð-и-ч-е-г-о нового не найдено. ЗанÑлаÑÑŒ малышом (204 Д-транÑверÑали). Ищу в нём визуально цикличеÑкие блоки. ПоÑмотрю, иÑпортÑÑ‚ ли его Ð¿Ñ€ÐµÐ¾Ð±Ñ€Ð°Ð·Ð¾Ð²Ð°Ð½Ð¸Ñ Ñ†Ð¸ÐºÐ»Ð¸Ñ‡ÐµÑких блоков. Ðадежды мало, ну а вдруг... |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вот Ñто фокуÑ!!! order? 12 Type of transversals, 1 all or 2 diagonal? 2 File name? inp .. writing counts to file 12Transversals_5.txt square 1 max transversals 204 square 2 max transversals 204 square 3 max transversals 204 square 4 max transversals 204 square 5 max transversals 204 square 6 max transversals 204 square 7 max transversals 204 Я Ñделала три полных цикличеÑких блока. Преобразованием их получила 7 новых ДЛК. Во вÑех Ñтих ДЛК 204 Д-транÑверÑали! Пойду ÑочинÑÑ‚ÑŒ неполные цикличеÑкие блоки. PS. Полный цикличеÑкий блок Ñквивалентен переобозначению Ñлементов. ПоÑтому вÑе ДЛК получилиÑÑŒ изоморфные и, еÑтеÑтвенно, количеÑтво Д-транÑверÑалей в них одинаковое. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese