Thread 'MOLS and MODLS of order 14'
Message boards : Science : MOLS and MODLS of order 14
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
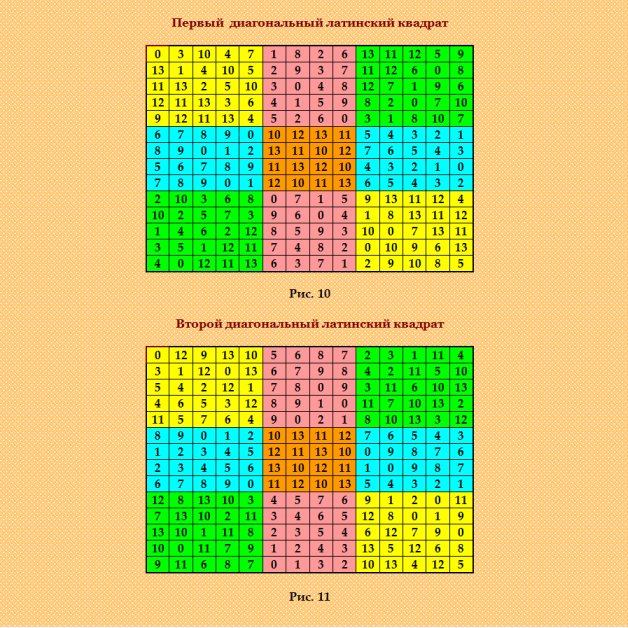
С группами MOLS и MODLS 12-го порÑдка немного поработала. Получила неплохой результат. Смотрите тему "MOLS and MODLS of order 12" https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=120 Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 13 извеÑтна Ð¿Ð¾Ð»Ð½Ð°Ñ ÑиÑтема MOLS, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· 12 взаимно ортогональных ЛК, 10 из которых ÑвлÑÑŽÑ‚ÑÑ Ð”Ð›Ðš, то еÑÑ‚ÑŒ образуют группу MODLS. Я думаю, что группа MODLS 13-го порÑдка не может Ñодержать более 10 взаимно ортогональных ДЛК. Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 9 у Ð¼ÐµÐ½Ñ Ð±Ñ‹Ð»Ð° гипотеза по Ñтому поводу. Теперь Ñто уже не гипотеза, а доказанный факт. Впрочем, гипотеза Ð¼Ð¾Ñ Ð±Ñ‹Ð»Ð° доказана и доказана правильно, по моему мнению. Были другие мнениÑ. Теперь их уже не может быть, потому что гоÑподин Ватутин алгоритмом грубой Ñилы доказал, что группа MODLS 9-го порÑдка не может Ñодержать более 6 взаимно ортогональных ДЛК. Ðу, Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 13 (а также и Ð´Ð»Ñ Ð²Ñех других порÑдков, ÑвлÑющихÑÑ Ð¿Ñ€Ð¾Ñтым чиÑлом) пуÑÑ‚ÑŒ Ñто будет гипотеза, потому что такого доказательÑтва, как Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 9, у Ð¼ÐµÐ½Ñ Ð½ÐµÑ‚. ПроверÑÑ‚ÑŒ Ñтот порÑдок алгоритмом грубой Ñилы - занÑтие не Ð´Ð»Ñ Ð¼Ð¾ÐµÐ³Ð¾ ПК, думаю, что и вообще не Ð´Ð»Ñ ÐŸÐš. Тут нужны реÑурÑÑ‹ поÑолиднее. Ртеперь займуÑÑŒ группами MOLS и MODLS порÑдка 14. Дублирую Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=120&postid=2482 Программа SageMath выдаёт такую группу MOLS 14-го порÑдка, ÑоÑтоÑщую из четырёх взаимно ортогональных ЛК Уже чуть-чуть поÑкÑпериментировала. Ðо пока раÑÑкажу о другой группе. Ðто Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° ДЛК 14-го порÑдка, поÑÑ‚Ñ€Ð¾ÐµÐ½Ð½Ð°Ñ Ð¼Ð½Ð¾Ð¹ очень давно по извеÑтному алгоритму. Смотрите далее. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата Далее рекомендую очень интереÑную Ñтатью о поÑтроении ортогональных пар ЛК и ДЛК 14-го порÑдка Как видите, Ð²Ð¾Ð¿Ñ€Ð¾Ñ Ñ€Ð°ÑÑˆÐ¸Ñ€ÐµÐ½Ð¸Ñ Ñтой минимальной группы MODLS 14-го порÑдка интереÑовал Ð¼ÐµÐ½Ñ Ð´Ð°Ð²Ð½Ð¾. Группа MODLS 14-го порÑдка, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· трёх ортогональных ДЛК, до Ñих пор не найдена, наÑколько мне извеÑтно. Во вÑÑком Ñлучае, в Ñтатье OEIS о такой группе не ÑообщаетÑÑ. С Ñтой ортогональной парой Ñ ÑÐµÐ¹Ñ‡Ð°Ñ Ð´Ð¾Ñтаточно много поработала. Ðлгоритм тот же Ñамый, который применÑлÑÑ Ð¿Ñ€Ð¸ поиÑке группы MODLS 12-го порÑдка: переÑтановка Ñтрок и Ñтолбцов. Ðтот алгоритм хорошо извеÑтен, однако Ñ Ð¿Ñ€Ð¸Ð´ÑƒÐ¼Ð°Ð»Ð° неÑколько интереÑных программных реализаций, которые позволÑÑŽÑ‚ очень быÑтро переÑтавлÑÑ‚ÑŒ Ñтроки и Ñтолбцы. О результатах раÑÑкажу далее. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðашла набор, ÑоÑтоÑщий из 304 ЛК и ДЛК. Ð’ результате проверки программой GetOrthogonal получена ÑÐ»ÐµÐ´ÑƒÑŽÑ‰Ð°Ñ Ñ‚Ð°Ð±Ð»Ð¸Ñ†Ð° ортогональных пар 1: [53,111,152], 2: [185,211,281], 6: [46,227,229], 7: [131,189,290], 11: [66,144,216], 28: [71,72,228], 29: [107,146,186], 31: [67,112,193], 32: [85,114,210], 33: [79,224,299], 46: [6,227,229], 47: [117,130,194], 53: [1,111,152], 64: [147,192,279], 65: [104,205,241], 66: [11,144,216], 67: [31,112,193], 71: [28,72,228], 72: [28,71,228], 73: [129,280,301], 79: [33,224,299], 80: [135,236,289], 85: [32,114,210], 104: [65,205,241], 107: [29,146,186], 110: [121,287,291], 111: [1,53,152], 112: [31,67,193], 114: [32,85,210], 117: [47,130,194], 121: [110,287,291], 129: [73,280,301], 130: [47,117,194], 131: [7,189,290], 135: [80,236,289], 142: [195], 144: [11,66,216], 146: [29,107,186], 147: [64,192,279], 151: [199], 152: [1,53,111], 185: [2,211,281], 186: [29,107,146], 189: [7,131,290], 192: [64,147,279], 193: [31,67,112], 194: [47,117,130], 195: [142], 196: [226], 197: [286], 198: [285], 199: [151], 200: [225], 205: [65,104,241], 206: [300], 207: [298], 210: [32,85,114], 211: [2,185,281], 216: [11,66,144], 224: [33,79,299], 225: [200], 226: [196], 227: [6,46,229], 228: [28,71,72], 229: [6,46,227], 236: [80,135,289], 241: [65,104,205], 279: [64,147,192], 280: [73,129,301], 281: [2,185,211], 285: [198], 286: [197], 287: [110,121,291], 289: [80,135,236], 290: [7,131,189], 291: [110,121,287], 298: [207], 299: [33,79,224], 300: [206], 301: [73,129,280] ПоиÑкала в программе SageMath макÑимальные клики в Ñтом графе. И они найдены! Программа SageMath выдала 16 клик размера 4. Отлично! [[11, 66, 144, 216], [28, 71, 72, 228], [29, 107, 146, 186], [31, 67, 112, 193], [32, 85, 114, 210], [33, 79, 224, 299], [46, 227, 229, 6], [47, 117, 130, 194], [53, 111, 152, 1], [64, 147, 192, 279], [65, 104, 205, 241], [73, 129, 280, 301], [80, 135, 236, 289], [110, 121, 287, 291], [131, 189, 290, 7], [185, 211, 281, 2]] Таким образом, иÑÑ…Ð¾Ð´Ð½Ð°Ñ Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ð°Ñ Ð¿Ð°Ñ€Ð° раÑширена до групп MOLS, ÑоÑтоÑщих из четырёх ЛК (макÑимально извеÑтное количеÑтво ЛК в группе MOLS 14-го порÑдка на данный момент). ИнтереÑно: в каждой найденной группе еÑÑ‚ÑŒ один ДЛК. Я отметила в каждой группе ДЛК буквой Д [[11, 66, 144, 216Д], [28, 71Д, 72, 228], [29, 107Д, 146, 186], [31, 67, 112Д, 193], [32Д, 85, 114, 210], [33Д, 79, 224, 299], [46, 227Д, 229, 6], [47Д, 117, 130, 194], [53, 111, 152Д, 1], [64, 147, 192Д, 279], [65, 104, 205Д, 241], [73Д, 129, 280, 301], [80, 135, 236, 289Д], [110, 121Д, 287, 291], [131Д, 189, 290, 7], [185, 211Д, 281, 2]] Далее покажу одну из Ñтих групп MOLS 14-го порÑдка. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Показываю Ñту группу MOLS 14-го порÑдка [53, 111, 152Д, 1] квадрат 1 - ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 1 2 12 11 9 7 8 3 13 0 5 6 4 10 5 9 7 0 13 10 4 8 12 6 2 3 11 1 6 0 4 8 2 12 10 5 1 13 11 7 9 3 11 7 1 4 6 13 5 0 9 3 12 8 10 2 8 6 3 13 5 1 12 10 4 11 0 2 7 9 3 4 5 10 11 0 7 9 2 12 8 13 1 6 4 5 11 6 7 2 3 12 10 8 1 9 13 0 2 11 10 9 0 8 1 13 6 7 4 5 3 12 10 3 8 7 1 9 13 4 5 2 6 12 0 11 9 10 13 12 8 6 0 11 3 1 7 4 2 5 12 13 6 2 10 3 11 1 7 5 9 0 8 4 13 8 0 5 12 4 9 2 11 10 3 1 6 7 7 12 9 1 3 11 2 6 0 4 13 10 5 8 квадрат 53 - ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 3 0 4 2 8 1 5 10 6 13 12 7 9 11 11 7 13 9 2 6 12 3 0 10 1 5 4 8 9 2 5 6 11 8 0 13 4 12 3 10 1 7 10 4 11 13 3 0 7 1 12 8 6 2 5 9 7 11 12 10 9 13 3 4 2 1 5 8 0 6 13 8 0 1 12 3 2 5 10 7 11 9 6 4 1 10 6 8 5 7 4 9 13 0 2 3 11 12 12 13 3 0 6 4 9 8 5 11 7 1 2 10 8 6 9 12 10 2 1 11 3 4 0 13 7 5 4 9 7 11 13 12 10 0 1 5 8 6 3 2 2 3 1 5 7 11 8 12 9 6 13 4 10 0 5 12 8 4 1 10 11 6 7 2 9 0 13 3 6 5 10 7 0 9 13 2 11 3 4 12 8 1 квадрат 111 - ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 5 9 6 13 1 0 7 8 12 11 3 2 10 4 2 6 3 7 10 11 0 13 5 4 8 9 1 12 1 5 12 4 0 7 8 9 3 6 2 13 11 10 6 11 8 1 12 3 4 10 7 2 9 0 13 5 12 7 13 0 6 10 11 2 9 5 1 3 4 8 7 13 10 12 9 6 1 4 11 3 5 8 2 0 3 12 7 11 8 13 5 0 6 1 4 10 9 2 4 8 0 2 3 9 13 5 10 12 11 7 6 1 9 0 11 5 7 12 2 6 1 10 13 4 8 3 13 3 1 10 2 8 9 12 4 0 6 5 7 11 8 4 9 6 5 1 10 11 2 13 0 12 3 7 11 10 4 8 13 2 3 1 0 7 12 6 5 9 10 2 5 9 11 4 12 3 13 8 7 1 0 6 квадрат 152 - ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 7 13 5 6 0 3 12 1 9 10 11 4 2 8 12 3 8 11 5 1 13 2 6 0 7 10 9 4 8 9 3 5 6 13 2 0 10 7 1 12 4 11 13 6 0 12 11 4 9 8 2 5 3 1 7 10 10 5 4 8 1 6 0 3 7 2 13 9 11 12 9 11 7 0 8 12 10 6 5 1 4 3 13 2 5 2 10 7 9 0 8 4 11 3 12 13 1 6 3 4 9 10 2 11 5 12 1 13 8 6 0 7 6 7 13 1 3 8 11 10 4 12 9 2 5 0 1 12 6 9 7 10 4 5 13 11 2 0 8 3 11 10 12 4 13 2 3 9 0 8 5 7 6 1 2 0 1 13 10 9 7 11 12 4 6 8 3 5 4 8 11 2 12 7 1 13 3 6 0 5 10 9 Проверка программой GetOrthogonal Order? 14 Enter the name of the squares file: inp14 Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file inp14-orthCounts.txt ..output file inp14-orthNos.txt squares 4 total orthogonal pairs 6 Maximum pairs for square 1: 3 There are 3 other squares with this maximum number of pairs. ..output file inp14-1orths.txt Pairs for square 1: 3 Ð’ÑÑ‘ верно. Таблица ортогональных пар 1: [2,3,4], 2: [1,3,4], 3: [1,2,4], 4: [1,2,3] Однако группа MODLS 14-го порÑдка, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· трёх взаимно ортогональных ДЛК, пока не найдена. Группа MOLS данного порÑдка, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· пÑти взаимно ортогональных ЛК, тоже пока не найдена. СущеÑтвует ли Ñ‚Ð°ÐºÐ°Ñ Ð² природе? Математикам она пока неизвеÑтна. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Итак, Ñ Ð½Ð°ÑˆÐ»Ð° 16 альтернативных групп MOLS 14-го порÑдка из четырёх взаимно ортогональных ЛК, ÐºÐ°Ð¶Ð´Ð°Ñ Ð¸Ð· которых Ñодержит один ДЛК. Продолжаю ÑкÑперимент. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Работаю Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð¾Ð¹ MOLS 14-го порÑдка из четырёх ЛК, показанной в Ñтартовом поÑте. Ðормализовала ЛК Ñтой группы, мне Ñ Ð½Ð¾Ñ€Ð¼Ð°Ð»Ð¸Ð·Ð¾Ð²Ð°Ð½Ð½Ñ‹Ð¼Ð¸ ЛК удобнее работать 0 1 2 3 4 5 6 7 8 9 10 11 12 13 11 7 5 1 0 3 9 6 13 2 12 8 4 10 12 4 13 9 5 7 0 8 11 6 1 10 2 3 7 10 3 6 12 9 13 0 2 4 11 5 8 1 6 13 8 0 11 10 12 5 7 1 3 4 9 2 10 11 6 2 7 4 8 1 9 13 5 0 3 12 2 8 4 11 1 13 3 10 5 12 6 9 7 0 13 9 10 5 6 8 11 2 12 3 7 1 0 4 4 6 12 8 9 11 2 3 1 10 0 13 5 7 1 3 11 10 2 12 4 13 0 5 8 7 6 9 3 5 0 4 8 1 10 12 6 7 9 2 13 11 8 0 9 7 3 2 5 4 10 11 13 12 1 6 9 2 7 12 13 0 1 11 3 8 4 6 10 5 5 12 1 13 10 6 7 9 4 0 2 3 11 8 0 1 2 3 4 5 6 7 8 9 10 11 12 13 9 3 8 5 7 1 11 12 4 10 13 0 6 2 6 13 7 10 11 4 8 5 2 1 0 12 3 9 10 9 12 4 0 6 1 13 11 5 8 3 2 7 8 0 13 2 1 3 9 4 12 6 11 10 7 5 13 10 3 12 5 8 7 11 1 2 9 6 0 4 4 12 0 7 2 11 10 1 6 8 5 13 9 3 3 4 11 0 13 9 5 6 10 7 2 8 1 12 11 7 1 6 3 12 13 2 9 0 4 5 10 8 12 6 4 8 9 7 2 10 5 13 3 1 11 0 5 2 9 1 10 13 4 3 0 11 12 7 8 6 1 11 5 13 8 0 12 9 7 3 6 2 4 10 2 8 6 11 12 10 3 0 13 4 7 9 5 1 7 5 10 9 6 2 0 8 3 12 1 4 13 11 0 1 2 3 4 5 6 7 8 9 10 11 12 13 5 12 9 8 2 11 7 1 10 0 6 13 3 4 10 7 4 6 0 8 3 11 9 13 12 5 1 2 2 13 10 11 5 12 0 8 3 6 1 4 7 9 12 8 1 13 3 7 4 6 0 2 5 9 11 10 11 4 0 9 1 2 10 13 5 12 8 7 6 3 13 3 11 12 6 9 8 2 1 7 4 0 10 5 6 2 12 7 9 0 13 5 11 1 3 10 4 8 1 5 8 4 10 6 12 0 7 3 9 2 13 11 4 9 7 0 11 13 5 3 12 10 2 6 8 1 7 11 6 10 12 3 1 9 2 4 13 8 5 0 9 10 3 5 13 4 2 12 6 8 11 1 0 7 8 6 13 2 7 1 11 10 4 5 0 3 9 12 3 0 5 1 8 10 9 4 13 11 7 12 2 6 0 1 2 3 4 5 6 7 8 9 10 11 12 13 8 4 10 6 12 9 13 3 1 11 5 2 7 0 3 11 9 2 8 0 5 4 12 10 7 13 6 1 13 12 7 5 6 11 4 10 9 0 2 1 3 8 9 3 0 1 13 8 7 11 2 5 4 6 10 12 1 5 12 4 10 3 11 0 7 6 13 9 8 2 7 10 13 0 9 2 12 6 4 1 8 3 5 11 10 8 5 12 7 6 3 1 0 13 11 4 2 9 12 2 11 13 0 1 8 5 10 4 3 7 9 6 11 0 6 7 3 4 10 8 13 2 9 12 1 5 2 7 4 8 1 12 9 13 11 3 6 5 0 10 5 6 1 9 11 10 0 2 3 7 12 8 13 4 4 13 8 10 5 7 2 9 6 12 1 0 11 3 6 9 3 11 2 13 1 12 5 8 0 10 4 7 ИнтереÑны ÑвойÑтва Ñтих ЛК Order? 14
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt
Counts
------
4 Latin
4 nfr
3 orthogonal pair
4 self-orthogonalÐ’Ñе ЛК ÑвлÑÑŽÑ‚ÑÑ SOLK. Ðто полезное ÑвойÑтво. Затем поиÑкала ДЛК переÑтановками Ñтрок и Ñтолбцов в каждом ЛК данной группы. Ðтим ÑпоÑобом удалоÑÑŒ получить неÑколько групп MOLS, Ñодержащие один ДЛК и три ЛК. Именно такую группу Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»Ð° на первом Ñтапе, Ñ€Ð°Ð±Ð¾Ñ‚Ð°Ñ Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð¾Ð¹ MOLS 12-го порÑдка. Показываю таблицу ортогональных пар от полученного набора ЛК и ДЛК 1: [13,27,39], 2: [40,48,58], 3: [11,51,53], 4: [34,42,61], 5: [16,36,49], 6: [18,19,52], 7: [25,37,41], 8: [17,28,44], 9: [23,29,47], 10: [21,50,63], 11: [3,51,53], 12: [30,33,45], 13: [1,27,39], 14: [38,43,56], 15: [24,46,55], 16: [5,36,49], 17: [8,28,44], 18: [6,19,52], 19: [6,18,52], 20: [32,57,64], 21: [10,50,63], 22: [35,54,60], 23: [9,29,47], 24: [15,46,55], 25: [7,37,41], 26: [31,59,62], 27: [1,13,39], 28: [8,17,44], 29: [9,23,47], 30: [12,33,45], 31: [26,59,62], 32: [20,57,64], 33: [12,30,45], 34: [4,42,61], 35: [22,54,60], 36: [5,16,49], 37: [7,25,41], 38: [14,43,56], 39: [1,13,27], 40: [2,48,58], 41: [7,25,37], 42: [4,34,61], 43: [14,38,56], 44: [8,17,28], 45: [12,30,33], 46: [15,24,55], 47: [9,23,29], 48: [2,40,58], 49: [5,16,36], 50: [10,21,63], 51: [3,11,53], 52: [6,18,19], 53: [3,11,51], 54: [22,35,60], 55: [15,24,46], 56: [14,38,43], 57: [20,32,64], 58: [2,40,48], 59: [26,31,62], 60: [22,35,54], 61: [4,34,42], 62: [26,31,59], 63: [10,21,50], 64: [20,32,57] Каждый ЛК в наборе имеет три ОЛК. Программой SageMath нашла клики размера 4. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Покажу одну из полученных групп MOLS 14-го порÑдка, Ñодержащих один ДЛК и три ЛК ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 10 13 8 11 12 0 1 2 6 4 7 5 9 3 2 3 11 4 9 7 8 12 0 13 5 10 6 1 1 9 0 7 3 8 12 13 10 11 6 2 4 5 11 8 9 12 5 1 7 10 3 2 4 6 13 0 12 7 1 8 10 2 13 11 4 0 9 3 5 6 3 12 5 0 2 6 10 8 13 7 1 9 11 4 9 2 7 6 8 11 0 4 5 10 13 1 3 12 5 11 13 9 0 3 2 6 12 1 8 4 7 10 4 0 10 2 11 9 5 3 1 6 12 13 8 7 13 4 6 1 7 10 11 0 9 5 3 12 2 8 6 10 12 13 1 4 9 5 7 3 11 8 0 2 8 5 4 10 6 13 3 9 2 12 0 7 1 11 7 6 3 5 13 12 4 1 11 8 2 0 10 9 ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 1 5 12 10 0 7 9 4 11 3 2 8 13 6 9 4 6 8 10 12 0 13 5 11 1 7 3 2 8 3 1 11 5 13 4 6 9 7 0 10 2 12 13 6 8 7 9 0 1 5 10 12 11 2 4 3 10 9 11 5 2 3 8 12 7 13 4 0 6 1 7 11 4 9 6 10 3 2 12 8 13 5 1 0 2 0 5 13 11 4 10 1 3 6 7 12 9 8 11 8 10 6 12 1 7 9 2 5 3 13 0 4 12 2 0 1 3 11 13 8 6 4 5 9 7 10 3 10 7 4 13 8 2 11 1 0 12 6 5 9 5 13 3 0 7 6 12 10 4 2 9 1 8 11 4 7 9 12 8 2 11 0 13 1 6 3 10 5 6 12 13 2 1 9 5 3 0 10 8 4 11 7 ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 2 8 1 4 7 9 11 6 10 0 13 3 5 12 3 13 10 1 8 4 9 11 7 12 6 0 2 5 12 11 5 2 0 3 10 4 1 6 8 13 9 7 7 2 4 8 12 13 0 9 11 10 5 1 3 6 9 6 7 10 3 8 5 13 12 1 2 4 0 11 5 3 9 13 1 12 7 0 2 11 4 6 8 10 10 5 12 9 6 1 2 3 4 13 11 8 7 0 13 9 0 7 11 10 4 5 6 3 12 2 1 8 6 4 11 12 5 0 8 2 9 7 1 10 13 3 1 7 3 0 10 6 12 8 13 2 9 5 11 4 4 12 13 6 2 11 3 1 5 8 0 7 10 9 11 10 8 5 13 7 1 12 0 4 3 9 6 2 8 0 6 11 9 2 13 10 3 5 7 12 4 1 ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 11 0 5 6 13 2 8 3 7 1 12 9 4 10 12 5 4 10 1 13 7 0 3 2 8 6 9 11 4 2 9 0 12 11 1 8 13 10 5 7 3 6 1 3 12 11 7 6 2 4 9 8 13 0 10 5 5 11 10 2 8 4 3 9 0 6 7 1 13 12 8 6 0 4 11 3 12 10 1 5 2 13 7 9 6 10 1 8 9 12 13 5 11 0 4 3 2 7 3 13 11 5 10 0 9 1 4 7 6 12 8 2 2 7 3 13 0 8 10 6 12 11 9 5 1 4 7 8 13 9 3 1 5 12 10 4 11 2 6 0 10 9 8 12 5 7 0 2 6 13 3 4 11 1 13 12 6 7 2 9 4 11 5 3 1 10 0 8 9 4 7 1 6 10 11 13 2 12 0 8 5 3 Теперь нашла раÑширенный набор ДЛК и ЛК, 135336 штук вмеÑте - тех и других. ЗапуÑтила обработку набора программой GetOrthogonal Order? 14
Enter the name of the squares file: inp14
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file inp14-orthCounts.txt
..output file inp14-orthNos.txt
.. increasing LS store to 100,000
.. increasing LS store to 200,000
squares 135336Программа пыхтит :) Жду результат. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Программа завершилаÑÑŒ. Результат Order? 14
Enter the name of the squares file: inp14
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file inp14-orthCounts.txt
..output file inp14-orthNos.txt
.. increasing LS store to 100,000
.. increasing LS store to 200,000
squares 135336 total orthogonal pairs 96
Maximum pairs for square 1: 3
There are 63 other squares with this maximum number of pairs.
..output file inp14-1orths.txt
Pairs for square 1: 3
elapsed time 2:57:26К Ñожалению, ничего нового не добавилоÑÑŒ. PS. Получила ещё один раÑширенный набор ДЛК и ЛК, который Ñодержит более 500 Ñ‚Ñ‹ÑÑч квадратов. Ðтот набор Ñ Ð½Ðµ Ñмогу обработать программой GetOrthogonal. И даже еÑли его обработать Ñтой программой, проверить потом на макÑимальную клику врÑд ли удаÑÑ‚ÑÑ. Мы Ñ Ð¿Ð¾Ð¼Ð¾Ñ‰Ð½Ð¸ÐºÐ¾Ð¼ уже ÑтолкнулиÑÑŒ Ñ Ñ‚Ð°ÐºÐ¾Ð¹ проблемой Ð´Ð»Ñ Ð½Ð°Ð±Ð¾Ñ€Ð° ДЛК и ЛК 12-го порÑдка. Попробовать, конечно, можно. Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 14 будет меньше ортогональных пар, нежели Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 12. Вдруг и получитÑÑ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПредÑтавлю Ñвою давнишнюю Ñтатью (2009 год) "ПОСТРОЕÐИЕ ГРУПП MOLS ЧЕТЫРÐÐДЦÐТОГО ПОРЯДКÐ" http://www.natalimak1.narod.ru/mols14.htm Ð¡Ñ‚Ð°Ñ‚ÑŒÑ Ð½Ð°Ð¿Ð¸Ñана в то времÑ, когда Ñ Ñ‚Ð¾Ð»ÑŒÐºÐ¾ начинала заниматьÑÑ Ð›Ðš/ДЛК/ОДЛК. Ð’ то Ð²Ñ€ÐµÐ¼Ñ Ð±Ñ‹Ð»Ð¸ извеÑтны только MOLS 14-го порÑдка из трёх взаимно ортогональных ЛК. Ðекоторые из Ñтих групп MOLS Ñ Ñ€Ð°ÑÑмотрела в Ñвоей Ñтатье. Ðу вот, прогреÑÑ Ð·Ð° прошедшие 12 лет еÑÑ‚ÑŒ у математиков: найдена группа MOLS 14-го порÑдка, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· четырёх взаимно ортогональных ЛК. Пару групп из Ñтой Ñтатьи Ñ ÑƒÐ¶Ðµ проверила раньше на предмет группы MODLS 14-го порÑдка, ÑоÑтоÑщей из трёх взаимно ортогональных ДЛК. Ðе найдена Ñ‚Ð°ÐºÐ°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð°. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ñмотрю другие группы в Ñтатье. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðапример, Ð¿ÐµÑ€Ð²Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° MOLS 14-го порÑдка из указанной Ñтатьи 1 2 3 4 5 6 7 8 9 10 11 12 13 14 2 1 6 10 4 13 8 12 14 5 7 9 11 3 3 4 1 7 11 5 14 9 13 2 6 8 10 12 4 13 5 1 8 12 6 2 10 14 3 7 9 11 5 12 14 6 1 9 13 7 3 11 2 4 8 10 6 11 13 2 7 1 10 14 8 4 12 3 5 9 7 10 12 14 3 8 1 11 2 9 5 13 4 6 8 7 11 13 2 4 9 1 12 3 10 6 14 5 9 6 8 12 14 3 5 10 1 13 4 11 7 2 10 3 7 9 13 2 4 6 11 1 14 5 12 8 11 9 4 8 10 14 3 5 7 12 1 2 6 13 12 14 10 5 9 11 2 4 6 8 13 1 3 7 13 8 2 11 6 10 12 3 5 7 9 14 1 4 14 5 9 3 12 7 11 13 4 6 8 10 2 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 4 10 7 1 3 8 12 2 6 11 14 5 9 13 5 14 11 8 1 4 9 13 3 7 12 2 6 10 6 11 2 12 9 1 5 10 14 4 8 13 3 7 7 8 12 3 13 10 1 6 11 2 5 9 14 4 8 5 9 13 4 14 11 1 7 12 3 6 10 2 9 3 6 10 14 5 2 12 1 8 13 4 7 11 10 12 4 7 11 2 6 3 13 1 9 14 5 8 11 9 13 5 8 12 3 7 4 14 1 10 2 6 12 7 10 14 6 9 13 4 8 5 2 1 11 3 13 4 8 11 2 7 10 14 5 9 6 3 1 12 14 13 5 9 12 3 8 11 2 6 10 7 4 1 2 1 14 6 10 13 4 9 12 3 7 11 8 5 3 6 1 2 7 11 14 5 10 13 4 8 12 9 1 2 3 4 5 6 7 8 9 10 11 12 13 14 14 3 11 13 8 10 6 5 2 12 9 4 7 1 2 1 4 12 14 9 11 7 6 3 13 10 5 8 3 9 1 5 13 2 10 12 8 7 4 14 11 6 4 7 10 1 6 14 3 11 13 9 8 5 2 12 5 13 8 11 1 7 2 4 12 14 10 9 6 3 6 4 14 9 12 1 8 3 5 13 2 11 10 7 7 8 5 2 10 13 1 9 4 6 14 3 12 11 8 12 9 6 3 11 14 1 10 5 7 2 4 13 9 14 13 10 7 4 12 2 1 11 6 8 3 5 10 6 2 14 11 8 5 13 3 1 12 7 9 4 11 5 7 3 2 12 9 6 14 4 1 13 8 10 12 11 6 8 4 3 13 10 7 2 5 1 14 9 13 10 12 7 9 5 4 14 11 8 3 6 1 2 ЛК приведены в нетрадиционной форме. Чтобы привеÑти их к традиционной форме, надо вÑе Ñлементы уменьшить на 1. Превратила ЛК в традиционную форму 0 1 2 3 4 5 6 7 8 9 10 11 12 13 1 0 5 9 3 12 7 11 13 4 6 8 10 2 2 3 0 6 10 4 13 8 12 1 5 7 9 11 3 12 4 0 7 11 5 1 9 13 2 6 8 10 4 11 13 5 0 8 12 6 2 10 1 3 7 9 5 10 12 1 6 0 9 13 7 3 11 2 4 8 6 9 11 13 2 7 0 10 1 8 4 12 3 5 7 6 10 12 1 3 8 0 11 2 9 5 13 4 8 5 7 11 13 2 4 9 0 12 3 10 6 1 9 2 6 8 12 1 3 5 10 0 13 4 11 7 10 8 3 7 9 13 2 4 6 11 0 1 5 12 11 13 9 4 8 10 1 3 5 7 12 0 2 6 12 7 1 10 5 9 11 2 4 6 8 13 0 3 13 4 8 2 11 6 10 12 3 5 7 9 1 0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 3 9 6 0 2 7 11 1 5 10 13 4 8 12 4 13 10 7 0 3 8 12 2 6 11 1 5 9 5 10 1 11 8 0 4 9 13 3 7 12 2 6 6 7 11 2 12 9 0 5 10 1 4 8 13 3 7 4 8 12 3 13 10 0 6 11 2 5 9 1 8 2 5 9 13 4 1 11 0 7 12 3 6 10 9 11 3 6 10 1 5 2 12 0 8 13 4 7 10 8 12 4 7 11 2 6 3 13 0 9 1 5 11 6 9 13 5 8 12 3 7 4 1 0 10 2 12 3 7 10 1 6 9 13 4 8 5 2 0 11 13 12 4 8 11 2 7 10 1 5 9 6 3 0 1 0 13 5 9 12 3 8 11 2 6 10 7 4 2 5 0 1 6 10 13 4 9 12 3 7 11 8 0 1 2 3 4 5 6 7 8 9 10 11 12 13 13 2 10 12 7 9 5 4 1 11 8 3 6 0 1 0 3 11 13 8 10 6 5 2 12 9 4 7 2 8 0 4 12 1 9 11 7 6 3 13 10 5 3 6 9 0 5 13 2 10 12 8 7 4 1 11 4 12 7 10 0 6 1 3 11 13 9 8 5 2 5 3 13 8 11 0 7 2 4 12 1 10 9 6 6 7 4 1 9 12 0 8 3 5 13 2 11 10 7 11 8 5 2 10 13 0 9 4 6 1 3 12 8 13 12 9 6 3 11 1 0 10 5 7 2 4 9 5 1 13 10 7 4 12 2 0 11 6 8 3 10 4 6 2 1 11 8 5 13 3 0 12 7 9 11 10 5 7 3 2 12 9 6 1 4 0 13 8 12 9 11 6 8 4 3 13 10 7 2 5 0 1 ЛК нормализованные. Можно начинать Ñ Ð½Ð¸Ð¼Ð¸ работать. Группу MODLS Ñ ÑƒÐ¶Ðµ иÑкала от данной группы MOLS, а группу MOLS побольше ещё не иÑкала. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Проверила показанную выше группу MOLS из трёх взаимно ортогональных ЛК на раÑширение. Ðашла набор из 61921 нормализованных ЛК. Проверила набор на ортогональные пары. Таблица ортогональных пар 1: [12682,61921], 444: [61895], 12682: [1,61921], 26432: [59631], 59631: [26432], 61895: [444], 61921: [1,12682] Очевидно, что клика размера 3 тут вÑего одна [1, 12682, 61921]. Ðто иÑÑ…Ð¾Ð´Ð½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° MOLS. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ой, Ñоблазн раÑÑˆÐ¸Ñ€ÐµÐ½Ð¸Ñ Ð½Ð°Ð±Ð¾Ñ€Ð° ЛК (от переÑтановок Ñтрок и Ñтолбцов) очень велик :) Вот ÑоÑтавила другой набор, проверила его на ортогональные пары, Ñ‚Ð°ÐºÐ°Ñ Ñ‚Ð°Ð±Ð»Ð¸Ñ†Ð° ортогональных пар получилаÑÑŒ 1: [15120,55211], 15119: [53016,53017], 15120: [1,55211], 15178: [51834], 40549: [66869], 51834: [15178], 53016: [15119,53017], 53017: [15119,53016], 55211: [1,15120], 66869: [40549] КажетÑÑ, тут две клики размера 3 [1, 15120, 55211] [15119, 53016, 53017] Ðто уже интереÑно: получилаÑÑŒ ещё одна группа MOLS из трёх взаимно ортогональных ЛК. Может быть, ЛК Ñтой группы изоморфны ЛК иÑходной группы. Я ÑÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾ÐºÐ°Ð¶Ñƒ Ñти группы MOLS. Ð’ моей давнишней Ñтатье напиÑано, что по одной квази-разноÑтной матрице можно ÑоÑтавить много групп MOLS. Ðу вот, отÑюда, видимо, и Ð¿Ð¾Ð»ÑƒÑ‡ÐµÐ½Ð½Ð°Ñ Ð½Ð¾Ð²Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° MOLS у Ð¼ÐµÐ½Ñ Ð² ÑкÑперименте. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Показываю две группы MOLS. ÐŸÐµÑ€Ð²Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° квадрат 1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 1 0 5 9 3 12 7 11 13 4 6 8 10 2 2 3 0 6 10 4 13 8 12 1 5 7 9 11 3 12 4 0 7 11 5 1 9 13 2 6 8 10 4 11 13 5 0 8 12 6 2 10 1 3 7 9 5 10 12 1 6 0 9 13 7 3 11 2 4 8 6 9 11 13 2 7 0 10 1 8 4 12 3 5 7 6 10 12 1 3 8 0 11 2 9 5 13 4 8 5 7 11 13 2 4 9 0 12 3 10 6 1 9 2 6 8 12 1 3 5 10 0 13 4 11 7 10 8 3 7 9 13 2 4 6 11 0 1 5 12 11 13 9 4 8 10 1 3 5 7 12 0 2 6 12 7 1 10 5 9 11 2 4 6 8 13 0 3 13 4 8 2 11 6 10 12 3 5 7 9 1 0 квадрат 15120 0 1 2 3 4 5 6 7 8 9 10 11 12 13 3 9 6 0 2 7 11 1 5 10 13 4 8 12 4 13 10 7 0 3 8 12 2 6 11 1 5 9 5 10 1 11 8 0 4 9 13 3 7 12 2 6 6 7 11 2 12 9 0 5 10 1 4 8 13 3 7 4 8 12 3 13 10 0 6 11 2 5 9 1 8 2 5 9 13 4 1 11 0 7 12 3 6 10 9 11 3 6 10 1 5 2 12 0 8 13 4 7 10 8 12 4 7 11 2 6 3 13 0 9 1 5 11 6 9 13 5 8 12 3 7 4 1 0 10 2 12 3 7 10 1 6 9 13 4 8 5 2 0 11 13 12 4 8 11 2 7 10 1 5 9 6 3 0 1 0 13 5 9 12 3 8 11 2 6 10 7 4 2 5 0 1 6 10 13 4 9 12 3 7 11 8 квадрат 55211 0 1 2 3 4 5 6 7 8 9 10 11 12 13 13 2 10 12 7 9 5 4 1 11 8 3 6 0 1 0 3 11 13 8 10 6 5 2 12 9 4 7 2 8 0 4 12 1 9 11 7 6 3 13 10 5 3 6 9 0 5 13 2 10 12 8 7 4 1 11 4 12 7 10 0 6 1 3 11 13 9 8 5 2 5 3 13 8 11 0 7 2 4 12 1 10 9 6 6 7 4 1 9 12 0 8 3 5 13 2 11 10 7 11 8 5 2 10 13 0 9 4 6 1 3 12 8 13 12 9 6 3 11 1 0 10 5 7 2 4 9 5 1 13 10 7 4 12 2 0 11 6 8 3 10 4 6 2 1 11 8 5 13 3 0 12 7 9 11 10 5 7 3 2 12 9 6 1 4 0 13 8 12 9 11 6 8 4 3 13 10 7 2 5 0 1 Очевидно, что Ñто иÑÑ…Ð¾Ð´Ð½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð°. Ð’Ñ‚Ð¾Ñ€Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° квадрат 15119 0 1 2 3 4 5 6 7 8 9 10 11 12 13 3 2 8 7 12 1 5 9 0 6 4 13 10 11 1 7 6 11 0 4 8 12 5 3 13 9 2 10 6 5 10 12 3 7 11 4 2 13 8 1 0 9 4 9 11 2 6 10 3 1 13 7 0 12 5 8 8 10 1 5 9 2 0 13 6 12 11 4 3 7 9 0 4 8 1 12 13 5 11 10 3 2 7 6 12 3 7 0 11 13 4 10 9 2 1 6 8 5 2 6 12 10 13 3 9 8 1 0 5 7 11 4 5 11 9 13 2 8 7 0 12 4 6 10 1 3 10 8 13 1 7 6 12 11 3 5 9 0 4 2 7 13 0 6 5 11 10 2 4 8 12 3 9 1 13 12 5 4 10 9 1 3 7 11 2 8 6 0 11 4 3 9 8 0 2 6 10 1 7 5 13 12 квадрат 53016 0 1 2 3 4 5 6 7 8 9 10 11 12 13 9 6 0 5 11 8 7 4 3 2 1 10 13 12 5 12 4 10 7 6 3 2 1 0 9 13 8 11 11 3 9 6 5 2 1 0 12 8 13 7 4 10 2 8 5 4 1 0 12 11 7 13 6 3 10 9 7 4 3 0 12 11 10 6 13 5 2 9 1 8 3 2 12 11 10 9 5 13 4 1 8 0 6 7 1 11 10 9 8 4 13 3 0 7 12 5 2 6 10 9 8 7 3 13 2 12 6 11 4 1 0 5 8 7 6 2 13 1 11 5 10 3 0 12 9 4 6 5 1 13 0 10 4 9 2 12 11 8 7 3 4 0 13 12 9 3 8 1 11 10 7 6 5 2 12 13 11 8 2 7 0 10 9 6 5 4 3 1 13 10 7 1 6 12 9 8 5 4 3 2 11 0 квадрат 53017 0 1 2 3 4 5 6 7 8 9 10 11 12 13 10 13 3 12 9 7 4 0 11 8 5 2 6 1 13 2 11 8 6 3 12 10 7 4 1 5 9 0 1 10 7 5 2 11 9 6 3 0 4 8 13 12 9 6 4 1 10 8 5 2 12 3 7 13 0 11 5 3 0 9 7 4 1 11 2 6 13 12 8 10 2 12 8 6 3 0 10 1 5 13 11 7 4 9 11 7 5 2 12 9 0 4 13 10 6 3 1 8 6 4 1 11 8 12 3 13 9 5 2 0 10 7 3 0 10 7 11 2 13 8 4 1 12 9 5 6 12 9 6 10 1 13 7 3 0 11 8 4 2 5 8 5 9 0 13 6 2 12 10 7 3 1 11 4 4 8 12 13 5 1 11 9 6 2 0 10 7 3 7 11 13 4 0 10 8 5 1 12 9 6 3 2 Да, ЛК Ñтой группы изоморфны ЛК иÑходной группы. ИнтереÑно, а что там от Ð²Ð°Ñ€ÑŒÐ¸Ñ€Ð¾Ð²Ð°Ð½Ð¸Ñ ÐºÐ²Ð°Ð·Ð¸-разноÑтной матрицы получаетÑÑ. Может быть, тоже изоморфы? Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð½Ðµ помню Ñтот момент. Так что, пока ничего нового от Ñтой группы MOLS не получено. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ЕÑÑ‚ÑŒ у Ð¼ÐµÐ½Ñ Ð¸ ещё один раÑширенный набор Ð´Ð»Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€Ñемой группы MOLS, ÑоÑтоÑщий из 133785 нормализованных ЛК. Ðо проверÑÑ‚ÑŒ его не буду программой GetOrthogonal, потому что Ñто Ñлишком долго. Ррезультата хорошего не ожидаетÑÑ. Ðу, даже еÑли и раÑширитÑÑ Ð³Ñ€ÑƒÐ¿Ð¿Ð° до четырёх взаимно ортогональных ЛК, так ведь такие группы MOLS уже извеÑтны. Ð’Ñ€Ñд ли раÑширитÑÑ Ð´Ð¾ пÑти взаимно ортогональных ЛК. Отмечу, что Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 14 еÑÑ‚ÑŒ Ñ…Ð¾Ñ€Ð¾ÑˆÐ°Ñ Ð¾ÑобенноÑÑ‚ÑŒ: ортогональных пар при обработке программой GetOrthogonal получаетÑÑ Ð¼Ð°Ð»Ð¾ (по Ñравнению Ñ Ð¿Ð¾Ñ€Ñдком 12). ПоÑтому здеÑÑŒ будет легче иÑкать клику макÑимального размера, граф будет не Ñильно большой. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Можно поработать Ñ Ð´Ñ€ÑƒÐ³Ð¸Ð¼Ð¸ группами MOLS 14-го порÑдка из Ñтатьи http://www.natalimak1.narod.ru/mols14.htm Ðо... очень жарко... Черепашка пыхтит Ñ Ñ‚Ñ€ÑƒÐ´Ð¾Ð¼. Ð Ñ Ñ‚ÐµÐ¼ более :) Пока понÑтно, что алгоритм переÑтановки Ñтрок и Ñтолбцов работает хорошо, тем более, Ñ Ð¼Ð¾Ð¸Ð¼Ð¸ ÑвриÑтиками. Хочу ещё поработать Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð¾Ð¹ MOLS из четырёх взаимно ортогональных ЛК. Там еÑÑ‚ÑŒ уже небольшой результат: получены группы MOLS, Ñодержащие один ДЛК и три ЛК. ЕÑÑ‚ÑŒ и большой раÑширенный набор ЛК, полученный от Ñтой группы, который, конечно, Ñ Ð½Ðµ обработала программой GetOrthogonal. Ðадо ещё поработать над Ñтим раÑширенным набором ЛК и выложить его Ð´Ð»Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÐºÐ¸. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðто минимальный набор ЛК, полученный от группы MOLS из четырёх взаимно ортогональных ЛК, ÑоÑтоит из 33826 нормализованных ЛК (тут только ЛК, ДЛК нет). При обработке программой GetOrthogonal набор даёт Order? 14 Enter the name of the squares file: inp14 Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file inp14-orthCounts.txt ..output file inp14-orthNos.txt squares 33826 total orthogonal pairs 12 Maximum pairs for square 1: 3 There are 7 other squares with this maximum number of pairs. ..output file inp14-1orths.txt Pairs for square 1: 3 Как видим, ортогональных пар ÑовÑем мало - вÑего 12. Ðу, на клику тут проверить очень проÑто: малюÑенький граф. Можно даже и без помощи программы SageMath проверить. Таблица ортогональных пар (граф) 1: [2,3,4], 2: [1,3,4], 3: [1,2,4], 4: [1,2,3], 5: [6,7,8], 6: [5,7,8], 7: [5,6,8], 8: [5,6,7] Очевидно, что здеÑÑŒ две клики размера 4 [1, 2, 3, 4] [5, 6, 7, 8] Одна из клик ÑоответÑтвует иÑходной группе MOLS, Ð²Ñ‚Ð¾Ñ€Ð°Ñ Ñодержит изоморфные ЛК. Ðто был минимальный набор ЛК (без ДЛК), полученный от иÑходной группы MOLS, ÑоÑтоÑщей из четырёх взаимно ортогональных ЛК. Далее Ñ Ñтот набор раÑширÑла, раÑширÑла... Ð’ конце концов, раÑширенный набор удалила (он Ñодержал более 500 Ñ‚Ñ‹ÑÑч нормализованных ДЛК и ЛК), и ÑÐµÐ¹Ñ‡Ð°Ñ Ð±ÑƒÐ´Ñƒ раÑширÑÑ‚ÑŒ Ñнова :) |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
К ÑчаÑтью, не удалила набор ДЛК, полученных от Ñтой группы MOLS. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¾Ð±ÑŠÐµÐ´Ð¸Ð½Ð¸Ð»Ð° первый минимальный набор ЛК Ñ Ð½Ð°Ð±Ð¾Ñ€Ð¾Ð¼ ДЛК, получила набор из 33998 нормализованных ДЛК и ЛК. ЗапуÑтила обработку программой GetOrthogonal. Жду результат. Результат получилÑÑ Ð½ÐµÐ¿Ð»Ð¾Ñ…Ð¾Ð¹ Order? 14 Enter the name of the squares file: inp14 Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file inp14-orthCounts_1.txt ..output file inp14-orthNos_1.txt squares 33898 total orthogonal pairs 120 Maximum pairs for square 1: 3 There are 79 other squares with this maximum number of pairs. ..output file inp14-1orths_1.txt Pairs for square 1: 3 elapsed time 0:11:02 Ðто пока быÑтро обработалоÑÑŒ, вÑего 11 минут. Образовано 120 ортогональных пар, уже кое-что. Ðайдено 80 троек. Ðу, и клики поищу, конечно, программой SageMath. Ð”Ð»Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ñ‹ Ñто легко, граф маленький. ПонÑтно, что здеÑÑŒ еÑÑ‚ÑŒ группы MOLS, ÑоÑтоÑщие из одного ДЛК и трёх ЛК, о которых Ñ ÑƒÐ¶Ðµ пиÑала выше. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Рвот и клики размера 4, выданные программой SageMath, - 20 штук [[70, 2841, 25577, 25579], [71, 18007, 33893, 6017], [72, 5730, 22127, 10153], [73, 5733, 5735, 25578], [3328, 21860, 6013, 6016], [5728, 28831, 10409, 21857], [5729, 5978, 21928, 25581], [5731, 33896, 28829, 21861], [5732, 2837, 5983, 21859], [5734, 33898, 28830, 2840], [5736, 33897, 28832, 6015], [5806, 2838, 6011, 21929], [12532, 3329, 5982, 1], [17987, 69, 28833, 21930], [17988, 2836, 5979, 10154], [28828, 17184, 21858, 6012], [33490, 12531, 5950, 5980], [33891, 33894, 5981, 6014], [33892, 5805, 6018, 25580], [33895, 5804, 2839, 22995]] Ðапример, группа MOLS, Ð²Ñ‹Ð´Ð°Ð½Ð½Ð°Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð¾Ð¹ GetOrthogonal, от квадрата 1; Ñреди клик Ñтой группе ÑоответÑтвует клика [12532, 3329, 5982, 1] 0 1 2 3 4 5 6 7 8 9 10 11 12 13 1 2 12 11 9 7 8 3 13 0 5 6 4 10 5 9 7 0 13 10 4 8 12 6 2 3 11 1 6 0 4 8 2 12 10 5 1 13 11 7 9 3 11 7 1 4 6 13 5 0 9 3 12 8 10 2 8 6 3 13 5 1 12 10 4 11 0 2 7 9 3 4 5 10 11 0 7 9 2 12 8 13 1 6 4 5 11 6 7 2 3 12 10 8 1 9 13 0 2 11 10 9 0 8 1 13 6 7 4 5 3 12 10 3 8 7 1 9 13 4 5 2 6 12 0 11 9 10 13 12 8 6 0 11 3 1 7 4 2 5 12 13 6 2 10 3 11 1 7 5 9 0 8 4 13 8 0 5 12 4 9 2 11 10 3 1 6 7 7 12 9 1 3 11 2 6 0 4 13 10 5 8 0 1 2 3 4 5 6 7 8 9 10 11 12 13 3 0 4 2 8 1 5 10 6 13 12 7 9 11 11 7 13 9 2 6 12 3 0 10 1 5 4 8 9 2 5 6 11 8 0 13 4 12 3 10 1 7 10 4 11 13 3 0 7 1 12 8 6 2 5 9 7 11 12 10 9 13 3 4 2 1 5 8 0 6 13 8 0 1 12 3 2 5 10 7 11 9 6 4 1 10 6 8 5 7 4 9 13 0 2 3 11 12 12 13 3 0 6 4 9 8 5 11 7 1 2 10 8 6 9 12 10 2 1 11 3 4 0 13 7 5 4 9 7 11 13 12 10 0 1 5 8 6 3 2 2 3 1 5 7 11 8 12 9 6 13 4 10 0 5 12 8 4 1 10 11 6 7 2 9 0 13 3 6 5 10 7 0 9 13 2 11 3 4 12 8 1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 5 9 6 13 1 0 7 8 12 11 3 2 10 4 2 6 3 7 10 11 0 13 5 4 8 9 1 12 1 5 12 4 0 7 8 9 3 6 2 13 11 10 6 11 8 1 12 3 4 10 7 2 9 0 13 5 12 7 13 0 6 10 11 2 9 5 1 3 4 8 7 13 10 12 9 6 1 4 11 3 5 8 2 0 3 12 7 11 8 13 5 0 6 1 4 10 9 2 4 8 0 2 3 9 13 5 10 12 11 7 6 1 9 0 11 5 7 12 2 6 1 10 13 4 8 3 13 3 1 10 2 8 9 12 4 0 6 5 7 11 8 4 9 6 5 1 10 11 2 13 0 12 3 7 11 10 4 8 13 2 3 1 0 7 12 6 5 9 10 2 5 9 11 4 12 3 13 8 7 1 0 6 0 1 2 3 4 5 6 7 8 9 10 11 12 13 7 13 5 6 0 3 12 1 9 10 11 4 2 8 12 3 8 11 5 1 13 2 6 0 7 10 9 4 8 9 3 5 6 13 2 0 10 7 1 12 4 11 13 6 0 12 11 4 9 8 2 5 3 1 7 10 10 5 4 8 1 6 0 3 7 2 13 9 11 12 9 11 7 0 8 12 10 6 5 1 4 3 13 2 5 2 10 7 9 0 8 4 11 3 12 13 1 6 3 4 9 10 2 11 5 12 1 13 8 6 0 7 6 7 13 1 3 8 11 10 4 12 9 2 5 0 1 12 6 9 7 10 4 5 13 11 2 0 8 3 11 10 12 4 13 2 3 9 0 8 5 7 6 1 2 0 1 13 10 9 7 11 12 4 6 8 3 5 4 8 11 2 12 7 1 13 3 6 0 5 10 9 ПроверÑÑŽ ÑвойÑтва утилитой GetType1 Order? 14
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
3 Latin
1 diagonal Latin
4 nfr
3 orthogonal pairÐ’ группе один ДЛК и три ЛК. Ð’ÑÑ‘ замечательно. ТÑк-Ñ, теперь вÑÑ‘, что было, Ñобрала. Буду дальше раÑширÑÑ‚ÑŒ набор ДЛК/ЛК. Главное - опÑÑ‚ÑŒ не удалить, что Ñобрала :) Ð”ÑƒÑ€Ð½Ð°Ñ Ð³Ð¾Ð»Ð¾Ð²Ð° черепашке Ð¿Ð¾ÐºÐ¾Ñ Ð½Ðµ даёт! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’ проверенном наборе из 33998 ДЛК и ЛК ÑодержитÑÑ 16 ДЛК, вÑе они входÑÑ‚ в найденные группы MOLS; пометила их в кликах буквой Д [[70, 2841, 25577Д, 25579], [71, 18007, 33893, 6017Д], [72, 5730, 22127Д, 10153], [73, 5733Д, 5735, 25578], [3328Д, 21860, 6013, 6016], [5728, 28831, 10409, 21857Д], [5729, 5978, 21928Д, 25581], [5731, 33896, 28829, 21861], [5732, 2837, 5983Д, 21859], [5734, 33898, 28830, 2840], [5736Д, 33897, 28832, 6015], [5806, 2838Д, 6011, 21929], [12532Д, 3329, 5982, 1], [17987, 69, 28833, 21930Д], [17988, 2836, 5979Д, 10154], [28828, 17184, 21858, 6012], [33490, 12531, 5950, 5980], [33891, 33894, 5981, 6014Д], [33892Д, 5805, 6018, 25580], [33895, 5804, 2839Д, 22995]] Значит, 16 групп MOLS Ñодержат один ДЛК и три ЛК, оÑтальные четыре группы MOLS ÑоÑтоÑÑ‚ из ЛК. ПонÑтно, что одна из них - иÑÑ…Ð¾Ð´Ð½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° MOLS. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
РаÑширила набор, получила только 270624 нормализованных ДЛК и ЛК. Совершенно не помню, как у Ð¼ÐµÐ½Ñ Ñ€Ð°Ð½ÑŒÑˆÐµ получилоÑÑŒ более 500 Ñ‚Ñ‹ÑÑч, может быть, Ñ Ð¸Ñ… забыла нормализовать и удалить дубликаты. Ðу и ладно, выложила новый набор на ЯндекÑ.ДиÑк https://disk.yandex.ru/d/66OjkP6Zi0_e6g текÑтовый файл Ñжат, 13 МБ. Ð’Ñ‹ можете проверить Ñтот набор, гоÑпода. Сначала обработка программой GetOrthogonal. Ðтот Ñтап трудный Ð´Ð»Ñ Ñ‡ÐµÑ€ÐµÐ¿Ð°ÑˆÐºÐ¸ - неÑколько чаÑов займёт. Затем полученный граф (таблицу ортогональных пар) надо проверить на макÑимальную клику в программе SageMath. Ðто должно быть проÑто, поÑкольку граф получаетÑÑ Ð¼Ð°Ð»ÐµÐ½ÑŒÐºÐ¸Ð¹. ВероÑтноÑÑ‚ÑŒ Ð¿Ð¾Ð»ÑƒÑ‡ÐµÐ½Ð¸Ñ ÐºÐ»Ð¸ÐºÐ¸ размера 5 в Ñтом наборе очень мала, но проверить надо. Пришла в голову ещё одна ÑвриÑтика - Ð´Ð»Ñ Ñ€Ð°ÑÑˆÐ¸Ñ€ÐµÐ½Ð¸Ñ Ñтого набора. Завтра попробую реализовать. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese