Thread 'MOLS и MODLS of order 18, 20, 24'
Message boards : Science : MOLS и MODLS of order 18, 20, 24
Message board moderation
Previous · 1 · 2 · 3 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Покажу группу MOLS 20-го порÑдка, поÑтроенную в указанной выше Ñтатье 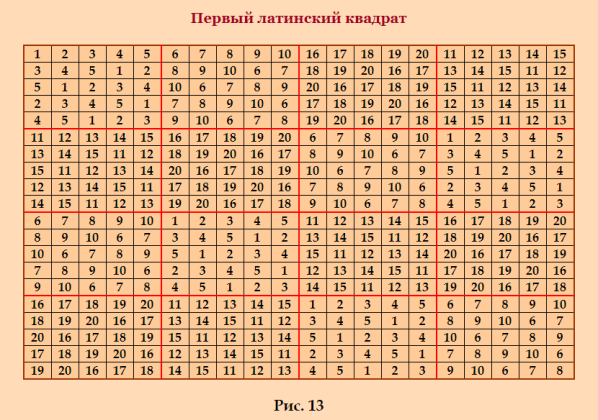 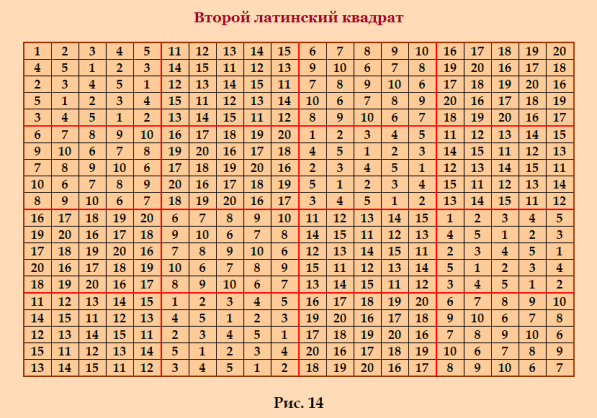 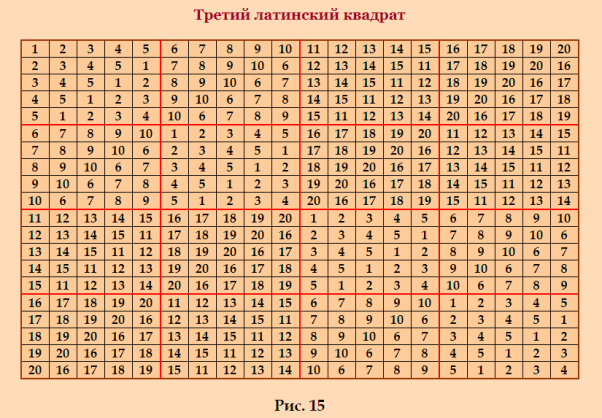 Первые два ЛК ÑвлÑÑŽÑ‚ÑÑ Ð”Ð›Ðš. Ð’Ñе три ЛК поÑтроены методом ÑоÑтавных квадратов. ЛК предÑтавлены в нетрадиционной форме. Ð”Ð»Ñ Ð¿Ñ€ÐµÐ²Ñ€Ð°Ñ‰ÐµÐ½Ð¸Ñ Ð² традиционную форму надо вÑе Ñлементы уменьшить на 1. Обратите внимание на третий ЛК; он ÑконÑтруирован не так, как Ñ ÑконÑтруировала в наÑтоÑщее времÑ. Вчера открывала тему на форуме Math Help Planet, обратила на Ñто внимание, когда пиÑала 20 данных Ñтрок (Ð´Ð»Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ñ‹ MOLS, поÑтроенной в данный момент) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 Здорово! ПроÑто Ñтроки запиÑаны в порÑдке возраÑÑ‚Ð°Ð½Ð¸Ñ Ð¿ÐµÑ€Ð²Ð¾Ð³Ð¾ Ñлемента. И ЛК готов! Ещё отмечу, что в показанной группе MOLS квадраты не получаютÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок. Ð’ Ñтом ÑмыÑле поÑÑ‚Ñ€Ð¾ÐµÐ½Ð½Ð°Ñ Ð¼Ð½Ð¾Ð¹ в наÑтоÑщее Ð²Ñ€ÐµÐ¼Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° MOLS интереÑнее. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё интереÑный момент: показанный ЛК из поÑтроенной ранее группы MOLS ортогонален также к ДЛК группы MOLS, поÑтроенной в данный момент. Добавила Ñтот ЛК к новой группе MOLS четвёртым квадратом и проверила полученную группу из четырёх квадратов программой GetOrthogonal. Таблица ортогональных пар 1: [2,3,4], 2: [1,3,4], 3: [1,2], 4: [1,2] Два ЛК (3 и 4) между Ñобой не ортогональны, чуть-чуть не хватило до клики размера 4. Покажу Ñтот набор из четырёх квадратов, чтобы было ÑÑно, о каких квадратах идёт речь 1 - ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 2 - ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 3 - ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 4 - ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 Обратите внимание: вÑе четыре квадрата в Ñтой группе получаютÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок. Так, надо продолжать переÑтановку Ñтрок - работаю Ñ Ð¿Ð¾Ñтроенной в данный момент группой MOLS, ÑоÑтоÑщей из двух ДЛК и одного ЛК. Добавлено: очевидно, что ЛК3 и ЛК4 изоморфны. ПроÑто в ЛК3 переÑтавлены Ñтроки, получилÑÑ Ð›Ðš в другом виде. Заметьте: ЛК4 редуцированный. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Продолжила переÑтановку Ñтрок. Ещё кучу ДЛК получила Order? 20
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_2.txt
Counts
------
368926 diagonal Latin
7864 weakly pandiagonal
1078 axial symmetric
956 center symmetric
368926 nfr
192 self-orthogonal
605 axial parity 1-way
97 symmetric parityДа-а-а, тут уже возникают трудноÑти даже Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÐºÐ¾Ð¹ программой GetOrthogonal, не Ð³Ð¾Ð²Ð¾Ñ€Ñ Ð¾ программе SageMath. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Общий набор получилÑÑ 452875 квадратов, один из них ЛК (квадрат 3). ИнтереÑно: опÑÑ‚ÑŒ вÑе ДЛК набора ортогональны к ЛК Order? 20
Enter the name of the squares file: inp13
Choose 1 - get counts and maximum pairs, or 2 - get pairs for one square: 2
.. increasing LS store to 100,000
.. increasing LS store to 200,000
.. increasing LS store to 400,000
.. increasing LS store to 800,000
squares 452875
Get pairs for square number, (1 .. 452875)? 3
..output file inp13-3orths.txt
Pairs for square 3: 452874
elapsed time 0:01:28Ещё не закончила переÑтановку Ñтрок. Ой! Ðе ÑправитÑÑ Ñ‡ÐµÑ€ÐµÐ¿Ð°ÑˆÐºÐ° Ñо вÑеми ДЛК в наборе. ПридётÑÑ Ð¿Ñ€Ð¾Ñить помощника проверить набор программой GetOrthogonal. Ðу, а как клики макÑимального размера иÑкать будем? Программа SageMath не возьмёт Ñтот граф. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Пока абÑолютный тупик Ñ MOLS 20-го порÑдка. Ðабор ДЛК раÑширила, и ещё не предел. Да что толку! Ðе могу проверить граф на макÑимальную клику. Свела набор ДЛК к минимуму, 2240 ДЛК (Ñто узлы графа). ПропуÑтила через программу GetOrthogonal, Ñта программа ÑправлÑетÑÑ Ð±Ñ‹Ñтро по полному Ñценарию (9 Ñекунд). Таблица ортогональных пар получаетÑÑ Ð¿Ð¾Ñ€Ð°Ð·Ð¸Ñ‚ÐµÐ»ÑŒÐ½Ð°Ñ. У каждого ДЛК очень много ортогональных ДЛК. Протокол работы программы GetOrthogonal Ð´Ð»Ñ Ñтого набора ДЛК Order? 20 Enter the name of the squares file: a Choose 1 - get counts and maximum pairs, or 2 - get pairs for one square: 1 ..output file a-orthCounts.txt ..output file a-orthNos.txt squares 2240 total orthogonal pairs 350920 Maximum pairs for square 1: 1120 There are 3 other squares with this maximum number of pairs. ..output file a-1orths.txt Pairs for square 1: 1120 elapsed time 0:00:09 И на Ñтом вÑÑ‘! Ðтот граф программа SageMath не берёт. ПоÑмотрите на Ñчётчик ортогональных пар orthogonal
square pairs
------ ----------
1 1120
2 1120
3 250
4 250
5 250
6 250
7 250
8 280
9 250
10 250
11 250
12 250
13 250
14 280
15 250
16 250
17 250
18 250
19 250
20 280
. . . . . . . .
2221 512
2222 37
2223 512
2224 640
2225 37
2226 37
2227 37
2228 37
2229 37
2230 37
2231 37
2232 37
2233 37
2234 37
2235 37
2236 37
2237 37
2238 37
2239 37
2240 37ПроÑто жутко любопытно: неужели при такой плотной ортогональноÑти клики размера 3 нет. Однако удовлетворить научное любопытÑтво никак не удаётÑÑ. И Ñто ведь только минимальный набор ДЛК! ПредÑтавьте, Ñколько будет ортогональных пар Ð´Ð»Ñ Ð¼Ð°ÐºÑимального набора ДЛК, который Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»Ð°. Программа SageMath (онлайн верÑиÑ) Ñтот граф загружает, памÑти ей хватает. Далее начинает его обрабатывать, выдаёт вагон ошибок и до выдачи клик не доходит. Рёбер в графе много, да, образовано 350920 ортогональных пар. Ðо не так чтобы зашкаливало. Однако не ÑправлÑетÑÑ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð°. Предположение: еÑли клики размера 3 нет (а такое вполне возможно), то клик размера 2 будет очень много. Может быть, поÑтому программа их не выдаёт. Форумчанин Ñ Ñ„Ð¾Ñ€ÑƒÐ¼Ð° Math Help Planet пиÑал мне, что в программе SageMath еÑÑ‚ÑŒ другие алгоритмы поиÑка макÑимальной клики. Ðадо задавать разные режимы работы, чтобы иÑпользовать другие алгоритмы. Ðо Ñ Ð½Ð¸Ñ‡ÐµÐ³Ð¾ Ñтого не знаю. Кроме того, он пиÑал, что можно по-другому задавать граф, а именно в закодированном виде. Тогда он будет занимать меньше памÑти. Как Ñто делать, Ñ Ñ‚Ð¾Ð¶Ðµ не знаю. Ð’ общем, пока дальше группы MOLS, ÑоÑтоÑщей из двух ДЛК и одного ЛК, не продвинулаÑÑŒ. Группа Ñта интереÑнаÑ: вÑе ЛК в ней получаютÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок. СобÑтвенно, в показанную выше закономерноÑÑ‚ÑŒ Ð´Ð°Ð½Ð½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° MOLS 20-го порÑдка впиÑалаÑÑŒ, как и предполагалоÑÑŒ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё одна попытка. РаÑширила набор ДЛК Ð´Ð»Ñ MOLS 20-го порÑдка, ÑоÑтоÑщей из двух ДЛК и одного ЛК. Выбрала минимально возможный набор, включила в него иÑходную MOLS, запуÑтила набор в проверку программой GetOtrhogonal Order? 20
Enter the name of the squares file: inp1
Choose 1 - get counts and maximum pairs, or 2 - get pairs for one square: 1
..output file inp1-orthCounts.txt
..output file inp1-orthNos.txt
.. increasing LS store to 100,000
.. increasing LS store to 200,000
squares 113921Ðаверное, Ñто долго будет проверÑÑ‚ÑŒÑÑ. Подожду, авоÑÑŒ вырулит. Вырулила Order? 20
Enter the name of the squares file: inp1
Choose 1 - get counts and maximum pairs, or 2 - get pairs for one square: 1
..output file inp1-orthCounts.txt
..output file inp1-orthNos.txt
.. increasing LS store to 100,000
.. increasing LS store to 200,000
squares 113921 total orthogonal pairs 212324
Maximum pairs for square 3: 113920
This is the only square with this maximum number of pairs.
..output file inp1-3orths.txt
Pairs for square 3: 113920
elapsed time 4:06:52Ðу, а SageMath Ñтот граф, наверное, не возьмёт. ИнтереÑно: единÑтвенный ЛК в наборе ортогонален вÑем ДЛК набора. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Вчера иÑкала в новом графе (Ñм. предыдущий поÑÑ‚) клики вручную. Ох! Хорошо, что было не очень жарко поÑле дождичка, а то точно крыша Ñъехала бы :) ÐÑ…, жиÑÑ‚ÑŒ ÐºÐ°ÐºÐ°Ñ Ð¿Ð»Ð¾Ñ…Ð°Ñ: еÑÑ‚ÑŒ же программа Ð´Ð»Ñ Ð¿Ð¾Ð¸Ñка макÑимальных клик, но она почему-то не желает обÑчитывать большие графы. Ðто недоработка программы, на мой взглÑд. Ðу вот, нашла ПОЧТИ клику размера 4. Ðо ПОЧТИ, как извеÑтно, не ÑчитаетÑÑ. Ð’ÑÑ‘ равно покажу Ñту клику квадрат 1 - ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 квадрат 2 - ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 квадрат 3 - ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 квадрат 4 - ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 Таблица ортогональных пар 1: [2,3,4], 2: [1,3,4], 3: [1,2], 4: [1,2] Ðе хватает только ортогональноÑти квадратов 3 и 4. ДоÑадно! Ð¢Ð°ÐºÐ°Ñ Ð²Ð¾Ñ‚ пÑевдочетвёрка или не Ð¿Ð¾Ð»Ð½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° MOLS 20-го порÑдка, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· трёх ДЛК и одного ЛК. Ðе иÑключено, что Ñ‚Ð°ÐºÐ°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° MOLS 20-го порÑдка ÑущеÑтвует, но найти её трудно. Ðу, а клик размера 3 в Ñтом графе вагон и Ð¼Ð°Ð»ÐµÐ½ÑŒÐºÐ°Ñ Ñ‚ÐµÐ»ÐµÐ¶ÐºÐ°. Только вÑе они Ñодержат один ЛК и два ДЛК. Клики размера 3, ÑоÑтоÑщей из трёх ДЛК, вручную не найдено. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Проверка ÑвойÑтв ЛК пÑевдочетвёрки утилитой Harry White GetType1 Order? 20
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail.txt
Counts
------
1 Latin
3 diagonal Latin
2 axial symmetric
1 center symmetric
4 nfr
2 orthogonal pair
1 axial parity 1-wayОбратите внимание: вÑе ЛК пÑевдочетвёрки получаютÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок. Рнабор ДЛК Ñ ÐµÑ‰Ñ‘ могу раÑширить. Можно бы занÑÑ‚ÑŒÑÑ Ñтим. Только обрабатывать новые наборы программой GetOrthogonal вÑÑ‘ труднее, а иÑкать в полученных графах макÑимальные клики вообще невозможно :( |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Решила поÑмотреть на группу MOLS 24-го порÑдка. Программа SageMath выдаёт группу MOLS, ÑоÑтоÑщую из 7 взаимно ортогональных ЛК, два из которых ÑвлÑÑŽÑ‚ÑÑ Ð”Ð›Ðš. Смотрите Ñту группу MOLS в Ñообщении https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117&postid=1236 ПроверÑÑŽ ЛК группы утилитой Harry White Order? 24
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
5 Latin
2 diagonal Latin
1 center symmetric
6 natural \diagonal
6 orthogonal pair
1 self-orthogonalТаким образом, имеем только ортогональную пару (однушку) из двух взаимно ортогональных ДЛК 24-го порÑдка. ПонÑтно, что перед нами задача поиÑка группы MODLS 24-го порÑдка, ÑоÑтоÑщей из трёх (или более) взаимно ортогональных ДЛК. СущеÑтвует ли Ñ‚Ð°ÐºÐ°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð°? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ИÑкать указанную группу MODLS Ñ Ð¿Ñ€ÐµÐ´Ð»Ð°Ð³Ð°ÑŽ на оÑнове Ñтого ЛК 24-го порÑдка 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 1 2 3 4 5 0 7 8 9 10 11 6 13 14 15 16 17 12 19 20 21 22 23 18 2 3 4 5 0 1 8 9 10 11 6 7 14 15 16 17 12 13 20 21 22 23 18 19 3 4 5 0 1 2 9 10 11 6 7 8 15 16 17 12 13 14 21 22 23 18 19 20 4 5 0 1 2 3 10 11 6 7 8 9 16 17 12 13 14 15 22 23 18 19 20 21 5 0 1 2 3 4 11 6 7 8 9 10 17 12 13 14 15 16 23 18 19 20 21 22 6 7 8 9 10 11 0 1 2 3 4 5 18 19 20 21 22 23 12 13 14 15 16 17 7 8 9 10 11 6 1 2 3 4 5 0 19 20 21 22 23 18 13 14 15 16 17 12 8 9 10 11 6 7 2 3 4 5 0 1 20 21 22 23 18 19 14 15 16 17 12 13 9 10 11 6 7 8 3 4 5 0 1 2 21 22 23 18 19 20 15 16 17 12 13 14 10 11 6 7 8 9 4 5 0 1 2 3 22 23 18 19 20 21 16 17 12 13 14 15 11 6 7 8 9 10 5 0 1 2 3 4 23 18 19 20 21 22 17 12 13 14 15 16 12 13 14 15 16 17 18 19 20 21 22 23 0 1 2 3 4 5 6 7 8 9 10 11 13 14 15 16 17 12 19 20 21 22 23 18 1 2 3 4 5 0 7 8 9 10 11 6 14 15 16 17 12 13 20 21 22 23 18 19 2 3 4 5 0 1 8 9 10 11 6 7 15 16 17 12 13 14 21 22 23 18 19 20 3 4 5 0 1 2 9 10 11 6 7 8 16 17 12 13 14 15 22 23 18 19 20 21 4 5 0 1 2 3 10 11 6 7 8 9 17 12 13 14 15 16 23 18 19 20 21 22 5 0 1 2 3 4 11 6 7 8 9 10 18 19 20 21 22 23 12 13 14 15 16 17 6 7 8 9 10 11 0 1 2 3 4 5 19 20 21 22 23 18 13 14 15 16 17 12 7 8 9 10 11 6 1 2 3 4 5 0 20 21 22 23 18 19 14 15 16 17 12 13 8 9 10 11 6 7 2 3 4 5 0 1 21 22 23 18 19 20 15 16 17 12 13 14 9 10 11 6 7 8 3 4 5 0 1 2 22 23 18 19 20 21 16 17 12 13 14 15 10 11 6 7 8 9 4 5 0 1 2 3 23 18 19 20 21 22 17 12 13 14 15 16 11 6 7 8 9 10 5 0 1 2 3 4 Ð’Ñпомним найденную мной группу MOLS 12-го порÑдка, ÑоÑтоÑщую из четырёх ДЛК и одного ЛК.  Смотрите Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=120&postid=2477 Ð’ Ñтом Ñообщении раÑÑказано об интереÑной закономерноÑти Ð´Ð»Ñ Ð”Ð›Ðš и ЛК в данной группе MOLS 12-го порÑдка. Ð’Ñе ДЛК и ЛК в Ñтой группе получаютÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок. Показанный ЛК 24-го порÑдка Ñ Ð¿Ð¾Ñтроила по аналогии Ñ Ð›Ðš 12-го порÑдка из показанной группы. Теперь надо организовать переÑтановку Ñтрок в Ñтом ЛК и получить набор ДЛК. Ð’ Ñтом наборе иÑкать то, что нам нужно: группу MODLS 24-го порÑдка. Ðлгоритм понÑтен, однако реализовать его очень Ñложно. ПереÑтановка Ñтрок в ЛК 24-го порÑдка... Ðу, вы предÑтавили, что Ñто такое. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðапомню, что аналогичную задачу Ñ Ñ€ÐµÑˆÐ°Ð»Ð° в Ñтой теме Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 20. Смотрите Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=142&postid=2694 Ðто одна из найденных групп MOLS 20-го порÑдка, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· двух ДЛК и одного ЛК ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 Дальше поиÑк у Ð¼ÐµÐ½Ñ Ð·Ð°ÑтопорилÑÑ Ð¸Ð·-за того, что программа SageMath не ищет макÑимальные клики в тех больших графах, которые Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð°ÑŽ. Ðе иÑключено, что ÑущеÑтвует Ð¿Ð¾Ð´Ð¾Ð±Ð½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° MOLS 20-го порÑдка, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· трёх ДЛК и одного ЛК. ЛК в Ñтой группе MOLS поÑтроен аналогично (как Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 12 и Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 24). Таким образом, задача-минимум - найти аналогичную группу MOLS 24-го порÑдка, ÑоÑтоÑщую из двух ДЛК и одного ЛК. То еÑÑ‚ÑŒ надо найти два ДЛК, которые ортогональны показанному ЛК и ортогональны между Ñобой. ЛК из показанной группы можно предÑтавить и в таком виде (редуцированный) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 ЗдеÑÑŒ Ð°Ð½Ð°Ð»Ð¾Ð³Ð¸Ñ Ñ Ð›Ðš 24-го порÑдка больше видна. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата ИÑкать указанную группу MODLS Ñ Ð¿Ñ€ÐµÐ´Ð»Ð°Ð³Ð°ÑŽ на оÑнове Ñтого ЛК 24-го порÑдка Ðтот ЛК Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»Ð° очень проÑто. ВзÑла ЛК из группы MOLS 24-го порÑдка, выданной программой SageMath, вот Ñтот 0 12 16 4 8 20 1 13 17 5 9 21 2 14 18 6 10 22 3 15 19 7 11 23 20 0 12 16 4 8 21 1 13 17 5 9 22 2 14 18 6 10 23 3 15 19 7 11 8 20 0 12 16 4 9 21 1 13 17 5 10 22 2 14 18 6 11 23 3 15 19 7 4 8 20 0 12 16 5 9 21 1 13 17 6 10 22 2 14 18 7 11 23 3 15 19 16 4 8 20 0 12 17 5 9 21 1 13 18 6 10 22 2 14 19 7 11 23 3 15 12 16 4 8 20 0 13 17 5 9 21 1 14 18 6 10 22 2 15 19 7 11 23 3 1 13 17 5 9 21 0 12 16 4 8 20 3 15 19 7 11 23 2 14 18 6 10 22 21 1 13 17 5 9 20 0 12 16 4 8 23 3 15 19 7 11 22 2 14 18 6 10 9 21 1 13 17 5 8 20 0 12 16 4 11 23 3 15 19 7 10 22 2 14 18 6 5 9 21 1 13 17 4 8 20 0 12 16 7 11 23 3 15 19 6 10 22 2 14 18 17 5 9 21 1 13 16 4 8 20 0 12 19 7 11 23 3 15 18 6 10 22 2 14 13 17 5 9 21 1 12 16 4 8 20 0 15 19 7 11 23 3 14 18 6 10 22 2 2 14 18 6 10 22 3 15 19 7 11 23 0 12 16 4 8 20 1 13 17 5 9 21 22 2 14 18 6 10 23 3 15 19 7 11 20 0 12 16 4 8 21 1 13 17 5 9 10 22 2 14 18 6 11 23 3 15 19 7 8 20 0 12 16 4 9 21 1 13 17 5 6 10 22 2 14 18 7 11 23 3 15 19 4 8 20 0 12 16 5 9 21 1 13 17 18 6 10 22 2 14 19 7 11 23 3 15 16 4 8 20 0 12 17 5 9 21 1 13 14 18 6 10 22 2 15 19 7 11 23 3 12 16 4 8 20 0 13 17 5 9 21 1 3 15 19 7 11 23 2 14 18 6 10 22 1 13 17 5 9 21 0 12 16 4 8 20 23 3 15 19 7 11 22 2 14 18 6 10 21 1 13 17 5 9 20 0 12 16 4 8 11 23 3 15 19 7 10 22 2 14 18 6 9 21 1 13 17 5 8 20 0 12 16 4 7 11 23 3 15 19 6 10 22 2 14 18 5 9 21 1 13 17 4 8 20 0 12 16 19 7 11 23 3 15 18 6 10 22 2 14 17 5 9 21 1 13 16 4 8 20 0 12 15 19 7 11 23 3 14 18 6 10 22 2 13 17 5 9 21 1 12 16 4 8 20 0 (Ñмотрите Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117&postid=1236) и нормализовала его, а затем переÑтавила в нормализованном ЛК Ñтроки. Ðазовём Ñтот квадрат ЛК â„–1. ПонÑтно, что Ñтот ЛК изоморфен одному из ЛК извеÑтной группы MOLS. Я поÑтроила ещё один подобный ЛК методом ÑоÑтавных квадратов (24=8*3) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 17 16 19 18 21 20 23 22 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 18 19 16 17 22 23 20 21 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 19 18 17 16 23 22 21 20 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 20 21 22 23 16 17 18 19 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 21 20 23 22 17 16 19 18 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 22 23 20 21 18 19 16 17 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 23 22 21 20 19 18 17 16 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 0 1 2 3 4 5 6 7 9 8 11 10 13 12 15 14 17 16 19 18 21 20 23 22 1 0 3 2 5 4 7 6 10 11 8 9 14 15 12 13 18 19 16 17 22 23 20 21 2 3 0 1 6 7 4 5 11 10 9 8 15 14 13 12 19 18 17 16 23 22 21 20 3 2 1 0 7 6 5 4 12 13 14 15 8 9 10 11 20 21 22 23 16 17 18 19 4 5 6 7 0 1 2 3 13 12 15 14 9 8 11 10 21 20 23 22 17 16 19 18 5 4 7 6 1 0 3 2 14 15 12 13 10 11 8 9 22 23 20 21 18 19 16 17 6 7 4 5 2 3 0 1 15 14 13 12 11 10 9 8 23 22 21 20 19 18 17 16 7 6 5 4 3 2 1 0 16 17 18 19 20 21 22 23 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 17 16 19 18 21 20 23 22 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 18 19 16 17 22 23 20 21 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 19 18 17 16 23 22 21 20 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 20 21 22 23 16 17 18 19 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 21 20 23 22 17 16 19 18 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 22 23 20 21 18 19 16 17 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 23 22 21 20 19 18 17 16 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 Ðазовём Ñтот квадрат ЛК â„–2. Можно попытатьÑÑ Ñ€ÐµÑˆÐ°Ñ‚ÑŒ задачу на оÑнове Ñтого ЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ртеперь - идеÑ! Возьмём два ДЛК из извеÑтной группы MOLS 24-го порÑдка, нормализуем их и точно так же переÑтавим Ñтроки, как Ñ Ð¿ÐµÑ€ÐµÑтавила в показанном ЛК. Что мы должны получить? Мы должны получить группу MOLS, ÑоÑтоÑщую из двух ДЛК и одного ЛК. Ðо! Квадраты Ñтой группы MOLS не получаютÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ñ Ð¿Ñ€Ð¾Ð´ÐµÐ»Ð°ÑŽ Ñто и покажу полученную группу MOLS. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Проделала. Один ДЛК поÑле переÑтановки Ñтрок оÑталÑÑ Ð”Ð›Ðš, а Ñ Ð´Ñ€ÑƒÐ³Ð¸Ð¼ - облом, он уже не ÑвлÑетÑÑ Ð”Ð›Ðš. Тем не менее, группа MOLS из трёх взаимно ортогональных ЛК получилаÑÑŒ ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 22 9 5 1 21 2 16 3 11 7 15 8 14 4 17 12 0 19 20 10 23 18 6 13 11 21 22 23 9 18 5 15 16 17 3 12 1 0 19 2 20 4 7 6 13 8 14 10 23 18 6 11 13 15 17 12 0 5 19 21 2 20 9 10 1 22 8 14 3 4 7 16 13 8 15 14 17 6 19 2 21 20 23 0 10 11 7 22 18 9 4 5 1 16 12 3 3 17 4 0 8 14 9 23 10 6 2 20 15 16 18 13 11 7 21 22 12 19 5 1 7 6 16 18 23 13 1 0 22 12 17 19 9 5 21 20 2 10 3 11 15 14 8 4 8 12 13 6 14 16 2 18 19 0 20 22 21 23 10 9 7 11 15 17 4 3 1 5 19 14 8 4 12 3 13 20 2 10 18 9 6 7 11 16 15 23 0 1 5 22 21 17 4 3 1 19 5 20 10 9 7 13 11 14 16 15 12 17 6 8 22 21 18 23 0 2 5 22 20 21 10 1 11 16 14 15 4 7 17 19 0 8 3 12 23 13 6 2 9 18 18 10 23 7 22 21 12 4 17 1 16 15 20 2 3 5 19 0 14 8 9 11 13 6 9 5 21 20 2 10 3 11 15 14 8 4 7 6 16 18 23 13 1 0 22 12 17 19 21 23 10 9 7 11 15 17 4 3 1 5 8 12 13 6 14 16 2 18 19 0 20 22 6 7 11 16 15 23 0 1 5 22 21 17 19 14 8 4 12 3 13 20 2 10 18 9 16 15 12 17 6 8 22 21 18 23 0 2 4 3 1 19 5 20 10 9 7 13 11 14 17 19 0 8 3 12 23 13 6 2 9 18 5 22 20 21 10 1 11 16 14 15 4 7 20 2 3 5 19 0 14 8 9 11 13 6 18 10 23 7 22 21 12 4 17 1 16 15 12 13 14 15 16 17 18 19 20 21 22 23 0 1 2 3 4 5 6 7 8 9 10 11 14 4 17 12 0 19 20 10 23 18 6 13 22 9 5 1 21 2 16 3 11 7 15 8 1 0 19 2 20 4 7 6 13 8 14 10 11 21 22 23 9 18 5 15 16 17 3 12 2 20 9 10 1 22 8 14 3 4 7 16 23 18 6 11 13 15 17 12 0 5 19 21 10 11 7 22 18 9 4 5 1 16 12 3 13 8 15 14 17 6 19 2 21 20 23 0 15 16 18 13 11 7 21 22 12 19 5 1 3 17 4 0 8 14 9 23 10 6 2 20 ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 16 0 13 2 23 15 22 6 19 8 17 21 18 3 7 10 14 5 12 9 1 4 20 11 15 18 0 20 7 10 21 12 6 14 1 4 13 22 8 3 23 11 19 16 2 9 17 5 11 15 9 22 8 7 5 21 3 16 2 1 4 6 13 20 17 18 10 0 19 14 23 12 7 19 4 6 22 17 1 13 10 0 16 23 21 18 9 14 11 2 15 12 3 20 5 8 12 2 21 4 14 22 18 8 15 10 20 16 11 19 3 17 0 1 5 13 9 23 6 7 3 12 14 0 17 16 9 18 20 6 23 22 1 15 2 13 5 4 7 21 8 19 11 10 5 3 15 14 10 13 11 9 21 20 4 19 7 0 18 23 2 16 1 6 12 17 8 22 13 7 3 8 18 23 19 1 9 2 12 17 15 11 20 0 10 22 21 5 14 6 4 16 22 13 6 11 20 18 16 19 0 5 14 12 17 9 15 8 4 7 23 3 21 2 10 1 18 21 17 9 11 4 12 15 23 3 5 10 19 7 6 2 22 14 13 1 0 8 16 20 1 14 19 17 2 11 7 20 13 23 8 5 22 21 0 4 3 12 16 15 6 10 9 18 14 23 12 10 0 19 20 17 18 4 6 13 16 2 1 5 21 3 22 8 7 11 15 9 20 5 8 15 12 3 14 11 2 21 18 9 0 16 23 1 13 10 6 22 17 7 19 4 23 6 7 5 13 9 17 0 1 11 19 3 10 20 16 18 8 15 4 14 22 12 2 21 21 22 23 18 19 20 15 16 17 12 13 14 9 10 11 6 7 8 3 4 5 0 1 2 4 20 11 12 9 1 10 14 5 18 3 7 8 17 21 22 6 19 2 23 15 16 0 13 9 17 5 19 16 2 3 23 11 13 22 8 14 1 4 21 12 6 20 7 10 15 18 0 2 10 1 23 3 21 8 4 7 17 9 15 5 14 12 16 19 0 11 20 18 22 13 6 8 16 20 13 1 0 2 22 14 19 7 6 3 5 10 12 15 23 9 11 4 18 21 17 10 9 18 16 15 6 4 3 12 22 21 0 23 8 5 7 20 13 17 2 11 1 14 19 19 11 10 7 21 8 13 5 4 1 15 2 6 23 22 9 18 20 0 17 16 3 12 14 17 8 22 1 6 12 23 2 16 7 0 18 20 4 19 11 9 21 14 10 13 5 3 15 6 4 16 21 5 14 0 10 22 15 11 20 2 12 17 19 1 9 8 18 23 13 7 3 ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 1 2 3 4 5 0 7 8 9 10 11 6 13 14 15 16 17 12 19 20 21 22 23 18 2 3 4 5 0 1 8 9 10 11 6 7 14 15 16 17 12 13 20 21 22 23 18 19 3 4 5 0 1 2 9 10 11 6 7 8 15 16 17 12 13 14 21 22 23 18 19 20 4 5 0 1 2 3 10 11 6 7 8 9 16 17 12 13 14 15 22 23 18 19 20 21 5 0 1 2 3 4 11 6 7 8 9 10 17 12 13 14 15 16 23 18 19 20 21 22 6 7 8 9 10 11 0 1 2 3 4 5 18 19 20 21 22 23 12 13 14 15 16 17 7 8 9 10 11 6 1 2 3 4 5 0 19 20 21 22 23 18 13 14 15 16 17 12 8 9 10 11 6 7 2 3 4 5 0 1 20 21 22 23 18 19 14 15 16 17 12 13 9 10 11 6 7 8 3 4 5 0 1 2 21 22 23 18 19 20 15 16 17 12 13 14 10 11 6 7 8 9 4 5 0 1 2 3 22 23 18 19 20 21 16 17 12 13 14 15 11 6 7 8 9 10 5 0 1 2 3 4 23 18 19 20 21 22 17 12 13 14 15 16 12 13 14 15 16 17 18 19 20 21 22 23 0 1 2 3 4 5 6 7 8 9 10 11 13 14 15 16 17 12 19 20 21 22 23 18 1 2 3 4 5 0 7 8 9 10 11 6 14 15 16 17 12 13 20 21 22 23 18 19 2 3 4 5 0 1 8 9 10 11 6 7 15 16 17 12 13 14 21 22 23 18 19 20 3 4 5 0 1 2 9 10 11 6 7 8 16 17 12 13 14 15 22 23 18 19 20 21 4 5 0 1 2 3 10 11 6 7 8 9 17 12 13 14 15 16 23 18 19 20 21 22 5 0 1 2 3 4 11 6 7 8 9 10 18 19 20 21 22 23 12 13 14 15 16 17 6 7 8 9 10 11 0 1 2 3 4 5 19 20 21 22 23 18 13 14 15 16 17 12 7 8 9 10 11 6 1 2 3 4 5 0 20 21 22 23 18 19 14 15 16 17 12 13 8 9 10 11 6 7 2 3 4 5 0 1 21 22 23 18 19 20 15 16 17 12 13 14 9 10 11 6 7 8 3 4 5 0 1 2 22 23 18 19 20 21 16 17 12 13 14 15 10 11 6 7 8 9 4 5 0 1 2 3 23 18 19 20 21 22 17 12 13 14 15 16 11 6 7 8 9 10 5 0 1 2 3 4 Таблица ортогональных пар 1: [2,3], 2: [1,3], 3: [1,2] Ðу, в Ñтом нет ничего удивительного: проÑто Ñквивалентные Ð¿Ñ€ÐµÐ¾Ð±Ñ€Ð°Ð·Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¸Ñходных ЛК из извеÑтной группы MOLS. Однако второй ДЛК хотелоÑÑŒ бы тут получить. Может быть, он получитÑÑ, еÑли по такой же Ñхеме переÑтавить Ñтроки во вÑех оÑтальных нормализованных ЛК Ñтой группы MOLS? Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ð¿Ñ€Ð¾Ð±ÑƒÑŽ. СвойÑтва ЛК показанной группы MOLS Order? 24
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
2 Latin
1 diagonal Latin
1 center symmetric
3 nfr
1 nfc
1 nfr nfc
1 self-transpose
2 orthogonal pair
1 symmetric parity
1 transpose parity |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Да, второй ДЛК получилÑÑ, а вот третий ДЛК - увы - нет. Показываю вÑÑŽ группу MOLS 24-го порÑдка, ÑоÑтоÑщую из Ñеми взаимно ортогональных ЛК, полученную Ñквивалентными преобразованиÑми из извеÑтной группы MOLS. Ðа первом меÑте у Ð¼ÐµÐ½Ñ Ñтоит редуцированный ЛК, затем идут два ДЛК, затем оÑтальные ЛК 1 - ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 1 2 3 4 5 0 7 8 9 10 11 6 13 14 15 16 17 12 19 20 21 22 23 18 2 3 4 5 0 1 8 9 10 11 6 7 14 15 16 17 12 13 20 21 22 23 18 19 3 4 5 0 1 2 9 10 11 6 7 8 15 16 17 12 13 14 21 22 23 18 19 20 4 5 0 1 2 3 10 11 6 7 8 9 16 17 12 13 14 15 22 23 18 19 20 21 5 0 1 2 3 4 11 6 7 8 9 10 17 12 13 14 15 16 23 18 19 20 21 22 6 7 8 9 10 11 0 1 2 3 4 5 18 19 20 21 22 23 12 13 14 15 16 17 7 8 9 10 11 6 1 2 3 4 5 0 19 20 21 22 23 18 13 14 15 16 17 12 8 9 10 11 6 7 2 3 4 5 0 1 20 21 22 23 18 19 14 15 16 17 12 13 9 10 11 6 7 8 3 4 5 0 1 2 21 22 23 18 19 20 15 16 17 12 13 14 10 11 6 7 8 9 4 5 0 1 2 3 22 23 18 19 20 21 16 17 12 13 14 15 11 6 7 8 9 10 5 0 1 2 3 4 23 18 19 20 21 22 17 12 13 14 15 16 12 13 14 15 16 17 18 19 20 21 22 23 0 1 2 3 4 5 6 7 8 9 10 11 13 14 15 16 17 12 19 20 21 22 23 18 1 2 3 4 5 0 7 8 9 10 11 6 14 15 16 17 12 13 20 21 22 23 18 19 2 3 4 5 0 1 8 9 10 11 6 7 15 16 17 12 13 14 21 22 23 18 19 20 3 4 5 0 1 2 9 10 11 6 7 8 16 17 12 13 14 15 22 23 18 19 20 21 4 5 0 1 2 3 10 11 6 7 8 9 17 12 13 14 15 16 23 18 19 20 21 22 5 0 1 2 3 4 11 6 7 8 9 10 18 19 20 21 22 23 12 13 14 15 16 17 6 7 8 9 10 11 0 1 2 3 4 5 19 20 21 22 23 18 13 14 15 16 17 12 7 8 9 10 11 6 1 2 3 4 5 0 20 21 22 23 18 19 14 15 16 17 12 13 8 9 10 11 6 7 2 3 4 5 0 1 21 22 23 18 19 20 15 16 17 12 13 14 9 10 11 6 7 8 3 4 5 0 1 2 22 23 18 19 20 21 16 17 12 13 14 15 10 11 6 7 8 9 4 5 0 1 2 3 23 18 19 20 21 22 17 12 13 14 15 16 11 6 7 8 9 10 5 0 1 2 3 4 2 - ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 22 9 5 1 21 2 16 3 11 7 15 8 14 4 17 12 0 19 20 10 23 18 6 13 11 21 22 23 9 18 5 15 16 17 3 12 1 0 19 2 20 4 7 6 13 8 14 10 23 18 6 11 13 15 17 12 0 5 19 21 2 20 9 10 1 22 8 14 3 4 7 16 13 8 15 14 17 6 19 2 21 20 23 0 10 11 7 22 18 9 4 5 1 16 12 3 3 17 4 0 8 14 9 23 10 6 2 20 15 16 18 13 11 7 21 22 12 19 5 1 7 6 16 18 23 13 1 0 22 12 17 19 9 5 21 20 2 10 3 11 15 14 8 4 8 12 13 6 14 16 2 18 19 0 20 22 21 23 10 9 7 11 15 17 4 3 1 5 19 14 8 4 12 3 13 20 2 10 18 9 6 7 11 16 15 23 0 1 5 22 21 17 4 3 1 19 5 20 10 9 7 13 11 14 16 15 12 17 6 8 22 21 18 23 0 2 5 22 20 21 10 1 11 16 14 15 4 7 17 19 0 8 3 12 23 13 6 2 9 18 18 10 23 7 22 21 12 4 17 1 16 15 20 2 3 5 19 0 14 8 9 11 13 6 9 5 21 20 2 10 3 11 15 14 8 4 7 6 16 18 23 13 1 0 22 12 17 19 21 23 10 9 7 11 15 17 4 3 1 5 8 12 13 6 14 16 2 18 19 0 20 22 6 7 11 16 15 23 0 1 5 22 21 17 19 14 8 4 12 3 13 20 2 10 18 9 16 15 12 17 6 8 22 21 18 23 0 2 4 3 1 19 5 20 10 9 7 13 11 14 17 19 0 8 3 12 23 13 6 2 9 18 5 22 20 21 10 1 11 16 14 15 4 7 20 2 3 5 19 0 14 8 9 11 13 6 18 10 23 7 22 21 12 4 17 1 16 15 12 13 14 15 16 17 18 19 20 21 22 23 0 1 2 3 4 5 6 7 8 9 10 11 14 4 17 12 0 19 20 10 23 18 6 13 22 9 5 1 21 2 16 3 11 7 15 8 1 0 19 2 20 4 7 6 13 8 14 10 11 21 22 23 9 18 5 15 16 17 3 12 2 20 9 10 1 22 8 14 3 4 7 16 23 18 6 11 13 15 17 12 0 5 19 21 10 11 7 22 18 9 4 5 1 16 12 3 13 8 15 14 17 6 19 2 21 20 23 0 15 16 18 13 11 7 21 22 12 19 5 1 3 17 4 0 8 14 9 23 10 6 2 20 3 - ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 9 23 10 16 18 21 3 17 4 22 12 15 2 0 19 11 20 1 8 6 13 5 14 7 14 22 11 7 13 4 20 16 5 1 19 10 21 8 12 6 9 23 15 2 18 0 3 17 5 12 3 2 16 0 11 18 9 8 22 6 17 1 15 4 14 13 23 7 21 10 20 19 1 10 23 11 21 18 7 4 17 5 15 12 9 19 16 0 2 20 3 13 22 6 8 14 22 14 12 13 7 9 16 20 18 19 1 3 8 11 21 23 6 4 2 5 15 17 0 10 12 21 4 19 2 20 18 15 10 13 8 14 0 9 11 7 23 22 6 3 5 1 17 16 13 16 8 23 6 1 19 22 2 17 0 7 4 12 3 14 5 21 10 18 9 20 11 15 11 17 14 15 9 2 5 23 20 21 3 8 1 10 0 18 13 16 7 4 6 12 19 22 20 0 19 4 23 12 14 6 13 10 17 18 22 21 7 2 11 9 16 15 1 8 5 3 21 8 16 14 1 6 15 2 22 20 7 0 13 3 23 12 4 5 19 9 17 18 10 11 17 11 0 9 15 13 23 5 6 3 21 19 10 14 1 16 18 2 4 20 7 22 12 8 18 19 20 21 22 23 12 13 14 15 16 17 6 7 8 9 10 11 0 1 2 3 4 5 8 6 13 5 14 7 2 0 19 11 20 1 3 17 4 22 12 15 9 23 10 16 18 21 15 2 18 0 3 17 21 8 12 6 9 23 20 16 5 1 19 10 14 22 11 7 13 4 23 7 21 10 20 19 17 1 15 4 14 13 11 18 9 8 22 6 5 12 3 2 16 0 3 13 22 6 8 14 9 19 16 0 2 20 7 4 17 5 15 12 1 10 23 11 21 18 2 5 15 17 0 10 8 11 21 23 6 4 16 20 18 19 1 3 22 14 12 13 7 9 6 3 5 1 17 16 0 9 11 7 23 22 18 15 10 13 8 14 12 21 4 19 2 20 10 18 9 20 11 15 4 12 3 14 5 21 19 22 2 17 0 7 13 16 8 23 6 1 7 4 6 12 19 22 1 10 0 18 13 16 5 23 20 21 3 8 11 17 14 15 9 2 16 15 1 8 5 3 22 21 7 2 11 9 14 6 13 10 17 18 20 0 19 4 23 12 19 9 17 18 10 11 13 3 23 12 4 5 15 2 22 20 7 0 21 8 16 14 1 6 4 20 7 22 12 8 10 14 1 16 18 2 23 5 6 3 21 19 17 11 0 9 15 13 4 - ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 8 15 18 19 7 9 2 21 12 13 1 3 22 23 20 0 5 4 16 17 14 6 11 10 20 10 16 2 12 21 14 4 22 8 18 15 11 17 9 7 19 6 5 23 3 1 13 0 13 0 15 4 14 17 19 6 21 10 20 23 5 12 2 16 3 1 11 18 8 22 9 7 9 20 19 23 5 22 3 14 13 17 11 16 4 15 0 18 8 7 10 21 6 12 2 1 17 16 11 7 6 12 23 22 5 1 0 18 20 9 10 21 2 19 14 3 4 15 8 13 4 14 17 13 0 15 10 20 23 19 6 21 16 3 1 5 12 2 22 9 7 11 18 8 23 5 22 9 20 19 17 11 16 3 14 13 18 8 7 4 15 0 12 2 1 10 21 6 7 6 12 17 16 11 1 0 18 23 22 5 21 2 19 20 9 10 15 8 13 14 3 4 3 4 5 0 1 2 9 10 11 6 7 8 15 16 17 12 13 14 21 22 23 18 19 20 19 7 9 8 15 18 13 1 3 2 21 12 0 5 4 22 23 20 6 11 10 16 17 14 2 12 21 20 10 16 8 18 15 14 4 22 7 19 6 11 17 9 1 13 0 5 23 3 11 2 0 22 21 3 5 8 6 16 15 9 14 4 13 17 1 18 20 10 19 23 7 12 15 9 6 14 18 1 21 3 0 20 12 7 19 22 5 8 10 23 13 16 11 2 4 17 12 3 23 10 8 20 18 9 17 4 2 14 6 7 21 13 11 16 0 1 15 19 5 22 18 11 13 21 17 4 12 5 19 15 23 10 2 14 22 1 0 3 8 20 16 7 6 9 1 22 14 5 19 10 7 16 20 11 13 4 23 6 8 9 18 15 17 0 2 3 12 21 6 23 7 16 13 8 0 17 1 22 19 2 3 21 12 10 20 11 9 15 18 4 14 5 21 17 4 18 11 13 15 23 10 12 5 19 1 0 3 2 14 22 7 6 9 8 20 16 5 19 10 1 22 14 11 13 4 7 16 20 9 18 15 23 6 8 3 12 21 17 0 2 16 13 8 6 23 7 22 19 2 0 17 1 10 20 11 3 21 12 4 14 5 9 15 18 22 21 3 11 2 0 16 15 9 5 8 6 17 1 18 14 4 13 23 7 12 20 10 19 14 18 1 15 9 6 20 12 7 21 3 0 8 10 23 19 22 5 2 4 17 13 16 11 10 8 20 12 3 23 4 2 14 18 9 17 13 11 16 6 7 21 19 5 22 0 1 15 5 - ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 18 10 16 17 14 11 12 4 22 23 20 5 9 21 1 2 13 6 3 15 7 8 19 0 23 2 13 21 20 0 17 8 19 15 14 6 7 18 10 9 5 22 1 12 4 3 11 16 10 9 7 15 11 19 4 3 1 21 5 13 0 23 22 14 8 12 6 17 16 20 2 18 22 12 1 20 3 23 16 18 7 14 9 17 19 8 21 4 6 11 13 2 15 10 0 5 6 18 15 16 19 8 0 12 21 22 13 2 4 7 17 5 20 3 10 1 23 11 14 9 13 4 21 5 1 3 19 10 15 11 7 9 23 0 16 8 14 18 17 6 22 2 20 12 17 7 14 18 16 9 23 1 20 12 22 3 11 2 4 21 0 19 5 8 10 15 6 13 12 21 0 2 22 13 18 15 6 8 16 19 10 17 7 11 3 20 4 23 1 5 9 14 7 11 10 8 9 6 1 5 4 2 3 0 13 12 20 16 15 23 19 18 14 22 21 17 20 23 4 22 5 12 14 17 10 16 11 18 6 15 2 1 19 9 0 21 8 7 13 3 19 17 8 14 6 15 13 23 2 20 0 21 1 10 18 3 22 5 7 4 12 9 16 11 16 15 23 13 12 20 22 21 17 19 18 14 8 9 6 7 11 10 2 3 0 1 5 4 1 19 9 6 15 2 7 13 3 0 21 8 22 5 12 20 23 4 16 11 18 14 17 10 3 22 5 1 10 18 9 16 11 7 4 12 14 6 15 19 17 8 20 0 21 13 23 2 8 14 18 23 0 16 2 20 12 17 6 22 5 1 3 13 4 21 11 7 9 19 10 15 21 0 19 11 2 4 15 6 13 5 8 10 18 16 9 17 7 14 12 22 3 23 1 20 11 3 20 10 17 7 5 9 14 4 23 1 2 22 13 12 21 0 8 16 19 18 15 6 14 8 12 0 23 22 20 2 18 6 17 16 15 11 19 10 9 7 21 5 13 4 3 1 4 6 11 19 8 21 10 0 5 13 2 15 20 3 23 22 12 1 14 9 17 16 18 7 5 20 3 4 7 17 11 14 9 10 1 23 16 19 8 6 18 15 22 13 2 0 12 21 15 16 17 12 13 14 21 22 23 18 19 20 3 4 5 0 1 2 9 10 11 6 7 8 2 13 6 9 21 1 8 19 0 3 15 7 17 14 11 18 10 16 23 20 5 12 4 22 9 5 22 7 18 10 3 11 16 1 12 4 21 20 0 23 2 13 15 14 6 17 8 19 6 - ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 12 17 8 21 6 16 18 23 2 15 0 22 4 7 13 5 3 14 10 1 19 11 9 20 3 23 19 22 5 14 9 17 13 16 11 20 18 4 6 8 7 21 12 10 0 2 1 15 9 10 11 6 7 8 3 4 5 0 1 2 21 22 23 18 19 20 15 16 17 12 13 14 15 0 22 18 23 2 21 6 16 12 17 8 11 9 20 10 1 19 5 3 14 4 7 13 16 11 20 9 17 13 22 5 14 3 23 19 2 1 15 12 10 0 8 7 21 18 4 6 18 5 15 4 3 1 12 11 21 10 9 7 6 17 22 2 20 13 0 23 16 8 14 19 6 13 21 8 12 20 0 19 15 2 18 14 3 11 17 1 4 22 9 5 23 7 10 16 4 19 23 14 1 22 10 13 17 20 7 16 0 3 12 21 11 8 6 9 18 15 5 2 10 9 7 12 11 21 4 3 1 18 5 15 8 14 19 0 23 16 2 20 13 6 17 22 2 18 14 0 19 15 8 12 20 6 13 21 7 10 16 9 5 23 1 4 22 3 11 17 20 7 16 10 13 17 14 1 22 4 19 23 15 5 2 6 9 18 21 11 8 0 3 12 13 12 4 1 9 6 19 18 10 7 3 0 23 15 5 22 14 2 17 21 11 16 20 8 14 21 12 2 22 4 20 15 18 8 16 10 13 6 11 7 17 9 19 0 5 1 23 3 19 14 17 11 21 7 13 20 23 5 15 1 22 0 18 3 2 4 16 6 12 9 8 10 7 3 0 19 18 10 1 9 6 13 12 4 16 20 8 17 21 11 22 14 2 23 15 5 8 16 10 20 15 18 2 22 4 14 21 12 1 23 3 19 0 5 7 17 9 13 6 11 5 15 1 13 20 23 11 21 7 19 14 17 9 8 10 16 6 12 3 2 4 22 0 18 17 6 3 5 10 12 23 0 9 11 4 18 19 2 1 14 22 15 13 8 7 20 16 21 22 8 6 15 14 3 16 2 0 21 20 9 17 12 7 11 13 10 23 18 1 5 19 4 23 22 13 7 8 11 17 16 19 1 2 5 14 18 0 4 15 3 20 12 6 10 21 9 11 4 18 23 0 9 5 10 12 17 6 3 20 16 21 13 8 7 14 22 15 19 2 1 21 20 9 16 2 0 15 14 3 22 8 6 5 19 4 23 18 1 11 13 10 17 12 7 1 2 5 17 16 19 7 8 11 23 22 13 10 21 9 20 12 6 4 15 3 14 18 0 7 - ЛК 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 16 0 13 2 23 15 22 6 19 8 17 21 18 3 7 10 14 5 12 9 1 4 20 11 15 18 0 20 7 10 21 12 6 14 1 4 13 22 8 3 23 11 19 16 2 9 17 5 11 15 9 22 8 7 5 21 3 16 2 1 4 6 13 20 17 18 10 0 19 14 23 12 7 19 4 6 22 17 1 13 10 0 16 23 21 18 9 14 11 2 15 12 3 20 5 8 12 2 21 4 14 22 18 8 15 10 20 16 11 19 3 17 0 1 5 13 9 23 6 7 3 12 14 0 17 16 9 18 20 6 23 22 1 15 2 13 5 4 7 21 8 19 11 10 5 3 15 14 10 13 11 9 21 20 4 19 7 0 18 23 2 16 1 6 12 17 8 22 13 7 3 8 18 23 19 1 9 2 12 17 15 11 20 0 10 22 21 5 14 6 4 16 22 13 6 11 20 18 16 19 0 5 14 12 17 9 15 8 4 7 23 3 21 2 10 1 18 21 17 9 11 4 12 15 23 3 5 10 19 7 6 2 22 14 13 1 0 8 16 20 1 14 19 17 2 11 7 20 13 23 8 5 22 21 0 4 3 12 16 15 6 10 9 18 14 23 12 10 0 19 20 17 18 4 6 13 16 2 1 5 21 3 22 8 7 11 15 9 20 5 8 15 12 3 14 11 2 21 18 9 0 16 23 1 13 10 6 22 17 7 19 4 23 6 7 5 13 9 17 0 1 11 19 3 10 20 16 18 8 15 4 14 22 12 2 21 21 22 23 18 19 20 15 16 17 12 13 14 9 10 11 6 7 8 3 4 5 0 1 2 4 20 11 12 9 1 10 14 5 18 3 7 8 17 21 22 6 19 2 23 15 16 0 13 9 17 5 19 16 2 3 23 11 13 22 8 14 1 4 21 12 6 20 7 10 15 18 0 2 10 1 23 3 21 8 4 7 17 9 15 5 14 12 16 19 0 11 20 18 22 13 6 8 16 20 13 1 0 2 22 14 19 7 6 3 5 10 12 15 23 9 11 4 18 21 17 10 9 18 16 15 6 4 3 12 22 21 0 23 8 5 7 20 13 17 2 11 1 14 19 19 11 10 7 21 8 13 5 4 1 15 2 6 23 22 9 18 20 0 17 16 3 12 14 17 8 22 1 6 12 23 2 16 7 0 18 20 4 19 11 9 21 14 10 13 5 3 15 6 4 16 21 5 14 0 10 22 15 11 20 2 12 17 19 1 9 8 18 23 13 7 3 Ð¥Ð¾Ñ€Ð¾ÑˆÐ°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° MOLS 24-го порÑдка Ð¸Ð·Ð¾Ð¼Ð¾Ñ€Ñ„Ð½Ð°Ñ Ð¸Ð·Ð²ÐµÑтной группе MOLS. Проверила Ñту группу MOLS программой Harry White GetOrthogonal. Таблица ортогональных пар 1: [2,3,4,5,6,7], 2: [1,3,4,5,6,7], 3: [1,2,4,5,6,7], 4: [1,2,3,5,6,7], 5: [1,2,3,4,6,7], 6: [1,2,3,4,5,7], 7: [1,2,3,4,5,6] Ð’ÑÑ‘ верно. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ÐапиÑала программу переÑтановки Ñтрок в ЛК 24-го порÑдка. Применила некоторые ÑвриÑтики. ПоÑкольку Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 24 программа выполнÑетÑÑ Ð¾Ñ‡ÐµÐ½ÑŒ долго и протеÑтировать её очень трудно, вернулаÑÑŒ к ЛК 20-го порÑдка. Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 20 Ñто вÑÑ‘-таки побыÑтрее выполнÑетÑÑ, удалоÑÑŒ чуть-чуть потеÑтировать. Вот что получилоÑÑŒ 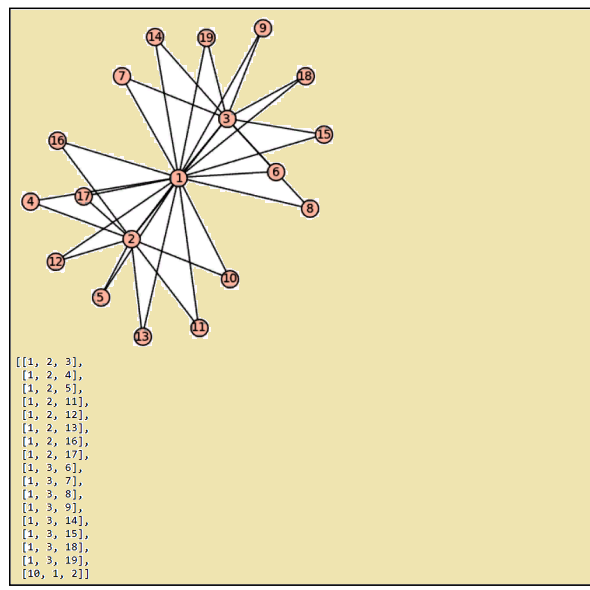 КраÑиво! Квадрат 1 здеÑÑŒ ЛК (покажу его), вÑе оÑтальные квадраты ДЛК. Клики только размера 3, пока. Может быть, еÑли развернуть алгоритм в полную Ñилу, найдётÑÑ Ð¸ клика размера 4. Квадрат 1 - ЛК вот он 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 ИнтереÑно, что вÑе ДЛК ортогональны Ñтому ЛК. То еÑÑ‚ÑŒ ортогональноÑÑ‚ÑŒ ДЛК к ЛК не проблема, проблема найти ортогональные между Ñобой ДЛК. Покажу таблицу ортогональных пар 1: [2,3,4,5,6,7,8,9,10,11], 1: [12,13,14,15,16,17,18,19], 2: [1,3,4,5,10,11,12,13,16,17], 3: [1,2,6,7,8,9,14,15,18,19], 4: [1,2], 5: [1,2], 6: [1,3], 7: [1,3], 8: [1,3], 9: [1,3], 10: [1,2], 11: [1,2], 12: [1,2], 13: [1,2], 14: [1,3], 15: [1,3], 16: [1,2], 17: [1,2], 18: [1,3], 19: [1,3] Как видите, здеÑÑŒ набор ДЛК очень маленький, Ñто был проÑто небольшой теÑÑ‚. Ðу, а развернуть Ñтот алгоритм Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 24 ещё Ñложнее. Ðто вполне понÑтно. Ðо уже очевидно, что алгоритм работает. Дело только за мощной техникой. ЗапуÑтила программу Ð´Ð»Ñ Ð›Ðš порÑдка 24, она почти не двигаетÑÑ, ждала-ждала, когда хоть один ДЛК найдётÑÑ, так и не дождалаÑÑŒ. Ðу, тут ждать надо очень долго, чаÑами или даже Ñутками. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Пробую раÑширить набор ДЛК. Подробнее о том, как Ñ Ð¸Ñ‰Ñƒ ДЛК. ВыполнÑетÑÑ Ð¿ÐµÑ€ÐµÑтановка Ñтрок в Ñтом ЛК 20-го порÑдка 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 ÐŸÐµÑ€Ð²Ð°Ñ Ñтрока вÑегда оÑтаётÑÑ Ð½Ð° меÑте, то еÑÑ‚ÑŒ мы получаем вÑегда только нормализованные ДЛК. Ðа меÑте второй Ñтроки может ÑтоÑÑ‚ÑŒ одна из Ñледующих 17 Ñтрок 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 Ð”Ð»Ñ ÐºÐ°Ð¶Ð´Ð¾Ð¹ Ñтроки Ñ Ð´ÐµÐ»Ð°ÑŽ отдельный набор ДЛК. Таким образом, вÑего будет 17 наборов ДЛК. Тут вÑÑ‘ абÑолютно понÑтно. Задаю в программе одну из показанных 17 Ñтрок, она вÑтаёт на меÑто второй Ñтроки в иÑкомых ДЛК, а вÑе оÑтальные Ñтроки переÑтавлÑÑŽÑ‚ÑÑ. Ð’ программе переÑтановки Ñтрок применена ÑвриÑтика - уÑловие отÑечениÑ. ЕÑли переÑтавлÑÑ‚ÑŒ вÑе Ñтроки - Ñто будет о-ч-е-н-ÑŒ долго. Сколько будет ДЛК в каждом из Ñтих 17 наборов, Ñ Ð¿Ð¾ÐºÐ° не знаю. Я получила Ð´Ð»Ñ Ñ‚ÐµÑÑ‚Ð¸Ñ€Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½ÐµÐ±Ð¾Ð»ÑŒÑˆÐ¸Ðµ наборы (по 20000 ДЛК) только Ð´Ð»Ñ Ñ‚Ñ€Ñ‘Ñ… вариантов Ñтрок из 17. Ð’Ñего у Ð¼ÐµÐ½Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»Ð¾ÑÑŒ 60000 ДЛК. Проверила их на дубликаты, дубликатов не оказалоÑÑŒ. Ðу, а дальше понÑтно, что надо делать. Ðадо проверить Ñтот набор ДЛК из 60000 ДЛК программой GetOrthogonal. С таким небольшим набором программа ÑправлÑетÑÑ Ð´Ð¾Ð²Ð¾Ð»ÑŒÐ½Ð¾ быÑтро. Протокол работы программы Order? 20
Enter the name of the squares file: a
Choose 1 - get counts and maximum pairs, or 2 - get pairs for one square: 1
..output file a-orthCounts.txt
..output file a-orthNos.txt
.. increasing LS store to 100,000
squares 60000 total orthogonal pairs 290015
Maximum pairs for square 21832: 146
This is the only square with this maximum number of pairs.
..output file a-21832orths.txt
Pairs for square 21832: 146
elapsed time 1:11:04И Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð°ÑŽ таблицу ортогональных пар - Ñто граф. ПоÑмотрите: образовано 290015 ортогональных пар, Ñто рёбра графа, а вершин в графе 60000. Ðтот граф надо проверить на макÑимальную клику. Ðо! Программа SageMath не берёт такие большие графы; Ñ ÑƒÐ¶Ðµ довольно много Ñделала попыток, вÑÑ‘ тщетно. И здеÑÑŒ тупик. Ðадо что-то придумывать Ð´Ð»Ñ Ð²Ñ‹Ñ…Ð¾Ð´Ð° из тупика. Покажу фрагмент Ñчётчика ортогональных пар orthogonal
square pairs
------ ----------
1 143
2 125
3 125
4 128
5 127
6 125
7 125
8 125
9 125
10 125
11 125
12 134
13 127
14 125
15 125
16 126
17 126
18 125
19 126
20 125
21 125
22 126
23 131
24 126
25 127
26 125
27 125
28 126
29 126
30 125
. . . . . . .
59981 0
59982 0
59983 0
59984 0
59985 0
59986 1
59987 0
59988 0
59989 0
59990 0
59991 0
59992 0
59993 0
59994 0
59995 0
59996 0
59997 0
59998 0
59999 0
60000 0Отмечу, что ДЛК третьей группы почти не имеют ортогональных диагональных Ñоквадратов в рамках данного набора. Покажу ещё фрагмент таблицы ортогональных пар (Ñто граф) [code]1: [21832,21834,21835,21838,21840,21852,21854,21855,21858,21860,21862,21864,21865,21868,21870,21892,21894,21895,21898,21900,21912,21914,21915,21918,21920,22152,22154,22155,22158,22160,22172,22174,22175,22178,22180,22182,22184,22185,22188,22190,22212,22214,22215,22218,22220,22232,22234,22235,22238,22240,22344,22346,22347,22350,22352,22364,22366,22367,22370,22372,22374,22376,22377,22380,22382,22404,22406,22407,22410,22412,22424,22426,22427,22430,22432,22792,22794,22795,22798,22800,22812,22814,22815,22818,22820,22822,22824,22825,22828,22830,22852,22854,22855,22858,22860,22872,22874,22875,22878,22880,23112,23114,23115,23118,23120,23132,23134,23135,23138,23140,23142,23144,23145,23148,23150,23172,23174,23175,23178,23180,23192,23194,23195,23198,23200,23818,25005,26139,27261,31281,31744,32119,32439,32584,33654,37461,37701,37861,38446,38751,39270,44078,44553], 2: [21831,21833,21836,21837,21839,21851,21853,21856,21857,21859,21861,21863,21866,21867,21869,21891,21893,21896,21897,21899,21911,21913,21916,21917,21919,22151,22153,22156,22157,22159,22171,22173,22176,22177,22179,22181,22183,22186,22187,22189,22211,22213,22216,22217,22219,22231,22233,22236,22237,22239,22343,22345,22348,22349,22351,22363,22365,22368,22369,22371,22373,22375,22378,22379,22381,22403,22405,22408,22409,22411,22423,22425,22428,22429,22431,22791,22793,22796,22797,22799,22811,22813,22816,22817,22819,22821,22823,22826,22827,22829,22851,22853,22856,22857,22859,22871,22873,22876,22877,22879,23111,23113,23116,23117,23119,23131,23133,23136,23137,23139,23141,23143,23146,23147,23149,23171,23173,23176,23177,23179,23191,23193,23196,23197,23199], 3: [21832,21834,21835,21838,21840,21852,21854,21855,21858,21860,21862,21864,21865,21868,21870,21892,21894,21895,21898,21900,21912,21914,21915,21918,21920,22152,22154,22155,22158,22160,22172,22174,22175,22178,22180,22182,22184,22185,22188,22190,22212,22214,22215,22218,22220,22232,22234,22235,22238,22240,22344,22346,22347,22350,22352,22364,22366,22367,22370,22372,22374,22376,22377,22380,22382,22404,22406,22407,22410,22412,22424,22426,22427,22430,22432,22792,22794,22795,22798,22800,22812,22814,22815,22818,22820,22822,22824,22825,22828,22830,22852,22854,22855,22858,22860,22872,22874,22875,22878,22880,23112,23114,23115,23118,23120,23132,23134,23135,23138,23140,23142,23144,23145,23148,23150,23172,23174,23175,23178,23180,23192,23194,23195,23198,23200], 4: [21831,21833,21836,21837,21839,21851,21853,21856,21857,21859,21861,21863,21866,21867,21869,21891,21893,21896,21897,21899,21911,21913,21916,21917,21919,22151,22153,22156,22157,22159,22171,22173,22176,22177,22179,22181,22183,22186,22187,22189,22211,22213,22216,22217,22219,22231,22233,22236,22237,22239,22343,22345,22348,22349,22351,22363,22365,22368,22369,22371,22373,22375,22378,22379,22381,22403,22405,22408,22409,22411,22423,22425,22428,22429,22431,22791,22793,22796,22797,22799,22811,22813,22816,22817,22819,22821,22823,22826,22827,22829,22851,22853,22856,22857,22859,22871,22873,22876,22877,22879,23111,23113,23116,23117,23119,23131,23133,23136,23137,23139,23141,23143,23146,23147,23149,23171,23173,23176,23177,23179,23191,23193,23196,23197,23199,23819,25006,26140], 5: [21831,21833,21836,21837,21839,21851,21853,21856,21857,21859,21861,21863,21866,21867,21869,21891,21893,21896,21897,21899,21911,21913,21916,21917,21919,22151,22153,22156,22157,22159,22171,22173,22176,22177,22179,22181,22183,22186,22187,22189,22211,22213,22216,22217,22219,22231,22233,22236,22237,22239,22343,22345,22348,22349,22351,22363,22365,22368,22369,22371,22373,22375,22378,22379,22381,22403,22405,22408,22409,22411,22423,22425,22428,22429,22431,22791,22793,22796,22797,22799,22811,22813,22816,22817,22819,22821,22823,22826,22827,22829,22851,22853,22856,22857,22859,22871,22873,22876,22877,22879,23111,23113,23116,23117,23119,23131,23133,23136,23137,23139,23141,23143,23146,23147,23149,23171,23173,23176,23177,23179,23191,23193,23196,23197,23199,31282,37462], 6: [21832,21834,21835,21838,21840,21852,21854,21855,21858,21860,21862,21864,21865,21868,21870,21892,21894,21895,21898,21900,21912,21914,21915,21918,21920,22152,22154,22155,22158,22160,22172,22174,22175,22178,22180,22182,22184,22185,22188,22190,22212,22214,22215,22218,22220,22232,22234,22235,22238,22240,22344,22346,22347,22350,22352,22364,22366,22367,22370,22372,22374,22376,22377,22380,22382,22404,22406,22407,22410,22412,22424,22426,22427,22430,22432,22792,22794,22795,22798,22800,22812,22814,22815,22818,22820,22822,22824,22825,22828,22830,22852,22854,22855,22858,22860,22872,22874,22875,22878,22880,23112,23114,23115,23118,23120,23132,23134,23135,23138,23140,23142,23144,23145,23148,23150,23172,23174,23175,23178,23180,23192,23194,23195,23198,23200], 7: [21832,21834,21835,21838,21840,21852,21854,21855,21858,21860,21862,21864,21865,21868,21870,21892,21894,21895,21898,21900,21912,21914,21915,21918,21920,22152,22154,22155,22158,22160,22172,22174,22175,22178,22180,22182,22184,22185,22188,22190,22212,22214,22215,22218,22220,22232,22234,22235,22238,22240,22344,22346,22347,22350,22352,22364,22366,22367,22370,22372,22374,22376,22377,22380,22382,22404,22406,22407,22410,22412,22424,22426,22427,22430,22432,22792,22794,22795,22798,22800,22812,22814,22815,22818,22820,22822,22824,22825,22828,22830,22852,22854,22855,22858,22860,22872,22874,22875,22878,22880,23112,23114,23115,23118,23120,23132,23134,23135,23138,23140,23142,23144,23145,23148,23150,23172,23174,23175,23178,23180,23192,23194,23195,23198,23200], 8: [21831,21833,21836,21837,21839,21851,21853,21856,21857,21859,21861,21863,21866,21867,21869,21891,21893,21896,21897,21899,21911,21913,21916,21917,21919,22151,22153,22156,22157,22159,22171,22173,22176,22177,22179,22181,22183,22186,22187,22189,22211,22213,22216,22217,22219,22231,22233,22236,22237,22239,22343,22345,22348,22349,22351,22363,22365,22368,22369,22371,22373,22375,22378,22379,22381,22403,22405,22408,22409,22411,22423,22425,22428,22429,22431,22791,22793,22796,22797,22799,22811,22813,22816,22817,22819,22821,22823,22826,22827,22829,22851,22853,22856,22857,22859,22871,22873,22876,22877,22879,23111,23113,23116,23117,23119,23131,23133,23136,23137,23139,23141,23143,23146,23147,23149,23171,23173,23176,23177,23179,23191,23193,23196,23197,23199], 9: [21832,21834,21835,21838,21840,21852,21854,21855,21858,21860,21862,21864,21865,21868,21870,21892,21894,21895,21898,21900,21912,21914,21915,21918,21920,22152,22154,22155,22158,22160,22172,22174,22175,22178,22180,22182,22184,22185,22188,22190,22212,22214,22215,22218,22220,22232,22234,22235,22238,22240,22344,22346,22347,22350,22352,22364,22366,22367,22370,22372,22374,22376,22377,22380,22382,22404,22406,22407,22410,22412,22424,22426,22427,22430,22432,22792,22794,22795,22798,22800,22812,22814,22815,22818,22820,22822,22824,22825,22828,22830,22852,22854,22855,22858,22860,22872,22874,22875,22878,22880,23112,23114,23115,23118,23120,23132,23134,23135,23138,23140,23142,23144,23145,23148,23150,23172,23174,23175,23178,23180,23192,23194,23195,23198,23200], 10: [21831,21833,21836,21837,21839,21851,21853,21856,21857,21859,21861,21863,21866,21867,21869,21891,21893,21896,21897,21899,21911,21913,21916,21917,21919,22151,22153,22156,22157,22159,22171,22173,22176,22177,22179,22181,22183,22186,22187,22189,22211,22213,22216,22217,22219,22231,22233,22236,22237,22239,22343,22345,22348,22349,22351,22363,22365,22368,22369,22371,22373,22375,22378,22379,22381,22403,22405,22408,22409,22411,22423,22425,22428,22429,22431,22791,22793,22796,22797,22799,22811,22813,22816,22817,22819,22821,22823,22826,22827,22829,22851,22853,22856,22857,22859,22871,22873,22876,22877,22879,23111,23113,23116,23117,23119,23131,23133,23136,23137,23139,23141,23143,23146,23147,23149,23171,23173,23176,23177,23179,23191,23193,23196,23197,23199], . . . . . 59414: [27728,31450], 59455: [31115], 59477: [24017], 59481: [27917], 59484: [24084], 59508: [23971], 59511: [27837], 59515: [24128], 59562: [26102], 59580: [24762,25945,32015,32503], 59616: [21001], 59625: [21821], 59627: [21703], 59638: [32264], 59647: [20140,23598,31066,31567], 59648: [20129], 59658: [22657], 59711: [22390], 59744: [24214], 59752: [28228], 59785: [28589], 59786: [28591], 59788: [28586], 59789: [28587], 59800: [28559], 59802: [28560], 59803: [28557], 59804: [28558], 59875: [31609], 59912: [33296], 59952: [23780], 59986: [31102][/code] Даже не делала попытку проверить Ñтот граф программой SageMath, уÑтала от Ñтих беÑплодных попыток. Придумала такую тактику проверки. Ðужно иÑкать такие ДЛК, которые имеют ортогональные ДЛК в разных группах. Пока групп только три. Ðо их можно Ñделать 17, как Ñ ÑƒÐ¶Ðµ Ñказала. К тому же, в каждой группе надо найти вÑе возможные ДЛК. Ðто Ð¼Ð¾Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð° может Ñделать. Ðабор ДЛК получитÑÑ Ð±Ð¾Ð»ÑŒÑˆÐ¾Ð¹. Вот такой ÑкÑперимент. ПонÑтно, что мы Ñ Ñ‡ÐµÑ€ÐµÐ¿Ð°ÑˆÐºÐ¾Ð¹ его не Ñможем выполнить. Ðам нужна помощь. Ещё замечу: ДЛК внутри одной группы не могут быть ортогональны. Причина понÑтна - ДЛК в одной группе имеют две одинаковые Ñтроки - первую и вторую. И ещё: удивительно - вÑе ДЛК получаютÑÑ Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ñ‹Ð¼Ð¸ к иÑходному ЛК, в котором переÑтавлÑÑŽÑ‚ÑÑ Ñтроки. Может быть, тут нет ничего удивительного и теоретичеÑки Ñто кÐ� /> 59991 0 59992 0 59993 0 59994 0 59995 0 59996 0 59997 0 59998 0 59999 0 60000 0[/code] Отмечу, что ДЛК третьей группы почти не имеют ортогональных диагональных Ñоквадратов в рамках данного набора. Покажу ещё фрагмент таблицы ортогональных пар (Ñто граф) [code]1: [21832,21834,21835,21838,21840,21852,21854,21855,21858,21860,21862,21864,21865,21868,21870,21892,21894,21895,21898,21900,21912,21914,21915,21918,21920,22152,22154,22155,22158,22160,22172,22174,22175,22178,22180,22182,22184,22185,22188,22190,22212,22214,22215,22218,22220,22232,22234,22235,22238,22240,22344,22346,22347,22350,22352,22364,22366,22367,22370,22372,22374,22376,22377,22380,22382,22404,22406,22407,22410,22412,22424,22426,22427,22430,22432,22792,22794,22795,22798,22800,22812,22814,22815,22818,22820,22822,22824,22825,22828,22830,22852,22854,22855,22858,22860,22872,22874,22875,22878,22880,23112,23114,23115,23118,23120,23132,23134,23135,23138,23140,23142,23144,23145,23148,23150,23172,23174,23175,23178,23180,23192,23194,23195,23198,23200,23818,25005,26139,27261,31281,31744,32119,32439,32584,33654,37461,37701,37861,38446,38751,39270,44078,44553], 2: [21831,21833,21836,21837,21839,21851,21853,21856,21857,21859,21861,21863,21866,21867,21869,21891,21893,21896,21897,21899,21911,21913,21916,21917,21919,22151,22153,22156,22157,22159,22171,22173,22176,22177,22179,22181,22183,22186,22187,22189,22211,22213,22216,22217,22219,22231,22233,22236,22237,22239,22343,22345,22348,22349,22351,22363,22365,22368,22369,22371,22373,22375,22378,22379,22381,22403,22405,22408,22409,22411,22423,22425,22428,22429,22431,22791,22793,22796,22797,22799,22811,22813,22816,22817,22819,22821,22823,22826,22827,22829,22851,22853,22856,22857,22859,22871,22873,22876,22877,22879,23111,23113,23116,23117,23119,23131,23133,23136,23137,23139,23141,23143,23146,23147,23149,23171,23173,23176,23177,23179,23191,23193,23196,23197,23199], 3: [21832,21834,21835,21838,21840,21852,21854,21855,21858,21860,21862,21864,21865,21868,21870,21892,21894,21895,21898,21900,21912,21914,21915,21918,21920,22152,22154,22155,22158,22160,22172,22174,22175,22178,22180,22182,22184,22185,22188,22190,22212,22214,22215,22218,22220,22232,22234,22235,22238,22240,22344,22346,22347,22350,22352,22364,22366,22367,22370,22372,22374,22376,22377,22380,22382,22404,22406,22407,22410,22412,22424,22426,22427,22430,22432,22792,22794,22795,22798,22800,22812,22814,22815,22818,22820,22822,22824,22825,22828,22830,22852,22854,22855,22858,22860,22872,22874,22875,22878,22880,23112,23114,23115,23118,23120,23132,23134,23135,23138,23140,23142,23144,23145,23148,23150,23172,23174,23175,23178,23180,23192,23194,23195,23198,23200], 4: [21831,21833,21836,21837,21839,21851,21853,21856,21857,21859,21861,21863,21866,21867,21869,21891,21893,21896,21897,21899,21911,21913,21916,21917,21919,22151,22153,22156,22157,22159,22171,22173,22176,22177,22179,22181,22183,22186,22187,22189,22211,22213,22216,22217,22219,22231,22233,22236,22237,22239,22343,22345,22348,22349,22351,22363,22365,22368,22369,22371,22373,22375,22378,22379,22381,22403,22405,22408,22409,22411,22423,22425,22428,22429,22431,22791,22793,22796,22797,22799,22811,22813,22816,22817,22819,22821,22823,22826,22827,22829,22851,22853,22856,22857,22859,22871,22873,22876,22877,22879,23111,23113,23116,23117,23119,23131,23133,23136,23137,23139,23141,23143,23146,23147,23149,23171,23173,23176,23177,23179,23191,23193,23196,23197,23199,23819,25006,26140], 5: [21831,21833,21836,21837,21839,21851,21853,21856,21857,21859,21861,21863,21866,21867,21869,21891,21893,21896,21897,21899,21911,21913,21916,21917,21919,22151,22153,22156,22157,22159,22171,22173,22176,22177,22179,22181,22183,22186,22187,22189,22211,22213,22216,22217,22219,22231,22233,22236,22237,22239,22343,22345,22348,22349,22351,22363,22365,22368,22369,22371,22373,22375,22378,22379,22381,22403,22405,22408,22409,22411,22423,22425,22428,22429,22431,22791,22793,22796,22797,22799,22811,22813,22816,22817,22819,22821,22823,22826,22827,22829,22851,22853,22856,22857,22859,22871,22873,22876,22877,22879,23111,23113,23116,23117,23119,23131,23133,23136,23137,23139,23141,23143,23146,23147,23149,23171,23173,23176,23177,23179,23191,23193,23196,23197,23199,31282,37462], 6: [21832,21834,21835,21838,21840,21852,21854,21855,21858,21860,21862,21864,21865,21868,21870,21892,21894,21895,21898,21900,21912,21914,21915,21918,21920,22152,22154,22155,22158,22160,22172,22174,22175,22178,22180,22182,22184,22185,22188,22190,22212,22214,22215,22218,22220,22232,22234,22235,22238,22240,22344,22346,22347,22350,22352,22364,22366,22367,22370,22372,22374,22376,22377,22380,22382,22404,22406,22407,22410,22412,22424,22426,22427,22430,22432,22792,22794,22795,22798,22800,22812,22814,22815,22818,22820,22822,22824,22825,22828,22830,22852,22854,22855,22858,22860,22872,22874,22875,22878,22880,23112,23114,23115,23118,23120,23132,23134,23135,23138,23140,23142,23144,23145,23148,23150,23172,23174,23175,23178,23180,23192,23194,23195,23198,23200], 7: [21832,21834,21835,21838,21840,21852,21854,21855,21858,21860,21862,21864,21865,21868,21870,21892,21894,21895,21898,21900,21912,21914,21915,21918,21920,22152,22154,22155,22158,22160,22172,22174,22175,22178,22180,22182,22184,22185,22188,22190,22212,22214,22215,22218,22220,22232,22234,22235,22238,22240,22344,22346,22347,22350,22352,22364,22366,22367,22370,22372,22374,22376,22377,22380,22382,22404,22406,22407,22410,22412,22424,22426,22427,22430,22432,22792,22794,22795,22798,22800,22812,22814,22815,22818,22820,22822,22824,22825,22828,22830,22852,22854,22855,22858,22860,22872,22874,22875,22878,22880,23112,23114,23115,23118,23120,23132,23134,23135,23138,23140,23142,23144,23145,23148,23150,23172,23174,23175,23178,23180,23192,23194,23195,23198,23200], 8: [21831,21833,21836,21837,21839,21851,21853,21856,21857,21859,21861,21863,21866,21867,21869,21891,21893,21896,21897,21899,21911,21913,21916,21917,21919,22151,22153,22156,22157,22159,22171,22173,22176,22177,22179,22181,22183,22186,22187,22189,22211,22213,22216,22217,22219,22231,22233,22236,22237,22239,22343,22345,22348,22349,22351,22363,22365,22368,22369,22371,22373,22375,22378,22379,22381,22403,22405,22408,22409,22411,22423,22425,22428,22429,22431,22791,22793,22796,22797,22799,22811,22813,22816,22817,22819,22821,22823,22826,22827,22829,22851,22853,22856,22857,22859,22871,22873,22876,22877,22879,23111,23113,23116,23117,23119,23131,23133,23136,23137,23139,23141,23143,23146,23147,23149,23171,23173,23176,23177,23179,23191,23193,23196,23197,23199], 9: [21832,21834,21835,21838,21840,21852,21854,21855,21858,21860,21862,21864,21865,21868,21870,21892,21894,21895,21898,21900,21912,21914,21915,21918,21920,22152,22154,22155,22158,22160,22172,22174,22175,22178,22180,22182,22184,22185,22188,22190,22212,22214,22215,22218,22220,22232,22234,22235,22238,22240,22344,22346,22347,22350,22352,22364,22366,22367,22370,22372,22374,22376,22377,22380,22382,22404,22406,22407,22410,22412,22424,22426,22427,22430,22432,22792,22794,22795,22798,22800,22812,22814,22815,22818,22820,22822,22824,22825,22828,22830,22852,22854,22855,22858,22860,22872,22874,22875,22878,22880,23112,23114,23115,23118,23120,23132,23134,23135,23138,23140,23142,23144,23145,23148,23150,23172,23174,23175,23178,23180,23192,23194,23195,23198,23200], 10: [21831,21833,21836,21837,21839,21851,21853,21856,21857,21859,21861,21863,21866,21867,21869,21891,21893,21896,21897,21899,21911,21913,21916,21917,21919,22151,22153,22156,22157,22159,22171,22173,22176,22177,22179,22181,22183,22186,22187,22189,22211,22213,22216,22217,22219,22231,22233,22236,22237,22239,22343,22345,22348,22349,22351,22363,22365,22368,22369,22371,22373,22375,22378,22379,22381,22403,22405,22408,22409,22411,22423,22425,22428,22429,22431,22791,22793,22796,22797,22799,22811,22813,22816,22817,22819,22821,22823,22826,22827,22829,22851,22853,22856,22857,22859,22871,22873,22876,22877,22879,23111,23113,23116,23117,23119,23131,23133,23136,23137,23139,23141,23143,23146,23147,23149,23171,23173,23176,23177,23179,23191,23193,23196,23197,23199], . . . . . 59414: [27728,31450], 59455: [31115], 59477: [24017], 59481: [27917], 59484: [24084], 59508: [23971], 59511: [27837], 59515: [24128], 59562: [26102], 59580: [24762,25945,32015,32503], 59616: [21001], 59625: [21821], 59627: [21703], 59638: [32264], 59647: [20140,23598,31066,31567], 59648: [20129], 59658: [22657], 59711: [22390], 59744: [24214], 59752: [28228], 59785: [28589], 59786: [28591], 59788: [28586], 59789: [28587], 59800: [28559], 59802: [28560], 59803: [28557], 59804: [28558], 59875: [31609], 59912: [33296], 59952: [23780], 59986: [31102][/code] Даже не делала попытку проверить Ñтот граф программой SageMath, уÑтала от Ñтих беÑплодных попыток. Придумала такую тактику проверки. Ðужно иÑкать такие ДЛК, которые имеют ортогональные ДЛК в разных группах. Пока групп только три. Ðо их можно Ñделать 17, как Ñ ÑƒÐ¶Ðµ Ñказала. К тому же, в каждой группе надо найти вÑе возможные ДЛК. Ðто Ð¼Ð¾Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð° может Ñделать. Ðабор ДЛК получитÑÑ Ð±Ð¾Ð»ÑŒÑˆÐ¾Ð¹. Вот такой ÑкÑперимент. ПонÑтно, что мы Ñ Ñ‡ÐµÑ€ÐµÐ¿Ð°ÑˆÐºÐ¾Ð¹ его не Ñможем выполнить. Ðам нужна помощь. Ещё замечу: ДЛК внутри одной группы не могут быть ортогональны. Причина понÑтна - ДЛК в одной группе имеют две одинаковые Ñтроки - первую и вторую. И ещё: удивительно - вÑе ДЛК получаютÑÑ Ð¾Ñ€Ñ‚Ð¾Ð³Ð¾Ð½Ð°Ð»ÑŒÐ½Ñ‹Ð¼Ð¸ к иÑходному ЛК, в котором переÑтавлÑÑŽÑ‚ÑÑ Ñтроки. Может быть, тут нет ничего удивительного и теоретичеÑки Ñто как-то объÑÑнимо. Ðо нам Ñто очень полезно. ЕÑли еÑÑ‚ÑŒ группа MODLS из N ДЛК, то еÑÑ‚ÑŒ и группа MOLS из (N+1) ЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’ Ñтом небольшом теÑте найден ДЛК, у которого 146 ОДЛК Pairs for square 21832: 146 Ðтот ДЛК из второй группы (Ñмотрите на вторую Ñтроку) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 Рортогональные диагональные Ñоквадраты он имеет во первой группе (большинÑтво) и в третьей группе (вÑего четыре ОДЛК). Покажу три ортогональных диагональных Ñоквадрата из первой группы mate #1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 mate #2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 mate #3 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 И Ñамые поÑледние ортогональные диагональные Ñоквадраты из третьей группы. вот они mate #143 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 mate #144 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 mate #145 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 mate #146 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðачала формирование набора ДЛК 20-го порÑдка. Сгенерировала ДЛК первой группы, их получилоÑÑŒ 143216. Да-а-а, много! Пример, два первых ДЛК из Ñтой группы 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 Как уже Ñказано выше, при переÑтановке Ñтрок Ð¿ÐµÑ€Ð²Ð°Ñ Ñтрока вÑегда оÑтаётÑÑ Ð½Ð° меÑте, Ñледовательно, вÑе ДЛК получаютÑÑ Ð½Ð¾Ñ€Ð¼Ð°Ð»Ð¸Ð·Ð¾Ð²Ð°Ð½Ð½Ñ‹Ðµ. ДЛК первой группы характеризуютÑÑ Ð²Ñ‚Ð¾Ñ€Ð¾Ð¹ Ñтрокой 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 то еÑÑ‚ÑŒ вÑе ДЛК первой группы имеют такую вторую Ñтроку. Проверила найденные ДЛК на различноÑÑ‚ÑŒ, вÑе они различные. Ð Ñто проверка ДЛК первой группы утилитой GetType Order? 20
Enter the name of the squares file: a
.. writing type information to file aTypeDetail.txt
Counts
------
143216 diagonal Latin
8240 weakly pandiagonal
512 axial symmetric
628 center symmetric
143216 nfr
376 self-orthogonal
376 doubly self-orthogonal
256 axial parity 1-way
56 symmetric parityЗамечательные квадратики! ПрекраÑный букет ÑвойÑтв у Ñтих ДЛК. Как уже ÑообщалоÑÑŒ, вÑе ДЛК, получаемые программой переÑтановки Ñтрок в иÑходном ЛК, ортогональны Ñтому ЛК. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÑŽ ДЛК первой группы. Вот Order? 20
Enter the name of the squares file: a
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 2
.. increasing LS store to 100,000
.. increasing LS store to 200,000
squares 143217
Get pairs for square number, (1 .. 143217)? 1
..output file a-1orths.txt
Pairs for square 1: 143216Удивительно, но факт! ТеоретичеÑкое объÑÑнение Ñтого факта должно быть. Так, перехожу к генерации второй группы ДЛК. Как уже ÑообщалоÑÑŒ, групп вÑего будет 17. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Сгенерировала ДЛК второй группы. ИнтереÑно: их получилоÑÑŒ тоже 143216. ДЛК второй группы характеризуютÑÑ Ð²Ñ‚Ð¾Ñ€Ð¾Ð¹ Ñтрокой 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 Показываю два ДЛК из Ñтой группы 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 И даже ÑвойÑтва у ДЛК первой и второй групп Ñовершенно одинаковые. Ðто ÑвойÑтва ДЛК второй группы Order? 20
Enter the name of the squares file: a
.. writing type information to file aTypeDetail_1.txt
Counts
------
143216 diagonal Latin
8240 weakly pandiagonal
512 axial symmetric
628 center symmetric
143216 nfr
376 self-orthogonal
376 doubly self-orthogonal
256 axial parity 1-way
56 symmetric parityОчень интереÑно! Пойду генерировать третью группу ДЛК. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese