Thread 'MOLS and MODLS of order 12'
Message boards : Science : MOLS and MODLS of order 12
Message board moderation
Previous · 1 · 2 · 3 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё раз поÑмотрим на ДЛК группы MODLS 12-го порÑдка 0 1 2 3 4 5 6 7 8 9 10 11 1 3 5 0 9 7 4 2 11 6 8 10 4 9 8 6 1 11 0 10 5 3 2 7 5 7 1 2 11 3 8 0 9 10 4 6 7 2 3 5 10 0 11 1 6 8 9 4 11 10 9 8 7 6 5 4 3 2 1 0 3 0 7 1 6 2 9 5 10 4 11 8 6 4 10 9 0 8 3 11 2 1 7 5 2 5 0 7 8 1 10 3 4 11 6 9 8 11 4 10 5 9 2 6 1 7 0 3 9 6 11 4 3 10 1 8 7 0 5 2 10 8 6 11 2 4 7 9 0 5 3 1 0 1 2 3 4 5 6 7 8 9 10 11 2 5 0 7 8 1 10 3 4 11 6 9 3 0 7 1 6 2 9 5 10 4 11 8 11 10 9 8 7 6 5 4 3 2 1 0 5 7 1 2 11 3 8 0 9 10 4 6 10 8 6 11 2 4 7 9 0 5 3 1 9 6 11 4 3 10 1 8 7 0 5 2 8 11 4 10 5 9 2 6 1 7 0 3 6 4 10 9 0 8 3 11 2 1 7 5 4 9 8 6 1 11 0 10 5 3 2 7 7 2 3 5 10 0 11 1 6 8 9 4 1 3 5 0 9 7 4 2 11 6 8 10 0 1 2 3 4 5 6 7 8 9 10 11 6 4 10 9 0 8 3 11 2 1 7 5 7 2 3 5 10 0 11 1 6 8 9 4 4 9 8 6 1 11 0 10 5 3 2 7 2 5 0 7 8 1 10 3 4 11 6 9 8 11 4 10 5 9 2 6 1 7 0 3 10 8 6 11 2 4 7 9 0 5 3 1 3 0 7 1 6 2 9 5 10 4 11 8 1 3 5 0 9 7 4 2 11 6 8 10 5 7 1 2 11 3 8 0 9 10 4 6 11 10 9 8 7 6 5 4 3 2 1 0 9 6 11 4 3 10 1 8 7 0 5 2 0 1 2 3 4 5 6 7 8 9 10 11 7 2 3 5 10 0 11 1 6 8 9 4 8 11 4 10 5 9 2 6 1 7 0 3 10 8 6 11 2 4 7 9 0 5 3 1 4 9 8 6 1 11 0 10 5 3 2 7 5 7 1 2 11 3 8 0 9 10 4 6 11 10 9 8 7 6 5 4 3 2 1 0 9 6 11 4 3 10 1 8 7 0 5 2 3 0 7 1 6 2 9 5 10 4 11 8 1 3 5 0 9 7 4 2 11 6 8 10 6 4 10 9 0 8 3 11 2 1 7 5 2 5 0 7 8 1 10 3 4 11 6 9 Ðти ДЛК не проÑтые, а золотые :) Ð’Ñ‹ ничего не заметили в Ñтих ДЛК? Ð’Ñе они получаютÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок!! Мы знаем, что так получаютÑÑ Ð”Ð›Ðš в группах MODLS порÑдков 5, 7, 8, 9 (и не только!). Теперь видим Ñто и в группе MODLS 12-го порÑдка. Таким образом, алгоритм поиÑка ЛК (пÑтого в Ñтой группе) можно упроÑтить, Ñделать "крупнопанельным". Имеем 11 Ñтрок (первую Ñтроку не Ñчитаем, она будет первой и в иÑкомом ЛК, то еÑÑ‚ÑŒ в переÑтановках она не учаÑтвует). Ðадо их вÑе переÑтавить, получить вÑе ЛК, а затем проверить их на ортогональноÑÑ‚ÑŒ четырём ДЛК группы MODLS. Однако... переÑтановок из 11 Ñтрок будет 11! = 39916800. Черепашка Ñто не оÑилит. Вот так вÑÑ‘ проÑто в теории, а на практике не так проÑто. Я занималаÑÑŒ переÑтановками Ñтрок и Ñтолбцов, но иÑкала ДЛК; понÑтно, что ДЛК будет в разы меньше, чем ЛК. И вÑÑ‘ равно до конца Ñ Ñту процедуру не выполнила. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПоÑмотрите на полные ÑиÑтемы MOLS порÑдков 8 и 9   Ð’ каждой из Ñтих групп и ДЛК, и ЛК получаютÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок. Ð’Ñе ЛК и ДЛК в Ñтих группах нормализованные. ЕÑли найдём пÑтый ЛК к найденной группе MODLS 12-го порÑдка путём переÑтановок Ñтрок, будет Ð¿Ð¾Ð»Ð½Ð°Ñ Ð°Ð½Ð°Ð»Ð¾Ð³Ð¸Ñ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Итак, требуетÑÑ Ð½Ð°Ð¹Ñ‚Ð¸ 39916800 нормализованных ЛК переÑтановкой 11 извеÑтных Ñтрок. Ðу, нашлёпать Ñти ЛК не очень Ð±Ð¾Ð»ÑŒÑˆÐ°Ñ Ð¿Ñ€Ð¾Ð±Ð»ÐµÐ¼Ð°, у кого компьютер Ñ Ñ…Ð¾Ñ€Ð¾ÑˆÐµÐ¹ памÑтью и нормальной производительноÑтью. Рвот проверить их на ортогональноÑÑ‚ÑŒ четырём ДЛК группы MODLS - Ñложнее проблема. РеÑли по чаÑÑ‚Ñм проверÑÑ‚ÑŒ? Ðадо ведь, чтобы нашёлÑÑ Ñ‚Ð°ÐºÐ¾Ð¹ ЛК, который будет ортогонален вÑем четырём ДЛК группы MODLS. Ðу, Ñкажем, мы нашлёпали Ñти 39916800 нормализованных ЛК. Берём один миллион ЛК, приÑоединÑем к ним четыре ДЛК группы MODLS и проверÑем на ортогональноÑÑ‚ÑŒ программой GetOrthogonal. СправитÑÑ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð° Ñ Ð¼Ð¸Ð»Ð»Ð¸Ð¾Ð½Ð¾Ð¼ ЛК и 4 ДЛК? ЕÑли ÑправитÑÑ, хорошо. Можно дальше проверÑÑ‚ÑŒ - Ñледующий миллион ЛК. ЕÑли миллион ЛК много Ð´Ð»Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ñ‹, можно по полмиллиона проверÑÑ‚ÑŒ. PS. Рвдруг ДЛК найдётÑÑ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
И в полной ÑиÑтеме MOLS 11-го порÑдка вÑÑ‘ точно так же! Смотрите 0 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 0 2 3 4 5 6 7 8 9 10 0 1 3 4 5 6 7 8 9 10 0 1 2 4 5 6 7 8 9 10 0 1 2 3 5 6 7 8 9 10 0 1 2 3 4 6 7 8 9 10 0 1 2 3 4 5 7 8 9 10 0 1 2 3 4 5 6 8 9 10 0 1 2 3 4 5 6 7 9 10 0 1 2 3 4 5 6 7 8 10 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 10 2 3 4 5 6 7 8 9 10 0 1 4 5 6 7 8 9 10 0 1 2 3 6 7 8 9 10 0 1 2 3 4 5 8 9 10 0 1 2 3 4 5 6 7 10 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 10 0 3 4 5 6 7 8 9 10 0 1 2 5 6 7 8 9 10 0 1 2 3 4 7 8 9 10 0 1 2 3 4 5 6 9 10 0 1 2 3 4 5 6 7 8 0 1 2 3 4 5 6 7 8 9 10 3 4 5 6 7 8 9 10 0 1 2 6 7 8 9 10 0 1 2 3 4 5 9 10 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 0 4 5 6 7 8 9 10 0 1 2 3 7 8 9 10 0 1 2 3 4 5 6 10 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 10 0 1 5 6 7 8 9 10 0 1 2 3 4 8 9 10 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 10 4 5 6 7 8 9 10 0 1 2 3 8 9 10 0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 8 9 10 0 5 6 7 8 9 10 0 1 2 3 4 9 10 0 1 2 3 4 5 6 7 8 2 3 4 5 6 7 8 9 10 0 1 6 7 8 9 10 0 1 2 3 4 5 10 0 1 2 3 4 5 6 7 8 9 3 4 5 6 7 8 9 10 0 1 2 7 8 9 10 0 1 2 3 4 5 6 0 1 2 3 4 5 6 7 8 9 10 5 6 7 8 9 10 0 1 2 3 4 10 0 1 2 3 4 5 6 7 8 9 4 5 6 7 8 9 10 0 1 2 3 9 10 0 1 2 3 4 5 6 7 8 3 4 5 6 7 8 9 10 0 1 2 8 9 10 0 1 2 3 4 5 6 7 2 3 4 5 6 7 8 9 10 0 1 7 8 9 10 0 1 2 3 4 5 6 1 2 3 4 5 6 7 8 9 10 0 6 7 8 9 10 0 1 2 3 4 5 0 1 2 3 4 5 6 7 8 9 10 6 7 8 9 10 0 1 2 3 4 5 1 2 3 4 5 6 7 8 9 10 0 7 8 9 10 0 1 2 3 4 5 6 2 3 4 5 6 7 8 9 10 0 1 8 9 10 0 1 2 3 4 5 6 7 3 4 5 6 7 8 9 10 0 1 2 9 10 0 1 2 3 4 5 6 7 8 4 5 6 7 8 9 10 0 1 2 3 10 0 1 2 3 4 5 6 7 8 9 5 6 7 8 9 10 0 1 2 3 4 0 1 2 3 4 5 6 7 8 9 10 7 8 9 10 0 1 2 3 4 5 6 3 4 5 6 7 8 9 10 0 1 2 10 0 1 2 3 4 5 6 7 8 9 6 7 8 9 10 0 1 2 3 4 5 2 3 4 5 6 7 8 9 10 0 1 9 10 0 1 2 3 4 5 6 7 8 5 6 7 8 9 10 0 1 2 3 4 1 2 3 4 5 6 7 8 9 10 0 8 9 10 0 1 2 3 4 5 6 7 4 5 6 7 8 9 10 0 1 2 3 0 1 2 3 4 5 6 7 8 9 10 8 9 10 0 1 2 3 4 5 6 7 5 6 7 8 9 10 0 1 2 3 4 2 3 4 5 6 7 8 9 10 0 1 10 0 1 2 3 4 5 6 7 8 9 7 8 9 10 0 1 2 3 4 5 6 4 5 6 7 8 9 10 0 1 2 3 1 2 3 4 5 6 7 8 9 10 0 9 10 0 1 2 3 4 5 6 7 8 6 7 8 9 10 0 1 2 3 4 5 3 4 5 6 7 8 9 10 0 1 2 0 1 2 3 4 5 6 7 8 9 10 9 10 0 1 2 3 4 5 6 7 8 7 8 9 10 0 1 2 3 4 5 6 5 6 7 8 9 10 0 1 2 3 4 3 4 5 6 7 8 9 10 0 1 2 1 2 3 4 5 6 7 8 9 10 0 10 0 1 2 3 4 5 6 7 8 9 8 9 10 0 1 2 3 4 5 6 7 6 7 8 9 10 0 1 2 3 4 5 4 5 6 7 8 9 10 0 1 2 3 2 3 4 5 6 7 8 9 10 0 1 0 1 2 3 4 5 6 7 8 9 10 10 0 1 2 3 4 5 6 7 8 9 9 10 0 1 2 3 4 5 6 7 8 8 9 10 0 1 2 3 4 5 6 7 7 8 9 10 0 1 2 3 4 5 6 6 7 8 9 10 0 1 2 3 4 5 5 6 7 8 9 10 0 1 2 3 4 4 5 6 7 8 9 10 0 1 2 3 3 4 5 6 7 8 9 10 0 1 2 2 3 4 5 6 7 8 9 10 0 1 1 2 3 4 5 6 7 8 9 10 0 Ð’ ÑиÑтеме 2 ЛК и 8 ДЛК, вÑе они получаютÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок. Ð¥Ð¾Ñ€Ð¾ÑˆÐ°Ñ Ð·Ð°ÐºÐ¾Ð½Ð¾Ð¼ÐµÑ€Ð½Ð¾ÑÑ‚ÑŒ, однако. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ÐариÑовала Ñти золотые ДЛК :) Группа MODLS 12-го порÑдка  Ðа иллюÑтрации хорошо видно, что вÑе ДЛК получаютÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок. ÐÑ…, найти бы Ñюда пÑтый квадратик (еÑли он ÑущеÑтвует), пуÑÑ‚ÑŒ он будет ЛК, вÑÑ‘ равно краÑÐ¸Ð²Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° MOLS получитÑÑ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
У-Ñ€-Ñ€-Ñ€-а-а-а!!! Я его нашла! С утра пришла в голову Ð¾Ð¿Ñ‚Ð¸Ð¼Ð¸Ð·Ð°Ñ†Ð¸Ñ Ð² процедуре переÑтановки Ñтрок. Ðу и, конечно, раÑпараллеливание. Ð’ математике много чего делаетÑÑ Ð¿Ð¾ чаÑÑ‚Ñм. Итак, Ñто у Ð¼ÐµÐ½Ñ Ð¿ÑÑ‚Ð°Ñ Ð¿Ð¾Ñ€Ñ†Ð¸Ñ Ð›Ðš, ÐºÐ¾Ñ‚Ð¾Ñ€Ð°Ñ Ñодержит 52082 ЛК. ДобавлÑÑŽ к Ñтим ЛК 4 ДЛК из группы MODLS, запиÑываю ДЛК первыми в наборе. ВыполнÑÑŽ Ð´Ð»Ñ Ð¿Ð¾Ð»ÑƒÑ‡ÐµÐ½Ð½Ð¾Ð³Ð¾ набора программу GetOrthogonal. Смотрю таблицу ортогональных пар 1: [2,3,4,1459,1526,1697,1780,2739,2797,2979], 1: [4146,4249,4299,4630,4649,4755,5528,6866,7233,7235], 1: [7611,7873,9330,10075,10101,10140,10245,10470,10772,11578], 1: [11722,11873,12064,12739,12931,12963,12965,13116,15244,15712], 1: [15917,17631,18225,18275,18660,19760,20098,20109,20160,20392], 1: [20914,20927,21144,21154,21191,21375,22627,22783,23829,24036], 1: [24167,27752,28268,28451,29224,29866,29910,32350,32616,33487], 1: [35059,46823,47043,48175,50995], 2: [1,3,4,244,1006,1627,2078,2818,3348,3362], 2: [3452,5909,5929,6430,16797,17316,17589,18347,19139,19338], 2: [19410,20123,20840,22660,22982,23365,23812,24070,25507,26325], 2: [27359,29232,29233,29407,29431,29682,29866,30130,31593,33634], 2: [34505,35591,36966,37605,37785,37793,37870,38940,38956,39089], 2: [39113,39485,39632,40727,41162,42311,42331,42839,43899,43941], 2: [43987,44012,44063,44749,45783,45954,46608,46793,47872,50939], 2: [50942,50978,51025,51602,51676], 3: [1,2,4,445,615,1812,1907,3148,3238,3324], 3: [5178,5548,7054,7626,8088,8447,10605,10742,11264,11313], 3: [11410,11936,12663,13304,13656,13867,13999,23312,23627,23739], 3: [23743,24309,26137,26335,26418,27305,27312,29023,29643,29866], 3: [30473,30479,31208,31550,31558,32601,32639,32646,32899,32981], 3: [34006,34365,37876,38019,39290,39932,39984,42453,42803,45356], 3: [45617,47435,47443,47481,47604,48108,48310,50014,50129,50291], 3: [50369,50396], 4: [1,2,3,871,1011,1068,2803,3665,4129,7855], 4: [8545,8887,8947,8975,12262,12987,13029,13711,14090,16137], 4: [16148,16476,16508,16674,17358,20034,20073,20097,21448,21452], 4: [21778,22030,22050,24464,24614,25141,25782,25833,26352,26374], 4: [26777,27111,27123,27225,29866,30776,33434,33679,33767,34813], 4: [34818,34925,35129,35467,35512,37527,37759,38002,42173,42187], 4: [42192,43292,43296,43881,43886,43959,45418,45446,45666,46297], 4: [49187,49250,49636,49738,50619,50622,51045], 244: [2], 445: [3], 615: [3], 871: [4], 1006: [2], 1011: [4], 1068: [4], 1459: [1], 1526: [1], 1627: [2], . . . . . . . 29233: [2], 29407: [2], 29431: [2], 29643: [3], 29682: [2], 29866: [1,2,3,4], 29910: [1], 30130: [2], 30473: [3], 30479: [3], 30776: [4], 31208: [3], . . . . . . Вот она - клика размера 5 [1, 2, 3, 4, 29866] Первые четыре квадрата - ДЛК, 29866-й квадрат - ЛК. Показываю найденную группу MOLS 12-го порÑдка, ÑоÑтоÑщую из четырёх ДЛК и одного ЛК ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 1 3 5 0 9 7 4 2 11 6 8 10 4 9 8 6 1 11 0 10 5 3 2 7 5 7 1 2 11 3 8 0 9 10 4 6 7 2 3 5 10 0 11 1 6 8 9 4 11 10 9 8 7 6 5 4 3 2 1 0 3 0 7 1 6 2 9 5 10 4 11 8 6 4 10 9 0 8 3 11 2 1 7 5 2 5 0 7 8 1 10 3 4 11 6 9 8 11 4 10 5 9 2 6 1 7 0 3 9 6 11 4 3 10 1 8 7 0 5 2 10 8 6 11 2 4 7 9 0 5 3 1 ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 2 5 0 7 8 1 10 3 4 11 6 9 3 0 7 1 6 2 9 5 10 4 11 8 11 10 9 8 7 6 5 4 3 2 1 0 5 7 1 2 11 3 8 0 9 10 4 6 10 8 6 11 2 4 7 9 0 5 3 1 9 6 11 4 3 10 1 8 7 0 5 2 8 11 4 10 5 9 2 6 1 7 0 3 6 4 10 9 0 8 3 11 2 1 7 5 4 9 8 6 1 11 0 10 5 3 2 7 7 2 3 5 10 0 11 1 6 8 9 4 1 3 5 0 9 7 4 2 11 6 8 10 ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 6 4 10 9 0 8 3 11 2 1 7 5 7 2 3 5 10 0 11 1 6 8 9 4 4 9 8 6 1 11 0 10 5 3 2 7 2 5 0 7 8 1 10 3 4 11 6 9 8 11 4 10 5 9 2 6 1 7 0 3 10 8 6 11 2 4 7 9 0 5 3 1 3 0 7 1 6 2 9 5 10 4 11 8 1 3 5 0 9 7 4 2 11 6 8 10 5 7 1 2 11 3 8 0 9 10 4 6 11 10 9 8 7 6 5 4 3 2 1 0 9 6 11 4 3 10 1 8 7 0 5 2 ДЛК 0 1 2 3 4 5 6 7 8 9 10 11 7 2 3 5 10 0 11 1 6 8 9 4 8 11 4 10 5 9 2 6 1 7 0 3 10 8 6 11 2 4 7 9 0 5 3 1 4 9 8 6 1 11 0 10 5 3 2 7 5 7 1 2 11 3 8 0 9 10 4 6 11 10 9 8 7 6 5 4 3 2 1 0 9 6 11 4 3 10 1 8 7 0 5 2 3 0 7 1 6 2 9 5 10 4 11 8 1 3 5 0 9 7 4 2 11 6 8 10 6 4 10 9 0 8 3 11 2 1 7 5 2 5 0 7 8 1 10 3 4 11 6 9 ЛК 0 1 2 3 4 5 6 7 8 9 10 11 3 0 7 1 6 2 9 5 10 4 11 8 2 5 0 7 8 1 10 3 4 11 6 9 1 3 5 0 9 7 4 2 11 6 8 10 6 4 10 9 0 8 3 11 2 1 7 5 7 2 3 5 10 0 11 1 6 8 9 4 4 9 8 6 1 11 0 10 5 3 2 7 5 7 1 2 11 3 8 0 9 10 4 6 10 8 6 11 2 4 7 9 0 5 3 1 9 6 11 4 3 10 1 8 7 0 5 2 8 11 4 10 5 9 2 6 1 7 0 3 11 10 9 8 7 6 5 4 3 2 1 0 Очень Ñимпатичный ЛК! Ðто ж надо так выÑтроитьÑÑ Ð´Ð¸Ð°Ð³Ð¾Ð½Ð°Ð»Ñм! ПроверÑÑŽ ÑвойÑтва квадратов группы утилитой Harry White GetType1 Order? 12
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_6.txt
Counts
------
1 Latin
4 diagonal Latin
4 axial symmetric
1 double axial symmetric
1 center symmetric
5 nfr
4 orthogonal pair
1 symmetric parity
1 transpose parityИ подтверждение взаимной ортогональноÑти квадратов группы Order? 12 Enter the name of the squares file: inp6 Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file inp6-orthCounts.txt ..output file inp6-orthNos.txt squares 5 total orthogonal pairs 10 Maximum pairs for square 1: 4 There are 4 other squares with this maximum number of pairs. ..output file inp6-1orths.txt Pairs for square 1: 4 Таблица ортогональных пар 1: [2,3,4,5], 2: [1,3,4,5], 3: [1,2,4,5], 4: [1,2,3,5], 5: [1,2,3,4] Ð ÑкÑперимент ещё не закончен. Дальше буду переÑтавлÑÑ‚ÑŒ Ñтроки. Рзатем надо будет Ñобрать вÑе порции ЛК, добавить к ним 4 ДЛК группы MODLS и проверить полученный набор на макÑимальную клику. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
РкÑтати... поÑмотрите на группу MOLS 12-го порÑдка, выданную программой SageMath, https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=120&postid=1290 0 1 2 3 4 5 6 7 8 9 10 11 1 0 3 2 5 4 7 6 9 8 11 10 2 3 0 1 6 7 4 5 10 11 8 9 3 2 1 0 7 6 5 4 11 10 9 8 8 9 10 11 0 1 2 3 4 5 6 7 9 8 11 10 1 0 3 2 5 4 7 6 10 11 8 9 2 3 0 1 6 7 4 5 11 10 9 8 3 2 1 0 7 6 5 4 4 5 6 7 8 9 10 11 0 1 2 3 5 4 7 6 9 8 11 10 1 0 3 2 6 7 4 5 10 11 8 9 2 3 0 1 7 6 5 4 11 10 9 8 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10 11 6 7 4 5 10 11 8 9 2 3 0 1 4 5 6 7 8 9 10 11 0 1 2 3 2 3 0 1 6 7 4 5 10 11 8 9 10 11 8 9 2 3 0 1 6 7 4 5 5 4 7 6 9 8 11 10 1 0 3 2 7 6 5 4 11 10 9 8 3 2 1 0 8 9 10 11 0 1 2 3 4 5 6 7 9 8 11 10 1 0 3 2 5 4 7 6 3 2 1 0 7 6 5 4 11 10 9 8 1 0 3 2 5 4 7 6 9 8 11 10 11 10 9 8 3 2 1 0 7 6 5 4 0 1 2 3 4 5 6 7 8 9 10 11 3 2 1 0 7 6 5 4 11 10 9 8 11 10 9 8 3 2 1 0 7 6 5 4 6 7 4 5 10 11 8 9 2 3 0 1 4 5 6 7 8 9 10 11 0 1 2 3 7 6 5 4 11 10 9 8 3 2 1 0 9 8 11 10 1 0 3 2 5 4 7 6 1 0 3 2 5 4 7 6 9 8 11 10 5 4 7 6 9 8 11 10 1 0 3 2 2 3 0 1 6 7 4 5 10 11 8 9 10 11 8 9 2 3 0 1 6 7 4 5 8 9 10 11 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 10 11 9 8 11 10 1 0 3 2 5 4 7 6 8 9 10 11 0 1 2 3 4 5 6 7 1 0 3 2 5 4 7 6 9 8 11 10 5 4 7 6 9 8 11 10 1 0 3 2 3 2 1 0 7 6 5 4 11 10 9 8 2 3 0 1 6 7 4 5 10 11 8 9 4 5 6 7 8 9 10 11 0 1 2 3 11 10 9 8 3 2 1 0 7 6 5 4 6 7 4 5 10 11 8 9 2 3 0 1 7 6 5 4 11 10 9 8 3 2 1 0 10 11 8 9 2 3 0 1 6 7 4 5 0 1 2 3 4 5 6 7 8 9 10 11 10 11 8 9 2 3 0 1 6 7 4 5 5 4 7 6 9 8 11 10 1 0 3 2 7 6 5 4 11 10 9 8 3 2 1 0 9 8 11 10 1 0 3 2 5 4 7 6 11 10 9 8 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 11 10 9 8 6 7 4 5 10 11 8 9 2 3 0 1 2 3 0 1 6 7 4 5 10 11 8 9 1 0 3 2 5 4 7 6 9 8 11 10 8 9 10 11 0 1 2 3 4 5 6 7 4 5 6 7 8 9 10 11 0 1 2 3 Ð’Ñе Ñти ЛК тоже получаютÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок. ÐŸÐ¾Ð»ÑƒÑ‡ÐµÐ½Ð½Ð°Ñ Ð¼Ð½Ð¾Ð¹ группа MOLS лучше, потому что она Ñодержит четыре ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПереÑтановку Ñтрок закончила. Ðайдены ещё две клики размера 4, то еÑÑ‚ÑŒ к трём ДЛК прибавлÑетÑÑ Ð¾Ð´Ð¸Ð½ ЛК, получаютÑÑ Ð³Ñ€ÑƒÐ¿Ð¿Ñ‹ MOLS из 3-Ñ… ДЛК и одного ЛК. Ðу, Ñто не так интереÑно. Теперь Ñоберу вÑе найденные ЛК и отправлю помощнику Ð´Ð»Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÐºÐ¸ на макÑимальную клику. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Изобразила группу MOLS 12-го порÑдка, найденную мной: четыре ДЛК и один ЛК  Лепота! Я в воÑторге от Ñтой группы! Группа MODLS из пÑти ДЛК пока не получилаÑÑŒ. Может быть, и не получитÑÑ - проÑто потому, что (вполне возможно) её не ÑущеÑтвует. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Черепашка очень довольна :) Только огорчаетÑÑ, что не может проверить вÑе ЛК на макÑимальную клику. Ðу, попроÑим нашего замечательного помощника. Он, кÑтати, недавно и программу SageMath уÑтановил. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ñоберём вÑе ЛК и отправим ему. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Помощника поÑтигла неудача Ñ Ð¿Ñ€Ð¾Ð³Ñ€Ð°Ð¼Ð¼Ð¾Ð¹ SageMath, что вполне ожидаемо. Граф получилÑÑ Ð¾Ð³Ñ€Ð¾Ð¼Ð½Ñ‹Ð¹, он занимает примерно 500 МБ. И программа SageMath граф не Ñмогла Ñчитать из входного файла. Помощник пишет, что он ждал 10 чаÑов, когда программа введёт граф, но так и не дождалÑÑ. Я вижу только протокол работы программы GetOrthogonal (помощник мне его приÑлал) Order? 12
Enter the name of the squares file: lk12_502602
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1
..output file lk12_502602-orthCounts.txt
..output file lk12_502602-orthNos.txt
.. increasing LS store to 100,000
.. increasing LS store to 200,000
.. increasing LS store to 400,000
.. increasing LS store to 800,000
squares 502602 total orthogonal pairs 31947721
Maximum pairs for square 1: 687
This is the only square with this maximum number of pairs.
..output file lk12_502602-1orths.txt
Pairs for square 1: 687
elapsed time 6:58:39Мы видим в протоколе: проверÑемый набор ÑоÑтоит из 502602 ЛК, из них первые четыре ÑвлÑÑŽÑ‚ÑÑ Ð”Ð›Ðš (из группы MODLS 12-го порÑдка). Образовано 31947721 ортогональных пар. При Ñтом макÑÐ¸Ð¼Ð°Ð»ÑŒÐ½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° ОЛК у квадрата 1, Ñтот квадрат ÑвлÑетÑÑ Ð”Ð›Ðš. МакÑÐ¸Ð¼Ð°Ð»ÑŒÐ½Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° Ñодержит 687 ОЛК, и она одна. Среди ОЛК к квадрату 1 еÑÑ‚ÑŒ три ДЛК, вÑе оÑтальные - ЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ПопроÑила помощника попробовать поиÑк по файлу (Ñодержащему граф). МакÑÐ¸Ð¼Ð°Ð»ÑŒÐ½Ð°Ñ ÐºÐ»Ð¸ÐºÐ° размера 5 выглÑдит в таблице ортогональноÑти так 29866: [1, 2, 3, 4] Следовательно, надо иÑкать такой набор Ñимволов в Ñтроке [1, 2, 3, 4 Ðо так мы проверим только ортогональноÑÑ‚ÑŒ каждого ЛК четырём ДЛК. Рещё ведь надо проверить, например, наличие таких клик [1,2,3, или варианты [1,2,4, [1,2,5, и так далее. То еÑÑ‚ÑŒ могут быть, вполне вероÑтно, группы, в которых три ДЛК и, как минимум, два ЛК. Рещё интереÑнее, еÑли будет три ДЛК и три ЛК, да пуÑÑ‚ÑŒ даже вÑе шеÑÑ‚ÑŒ ЛК. Однако группа MOLS 12-го порÑдка из шеÑти ЛК пока науке неизвеÑтна, извеÑтна только из пÑти ЛК. Вдруг в найденном мной наборе ÑущеÑтвует макÑÐ¸Ð¼Ð°Ð»ÑŒÐ½Ð°Ñ ÐºÐ»Ð¸ÐºÐ° размера 6, пуÑÑ‚ÑŒ даже ÑоÑтоÑÑ‰Ð°Ñ Ñ‚Ð¾Ð»ÑŒÐºÐ¾ из ЛК. Ргде-то напиÑано, что группа MOLS 12-го порÑдка из шеÑти ЛК не ÑущеÑтвует? ГоÑпода, еÑли вам Ñто извеÑтно, пожалуйÑта, Ñообщите. Программа SageMath не знает группу MOLS 12-го порÑдка, ÑоÑтоÑщую из шеÑти взаимно ортогональных ЛК. Я думаю, что в программу введены вÑе новейшие результаты в Ñтой облаÑти. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Смотрим поÑледовательноÑÑ‚ÑŒ OEIS https://oeis.org/A001438 Maximal number of mutually orthogonal Latin squares (or MOLS) of order n. Цитирую Parker and others conjecture that a(10) = 2. Комментарий довольно Ñвежий, вÑего год назад. Значит, пока вÑÑ‘-таки неизвеÑтна группа MOLS 12-го порÑдка, ÑоÑтоÑÑ‰Ð°Ñ Ð¸Ð· шеÑти взаимно ортогональных ЛК. Ðо и не утверждаетÑÑ, что Ñ‚Ð°ÐºÐ°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° не ÑущеÑтвует, потому что в таком Ñлучае было бы напиÑано a(12) = 5. КÑтати, в Ñтой Ñтатье OEIS был бы хорош пример найденной мной группы MOLS 12-го порÑдка, ÑоÑтоÑщей из четырёх ДЛК и одного ЛК  Очень краÑÐ¸Ð²Ð°Ñ Ð³Ñ€ÑƒÐ¿Ð¿Ð° MOLS, к тому же, оригинальнаÑ, потому что такую группу программа SageMath, например, не знает, она выдаёт ÑовÑем другую группу, ÑоÑтоÑщую из пÑти ЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитата из ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117&postid=1189 Ура! Я её нашла! Сделала новый Ñкриншот 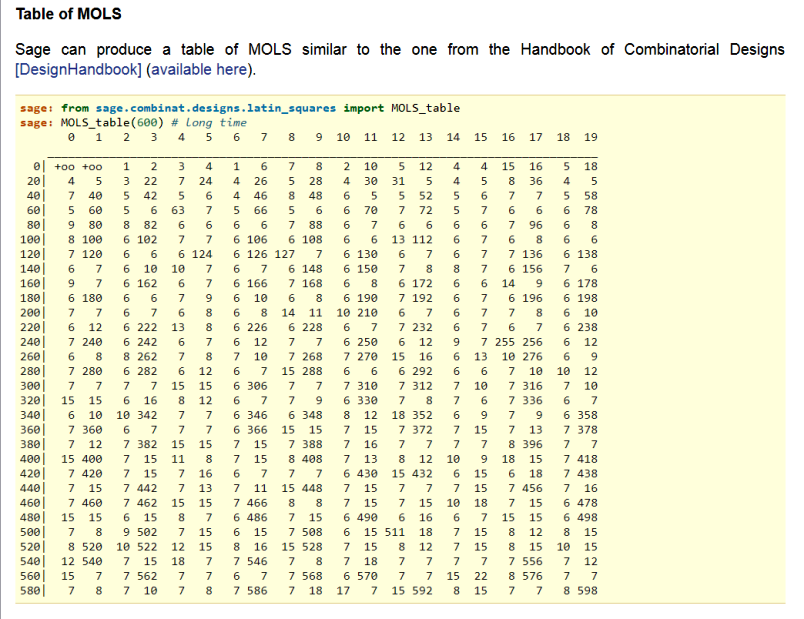 Ðу вот, здеÑÑŒ тоже напиÑано, что Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 12 извеÑтна группа MOLS из пÑти ЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ЗдеÑÑŒ https://math.stackexchange.com/questions/4156562/modls-of-order-12 по-прежнему Ð¿Ð¾Ð»Ð½Ð°Ñ Ñ‚Ð¸ÑˆÐ¸Ð½Ð°. Добавила комментарий о том, что Ñ Ð½Ð°ÑˆÐ»Ð° пÑтый квадрат к найденной группе MODLS, Ñодержащей четыре ДЛК. Вот как выглÑдит комментарий I found the fifth square for the MODLS group I found, containing four diagonal Latin squares (see question). Может, кто-нибудь чего-нибудь Ñкажет по Ñтому поводу. Уже никакой надежды не оÑталоÑÑŒ. Ðаверное, в Ñамом деле, Ñ Ð½Ð°ÑˆÐ»Ð° уникальную группу MODLS, доÑеле неизвеÑтную науке. Поразительно, что в OEIS Ñту группу MODLS до Ñих пор не утвердили. Ð¡Ñ‚Ð°Ñ‚ÑŒÑ Ð² OEIS https://oeis.org/A328873 Моё добавление COMMENTS a(12) >= 4. - Natalia Makarova, May 30 2021 Ð, они ÑомневаютÑÑ, что группа правильнаÑ. Им надо, чтобы гоÑподин Ватутин Ñто подтвердил :) П-о-н-и-м-а-ÑŽ... Ðу, он и подтвердил :) Добавил группу в Ñвой "подтверждающий ÑпиÑок". ОпÑÑ‚ÑŒ не утверждают. Чего-то ещё ждут. Может быть, поÑлали группу какому-нибудь ÑкÑперту и ждут заключениÑ. Ðу, Ñто Ñ Ñ‚Ð°Ðº фантазирую :) ХотÑ... редактор пиÑал же: "Ð’ OEIS еÑÑ‚ÑŒ Ñтандарты качеÑтва и процеÑÑ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÐºÐ¸". Ладно, пуÑÑ‚ÑŒ проверÑÑŽÑ‚. Думаю, что не пройдёт и года, как утвердÑÑ‚. Впрочем, может быть, и не утвердÑÑ‚, а удалÑÑ‚ добавление. И вÑе дела! Ðет Ð´Ð¾Ð±Ð°Ð²Ð»ÐµÐ½Ð¸Ñ - нет вопроÑов. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
У Ð½Ð°Ñ Ñ Ð¿Ð¾Ð¼Ð¾Ñ‰Ð½Ð¸ÐºÐ¾Ð¼ еÑÑ‚ÑŒ огромный граф, в котором нам пока не удалоÑÑŒ найти клику макÑимального размера. Программа SageMath что-то забукÑовала на проверке Ñтого графа. Пока думаем, что делать Ñ Ñтим графом. Решили одну подзадачу. Помощник поиÑком по файлу нашёл только один ЛК, которому ортогональны вÑе четыре ДЛК (1, 2, 3, 4) 232546: [1,2,3,4,4160,4197,5232,13227,26395,28179], 232546: [28236,37561,38880,43155,43178,43767,45433,49360,49368,68176], 232546: [68814,71421,75756,76699,88603,88620,91100,91381,93818,94433], 232546: [94482,96544,99871,103053,103142,105990,113031,114800,118952,121596], 232546: [123247,125412,137754,141965,142256,144878,146487,152173,153656,154834], 232546: [155076,157011,159949,162469,164407,166309,167101,167237,187348,189063], 232546: [189754,189808,190487,190755,194776,195898,198243,199669,202352,202370], 232546: [202522,202534,202673,256134,259456,263133,263244,265777,267231,271276], 232546: [272415,272570,274385,275651,287974,290407,293324,293389,295354,295941], 232546: [312034,312616,320117,321010,322543,322571,325273,334560,334679,335765], 232546: [336330,336553,339846,342177,342199,342491,343532,343726,343767,344364], 232546: [347527,347899,348365,349186,349690,351269,356214,356566,356758,357252], 232546: [357621,357670,359073,362430,363397,365610,366527,371222,373449,391229], 232546: [391485,392045,392146,392811,393296,394670,395172,395212,399663,401186], 232546: [405847,412076,412618,414582,418475,424722,424733,424751,426769,428571], 232546: [428793,429570,430533,452769,452853,452977,453086,453132,454305,456243], 232546: [456636,462350,462870,462890,469075,469202,470833,470943,473041,495201], 232546: [495427,497409,498658,499048], Тут, конечно, клика размера 5, ÑÐ¾Ð´ÐµÑ€Ð¶Ð°Ñ‰Ð°Ñ Ñ‡ÐµÑ‚Ñ‹Ñ€Ðµ ДЛК и один ЛК. И Ñто та ÑÐ°Ð¼Ð°Ñ ÐºÐ»Ð¸ÐºÐ°, которую Ñ ÑƒÐ¶Ðµ нашла ранее. Квадрат 232546 - вот он 0 1 2 3 4 5 6 7 8 9 10 11 3 0 7 1 6 2 9 5 10 4 11 8 2 5 0 7 8 1 10 3 4 11 6 9 1 3 5 0 9 7 4 2 11 6 8 10 6 4 10 9 0 8 3 11 2 1 7 5 7 2 3 5 10 0 11 1 6 8 9 4 4 9 8 6 1 11 0 10 5 3 2 7 5 7 1 2 11 3 8 0 9 10 4 6 10 8 6 11 2 4 7 9 0 5 3 1 9 6 11 4 3 10 1 8 7 0 5 2 8 11 4 10 5 9 2 6 1 7 0 3 11 10 9 8 7 6 5 4 3 2 1 0 ПоÑмотрите, Ñколько у Ñтого ЛК ортогональных Ñоквадратов (помимо четырёх ДЛК)! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Далее, помощник приÑлал мне ÑпиÑок вÑех ортогональных Ñоквадратов к ДЛК 1, 2, 3, 4 1: [2,3,4,403,480,484,631,1225,1254,2609], 1: [2828,2831,3595,3663,3705,3901,3961,5667,5853,6295], 1: [6307,7546,8221,8225,8450,8713,9367,9629,9655,9820], 1: [10776,10884,11082,11770,14554,15549,15811,15841,16050,16053], 1: [18595,18699,19016,19683,21181,21193,21843,22268,22746,22937], 1: [23239,23274,23279,25287,27765,27940,30619,30636,30975,31502], 1: [33223,34580,34630,34633,34966,35011,35408,35790,36414,36582], 1: [38480,38998,39009,39975,40392,41961,44580,44728,45094,45097], 1: [45760,46722,46840,47822,48010,49041,51453,51938,52231,52610], 1: [52977,55452,55501,55504,55520,55953,56830,58678,61933,64637], 1: [66336,68025,68823,69332,71629,71703,72845,74457,75824,76031], 1: [77105,77188,78812,79100,79267,80208,82214,82236,82396,83832], 1: [83833,83944,85217,85247,89082,89459,89839,90094,90241,90537], 1: [90610,91181,91253,91295,91659,92216,92664,92726,92985,93424], 1: [93494,93641,93806,94960,95031,97452,97468,97785,98317,99139], 1: [99299,100187,100190,100890,100961,101189,101536,102280,102324,102349], 1: [102414,102679,103348,105779,106224,106358,106385,106793,107209,107217], 1: [107508,108395,108404,108424,108539,108549,108553,109277,109536,110502], 1: [111285,111292,111306,113395,113683,113871,114356,114531,114537,114796], 1: [114902,114917,115826,124977,125223,128732,130140,132641,133483,134010], 1: [134456,134889,135142,135524,135561,136187,136788,138800,139531,140308], 1: [140327,141693,142016,142558,142611,142777,143530,143783,146684,147053], 1: [147266,147396,147957,148622,149164,149245,150596,150708,152220,152277], 1: [152742,153157,155025,155063,156345,168049,168051,168353,168442,168646], 1: [169190,169512,169816,169939,170239,171189,171260,172906,173939,176406], 1: [177676,177786,178457,178870,179559,179598,179603,180000,180027,180194], 1: [181144,181212,181336,184897,184996,185529,188231,188387,189164,189210], 1: [189217,189356,189436,190421,190506,190572,190730,191186,192242,193148], 1: [194576,194660,196592,197020,197687,198093,199550,199848,200198,200952], 1: [204139,204206,204377,204460,205419,205477,205659,206826,206929,206979], 1: [207310,207329,207435,208208,209546,209913,209915,210291,210553,212010], 1: [212755,212781,212820,212925,213150,213452,214258,214402,214553,214744], 1: [215419,215611,215643,215645,215796,217924,218392,218597,220311,220905], 1: [220955,221340,222440,222778,222789,222840,223072,223594,223607,223824], 1: [223834,223871,224055,225307,225463,226509,226716,226847,230432,230948], 1: [231131,231904,232546,232590,235030,235296,236167,237739,249503,249723], 1: [250855,253675,254952,255027,255912,256119,257394,258176,259125,259317], 1: [259336,259872,260318,261421,261456,262228,262235,262937,263511,264710], 1: [264923,264926,265353,266553,270204,270247,270330,270655,271943,274304], 1: [274647,276168,276441,278728,281162,283091,283355,283452,283510,284316], 1: [284387,285664,287336,288294,290360,291905,293062,293617,296041,297122], 1: [297917,299421,301685,301686,301702,302604,303114,304406,304415,304638], 1: [305327,305408,305684,305685,305701,306330,306337,306766,307673,307674], 1: [308785,309171,309607,309969,309971,310472,310619,310913,311034,311993], 1: [312475,312792,315175,315526,316417,316631,316765,319505,320360,321042], 1: [321607,322260,322318,323746,324006,324333,326268,326516,326531,327796], 1: [328243,328292,328515,328794,328889,329797,332964,334583,334619,336363], 1: [336719,336841,337305,345525,346080,347057,347093,347115,347116,349338], 1: [349348,349896,349916,350909,351168,351190,351191,353513,353650,353720], 1: [353816,353818,353888,354654,354692,354693,355727,355747,355929,355996], 1: [355997,357183,357235,357522,360481,361417,361549,361642,361847,362345], 1: [364021,366393,366402,366958,367107,367135,368091,369229,369238,370560], 1: [370575,371662,371838,373628,374307,374858,381761,382629,382630,382732], 1: [383194,383258,385409,385422,386405,387458,387491,387500,387518,388547], 1: [389319,389656,389761,389862,391449,391681,391930,394195,394390,396924], 1: [397542,406182,407739,408541,409293,409315,410001,410070,411350,411399], 1: [411402,411418,411460,411506,411611,411814,413000,414272,414279,416474], 1: [417741,418203,418257,420466,420699,420730,420840,421021,421202,422043], 1: [422508,422546,422640,422660,423612,424436,424453,425143,425412,426053], 1: [426846,426986,427283,428356,428409,428789,431469,432835,432919,434716], 1: [434977,435441,436487,436512,436514,437817,437853,438494,438511,438969], 1: [440028,440791,440877,442932,444069,444406,447350,447676,447691,448356], 1: [449382,451366,451657,451664,451684,453939,455962,456071,456299,457067], 1: [457074,457094,458005,458270,459257,459719,460698,461661,461832,463656], 1: [463692,465586,468568,469417,469771,473314,473805,473816,474198,474932], 1: [475659,475747,475920,476383,476451,476786,476923,479534,480480,482364], 1: [484443,484449,484597,484699,485132,485881,486563,488201,488204,491027], 1: [491168,491193,492480,492483,493386,493443,494604,494667,496627,496641], 1: [496715,497044,497157,497534,499903,501953,501987], 2: [1,3,4,393,903,2206,2555,2668,2963,5388], 2: [5652,6717,7259,7265,8491,9710,10724,11127,13157,13742], 2: [15549,15570,15807,17500,19213,19973,20074,20156,20366,21714], 2: [22042,22133,22553,22558,22912,22923,25958,26031,26034,27506], 2: [27672,28569,28916,29149,29487,30576,30581,30622,30665,30667], 2: [31043,33892,33949,34732,35340,36013,36045,36369,36386,36643], 2: [36654,37227,37280,37303,37658,37686,38307,40031,40166,40180], 2: [41356,41609,41661,41770,43233,43440,43741,43745,43793,43986], 2: [52958,53972,54783,55273,55396,58471,59048,59100,61628,61710], 2: [61938,62063,62231,62439,62477,62625,62681,62838,65061,65469], 2: [68705,69646,69742,69855,70429,70583,71971,72962,74000,74026], 2: [75044,75374,75694,76397,76433,76855,77298,77843,79109,79505], 2: [79991,80043,83040,83257,84603,84890,85966,86238,88226,88279], 2: [88425,88731,88865,89367,90401,90436,91761,92284,92377,92428], 2: [92598,93923,94157,95157,95272,95306,95347,95762,96465,97193], 2: [99174,99236,103304,103335,103738,111228,112881,113505,114223,116927], 2: [118460,118949,119470,120200,120281,120284,120416,120628,120984,121462], 2: [121603,123480,125211,126457,126473,127215,127265,127320,127386,129324], 2: [130021,130753,130769,130997,131724,132204,134938,135388,136354,136442], 2: [136541,137401,137554,137630,138625,138687,138836,139150,139835,140144], 2: [140352,140415,140471,140913,142838,142996,143094,143502,143686,145245], 2: [145564,145566,146784,146937,147030,149034,149246,149575,149577,149748], 2: [149924,150731,150812,150884,151258,151804,151815,153182,153190,153376], 2: [153389,153397,153527,153535,157369,158790,159215,159336,159463,160420], 2: [160542,160791,161312,162645,163152,165148,166401,166558,166881,167146], 2: [167239,168388,168439,170412,170514,170603,173423,173499,173602,173688], 2: [174656,174830,174851,175110,175115,175217,175255,176428,176471,176480], 2: [176633,176642,177572,177727,177767,177807,178293,178643,181697,181846], 2: [182047,182065,184822,186156,186177,186385,186418,192629,192791,193009], 2: [193558,194344,194914,195054,195119,195272,195340,197265,197339,198062], 2: [200356,200734,201654,201773,202132,202434,202547,202924,203686,204307], 2: [204758,205498,206028,206042,206132,208589,208609,209110,219477,219996], 2: [220269,221027,221819,222018,222090,222803,223520,225340,225662,226045], 2: [226492,226750,228187,229005,230039,231912,231913,232087,232111,232362], 2: [232546,232810,234273,236314,237185,238271,239646,240285,240465,240473], 2: [240550,241620,241636,241769,241793,242165,242312,243407,243842,244991], 2: [245011,245519,246579,246621,246667,246692,246743,247429,248463,248634], 2: [249288,249473,250552,253619,253622,253658,253705,254282,254356,255695], 2: [256256,256491,257549,257558,257894,257909,258063,258078,259840,260405], 2: [260539,263075,263420,263650,264089,265393,265816,267073,267470,267481], 2: [268160,268734,279607,280243,280372,280440,281455,282364,282521,283096], 2: [285840,287358,287482,288570,288972,289081,291809,293364,293412,293666], 2: [293966,295830,296211,296546,297708,297960,299049,299716,300095,300099], 2: [347122,347746,347907,349077,349195,349220,352991,353245,353340,355672], 2: [356841,356852,356940,357575,357714,357925,358028,358111,359435,362871], 2: [363578,363649,363732,364080,364633,365503,365570,365642,367006,367152], 2: [367180,367852,375569,375649,375706,376110,377340,377342,378558,378591], 2: [381280,381299,381537,381620,381628,382342,382448,382621,384819,384884], 2: [386037,386073,386184,386291,386603,386709,387680,387901,388802,389059], 2: [389420,390138,390209,393758,393926,395648,395681,395868,395873,395936], 2: [397159,397204,397327,397668,398374,399424,399486,399594,399598,400203], 2: [400863,401223,402107,402325,403560,405856,406080,406488,407183,407514], 2: [408158,408599,408810,409027,409280,409397,409519,411172,411174,412500], 2: [413758,414089,414192,414910,415690,418800,419098,421446,422391,422925], 2: [425890,429378,429761,430762,432601,434099,435441,436227,439341,440876], 2: [442007,442164,442194,442212,442321,445229,445231,445554,446706,447207], 2: [448317,448881,449051,450349,450574,450897,450973,451372,451399,451414], 2: [451597,452753,452755,453807,453879,454228,454243,454369,454381,454565], 2: [454864,455137,457314,457316,457359,458486,458720,458734,459348,459737], 2: [460279,460650,460764,462015,462134,462136,463486,464814,466226,466288], 2: [466314,467096,469208,469296,469407,469942,470126,470197,470427,472772], 2: [473663,473874,474440,475151,475208,475975,476356,479348,479515,479522], 2: [479601,481231,481248,481808,482014,483058,483204,483363,484365,485236], 2: [486233,486956,487252,487264,487436,487752,487864,490281,490414,490563], 2: [490656,490681,492112], 3: [1,2,4,93,128,363,1535,1823,2036,2040], 3: [2726,3303,4156,6979,7466,7474,7547,7607,7785,7925], 3: [8485,9192,9514,9693,11873,12057,12608,12747,12749,14248], 3: [14596,15549,15819,16396,16960,18261,18654,18687,18716,19403], 3: [20620,20635,23844,24964,25543,26465,26988,27181,35921,36081], 3: [36319,37390,38644,39412,39587,39691,39939,39955,40015,40148], 3: [40672,40863,41032,43101,43130,46661,46720,47054,47352,47355], 3: [47631,47824,48242,48244,48478,48740,48816,49472,50212,50680], 3: [53609,53722,53898,53952,54363,54585,54711,55673,55675,55861], 3: [55906,56076,57077,57734,58153,59050,59152,59301,59706,59792], 3: [60095,60251,60273,62551,62709,62784,64137,65252,65327,66773], 3: [67782,67951,68507,69752,71759,73083,73352,74301,77243,77768], 3: [80992,81017,81264,82434,82660,83095,85632,85892,86900,86907], 3: [88609,90418,90488,93708,94073,94947,95048,98189,99532,99576], 3: [100632,102217,102886,103030,103441,103909,105329,105664,106118,106326], 3: [107880,109223,109932,110120,110432,110750,111253,111261,111277,111588], 3: [112085,112222,112477,115037,115068,115257,115937,116066,116953,116961], 3: [117266,117493,118151,118157,118452,118959,119049,119597,119634,120252], 3: [120288,121872,122059,123790,123934,123940,124689,125973,126249,127952], 3: [127988,128890,129142,129810,129985,130394,130970,131812,132126,132536], 3: [132955,133355,133700,133705,134352,134545,145259,146154,147886,148095], 3: [148644,148747,149174,149232,159137,159141,159419,159444,159530,159803], 3: [161350,161449,161946,164258,165332,165397,165399,165453,165628,165922], 3: [166044,167233,167359,167366,168654,170025,170167,170715,171249,171625], 3: [172427,172782,172971,173673,174015,174030,174443,174447,175104,175251], 3: [175336,176627,176631,176941,177042,177815,178066,178241,179007,179352], 3: [180336,180411,181621,181626,181667,182214,185424,186755,186823,187837], 3: [187876,187909,187957,188173,189701,196813,196867,196871,197341,198242], 3: [198524,198596,198600,199567,199573,201331,201513,202248,203125,203295], 3: [204492,204587,205828,205918,206004,207858,208228,209734,210306,210768], 3: [211127,213285,213422,213944,213993,214090,214616,215343,215984,216336], 3: [216547,216679,225992,226307,226419,226423,226989,228817,229015,229098], 3: [229985,229992,231703,232323,232546,233153,233159,233888,234230,234238], 3: [235281,235319,235326,235579,235661,236686,237045,240556,240699,241970], 3: [242612,242664,245133,245483,248036,248297,250115,250123,250161,250284], 3: [250788,250990,252694,252809,252971,253049,253076,301049,301703,301908], 3: [301949,303306,306141,306243,306363,306422,306528,306998,307499,307647], 3: [308902,308946,309495,310218,311651,312148,312710,314263,314452,314731], 3: [314766,315429,315601,316320,316437,317822,317829,318564,319372,320156], 3: [320419,320565,321967,322359,322364,322435,322443,322513,329485,329802], 3: [332191,332455,332724,333646,333800,334230,334254,335118,336249,336493], 3: [337187,340424,341029,341789,342377,344409,344413,344654,344966,346386], 3: [348073,349380,351654,351679,351747,351924,352451,355111,355488,357387], 3: [357479,358261,359180,359322,359613,361595,361638,362867,363409,364198], 3: [365395,365447,367190,367394,367552,367659,373131,373794,374227,374410], 3: [374629,375184,375903,376530,378394,378966,379217,379485,379558,379837], 3: [381738,381908,381915,382139,382497,383128,383165,383716,384090,387176], 3: [387331,387523,387737,393241,393330,393595,393604,395354,396325,396983], 3: [397017,397179,397267,397510,397733,398008,398594,399036,399064,399101], 3: [399910,400187,400481,400486,402643,403665,405251,415712,415793,416136], 3: [416192,416318,416423,417401,417963,417999,418766,419574,421955,422833], 3: [422895,422960,423080,423798,423997,424311,424350,425474,426431,426439], 3: [426477,426919,428077,428345,429073,429716,429740,430604,431449,431851], 3: [432124,432184,433150,433532,433996,434053,434055,435441,436311,436455], 3: [439148,440240,440361,440474,443078,443963,443968,444504,446850,446914], 3: [447455,449024,450616,450805,453636,453852,457517,458074,458182,458583], 3: [459327,459481,459668,460663,461426,461546,461795,465893,466157,466945], 3: [467071,467350,467929,468465,468663,468710,468909,469262,472203,472237], 3: [472635,473461,475321,475683,476606,478512,478517,478571,478792,480659], 3: [480669,481082,481133,483691,484487,484491,484543,485245,485458,485466], 3: [486271,486281,486415,486600,487025,488159,488373,488470,488477,488764], 3: [489524,493577,493755,495023,495147,495383,496172,497620,498027,498058], 4: [1,2,3,1954,3064,3194,4335,4667,5218,6389], 4: [8358,8401,8455,10720,10780,12070,12264,12338,12414,12431], 4: [12719,15571,15706,15947,16727,16740,18993,19338,21532,23759], 4: [23772,24911,25220,25221,26005,26174,26249,26672,26830,27020], 4: [32434,33243,33891,34539,35145,39122,39128,39872,41190,41822], 4: [42449,42853,43446,43510,45289,45983,46849,47317,47949,48394], 4: [49268,49394,49785,49818,49830,49853,52016,52765,52892,53130], 4: [53287,53853,54448,55325,55656,56128,57112,58141,60056,60572], 4: [60761,61546,61547,61934,61956,61981,63090,63553,63677,63806], 4: [65080,65327,65498,65499,65815,65857,68163,68886,69346,69850], 4: [69891,70091,70094,70951,71232,71455,71460,71819,72040,72119], 4: [72234,73609,73816,77637,78130,78171,78269,78575,80762,80763], 4: [80824,80888,81949,82065,82220,82629,83602,84086,84177,84189], 4: [84370,84374,85006,87577,88297,89656,90002,90987,91564,91608], 4: [92526,93331,94382,94838,94842,151691,152114,152188,152413,153609], 4: [153798,154834,154903,155087,155368,155510,155704,156529,157093,157194], 4: [157394,157942,158642,159184,159314,159683,161544,161548,161804,162581], 4: [163007,163146,163414,165444,166467,167143,167203,167272,167721,168135], 4: [170441,170442,170484,170873,171916,171917,172212,172580,173335,184507], 4: [185264,187213,187337,187365,187557,188124,188260,188760,189234,189237], 4: [189319,190105,190146,190600,191283,191458,191561,191808,192280,192282], 4: [192699,193670,194104,194175,194473,196085,196619,196845,196860,197476], 4: [197649,197768,198387,198432,201456,203551,203691,203748,205483,206345], 4: [206809,210535,211225,211567,211627,211655,214942,215667,215709,216391], 4: [216770,218817,218828,219156,219188,219354,220038,222714,222753,222777], 4: [224128,224132,224458,224710,224730,227144,227294,227821,228462,228513], 4: [229032,229054,229457,229791,229803,229905,232546,233456,236114,236359], 4: [236447,237493,237498,237605,237809,238147,238192,240207,240439,240682], 4: [244853,244867,244872,245972,245976,246561,246566,246639,248098,248126], 4: [248346,248977,251867,251930,252316,252418,253299,253302,253725,262196], 4: [262492,263430,263524,263599,264854,264857,264964,268245,269048,269606], 4: [269850,271432,273000,273024,273563,273973,277626,278717,280748,281750], 4: [282451,282465,282678,282869,283285,283845,284736,285831,285961,286497], 4: [286878,287065,287257,288220,289706,289764,290013,290031,290267,290504], 4: [292166,292602,292849,293467,293666,293980,293992,294275,296824,296956], 4: [297182,297540,297551,298547,298595,299082,299097,299378,300235,300519], 4: [301109,302357,302367,305621,306692,307377,307876,308120,308418,308595], 4: [309316,309366,309520,309523,309693,310209,310532,310843,311532,313178], 4: [313525,313679,314206,314227,323119,323249,324531,324714,325369,325372], 4: [325385,325692,331118,331272,331669,333983,334082,337479,338066,339026], 4: [339983,340187,341243,341411,341815,344183,344603,345333,345338,345927], 4: [346721,348127,349060,349383,350029,350251,350344,352353,352915,353173], 4: [353175,353241,354122,355592,356096,356170,356718,356953,360315,360426], 4: [361132,361269,361871,362844,363720,363890,366678,366941,368316,370895], 4: [370901,372302,375063,375423,375748,377516,378811,378973,380064,380380], 4: [381144,382608,383629,385032,386538,386745,386778,388038,389094,389127], 4: [389275,389682,392327,392354,392710,393841,393866,394038,394886,395232], 4: [395443,396127,396213,396303,396401,396512,398149,398501,398675,399359], 4: [401113,402658,403348,403626,404014,404107,404123,404176,406952,407840], 4: [408274,408279,408303,408739,408945,411191,412279,414408,415071,415275], 4: [415432,416330,416937,417105,417503,417688,417691,420616,421001,421028], 4: [422473,422525,423026,423140,423394,425412,425766,425770,426242,426791], 4: [426828,426833,426975,429900,430191,431289,431301,431307,433169,437418], 4: [437537,438816,438984,439211,439967,440211,442245,442386,442779,445262], 4: [445354,447070,447080,447636,448179,448626,448694,448807,450982,451844], 4: [452282,452294,453547,453785,455487,455618,455797,456547,457226,457308], 4: [457356,457866,458021,467685,468174,468370,468388,470829,475630,476061], 4: [477117,477538,477685,480323,480338,480644,482887,485276,485525,485683], 4: [488193,488818,489300,490154,490634,491164,491950,492197,492265,492432], 4: [494479,494515,494751,494764,495445,495643,495692,496082,497013,497241], 4: [497670,498849,502118,502324,502341], Тут надо придумать, как поиÑкать общие ортогональные ЛК, Ñкажем, к ДЛК 1, 2 и 3, или к ДЛК 1 и 2; ну, тут много вариантов. Пока не придумываетÑÑ Ð°Ð²Ñ‚Ð¾Ð¼Ð°Ñ‚Ð¸Ð·Ð°Ñ†Ð¸Ñ Ñтого поиÑка. Ðо ÑÐ°Ð¼Ð°Ñ Ð³Ð»Ð°Ð²Ð½Ð°Ñ Ð·Ð°Ð´Ð°Ñ‡Ð°: проверить граф на клику размера 6, паче чаÑÐ½Ð¸Ñ Ñ‚Ð°ÐºÐ°Ñ Ð²Ð¾Ð¾Ð±Ñ‰Ðµ ÑущеÑтвует в природе. ПуÑÑ‚ÑŒ Ñта клика ÑоÑтоит из вÑех ЛК, Ñто тоже очень хорошо. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Я попроÑила помощника выложить таблицу ортогональных пар (Ñтот Ñамый огромный граф) на ЯндекÑ.ДиÑк Вот здеÑÑŒ https://disk.yandex.ru/d/wfQVzrZvfW35PQ текÑтовый файл Ñжат, в Ñжатом виде 172,3 МБ. ГоÑпода! Ð’Ñ‹ можете поиÑкать в Ñтом графе макÑимальную клику. ПожалуйÑта, раÑÑкажите, еÑли у Ð²Ð°Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ñ‚ÑÑ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Я тут Ñравнила группы MOLS... Цитата из ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=138&postid=2452 Мне удалоÑÑŒ раÑширить Ñту группу до пÑти взаимно ортогональных ЛК, только пÑтый ЛК не ÑвлÑетÑÑ Ð”Ð›Ðš. Ð”Ð»Ñ Ð¿Ð¾Ñ€Ñдка 32, наверное, Ð¿Ð¾Ð´Ð¾Ð±Ð½Ð°Ñ Ð¿Ð¾Ð»Ð½Ð°Ñ ÑиÑтема MOLS. Ðту полную ÑиÑтему MOLS можно поÑмотреть в теме https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117 ИнтереÑÐ½Ð°Ñ Ð·Ð°ÐºÐ¾Ð½Ð¾Ð¼ÐµÑ€Ð½Ð¾ÑÑ‚ÑŒ! PS. Добавлю полную ÑиÑтему MOLS 4-го порÑдка [code]0 1 2 3 3 2 1 0 1 0 3 2 2 3 0 1 0 1 2 3 2 3 0 1 3 2 1 0 1 0 3 2 0 1 2 3 1 0 3 2 2 3 0 1 3 2 1 0[/code] |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Я поÑмотрела на полную ÑиÑтему MOLS 32-го порÑдка. Да! Ð’ÑÑ‘ точно так же! Ð’Ñе квадраты получаютÑÑ Ð´Ñ€ÑƒÐ³ из друга переÑтановкой Ñтрок. ЕдинÑтвенный ЛК имеет похожую Ñтруктуру (Ñмотрите на диагонали) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 17 16 19 18 21 20 23 22 25 24 27 26 29 28 31 30 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 18 19 16 17 22 23 20 21 26 27 24 25 30 31 28 29 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 19 18 17 16 23 22 21 20 27 26 25 24 31 30 29 28 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 20 21 22 23 16 17 18 19 28 29 30 31 24 25 26 27 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 21 20 23 22 17 16 19 18 29 28 31 30 25 24 27 26 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 22 23 20 21 18 19 16 17 30 31 28 29 26 27 24 25 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 23 22 21 20 19 18 17 16 31 30 29 28 27 26 25 24 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 24 25 26 27 28 29 30 31 16 17 18 19 20 21 22 23 9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6 25 24 27 26 29 28 31 30 17 16 19 18 21 20 23 22 10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5 26 27 24 25 30 31 28 29 18 19 16 17 22 23 20 21 11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4 27 26 25 24 31 30 29 28 19 18 17 16 23 22 21 20 12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3 28 29 30 31 24 25 26 27 20 21 22 23 16 17 18 19 13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2 29 28 31 30 25 24 27 26 21 20 23 22 17 16 19 18 14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1 30 31 28 29 26 27 24 25 22 23 20 21 18 19 16 17 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 17 16 19 18 21 20 23 22 25 24 27 26 29 28 31 30 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 18 19 16 17 22 23 20 21 26 27 24 25 30 31 28 29 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 19 18 17 16 23 22 21 20 27 26 25 24 31 30 29 28 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 20 21 22 23 16 17 18 19 28 29 30 31 24 25 26 27 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 21 20 23 22 17 16 19 18 29 28 31 30 25 24 27 26 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 22 23 20 21 18 19 16 17 30 31 28 29 26 27 24 25 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 23 22 21 20 19 18 17 16 31 30 29 28 27 26 25 24 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 24 25 26 27 28 29 30 31 16 17 18 19 20 21 22 23 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 25 24 27 26 29 28 31 30 17 16 19 18 21 20 23 22 9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6 26 27 24 25 30 31 28 29 18 19 16 17 22 23 20 21 10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5 27 26 25 24 31 30 29 28 19 18 17 16 23 22 21 20 11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4 28 29 30 31 24 25 26 27 20 21 22 23 16 17 18 19 12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3 29 28 31 30 25 24 27 26 21 20 23 22 17 16 19 18 13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2 30 31 28 29 26 27 24 25 22 23 20 21 18 19 16 17 14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 ВоÑÑ…Ð¸Ñ‚Ð¸Ñ‚ÐµÐ»ÑŒÐ½Ð°Ñ Ð·Ð°ÐºÐ¾Ð½Ð¾Ð¼ÐµÑ€Ð½Ð¾ÑÑ‚ÑŒ! И больше вÑего мне нравитÑÑ, что Ð½Ð°Ð¹Ð´ÐµÐ½Ð½Ð°Ñ Ð¼Ð½Ð¾Ð¹ группа MOLS 12-го порÑдка впиÑалаÑÑŒ в Ñту закономерноÑÑ‚ÑŒ. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese