В третьей группе сгенерировалось 67968 ДЛК.
ДЛК этой группы характеризуются второй строкой

5  6  7  8  9  0  1  2  3  4 15 16 17 18 19 10 11 12 13 14

Показываю два ДЛК из этой группы

 0  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17  18  19 
 5  6  7  8  9  0  1  2  3  4  15  16  17  18  19  10  11  12  13  14 
 1  2  3  4  0  6  7  8  9  5  11  12  13  14  10  16  17  18  19  15 
 4  0  1  2  3  9  5  6  7  8  14  10  11  12  13  19  15  16  17  18 
 2  3  4  0  1  7  8  9  5  6  12  13  14  10  11  17  18  19  15  16 
 10  11  12  13  14  15  16  17  18  19  0  1  2  3  4  5  6  7  8  9 
 12  13  14  10  11  17  18  19  15  16  2  3  4  0  1  7  8  9  5  6 
 14  10  11  12  13  19  15  16  17  18  4  0  1  2  3  9  5  6  7  8 
 11  12  13  14  10  16  17  18  19  15  1  2  3  4  0  6  7  8  9  5 
 15  16  17  18  19  10  11  12  13  14  5  6  7  8  9  0  1  2  3  4 
 17  18  19  15  16  12  13  14  10  11  7  8  9  5  6  2  3  4  0  1 
 13  14  10  11  12  18  19  15  16  17  3  4  0  1  2  8  9  5  6  7 
 18  19  15  16  17  13  14  10  11  12  8  9  5  6  7  3  4  0  1  2 
 16  17  18  19  15  11  12  13  14  10  6  7  8  9  5  1  2  3  4  0 
 19  15  16  17  18  14  10  11  12  13  9  5  6  7  8  4  0  1  2  3 
 7  8  9  5  6  2  3  4  0  1  17  18  19  15  16  12  13  14  10  11 
 9  5  6  7  8  4  0  1  2  3  19  15  16  17  18  14  10  11  12  13 
 6  7  8  9  5  1  2  3  4  0  16  17  18  19  15  11  12  13  14  10 
 8  9  5  6  7  3  4  0  1  2  18  19  15  16  17  13  14  10  11  12 
 3  4  0  1  2  8  9  5  6  7  13  14  10  11  12  18  19  15  16  17 

 0  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17  18  19 
 5  6  7  8  9  0  1  2  3  4  15  16  17  18  19  10  11  12  13  14 
 1  2  3  4  0  6  7  8  9  5  11  12  13  14  10  16  17  18  19  15 
 4  0  1  2  3  9  5  6  7  8  14  10  11  12  13  19  15  16  17  18 
 2  3  4  0  1  7  8  9  5  6  12  13  14  10  11  17  18  19  15  16 
 10  11  12  13  14  15  16  17  18  19  0  1  2  3  4  5  6  7  8  9 
 12  13  14  10  11  17  18  19  15  16  2  3  4  0  1  7  8  9  5  6 
 14  10  11  12  13  19  15  16  17  18  4  0  1  2  3  9  5  6  7  8 
 11  12  13  14  10  16  17  18  19  15  1  2  3  4  0  6  7  8  9  5 
 15  16  17  18  19  10  11  12  13  14  5  6  7  8  9  0  1  2  3  4 
 17  18  19  15  16  12  13  14  10  11  7  8  9  5  6  2  3  4  0  1 
 13  14  10  11  12  18  19  15  16  17  3  4  0  1  2  8  9  5  6  7 
 18  19  15  16  17  13  14  10  11  12  8  9  5  6  7  3  4  0  1  2 
 16  17  18  19  15  11  12  13  14  10  6  7  8  9  5  1  2  3  4  0 
 19  15  16  17  18  14  10  11  12  13  9  5  6  7  8  4  0  1  2  3 
 8  9  5  6  7  3  4  0  1  2  18  19  15  16  17  13  14  10  11  12 
 6  7  8  9  5  1  2  3  4  0  16  17  18  19  15  11  12  13  14  10 
 9  5  6  7  8  4  0  1  2  3  19  15  16  17  18  14  10  11  12  13 
 7  8  9  5  6  2  3  4  0  1  17  18  19  15  16  12  13  14  10  11 
 3  4  0  1  2  8  9  5  6  7  13  14  10  11  12  18  19  15  16  17 

ДЛК третьей группы обладают следующими свойствами

Order? 20

Enter the name of the squares file: group3
.. writing type information to file group3TypeDetail.txt

Counts
------
     67968 diagonal Latin
      1960 weakly pandiagonal
        80 axial symmetric
       236 center symmetric
     67968 nfr
        80 axial parity 1-way

В этой группе нет SODLS и DSODLS.

Ну вот, есть набор ДЛК, состоящий из 354400 ДЛК (три группы).
Проверить этот набор программой GetOrthogonal для меня уже проблема - очень долго будет проверяться.
А это только три группы!
Добавятся ещё ДЛК из 14 групп.

Пойду дальше генерировать ДЛК.

Вот проверить все полученные ДЛК набора (354400 шт.) на ортогональность исходному ЛК могу

Order? 20

Enter the name of the squares file: a
Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 2
    .. increasing LS store to     100,000
    .. increasing LS store to     200,000
    .. increasing LS store to     400,000
squares 354401
Get pairs for square number, (1 .. 354401)? 1
..output file a-1orths.txt
Pairs for square 1: 354400

Да! Все ДЛК набора ортогональны исходному ЛК.

А теперь представьте океан клик размера 3 в этом графе!
Очень многие ДЛК групп 1 и 2 ортогональны, это ортогональные пары; к каждой ортогональной паре добавляем исходный ЛК (который ортогонален обоим ДЛК) и - готова группа MOLS, состоящая из двух ДЛК и одного ЛК.
Но... нам нужна клика размера 4.
Нам нужно найти в наборе ДЛК клику размера З, это будет группа MODLS, состоящая из трёх взаимно ортогональных ДЛК.
Добавив к этой группе MOLDS исходный ЛК (которому ортогональны все ДЛК), получим группу MOLS, состоящую из трёх ДЛК и одного ЛК.
Это задача-минимум.
Я не знаю, существует ли такая группа MOLS 20-го порядка.
Очень хочется, чтобы она существовала :)
И очень хочется её найти, в случае существования.

Завершила генерацию ДЛК.
Набор состоит из 1454080 нормализованных различных ДЛК.
Распишу количество ДЛК в группах

группа 1 - 143216
группа 2 - 143216
группа 3 - 67968
группа 4 - 72944
группа 5 - 87680
группа 6 - 87680
группа 7 - 72944
группа 8 - 67968
группа 9 - 72944
группа 10 - 87680
группа 11 - 87680
группа 12 - 72944
группа 13 - 67968
группа 14 - 72944
группа 15 - 87680
группа 16 - 87680
группа 17 - 72944

Demis любезно согласился попробовать проверить этот набор ДЛК на ортогональные пары программой GetOrthogonal.
Пока не знаем, справится ли программа с таким большим набором.
Я такой большой набор, конечно, ни разу не проверяла.
Если удастся получить таблицу ортогональных пар (граф) для ДЛК этого набора, уже хорошо.
Правда дальше предстоит ещё более сложное дело: найти в этом графе максимальную клику.

Да, задача непростая.
Для каждого квадратика из 1454080 штук надо найти все его ортогональки (в рамках данного набора ДЛК).
И ортогональных пар получится ох как много, если, конечно, программа справится за приемлемое время.
А потом среди всех этих ортогональных соквадратов надо найти три взаимно ортогональных.

И в то же время задача абсолютно прозрачная: дано конечное число ДЛК. Очевидно, что среди этих ДЛК
1) либо есть три взаимно ортогональных ДЛК;
2) либо их нет.
Третьего не дано!

В этом сообщении
https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=142&postid=2681
показана очень интересная группа MOLS 18-го порядка, состоящая из двух ДЛК и одного ЛК

ДЛК
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
14  6 15  2  3  4  5  0  1  7  8  9 16 17 11 12 13 10
 7 17 10 11  2  3  4  6 15  0  1 12 13 14  9 16  8  5
 9  0 13  8 14  2  3 10 11  6 15 16 17  7 12  1  5  4
12  7  6 16  1 17  2  8 14 10 11 13  0  9 15  5  4  3
16  9  0 10 12 15 13  1 17  8 14  6  7 11  5  4  3  2
10 12  7  6  8  9 11 15 13  1 17  0 14  5  4  3  2 16
17 13 16 12  9  7  0  2  3  4  5 14 11 15  1  8 10  6
15 11 14 17 13 16 12  5  4  3  2  1  8 10  6  0  7  9
 1 15 11 14 17 13 16  3  2  5  4  8 10  6  0  7  9 12
11 14 17 13 16 12  9  4  5  2  3 15  1  8 10  6  0  7
 8  2  3  4  5  0 14  9 10 12  6  7 15 16 17 11  1 13
 2  3  4  5  7 11 17 12  6 16  0 10  9  1 13 14 15  8
 3  4  5  9 15 14 10 16  0 13  7  2  6 12  8 17 11  1
 4  5 12  1 11  6  8 13  7 17  9  3  2  0 16 10 14 15
 5 16  8 15  0 10  1 17  9 14 12  4  3  2  7 13  6 11
13 10  1  7  6  8 15 14 12 11 16  5  4  3  2  9 17  0
 6  8  9  0 10  1  7 11 16 15 13 17  5  4  3  2 12 14

ДЛК
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
 9 17  7  0  2  3  4 16 10  8  1 12 13 14 15  5  6 11
12  8  6 16 17  0  2  5  1 10  7 13 14 15  4 11  9  3
13 12 10 11  5  6 17  4  7  1 16 14 15  3  9  8  2  0
14 13 12  1  9  4 11  3 16  7  5 15  2  8 10  0 17  6
15 14 13 12  7  8  3  2  5 16  4  0 10  1 17  6 11  9
17 15 14 13 12 16 10  0  4  5  3  1  7  6 11  9  8  2
 2  0 17  6 11  9  8 12 13 14 15  3  4  5 16  7  1 10
11  9  8 10  1  7 16 14 15 12 13  6 17  0  2  3  4  5
 3  2  0 17  6 11  9 15 14 13 12  4  5 16  7  1 10  8
 6 11  9  8 10  1  7 13 12 15 14 17  0  2  3  4  5 16
10  3  4  5 16 17  0  1  9 11  8  2  6 12 13 14 15  7
 4  5 16  7  0  2  1 10 11  6  9  8  3 17 12 13 14 15
16  7  1  2  3 10 15  8  6 17 11  5  9  4  0 12 13 14
 1 10  3  4  8 15 14  9 17  0  6  7 16 11  5  2 12 13
 8  4  5  9 15 14 13 11  0  2 17 10  1  7  6 16  3 12
 5 16 11 15 14 13 12  6  2  3  0  9  8 10  1 17  7  4
 7  6 15 14 13 12  5 17  3  4  2 16 11  9  8 10  0  1

ЛК
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
11  0  1  7  5  8  9 10 12  4 15 16  6  3 13  2 17 14
 2 11  0  1 10  9 12 15 16  8 13 14  5  6  7 17  3  4
 3  7 11  0  1 15  4 13  2 12  6  9 14 10 17  5  8 16
 4  5 10 11  0  1 13  6  7 16 14  3 15 17  9 12  2  8
 5  8  9 15 11  0  1 14 10  2  3 13 17  4 16  7 12  6
 6  9 12  4 13 11  0  3 15  7  5 17  8  2 10 16 14  1
 7 10 15 13  6 14  3  0 17  1 11  2 16 12  8  4  9  5
 8 12 16  2  7 10 15 17  0 11  1  4  9  5  3 14  6 13
 9  4  8 12 16  2  7  1 11  0 17  5  3 14  6 13 15 10
10 15 13  6 14  3  5 11  1 17  0  7  2 16 12  8  4  9
 1 16 14  9  3 13 17  2  4  5  7  0 11  8 15  6 10 12
12  6  5 14 15 17  8 16  9  3  2  1  0 11  4 10 13  7
13  3  6 10 17  4  2 12  5 14 16  8  1  0 11  9  7 15
14 13  7 17  9 16 10  8  3  6 12 15  4  1  0 11  5  2
15  2 17  5 12  7 16  4 14 13  8  6 10  9  1  0 11  3
16 17  3  8  2 12 14  9  6 15  4 10 13  7  5  1  0 11
17 14  4 16  8  6 11  5 13 10  9 12  7 15  2  3  1  0

Эту группу я построила очень давно по известному алгоритму.
Очаровательный ЛК! Ну, пальчики оближешь :)
Сейчас хочу попробовать применить к этому ЛК мой новый алгоритм с перестановками строк.
Очень интересно, что тут получится.
Если граф будет сильно большой, опять не смогу проверить на максимальную клику.

Кстати, для группы MOLS 12-го порядка, найденной мной, я этот алгоритм опробовала.
Всё замечательно сработало!
ЛК в этой группе MOLS тоже очаровательный, он выше показан вместе со всей группой MOLS.
Набор ДЛК получился небольшой, всего 16512 ДЛК.
Программа SageMath справилась с полученным графом и выдала океан клик размера 4.
Клика размера 5 не найдена в этом графе.
Речь идёт о кликах только для ортогональных ДЛК, потому что ЛК при проверке на ортогональные пары отсутствовал в наборе.
Если ЛК добавить к любой из найденных групп MODLS, получится группа MOLS, состоящая из четырёх ДЛК и одного ЛК.
Одна из таких групп MOLS показана выше.

Эксперимент с MOLS 18-го порядка выполнила.
ДЛК получилось при перестановке строк в ЛК всего 6 штук.
И они не дали ни одной ортогональной пары.
Даже исходному ЛК они не ортогональны.

В показанной группе MOLS 18-го порядка ДЛК и ЛК не получаются друг из друга перестановкой строк.
Похоже, мой новый алгоритм работает только для порядков серии n = 4k, k = 1, 2, 3, ...

Demis ознакомился с работой программы GetOrthogonal пока в лёгком режиме 2.
То есть он проверил все ДЛК набора на ортогональность исходному ЛК.
Протокол работы программы

Order? 20
 
Enter the name of the squares file: all-1-17
Choose 1 - get counts and maximum pairs, or 2 - get pairs for one square: 2
    .. increasing LS store to     100,000
    .. increasing LS store to     200,000
    .. increasing LS store to     400,000
    .. increasing LS store to     800,000
    .. increasing LS store to   1,600,000
squares 1454081
Get pairs for square number, (1 .. 1454081)? 1
..output file all-1-17-1orths.txt
Pairs for square 1: 1454080

elapsed time 0:03:41

Замечательно!
Все ДЛК набора ортогональны исходному ЛК, как и ожидалось.
И выполнилась проверка очень быстро - 0:03:41.

Впереди проверка всех ДЛК на ортогональность - сложная часть эксперимента.
ЛК из набора в этой части эксперимента удаляется, проверяются только ДЛК на ортогональность.

Проверка у Demis ещё на закончилась.
Граф получится колоссальный, если вообще программа вырулит, что-то очень долго она работает.

Занималась архивированием своих статей о латинских квадратах с сайта.
Натолкнулась на статью "ЕЩЁ ОДНА ГРУППА MOLS 20-го ПОРЯДКА"
http://www.natalimak1.narod.ru/mols20a.htm
Очень интересная группа! Она состоит из четырёх взаимно ортогональных ЛК.
Первый квадрат в этой группе является ДЛК, я его уже показывала раньше, сейчас ещё раз покажу.
Вот он



Ещё более интересен последний ЛК в этой группе MOLS.
Сейчас скопирую и покажу.

Вот он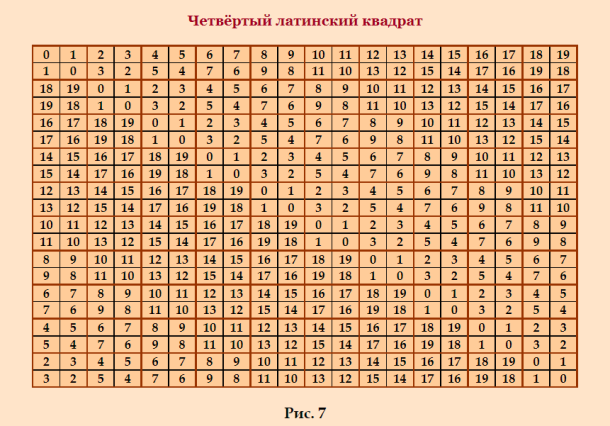



В этом ЛК классическая блочная структура!
Немного преобразовала этот ЛК, сделала его редуцированным (просто переставила строки)

 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1
 3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3
 5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2
 6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5
 7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4
 8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7
 9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6
10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9
11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8
12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11
13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10
14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13
15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12
16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16

Можно попробовать перестановку строк в этом ЛК.

Кстати, первый ЛК, который является ДЛК, тоже имеет классическую блочную структуру, просто в нём раскраска несколько другая - не показывает классические блоки.

PS. Сравните структуру показанного ЛК 20-го порядка со структурой ЛК 10-го порядка
(из сообщения https://boinc.progger.info/odlk/forum_thread.php?id=41&postid=762)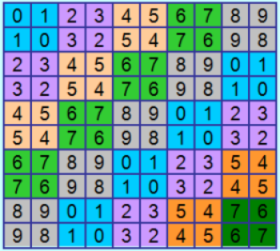



В этом ЛК блоки, окрашенные более тёмным цветом, повёрнуты.
Структура в этих ЛК совершенно аналогичная.

Поэкспериментировала с показанным выше редуцированным ЛК 20-го порядка блочной структуры.
Пока получила вот такие группы MOLS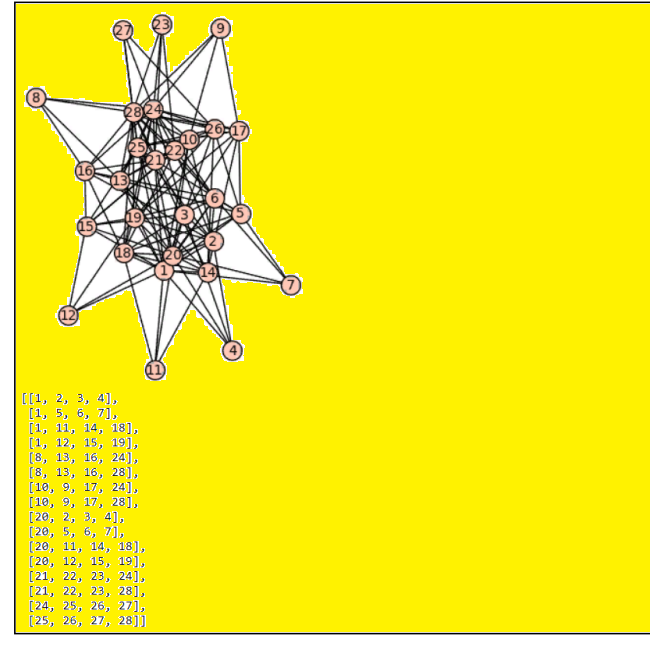



Видим тут клики размера 4.
Это граф, который дал показанную картинку

sage: d = {1: [2,3,4,5,6,7,10,11,12,13,14,15,18,19,21,25],
2: [1,3,4,10,16,19,20,22,25],
3: [1,2,4,6,15,17,18,20,24,26,28],
4: [1,2,3,20],
5: [1,6,7,13,17,18,20,21,26],
6: [1,3,5,7,14,16,19,20,22,24,28],
7: [1,5,6,20],
8: [13,16,24,28],
9: [10,17,24,28],
10: [1,2,9,13,15,17,20,21,24,26,28],
11: [1,14,18,20],
12: [1,15,19,20],
13: [1,5,8,10,14,16,20,22,24,25,28],
14: [1,6,11,13,17,18,20,21,26],
15: [1,3,10,12,16,19,20,22,25],
16: [2,6,8,13,15,18,21,24,28],
17: [3,5,9,10,14,19,24,25,28],
18: [1,3,5,11,14,16,19,20,22,24,28],
19: [1,2,6,12,15,17,18,20,24,26,28],
20: [2,3,4,5,6,7,10,11,12,13,14,15,18,19,21,25],
21: [1,5,10,14,16,20,22,23,24,25,28],
22: [2,6,13,15,18,21,23,24,28],
23: [21,22,24,28],
24: [3,6,8,9,10,13,16,17,18,19,21,22,23,25,26,27],
25: [1,2,13,15,17,20,21,24,26,27,28],
26: [3,5,10,14,19,24,25,27,28],
27: [24,25,26,28],
28: [3,6,8,9,10,13,16,17,18,19,21,22,23,25,26,27]}
sage: g = Graph (d)
sage: g.show ()
sage: g.cliques_maximum ()

Ну, такой граф поверяется программой SageMath легко.
В наборе всего 28 квадратов.
Кстати, вот их свойства

Order? 20

Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail.txt

Counts
------
        20 Latin
         8 diagonal Latin
         8 weakly pandiagonal
         4 center symmetric
         4 nfr
         4 nfc
         1 nfr nfc
         2 self-transpose
        18 orthogonal pair
         8 self-orthogonal
         8 doubly self-orthogonal
         4 symmetric parity
         4 transpose parity

Очень вкусные квадратики!
Интересно: все 8 ДЛК являются SODLS и DSODLS. Ктому же, они ещё и слабо пандиагональные.

Но, по-моему, клик, содержащих два ДЛК нет.
Завтра проверю.

Пока покажу группу MOLS, соответствующую первой клике, выданной программой SageMath
[1, 2, 3, 4]

ЛК (редуцированный)
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1
 3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3
 5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2
 6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5
 7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4
 8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7
 9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6
10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9
11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8
12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11
13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10
14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13
15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12
16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16

ЛК
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9
18 19  1  0  2  3  5  4  7  6  8  9 11 10 12 13 15 14 17 16
 8  9 11 10 12 13 15 14 17 16 18 19  1  0  2  3  5  4  7  6
16 17 18 19  0  1  3  2  5  4  6  7  8  9 10 11 13 12 15 14
 6  7  8  9 10 11 13 12 15 14 16 17 18 19  0  1  3  2  5  4
15 14 17 16 19 18  0  1  2  3  5  4  7  6  9  8 10 11 12 13
 5  4  7  6  9  8 10 11 12 13 15 14 17 16 19 18  0  1  2  3
13 12 14 15 17 16 18 19  0  1  3  2  4  5  7  6  8  9 10 11
 3  2  4  5  7  6  8  9 10 11 13 12 14 15 17 16 18 19  0  1
11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 9  8 10 11 13 12 14 15 16 17 19 18  0  1  3  2  4  5  6  7
19 18  0  1  3  2  4  5  6  7  9  8 10 11 13 12 14 15 16 17
 7  6  9  8 11 10 12 13 14 15 17 16 19 18  1  0  2  3  4  5
17 16 19 18  1  0  2  3  4  5  7  6  9  8 11 10 12 13 14 15
 4  5  6  7  8  9 11 10 13 12 14 15 16 17 18 19  1  0  3  2
14 15 16 17 18 19  1  0  3  2  4  5  6  7  8  9 11 10 13 12
 2  3  5  4  6  7  9  8 11 10 12 13 15 14 16 17 19 18  1  0
12 13 15 14 16 17 19 18  1  0  2  3  5  4  6  7  9  8 11 10

ДЛК
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8
15 14 17 16  8  9 10 11 13 12  5  4  7  6 18 19  0  1  3  2
 4  5  6  7 19 18  1  0  2  3 14 15 16 17  9  8 11 10 12 13
19 18 10 11 13 12  4  5 16 17  9  8  0  1  3  2 14 15  6  7
 8  9  1  0  2  3 15 14  7  6 18 19 11 10 12 13  5  4 17 16
13 12  4  5 17 16 18 19 11 10  3  2 14 15  7  6  8  9  1  0
 2  3 15 14  6  7  9  8  0  1 12 13  5  4 16 17 19 18 10 11
17 16 19 18  0  1 12 13 14 15  7  6  9  8 10 11  2  3  4  5
 6  7  8  9 11 10  3  2  5  4 16 17 18 19  1  0 13 12 15 14
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9
14 15 16 17  9  8 11 10 12 13  4  5  6  7 19 18  1  0  2  3
 5  4  7  6 18 19  0  1  3  2 15 14 17 16  8  9 10 11 13 12
18 19 11 10 12 13  5  4 17 16  8  9  1  0  2  3 15 14  7  6
 9  8  0  1  3  2 14 15  6  7 19 18 10 11 13 12  4  5 16 17
12 13  5  4 16 17 19 18 10 11  2  3 15 14  6  7  9  8  0  1
 3  2 14 15  7  6  8  9  1  0 13 12  4  5 17 16 18 19 11 10
16 17 18 19  1  0 13 12 15 14  6  7  8  9 11 10  3  2  5  4
 7  6  9  8 10 11  2  3  4  5 17 16 19 18  0  1 12 13 14 15

ЛК
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
13  5  6 11  0 19 14  3 15 10  2  8  1 17  9  7 12 18  4 16
 4  7 10 15 14 18 13 17  1 19  6  5 16 12 11  3  2  8  9  0
14 19  9  8 16  7 12  1  4 13  0  3 17 18  6  2 10 11  5 15
 1 12 16  2  5  3  0  8 14 15 11  6 19  7  4 13 17  9 10 18
17 13 11 18  6  0 10  5  9  7  3  2 14  4  1 19 15 12 16  8
11  4 15  7  9 13 16 12 19 14  8 18 10  5  3 17  1  2  0  6
19  2 14  9  1 15 17 18  7  4 16 10  0  8 12  6 11 13  3  5
12 18 17  5 11  6  8 16 13  2  1 15  7  3  0  4  9 14 19 10
16 17  0 12  3  2 18 10 11  1  9 13  6 14 19  5  7 15  8  4
 3 15 19 14 13 11  5  4  0 12 18  7  9 10 17 16  8  1  6  2
 9  6  7  4  2  1 19  0 17  5 14 16  8 15 18 12 13 10 11  3
 8 16  5 19 15 10  9  6  2 18 17  1  3 11 13  0 14  4  7 12
18 10  4  0  8  9  3 15 16 11 13 12  2  6  5  1 19  7 17 14
15  8 12  1 17 14  4  2  3  0  7 19  5  9 16 10 18  6 13 11
10  9 13 17  7 12 11 19  5  6  4 14 15  0  8 18  3 16  2  1
 6  0  3 16 10  4  7  9 18  8 15 17 11  1  2 14  5 19 12 13
 5  3 18  6 19  8 15 14 10 16 12  9 13  2  7 11  4  0  1 17
 7 11  1 10 18 17  2 13 12  3 19  0  4 16 15  8  6  5 14  9
 2 14  8 13 12 16  1 11  6 17  5  4 18 19 10  9  0  3 15  7

Проверила все 16 клик, выданных программой SageMath.
Как и предположила, в каждой клике есть только один ДЛК.
Пока ничего принципиально нового не найдено, несколько альтернативных групп MOLS, аналогичных исходной. Они получены с помощью эквивалентных преобразований ЛК исходной группы MOLS.
Одна из полученных альтернативных групп MOLS показана выше.

А теперь выполнила небольшой (усечённый) эксперимент по новому алгоритму.
Сгенерировала ДЛК в 10 группах и в каждой группе только 10000 ДЛК.
Получила набор из 100000 ДЛК.
Программа GetOrthogonal работала довольно долго (три часа с хвостиком), вот протокол работы

Order? 20

Enter the name of the squares file: inp2
Choose 1 - get counts and maximum pairs, or 2 - get pairs for one square: 1
..output file inp2-orthCounts.txt
..output file inp2-orthNos.txt
    .. increasing LS store to     100,000
    .. increasing LS store to     200,000
squares 100000 total orthogonal pairs 9169
Maximum pairs for square 88580: 25
There is 1 other square with this maximum number of pairs.
..output file inp2-88580orths.txt
Pairs for square 88580: 25

elapsed time 3:16:36

Здесь ортогональных пар получилось не очень много и программа SageMath справилась с поиском максимальной клики в этом графе.
Итак, найдено 9169 ортогональных пар ДЛК.
Как и ранее в аналогичном эксперименте, все ДЛК набора ортогональны исходному ЛК, в котором переставляются строки.
Таким образом, получено 9169 групп MOLS, состоящих из двух ДЛК и одного ЛК.
Покажу одну из этих групп MOLS

ДЛК
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1
 3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7
10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9
11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8
13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10
19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16
17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3
18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
 7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4
 5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2
16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
 6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5
12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11
14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13
15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12
 9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6

ДЛК
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1
12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11
15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12
13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10
10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9
 6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5
 5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2
19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3
18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
 7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4
16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
 8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7
11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8
 9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6
14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13

ЛК
 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18
 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1
 3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0
 4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3
 5  4  7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2
 6  7  8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5
 7  6  9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4
 8  9 10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7
 9  8 11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6
10 11 12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9
11 10 13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8
12 13 14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11
13 12 15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10
14 15 16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13
15 14 17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12
16 17 18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15
17 16 19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14
18 19  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
19 18  1  0  3  2  5  4  7  6  9  8 11 10 13 12 15 14 17 16

Как видите, в этой группе MOLS все квадраты получаются друг из друга перестановкой строк (таков алгоритм).
Не исключена вероятность существования группы MOLS, состоящей из трёх ДЛК и одного ЛК.
Но выполнить эксперимент в полном объёме я не могу.
Вот для другого ЛК этот эксперимент выполняется в полном объёме, только полученный набор ДЛК у Demis до сих пор проверяется программой GetOrthogonal.
Набор содержит 1454080 ДЛК.
С этим ЛК набор будет, наверное, не меньше.
Так что, с полным экспериментом пока всё глухо.
Даже если программа GetOrthogonal вырулит, в конце концов, поиск максимальной клики в полученном графе - задача очень сложная.
Программа SageMath этот граф точно не возьмёт, и надо что-то изобретать для поиска максимальной клики в этом графе.

Свойства ДЛК и ЛК показанной группы MOLS 20-го порядка

Order? 20

Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_3.txt

Counts
------
         1 Latin
         2 diagonal Latin
         1 center symmetric
         3 nfr
         1 nfc
         1 nfr nfc
         1 self-transpose
         2 orthogonal pair
         1 axial parity 1-way
         1 symmetric parity
         1 transpose parity

Свойства для каждого квадрата

1 ...
diagonal Latin, nfr
diagonal Latin, nfr, orthogonal pair, axial parity 1-way (up-down)
Latin, center symmetric, nfr, nfc, nfr nfc, self-transpose, orthogonal pair, symmetric parity, transpose parity

О-о-о!!
Программа GetOrthogonal справилась-таки у Demis.
Протокол работы программы

Order? 20

Enter the name of the squares file: all-1-17
Choose 1 - get counts and maximum pairs, or 2 - get pairs for one square: 1
..output file all-1-17-orthCounts.txt
..output file all-1-17-orthNos.txt
    .. increasing LS store to     100,000
    .. increasing LS store to     200,000
    .. increasing LS store to     400,000
    .. increasing LS store to     800,000
    .. increasing LS store to   1,600,000
squares 1454080 total orthogonal pairs 4604320
Maximum pairs for square 1: 560
There are 3 other squares with this maximum number of pairs.
..output file all-1-17-1orths.txt
Pairs for square 1: 560

elapsed time 245:46:47

Грандиозно! Больше 10 суток работала программа.
Граф получен! Важный такой граф, супер :)
Образовано 4604320 ортогональных пар.
Четыре ДЛК имеют 560 ОДЛК.

Напомню: проверялся на ортогональность набор ДЛК 20-го порядка, состоящий из 1454080 ДЛК.

Да-а-а-а, такой граф программа SageMath вряд ли проверит на максимальную клику.
Но, может быть, есть другие, более сильные программы поиска максимальной клики?
Подскажите, пожалуйста, господа.
Задачу очень хочется решить до конца.

А пока будем думать, как искать максимальную клику в таком огромном графе.
Demis огромная благодарность!
Первая часть эксперимента выполнена успешно.