Thread 'Спектр по Д-транÑверÑалÑм Ð´Ð»Ñ Ð”Ð›Ðš 15-го порÑдка'
Message boards : Science : Спектр по Д-транÑверÑалÑм Ð´Ð»Ñ Ð”Ð›Ðš 15-го порÑдка
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Дублирую Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=138&postid=2824 О Д-транÑверÑалÑÑ… ДЛК 15-го порÑдка Ðе помню, показывала ли Ñ Ð”-транÑверÑали Ð´Ð»Ñ Ð”Ð›Ðš 15-го порÑдка. Скорее вÑего, не показывала. У Ð¼ÐµÐ½Ñ ÐµÑÑ‚ÑŒ вÑего 308 КФ ДЛК данного порÑдка. Подчёркиваю: Ñто проÑто ÑущеÑтвенно различные ДЛК (не изоморфные), возможно, Ñреди них еÑÑ‚ÑŒ «пуÑтышки». ОДЛК Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 15 пыталаÑÑŒ иÑкать много раз и программой Белышева, и программой Tomas Brada. Программа Tomas Brada у Ð¼ÐµÐ½Ñ Ð²Ð¾Ð¾Ð±Ñ‰Ðµ входит в Ñтупор; программа Белышева работает, но ни черта не находит. ПроÑила помощника попробовать на Ñвоей мощной технике проверку программой Tomas Brada (поиÑк ОДЛК по чаÑÑ‚Ñм). Он попробовал, программа у него работает, но тоже ни черта не находит. Покрутил немного и прервал. Ð’ общем, Ñ ÐžÐ”Ð›Ðš 15-го порÑдка пока никакого уÑпеха. Ðедаром Ð´Ð»Ñ Ð¼Ð°ÐºÑимального чиÑла ОДЛК от одного ДЛК 15-го порÑдка имеем оценку a(15) >= 3. Ðта оценка получена из найденной мной группы MODLS 15-го порÑдка, ÑоÑтоÑщей из четырёх взаимно ортогональных ДЛК. Смотрите тему «MODLS of order 15» https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=115 ЗапуÑтила проверку на Д-транÑверÑали Ð´Ð»Ñ Ð¸Ð¼ÐµÑŽÑ‰ÐµÐ³Ð¾ÑÑ Ñƒ Ð¼ÐµÐ½Ñ Ð½Ð°Ð±Ð¾Ñ€Ð° КФ ДЛК 15-го порÑдка. Пока программа работает, покажу топовые ДЛК данного порÑдка по Д-транÑверÑалÑм из ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=130&postid=1741 (дублирую Ñообщение) Топ-8 ДЛК 15-го порÑдка по Д-транÑверÑалÑм в порÑдке ÑƒÐ±Ñ‹Ð²Ð°Ð½Ð¸Ñ Ð”Ð›Ðš предÑтавлены в виде КФ второго формата. 1. 389318 Д-транÑверÑалей ДЛК, поÑтроенный методом Гергели 0 8 9 14 7 3 4 10 5 2 13 12 6 11 1 9 1 7 4 8 10 2 12 3 13 11 5 14 0 6 4 14 2 13 9 1 7 8 11 0 6 10 3 12 5 7 9 4 3 1 8 13 14 10 11 0 2 5 6 12 10 3 8 1 4 12 9 6 7 14 5 0 11 2 13 8 7 1 9 3 5 14 13 12 4 2 6 0 10 11 13 2 11 0 5 14 6 4 9 12 7 1 8 3 10 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 5 12 3 10 6 0 11 2 8 1 9 13 7 14 4 2 4 13 7 14 6 0 11 1 9 12 8 10 5 3 1 11 6 12 13 2 5 0 4 3 10 14 9 8 7 3 5 10 8 12 7 1 9 0 6 14 11 13 4 2 6 0 14 5 11 13 3 1 2 10 8 4 12 7 9 11 10 0 6 2 4 12 5 14 7 3 9 1 13 8 12 6 5 2 0 11 10 3 13 8 1 7 4 9 14 ИллюÑÑ‚Ñ€Ð°Ñ†Ð¸Ñ (показан оригинальный ДЛК Гергели до Ð¿Ñ€ÐµÐ¾Ð±Ñ€Ð°Ð·Ð¾Ð²Ð°Ð½Ð¸Ñ Ð² КФ)  Смотрите мою Ñтатью http://www.natalimak1.narod.ru/dlk.htm 2. 308292 Д-транÑверÑалей 0 5 4 12 14 11 8 2 9 13 7 10 6 3 1 14 1 6 5 11 13 10 3 12 7 9 0 4 2 8 9 13 2 0 6 10 12 4 7 8 1 5 3 14 11 11 8 12 3 1 0 9 5 14 2 6 4 13 10 7 8 10 14 11 4 2 1 6 3 0 5 12 9 7 13 2 14 9 13 10 5 3 0 1 6 11 8 7 12 4 4 3 13 8 12 9 6 1 0 10 14 7 11 5 2 5 6 0 1 2 3 4 7 10 11 12 13 14 8 9 12 9 3 7 0 4 14 13 8 5 2 6 1 11 10 10 2 7 6 3 8 13 14 11 9 4 1 5 0 12 1 7 5 2 9 14 11 8 13 12 10 3 0 4 6 7 4 1 10 8 12 0 9 5 14 13 11 2 6 3 3 0 11 9 13 6 7 10 2 4 8 14 12 1 5 6 12 10 14 5 7 2 11 4 1 3 9 8 13 0 13 11 8 4 7 1 5 12 6 3 0 2 10 9 14 3. 308243 Д-транÑверÑалей 0 6 8 9 5 10 12 2 7 3 4 14 13 11 1 11 1 0 14 8 6 9 3 4 5 13 12 10 2 7 8 10 2 1 13 14 0 4 6 12 11 9 3 7 5 1 14 9 3 2 12 13 5 11 10 8 4 7 6 0 12 2 13 8 4 3 11 6 9 14 5 7 0 1 10 10 11 3 12 14 5 4 0 13 6 7 1 2 9 8 5 9 10 4 11 13 6 1 0 7 2 3 8 14 12 3 4 5 6 0 1 2 7 12 13 14 8 9 10 11 2 0 6 11 12 7 14 13 8 1 3 10 4 5 9 6 5 12 13 7 8 1 14 10 9 0 2 11 3 4 4 13 14 7 9 0 5 8 3 11 10 6 1 12 2 14 8 7 10 6 4 3 9 1 2 12 11 5 0 13 9 7 11 5 3 2 8 10 14 0 1 13 12 4 6 7 12 4 2 1 9 10 11 5 8 6 0 14 13 3 13 3 1 0 10 11 7 12 2 4 9 5 6 8 14 4. 306765 Д-транÑверÑалей 0 2 3 4 5 6 7 8 9 10 11 12 13 14 1 3 1 4 5 8 7 9 12 10 11 14 13 6 0 2 1 7 2 10 6 9 8 13 11 4 12 14 3 5 0 5 10 6 3 11 12 1 9 0 14 13 2 7 8 4 2 11 12 7 4 14 0 3 1 13 5 6 9 10 8 4 12 0 13 10 5 11 14 2 6 7 8 1 9 3 8 13 14 9 12 2 6 10 4 1 0 3 5 11 7 9 8 10 14 13 11 2 7 12 3 1 0 4 6 5 7 3 9 11 14 13 10 4 8 12 2 5 0 1 6 11 5 13 6 7 8 12 0 3 9 4 1 14 2 10 6 4 5 8 9 1 13 11 14 0 10 7 2 3 12 10 6 7 12 1 0 14 5 13 2 3 11 8 4 9 14 9 11 0 2 10 3 1 6 5 8 4 12 7 13 12 14 8 1 0 3 4 2 5 7 6 9 10 13 11 13 0 1 2 3 4 5 6 7 8 9 10 11 12 14 5. 306605 Д-транÑверÑалей 0 8 5 7 2 14 11 3 9 4 13 6 10 12 1 10 1 14 6 7 3 13 4 5 12 0 9 11 2 8 12 9 2 13 0 7 4 5 11 1 8 10 3 14 6 5 11 8 3 12 1 7 6 2 14 9 4 13 0 10 7 6 10 14 4 11 2 0 13 8 5 12 1 9 3 3 7 0 9 13 5 10 1 14 6 11 2 8 4 12 9 4 7 1 8 12 6 2 0 10 3 14 5 11 13 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 1 3 9 0 11 4 14 12 8 2 6 13 7 10 5 2 10 6 12 3 8 0 13 4 9 1 5 14 7 11 11 5 13 2 9 6 1 14 12 3 10 0 4 8 7 4 14 1 10 5 0 12 8 7 13 2 11 6 3 9 8 0 11 4 6 13 3 9 10 7 14 1 12 5 2 6 12 3 5 14 2 9 10 1 11 7 8 0 13 4 13 2 4 8 1 10 5 11 3 0 12 7 9 6 14 6. 305868 Д-транÑверÑалей [code] 0 8 13 7 6 9 4 12 11 2 14 10 5 3 1 5 1 14 12 7 0 8 11 3 13 9 6 4 2 10 14 6 2 13 11 7 1 10 12 8 0 5 3 9 4 2 13 0 3 12 10 7 9 14 1 6 4 8 5 11 7 3 12 1 4 11 9 8 2 0 5 14 6 10 13 8 7 4 11 2 5 10 14 1 6 13 0 9 12 3 9 14 7 5 10 3 6 13 0 12 1 8 11 4 2 6 0 1 2 3 4 5 7 9 10 11 12 13 14 8 12 10 3 6 13 2 14 1 8 11 4 9 7 0 5 11 2 5 14 1 8 13 0 4 9 12 3 10 7 6 1 4 8 0 9 14 12 6 5 3 10 13 2 11 7 3 9 6 10 8 13 0 5 7 4 2 11 14 1 12 10 5 11 9 14 6 2 4 13 7 3 1 12 8 0 4 12 10 8 5 1 11 3 6 14 7 2 0 13 9 13 11 9 4 0 12 3 2 10 5 8 7 1 6 14[/code] 7. 305408 Д-транÑверÑалей [code] 0 7 14 8 3 9 4 5 11 13 6 2 10 12 1 5 1 7 13 14 4 8 6 12 0 3 9 11 2 10 14 6 2 7 12 13 5 0 1 4 8 10 3 9 11 6 13 0 3 7 11 12 1 5 14 9 4 8 10 2 11 0 12 1 4 7 10 2 13 8 5 14 9 3 6 9 10 1 11 2 5 7 3 14 6 13 8 4 0 12 7 8 9 2 10 3 6 4 0 12 14 5 1 11 13 10 9 8 14 13 12 11 7 3 2 1 0 6 5 4 1 3 13 9 0 2 14 10 8 11 4 12 5 6 7 2 14 10 6 1 8 0 11 7 9 12 3 13 4 5 8 11 5 0 9 6 1 12 4 7 10 13 2 14 3 12 4 6 10 5 0 9 13 2 3 7 11 14 1 8 3 5 11 4 6 10 13 14 9 1 2 7 12 8 0 4 12 3 5 11 14 2 8 6 10 0 1 7 13 9 13 2 4 12 8 1 3 9 10 5 11 6 0 7 14[/code] 8. 304818 Д-транÑверÑалей [code] 0 7 9 12 8 6 2 11 10 3 4 14 13 5 1 3 1 7 8 11 14 0 10 4 5 13 12 6 2 9 1 4 2 7 14 10 13 9 6 12 11 0 3 8 5 12 2 5 3 7 13 9 8 11 10 1 4 14 6 0 8 11 3 6 4 7 12 14 9 2 5 13 0 1 10 11 14 10 4 0 5 7 13 3 6 12 1 2 9 8 7 10 13 9 5 1 6 12 0 11 2 3 8 14 4 2 3 4 5 6 0 1 7 13 14 8 9 10 11 12 10 0 6 11 12 3 14 2 8 13 9 5 1 4 7 6 5 12 13 2 8 11 1 7 9 14 10 4 0 3 4 13 14 1 9 12 5 0 2 7 10 8 11 3 6 14 8 0 10 13 4 3 6 5 1 7 11 9 12 2 9 6 11 14 3 2 8 5 1 4 0 7 12 10 13 5 12 8 2 1 9 10 4 14 0 3 6 7 13 11 13 9 1 0 10 11 4 3 12 8 6 2 5 7 14[/code] Покажу ÑвойÑтва Ñтих ДЛК, выданные утилитой Harry White [code]Order? 15 Enter the name of the squares file: inp .. writing type information to file inpTypeDetail_6.txt Counts ------ 8 diagonal Latin 7 associative 8 natural \diagonal 1 self-orthogonal[/code] ЗдеÑÑŒ вы видите 8 значений из верхней чаÑти Ñпектра Д-транÑверÑалей Ð´Ð»Ñ Ð”Ð›Ðš 15-го порÑдка. ЕÑÑ‚ÑŒ один SODLS, Ñтот ДЛК точно не «пуÑтышка». Ðто квадрат â„–4 в ÑпиÑке. ДЛК поÑтроен программой Harry White. КÑтати, Ñтот ДЛК ÑвлÑетÑÑ Ñ‚Ð°ÐºÐ¶Ðµ и DSODLS. Вот какие ÑвойÑтва у Ñтого ДЛК выдаёт Ð¼Ð¾Ð´Ð¸Ñ„Ð¸Ñ†Ð¸Ñ€Ð¾Ð²Ð°Ð½Ð½Ð°Ñ ÑƒÑ‚Ð¸Ð»Ð¸Ñ‚Ð° Harry White GetType [code]Order? 15 Enter the name of the squares file: inp .. writing type information to file inpTypeDetail_2.txt Counts ------ 1 diagonal Latin 1 associative 1 natural \diagonal 1 self-orthogonal 1 doubly self-orthogonal 1 symmetric parity[/code] ЗдеÑÑŒ отмечены оба ÑвойÑтва: self-orthogonal и doubly self-orthogonal. ______________________________________________________________________ конец дублируемого ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ ÐšÐ°Ðº видите, немного Ñпектром по Д-транÑверÑалÑм в ДЛК 15-го порÑдка Ñ Ð·Ð°Ð½Ð¸Ð¼Ð°Ð»Ð°ÑÑŒ уÐ�4 6 13 3 9 10 7 14 1 12 5 2 6 12 3 5 14 2 9 10 1 11 7 8 0 13 4 13 2 4 8 1 10 5 11 3 0 12 7 9 6 14[/code] 6. 305868 Д-транÑверÑалей [code] 0 8 13 7 6 9 4 12 11 2 14 10 5 3 1 5 1 14 12 7 0 8 11 3 13 9 6 4 2 10 14 6 2 13 11 7 1 10 12 8 0 5 3 9 4 2 13 0 3 12 10 7 9 14 1 6 4 8 5 11 7 3 12 1 4 11 9 8 2 0 5 14 6 10 13 8 7 4 11 2 5 10 14 1 6 13 0 9 12 3 9 14 7 5 10 3 6 13 0 12 1 8 11 4 2 6 0 1 2 3 4 5 7 9 10 11 12 13 14 8 12 10 3 6 13 2 14 1 8 11 4 9 7 0 5 11 2 5 14 1 8 13 0 4 9 12 3 10 7 6 1 4 8 0 9 14 12 6 5 3 10 13 2 11 7 3 9 6 10 8 13 0 5 7 4 2 11 14 1 12 10 5 11 9 14 6 2 4 13 7 3 1 12 8 0 4 12 10 8 5 1 11 3 6 14 7 2 0 13 9 13 11 9 4 0 12 3 2 10 5 8 7 1 6 14[/code] 7. 305408 Д-транÑверÑалей [code] 0 7 14 8 3 9 4 5 11 13 6 2 10 12 1 5 1 7 13 14 4 8 6 12 0 3 9 11 2 10 14 6 2 7 12 13 5 0 1 4 8 10 3 9 11 6 13 0 3 7 11 12 1 5 14 9 4 8 10 2 11 0 12 1 4 7 10 2 13 8 5 14 9 3 6 9 10 1 11 2 5 7 3 14 6 13 8 4 0 12 7 8 9 2 10 3 6 4 0 12 14 5 1 11 13 10 9 8 14 13 12 11 7 3 2 1 0 6 5 4 1 3 13 9 0 2 14 10 8 11 4 12 5 6 7 2 14 10 6 1 8 0 11 7 9 12 3 13 4 5 8 11 5 0 9 6 1 12 4 7 10 13 2 14 3 12 4 6 10 5 0 9 13 2 3 7 11 14 1 8 3 5 11 4 6 10 13 14 9 1 2 7 12 8 0 4 12 3 5 11 14 2 8 6 10 0 1 7 13 9 13 2 4 12 8 1 3 9 10 5 11 6 0 7 14[/code] 8. 304818 Д-транÑверÑалей [code] 0 7 9 12 8 6 2 11 10 3 4 14 13 5 1 3 1 7 8 11 14 0 10 4 5 13 12 6 2 9 1 4 2 7 14 10 13 9 6 12 11 0 3 8 5 12 2 5 3 7 13 9 8 11 10 1 4 14 6 0 8 11 3 6 4 7 12 14 9 2 5 13 0 1 10 11 14 10 4 0 5 7 13 3 6 12 1 2 9 8 7 10 13 9 5 1 6 12 0 11 2 3 8 14 4 2 3 4 5 6 0 1 7 13 14 8 9 10 11 12 10 0 6 11 12 3 14 2 8 13 9 5 1 4 7 6 5 12 13 2 8 11 1 7 9 14 10 4 0 3 4 13 14 1 9 12 5 0 2 7 10 8 11 3 6 14 8 0 10 13 4 3 6 5 1 7 11 9 12 2 9 6 11 14 3 2 8 5 1 4 0 7 12 10 13 5 12 8 2 1 9 10 4 14 0 3 6 7 13 11 13 9 1 0 10 11 4 3 12 8 6 2 5 7 14[/code] Покажу ÑвойÑтва Ñтих ДЛК, выданные утилитой Harry White [code]Order? 15 Enter the name of the squares file: inp .. writing type information to file inpTypeDetail_6.txt Counts ------ 8 diagonal Latin 7 associative 8 natural \diagonal 1 self-orthogonal[/code] ЗдеÑÑŒ вы видите 8 значений из верхней чаÑти Ñпектра Д-транÑверÑалей Ð´Ð»Ñ Ð”Ð›Ðš 15-го порÑдка. ЕÑÑ‚ÑŒ один SODLS, Ñтот ДЛК точно не «пуÑтышка». Ðто квадрат â„–4 в ÑпиÑке. ДЛК поÑтроен программой Harry White. КÑтати, Ñтот ДЛК ÑвлÑетÑÑ Ñ‚Ð°ÐºÐ¶Ðµ и DSODLS. Вот какие ÑвойÑтва у Ñтого ДЛК выдаёт Ð¼Ð¾Ð´Ð¸Ñ„Ð¸Ñ†Ð¸Ñ€Ð¾Ð²Ð°Ð½Ð½Ð°Ñ ÑƒÑ‚Ð¸Ð»Ð¸Ñ‚Ð° Harry White GetType [code]Order? 15 Enter the name of the squares file: inp .. writing type information to file inpTypeDetail_2.txt Counts ------ 1 diagonal Latin 1 associative 1 natural \diagonal 1 self-orthogonal 1 doubly self-orthogonal 1 symmetric parity[/code] ЗдеÑÑŒ отмечены оба ÑвойÑтва: self-orthogonal и doubly self-orthogonal. ______________________________________________________________________ конец дублируемого ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ ÐšÐ°Ðº видите, немного Ñпектром по Д-транÑверÑалÑм в ДЛК 15-го порÑдка Ñ Ð·Ð°Ð½Ð¸Ð¼Ð°Ð»Ð°ÑÑŒ уже давно. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾ÐºÐ°Ð¶Ñƒ, что Ñ Ñ‚Ð¾Ð³Ð´Ð° нашла. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Цитирую Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=138&postid=2825 Ðу вот, программа Tomas Brada раÑправилаÑÑŒ Ñ Ð”-транÑверÑалÑми в 308 ДЛК 15-го порÑдка. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Дублирую Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=138&postid=2826 Готово! Вот Ñ‚Ð°ÐºÐ°Ñ Ñ‡Ð°ÑÑ‚ÑŒ Ñпектра получилаÑÑŒ (в порÑдке возраÑтаниÑ) 304818 305408 305410 305534 305553 305650 305674 305678 305694 305770 305796 305863 305868 305880 305903 305917 305937 305972 305978 306009 306023 306026 306031 306035 306047 306054 306065 306079 306105 306108 306112 306125 306126 306149 306153 306163 306167 306169 306174 306197 306199 306212 306220 306227 306244 306247 306254 306264 306270 306276 306295 306300 306322 306324 306327 306333 306335 306341 306343 306345 306348 306352 306359 306360 306400 306414 306438 306439 306449 306478 306493 306495 306513 306525 306527 306532 306545 306555 306561 306562 306575 306583 306587 306588 306592 306604 306605 306617 306619 306621 306622 306638 306647 306651 306652 306653 306656 306673 306680 306683 306688 306690 306703 306720 306731 306733 306734 306741 306743 306748 306761 306765 306782 306798 306802 306808 306814 306839 306842 306851 306853 306861 306868 306881 306882 306889 306892 306897 306901 306909 306916 306921 306922 306948 306954 306967 306975 306985 306988 306989 306990 307012 307014 307015 307038 307044 307055 307059 307068 307075 307084 307088 307098 307108 307112 307130 307137 307165 307166 307177 307178 307181 307210 307213 307220 307225 307233 307240 307246 307251 307273 307315 307345 307359 307366 307409 307412 307423 307447 307454 307458 307483 307530 307532 307542 307571 307608 307682 307691 307728 307744 307814 307815 307843 307921 308243 308292 311140 311672 311749 311841 311972 312174 312196 312346 312396 312398 312441 312471 312504 312577 312657 312667 312674 312678 312765 312791 312807 312826 312845 312851 312859 312872 312875 312878 312904 312920 312929 312935 312988 313031 313032 313106 313116 313140 313144 313167 313178 313196 313214 313223 313248 313270 313288 313291 313296 313297 313302 313347 313354 313366 313419 313432 313478 313489 313492 313493 313494 313519 313550 313564 313607 313613 313642 313662 313665 313674 313708 313725 313736 313760 313836 313856 313986 314043 314044 314047 314053 314061 314127 314141 314145 314179 314204 314230 314264 314265 314278 314350 314374 314639 314978 315350 315596 315728 316084 389318 ИнтереÑные Ñлементы Ñпектра. Текущий макÑимум по Д-транÑверÑалÑм здеÑÑŒ приÑутÑтвует, конечно. ПоÑмотрим на предÑтавленный выше ÑпиÑок воÑьми топовых значений Д-транÑверÑалей 389318, 308292, 308243, 306765, 306605, 305868, 305408, 304818 Ð’Ñе Ñти Ð·Ð½Ð°Ñ‡ÐµÐ½Ð¸Ñ Ð² Ñпектре приÑутÑтвуют. Однако, ÑпиÑок топовых ДЛК по Д-транÑверÑалÑм можно изменить в ÑоответÑтвии Ñ Ð¿Ð¾Ð»ÑƒÑ‡ÐµÐ½Ð½Ñ‹Ð¼ Ñпектром. Ðапример, Топ-10 будет таким 314278, 314350, 314374, 314639, 314978, 315350, 315596, 315728, 316084, 389318 Какова оценка Ð´Ð»Ñ Ð¼Ð¸Ð½Ð¸Ð¼Ð°Ð»ÑŒÐ½Ð¾Ð³Ð¾ количеÑтва Д-транÑверÑалей в ДЛК 15-го порÑдка, мне пока неизвеÑтно. _______________________________________________________________________ конец дублируемого ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ Ð’Ð¾Ñ‚ такой у Ð¼ÐµÐ½Ñ Ð¿Ð¾Ð»ÑƒÑ‡Ð¸Ð»ÑÑ Ñпектр. Параметры Ñпектра Min = 304818 Max = 389318 ширина Ñпектра 84501 мощноÑÑ‚ÑŒ Ñпектра 297 коÑффициент плотноÑти Ñпектра K = 0,0035. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðу, и поÑледнее Ñообщение по Ñтой теме продублирую, пуÑÑ‚ÑŒ будет здеÑÑŒ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=138&postid=2827 Я не помню, ÑодержатÑÑ Ð»Ð¸ в проверенном наборе ДЛК из найденной мной группы MODLS 15-го порÑдка. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ñ€Ð¾Ð²ÐµÑ€ÑŽ. Показываю Ñту замечательную группу MODLS 15-го порÑдка в формате СРДЛК 0 6 10 12 13 2 7 14 1 8 11 3 9 4 5 2 1 14 9 11 12 3 13 0 10 4 8 5 6 7 1 3 2 13 8 10 11 12 9 5 0 6 14 7 4 8 2 4 3 12 0 9 11 6 1 14 13 7 5 10 14 0 3 5 4 11 1 10 2 13 12 7 6 9 8 3 13 1 4 6 5 10 9 12 11 7 14 8 0 2 11 4 12 2 5 14 6 8 10 7 13 0 1 3 9 13 12 11 10 9 8 0 7 14 6 5 4 3 2 1 5 11 13 14 1 7 4 6 8 0 9 12 2 10 3 12 14 6 0 7 3 2 5 4 9 8 10 13 1 11 6 5 8 7 2 1 12 4 13 3 10 9 11 14 0 4 9 7 1 0 13 8 3 5 14 2 11 10 12 6 10 7 0 8 14 9 5 2 3 4 6 1 12 11 13 7 8 9 6 10 4 14 1 11 2 3 5 0 13 12 9 10 5 11 3 6 13 0 7 12 1 2 4 8 14 0 11 14 2 5 10 13 8 6 1 12 4 7 9 3 14 1 10 13 3 6 9 0 2 11 5 7 8 4 12 3 13 2 9 12 4 14 1 10 6 7 0 5 11 8 9 4 12 3 8 11 5 2 14 7 1 6 10 0 13 13 8 5 11 4 0 10 3 7 2 14 9 1 12 6 7 12 0 6 10 5 1 4 3 13 8 2 11 14 9 4 7 11 1 14 9 6 5 12 0 3 10 13 8 2 10 9 8 0 1 2 3 7 11 12 13 14 6 5 4 12 6 1 4 11 14 2 9 8 5 0 13 3 7 10 5 0 3 12 6 1 11 10 13 9 4 8 14 2 7 8 2 13 5 0 12 7 11 4 14 10 3 9 6 1 1 14 4 8 13 7 0 12 9 3 6 11 2 10 5 6 3 9 14 7 8 4 13 0 10 2 5 12 1 11 2 10 6 7 9 3 12 14 5 8 11 1 4 13 0 11 5 7 10 2 13 8 6 1 4 9 12 0 3 14 0 13 6 9 2 1 10 4 14 7 3 8 11 5 12 13 1 12 14 8 3 2 5 7 4 0 10 6 11 9 7 12 2 11 13 0 4 6 5 1 9 14 10 8 3 6 7 11 3 10 12 1 14 2 8 13 9 0 4 5 3 14 7 10 4 9 11 13 0 12 8 1 5 6 2 1 4 13 7 9 5 8 12 11 0 2 6 14 3 10 10 2 5 12 7 8 6 11 1 3 14 13 4 9 0 8 0 1 2 3 4 5 7 9 10 11 12 13 14 6 14 5 10 1 0 11 13 3 8 6 7 2 9 12 4 4 11 0 8 12 14 3 2 6 9 5 7 1 10 13 12 8 9 13 6 2 14 1 3 5 10 4 7 0 11 9 10 14 5 1 6 12 0 13 2 4 11 3 7 8 11 6 4 0 5 13 9 8 10 14 1 3 12 2 7 5 3 8 4 14 10 7 9 12 11 6 0 2 13 1 2 9 3 6 11 7 0 10 4 13 12 5 8 1 14 0 5 9 6 10 4 14 2 13 12 7 1 3 11 8 12 1 6 8 14 9 5 3 11 7 2 4 10 0 13 10 11 2 14 0 13 8 4 7 3 5 9 1 12 6 7 9 10 3 13 1 12 5 4 6 8 2 11 14 0 5 7 8 9 4 12 2 6 14 0 3 10 13 1 11 13 6 7 0 8 5 11 14 1 4 9 12 2 10 3 2 12 14 7 1 0 6 13 5 8 11 3 9 4 10 9 8 0 1 2 3 4 7 10 11 12 13 14 6 5 4 10 5 11 3 6 9 1 8 14 13 7 0 2 12 11 4 12 2 5 10 13 0 3 9 6 14 7 8 1 3 13 1 4 11 14 0 8 12 2 10 5 6 7 9 14 0 3 12 6 8 10 9 2 13 1 11 4 5 7 8 2 13 5 9 11 7 10 6 1 14 0 12 3 4 1 14 4 10 12 7 3 11 9 5 0 6 8 13 2 6 3 11 13 7 2 1 12 0 10 4 8 5 9 14 из ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=115&postid=1272 ПоÑчитала Д-транÑверÑали в Ñтих ДЛК (количеÑтва Д-транÑверÑалей приведены в порÑдке раÑÐ¿Ð¾Ð»Ð¾Ð¶ÐµÐ½Ð¸Ñ Ð”Ð›Ðš в показанном ÑпиÑке) num_dtrans: 306605 num_dtrans: 305868 num_dtrans: 304818 num_dtrans: 308292 Ð’Ñе Ñти Ð·Ð½Ð°Ñ‡ÐµÐ½Ð¸Ñ Ð² полученном Ñпектре приÑутÑтвуют. ЗдеÑÑŒ и ДЛК Ñ Ð¼Ð¸Ð½Ð¸Ð¼Ð°Ð»ÑŒÐ½Ñ‹Ð¼ значением в Ñтой чаÑти Ñпектра num_dtrans: 304818 Ðаш малыш :) Ðти ДЛК не "пуÑтышки", более того: каждый из них имеет как минимум три ортогональных диагональных Ñоквадрата. СвойÑтва ДЛК Ñтой группы MODLS Order? 15
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_3.txt
Counts
------
4 diagonal Latin
4 associative
4 natural \diagonal
3 orthogonal pair
4 symmetric parity
Ð’Ñе ДЛК аÑÑоциативные. ЧудеÑные квадратики! ________________________________________ конец дублируемого ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Итак, извеÑтный на ÑÐµÐ³Ð¾Ð´Ð½Ñ Ð°Ð½Ñ‚Ð¸ÐºÐ²Ð°Ð´Ñ€Ð¾Ð·Ð°Ð²Ñ€Ð¸Ðº 15-го порÑдка 304818 Д-транÑверÑалей 0 13 6 9 2 1 10 4 14 7 3 8 11 5 12 13 1 12 14 8 3 2 5 7 4 0 10 6 11 9 7 12 2 11 13 0 4 6 5 1 9 14 10 8 3 6 7 11 3 10 12 1 14 2 8 13 9 0 4 5 3 14 7 10 4 9 11 13 0 12 8 1 5 6 2 1 4 13 7 9 5 8 12 11 0 2 6 14 3 10 10 2 5 12 7 8 6 11 1 3 14 13 4 9 0 8 0 1 2 3 4 5 7 9 10 11 12 13 14 6 14 5 10 1 0 11 13 3 8 6 7 2 9 12 4 4 11 0 8 12 14 3 2 6 9 5 7 1 10 13 12 8 9 13 6 2 14 1 3 5 10 4 7 0 11 9 10 14 5 1 6 12 0 13 2 4 11 3 7 8 11 6 4 0 5 13 9 8 10 14 1 3 12 2 7 5 3 8 4 14 10 7 9 12 11 6 0 2 13 1 2 9 3 6 11 7 0 10 4 13 12 5 8 1 14 Такой вот малыш :) Сколько же ОДЛК имеет Ñтот ДЛК? Ðу, как минимум три ОДЛК имеет, потому что Ñтот ДЛК из группы MODLS, ÑоÑтоÑщей из четырёх взаимно ортогональных ДЛК. Имеет ли ещё ОДЛК? Трудно Ñказать. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ñ€Ð¾Ð±ÑƒÑŽ поиÑк ОДЛК к Ñтому ОДЛК программой Tomas Brada (поиÑк ОДЛК по чаÑÑ‚Ñм). Программа вроде работает C:\Users\Дом\Downloads\libr>ortogonbw GsGzhdCArzC88TXLywPDxDTmvE2gw1vZyC6Z2Qi62 UMLkJ8vM6KmCZX3J3 1 1>output.txt init_trans(15) used 753 nodes num_dtrans: 304818 init_disjoint(15) used 226 heads and 4572496 nodes L(0) c(113) 1 / 18392 L(1) c(89) X / 8121 Видим, что программа разбила поиÑк на 18392 чаÑти. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð·Ð°Ð¿ÑƒÑ‰ÐµÐ½ поиÑк ОДЛК в первой чаÑти. Ðайдёт ли что-нибудь программа? Пока в выходном файле пуÑто. Программа работала больше чаÑа и не нашла ни одного ОДЛК. Прервала. Я пыталаÑÑŒ иÑкать ОДЛК к ДЛК 15-го порÑдка также программой Белышева. Ðичего не удалоÑÑŒ найти. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Проверила ÑвойÑтва 308 ДЛК 15-го порÑдка, в который поÑчитаны Д-транÑверÑали, утилитой Harry White Order? 15
Enter the name of the squares file: a
.. writing type information to file aTypeDetail.txt
Counts
------
308 diagonal Latin
107 associative
308 natural \diagonal
1 self-orthogonal
1 doubly self-orthogonal
107 symmetric parityТакие вот квадратики. Один из них ÑвлÑетÑÑ SODLS и DSODLS. 107 аÑÑоциативных ДЛК. Д-транÑверÑалей во вÑех Ñтих ДЛК много, прÑмо вÑе квадрозавры :) Показываю ДЛК, который ÑвлÑетÑÑ SODLS и DSODLS (поÑтроен программой Harry White) 306765 Д-транÑверÑалей 0 2 3 4 5 6 7 8 9 10 11 12 13 14 1 3 1 4 5 8 7 9 12 10 11 14 13 6 0 2 1 7 2 10 6 9 8 13 11 4 12 14 3 5 0 5 10 6 3 11 12 1 9 0 14 13 2 7 8 4 2 11 12 7 4 14 0 3 1 13 5 6 9 10 8 4 12 0 13 10 5 11 14 2 6 7 8 1 9 3 8 13 14 9 12 2 6 10 4 1 0 3 5 11 7 9 8 10 14 13 11 2 7 12 3 1 0 4 6 5 7 3 9 11 14 13 10 4 8 12 2 5 0 1 6 11 5 13 6 7 8 12 0 3 9 4 1 14 2 10 6 4 5 8 9 1 13 11 14 0 10 7 2 3 12 10 6 7 12 1 0 14 5 13 2 3 11 8 4 9 14 9 11 0 2 10 3 1 6 5 8 4 12 7 13 12 14 8 1 0 3 4 2 5 7 6 9 10 13 11 13 0 1 2 3 4 5 6 7 8 9 10 11 12 14 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Сгенерировала программой Harry White 500 Ñлучайных ДЛК 15-го порÑдка. ПоÑчитала в Ñтих ДЛК Д-транÑверÑали программой Tomas Brada. Ðайдено 323 новых Ñлемента Ñпектра. Объединила Ñти Ñлементы Ñ Ð½Ð°Ð¹Ð´ÐµÐ½Ð½Ñ‹Ð¼Ð¸ выше 297 Ñлементами, получилоÑÑŒ 620 Ñлементов Ñпектра. Показываю их вÑе 304818 305408 305410 305534 305553 305639 305650 305670 305674 305678 305694 305727 305740 305770 305796 305863 305868 305873 305880 305898 305903 305917 305924 305937 305953 305972 305978 306009 306023 306024 306026 306031 306035 306047 306048 306054 306056 306065 306067 306070 306079 306081 306086 306102 306105 306108 306112 306114 306125 306126 306140 306142 306149 306152 306153 306161 306162 306163 306167 306169 306174 306187 306197 306199 306212 306219 306220 306222 306224 306227 306244 306247 306254 306264 306269 306270 306272 306275 306276 306280 306283 306291 306295 306300 306305 306306 306322 306324 306326 306327 306330 306332 306333 306335 306336 306341 306343 306345 306348 306352 306353 306357 306359 306360 306361 306368 306370 306372 306375 306377 306386 306387 306396 306400 306414 306418 306422 306425 306438 306439 306443 306444 306449 306451 306452 306455 306457 306460 306462 306464 306465 306469 306472 306478 306482 306484 306486 306487 306488 306493 306494 306495 306501 306502 306503 306505 306507 306511 306512 306513 306514 306515 306520 306521 306522 306523 306525 306526 306527 306529 306531 306532 306540 306545 306552 306555 306558 306561 306562 306564 306568 306575 306577 306580 306583 306585 306586 306587 306588 306592 306593 306597 306598 306599 306604 306605 306610 306617 306619 306620 306621 306622 306629 306638 306644 306646 306647 306648 306651 306652 306653 306654 306656 306657 306659 306660 306661 306665 306673 306680 306683 306685 306686 306687 306688 306690 306695 306696 306701 306703 306704 306706 306707 306713 306716 306717 306720 306724 306727 306729 306731 306732 306733 306734 306735 306741 306742 306743 306746 306748 306749 306755 306760 306761 306765 306767 306769 306774 306776 306780 306781 306782 306784 306788 306790 306798 306799 306802 306804 306808 306814 306815 306817 306821 306824 306825 306829 306834 306839 306840 306842 306844 306847 306851 306853 306858 306861 306868 306870 306873 306877 306880 306881 306882 306889 306892 306897 306901 306902 306906 306909 306916 306921 306922 306925 306935 306938 306940 306943 306946 306948 306949 306953 306954 306955 306956 306963 306967 306968 306970 306974 306975 306985 306986 306987 306988 306989 306990 306996 307003 307004 307006 307012 307014 307015 307020 307023 307024 307026 307035 307038 307042 307044 307047 307048 307054 307055 307057 307059 307060 307065 307068 307070 307071 307072 307075 307081 307084 307088 307090 307091 307098 307099 307104 307108 307111 307112 307113 307121 307128 307130 307131 307134 307137 307140 307150 307154 307165 307166 307167 307173 307174 307176 307177 307178 307181 307185 307186 307193 307197 307199 307202 307210 307213 307220 307225 307233 307239 307240 307246 307250 307251 307261 307263 307264 307268 307273 307285 307291 307298 307306 307315 307316 307329 307331 307335 307340 307344 307345 307349 307350 307351 307358 307359 307360 307366 307369 307376 307381 307384 307385 307388 307393 307404 307406 307409 307411 307412 307421 307423 307435 307440 307444 307447 307448 307453 307454 307456 307457 307458 307460 307468 307469 307470 307478 307483 307487 307494 307510 307530 307532 307537 307542 307544 307556 307557 307571 307572 307573 307575 307580 307581 307585 307604 307608 307619 307628 307636 307638 307639 307658 307661 307664 307679 307682 307691 307693 307700 307715 307723 307728 307729 307740 307744 307750 307753 307765 307770 307778 307783 307784 307787 307792 307794 307798 307804 307805 307812 307814 307815 307843 307864 307882 307913 307921 307929 307946 307948 307983 307994 308096 308214 308241 308243 308288 308292 308317 308355 308540 308660 311140 311672 311749 311841 311972 312174 312196 312346 312396 312398 312441 312471 312504 312577 312657 312667 312674 312678 312765 312791 312807 312826 312845 312851 312859 312872 312875 312878 312904 312920 312929 312935 312988 313031 313032 313106 313116 313140 313144 313167 313178 313196 313214 313223 313248 313270 313288 313291 313296 313297 313302 313347 313354 313366 313419 313432 313478 313489 313492 313493 313494 313519 313550 313564 313607 313613 313642 313662 313665 313674 313708 313725 313736 313760 313836 313856 313986 314043 314044 314047 314053 314061 314127 314141 314145 314179 314204 314230 314264 314265 314278 314350 314374 314639 314978 315350 315596 315728 316084 389318 Очень интереÑно! Минимальный и макÑимальный Ñлементы не изменилиÑÑŒ. И опÑÑ‚ÑŒ одни квадрозавры! Ð’Ñе Ñлементы Ñпектра >300000. Я думала, что Ñлучайные ДЛК будут иметь меньше Д-транÑверÑалей. Однако нет. ÐœÐ¸Ð½Ð¸Ð¼Ð¸Ð·Ð°Ñ†Ð¸Ñ Ð² Ñтом Ñпектре вообще Ð·Ð°Ð¾Ð±Ð»Ð°Ñ‡Ð½Ð°Ñ Ð¼ÐµÑ‡Ñ‚Ð° :) Параметры Ñпектра Min = 304818 Max = 389318 ширина Ñпектра 84501 мощноÑÑ‚ÑŒ Ñпектра 620 коÑффициент плотноÑти Ñпектра K = 0,0073. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Дублирую Ñообщение https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=5734 Показываю ДЛК 15-го порÑдка, поÑтроенный методом Гергели в моей Ñтатье http://www.natalimak1.narod.ru/dlk.htm  Попытка найти ортогональные ДЛК к Ñтому ДЛК Проверка ДЛК15 на марьÑжноÑÑ‚ÑŒ (ОДЛК) Введено ДЛК: 1 Ðайдено ОДЛК: 0 Д-транÑверÑалей: 389318 Соквадратов: 0 Ð’Ñ€ÐµÐ¼Ñ Ð² Ñек: 4320 20371 8124 2757 857 134 40 12 1 Прервала программу. __________________________________________ конец дублируемого ÑÐ¾Ð¾Ð±Ñ‰ÐµÐ½Ð¸Ñ Ð—Ð´ÐµÑÑŒ вы видите попытку найти ОДЛК к квадрату Гергели (Ñамому главному квадрозавру на данный момент: 389318 Д-транÑверÑалей) программой Белышева ortogon_u Программа показывает в Ñтом ДЛК 20371 чаÑÑ‚ÑŒ. Крутила программу мало - Ñ‡Ð°Ñ Ñ Ð½ÐµÐ±Ð¾Ð»ÑŒÑˆÐ¸Ð¼, ОДЛК не нашлоÑÑŒ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Теперь поÑмотрим, как работает Ñ Ñамым главным квадрозавром 15-го порÑдка программа Tomas Brada (поиÑк ОДЛК по чаÑÑ‚Ñм). ЗапуÑтила поиÑк ОДЛК в первой чаÑти C:\Users\Дом\Downloads\libr>ortogonbw GoQFfXwz5VzQUCj6Bo1nmRbfreagPzdHR3RpZV3t1k bzVNeH576RZSF 1 1>output.txt init_trans(15) used 753 nodes num_dtrans: 389318 init_disjoint(15) used 226 heads and 5839996 nodes L(0) c(1) 1 / 20371 L(1) c(115) X / 8124 ЧаÑтей программа Ñделала ровно Ñтолько же, Ñколько показала программа Белышева. Программа вроде работает, в Ñтупор не вошла :) Покручу немного, вдруг найдётÑÑ Ñ…Ð¾Ñ‚ÑŒ один ОДЛК. Что-то Ñ Ð¿Ð¾Ð¸Ñком ОДЛК к ДЛК 15-го порÑдка вÑÑ‘ глухо, Ñколько раз пыталаÑÑŒ и - ничего не найдено! Три чаÑа крутилаÑÑŒ программа - ни одного ОДЛК не найдено! Прервала. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Поразительно! Сгенерировала 2500 Ñлучайных ДЛК 15-го порÑдка программой Harry White. ПоÑчитала в них Д-транÑверÑали. Ðайдено 1099 новых Ñлементов Ñпектра и - вÑе они находÑÑ‚ÑÑ Ð² интервале (304818,389318). ПроиÑходит уплотнение найденной чаÑтички Ñпектра. РраÑширÑÑ‚ÑŒÑÑ Ñта чаÑтичка не хочет! Ðи влево, ни вправо! Ладно, будем уплотнÑÑ‚ÑŒ, Ñто тоже надо делать. МощноÑÑ‚ÑŒ Ñпектра Ñтала равна 1719. КоÑффициент плотноÑти чуть-чуть увеличилÑÑ: K = 0,2. Показываю 1099 новых Ñлементов Ñпектра 305098 305107 305295 305347 305415 305445 305456 305508 305525 305540 305545 305563 305573 305580 305623 305627 305634 305635 305645 305671 305673 305679 305690 305706 305708 305723 305729 305731 305741 305749 305771 305773 305780 305782 305785 305786 305788 305795 305798 305808 305813 305814 305829 305830 305834 305835 305838 305845 305847 305859 305861 305865 305867 305877 305878 305879 305889 305895 305897 305901 305910 305911 305913 305915 305918 305932 305936 305940 305941 305943 305947 305949 305950 305951 305959 305960 305961 305962 305965 305966 305967 305974 305979 305983 305987 305989 305993 305995 305996 306006 306007 306011 306013 306015 306034 306040 306042 306046 306051 306057 306058 306062 306063 306066 306068 306072 306073 306074 306078 306084 306085 306087 306093 306095 306103 306104 306111 306115 306119 306120 306122 306127 306131 306134 306138 306139 306143 306145 306147 306148 306150 306155 306156 306159 306160 306165 306166 306168 306170 306173 306176 306180 306182 306184 306185 306186 306189 306201 306202 306204 306207 306208 306210 306211 306213 306214 306215 306226 306228 306236 306237 306239 306240 306243 306249 306252 306253 306255 306256 306260 306261 306262 306263 306265 306266 306268 306271 306273 306274 306277 306285 306286 306288 306289 306290 306292 306293 306307 306309 306311 306313 306317 306318 306319 306320 306321 306323 306328 306329 306331 306334 306337 306338 306339 306342 306344 306349 306350 306351 306362 306364 306365 306366 306367 306369 306371 306373 306374 306378 306379 306380 306383 306388 306389 306390 306391 306392 306395 306398 306399 306402 306404 306405 306407 306409 306410 306411 306413 306415 306416 306419 306424 306426 306428 306435 306436 306437 306442 306445 306446 306447 306458 306459 306463 306466 306468 306470 306473 306477 306481 306483 306485 306489 306490 306491 306492 306497 306498 306499 306500 306508 306510 306516 306517 306518 306519 306524 306528 306530 306537 306538 306542 306543 306546 306547 306548 306550 306551 306556 306557 306560 306563 306565 306566 306569 306570 306572 306573 306574 306576 306579 306581 306584 306590 306591 306594 306601 306602 306603 306607 306608 306609 306611 306612 306613 306614 306615 306616 306618 306623 306625 306626 306627 306630 306631 306632 306636 306637 306640 306641 306642 306643 306649 306650 306658 306662 306663 306664 306666 306667 306668 306670 306671 306672 306675 306677 306678 306681 306682 306684 306689 306691 306692 306693 306694 306697 306699 306700 306705 306708 306709 306710 306711 306714 306718 306719 306721 306722 306723 306725 306726 306728 306730 306736 306739 306740 306744 306745 306747 306750 306752 306753 306754 306756 306758 306759 306762 306764 306768 306770 306772 306773 306775 306778 306779 306785 306786 306787 306789 306791 306792 306794 306795 306796 306797 306800 306801 306803 306806 306807 306809 306810 306811 306812 306813 306816 306818 306819 306820 306822 306823 306826 306827 306828 306830 306831 306832 306833 306835 306836 306837 306838 306843 306848 306849 306852 306854 306855 306856 306857 306860 306862 306863 306864 306865 306867 306869 306871 306872 306874 306875 306876 306878 306879 306884 306885 306886 306887 306888 306891 306894 306895 306896 306898 306899 306900 306903 306904 306905 306907 306910 306911 306912 306913 306914 306915 306917 306918 306920 306924 306926 306927 306929 306930 306931 306932 306934 306936 306937 306939 306941 306942 306944 306945 306947 306950 306951 306952 306959 306962 306964 306966 306969 306971 306972 306973 306976 306977 306978 306979 306980 306981 306982 306983 306991 306992 306994 306995 306997 306998 306999 307000 307001 307002 307005 307007 307008 307009 307010 307011 307016 307017 307018 307019 307021 307022 307025 307027 307028 307029 307032 307033 307034 307037 307039 307040 307041 307043 307049 307051 307052 307053 307056 307058 307061 307062 307063 307064 307066 307067 307073 307074 307076 307078 307079 307080 307082 307083 307086 307087 307089 307092 307093 307094 307097 307100 307101 307102 307103 307105 307106 307107 307109 307110 307114 307115 307116 307117 307119 307120 307122 307124 307127 307129 307132 307133 307135 307136 307138 307139 307141 307142 307143 307145 307147 307148 307149 307151 307153 307155 307156 307157 307159 307160 307161 307162 307163 307164 307168 307169 307170 307171 307172 307175 307179 307182 307183 307184 307187 307188 307189 307190 307191 307192 307194 307195 307196 307198 307200 307201 307204 307207 307208 307211 307212 307214 307217 307218 307219 307221 307224 307226 307227 307228 307231 307232 307234 307236 307237 307238 307241 307242 307244 307249 307252 307253 307254 307255 307256 307258 307259 307260 307262 307265 307266 307267 307269 307270 307271 307272 307274 307275 307276 307277 307278 307279 307280 307282 307283 307284 307286 307288 307289 307290 307294 307295 307296 307302 307303 307307 307308 307310 307312 307313 307317 307318 307320 307322 307323 307324 307325 307326 307327 307328 307330 307332 307333 307334 307337 307338 307339 307341 307342 307343 307346 307348 307352 307353 307355 307356 307357 307361 307362 307363 307364 307365 307368 307370 307372 307374 307375 307377 307379 307380 307382 307383 307386 307389 307390 307391 307394 307395 307396 307398 307399 307400 307401 307402 307403 307405 307407 307410 307413 307414 307416 307417 307418 307419 307422 307424 307425 307427 307428 307429 307430 307431 307432 307433 307436 307437 307438 307441 307442 307445 307446 307449 307450 307452 307455 307461 307462 307465 307471 307472 307473 307474 307476 307477 307479 307481 307484 307485 307486 307488 307489 307493 307495 307496 307497 307499 307501 307502 307503 307504 307506 307507 307508 307509 307511 307513 307514 307515 307516 307517 307521 307523 307524 307525 307526 307528 307529 307533 307535 307538 307540 307541 307543 307545 307546 307547 307549 307550 307554 307558 307559 307561 307562 307563 307564 307565 307567 307568 307569 307574 307576 307578 307582 307583 307584 307586 307588 307591 307592 307596 307597 307598 307599 307602 307605 307606 307607 307609 307610 307611 307615 307617 307620 307621 307622 307623 307624 307625 307627 307629 307630 307631 307632 307635 307637 307641 307642 307643 307646 307647 307649 307650 307653 307656 307657 307659 307663 307666 307668 307670 307671 307673 307674 307675 307676 307686 307689 307690 307692 307694 307697 307699 307702 307711 307712 307714 307716 307718 307719 307721 307727 307730 307731 307732 307734 307737 307739 307741 307742 307743 307745 307747 307748 307751 307756 307757 307758 307760 307762 307763 307764 307766 307767 307768 307769 307771 307774 307781 307782 307788 307789 307790 307793 307806 307816 307817 307821 307824 307829 307831 307832 307834 307837 307840 307847 307848 307855 307856 307858 307859 307862 307863 307869 307870 307871 307874 307875 307876 307880 307881 307887 307888 307891 307894 307896 307898 307901 307904 307905 307910 307912 307914 307915 307918 307919 307920 307922 307926 307930 307933 307934 307935 307939 307955 307957 307960 307964 307965 307971 307972 307976 307980 307982 307985 307986 307987 307990 307992 307993 307997 307998 308000 308001 308002 308008 308011 308018 308035 308043 308044 308049 308054 308060 308065 308069 308070 308075 308086 308088 308091 308093 308105 308106 308108 308110 308113 308122 308125 308129 308131 308158 308162 308168 308189 308215 308216 308233 308239 308245 308251 308254 308258 308259 308262 308265 308273 308285 308296 308302 308319 308366 308371 308373 308387 308389 308398 308405 308448 308455 308465 308467 308470 308471 308476 308509 308590 308669 308707 308710 308753 308825 308930 308968 309183 309364 Ð’Ñе как на подбор - такие квадрозавриÑтые :) ИнтереÑно, где ДЛК Ñ Ð¼Ð°Ð»ÐµÐ½ÑŒÐºÐ¸Ð¼Ð¸ количеÑтвами Д-транÑверÑалей? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё 3000 Ñлучайных ДЛК 15-го порÑдка проверено на Д-транÑверÑали. Ðайдено 568 новых Ñлементов Ñпектра. Они вÑÑ‘ такие же квадрозавриÑтые :) и находÑÑ‚ÑÑ Ð² том же интервале. Показываю 305026 305264 305277 305304 305332 305389 305404 305407 305412 305418 305437 305442 305451 305468 305472 305477 305486 305499 305503 305504 305510 305539 305577 305581 305583 305589 305603 305612 305617 305621 305624 305632 305636 305653 305655 305662 305672 305689 305692 305696 305707 305709 305715 305719 305720 305742 305743 305747 305748 305755 305766 305769 305772 305775 305776 305778 305781 305783 305784 305787 305790 305791 305792 305794 305797 305804 305805 305806 305807 305816 305824 305825 305826 305840 305860 305862 305870 305871 305874 305876 305883 305891 305893 305896 305900 305907 305912 305914 305921 305922 305927 305928 305929 305935 305942 305944 305958 305970 305971 305973 305976 305977 305980 305982 305985 305988 305992 305994 305997 306001 306003 306004 306008 306010 306016 306017 306022 306025 306036 306038 306043 306044 306050 306053 306055 306059 306061 306080 306083 306089 306090 306091 306096 306097 306098 306099 306100 306107 306116 306117 306118 306123 306129 306130 306132 306133 306137 306141 306144 306146 306151 306157 306164 306177 306179 306181 306183 306188 306190 306191 306193 306194 306195 306196 306200 306203 306205 306206 306216 306217 306218 306221 306223 306225 306229 306230 306231 306233 306238 306242 306245 306246 306248 306250 306251 306257 306259 306278 306281 306282 306287 306294 306298 306301 306302 306303 306308 306310 306314 306316 306325 306340 306346 306347 306354 306355 306356 306363 306376 306382 306384 306393 306394 306397 306401 306403 306406 306408 306412 306417 306420 306421 306423 306430 306431 306434 306440 306441 306448 306450 306453 306454 306456 306461 306467 306471 306474 306475 306476 306496 306506 306509 306533 306534 306535 306536 306539 306541 306544 306553 306554 306559 306567 306571 306582 306589 306596 306600 306606 306628 306633 306634 306635 306639 306645 306655 306669 306674 306676 306679 306698 306702 306715 306738 306751 306757 306763 306766 306771 306777 306783 306793 306805 306841 306845 306846 306850 306859 306866 306883 306890 306893 306908 306919 306923 306928 306933 306957 306958 306960 306961 306965 306984 306993 307013 307030 307031 307036 307045 307046 307069 307077 307085 307095 307096 307118 307123 307125 307126 307144 307146 307152 307158 307180 307203 307205 307206 307209 307216 307222 307223 307229 307230 307235 307243 307245 307247 307248 307257 307281 307292 307293 307297 307300 307301 307305 307309 307311 307314 307319 307321 307336 307347 307354 307367 307371 307373 307378 307392 307397 307408 307420 307434 307439 307443 307451 307463 307464 307466 307475 307480 307482 307498 307500 307505 307512 307518 307527 307531 307534 307539 307548 307551 307560 307566 307570 307577 307587 307589 307594 307612 307613 307614 307616 307618 307626 307633 307640 307644 307645 307648 307651 307652 307655 307660 307662 307665 307667 307677 307678 307681 307684 307685 307687 307696 307704 307705 307708 307709 307710 307713 307724 307733 307736 307738 307746 307752 307754 307755 307759 307761 307786 307796 307797 307800 307801 307803 307810 307813 307819 307823 307825 307827 307828 307835 307836 307838 307839 307841 307844 307845 307850 307851 307852 307857 307860 307861 307865 307866 307868 307878 307879 307885 307892 307893 307897 307906 307909 307916 307917 307928 307931 307932 307936 307937 307938 307940 307944 307951 307952 307954 307956 307958 307967 307968 307973 307974 307977 307978 307995 308005 308010 308012 308015 308016 308017 308021 308022 308024 308032 308034 308040 308042 308045 308053 308056 308058 308066 308083 308085 308087 308090 308099 308103 308104 308107 308111 308112 308117 308123 308130 308132 308136 308141 308142 308144 308161 308169 308170 308172 308175 308180 308200 308204 308205 308207 308211 308218 308235 308237 308263 308271 308297 308306 308309 308315 308320 308325 308340 308353 308360 308361 308364 308386 308392 308402 308414 308487 308515 308536 308547 308555 308581 308720 308791 308851 308937 309020 УплотнÑетÑÑ, уплотнÑетÑÑ Ñпектр! МощноÑÑ‚ÑŒ Ñпектра Ñтала равна 2287. КоÑффициент плотноÑти K = 0,027. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ðайдено 265 новых Ñлементов Ñпектра, показываю 304684 304777 304934 304975 305099 305175 305213 305229 305234 305299 305302 305305 305322 305324 305370 305382 305399 305411 305416 305476 305481 305488 305494 305495 305497 305501 305505 305524 305546 305550 305557 305560 305565 305570 305571 305592 305598 305604 305610 305613 305622 305638 305640 305641 305643 305651 305654 305664 305665 305693 305702 305705 305717 305718 305725 305730 305733 305735 305737 305738 305739 305744 305746 305750 305751 305754 305757 305763 305779 305793 305799 305809 305810 305811 305815 305819 305823 305831 305833 305836 305842 305843 305846 305848 305850 305852 305856 305866 305882 305884 305885 305886 305899 305904 305905 305906 305909 305916 305920 305926 305930 305931 305934 305939 305945 305952 305956 305957 305963 305964 305969 305975 305981 305986 305999 306002 306005 306018 306019 306021 306028 306029 306030 306033 306039 306041 306049 306060 306069 306075 306076 306077 306082 306088 306092 306094 306101 306109 306110 306113 306124 306128 306135 306136 306154 306158 306172 306175 306192 306198 306209 306232 306234 306235 306241 306267 306279 306284 306297 306299 306304 306312 306315 306358 306381 306429 306432 306479 306480 306504 306549 306578 306595 306624 306712 307050 307287 307304 307387 307415 307426 307459 307467 307490 307491 307492 307519 307536 307552 307595 307634 307688 307695 307703 307707 307717 307720 307722 307725 307749 307772 307775 307777 307785 307809 307811 307818 307822 307826 307833 307842 307846 307853 307867 307884 307886 307889 307900 307902 307903 307911 307924 307949 307953 307959 307961 307963 307975 307988 308026 308033 308036 308039 308041 308047 308050 308062 308067 308072 308114 308120 308127 308138 308139 308185 308213 308222 308226 308227 308228 308244 308250 308277 308278 308291 308310 308341 308342 308370 308412 308523 308551 308650 308679 308703 ЕÑÑ‚ÑŒ минимизациÑ! Ðаконец-то, пробила границу. МощноÑÑ‚ÑŒ Ñпектра Ñтала равна 2552. Хорошее чиÑло, палиндромное :) И чуть-чуть увеличилаÑÑŒ ширина Ñпектра, теперь она равна 84635. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð½Ð°Ð¹Ð´Ñƒ новорожденного малыша и покажу. Вот он - наш новый малыш 304684 Д-транÑверÑали 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1 2 3 5 6 4 7 9 10 8 11 13 14 0 12 3 0 1 6 7 8 4 5 9 11 13 14 2 12 10 2 3 0 4 8 9 10 6 5 12 14 1 13 7 11 5 6 7 0 3 1 2 12 13 14 4 8 10 11 9 4 5 8 1 0 6 11 13 14 3 12 2 9 10 7 7 4 9 2 11 12 5 14 6 13 0 10 1 3 8 6 7 4 11 10 13 14 8 12 0 1 3 5 9 2 8 10 5 12 13 14 9 11 7 1 2 0 3 4 6 9 8 6 13 14 7 12 0 11 10 3 5 4 2 1 10 12 11 14 5 0 13 1 2 7 9 4 6 8 3 14 11 13 10 9 3 0 2 4 6 8 12 7 1 5 13 14 12 7 1 10 8 3 0 2 6 9 11 5 4 12 13 10 9 2 11 3 4 1 5 7 6 8 14 0 11 9 14 8 12 2 1 10 3 4 5 7 0 6 13 Оценка Ð´Ð»Ñ Ð¼Ð¸Ð½Ð¸Ð¼Ð°Ð»ÑŒÐ½Ð¾Ð³Ð¾ количеÑтва Д-транÑверÑалей в ДЛК 15-го порÑдка Ñтала такаÑ: a(15) <= 304684. Думаю, Ñто далеко не минимум, Ð´Ð»Ñ Ð¼Ð¸Ð½Ð¸Ð¼ÑƒÐ¼Ð° уж очень большое значение. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Покажу начало Ñпектра на данный момент 304684 304777 304818 304934 304975 305026 305098 305099 305107 305175 305213 305229 305234 305264 305277 305295 305299 305302 305304 305305 305322 305324 305332 305347 305370 305382 305389 305399 305404 305407 305408 305410 305411 305412 305415 305416 305418 305437 305442 305445 305451 305456 305468 305472 305476 305477 305481 305486 305488 305494 305495 305497 305499 305501 305503 305504 305505 305508 305510 305524 305525 305534 305539 305540 305545 305546 305550 305553 305557 305560 305563 305565 305570 305571 305573 305577 305580 305581 305583 305589 305592 305598 305603 305604 305610 305612 305613 305617 305621 305622 305623 305624 305627 305632 305634 305635 305636 305638 305639 305640 305641 305643 305645 305650 305651 305653 305654 305655 305662 305664 305665 305670 305671 305672 305673 305674 305678 305679 305689 305690 305692 305693 305694 305696 305702 305705 305706 305707 305708 305709 305715 305717 305718 305719 305720 305723 305725 305727 305729 305730 305731 305733 305735 305737 305738 305739 305740 305741 305742 305743 305744 305746 305747 305748 305749 305750 305751 305754 305755 305757 305763 305766 305769 305770 305771 305772 305773 305775 305776 305778 305779 305780 305781 305782 305783 305784 305785 305786 305787 305788 305790 305791 305792 305793 305794 305795 305796 305797 305798 305799 305804 305805 305806 305807 305808 305809 305810 305811 305813 305814 305815 305816 305819 305823 305824 305825 305826 305829 305830 305831 305833 305834 305835 305836 305838 305840 305842 305843 305845 305846 305847 305848 305850 305852 305856 305859 305860 305861 305862 305863 305865 305866 305867 305868 305870 305871 305873 305874 305876 305877 305878 305879 305880 305882 305883 305884 305885 305886 305889 305891 305893 305895 305896 305897 305898 305899 305900 305901 305903 305904 305905 305906 305907 305909 305910 305911 305912 305913 305914 305915 305916 305917 305918 305920 305921 305922 305924 305926 305927 305928 305929 305930 305931 305932 305934 305935 305936 305937 305939 305940 305941 305942 305943 305944 305945 305947 305949 305950 305951 305952 305953 305956 305957 305958 305959 305960 305961 305962 305963 305964 305965 305966 305967 305969 305970 305971 305972 305973 305974 305975 305976 305977 305978 305979 305980 305981 305982 305983 305985 305986 305987 305988 305989 305992 305993 305994 305995 305996 305997 305999 ... Уплотнение Ñпектра тоже произошло. КоÑффициент плотноÑти K= 0,03. Завтра мы Ñ Ñ‡ÐµÑ€ÐµÐ¿Ð°ÑˆÐºÐ¾Ð¹ продолжим пополнÑÑ‚ÑŒ Ñтот Ñпектр. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
С утра обÑчитала маленькую порцию (1000 ДЛК) на Д-транÑверÑали. Ðайдено 46 новых Ñлементов Ñпектра. Минимум и макÑимум без изменений. МощноÑÑ‚ÑŒ Ñпектра Ñтала равна 2598. ПродолжаетÑÑ ÑƒÐ¿Ð»Ð¾Ñ‚Ð½ÐµÐ½Ð¸Ðµ найденной чаÑти Ñпектра. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð²ÐºÐ»Ð¸Ð½Ð¸Ð»ÑÑ ÑкÑперимент Ñ Ð”Ð›Ðš 14-го порÑдка. ПорÑдок 15 пока отдыхает :) Показываю 46 новых Ñлементов Ñпектра 305081 305237 305261 305325 305465 305482 305625 305646 305675 305704 305821 305872 305875 305881 305954 306064 306071 307299 307601 307603 307669 307672 307779 307780 307802 307808 307873 307979 307981 307996 308027 308038 308048 308081 308098 308109 308148 308173 308195 308199 308209 308270 308303 308336 308415 308418 Ð’Ñе опÑÑ‚ÑŒ такие ровненькие, квадрозавриÑтые :) Лепота! Более-менее значительной непрерывной чаÑти визуально не вижу в начале Ñпектра. ЕÑÑ‚ÑŒ пока только такие маленькие непрерывные учаÑтки, например ... 305778 305779 305780 305781 305782 305783 305784 305785 305786 305787 305788 ... То еÑÑ‚ÑŒ разрывов пока много Ñреди Ñтих квадрозавриÑÑ‚Ñ‹Ñ… Ñлементов, ещё уплотнÑÑ‚ÑŒ и уплотнÑÑ‚ÑŒ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Так выглÑдит Ñ‚ÐµÐºÑƒÑ‰Ð°Ñ Ñ‡Ð°ÑÑ‚ÑŒ Ñпектра по Д-транÑверÑалÑм в ДЛК 15-го порÑдка графичеÑки 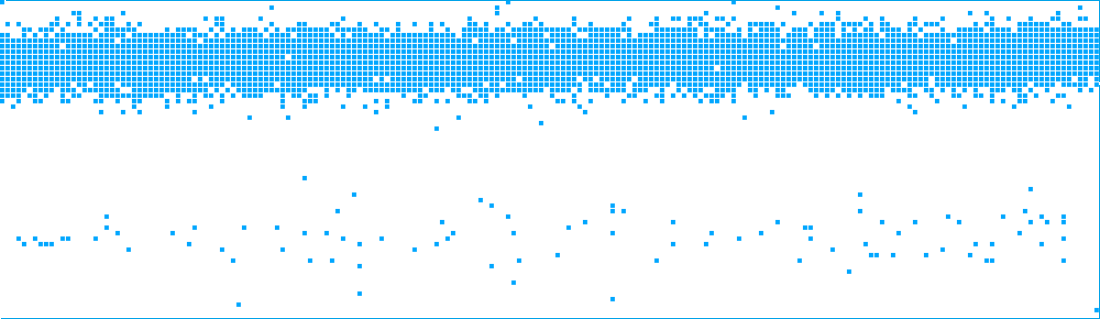 Изображение получено программой форумчанина Ñ Ñ„Ð¾Ñ€ÑƒÐ¼Ð° Math Help Planet Захара Пехтерева. Ðа картинке не показан поÑледний Ñамый-Ñамый квадрозавриÑтый Ñлемент: 389318 (текущий макÑимум), потому что он Ñлишком далеко отÑтоит от предшеÑтвующего ему Ñлемента 316084 (Ñтот Ñлемент вы видите в правом нижнем углу картинки). Да, между Ñтими Ñлементами Ñамый большой разрыв текущего Ñпектра. Пока единÑтвенный интереÑный результат в Ñпектре: новый минимальный Ñлемент 304684. Ðтот Ñлемент вы видите в левом верхнем углу картинки. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Смотрим поÑледовательноÑÑ‚ÑŒ OEIS https://oeis.org/A287647 Свежие обновлениÑ, цитата a(10) <= 3, a(11) <= 194, a(12) <= 50, a(13) <= 8795, a(14) <= 40648, a(15) <= 304818, a(16) <= 3994676, a(17) <= 204330233, a(19) <= 11232045257. - Eduard I. Vatutin, Sep 26 2021, updated Dec 20 2021 Однако оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 15 уже не актуальнаÑ, она улучшена мной. Цитирую Ñообщение https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=158&postid=3312 ЕÑÑ‚ÑŒ минимизациÑ! Ðаконец-то, пробила границу. ________________________________ конец цитаты Оценка Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 14 тоже не актуальнаÑ. Смотрите об Ñтом в теме о Ñпектре Ð´Ð»Ñ Ð¿Ð¾Ñ€Ñдка 14. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð¿Ð¾Ð¿Ñ€Ð¾Ð±Ð¾Ð²Ð°Ð»Ð° Ñгенерировать программой Harry White 1000 Ñлучайных ДЛК 15-го порÑдка. ПоÑчитала в них Д-транÑверÑали, получено 185 новых Ñлементов Ñпектра 304714 304743 304771 304773 304869 304959 304987 305005 305009 305024 305036 305046 305056 305072 305082 305096 305106 305114 305116 305117 305119 305122 305125 305136 305138 305162 305163 305165 305167 305169 305174 305176 305197 305199 305210 305216 305220 305221 305225 305235 305244 305250 305256 305258 305263 305268 305282 305291 305309 305311 305313 305318 305319 305323 305326 305329 305333 305341 305345 305354 305358 305371 305374 305385 305386 305390 305397 305409 305419 305427 305429 305431 305433 305441 305450 305453 305458 305460 305464 305467 305469 305470 305471 305473 305474 305480 305487 305490 305492 305496 305507 305509 305512 305514 305517 305522 305532 305535 305536 305537 305541 305542 305544 305547 305555 305559 305564 305569 305579 305585 305586 305590 305591 305593 305595 305596 305597 305599 305600 305602 305605 305606 305609 305614 305615 305626 305628 305630 305637 305642 305657 305660 305663 305666 305669 305676 305677 305680 305684 305691 305697 305699 305700 305701 305711 305712 305714 305728 305753 305756 305758 305759 305768 305774 305800 305801 305812 305818 305820 305827 305828 305844 305851 305853 305864 305869 305902 305908 305923 305925 305933 305938 305955 305968 305991 305998 306000 306012 306014 306052 306258 306296 306427 306433 306737 Минимум пока не изменилÑÑ, Ñ…Ð¾Ñ‚Ñ Ð¿ÐµÑ€Ð²Ñ‹Ð¹ новый Ñлемент довольно близок к текущему минимуму. МощноÑÑ‚ÑŒ Ñпектра Ñтала равна 2783. ИнтереÑно: даже ÑовÑем Ñлучайные ДЛК имеют много Д-транÑверÑалей. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё попытка. И... еÑÑ‚ÑŒ минимизациÑ! 138 новых Ñлементов Ñпектра получено 304349 304598 304791 304834 304855 304882 304889 304920 304952 304968 304985 304988 304999 305012 305027 305038 305050 305063 305070 305083 305102 305105 305133 305134 305150 305154 305179 305182 305206 305217 305239 305247 305251 305260 305265 305271 305272 305273 305276 305279 305281 305292 305293 305314 305334 305353 305355 305356 305359 305365 305368 305377 305378 305381 305388 305393 305395 305396 305398 305400 305401 305423 305424 305425 305426 305432 305434 305435 305440 305443 305444 305446 305452 305454 305455 305459 305462 305466 305475 305478 305484 305485 305489 305493 305500 305513 305521 305523 305526 305527 305533 305556 305568 305572 305574 305578 305587 305601 305608 305619 305631 305649 305661 305667 305681 305682 305685 305686 305687 305698 305716 305722 305724 305732 305734 305752 305760 305761 305765 305767 305817 305832 305841 305849 305857 305887 305890 305892 305946 305948 305984 306020 306027 306037 306106 306171 306385 307593 Ðовый минимум 304349. Ð¡ÐµÐ¹Ñ‡Ð°Ñ Ð½Ð°Ð¹Ð´Ñƒ и покажу нового малыша. МощноÑÑ‚ÑŒ Ñпектра Ñтала равна 2921. Хорошо раÑÑ‚Ñ‘Ñ‚! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ð’Ñтречайте нового малыша 304349 Д-транÑверÑалей 0 2 4 5 13 9 11 14 10 6 3 8 7 12 1 12 1 11 14 2 10 8 13 5 3 9 4 6 0 7 8 10 2 9 6 12 13 5 1 14 7 0 3 11 4 1 5 10 3 8 0 14 4 9 7 12 2 13 6 11 11 6 3 7 4 13 2 8 14 12 5 1 0 10 9 9 0 14 11 3 5 7 6 2 10 1 13 4 8 12 7 4 12 13 1 14 6 0 11 2 8 9 10 5 3 6 12 9 1 11 3 4 7 0 8 2 10 5 14 13 10 9 5 4 7 2 12 1 8 13 0 14 11 3 6 14 11 7 8 5 4 0 3 6 9 13 12 2 1 10 5 7 13 0 9 1 3 11 12 4 10 6 14 2 8 3 13 1 6 12 8 5 10 4 0 14 11 9 7 2 2 3 8 10 14 7 1 9 13 11 6 5 12 4 0 4 14 0 12 10 6 9 2 3 1 11 7 8 13 5 13 8 6 2 0 11 10 12 7 5 4 3 1 9 14 И оценка Ð´Ð»Ñ Ð¼Ð¸Ð½Ð¸Ð¼Ð°Ð»ÑŒÐ½Ð¾Ð³Ð¾ количеÑтва Д-транÑверÑалей в ДЛК 15-го порÑдка Ñтала Ñ‚Ð°ÐºÐ°Ñ a(15) <= 304349. Ðу, и какой ÑмыÑл вноÑить Ñту оценку в OEIS, еÑли она может ещё N раз изменитьÑÑ, еÑли Ñо Ñпектром активно работать?! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
Ещё одна попытка, получено 150 новых Ñлементов Ñпектра 304401 304468 304545 304617 304628 304718 304758 304775 304804 304810 304872 304902 304911 304912 304919 304921 304933 304957 304964 304966 304981 304990 305004 305007 305035 305040 305045 305053 305054 305060 305062 305067 305075 305084 305089 305095 305115 305120 305128 305130 305132 305135 305141 305153 305158 305164 305166 305171 305172 305180 305184 305187 305193 305195 305198 305200 305208 305212 305226 305231 305252 305262 305267 305275 305284 305286 305288 305306 305307 305315 305321 305330 305335 305336 305337 305340 305343 305344 305346 305349 305351 305352 305357 305361 305362 305363 305364 305372 305391 305392 305406 305417 305420 305421 305422 305428 305439 305457 305483 305502 305506 305516 305518 305528 305529 305531 305538 305543 305548 305549 305551 305552 305554 305562 305567 305584 305588 305607 305611 305616 305618 305629 305648 305658 305659 305668 305683 305688 305703 305710 305726 305736 305745 305762 305764 305777 305789 305803 305822 305837 305839 305858 305888 305894 305919 305990 306032 306045 306178 307890 ИнтереÑно: вÑе новые Ñлементы получаютÑÑ Ð² одной облаÑти, квадрозавриÑтые такие :) ÐœÐ¸Ð½Ð¸Ð¼Ð¸Ð·Ð°Ñ†Ð¸Ñ Ð² Ñтот раз не ÑлучилаÑÑŒ, Ñ…Ð¾Ñ‚Ñ Ð¿ÐµÑ€Ð²Ñ‹Ð¹ новый Ñлемент очень близок к текущему минимуму. МощноÑÑ‚ÑŒ Ñпектра выроÑла до 3071. |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese