Thread 'MOLS ГҗВё MODLS of order 18, 20, 24'
Message boards : Science : MOLS ГҗВё MODLS of order 18, 20, 24
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЕёГҗВҫ ГҗВәГҗВҫГҗВјГҗВ°ГҗВҪГҗВҙГҗВө sage: for x in designs.mutually_orthogonal_latin_squares(5,18): print(x,'\n') ГҗВІ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВө SageMath ГҗВҝГҗВҫГҗȄĄвҖЎГҗВ°ГҗВөГҗВј ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ MOLS 18-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘ВҸГ‘вҖ°Г‘Ж’Г‘ЕҪ ГҗВёГҗВ· ГҗВҝГ‘ВҸГ‘вҖҡГҗВё ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖәГҗЕЎ 0 3 6 16 10 13 1 4 7 11 14 17 15 9 12 2 5 8 7 1 4 14 17 11 8 2 5 15 9 12 13 16 10 6 0 3 5 8 2 9 12 15 3 6 0 13 16 10 11 14 17 4 7 1 4 7 1 3 6 0 10 13 16 5 8 2 14 17 11 9 12 15 2 5 8 1 4 7 17 11 14 0 3 6 9 12 15 16 10 13 6 0 3 8 2 5 12 15 9 7 1 4 16 10 13 14 17 11 13 16 10 7 1 4 6 0 3 12 15 9 8 2 5 17 11 14 11 14 17 5 8 2 4 7 1 10 13 16 3 6 0 12 15 9 15 9 12 0 3 6 2 5 8 17 11 14 1 4 7 10 13 16 14 17 11 6 0 3 9 12 15 8 2 5 10 13 16 1 4 7 9 12 15 4 7 1 16 10 13 3 6 0 17 11 14 8 2 5 16 10 13 2 5 8 14 17 11 1 4 7 12 15 9 3 6 0 12 15 9 17 11 14 0 3 6 4 7 1 2 5 8 13 16 10 10 13 16 12 15 9 7 1 4 2 5 8 6 0 3 11 14 17 17 11 14 10 13 16 5 8 2 6 0 3 4 7 1 15 9 12 3 6 0 15 9 12 11 14 17 16 10 13 7 1 4 5 8 2 1 4 7 13 16 10 15 9 12 14 17 11 5 8 2 0 3 6 8 2 5 11 14 17 13 16 10 9 12 15 0 3 6 7 1 4 0 7 5 12 10 17 16 14 9 2 6 4 13 11 15 1 8 3 3 1 8 15 13 11 10 17 12 5 0 7 16 14 9 4 2 6 6 4 2 9 16 14 13 11 15 8 3 1 10 17 12 7 5 0 10 17 12 3 1 8 15 13 11 4 2 6 5 0 7 16 14 9 13 11 15 6 4 2 9 16 14 7 5 0 8 3 1 10 17 12 16 14 9 0 7 5 12 10 17 1 8 3 2 6 4 13 11 15 9 16 14 13 11 15 6 4 2 10 17 12 7 5 0 8 3 1 12 10 17 16 14 9 0 7 5 13 11 15 1 8 3 2 6 4 15 13 11 10 17 12 3 1 8 16 14 9 4 2 6 5 0 7 11 15 13 7 5 0 2 6 4 9 16 14 3 1 8 17 12 10 14 9 16 1 8 3 5 0 7 12 10 17 6 4 2 11 15 13 17 12 10 4 2 6 8 3 1 15 13 11 0 7 5 14 9 16 5 0 7 14 9 16 1 8 3 11 15 13 12 10 17 6 4 2 8 3 1 17 12 10 4 2 6 14 9 16 15 13 11 0 7 5 2 6 4 11 15 13 7 5 0 17 12 10 9 16 14 3 1 8 4 2 6 8 3 1 17 12 10 0 7 5 14 9 16 15 13 11 7 5 0 2 6 4 11 15 13 3 1 8 17 12 10 9 16 14 1 8 3 5 0 7 14 9 16 6 4 2 11 15 13 12 10 17 0 8 4 14 10 15 11 16 12 9 17 13 7 3 2 5 1 6 5 1 6 16 12 11 13 9 17 14 10 15 0 8 4 7 3 2 7 3 2 9 17 13 15 14 10 16 12 11 5 1 6 0 8 4 14 10 15 3 2 7 17 13 9 8 4 0 12 11 16 1 6 5 16 12 11 8 4 0 10 15 14 1 6 5 17 13 9 3 2 7 9 17 13 1 6 5 12 11 16 3 2 7 10 15 14 8 4 0 11 16 12 17 13 9 6 5 1 4 0 8 2 7 3 15 14 10 13 9 17 10 15 14 2 7 3 6 5 1 4 0 8 11 16 12 15 14 10 12 11 16 4 0 8 2 7 3 6 5 1 13 9 17 6 5 1 11 16 12 7 3 2 0 8 4 9 17 13 14 10 15 2 7 3 13 9 17 0 8 4 5 1 6 14 10 15 16 12 11 4 0 8 15 14 10 5 1 6 7 3 2 16 12 11 9 17 13 1 6 5 0 8 4 14 10 15 17 13 9 3 2 7 12 11 16 3 2 7 5 1 6 16 12 11 10 15 14 8 4 0 17 13 9 8 4 0 7 3 2 9 17 13 12 11 16 1 6 5 10 15 14 17 13 9 4 0 8 3 2 7 15 14 10 11 16 12 6 5 1 10 15 14 6 5 1 8 4 0 11 16 12 13 9 17 2 7 3 12 11 16 2 7 3 1 6 5 13 9 17 15 14 10 4 0 8 0 5 7 4 6 2 16 9 14 3 8 1 17 10 12 13 15 11 8 1 3 0 5 7 12 17 10 2 4 6 13 15 11 9 14 16 4 6 2 8 1 3 11 13 15 7 0 5 9 14 16 17 10 12 10 12 17 3 8 1 7 0 5 16 9 14 6 2 4 11 13 15 15 11 13 2 4 6 3 8 1 12 17 10 5 7 0 16 9 14 14 16 9 7 0 5 2 4 6 11 13 15 1 3 8 12 17 10 1 3 8 13 15 11 6 2 4 14 16 9 10 12 17 0 5 7 6 2 4 9 14 16 5 7 0 10 12 17 15 11 13 8 1 3 5 7 0 17 10 12 1 3 8 15 11 13 14 16 9 4 6 2 9 14 16 15 11 13 0 5 7 4 6 2 12 17 10 3 8 1 17 10 12 14 16 9 8 1 3 0 5 7 11 13 15 2 4 6 13 15 11 10 12 17 4 6 2 8 1 3 16 9 14 7 0 5 3 8 1 12 17 10 9 14 16 6 2 4 7 0 5 15 11 13 2 4 6 11 13 15 17 10 12 5 7 0 3 8 1 14 16 9 7 0 5 16 9 14 13 15 11 1 3 8 2 4 6 10 12 17 12 17 10 6 2 4 15 11 13 9 14 16 0 5 7 1 3 8 11 13 15 5 7 0 14 16 9 17 10 12 8 1 3 6 2 4 16 9 14 1 3 8 10 12 17 13 15 11 4 6 2 5 7 0 0 2 1 9 11 10 3 5 4 8 7 6 17 16 15 14 13 12 2 1 0 11 10 9 5 4 3 7 6 8 16 15 17 13 12 14 1 0 2 10 9 11 4 3 5 6 8 7 15 17 16 12 14 13 6 8 7 3 5 4 12 14 13 17 16 15 2 1 0 11 10 9 8 7 6 5 4 3 14 13 12 16 15 17 1 0 2 10 9 11 7 6 8 4 3 5 13 12 14 15 17 16 0 2 1 9 11 10 15 17 16 0 2 1 6 8 7 14 13 12 11 10 9 5 4 3 17 16 15 2 1 0 8 7 6 13 12 14 10 9 11 4 3 5 16 15 17 1 0 2 7 6 8 12 14 13 9 11 10 3 5 4 4 3 5 14 13 12 9 11 10 2 1 0 6 8 7 16 15 17 3 5 4 13 12 14 11 10 9 1 0 2 8 7 6 15 17 16 5 4 3 12 14 13 10 9 11 0 2 1 7 6 8 17 16 15 12 14 13 7 6 8 17 16 15 10 9 11 5 4 3 0 2 1 14 13 12 6 8 7 16 15 17 9 11 10 4 3 5 2 1 0 13 12 14 8 7 6 15 17 16 11 10 9 3 5 4 1 0 2 11 10 9 15 17 16 1 0 2 3 5 4 13 12 14 8 7 6 10 9 11 17 16 15 0 2 1 5 4 3 12 14 13 7 6 8 9 11 10 16 15 17 2 1 0 4 3 5 14 13 12 6 8 7 ГҗвҖқГҗвҖәГҗЕЎ ГҗВІ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВө ГҗВҪГҗВөГ‘вҖҡ. ГҗвҖңГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВ° MODLS 18-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘ВҸГ‘вҖ°Гҗ°ÑВҸ ГҗВұГҗВҫГҗВ»ГҗВөГҗВө Г‘вҖЎГҗВөГҗВј ГҗВёГҗВ· ГҗВҙГҗВІГ‘Ж’Г‘вҖҰ ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ, ГҗВҝГҗВҫГҗВәГҗВ° ГҗВҪГҗВөГҗВёГҗВ·ГҗВІГҗВөГ‘ВҒГ‘вҖҡГҗВҪГҗВ°. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖқГҗВ°ГҗВ»ГҗВөГҗВө ГҗВҙГ‘Ж’ГҗВұГҗВ»ГҗВёГ‘вӮ¬Г‘Ж’Г‘ЕҪ Г‘вҖҡГ‘вӮ¬ГҗВё Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГ‘ВҸ ГҗВёГҗВ· ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВіГҗВҫГҗВ№ Г‘вҖҡГҗВөГҗВјГ‘вҖ№. https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=136&postid=2600 ГҗЕЎГҗВ°ГҗВ¶ГҗВҙГҗ°ÑВҸ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВҪГҗ°ÑВҸ ГҗВҝГҗВҫ ГҗЕЎГҗВ ГҗЕ“ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗ°ÑВҸ ГҗВҝГҗ°ÑвӮ¬ГҗВ° ГҗвҖәГҗЕЎ 18-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВҝГ‘вӮ¬ГҗВҫГ‘ВҒГ‘вҖҡГҗВҫ ГҗВҝГ‘вӮ¬ГҗВөГҗВІГ‘вӮ¬Гҗ°ÑвҖ°ГҗВ°ГҗВөГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВІ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВҝГҗ°ÑвӮ¬Г‘Ж’ ГҗвҖқГҗвҖәГҗЕЎ. ГҗвҖҷГҗВҫГ‘вҖҡ Г‘ВҚГ‘вҖҡГҗВ° ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗ°ÑВҸ ГҗВҝГҗ°ÑвӮ¬ГҗВ° ГҗвҖқГҗвҖәГҗЕЎ 18-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВҝГҗВҫГҗȄĄвҖЎГҗВөГҗВҪГҗВ° ГҗВёГҗВ· ГҗВёГ‘ВҒГ‘вҖҰГҗВҫГҗВҙГҗВҪГҗВҫГҗВ№ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ ГҗвҖәГҗЕЎ (Г‘ВҒГҗВј. ГҗЕЎГҗВ ГҗЕ“ ГҗВІГҗ°ÑвӮ¬ГҗВёГҗВ°ГҗВҪГ‘вҖҡ 1) 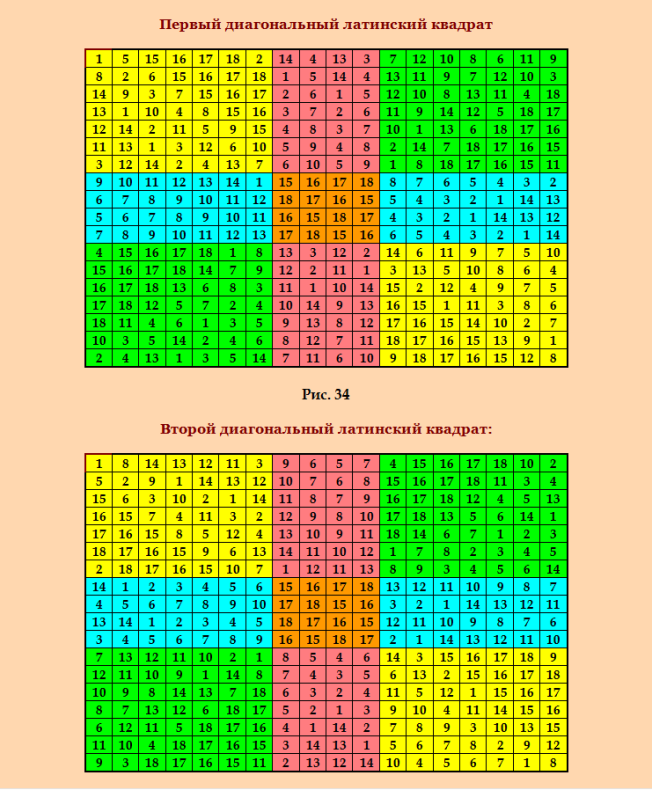 ГҗВЎ Г‘ВҚГ‘вҖҡГҗВҫГҗВіГҗВҫ ГҗВё ГҗВҪГҗ°ÑвҖЎГҗВёГҗВҪГҗВ°ГҗȄВҒГ‘ВҸ Г‘вӮ¬Гҗ°ÑВҒГ‘ВҒГҗВјГҗ°ÑвҖҡГ‘вӮ¬ГҗВёГҗВІГҗВ°ГҗВөГҗВјГ‘вҖ№ГҗВ№ ГҗВІ Г‘вҖҡГҗВөГҗВјГҗВө ГҗВ°ГҗВ»ГҗВіГҗВҫГ‘вӮ¬ГҗВёГ‘вҖҡГҗВј (Г‘ВҒГҗВј. Г‘ВҒГ‘вҖҡГҗ°ÑвӮ¬Г‘вҖҡГҗВҫГҗВІГ‘вҖ№ГҗВ№ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡ). ГҗЛңГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҪГҗВҫ ГҗВұГ‘вҖ№ГҗВ»ГҗВҫ ГҗВұГ‘вҖ№ ГҗВҝГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬ГҗВёГ‘вҖҡГ‘Е’ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ ГҗвҖәГҗЕЎ, ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВө ГҗВҝГҗВҫ ГҗВІГ‘ВҒГҗВөГҗВј ГҗВІГҗ°ÑвӮ¬ГҗВёГҗВ°ГҗВҪГ‘вҖҡГҗВ°ГҗВј ГҗЕЎГҗВ ГҗЕ“. ГҗвҖҳГ‘Ж’ГҗВҙГ‘Ж’Г‘вҖҡ ГҗВ»ГҗВё Г‘ВҒГ‘вӮ¬ГҗВөГҗВҙГҗВё ГҗВҪГҗВёГ‘вҖҰ SOLS ГҗВё Г‘ВҒГҗВҫГҗВҫГ‘вҖҡГҗВІГҗВөГ‘вҖҡГ‘ВҒГ‘вҖҡГҗВІГҗВөГҗВҪГҗВҪГҗВҫ SODLS? ------ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=136&postid=2602 ГҗЛң ГҗВІ ГҗВ·ГҗВ°ГҗВәГҗȄЕҪГ‘вҖЎГҗВөГҗВҪГҗВёГҗВө ГҗВҫ Г‘вҖҡГ‘вӮ¬ГҗВөГ‘вҖҡГ‘Е’ГҗВөГҗВј ГҗвҖәГҗЕЎ ГҗВІ Г‘вӮ¬Гҗ°ÑВҒГ‘ВҒГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВөГҗВҪГҗВҪГҗВҫГҗВ№ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВө MOLS 18-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗВӯГ‘вҖҡГҗВҫГ‘вҖҡ ГҗвҖәГҗЕЎ ГҗВІ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҪГҗВө ГҗВҝГ‘вӮ¬ГҗВөГҗВІГ‘вӮ¬Гҗ°ÑвҖ°ГҗВ°ГҗВөГ‘вҖҡГ‘ВҒГ‘ВҸ. ГҗЕҫГҗВҙГҗВҪГҗВ°ГҗВәГҗВҫ... ГҗВөГ‘ВҒГҗВ»ГҗВё ГҗВөГҗВіГҗВҫ ГҗВ°ГҗВҪГҗВ°ГҗВ»ГҗВҫГҗВіГҗВёГ‘вҖЎГҗВҪГҗВҫ ГҗВҝГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГҗ°ÑвҖҡГ‘Е’, ГҗВҫГҗВҪ Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВёГ‘вҖҡ Г‘ВҒ ГҗВҙГҗВІГ‘Ж’ГҗВјГ‘ВҸ ГҗвҖқГҗвҖәГҗЕЎ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ MOLS, Г‘вҖЎГ‘вҖҡГҗВҫ Г‘вҖҡГҗВҫГҗВ¶ГҗВө ГҗВІГҗВөГ‘ВҒГ‘Е’ГҗВјГҗВ° ГҗВёГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҪГҗВҫ. ГҗвҖҷ Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ГҗВө "ГҗЕҫ ГҗвҖңГҗВ ГҗВЈГҗЕёГҗЕёГҗВҗГҗВҘ MOLS ГҗвҖҷГҗЕҫГҗВЎГҗвҖўГҗЕ“ГҗВқГҗВҗГҗвҖқГҗВҰГҗВҗГҗВўГҗЕҫГҗвҖңГҗЕҫ ГҗЕёГҗЕҫГҗВ ГҗВҜГҗвҖқГҗЕЎГҗВҗ" http://www.natalimak1.narod.ru/mols18.htm ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪ Г‘вҖҡГ‘вӮ¬ГҗВөГ‘вҖҡГҗВёГҗВ№ ГҗвҖәГҗЕЎ ГҗВҙГҗВ°ГҗВҪГҗВҪГҗВҫГҗВ№ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘вҖ№ MOLS 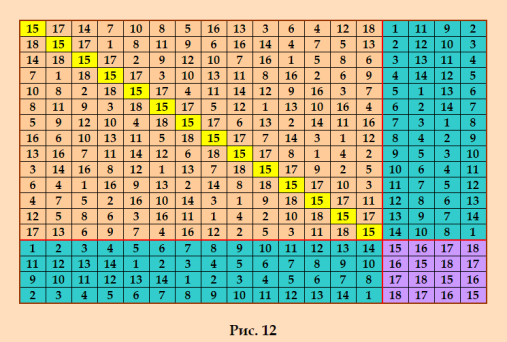 ГҗЕёГ‘вӮ¬ГҗВөГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВІГҗВ°ГҗВ»ГҗВ° Г‘ВҚГ‘вҖҡГҗВҫГ‘вҖҡ ГҗвҖәГҗЕЎ ГҗВ°ГҗВҪГҗВ°ГҗВ»ГҗВҫГҗВіГҗВёГ‘вҖЎГҗВҪГҗВҫ ГҗВҝГҗВөГ‘вӮ¬ГҗВІГ‘вҖ№ГҗВј ГҗВҙГҗВІГ‘Ж’ГҗВј ГҗвҖәГҗЕЎ, ГҗВҙГҗВ°ГҗВ»ГҗВөГҗВө ГҗВҝГ‘вӮ¬ГҗВөГҗВІГ‘вӮ¬Гҗ°ÑвҖҡГҗВёГҗВ»ГҗВ° ГҗВІГ‘ВҒГҗВө Г‘вҖҡГ‘вӮ¬ГҗВё ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ° ГҗВІ Г‘вҖҡГ‘вӮ¬ГҗВ°ГҗВҙГҗВёГ‘вҖ ГҗВёГҗВҫГҗВҪГҗВҪГ‘Ж’Г‘ЕҪ Г‘вҖһГҗВҫГ‘вӮ¬ГҗВјГ‘Ж’ ГҗВё ГҗВҪГҗВҫГ‘вӮ¬ГҗВјГҗВ°ГҗВ»ГҗВёГҗВ·ГҗВҫГҗВІГҗВ°ГҗВ»ГҗВ° ГҗВёГ‘вҖҰ. ГҗвҖҷ Г‘вӮ¬ГҗВөГҗВ·Г‘Ж’ГҗȄ΄вҖҡГҗ°ÑвҖҡГҗВө ГҗВҝГҗВҫГҗȄĄвҖЎГҗВөГҗВҪГҗВ° ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВ° MOLS 18-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘ВҸГ‘вҖ°Гҗ°ÑВҸ ГҗВёГҗВ· ГҗВҙГҗВІГ‘Ж’Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВё ГҗВҫГҗВҙГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖәГҗЕЎ ГҗвҖқГҗвҖәГҗЕЎ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 14 6 15 2 3 4 5 0 1 7 8 9 16 17 11 12 13 10 7 17 10 11 2 3 4 6 15 0 1 12 13 14 9 16 8 5 9 0 13 8 14 2 3 10 11 6 15 16 17 7 12 1 5 4 12 7 6 16 1 17 2 8 14 10 11 13 0 9 15 5 4 3 16 9 0 10 12 15 13 1 17 8 14 6 7 11 5 4 3 2 10 12 7 6 8 9 11 15 13 1 17 0 14 5 4 3 2 16 17 13 16 12 9 7 0 2 3 4 5 14 11 15 1 8 10 6 15 11 14 17 13 16 12 5 4 3 2 1 8 10 6 0 7 9 1 15 11 14 17 13 16 3 2 5 4 8 10 6 0 7 9 12 11 14 17 13 16 12 9 4 5 2 3 15 1 8 10 6 0 7 8 2 3 4 5 0 14 9 10 12 6 7 15 16 17 11 1 13 2 3 4 5 7 11 17 12 6 16 0 10 9 1 13 14 15 8 3 4 5 9 15 14 10 16 0 13 7 2 6 12 8 17 11 1 4 5 12 1 11 6 8 13 7 17 9 3 2 0 16 10 14 15 5 16 8 15 0 10 1 17 9 14 12 4 3 2 7 13 6 11 13 10 1 7 6 8 15 14 12 11 16 5 4 3 2 9 17 0 6 8 9 0 10 1 7 11 16 15 13 17 5 4 3 2 12 14 ГҗвҖқГҗвҖәГҗЕЎ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 9 17 7 0 2 3 4 16 10 8 1 12 13 14 15 5 6 11 12 8 6 16 17 0 2 5 1 10 7 13 14 15 4 11 9 3 13 12 10 11 5 6 17 4 7 1 16 14 15 3 9 8 2 0 14 13 12 1 9 4 11 3 16 7 5 15 2 8 10 0 17 6 15 14 13 12 7 8 3 2 5 16 4 0 10 1 17 6 11 9 17 15 14 13 12 16 10 0 4 5 3 1 7 6 11 9 8 2 2 0 17 6 11 9 8 12 13 14 15 3 4 5 16 7 1 10 11 9 8 10 1 7 16 14 15 12 13 6 17 0 2 3 4 5 3 2 0 17 6 11 9 15 14 13 12 4 5 16 7 1 10 8 6 11 9 8 10 1 7 13 12 15 14 17 0 2 3 4 5 16 10 3 4 5 16 17 0 1 9 11 8 2 6 12 13 14 15 7 4 5 16 7 0 2 1 10 11 6 9 8 3 17 12 13 14 15 16 7 1 2 3 10 15 8 6 17 11 5 9 4 0 12 13 14 1 10 3 4 8 15 14 9 17 0 6 7 16 11 5 2 12 13 8 4 5 9 15 14 13 11 0 2 17 10 1 7 6 16 3 12 5 16 11 15 14 13 12 6 2 3 0 9 8 10 1 17 7 4 7 6 15 14 13 12 5 17 3 4 2 16 11 9 8 10 0 1 ГҗвҖәГҗЕЎ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 11 0 1 7 5 8 9 10 12 4 15 16 6 3 13 2 17 14 2 11 0 1 10 9 12 15 16 8 13 14 5 6 7 17 3 4 3 7 11 0 1 15 4 13 2 12 6 9 14 10 17 5 8 16 4 5 10 11 0 1 13 6 7 16 14 3 15 17 9 12 2 8 5 8 9 15 11 0 1 14 10 2 3 13 17 4 16 7 12 6 6 9 12 4 13 11 0 3 15 7 5 17 8 2 10 16 14 1 7 10 15 13 6 14 3 0 17 1 11 2 16 12 8 4 9 5 8 12 16 2 7 10 15 17 0 11 1 4 9 5 3 14 6 13 9 4 8 12 16 2 7 1 11 0 17 5 3 14 6 13 15 10 10 15 13 6 14 3 5 11 1 17 0 7 2 16 12 8 4 9 1 16 14 9 3 13 17 2 4 5 7 0 11 8 15 6 10 12 12 6 5 14 15 17 8 16 9 3 2 1 0 11 4 10 13 7 13 3 6 10 17 4 2 12 5 14 16 8 1 0 11 9 7 15 14 13 7 17 9 16 10 8 3 6 12 15 4 1 0 11 5 2 15 2 17 5 12 7 16 4 14 13 8 6 10 9 1 0 11 3 16 17 3 8 2 12 14 9 6 15 4 10 13 7 5 1 0 11 17 14 4 16 8 6 11 5 13 10 9 12 7 15 2 3 1 0 ГҗЕҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ Г‘ВҒГҗВёГҗВјГҗВҝГҗ°ÑвҖҡГҗВёГ‘вҖЎГҗВҪГҗ°ÑВҸ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВ° MOLS! ГҗЕёГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬Г‘ВҸГ‘ЕҪ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВҫГҗВ№ GetOrthogonal Order? 18 Enter the name of the squares file: a Choose 1 - get counts and maximun pairs, or 2 - get pairs for one square: 1 ..output file a-orthCounts.txt ..output file a-orthNos.txt squares 3 total orthogonal pairs 3 Maximum pairs for square 1: 2 There are 2 other squares with this maximum number of pairs. ..output file a-1orths.txt Pairs for square 1: 2 ГҗвҖҷГ‘ВҒГ‘вҖҳ ГҗВІГҗВөГ‘вӮ¬ГҗВҪГҗВҫ: ГҗВІГ‘ВҒГҗВө Г‘вҖҡГ‘вӮ¬ГҗВё ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ° ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВі ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВіГ‘Ж’ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№. ГҗВўГҗВ°ГҗВұГҗВ»ГҗВёГ‘вҖ ГҗВ° ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВҝГҗ°ÑвӮ¬ 1: [2,3], 2: [1,3], 3: [1,2] ГҗВЎГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ° ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘вҖ№ MOLS Order? 18
Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail_7.txt
Counts
------
1 Latin
2 diagonal Latin
3 nfr
2 orthogonal pair
2 self-orthogonal
1 transpose parityГҗЛңГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҪГ‘вҖ№ГҗВ№ ГҗВІГҗВҫГҗВҝГ‘вӮ¬ГҗВҫГ‘ВҒ: ГҗВҪГҗВөГҗ»ÑŒГҗВ·Г‘ВҸ ГҗВ»ГҗВё ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГ‘вҖҡГ‘Е’ ГҗВёГҗВ· ГҗВҙГҗВ°ГҗВҪГҗВҪГҗВҫГҗВ№ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘вҖ№ MOLS ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ MODLS, Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘ВҸГ‘вҖ°Г‘Ж’Г‘ЕҪ ГҗВёГҗВ· Г‘вҖҡГ‘вӮ¬Г‘вҖҳГ‘вҖҰ ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ? ГҗВўГҗВ°ГҗВәГҗ°ÑВҸ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВ° MODLS 18-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВҝГҗВҫГҗВәГҗВ° ГҗВҪГҗВөГҗВёГҗВ·ГҗВІГҗВөГ‘ВҒГ‘вҖҡГҗВҪГҗВ°. ------- https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=136&postid=2604 ГҗВҗ Г‘ВҚГ‘вҖҡГҗВҫ ГҗВҝГ‘ВҒГҗВөГҗВІГҗВҙГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВ№ГҗВәГҗВ° MODLS 18-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° 1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 14 6 15 2 3 4 5 0 1 7 8 9 16 17 11 12 13 10 7 17 10 11 2 3 4 6 15 0 1 12 13 14 9 16 8 5 9 0 13 8 14 2 3 10 11 6 15 16 17 7 12 1 5 4 12 7 6 16 1 17 2 8 14 10 11 13 0 9 15 5 4 3 16 9 0 10 12 15 13 1 17 8 14 6 7 11 5 4 3 2 10 12 7 6 8 9 11 15 13 1 17 0 14 5 4 3 2 16 17 13 16 12 9 7 0 2 3 4 5 14 11 15 1 8 10 6 15 11 14 17 13 16 12 5 4 3 2 1 8 10 6 0 7 9 1 15 11 14 17 13 16 3 2 5 4 8 10 6 0 7 9 12 11 14 17 13 16 12 9 4 5 2 3 15 1 8 10 6 0 7 8 2 3 4 5 0 14 9 10 12 6 7 15 16 17 11 1 13 2 3 4 5 7 11 17 12 6 16 0 10 9 1 13 14 15 8 3 4 5 9 15 14 10 16 0 13 7 2 6 12 8 17 11 1 4 5 12 1 11 6 8 13 7 17 9 3 2 0 16 10 14 15 5 16 8 15 0 10 1 17 9 14 12 4 3 2 7 13 6 11 13 10 1 7 6 8 15 14 12 11 16 5 4 3 2 9 17 0 6 8 9 0 10 1 7 11 16 15 13 17 5 4 3 2 12 14 2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 9 17 7 0 2 3 4 16 10 8 1 12 13 14 15 5 6 11 12 8 6 16 17 0 2 5 1 10 7 13 14 15 4 11 9 3 13 12 10 11 5 6 17 4 7 1 16 14 15 3 9 8 2 0 14 13 12 1 9 4 11 3 16 7 5 15 2 8 10 0 17 6 15 14 13 12 7 8 3 2 5 16 4 0 10 1 17 6 11 9 17 15 14 13 12 16 10 0 4 5 3 1 7 6 11 9 8 2 2 0 17 6 11 9 8 12 15 13 14 3 4 5 16 7 1 10 11 9 8 10 1 7 16 13 14 12 15 6 17 0 2 3 4 5 3 2 0 17 6 11 9 14 13 15 12 4 5 16 7 1 10 8 6 11 9 8 10 1 7 15 12 14 13 17 0 2 3 4 5 16 10 3 4 5 16 17 0 1 9 11 8 2 6 12 13 14 15 7 4 5 16 7 0 2 1 10 11 6 9 8 3 17 12 13 14 15 16 7 1 2 3 10 15 8 6 17 11 5 9 4 0 12 13 14 1 10 3 4 8 15 14 9 17 0 6 7 16 11 5 2 12 13 8 4 5 9 15 14 13 11 0 2 17 10 1 7 6 16 3 12 5 16 11 15 14 13 12 6 2 3 0 9 8 10 1 17 7 4 7 6 15 14 13 12 5 17 3 4 2 16 11 9 8 10 0 1 3 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 9 17 7 0 2 3 4 16 10 8 1 12 13 14 15 5 6 11 12 8 6 16 17 0 2 5 1 10 7 13 14 15 4 11 9 3 13 12 10 11 5 6 17 4 7 1 16 14 15 3 9 8 2 0 14 13 12 1 9 4 11 3 16 7 5 15 2 8 10 0 17 6 15 14 13 12 7 8 3 2 5 16 4 0 10 1 17 6 11 9 17 15 14 13 12 16 10 0 4 5 3 1 7 6 11 9 8 2 2 0 17 6 11 9 8 12 13 14 15 3 4 5 16 7 1 10 11 9 8 10 1 7 16 14 15 12 13 6 17 0 2 3 4 5 3 2 0 17 6 11 9 15 14 13 12 4 5 16 7 1 10 8 6 11 9 8 10 1 7 13 12 15 14 17 0 2 3 4 5 16 10 3 4 5 16 17 0 1 9 11 8 2 6 12 13 14 15 7 4 5 16 7 0 2 1 10 11 6 9 8 3 17 12 13 14 15 16 7 1 2 3 10 15 8 6 17 11 5 9 4 0 12 13 14 1 10 3 4 8 15 14 9 17 0 6 7 16 11 5 2 12 13 8 4 5 9 15 14 13 11 0 2 17 10 1 7 6 16 3 12 5 16 11 15 14 13 12 6 2 3 0 9 8 10 1 17 7 4 7 6 15 14 13 12 5 17 3 4 2 16 11 9 8 10 0 1 ГҗвҖ”ГҗВҙГҗВөГ‘ВҒГ‘Е’ ГҗВІГ‘ВҒГҗВө ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ Г‘ВҸГҗВІГҗȄВҸГ‘ЕҪГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗвҖқГҗвҖәГҗЕЎ, ГҗВҪГҗВҫ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ 2 ГҗВё 3 ГҗВҪГҗВө ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№. ГҗВўГҗВ°ГҗВұГҗВ»ГҗВёГ‘вҖ ГҗВ° ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВҝГҗ°ÑвӮ¬ 1: [2,3], 2: [1], 3: [1] |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВқГҗВөГҗВјГҗВҪГҗВҫГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗВ°ГҗВ»ГҗВ° Г‘ВҒ ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГҗВҫГҗВ№ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВҫГҗВ№ MOLS 18-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘ВҸГ‘вҖ°ГҗВөГҗВ№ ГҗВёГҗВ· ГҗВҙГҗВІГ‘Ж’Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВё ГҗВҫГҗВҙГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖәГҗЕЎ. ГҗЕёГҗВҫГҗȄĄвҖЎГҗВөГҗВҪ ГҗВёГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҪГ‘вҖ№ГҗВ№ ГҗВҪГҗВ°ГҗВұГҗВҫГ‘вӮ¬ ГҗВёГҗВ· 384 ГҗвҖқГҗвҖәГҗЕЎ ГҗВё ГҗВҫГҗВҙГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖәГҗЕЎ, ГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬Г‘вҖ№ГҗВ№ ГҗВҙГҗ°ÑвҖҳГ‘вҖҡ Г‘вҖЎГҗВөГ‘вҖҡГ‘вҖ№Г‘вӮ¬ГҗВө ГҗВ°ГҗВҪГҗВ°ГҗВ»ГҗВҫГҗВіГҗВёГ‘вҖЎГҗВҪГ‘вҖ№ГҗВө ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘вҖ№ MOLS. ГҗВӯГ‘вҖҡГҗВҫ ГҗВҝГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬ГҗВәГҗВ° ГҗВҝГҗВҫГҗȄĄвҖЎГҗВөГҗВҪГҗВҪГҗВҫГҗВіГҗВҫ ГҗВіГ‘вӮ¬Гҗ°ÑвҖһГҗВ° ГҗВҪГҗВ° ГҗВәГҗВ»ГҗВёГҗВәГҗВё sage: d = { 1: [8,161,385],
2: [5,162],
3: [6,163],
4: [7,164],
5: [2,165],
6: [3,166],
7: [4,167],
8: [1,168,385],
17: [177],
18: [178],
19: [179],
20: [180],
21: [181],
22: [182],
23: [183],
24: [184],
41: [201],
42: [202],
43: [203],
44: [204],
45: [205],
46: [206],
47: [207],
48: [208],
57: [62,217],
58: [63,218],
59: [64,219],
60: [61,220],
61: [60,221],
62: [57,222],
63: [58,223],
64: [59,224],
161: [1,168,385],
162: [2,165],
163: [3,166],
164: [4,167],
165: [5,162],
166: [6,163],
167: [7,164],
168: [8,161,385],
177: [17],
178: [18],
179: [19],
180: [20],
181: [21],
182: [22],
183: [23],
184: [24],
201: [41],
202: [42],
203: [43],
204: [44],
205: [45],
206: [46],
207: [47],
208: [48],
217: [57,222],
218: [58,223],
219: [59,224],
220: [60,221],
221: [61,220],
222: [62,217],
223: [63,218],
224: [64,219],
385: [1,8,161,168]}
sage: g = Graph (d)
sage: g.cliques_maximum ()ГҗВқГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВө ГҗВәГҗВ»ГҗВёГҗВәГҗВё [[385, 1, 8], [385, 161, 1], [385, 161, 168], [385, 168, 8]] ГҗЕЎГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ 1, 8, 161 ГҗВё 168 - ГҗвҖқГҗвҖәГҗЕЎ, ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ 385 - ГҗвҖәГҗЕЎ. ГҗЕЎГҗВ»ГҗВёГҗВәГҗВ° ГҗВёГҗВ· Г‘вҖҡГ‘вӮ¬Г‘вҖҳГ‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГҗВәГҗВ° ГҗВҪГҗВө ГҗВҪГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВ°. ГҗВқГҗВҫ Г‘вҖҡГ‘Ж’Г‘вҖҡ ГҗВјГҗВҫГҗВ¶ГҗВҪГҗВҫ ГҗВҝГ‘вӮ¬ГҗВҫГҗВҙГҗВҫГҗВ»ГҗВ¶ГҗВёГ‘вҖҡГ‘Е’ ГҗВё ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГ‘вҖҡГ‘Е’ Г‘вӮ¬Гҗ°ÑВҒГ‘ЛҶГҗВёГ‘вӮ¬ГҗВөГҗВҪГҗВёГҗВө ГҗВҪГҗВ°ГҗВұГҗВҫГ‘вӮ¬ГҗВ° ГҗвҖқГҗвҖәГҗЕЎ. ГҗвҖҷГҗВҙГ‘вӮ¬Г‘Ж’ГҗВі ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВ° MODLS, Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘ВҸГ‘вҖ°Гҗ°ÑВҸ ГҗВёГҗВ· Г‘вҖҡГ‘вӮ¬Г‘вҖҳГ‘вҖҰ ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ. ГҗВқГҗВ°ГҗВҙГҗВҫ ГҗВҝГҗВҫГҗВҝГ‘вӮ¬ГҗВҫГҗВұГҗВҫГҗВІГҗ°ÑвҖҡГ‘Е’. ГҗЕёГҗВҫГҗВәГҗВ°Гҗ¶Ñƒ ГҗВҫГҗВҙГҗВҪГ‘Ж’ ГҗВёГҗВ· ГҗВҪГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВәГҗВ»ГҗВёГҗВә, ГҗВІГҗВҫГ‘вҖҡ Г‘ВҚГ‘вҖҡГ‘Ж’ [385, 161, 168] ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ 161 - ГҗвҖқГҗвҖәГҗЕЎ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 9 17 7 0 2 3 4 16 10 8 1 12 13 14 15 5 6 11 12 8 6 16 17 0 2 5 1 10 7 13 14 15 4 11 9 3 13 12 10 11 5 6 17 4 7 1 16 14 15 3 9 8 2 0 14 13 12 1 9 4 11 3 16 7 5 15 2 8 10 0 17 6 15 14 13 12 7 8 3 2 5 16 4 0 10 1 17 6 11 9 17 15 14 13 12 16 10 0 4 5 3 1 7 6 11 9 8 2 2 0 17 6 11 9 8 12 13 14 15 3 4 5 16 7 1 10 11 9 8 10 1 7 16 14 15 12 13 6 17 0 2 3 4 5 3 2 0 17 6 11 9 15 14 13 12 4 5 16 7 1 10 8 6 11 9 8 10 1 7 13 12 15 14 17 0 2 3 4 5 16 10 3 4 5 16 17 0 1 9 11 8 2 6 12 13 14 15 7 4 5 16 7 0 2 1 10 11 6 9 8 3 17 12 13 14 15 16 7 1 2 3 10 15 8 6 17 11 5 9 4 0 12 13 14 1 10 3 4 8 15 14 9 17 0 6 7 16 11 5 2 12 13 8 4 5 9 15 14 13 11 0 2 17 10 1 7 6 16 3 12 5 16 11 15 14 13 12 6 2 3 0 9 8 10 1 17 7 4 7 6 15 14 13 12 5 17 3 4 2 16 11 9 8 10 0 1 ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ 168 - ГҗвҖқГҗвҖәГҗЕЎ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 14 6 15 2 3 4 5 0 1 7 8 9 16 17 11 12 13 10 7 17 10 11 2 3 4 6 15 0 1 12 13 14 9 16 8 5 9 0 13 8 14 2 3 10 11 6 15 16 17 7 12 1 5 4 12 7 6 16 1 17 2 8 14 10 11 13 0 9 15 5 4 3 16 9 0 10 12 15 13 1 17 8 14 6 7 11 5 4 3 2 10 12 7 6 8 9 11 15 13 1 17 0 14 5 4 3 2 16 17 13 16 12 9 7 0 2 4 5 3 14 11 15 1 8 10 6 15 11 14 17 13 16 12 3 5 4 2 1 8 10 6 0 7 9 1 15 11 14 17 13 16 4 2 3 5 8 10 6 0 7 9 12 11 14 17 13 16 12 9 5 3 2 4 15 1 8 10 6 0 7 8 2 3 4 5 0 14 9 10 12 6 7 15 16 17 11 1 13 2 3 4 5 7 11 17 12 6 16 0 10 9 1 13 14 15 8 3 4 5 9 15 14 10 16 0 13 7 2 6 12 8 17 11 1 4 5 12 1 11 6 8 13 7 17 9 3 2 0 16 10 14 15 5 16 8 15 0 10 1 17 9 14 12 4 3 2 7 13 6 11 13 10 1 7 6 8 15 14 12 11 16 5 4 3 2 9 17 0 6 8 9 0 10 1 7 11 16 15 13 17 5 4 3 2 12 14 ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ 385 - ГҗвҖәГҗЕЎ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 11 0 1 7 5 8 9 10 12 4 15 16 6 3 13 2 17 14 2 11 0 1 10 9 12 15 16 8 13 14 5 6 7 17 3 4 3 7 11 0 1 15 4 13 2 12 6 9 14 10 17 5 8 16 4 5 10 11 0 1 13 6 7 16 14 3 15 17 9 12 2 8 5 8 9 15 11 0 1 14 10 2 3 13 17 4 16 7 12 6 6 9 12 4 13 11 0 3 15 7 5 17 8 2 10 16 14 1 7 10 15 13 6 14 3 0 17 1 11 2 16 12 8 4 9 5 8 12 16 2 7 10 15 17 0 11 1 4 9 5 3 14 6 13 9 4 8 12 16 2 7 1 11 0 17 5 3 14 6 13 15 10 10 15 13 6 14 3 5 11 1 17 0 7 2 16 12 8 4 9 1 16 14 9 3 13 17 2 4 5 7 0 11 8 15 6 10 12 12 6 5 14 15 17 8 16 9 3 2 1 0 11 4 10 13 7 13 3 6 10 17 4 2 12 5 14 16 8 1 0 11 9 7 15 14 13 7 17 9 16 10 8 3 6 12 15 4 1 0 11 5 2 15 2 17 5 12 7 16 4 14 13 8 6 10 9 1 0 11 3 16 17 3 8 2 12 14 9 6 15 4 10 13 7 5 1 0 11 17 14 4 16 8 6 11 5 13 10 9 12 7 15 2 3 1 0 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖ”ГҗВ°ГҗВіГҗȄВҸГҗВҪГҗВөГҗВј ГҗВІ Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’Г‘ЕҪ OEIS https://oeis.org/A328873 ГҗВҰГҗВёГ‘вҖҡГҗВёГ‘вӮ¬Г‘Ж’Г‘ЕҪ a(16) >= 14, a(17) >= 14, a(18) >= 2, a(19) >= 16, a(20) >= 2. - Natalia Makarova, Jan 08 2021 ГҗЕёГҗВҫГҗВәГҗВ° ГҗВҪГҗВёГҗВәГҗВ°ГҗВәГҗВёГ‘вҖҰ ГҗВёГҗВ·ГҗВјГҗВөГҗВҪГҗВөГҗВҪГҗВёГҗВ№ ГҗВҪГҗВөГ‘вҖҡ ГҗВІ Г‘ВҒГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВҫГҗВҪГ‘Ж’ Г‘Ж’ГҗȄĄвҖЎГ‘ЛҶГҗВөГҗВҪГҗВёГ‘ВҸ ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВҫГ‘вҖ ГҗВөГҗВҪГҗВҫГҗВә. ГҗВЎГҗВ»ГҗВөГҗВҙГҗВҫГҗВІГҗ°ÑвҖҡГҗВөГҗ»ÑŒГҗВҪГҗВҫ, ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВ° MODLS 18-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВёГҗВ· Г‘вҖҡГ‘вӮ¬Г‘вҖҳГ‘вҖҰ ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҪГҗВө ГҗВҪГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВ° ГҗВҪГҗВ° ГҗВҙГҗВ°ГҗВҪГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВҫГҗВјГҗВөГҗВҪГ‘вҖҡ. ГҗвҖ”ГҗВ°ГҗВҙГҗ°ÑвҖЎГҗВ° Г‘ВҒГҗВ»ГҗВҫГҗВ¶ГҗВҪГҗ°ÑВҸ. ГҗЕ“ГҗВҫГҗВ¶ГҗВҪГҗВҫ ГҗВҪГҗВ°ГҗВҙГҗВөГ‘ВҸГ‘вҖҡГ‘Е’Г‘ВҒГ‘ВҸ Г‘вҖҡГҗВҫГҗ»ÑŒГҗВәГҗВҫ ГҗВҪГҗВ° ГҗВІГҗВөГҗВ·ГҗВөГҗВҪГҗВёГҗВө, ГҗВІГҗВҙГ‘вӮ¬Г‘Ж’ГҗВі ГҗВҝГҗВҫГҗВІГҗВөГҗВ·Г‘вҖҳГ‘вҖҡ, ГҗВәГҗВ°ГҗВә ГҗВјГҗВҪГҗВө ГҗВҝГҗВҫГҗВІГҗВөГҗВ·ГҗВ»ГҗВҫ ГҗВІ ГҗВҝГҗВҫГҗВёГ‘ВҒГҗВәГҗВө MODLS 12-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗВўГҗВҫГҗВ¶ГҗВө ГҗВёГ‘ВҒГҗВәГҗВ°ГҗВ»ГҗВ° ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ MODLS ГҗВёГҗВ· Г‘вҖҡГ‘вӮ¬Г‘вҖҳГ‘вҖҰ ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ, ГҗВ° ГҗВҪГҗ°ÑЛҶГҗВ»ГҗВ° Г‘ВҒГ‘вӮ¬ГҗВ°ГҗВ·Г‘Ж’ ГҗВёГҗВ· Г‘вҖЎГҗВөГ‘вҖҡГ‘вҖ№Г‘вӮ¬Г‘вҖҳГ‘вҖҰ! ГҗвҖқГҗВ° ГҗВөГ‘вҖ°Г‘вҖҳ ГҗВҝГҗВҫГ‘вҖҡГҗВҫГҗВј ГҗВҙГҗВҫГҗВҝГҗВҫГҗВ»ГҗВҪГҗВёГҗВ»ГҗВ° ГҗВҪГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҪГ‘Ж’Г‘ЕҪ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ MODLS ГҗВҙГҗВҫ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘вҖ№ MOLS ГҗВёГҗВ· ГҗВҝГ‘ВҸГ‘вҖҡГҗВё ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖәГҗЕЎ (ГҗВҝГ‘ВҸГ‘вҖҡГ‘вҖ№ГҗВ№ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ - ГҗвҖәГҗЕЎ). ГҗЕёГҗВҫГ‘ВҒГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖҡГҗВө, ГҗВәГҗВ°ГҗВәГҗ°ÑВҸ ГҗВәГ‘вӮ¬Гҗ°ÑВҒГҗВёГҗВІГҗ°ÑВҸ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВ° MOLS ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГҗВ»Гҗ°ÑВҒГ‘Е’!  ГҗЛңГ‘вҖҡГҗВ°ГҗВә, ГҗВҪГҗВ°ГҗВҙГҗВҫ ГҗВҝГ‘вӮ¬ГҗВҫГҗВҙГҗВҫГҗВ»ГҗВ¶ГҗВёГ‘вҖҡГ‘Е’ Г‘ВҚГҗВәГ‘ВҒГҗВҝГҗВөГ‘вӮ¬ГҗВёГҗВјГҗВөГҗВҪГ‘вҖҡ Г‘ВҒ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВ°ГҗВјГҗВё MOLS 18-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЛңГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҪГҗВҫ: ГҗВІ ГҗВҪГҗВ°ГҗВұГҗВҫГ‘вӮ¬ГҗВө ГҗВёГҗВ· 385 ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ (384 ГҗвҖқГҗвҖәГҗЕЎ ГҗВё ГҗВҫГҗВҙГҗВёГҗВҪ ГҗвҖәГҗЕЎ) ГҗВөГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВјГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ - "ГҗВҝГ‘Ж’Г‘ВҒГ‘вҖҡГ‘вҖ№Г‘ЛҶГҗВөГҗВә" (ГҗВҝГҗВҫ ГҗВәГ‘вӮ¬ГҗВ°ГҗВ№ГҗВҪГҗВөГҗВ№ ГҗВјГҗВөГ‘вӮ¬ГҗВө. ГҗВІ Г‘вӮ¬ГҗВ°ГҗВјГҗВәГҗ°ÑвҖҰ ГҗВҙГҗВ°ГҗВҪГҗВҪГҗВҫГҗВіГҗВҫ ГҗВҪГҗВ°ГҗВұГҗВҫГ‘вӮ¬ГҗВ°; ГҗВјГҗВҫГҗВ¶ГҗВөГ‘вҖҡ ГҗВұГ‘вҖ№Г‘вҖҡГ‘Е’, ГҗВәГҗВҫГҗВҪГҗВөГ‘вҖЎГҗВҪГҗВҫ, ГҗВҫГҗВҪГҗВё ГҗВё ГҗВҪГҗВө "ГҗВҝГ‘Ж’Г‘ВҒГ‘вҖҡГ‘вҖ№Г‘ЛҶГҗВәГҗВё" ГҗВІГҗВҪГҗВө ГҗВҙГҗВ°ГҗВҪГҗВҪГҗВҫГҗВіГҗВҫ ГҗВҪГҗВ°ГҗВұГҗВҫГ‘вӮ¬ГҗВ°). ГҗЕёГҗВҫГҗВәГҗВ°ГҗВ·Г‘вҖ№ГҗВІГҗ°ÑЕҪ Г‘вҖҡГҗВ°ГҗВұГҗВ»ГҗВёГ‘вҖ Г‘Ж’ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВҝГҗ°ÑвӮ¬ (Г‘вҖЎГҗ°ÑВҒГ‘вҖҡГҗВёГ‘вҖЎГҗВҪГҗВҫ) orthogonal
square pairs
------ ----------
1 3
2 2
3 2
4 2
5 2
6 2
7 2
8 3
9 0
10 0
11 0
12 0
13 0
14 0
15 0
16 0
17 1
18 1
19 1
20 1
21 1
22 1
23 1
24 1
25 0
26 0
27 0
28 0
29 0
30 0
31 0
32 0
33 0
34 0
35 0
36 0
37 0
38 0
39 0
40 0
41 1
42 1
43 1
44 1
45 1
46 1
47 1
48 1
49 0
50 0
. . . . . . . . . .
381 0
382 0
383 0
384 0
385 4
ГҗЛң ГҗВөГ‘вҖ°Г‘вҖҳ ГҗВёГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҪГҗВҫ: ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡ 385 (ГҗвҖәГҗЕЎ) ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°ГҗВ»ГҗВөГҗВҪ ГҗвҖқГҗвҖәГҗЕЎ 1, 8, 161, 168. ГҗВҘГҗВҫГ‘вҖЎГ‘Ж’ ГҗВҙГҗȄВҸ Г‘вӮ¬Гҗ°ÑВҒГ‘ЛҶГҗВёГ‘вӮ¬ГҗВөГҗВҪГҗВёГ‘ВҸ ГҗВҪГҗВ°ГҗВұГҗВҫГ‘вӮ¬ГҗВ° ГҗВҝГҗВҫГ‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ Г‘ВҒ ГҗвҖқГҗвҖәГҗЕЎ, ГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬Г‘вҖ№ГҗВө ГҗВҪГҗВө "ГҗВҝГ‘Ж’Г‘ВҒГ‘вҖҡГ‘вҖ№Г‘ЛҶГҗВәГҗВё". ГҗВЁГҗВ°ГҗВҪГ‘ВҒГҗВҫГҗВІ ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГ‘вҖҡГ‘Е’ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ MODLS 18-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВёГҗВ· Г‘вҖҡГ‘вӮ¬Г‘вҖҳГ‘вҖҰ ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВјГҗВ°ГҗВ»ГҗВҫ, ГҗВҪГҗВҫ ГҗВҪГҗВёГҗВәГ‘вҖҡГҗВҫ ГҗВҪГҗВө ГҗВҙГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВ», Г‘вҖЎГ‘вҖҡГҗВҫ Г‘ЛҶГҗВ°ГҗВҪГ‘ВҒГҗВҫГҗВІ Г‘ВҒГҗВҫГҗВІГ‘ВҒГҗВөГҗВј ГҗВҪГҗВөГ‘вҖҡ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЕЎГ‘ВҒГ‘вҖҡГҗ°ÑвҖҡГҗВё, ГҗВөГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВөГ‘вҖ°Г‘вҖҳ ГҗВҫГҗВҙГҗВёГҗВҪ ГҗВҝГ‘Ж’Г‘вҖҡГ‘Е’ ГҗВә ГҗВҙГҗВҫГ‘ВҒГ‘вҖҡГҗВёГҗВ¶ГҗВөГҗВҪГҗВёГ‘ЕҪ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВ»ГҗВөГҗВҪГҗВҪГҗВҫГҗВ№ Г‘вҖ ГҗВөГҗВ»ГҗВё: ГҗВҝГҗВҫГ‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ Г‘ВҒ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВҫГҗВ№ MOLS 18-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВёГҗВ· ГҗВҝГ‘ВҸГ‘вҖҡГҗВё ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖәГҗЕЎ, ГҗВІГ‘вҖ№ГҗВҙГҗВ°ГҗВҪГҗВҪГҗВҫГҗВ№ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВҫГҗВ№ SageMath (Г‘ВҒГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖҡГҗВө Г‘ВҒГ‘вҖҡГҗ°ÑвӮ¬Г‘вҖҡГҗВҫГҗВІГ‘вҖ№ГҗВ№ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡ). ГҗЕёГ‘вӮ¬ГҗВҫГҗВұГ‘Ж’ГҗВ№Г‘вҖҡГҗВө, ГҗВіГҗВҫГ‘ВҒГҗВҝГҗВҫГҗВҙГҗВ°. ГҗвҖ”ГҗВ°ГҗВҙГҗ°ÑвҖЎГҗВ° ГҗВёГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҪГҗ°ÑВҸ! ГҗВҗГҗВ»ГҗВіГҗВҫГ‘вӮ¬ГҗВёГ‘вҖҡГҗВј ГҗВІГ‘ВҒГ‘вҖҳ Г‘вҖҡГҗВҫГ‘вҖҡ ГҗВ¶ГҗВө - ГҗВҝГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГ‘вҖҡГҗВ°ГҗВҪГҗВҫГҗВІГҗВәГҗВ° Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВә ГҗВё Г‘ВҒГ‘вҖҡГҗВҫГҗВ»ГҗВұГ‘вҖ ГҗВҫГҗВІ. ГҗВЈ ГҗВјГҗВөГҗВҪГ‘ВҸ ГҗВөГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВҪГҗВөГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬Г‘вҖ№ГҗВө Г‘ВҚГҗВІГ‘вӮ¬ГҗВёГ‘ВҒГ‘вҖҡГҗВёГҗВәГҗВё ГҗВІ Г‘ВҚГ‘вҖҡГҗВҫГҗВј ГҗВ°ГҗВ»ГҗВіГҗВҫГ‘вӮ¬ГҗВёГ‘вҖҡГҗВјГҗВө, ГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬Г‘вҖ№ГҗВө ГҗВҝГҗВҫГҗВ·ГҗВІГҗВҫГҗȄВҸГ‘ЕҪГ‘вҖҡ ГҗВұГ‘вҖ№Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫ ГҗВІГ‘вҖ№ГҗВҝГҗВҫГҗВ»ГҗВҪГ‘ВҸГ‘вҖҡГ‘Е’ ГҗВҝГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГ‘вҖҡГҗВ°ГҗВҪГҗВҫГҗВІГҗВәГ‘Ж’ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВә ГҗВё Г‘ВҒГ‘вҖҡГҗВҫГҗВ»ГҗВұГ‘вҖ ГҗВҫГҗВІ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВқГ‘Ж’ ГҗВІГҗВҫГ‘вҖҡ, ГҗВ·ГҗВ°ГҗВІГҗВөГ‘вӮ¬Г‘ЛҶГҗВёГҗВ»ГҗВ° Г‘ВҚГҗВәГ‘ВҒГҗВҝГҗВөГ‘вӮ¬ГҗВёГҗВјГҗВөГҗВҪГ‘вҖҡ Г‘ВҒГҗВҫ Г‘ВҒГҗВІГҗВҫГҗВёГҗВјГҗВё ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВ°ГҗВјГҗВё MOLS 18-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗВ Гҗ°ÑВҒГ‘ЛҶГҗВёГ‘вӮ¬ГҗВёГҗВ»ГҗВ° ГҗВҪГҗВ°ГҗВұГҗВҫГ‘вӮ¬ ГҗВҙГҗВҫ 722 ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ, ГҗВҙГҗВІГҗВ° ГҗВёГҗВ· ГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬Г‘вҖ№Г‘вҖҰ ГҗвҖәГҗЕЎ. ГҗВҫГ‘ВҒГ‘вҖҡГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ. ГҗЕЎ Г‘ВҒГҗВҫГҗВ¶ГҗВ°ГҗВ»ГҗВөГҗВҪГҗВёГ‘ЕҪ, ГҗВҪГҗВёГ‘вҖЎГҗВөГҗВіГҗВҫ ГҗВҝГ‘вӮ¬ГҗВёГҗВҪГ‘вҖ ГҗВёГҗВҝГҗВёГҗВ°Гҗ»ÑŒГҗВҪГҗВҫ ГҗВҪГҗВҫГҗВІГҗВҫГҗВіГҗВҫ ГҗВҪГҗВө ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГҗВ»ГҗВ°. ГҗВқГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГ‘вҖ№ Г‘вҖҡГҗВҫГ‘вҖЎГҗВҪГҗВҫ Г‘вҖҡГҗВ°ГҗВәГҗВёГҗВө ГҗВ¶ГҗВө ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘вҖ№ MOLS, Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘ВҸГ‘вҖ°ГҗВёГҗВө ГҗВёГҗВ· ГҗВҙГҗВІГ‘Ж’Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВё ГҗВҫГҗВҙГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖәГҗЕЎ, Г‘вҖҡГҗВҫГҗ»ÑŒГҗВәГҗВҫ ГҗВёГ‘вҖҰ Г‘ВҒГ‘вҖҡГҗВ°ГҗВ»ГҗВҫ ГҗВІ ГҗВҙГҗВІГҗВ° Г‘вӮ¬ГҗВ°ГҗВ·ГҗВ° ГҗВұГҗВҫГҗȄ΄ЛҶГҗВө. ГҗвҖҷГҗВҫГ‘вҖҡ ГҗВҫГҗВҪГҗВё - ГҗВІГҗВҫГ‘ВҒГҗВөГҗВјГ‘Е’ ГҗВәГҗВ»ГҗВёГҗВә Г‘вӮ¬ГҗВ°ГҗВ·ГҗВјГҗВөГ‘вӮ¬ГҗВ° 3 [[199, 722, 229], [199, 722, 231], [201, 722, 229], [201, 722, 231], [577, 721, 357], [577, 721, 359], [578, 721, 357], [578, 721, 359]] ГҗЕЎГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ 721 ГҗВё 722 - ГҗвҖәГҗЕЎ. ГҗЕҫГҗВ¶ГҗВёГҗВҙГҗВ°ГҗВөГҗВјГ‘вҖ№ГҗВ№ Г‘вӮ¬ГҗВөГҗВ·Г‘Ж’ГҗȄ΄вҖҡГҗ°ÑвҖҡ. ГҗЕҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВ»ГҗВҫГ‘ВҒГ‘Е’ ГҗВҝГҗВҫГҗВҝГ‘вӮ¬ГҗВҫГҗВұГҗВҫГҗВІГҗ°ÑвҖҡГ‘Е’ Г‘ВҒ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВҫГҗВ№ MOLS, ГҗВІГ‘вҖ№ГҗВҙГҗВ°ГҗВҪГҗВҪГҗВҫГҗВ№ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВҫГҗВ№ SageMath. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЕёГҗВҫГҗВәГҗВ°Гҗ¶Ñƒ ГҗВІГ‘ВҒГҗВө ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№, ГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·Г‘Ж’Г‘ЕҪГ‘вҖ°ГҗВёГҗВө ГҗВІГҗВҫГ‘ВҒГҗВөГҗВјГ‘Е’ ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВәГҗВ»ГҗВёГҗВә Г‘вӮ¬ГҗВ°ГҗВ·ГҗВјГҗВөГ‘вӮ¬ГҗВ° 3; ГҗВІГ‘вҖ№ ГҗВјГҗВҫГҗВ¶ГҗВөГ‘вҖҡГҗВө Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВёГ‘вҖҡГ‘Е’ ГҗВІГ‘ВҒГҗВө ГҗВІГҗВҫГ‘ВҒГҗВөГҗВјГ‘Е’ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝ MOLS ГҗВёГҗВ· Г‘ВҚГ‘вҖҡГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ ГҗВІ Г‘ВҒГҗВҫГҗВҫГ‘вҖҡГҗВІГҗВөГ‘вҖҡГ‘ВҒГ‘вҖҡГҗВІГҗВёГҗВё Г‘ВҒ ГҗВәГҗВ»ГҗВёГҗВәГҗВ°ГҗВјГҗВё 199 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 6 11 12 2 3 4 5 16 9 7 1 13 14 15 17 10 0 8 14 8 6 13 2 3 4 10 7 16 12 15 17 0 1 11 9 5 17 15 9 8 14 2 3 1 16 10 13 0 11 12 6 7 5 4 11 0 17 7 9 15 2 12 10 1 14 6 13 8 16 5 4 3 8 6 11 0 16 7 17 13 1 12 15 14 9 10 5 4 3 2 15 9 8 6 11 10 16 14 12 13 17 7 1 5 4 3 2 0 7 16 10 1 12 13 14 2 3 4 5 9 8 6 11 0 17 15 12 13 14 15 17 0 11 4 5 2 3 1 10 16 7 9 8 6 9 7 16 10 1 12 13 5 4 3 2 8 6 11 0 17 15 14 1 12 13 14 15 17 0 3 2 5 4 10 16 7 9 8 6 11 10 2 3 4 5 11 15 9 6 8 16 17 0 1 12 13 14 7 2 3 4 5 0 14 9 8 11 6 7 16 15 17 10 1 12 13 3 4 5 17 13 8 12 6 0 11 9 2 7 14 15 16 10 1 4 5 15 12 6 1 10 11 17 0 8 3 2 9 13 14 7 16 5 14 1 11 10 16 7 0 15 17 6 4 3 2 8 12 13 9 13 10 0 16 7 9 8 17 14 15 11 5 4 3 2 6 1 12 16 17 7 9 8 6 1 15 13 14 0 12 5 4 3 2 11 10 201 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 6 11 12 2 3 4 5 16 9 7 1 13 14 15 17 10 0 8 14 8 6 13 2 3 4 10 7 16 12 15 17 0 1 11 9 5 17 15 9 8 14 2 3 1 16 10 13 0 11 12 6 7 5 4 11 0 17 7 9 15 2 12 10 1 14 6 13 8 16 5 4 3 8 6 11 0 16 7 17 13 1 12 15 14 9 10 5 4 3 2 15 9 8 6 11 10 16 14 12 13 17 7 1 5 4 3 2 0 7 16 10 1 12 13 14 3 4 2 5 9 8 6 11 0 17 15 12 13 14 15 17 0 11 2 5 3 4 1 10 16 7 9 8 6 9 7 16 10 1 12 13 5 2 4 3 8 6 11 0 17 15 14 1 12 13 14 15 17 0 4 3 5 2 10 16 7 9 8 6 11 10 2 3 4 5 11 15 9 6 8 16 17 0 1 12 13 14 7 2 3 4 5 0 14 9 8 11 6 7 16 15 17 10 1 12 13 3 4 5 17 13 8 12 6 0 11 9 2 7 14 15 16 10 1 4 5 15 12 6 1 10 11 17 0 8 3 2 9 13 14 7 16 5 14 1 11 10 16 7 0 15 17 6 4 3 2 8 12 13 9 13 10 0 16 7 9 8 17 14 15 11 5 4 3 2 6 1 12 16 17 7 9 8 6 1 15 13 14 0 12 5 4 3 2 11 10 229 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 7 4 5 6 0 1 8 9 10 16 17 12 13 14 15 2 11 3 12 9 1 8 3 4 5 16 17 2 11 13 14 15 6 7 0 10 13 12 16 5 10 0 1 2 11 6 7 14 15 3 9 4 17 8 14 13 12 2 8 17 4 6 7 3 9 15 0 16 1 11 10 5 15 14 13 12 6 10 11 3 9 0 16 4 2 5 7 17 8 1 1 15 14 13 12 3 17 0 16 4 2 6 8 9 11 10 5 7 11 7 9 16 2 6 3 12 13 14 15 17 10 8 5 1 4 0 8 10 17 11 7 9 16 15 14 13 12 5 1 4 0 3 6 2 5 8 10 17 11 7 9 13 12 15 14 1 4 0 3 6 2 16 10 17 11 7 9 16 2 14 15 12 13 8 5 1 4 0 3 6 4 16 6 0 1 2 10 11 5 7 8 3 17 12 13 14 15 9 9 2 3 4 16 8 7 17 1 11 5 0 6 10 12 13 14 15 16 6 0 9 5 11 15 10 4 17 1 7 3 2 8 12 13 14 2 3 7 1 17 15 14 8 0 10 4 9 11 6 16 5 12 13 6 11 4 10 15 14 13 5 3 8 0 16 7 17 2 9 1 12 17 0 8 15 14 13 12 1 6 5 3 2 9 11 10 16 7 4 3 5 15 14 13 12 0 4 2 1 6 10 16 7 17 8 9 11 231 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 7 4 5 6 0 1 8 9 10 16 17 12 13 14 15 2 11 3 12 9 1 8 3 4 5 16 17 2 11 13 14 15 6 7 0 10 13 12 16 5 10 0 1 2 11 6 7 14 15 3 9 4 17 8 14 13 12 2 8 17 4 6 7 3 9 15 0 16 1 11 10 5 15 14 13 12 6 10 11 3 9 0 16 4 2 5 7 17 8 1 1 15 14 13 12 3 17 0 16 4 2 6 8 9 11 10 5 7 11 7 9 16 2 6 3 14 12 13 15 17 10 8 5 1 4 0 8 10 17 11 7 9 16 15 13 12 14 5 1 4 0 3 6 2 5 8 10 17 11 7 9 12 14 15 13 1 4 0 3 6 2 16 10 17 11 7 9 16 2 13 15 14 12 8 5 1 4 0 3 6 4 16 6 0 1 2 10 11 5 7 8 3 17 12 13 14 15 9 9 2 3 4 16 8 7 17 1 11 5 0 6 10 12 13 14 15 16 6 0 9 5 11 15 10 4 17 1 7 3 2 8 12 13 14 2 3 7 1 17 15 14 8 0 10 4 9 11 6 16 5 12 13 6 11 4 10 15 14 13 5 3 8 0 16 7 17 2 9 1 12 17 0 8 15 14 13 12 1 6 5 3 2 9 11 10 16 7 4 3 5 15 14 13 12 0 4 2 1 6 10 16 7 17 8 9 11 357 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 9 17 7 0 2 3 4 16 10 8 1 12 13 14 15 5 6 11 12 8 6 16 17 0 2 5 1 10 7 13 14 15 4 11 9 3 13 12 10 11 5 6 17 4 7 1 16 14 15 3 9 8 2 0 14 13 12 1 9 4 11 3 16 7 5 15 2 8 10 0 17 6 15 14 13 12 7 8 3 2 5 16 4 0 10 1 17 6 11 9 17 15 14 13 12 16 10 0 4 5 3 1 7 6 11 9 8 2 2 0 17 6 11 9 8 12 13 14 15 3 4 5 16 7 1 10 11 9 8 10 1 7 16 14 15 12 13 6 17 0 2 3 4 5 3 2 0 17 6 11 9 15 14 13 12 4 5 16 7 1 10 8 6 11 9 8 10 1 7 13 12 15 14 17 0 2 3 4 5 16 10 3 4 5 16 17 0 1 9 11 8 2 6 12 13 14 15 7 4 5 16 7 0 2 1 10 11 6 9 8 3 17 12 13 14 15 16 7 1 2 3 10 15 8 6 17 11 5 9 4 0 12 13 14 1 10 3 4 8 15 14 9 17 0 6 7 16 11 5 2 12 13 8 4 5 9 15 14 13 11 0 2 17 10 1 7 6 16 3 12 5 16 11 15 14 13 12 6 2 3 0 9 8 10 1 17 7 4 7 6 15 14 13 12 5 17 3 4 2 16 11 9 8 10 0 1 359 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 9 17 7 0 2 3 4 16 10 8 1 12 13 14 15 5 6 11 12 8 6 16 17 0 2 5 1 10 7 13 14 15 4 11 9 3 13 12 10 11 5 6 17 4 7 1 16 14 15 3 9 8 2 0 14 13 12 1 9 4 11 3 16 7 5 15 2 8 10 0 17 6 15 14 13 12 7 8 3 2 5 16 4 0 10 1 17 6 11 9 17 15 14 13 12 16 10 0 4 5 3 1 7 6 11 9 8 2 2 0 17 6 11 9 8 12 15 13 14 3 4 5 16 7 1 10 11 9 8 10 1 7 16 13 14 12 15 6 17 0 2 3 4 5 3 2 0 17 6 11 9 14 13 15 12 4 5 16 7 1 10 8 6 11 9 8 10 1 7 15 12 14 13 17 0 2 3 4 5 16 10 3 4 5 16 17 0 1 9 11 8 2 6 12 13 14 15 7 4 5 16 7 0 2 1 10 11 6 9 8 3 17 12 13 14 15 16 7 1 2 3 10 15 8 6 17 11 5 9 4 0 12 13 14 1 10 3 4 8 15 14 9 17 0 6 7 16 11 5 2 12 13 8 4 5 9 15 14 13 11 0 2 17 10 1 7 6 16 3 12 5 16 11 15 14 13 12 6 2 3 0 9 8 10 1 17 7 4 7 6 15 14 13 12 5 17 3 4 2 16 11 9 8 10 0 1 577 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 14 6 15 2 3 4 5 0 1 7 8 9 16 17 11 12 13 10 7 17 10 11 2 3 4 6 15 0 1 12 13 14 9 16 8 5 9 0 13 8 14 2 3 10 11 6 15 16 17 7 12 1 5 4 12 7 6 16 1 17 2 8 14 10 11 13 0 9 15 5 4 3 16 9 0 10 12 15 13 1 17 8 14 6 7 11 5 4 3 2 10 12 7 6 8 9 11 15 13 1 17 0 14 5 4 3 2 16 17 13 16 12 9 7 0 2 3 4 5 14 11 15 1 8 10 6 15 11 14 17 13 16 12 5 4 3 2 1 8 10 6 0 7 9 1 15 11 14 17 13 16 3 2 5 4 8 10 6 0 7 9 12 11 14 17 13 16 12 9 4 5 2 3 15 1 8 10 6 0 7 8 2 3 4 5 0 14 9 10 12 6 7 15 16 17 11 1 13 2 3 4 5 7 11 17 12 6 16 0 10 9 1 13 14 15 8 3 4 5 9 15 14 10 16 0 13 7 2 6 12 8 17 11 1 4 5 12 1 11 6 8 13 7 17 9 3 2 0 16 10 14 15 5 16 8 15 0 10 1 17 9 14 12 4 3 2 7 13 6 11 13 10 1 7 6 8 15 14 12 11 16 5 4 3 2 9 17 0 6 8 9 0 10 1 7 11 16 15 13 17 5 4 3 2 12 14 578 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 14 6 15 2 3 4 5 0 1 7 8 9 16 17 11 12 13 10 7 17 10 11 2 3 4 6 15 0 1 12 13 14 9 16 8 5 9 0 13 8 14 2 3 10 11 6 15 16 17 7 12 1 5 4 12 7 6 16 1 17 2 8 14 10 11 13 0 9 15 5 4 3 16 9 0 10 12 15 13 1 17 8 14 6 7 11 5 4 3 2 10 12 7 6 8 9 11 15 13 1 17 0 14 5 4 3 2 16 17 13 16 12 9 7 0 2 4 5 3 14 11 15 1 8 10 6 15 11 14 17 13 16 12 3 5 4 2 1 8 10 6 0 7 9 1 15 11 14 17 13 16 4 2 3 5 8 10 6 0 7 9 12 11 14 17 13 16 12 9 5 3 2 4 15 1 8 10 6 0 7 8 2 3 4 5 0 14 9 10 12 6 7 15 16 17 11 1 13 2 3 4 5 7 11 17 12 6 16 0 10 9 1 13 14 15 8 3 4 5 9 15 14 10 16 0 13 7 2 6 12 8 17 11 1 4 5 12 1 11 6 8 13 7 17 9 3 2 0 16 10 14 15 5 16 8 15 0 10 1 17 9 14 12 4 3 2 7 13 6 11 13 10 1 7 6 8 15 14 12 11 16 5 4 3 2 9 17 0 6 8 9 0 10 1 7 11 16 15 13 17 5 4 3 2 12 14 721 ГўвӮ¬вҖң ГҗвҖәГҗЕЎ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 11 0 1 7 5 8 9 10 12 4 15 16 6 3 13 2 17 14 2 11 0 1 10 9 12 15 16 8 13 14 5 6 7 17 3 4 3 7 11 0 1 15 4 13 2 12 6 9 14 10 17 5 8 16 4 5 10 11 0 1 13 6 7 16 14 3 15 17 9 12 2 8 5 8 9 15 11 0 1 14 10 2 3 13 17 4 16 7 12 6 6 9 12 4 13 11 0 3 15 7 5 17 8 2 10 16 14 1 7 10 15 13 6 14 3 0 17 1 11 2 16 12 8 4 9 5 8 12 16 2 7 10 15 17 0 11 1 4 9 5 3 14 6 13 9 4 8 12 16 2 7 1 11 0 17 5 3 14 6 13 15 10 10 15 13 6 14 3 5 11 1 17 0 7 2 16 12 8 4 9 1 16 14 9 3 13 17 2 4 5 7 0 11 8 15 6 10 12 12 6 5 14 15 17 8 16 9 3 2 1 0 11 4 10 13 7 13 3 6 10 17 4 2 12 5 14 16 8 1 0 11 9 7 15 14 13 7 17 9 16 10 8 3 6 12 15 4 1 0 11 5 2 15 2 17 5 12 7 16 4 14 13 8 6 10 9 1 0 11 3 16 17 3 8 2 12 14 9 6 15 4 10 13 7 5 1 0 11 17 14 4 16 8 6 11 5 13 10 9 12 7 15 2 3 1 0 722 ГўвӮ¬вҖң ГҗвҖәГҗЕЎ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 3 0 15 4 14 11 1 2 13 5 7 8 9 12 10 16 17 6 13 14 0 10 11 12 3 4 9 1 2 5 8 7 16 17 6 15 1 9 12 0 7 3 8 11 5 15 4 13 2 16 17 6 10 14 9 15 5 8 0 2 14 3 1 10 11 4 16 17 6 7 12 13 11 5 10 1 13 0 4 14 15 7 3 16 17 6 2 8 9 12 16 3 1 7 15 9 0 12 10 2 14 17 6 4 13 5 8 11 12 8 13 9 5 1 15 16 6 0 17 14 3 11 4 2 7 10 4 11 3 14 12 8 13 6 16 17 0 2 7 10 15 1 5 9 7 2 4 11 3 14 12 0 17 16 6 10 15 1 5 9 13 8 8 13 9 5 1 15 10 17 0 6 16 12 14 3 11 4 2 7 5 7 11 2 9 6 17 10 12 13 15 0 4 14 8 3 1 16 10 4 7 13 6 17 16 15 14 8 1 9 0 2 3 12 11 5 2 10 8 6 17 16 9 1 3 12 5 15 13 0 7 11 14 4 15 12 6 17 16 13 2 5 11 14 9 7 1 8 0 10 4 3 14 6 17 16 8 7 11 9 4 3 13 1 10 5 12 0 15 2 6 17 16 12 10 4 7 13 2 11 8 3 5 15 9 14 0 1 17 16 14 15 2 10 5 8 7 4 12 6 11 9 1 13 3 0 ГҗвҖқГҗВІГҗВ° ГҗВҝГҗВҫГ‘ВҒГҗВ»ГҗВөГҗВҙГҗВҪГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖ17 5 3 14 6 13 15 10 10 15 13 6 14 3 5 11 1 17 0 7 2 16 12 8 4 9 1 16 14 9 3 13 17 2 4 5 7 0 11 8 15 6 10 12 12 6 5 14 15 17 8 16 9 3 2 1 0 11 4 10 13 7 13 3 6 10 17 4 2 12 5 14 16 8 1 0 11 9 7 15 14 13 7 17 9 16 10 8 3 6 12 15 4 1 0 11 5 2 15 2 17 5 12 7 16 4 14 13 8 6 10 9 1 0 11 3 16 17 3 8 2 12 14 9 6 15 4 10 13 7 5 1 0 11 17 14 4 16 8 6 11 5 13 10 9 12 7 15 2 3 1 0 722 ГўвӮ¬вҖң ГҗвҖәГҗЕЎ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 3 0 15 4 14 11 1 2 13 5 7 8 9 12 10 16 17 6 13 14 0 10 11 12 3 4 9 1 2 5 8 7 16 17 6 15 1 9 12 0 7 3 8 11 5 15 4 13 2 16 17 6 10 14 9 15 5 8 0 2 14 3 1 10 11 4 16 17 6 7 12 13 11 5 10 1 13 0 4 14 15 7 3 16 17 6 2 8 9 12 16 3 1 7 15 9 0 12 10 2 14 17 6 4 13 5 8 11 12 8 13 9 5 1 15 16 6 0 17 14 3 11 4 2 7 10 4 11 3 14 12 8 13 6 16 17 0 2 7 10 15 1 5 9 7 2 4 11 3 14 12 0 17 16 6 10 15 1 5 9 13 8 8 13 9 5 1 15 10 17 0 6 16 12 14 3 11 4 2 7 5 7 11 2 9 6 17 10 12 13 15 0 4 14 8 3 1 16 10 4 7 13 6 17 16 15 14 8 1 9 0 2 3 12 11 5 2 10 8 6 17 16 9 1 3 12 5 15 13 0 7 11 14 4 15 12 6 17 16 13 2 5 11 14 9 7 1 8 0 10 4 3 14 6 17 16 8 7 11 9 4 3 13 1 10 5 12 0 15 2 6 17 16 12 10 4 7 13 2 11 8 3 5 15 9 14 0 1 17 16 14 15 2 10 5 8 7 4 12 6 11 9 1 13 3 0[/code] ГҗвҖқГҗВІГҗВ° ГҗВҝГҗВҫГ‘ВҒГҗВ»ГҗВөГҗВҙГҗВҪГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ° (721 ГҗВё 722) Г‘ВҸГҗВІГҗȄВҸГ‘ЕҪГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗвҖәГҗЕЎ, ГҗВІГ‘ВҒГҗВө ГҗВҫГ‘ВҒГ‘вҖҡГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ - ГҗвҖқГҗвҖәГҗЕЎ. ГҗвҖҷГ‘ВҒГҗВө ГҗвҖқГҗвҖәГҗЕЎ ГҗВҪГҗВҫГ‘вӮ¬ГҗВјГҗВ°ГҗВ»ГҗВёГҗВ·ГҗВҫГҗВІГҗВ°ГҗВҪГҗВҪГ‘вҖ№ГҗВө ГҗВё Г‘вӮ¬ГҗВ°ГҗВ·ГҗВ»ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№ГҗВө. ГҗвҖәГҗЕЎ Г‘вҖҡГҗВҫГҗВ¶ГҗВө ГҗВҪГҗВҫГ‘вӮ¬ГҗВјГҗВ°ГҗВ»ГҗВёГҗВ·ГҗВҫГҗВІГҗВ°ГҗВҪГҗВҪГ‘вҖ№ГҗВө ГҗВё Г‘вӮ¬ГҗВ°ГҗВ·ГҗВ»ГҗВёГ‘вҖЎГҗВҪГ‘вҖ№ГҗВө. ГҗВқГҗВ° ГҗВёГҗВ·ГҗВҫГҗВјГҗВҫГ‘вӮ¬Г‘вҖһГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ ГҗВҪГҗВө ГҗВҝГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬Г‘ВҸГҗВ»ГҗВёГ‘ВҒГ‘Е’. ГҗВўГҗВ°ГҗВәГҗВёГҗВј ГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВј, ГҗВІГ‘ВҒГҗВө ГҗВІГҗВҫГ‘ВҒГҗВөГҗВјГ‘Е’ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝ MOLS, Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘ВҸГ‘вҖ°ГҗВёГҗВө ГҗВёГҗВ· ГҗВҙГҗВІГ‘Ж’Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВё ГҗВҫГҗВҙГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖәГҗЕЎ, Г‘вӮ¬ГҗВ°ГҗВ·ГҗВҪГ‘вҖ№ГҗВө. ГҗВЎГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ° ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ [code]Order? 18 Enter the name of the squares file: inp1 .. writing type information to file inp1TypeDetail_6.txt Counts ------ 2 Latin 8 diagonal Latin 10 nfr 3 orthogonal pair 4 self-orthogonal 1 transpose parity[/code] |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВқГҗВҫГ‘вӮ¬ГҗВјГҗВ°ГҗВ»ГҗВёГҗВ·ГҗВҫГҗВІГҗВ°ГҗВ»ГҗВ° ГҗвҖәГҗЕЎ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘вҖ№ MOLS, ГҗВІГ‘вҖ№ГҗВҙГҗВ°ГҗВҪГҗВҪГҗВҫГҗВ№ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВҫГҗВ№ SageMath, ГҗВјГҗВҪГҗВө Г‘ВҒ ГҗВҪГҗВҫГ‘вӮ¬ГҗВјГҗВ°ГҗВ»ГҗВёГҗВ·ГҗВҫГҗВІГҗВ°ГҗВҪГҗВҪГ‘вҖ№ГҗВјГҗВё ГҗвҖәГҗЕЎ Г‘Ж’ГҗВҙГҗВҫГҗВұГҗВҪГҗВөГҗВө Г‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1 2 0 4 5 3 7 8 6 10 11 9 13 14 12 16 17 15 2 0 1 5 3 4 8 6 7 11 9 10 14 12 13 17 15 16 11 9 10 6 7 8 17 15 16 12 13 14 1 2 0 4 5 3 9 10 11 7 8 6 15 16 17 13 14 12 2 0 1 5 3 4 10 11 9 8 6 7 16 17 15 14 12 13 0 1 2 3 4 5 14 12 13 0 1 2 11 9 10 15 16 17 4 5 3 7 8 6 12 13 14 1 2 0 9 10 11 16 17 15 5 3 4 8 6 7 13 14 12 2 0 1 10 11 9 17 15 16 3 4 5 6 7 8 8 6 7 15 16 17 3 4 5 1 2 0 11 9 10 13 14 12 6 7 8 16 17 15 4 5 3 2 0 1 9 10 11 14 12 13 7 8 6 17 15 16 5 3 4 0 1 2 10 11 9 12 13 14 17 15 16 10 11 9 12 13 14 5 3 4 7 8 6 0 1 2 15 16 17 11 9 10 13 14 12 3 4 5 8 6 7 1 2 0 16 17 15 9 10 11 14 12 13 4 5 3 6 7 8 2 0 1 4 5 3 14 12 13 2 0 1 6 7 8 16 17 15 9 10 11 5 3 4 12 13 14 0 1 2 7 8 6 17 15 16 10 11 9 3 4 5 13 14 12 1 2 0 8 6 7 15 16 17 11 9 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 8 6 7 10 11 9 17 15 16 12 13 14 5 3 4 2 0 1 16 17 15 13 14 12 1 2 0 5 3 4 9 10 11 7 8 6 7 8 6 1 2 0 4 5 3 16 17 15 10 11 9 13 14 12 15 16 17 6 7 8 11 9 10 0 1 2 13 14 12 3 4 5 2 0 1 17 15 16 14 12 13 8 6 7 3 4 5 10 11 9 5 3 4 8 6 7 2 0 1 14 12 13 17 15 16 11 9 10 9 10 11 16 17 15 7 8 6 4 5 3 1 2 0 14 12 13 12 13 14 0 1 2 15 16 17 11 9 10 6 7 8 4 5 3 10 11 9 2 0 1 13 14 12 17 15 16 4 5 3 6 7 8 13 14 12 7 8 6 3 4 5 1 2 0 11 9 10 17 15 16 3 4 5 15 16 17 10 11 9 6 7 8 14 12 13 1 2 0 14 12 13 11 9 10 0 1 2 7 8 6 15 16 17 5 3 4 4 5 3 14 12 13 8 6 7 15 16 17 2 0 1 9 10 11 11 9 10 4 5 3 16 17 15 2 0 1 7 8 6 12 13 14 1 2 0 12 13 14 9 10 11 3 4 5 8 6 7 16 17 15 6 7 8 5 3 4 12 13 14 10 11 9 16 17 15 0 1 2 17 15 16 9 10 11 5 3 4 13 14 12 0 1 2 8 6 7 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 10 11 9 0 1 2 14 12 13 5 3 4 15 16 17 7 8 6 3 4 5 10 11 9 17 15 16 2 0 1 7 8 6 12 13 14 13 14 12 9 10 11 2 0 1 6 7 8 4 5 3 17 15 16 16 17 15 5 3 4 9 10 11 14 12 13 1 2 0 6 7 8 8 6 7 2 0 1 5 3 4 17 15 16 11 9 10 14 12 13 11 9 10 15 16 17 4 5 3 8 6 7 13 14 12 0 1 2 4 5 3 7 8 6 1 2 0 13 14 12 16 17 15 10 11 9 1 2 0 12 13 14 11 9 10 16 17 15 8 6 7 3 4 5 7 8 6 16 17 15 0 1 2 3 4 5 14 12 13 9 10 11 12 13 14 8 6 7 10 11 9 0 1 2 17 15 16 5 3 4 15 16 17 13 14 12 3 4 5 10 11 9 6 7 8 2 0 1 9 10 11 14 12 13 7 8 6 4 5 3 2 0 1 16 17 15 5 3 4 17 15 16 12 13 14 1 2 0 9 10 11 8 6 7 2 0 1 6 7 8 15 16 17 11 9 10 5 3 4 13 14 12 14 12 13 4 5 3 16 17 15 7 8 6 0 1 2 11 9 10 17 15 16 1 2 0 8 6 7 12 13 14 10 11 9 4 5 3 6 7 8 11 9 10 13 14 12 15 16 17 3 4 5 1 2 0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 15 16 17 7 8 6 11 9 10 3 4 5 0 1 2 12 13 14 12 13 14 9 10 11 5 3 4 7 8 6 15 16 17 0 1 2 3 4 5 13 14 12 10 11 9 1 2 0 8 6 7 16 17 15 7 8 6 1 2 0 4 5 3 16 17 15 10 11 9 13 14 12 9 10 11 16 17 15 8 6 7 13 14 12 4 5 3 1 2 0 6 7 8 10 11 9 17 15 16 2 0 1 14 12 13 5 3 4 11 9 10 4 5 3 14 12 13 17 15 16 2 0 1 6 7 8 5 3 4 8 6 7 2 0 1 14 12 13 17 15 16 11 9 10 17 15 16 6 7 8 12 13 14 0 1 2 9 10 11 3 4 5 14 12 13 11 9 10 0 1 2 15 16 17 3 4 5 7 8 6 2 0 1 5 3 4 15 16 17 12 13 14 7 8 6 9 10 11 16 17 15 0 1 2 3 4 5 10 11 9 13 14 12 8 6 7 13 14 12 15 16 17 7 8 6 4 5 3 1 2 0 10 11 9 1 2 0 12 13 14 9 10 11 8 6 7 16 17 15 4 5 3 10 11 9 2 0 1 13 14 12 5 3 4 6 7 8 17 15 16 4 5 3 17 15 16 1 2 0 6 7 8 11 9 10 14 12 13 8 6 7 14 12 13 16 17 15 11 9 10 5 3 4 2 0 1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 17 15 16 14 12 13 4 5 3 2 0 1 6 7 8 11 9 10 10 11 9 8 6 7 12 13 14 16 17 15 4 5 3 1 2 0 4 5 3 17 15 16 14 12 13 11 9 10 2 0 1 6 7 8 12 13 14 10 11 9 8 6 7 1 2 0 16 17 15 4 5 3 6 7 8 0 1 2 3 4 5 15 16 17 9 10 11 12 13 14 8 6 7 12 13 14 10 11 9 4 5 3 1 2 0 16 17 15 3 4 5 6 7 8 0 1 2 12 13 14 15 16 17 9 10 11 14 12 13 4 5 3 17 15 16 6 7 8 11 9 10 2 0 1 13 14 12 1 2 0 9 10 11 8 6 7 17 15 16 5 3 4 7 8 6 15 16 17 2 0 1 3 4 5 10 11 9 13 14 12 5 3 4 11 9 10 16 17 15 14 12 13 0 1 2 7 8 6 2 0 1 7 8 6 15 16 17 13 14 12 3 4 5 10 11 9 16 17 15 5 3 4 11 9 10 7 8 6 14 12 13 0 1 2 9 10 11 13 14 12 1 2 0 5 3 4 8 6 7 17 15 16 11 9 10 16 17 15 5 3 4 0 1 2 7 8 6 14 12 13 1 2 0 9 10 11 13 14 12 17 15 16 5 3 4 8 6 7 15 16 17 2 0 1 7 8 6 10 11 9 13 14 12 3 4 5 ГҗВЎГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ ГҗВҪГҗ°ÑвҖЎГҗВҪГ‘Ж’ Г‘ВҒ ГҗВҪГҗВёГҗВјГҗВё Г‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗ°ÑвҖҡГ‘Е’. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗВқГҗВёГ‘вҖЎГҗВөГҗВіГҗВҫ ГҗВҪГҗВө ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГҗВ»ГҗВҫГ‘ВҒГ‘Е’ Г‘ВҒ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВҫГҗВ№ MOLS ГҗВҫГ‘вҖҡ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГ‘вҖ№ SageMath. ГҗвҖқГҗВ°ГҗВ¶ГҗВө ГҗВҪГҗВө Г‘Ж’ГҗВҙГҗВ°ГҗВ»ГҗВҫГ‘ВҒГ‘Е’ Г‘ВҒГҗВҙГҗВөГҗВ»Гҗ°ÑвҖҡГ‘Е’ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ MOLS Г‘ВҒ ГҗВҫГҗВҙГҗВҪГҗВёГҗВј ГҗвҖқГҗвҖәГҗЕЎ ГҗВё Г‘вҖЎГҗВөГ‘вҖҡГ‘вҖ№Г‘вӮ¬Г‘Е’ГҗВјГ‘ВҸ ГҗвҖәГҗЕЎ. ГҗЕЎГҗВ°ГҗВәГҗВёГҗВө-Г‘вҖҡГҗВҫ ГҗВҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВҪГҗВөГ‘Ж’ГҗВҙГҗ°ÑвҖЎГҗВҪГ‘вҖ№ГҗВө ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ ГҗВІ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВө. ГҗЕ“ГҗВҫГҗВ¶ГҗВөГ‘вҖҡ ГҗВұГ‘вҖ№Г‘вҖҡГ‘Е’, ГҗВҫГ‘ЛҶГҗВёГҗВұГҗВ»Гҗ°ÑВҒГ‘Е’ ГҗВіГҗВҙГҗВө-ГҗВҪГҗВёГҗВұГ‘Ж’ГҗВҙГ‘Е’ ГҗВІ ГҗВҝГ‘вӮ¬ГҗВҫГ‘вҖ ГҗВөГ‘ВҒГ‘ВҒГҗВө ГҗВҝГҗВҫГҗВҙГҗВіГҗВҫГ‘вҖҡГҗВҫГҗВІГҗВәГҗВё ГҗВҪГҗВ°ГҗВұГҗВҫГ‘вӮ¬ГҗВ° ГҗвҖқГҗвҖәГҗЕЎ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЕёГ‘вӮ¬ГҗВөГҗВ¶ГҗВҙГҗВө Г‘вҖЎГҗВөГҗВј ГҗВҝГ‘вӮ¬ГҗВёГ‘ВҒГ‘вҖҡГ‘Ж’ГҗВҝГҗВёГ‘вҖҡГ‘Е’ ГҗВә Г‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗВө Г‘ВҒ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВҫГҗВ№ MOLS 20-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВҝГҗВҫГҗВәГҗВ°Гҗ¶Ñƒ ГҗВёГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҪГ‘Ж’Г‘ЕҪ ГҗВ·ГҗВ°ГҗВәГҗВҫГҗВҪГҗВҫГҗВјГҗВөГ‘вӮ¬ГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’, ГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬Г‘Ж’Г‘ВҸ Г‘ВҸ ГҗВІГ‘вҖ№Г‘ВҸГҗВІГҗВёГҗВ»ГҗВ° ГҗВІГҗВҫ ГҗВІГ‘вӮ¬ГҗВөГҗВјГ‘ВҸ Г‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГ‘вҖ№ Г‘ВҒ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВҫГҗВ№ MOLS 12-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗвҖқГ‘Ж’ГҗВұГҗВ»ГҗВёГ‘вӮ¬Г‘Ж’Г‘ЕҪ Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГҗВө https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=120&postid=2477 ГҗВҜ Г‘вҖҡГ‘Ж’Г‘вҖҡ Г‘ВҒГ‘вӮ¬ГҗВ°ГҗВІГҗВҪГҗВёГҗВ»ГҗВ° ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘вҖ№ MOLS... ГҗВҰГҗВёГ‘вҖҡГҗ°ÑвҖҡГҗВ° ГҗВёГҗВ· Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГ‘ВҸ https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=138&postid=2452 ГҗЕ“ГҗВҪГҗВө Г‘Ж’ГҗВҙГҗВ°ГҗВ»ГҗВҫГ‘ВҒГ‘Е’ Г‘вӮ¬Гҗ°ÑВҒГ‘ЛҶГҗВёГ‘вӮ¬ГҗВёГ‘вҖҡГ‘Е’ Г‘ВҚГ‘вҖҡГ‘Ж’ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ ГҗВҙГҗВҫ ГҗВҝГ‘ВҸГ‘вҖҡГҗВё ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖәГҗЕЎ, Г‘вҖҡГҗВҫГҗ»ÑŒГҗВәГҗВҫ ГҗВҝГ‘ВҸГ‘вҖҡГ‘вҖ№ГҗВ№ ГҗвҖәГҗЕЎ ГҗВҪГҗВө Г‘ВҸГҗВІГҗȄВҸГҗВөГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗвҖқГҗвҖәГҗЕЎ. ГҗвҖқГҗȄВҸ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° 32, ГҗВҪГҗВ°ГҗВІГҗВөГ‘вӮ¬ГҗВҪГҗВҫГҗВө, ГҗВҝГҗВҫГҗВҙГҗВҫГҗВұГҗВҪГҗ°ÑВҸ ГҗВҝГҗВҫГҗВ»ГҗВҪГҗ°ÑВҸ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГҗВ° MOLS. ГҗВӯГ‘вҖҡГ‘Ж’ ГҗВҝГҗВҫГҗВ»ГҗВҪГ‘Ж’Г‘ЕҪ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГ‘Ж’ MOLS ГҗВјГҗВҫГҗВ¶ГҗВҪГҗВҫ ГҗВҝГҗВҫГ‘ВҒГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВөГ‘вҖҡГ‘Е’ ГҗВІ Г‘вҖҡГҗВөГҗВјГҗВө https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117 ГҗЛңГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҪГҗ°ÑВҸ ГҗВ·ГҗВ°ГҗВәГҗВҫГҗВҪГҗВҫГҗВјГҗВөГ‘вӮ¬ГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’! PS. ГҗвҖқГҗВҫГҗВұГҗВ°ГҗВІГҗȄЕҪ ГҗВҝГҗВҫГҗВ»ГҗВҪГ‘Ж’Г‘ЕҪ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГ‘Ж’ MOLS 4-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° [code]0 1 2 3 3 2 1 0 1 0 3 2 2 3 0 1 0 1 2 3 2 3 0 1 3 2 1 0 1 0 3 2 0 1 2 3 1 0 3 2 2 3 0 1 3 2 1 0[/code] ____________________ ГҗВәГҗВҫГҗВҪГҗВөГ‘вҖ ГҗВҙГ‘Ж’ГҗВұГҗВ»ГҗВёГ‘вӮ¬Г‘Ж’ГҗВөГҗВјГҗВҫГҗВіГҗВҫ Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГ‘ВҸ ГҗвҖҷ Г‘ВҒГҗВ»ГҗВөГҗВҙГ‘Ж’Г‘ЕҪГ‘вҖ°ГҗВөГҗВј Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГҗВё https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=120&postid=2478 ГҗВіГҗВҫГҗВІГҗВҫГ‘вӮ¬ГҗВёГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВҫ ГҗВҝГҗВҫГҗВ»ГҗВҪГҗВҫГҗВ№ Г‘ВҒГҗВёГ‘ВҒГ‘вҖҡГҗВөГҗВјГҗВө MOLS 32-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВІ ГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬ГҗВҫГҗВ№ ГҗВ°ГҗВҪГҗВ°ГҗВ»ГҗВҫГҗВіГҗВёГ‘вҖЎГҗВҪГҗ°ÑВҸ Г‘ВҒГ‘вҖҡГ‘вӮ¬Г‘Ж’ГҗВәГ‘вҖҡГ‘Ж’Г‘вӮ¬ГҗВ° ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ. ГҗЛңГ‘вҖҡГҗВ°ГҗВә, ГҗВ·ГҗВ°ГҗВәГҗВҫГҗВҪГҗВҫГҗВјГҗВөГ‘вӮ¬ГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВёГҗВјГҗВөГҗВөГ‘вҖҡ ГҗВјГҗВөГ‘ВҒГ‘вҖҡГҗВҫ ГҗВҙГҗȄВҸ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝ MOLS ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВҫГҗВІ 4, 8, 12, 16 ГҗВё 32, Г‘вҖҡГҗВҫ ГҗВөГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВҙГҗȄВҸ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВҫГҗВІ Г‘ВҒГҗВөГ‘вӮ¬ГҗВёГҗВё n=4k ГҗВҝГ‘вӮ¬ГҗВё k=1, 2, 3, 4, 8. ГҗЕ“ГҗВҫГҗВ¶ГҗВҪГҗВҫ ГҗВҝГ‘вӮ¬ГҗВөГҗВҙГҗВҝГҗВҫГҗВ»ГҗВҫГҗВ¶ГҗВёГ‘вҖҡГ‘Е’, Г‘вҖЎГ‘вҖҡГҗВҫ Г‘ВҒГ‘Ж’Г‘вҖ°ГҗВөГ‘ВҒГ‘вҖҡГҗВІГ‘Ж’ГҗВөГ‘вҖҡ ГҗВ°ГҗВҪГҗВ°ГҗВ»ГҗВҫГҗВіГҗВёГ‘вҖЎГҗВҪГ‘вҖ№ГҗВө ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘вҖ№ MOLS ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВҫГҗВІ 20, 24, 28. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷ Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГҗВё https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=120&postid=2479 ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВ° ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВ° MOLS 20-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВІГ‘вҖ№ГҗВҙГҗВ°ГҗВҪГҗВҪГҗ°ÑВҸ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВҫГҗВ№ SageMath. ГҗВқГҗВҫГ‘вӮ¬ГҗВјГҗВ°ГҗВ»ГҗВёГҗВ·ГҗВҫГҗВІГҗВ°ГҗВ»ГҗВ° ГҗвҖәГҗЕЎ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘вҖ№ MOLS 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 7 15 4 12 1 9 17 6 14 5 11 0 3 16 8 13 2 10 19 18 14 3 11 0 8 16 5 13 4 10 18 2 15 7 12 1 9 19 6 17 2 10 18 7 15 4 12 3 9 17 1 14 6 11 0 8 19 5 13 16 9 17 6 14 3 11 2 8 16 0 13 5 10 18 7 19 4 12 1 15 16 5 13 2 10 1 7 15 18 12 4 9 17 6 19 3 11 0 8 14 4 12 1 9 0 6 14 17 11 3 8 16 5 19 2 10 18 7 15 13 11 0 8 18 5 13 16 10 2 7 15 4 19 1 9 17 6 14 3 12 18 7 17 4 12 15 9 1 6 14 3 19 0 8 16 5 13 2 10 11 6 16 3 11 14 8 0 5 13 2 19 18 7 15 4 12 1 9 17 10 15 2 10 13 7 18 4 12 1 19 17 6 14 3 11 0 8 16 5 9 1 9 12 6 17 3 11 0 19 16 5 13 2 10 18 7 15 4 14 8 8 11 5 16 2 10 18 19 15 4 12 1 9 17 6 14 3 13 0 7 10 4 15 1 9 17 19 14 3 11 0 8 16 5 13 2 12 18 7 6 3 14 0 8 16 19 13 2 10 18 7 15 4 12 1 11 17 6 9 5 13 18 7 15 19 12 1 9 17 6 14 3 11 0 10 16 5 8 2 4 17 6 14 19 11 0 8 16 5 13 2 10 18 9 15 4 7 1 12 3 5 13 19 10 18 7 15 4 12 1 9 17 8 14 3 6 0 11 16 2 12 19 9 17 6 14 3 11 0 8 16 7 13 2 5 18 10 15 4 1 19 8 16 5 13 2 10 18 7 15 6 12 1 4 17 9 14 3 11 0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 15 11 16 9 2 7 5 1 17 10 13 18 19 6 0 4 8 14 3 12 10 15 8 1 6 4 0 16 9 12 17 19 5 18 3 7 13 2 14 11 14 7 0 5 3 18 15 8 11 16 19 4 17 2 6 12 1 13 9 10 6 18 4 2 17 14 7 10 15 19 3 16 1 5 11 0 12 8 13 9 17 3 1 16 13 6 9 14 19 2 15 0 4 10 18 11 7 12 5 8 2 0 15 12 5 8 13 19 1 14 18 3 9 17 10 6 11 4 16 7 18 14 11 4 7 12 19 0 13 17 2 8 16 9 5 10 3 15 1 6 13 10 3 6 11 19 18 12 16 1 7 15 8 4 9 2 14 0 17 5 9 2 5 10 19 17 11 15 0 6 14 7 3 8 1 13 18 16 12 4 1 4 9 19 16 10 14 18 5 13 6 2 7 0 12 17 15 11 8 3 3 8 19 15 9 13 17 4 12 5 1 6 18 11 16 14 10 7 0 2 7 19 14 8 12 16 3 11 4 0 5 17 10 15 13 9 6 18 2 1 19 13 7 11 15 2 10 3 18 4 16 9 14 12 8 5 17 1 6 0 12 6 10 14 1 9 2 17 3 15 8 13 11 7 4 16 0 5 19 18 5 9 13 0 8 1 16 2 14 7 12 10 6 3 15 18 4 19 11 17 8 12 18 7 0 15 1 13 6 11 9 5 2 14 17 3 19 10 4 16 11 17 6 18 14 0 12 5 10 8 4 1 13 16 2 19 9 3 7 15 16 5 17 13 18 11 4 9 7 3 0 12 15 1 19 8 2 6 10 14 4 16 12 17 10 3 8 6 2 18 11 14 0 19 7 1 5 9 15 13 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 8 0 17 7 16 14 1 12 11 19 4 2 10 15 6 3 13 18 5 9 18 16 6 15 13 0 11 10 19 3 1 9 14 5 2 12 17 4 7 8 15 5 14 12 18 10 9 19 2 0 8 13 4 1 11 16 3 6 17 7 4 13 11 17 9 8 19 1 18 7 12 3 0 10 15 2 5 16 14 6 12 10 16 8 7 19 0 17 6 11 2 18 9 14 1 4 15 13 3 5 9 15 7 6 19 18 16 5 10 1 17 8 13 0 3 14 12 2 11 4 14 6 5 19 17 15 4 9 0 16 7 12 18 2 13 11 1 10 8 3 5 4 19 16 14 3 8 18 15 6 11 17 1 12 10 0 9 7 13 2 3 19 15 13 2 7 17 14 5 10 16 0 11 9 18 8 6 12 4 1 19 14 12 1 6 16 13 4 9 15 18 10 8 17 7 5 11 3 2 0 13 11 0 5 15 12 3 8 14 17 9 7 16 6 4 10 2 1 19 18 10 18 4 14 11 2 7 13 16 8 6 15 5 3 9 1 0 19 12 17 17 3 13 10 1 6 12 15 7 5 14 4 2 8 0 18 19 11 9 16 2 12 9 0 5 11 14 6 4 13 3 1 7 18 17 19 10 8 16 15 11 8 18 4 10 13 5 3 12 2 0 6 17 16 19 9 7 15 1 14 7 17 3 9 12 4 2 11 1 18 5 16 15 19 8 6 14 0 10 13 16 2 8 11 3 1 10 0 17 4 15 14 19 7 5 13 18 9 6 12 1 7 10 2 0 9 18 16 3 14 13 19 6 4 12 17 8 5 15 11 6 9 1 18 8 17 15 2 13 12 19 5 3 11 16 7 4 14 0 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 4 10 17 5 11 16 18 12 6 3 9 0 7 19 1 15 13 8 14 3 9 16 4 10 15 17 11 5 2 8 18 6 19 0 14 12 7 1 13 8 15 3 9 14 16 10 4 1 7 17 5 19 18 13 11 6 0 2 12 14 2 8 13 15 9 3 0 6 16 4 19 17 12 10 5 18 1 7 11 1 7 12 14 8 2 18 5 15 3 19 16 11 9 4 17 0 6 13 10 6 11 13 7 1 17 4 14 2 19 15 10 8 3 16 18 5 12 0 9 10 12 6 0 16 3 13 1 19 14 9 7 2 15 17 4 11 18 5 8 11 5 18 15 2 12 0 19 13 8 6 1 14 16 3 10 17 4 9 7 4 17 14 1 11 18 19 12 7 5 0 13 15 2 9 16 3 8 10 6 16 13 0 10 17 19 11 6 4 18 12 14 1 8 15 2 7 9 3 5 12 18 9 16 19 10 5 3 17 11 13 0 7 14 1 6 8 2 15 4 17 8 15 19 9 4 2 16 10 12 18 6 13 0 5 7 1 14 11 3 7 14 19 8 3 1 15 9 11 17 5 12 18 4 6 0 13 10 16 2 13 19 7 2 0 14 8 10 16 4 11 17 3 5 18 12 9 15 6 1 19 6 1 18 13 7 9 15 3 10 16 2 4 17 11 8 14 5 12 0 5 0 17 12 6 8 14 2 9 15 1 3 16 10 7 13 4 11 19 18 18 16 11 5 7 13 1 8 14 0 2 15 9 6 12 3 10 19 4 17 15 10 4 6 12 0 7 13 18 1 14 8 5 11 2 9 19 3 17 16 9 3 5 11 18 6 12 17 0 13 7 4 10 1 8 19 2 16 14 15 ГҗЕёГҗВҫГҗВҝГ‘вӮ¬ГҗВҫГҗВұГ‘Ж’Г‘ЕҪ ГҗВҝГҗВҫГ‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ Г‘ВҒ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВҫГҗВ№ MOLS. ГҗЕёГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗȄВҸГ‘вҖҡГ‘Е’ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВәГҗВё/Г‘ВҒГ‘вҖҡГҗВҫГҗВ»ГҗВұГ‘вҖ Г‘вҖ№ ГҗВІ ГҗвҖәГҗЕЎ 20-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВҙГҗВҫГҗВІГҗВҫГҗ»ÑŒГҗВҪГҗВҫ Г‘вҖҡГ‘вӮ¬Г‘Ж’ГҗВҙГҗВҪГҗВҫ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЕЎГ‘ВҒГ‘вҖҡГҗ°ÑвҖҡГҗВё, Г‘ВҚГ‘вҖҡГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗ°ÑВҸ ГҗВҝГҗ°ÑвӮ¬ГҗВ° ГҗвҖқГҗвҖәГҗЕЎ 20-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 ГҗвҖқГҗвҖәГҗЕЎ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ ГҗВҝГҗ°ÑвӮ¬Г‘вҖ№ ГҗВҝГҗВҫГҗȄĄвҖЎГҗ°ÑЕҪГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВі ГҗВёГҗВ· ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВіГҗВ° ГҗВҝГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГ‘вҖҡГҗВ°ГҗВҪГҗВҫГҗВІГҗВәГҗВҫГҗВ№ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВә. ГҗВқГҗВөГҗ»ÑŒГҗВ·Г‘ВҸ ГҗВ»ГҗВё ГҗВҙГҗВҫГҗВұГҗВ°ГҗВІГҗВёГ‘вҖҡГ‘Е’ ГҗВә Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГҗВҫГҗВ№ ГҗВҝГҗ°ÑвӮ¬ГҗВө ГҗвҖәГҗЕЎ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВ№ ГҗВҫГҗВұГҗВҫГҗВёГҗВј ГҗвҖқГҗвҖәГҗЕЎ, Г‘вҖЎГ‘вҖҡГҗВҫГҗВұГ‘вҖ№ ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГҗВ»Гҗ°ÑВҒГ‘Е’ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВ° MOLS ГҗВёГҗВ· Г‘вҖҡГ‘вӮ¬Г‘вҖҳГ‘вҖҰ ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖәГҗЕЎ? ГҗВҘГҗВҫГ‘вӮ¬ГҗВҫГ‘ЛҶГҗВёГҗВ№ ГҗВІГҗВҫГҗВҝГ‘вӮ¬ГҗВҫГ‘ВҒ! |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷГҗВҫГҗВҝГ‘вӮ¬ГҗВҫГ‘ВҒ ГҗВҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВұГ‘вҖ№Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫ Г‘вӮ¬ГҗВ°ГҗВ·Г‘вӮ¬ГҗВөГ‘ЛҶГҗВёГҗȄВҒГ‘ВҸ! ГҗЛңГ‘вҖҡГҗВ°ГҗВә, ГҗВёГҗВјГҗВөГ‘ЕҪ Г‘ВҒГҗВ»ГҗВөГҗВҙГ‘Ж’Г‘ЕҪГ‘вҖ°Г‘Ж’Г‘ЕҪ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ ГҗВёГҗВ· Г‘вҖЎГҗВөГ‘вҖҡГ‘вҖ№Г‘вӮ¬Г‘вҖҳГ‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ 20-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° (ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГ‘вҖ№ ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 ГҗВЎГҗВәГҗВҫГҗВҪГ‘ВҒГ‘вҖҡГ‘вӮ¬Г‘Ж’ГҗВёГ‘вӮ¬ГҗВҫГҗВІГҗВ°ГҗВ»ГҗВ° Г‘вҖҡГҗВ°ГҗВәГҗВҫГҗВ№ ГҗвҖәГҗЕЎ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 ГҗЕЎГҗВ°ГҗВә ГҗВҫГҗВҪ Г‘ВҒГҗВәГҗВҫГҗВҪГ‘ВҒГ‘вҖҡГ‘вӮ¬Г‘Ж’ГҗВёГ‘вӮ¬ГҗВҫГҗВІГҗВ°ГҗВҪ - ГҗВҫГ‘вҖЎГҗВөГҗВІГҗВёГҗВҙГҗВҪГҗВҫ. ГҗвҖқГҗВҫГҗВұГҗВ°ГҗВІГҗВёГҗВ»ГҗВ° Г‘ВҚГ‘вҖҡГҗВҫГ‘вҖҡ ГҗвҖәГҗЕЎ ГҗВә ГҗВҝГҗВҫГҗВәГҗВ°ГҗВ·ГҗВ°ГҗВҪГҗВҪГҗВҫГҗВ№ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВө ГҗвҖқГҗвҖәГҗЕЎ. ГҗвҖҷГҗВҫГ‘вҖҡ Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГҗВ»ГҗВ° 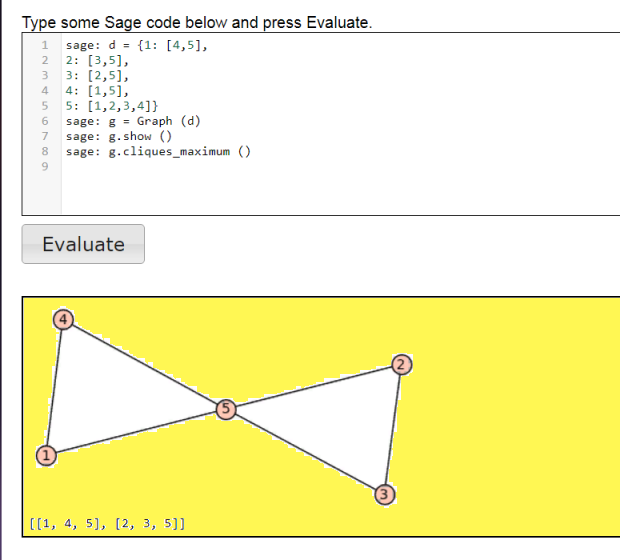 ГҗЕҫГ‘вҖЎГҗ°ÑвӮ¬ГҗВҫГҗВІГҗ°ÑвҖҡГҗВөГҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө ГҗВәГҗВ»ГҗВёГҗВәГҗВё Г‘вӮ¬ГҗВ°ГҗВ·ГҗВјГҗВөГ‘вӮ¬ГҗВ° 3! ГҗвҖқГҗВІГҗВө Г‘ЛҶГ‘вҖҡГ‘Ж’ГҗВәГҗВё. ГҗВўГҗВ°ГҗВәГҗВёГҗВј ГҗВҫГҗВұГ‘вӮ¬ГҗВ°ГҗВ·ГҗВҫГҗВј, ГҗВёГҗВјГҗВөГҗВөГҗВј ГҗВҙГҗВІГҗВө ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘вҖ№ MOLS 20-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘ВҸГ‘вҖ°ГҗВёГҗВө ГҗВёГҗВ· ГҗВҙГҗВІГ‘Ж’Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВё ГҗВҫГҗВҙГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖәГҗЕЎ. ГҗвҖҷГ‘ВҒГҗВө ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ ГҗВІ Г‘ВҚГ‘вҖҡГҗВёГ‘вҖҰ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗ°ÑвҖҰ MOLS ГҗВҝГҗВҫГҗȄĄвҖЎГҗ°ÑЕҪГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВі ГҗВёГҗВ· ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВіГҗВ° ГҗВҝГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГ‘вҖҡГҗВ°ГҗВҪГҗВҫГҗВІГҗВәГҗВҫГҗВ№ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВә. ГҗВЎГ‘Ж’ГҗВҝГҗВөГ‘вӮ¬! ГҗВўГҗВөГҗВҝГҗВөГ‘вӮ¬Г‘Е’ ГҗВ·ГҗВ°ГҗВҙГҗ°ÑвҖЎГҗВ° Г‘вӮ¬Гҗ°ÑВҒГ‘ЛҶГҗВёГ‘вӮ¬ГҗВөГҗВҪГҗВёГ‘ВҸ ГҗВҝГҗВҫГҗȄĄвҖЎГҗВөГҗВҪГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝ MOLS ГҗВҙГҗВҫ Г‘вҖЎГҗВөГ‘вҖҡГ‘вҖ№Г‘вӮ¬Г‘вҖҳГ‘вҖҰ ГҗвҖәГҗЕЎ. ГҗЛңГҗВ»ГҗВё ГҗВ¶ГҗВө ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВіГҗ°ÑВҸ ГҗВ·ГҗВ°ГҗВҙГҗ°ÑвҖЎГҗВ°: ГҗВҪГҗВ°ГҗВ№Г‘вҖҡГҗВё ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ MODLS 20-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘ВҸГ‘вҖ°Г‘Ж’Г‘ЕҪ ГҗВёГҗВ· Г‘вҖҡГ‘вӮ¬Г‘вҖҳГ‘вҖҰ ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЕёГҗВҫГҗВәГҗВ°ГҗВ·Г‘вҖ№ГҗВІГҗ°ÑЕҪ ГҗВҫГҗВҙГҗВҪГ‘Ж’ ГҗВёГҗВ· ГҗВҪГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝ MOLS 20-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, Г‘ВҒГҗВҫГҗВҫГ‘вҖҡГҗВІГҗВөГ‘вҖҡГ‘ВҒГ‘вҖҡГҗВІГ‘Ж’Г‘ЕҪГ‘вҖ°Г‘Ж’Г‘ЕҪ ГҗВәГҗВ»ГҗВёГҗВәГҗВө [1, 4, 5] 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18 3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17 2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16 1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15 5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14 9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13 8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12 7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11 6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10 10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9 14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8 13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7 12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6 11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5 15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4 19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3 18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2 17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0 ГҗЕёГ‘вӮ¬ГҗВҫГҗВІГҗВөГ‘вӮ¬Г‘ВҸГ‘ЕҪ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ MOLS ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВҫГҗВ№ Harry White GetOrthogonal Order? 20 Enter the name of the squares file: inp13 Choose 1 - get counts and maximum pairs, or 2 - get pairs for one square: 1 ..output file inp13-orthCounts_2.txt ..output file inp13-orthNos_2.txt squares 3 total orthogonal pairs 3 Maximum pairs for square 1: 2 There are 2 other squares with this maximum number of pairs. ..output file inp13-1orths_1.txt Pairs for square 1: 2 ГҗвҖҷГ‘ВҒГ‘вҖҳ ГҗВІГҗВөГ‘вӮ¬ГҗВҪГҗВҫ. ГҗВўГҗВ°ГҗВұГҗВ»ГҗВёГ‘вҖ ГҗВ° ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВҝГҗ°ÑвӮ¬ 1: [2,3], 2: [1,3], 3: [1,2] ГҗвҖҷГҗВҫГ‘вҖҡ Г‘вҖҡГҗВ°ГҗВә ГҗВҝГ‘вӮ¬ГҗВҫГ‘ВҒГ‘вҖҡГҗВҫ Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗȄВҸГ‘ЕҪГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘вҖ№ MOLS 20-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘ВҸГ‘вҖ°ГҗВёГҗВө ГҗВёГҗВ· Г‘вҖҡГ‘вӮ¬Г‘вҖҳГ‘вҖҰ ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖәГҗЕЎ. ГҗЕ“Гҗ°ÑвҖҡГҗВөГҗВјГҗ°ÑвҖҡГҗВёГҗВәГҗВ°ГҗВј Г‘Ж’ГҗВҙГҗВ°ГҗВ»ГҗВҫГ‘ВҒГ‘Е’ ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГ‘вҖҡГ‘Е’ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ MOLS ГҗВҙГҗВ°ГҗВҪГҗВҪГҗВҫГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘ВҸГ‘вҖ°Г‘Ж’Г‘ЕҪ ГҗВёГҗВ· Г‘вҖЎГҗВөГ‘вҖҡГ‘вҖ№Г‘вӮ¬Г‘вҖҳГ‘вҖҰ ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖәГҗЕЎ, ГҗВҪГҗВҫ ГҗВІ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВө ГҗВҪГҗВөГ‘вҖҡ ГҗВҪГҗВё ГҗВҫГҗВҙГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖқГҗвҖәГҗЕЎ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖқГ‘Ж’ГҗВұГҗВ»ГҗВёГ‘вӮ¬Г‘Ж’Г‘ЕҪ Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГҗВө https://boinc.multi-pool.info/latinsquares/forum_thread.php?id=117&postid=1160 ГҗвҖ”ГҗВ°ГҗВҙГҗ°ÑЕҪ ГҗВәГҗВҫГҗВјГҗВ°ГҗВҪГҗВҙГ‘Ж’ sage: designs.mutually_orthogonal_latin_squares(4,20) ГҗЕёГҗВҫГҗȄĄвҖЎГҗ°ÑЕҪ [20 x 20 dense matrix over Integer Ring, 20 x 20 dense matrix over Integer Ring, 20 x 20 dense matrix over Integer Ring, 20 x 20 dense matrix over Integer Ring] ГҗЕЎГҗВҫГҗȄ΄вҖ ГҗВҫ! ГҗвҖ”ГҗВ°ГҗВҙГҗ°ÑЕҪ ГҗВәГҗВҫГҗВјГҗВ°ГҗВҪГҗВҙГ‘Ж’ sage: designs.mutually_orthogonal_latin_squares(5,20) ГҗЕёГҗВҫГҗȄĄвҖЎГҗ°ÑЕҪ ГҗВІ ГҗВҫГ‘вҖҡГҗВІГҗВөГ‘вҖҡ NotImplementedError: I don't know how to build 5 MOLS of order 20 ГҗВқГҗВө ГҗВ·ГҗВҪГҗВ°ГҗВөГ‘вҖҡ :) ГҗВҜ Г‘вҖҡГҗВҫГҗВ¶ГҗВө ГҗВҪГҗВө ГҗВ·ГҗВҪГҗ°ÑЕҪ :) ________________________ ГҗВәГҗВҫГҗВҪГҗВөГ‘вҖ ГҗВҙГ‘Ж’ГҗВұГҗВ»ГҗВёГ‘вӮ¬Г‘Ж’ГҗВөГҗВјГҗВҫГҗВіГҗВҫ Г‘ВҒГҗВҫГҗВҫГҗВұГ‘вҖ°ГҗВөГҗВҪГҗВёГ‘ВҸ ГҗВҗГҗВұГ‘ВҒГҗВҫГҗȄЕҪГ‘вҖҡГҗВҪГҗВҫ Г‘вҖҡГ‘вҖҳГҗВјГҗВҪГҗ°ÑВҸ ГҗВҪГҗ°ÑВҒГ‘вҖЎГ‘вҖҳГ‘вҖҡ ГҗВәГҗВҫГҗВ»ГҗВөГ‘вҖ . ГҗвҖңГҗВҫГ‘ВҒГҗВҝГҗВҫГҗВҙГҗВ°! ГҗЕёГ‘вӮ¬ГҗВҫГ‘ВҒГҗВІГҗВөГ‘вҖҡГҗВёГ‘вҖҡГҗВө, ГҗВҝГҗВҫГҗВ¶ГҗВ°Гҗ»ÑƒГҗВ№Г‘ВҒГ‘вҖҡГҗВ°. Гҗ§ÑвҖҡГҗВҫ Г‘ВҚГ‘вҖҡГҗВҫ ГҗВҫГҗВ·ГҗВҪГҗ°ÑвҖЎГҗВ°ГҗВөГ‘вҖҡ 20 x 20 dense matrix over Integer Ring ГҗВЈ ГҗВјГҗВөГҗВҪГ‘ВҸ ГҗВөГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВҝГҗВҫГҗВҙГҗВҫГҗВ·Г‘вӮ¬ГҗВөГҗВҪГҗВёГҗВө, Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВІ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗ°ÑвҖҰ MOLS, ГҗВіГҗВҙГҗВө ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ ГҗВҝГҗВҫГҗȄĄвҖЎГҗ°ÑЕҪГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВі ГҗВёГҗВ· ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВіГҗВ° ГҗВҝГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГ‘вҖҡГҗВ°ГҗВҪГҗВҫГҗВІГҗВәГҗВҫГҗВ№ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВә, Г‘вҖҡГҗВҫГҗВ¶ГҗВө ГҗВөГ‘ВҒГ‘вҖҡГ‘Е’ ГҗВәГҗВ°ГҗВәГҗВҫГҗВө-Г‘вҖҡГҗВҫ ГҗВәГҗВҫГҗȄ΄вҖ ГҗВҫ. ГҗВқГҗВҫ ГҗВІ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВө MOLS 20-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, ГҗВІГ‘вҖ№ГҗВҙГҗВ°ГҗВҪГҗВҪГҗВҫГҗВ№ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВҫГҗВ№ SageMath, ГҗВә Г‘ВҒГҗВҫГҗВ¶ГҗВ°ГҗВ»ГҗВөГҗВҪГҗВёГ‘ЕҪ, ГҗВҪГҗВө ГҗВІГҗВёГҗВҙГҗВҪГҗВҫ ГҗВҝГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГ‘вҖҡГҗВ°ГҗВҪГҗВҫГҗВІГҗВҫГҗВә Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВә ГҗВІ ГҗвҖәГҗЕЎ. ГҗЕ“ГҗВҫГҗВ¶ГҗВөГ‘вҖҡ ГҗВұГ‘вҖ№Г‘вҖҡГ‘Е’, ГҗВ·ГҗВ°ГҗВІГ‘Ж’ГҗВ°ГҗВ»ГҗВёГ‘вӮ¬ГҗВҫГҗВІГҗВ°ГҗВҪГ‘вҖ№ ГҗВәГҗВ°ГҗВә-Г‘вҖҡГҗВҫ. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗвҖҷГҗВіГ‘вӮ¬Г‘вҖ№ГҗВ·Гҗ°ÑЕҪГ‘ВҒГ‘Е’ ГҗВІ ГҗВҝГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГ‘вҖҡГҗВ°ГҗВҪГҗВҫГҗВІГҗВәГ‘Ж’ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВә ГҗВІ ГҗвҖқГҗвҖәГҗЕЎ 20-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°. ГҗВЎГҗВҪГҗ°ÑвҖЎГҗВ°ГҗВ»ГҗВ° Г‘вӮ¬ГҗВөГ‘ЛҶГҗВёГҗВ»ГҗВ° ГҗВҝГҗВҫГ‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ Г‘ВҒГҗВҫ Г‘ВҒГҗВІГҗВҫГҗВөГҗВ№ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВҫГҗВ№ MOLS, Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘ВҸГ‘вҖ°ГҗВөГҗВ№ ГҗВёГҗВ· ГҗВҙГҗВІГ‘Ж’Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВё ГҗВҫГҗВҙГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖәГҗЕЎ.ГҗвҖҷ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВө ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ ГҗВҝГҗВҫГҗȄĄвҖЎГҗ°ÑЕҪГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВі ГҗВёГҗВ· ГҗВҙГ‘вӮ¬Г‘Ж’ГҗВіГҗВ° ГҗВҝГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГ‘вҖҡГҗВ°ГҗВҪГҗВҫГҗВІГҗВәГҗВҫГҗВ№ Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВә, Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВҝГҗВҫГҗВҙГҗ°ÑвҖҳГ‘вҖҡ ГҗВҪГҗВ°ГҗВҙГҗВөГҗВ¶ГҗВҙГ‘Ж’ ГҗВҪГҗВ° Г‘вӮ¬Гҗ°ÑВҒГ‘ЛҶГҗВёГ‘вӮ¬ГҗВөГҗВҪГҗВёГҗВө ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘вҖ№ MOLS (Г‘вҖҡГҗВ°ГҗВәГҗВёГҗВө ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ ГҗВұГ‘вҖ№ГҗВ»ГҗВё ГҗВІ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗ°ÑвҖҰ MOLS 12-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°). ГҗВқГҗВөГ‘ВҒГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬Г‘ВҸ ГҗВҪГҗВ° ГҗВІГ‘ВҒГҗВө Г‘ВҚГҗВІГ‘вӮ¬ГҗВёГ‘ВҒГ‘вҖҡГҗВёГҗВәГҗВё ГҗВҝГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГ‘вҖҡГҗВ°ГҗВҪГҗВҫГҗВІГҗВәГҗВ° Г‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВә ГҗВІ ГҗвҖқГҗвҖәГҗЕЎ 20-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВІГ‘вҖ№ГҗВҝГҗВҫГҗВ»ГҗВҪГ‘ВҸГҗВөГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВҙГҗВҫГҗВІГҗВҫГҗ»ÑŒГҗВҪГҗВҫ ГҗВјГҗВөГҗВҙГҗВ»ГҗВөГҗВҪГҗВҪГҗВҫ. ГҗВӯГ‘вҖҡГҗВҫ ГҗВІГҗВҝГҗВҫГҗВ»ГҗВҪГҗВө ГҗВҫГҗВұГ‘Е Г‘ВҸГ‘ВҒГҗВҪГҗВёГҗВјГҗВҫ. ГҗВқГҗВҫ ГҗВІГ‘вҖ№ГҗВҝГҗВҫГҗВ»ГҗВҪГ‘ВҸГҗВөГ‘вҖҡГ‘ВҒГ‘ВҸ! ГҗвҖҷГҗВҫГ‘вҖҡ ГҗВҝГҗВҫГ‘ВҒГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖҡГҗВө, Г‘ВҒГҗВәГҗВҫГҗ»ÑŒГҗВәГҗВҫ Г‘Ж’ГҗВ¶ГҗВө ГҗВҪГҗВҫГҗВІГ‘вҖ№Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ Г‘ВҸ ГҗВҝГҗВҫГҗȄĄвҖЎГҗВёГҗВ»ГҗВ° (Г‘ВҚГ‘вҖҡГҗВҫ ГҗВёГ‘вҖҰ Г‘ВҒГҗВІГҗВҫГҗВ№Г‘ВҒГ‘вҖҡГҗВІГҗВ°, ГҗВІГ‘вҖ№ГҗВҙГҗВ°ГҗВҪГҗВҪГ‘вҖ№ГҗВө Г‘Ж’Г‘вҖҡГҗВёГҗВ»ГҗВёГ‘вҖҡГҗВҫГҗВ№ Harry White) Order? 20
Enter the name of the squares file: INP1
.. writing type information to file INP1TypeDetail.txt
Counts
------
61463 diagonal Latin
1818 weakly pandiagonal
278 axial symmetric
276 center symmetric
61463 nfr
188 self-orthogonal
112 axial parity 1-way
38 symmetric parityГҗЕЎГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВёГҗВәГҗВё Г‘вҖҰГҗВҫГ‘вӮ¬ГҗВҫГ‘ЛҶГҗВёГҗВө. ГҗВқГ‘Ж’, ГҗВҝГҗВҫГҗВәГҗВ° Г‘вҖҡГҗВҫГҗ»ÑŒГҗВәГҗВҫ ГҗВҫГ‘вҖҡГҗВ»ГҗВ°ГҗВҙГҗВёГҗВ»ГҗВ° ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГ‘Ж’ ГҗВё Г‘ВҒГҗВҙГҗВөГҗВ»ГҗВ°ГҗВ»ГҗВ° ГҗВҫГҗВҙГҗВёГҗВҪ ГҗВҝГ‘вӮ¬ГҗВҫГ‘вҖҰГҗВҫГҗВҙ ГҗВҙГҗȄВҸ ГҗВҫГҗВәГҗВҫГҗВҪГ‘вҖЎГҗ°ÑвҖҡГҗВөГҗ»ÑŒГҗВҪГҗВҫГҗВіГҗВҫ Г‘вҖҡГҗВөГ‘ВҒГ‘вҖҡГҗВёГ‘вӮ¬ГҗВҫГҗВІГҗВ°ГҗВҪГҗВёГ‘ВҸ. ГҗвҖҷГ‘вӮ¬ГҗВҫГҗВҙГҗВө ГҗВІГ‘ВҒГ‘вҖҳ ГҗВҝГ‘вӮ¬ГҗВ°ГҗВІГҗВёГҗ»ÑŒГҗВҪГҗВҫ, ГҗвҖқГҗвҖәГҗЕЎ ГҗВҝГҗВҫГҗȄĄвҖЎГҗ°ÑЕҪГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВҝГ‘вӮ¬ГҗВ°ГҗВІГҗВёГҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө. ГҗЕ“ГҗВҫГҗВ¶ГҗВҪГҗВҫ ГҗВҝГ‘вӮ¬ГҗВҫГҗВҙГҗВҫГҗВ»ГҗВ¶Гҗ°ÑвҖҡГ‘Е’. |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЕҫГ‘вҖЎГҗВөГҗВҪГ‘Е’ ГҗВёГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҪГ‘вҖ№ГҗВ№ ГҗВјГҗВҫГҗВјГҗВөГҗВҪГ‘вҖҡ! ГҗвҖҷГ‘ВҒГҗВө ГҗВҪГҗВ°ГҗВ№ГҗВҙГҗВөГҗВҪГҗВҪГ‘вҖ№ГҗВө ГҗВҪГҗВҫГҗВІГ‘вҖ№ГҗВө ГҗвҖқГҗвҖәГҗЕЎ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ ГҗВә ГҗвҖәГҗЕЎ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘вҖ№ MOLS Order? 20
Enter the name of the squares file: inp1
Choose 1 - get counts and maximum pairs, or 2 - get pairs for one square: 2
.. increasing LS store to 100,000
squares 61465
Get pairs for square number, (1 .. 61465)? 3
..output file inp1-3orths.txt
Pairs for square 3: 61464
elapsed time 0:00:28 |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЕҫГҗВҝГ‘Ж’ГҗВұГҗВ»ГҗВёГҗВәГҗВҫГҗВІГҗВ°ГҗВ»ГҗВ° ГҗВ·ГҗВ°ГҗВҙГҗ°ÑвҖЎГ‘Ж’ ГҗВҪГҗВ° Г‘вҖһГҗВҫГ‘вӮ¬Г‘Ж’ГҗВјГҗВө Math Help Planet http://mathhelpplanet.com/viewtopic.php?f=54&t=74774&p=422243#p422243 ГҗВқГҗВҫ Г‘ВҚГ‘вҖҡГҗВ° Г‘вҖҡГҗВөГҗВјГҗВ° ГҗВҙГҗВҫГҗВ»ГҗВіГҗВҫ ГҗВҪГҗВө ГҗВҝГ‘вӮ¬ГҗВҫГҗВ¶ГҗВёГҗВІГ‘вҖҳГ‘вҖҡ. ГҗВЈ ГҗвҖҷГҗВөГ‘вӮ¬Г‘вҖҰГҗВҫГҗВІГҗВҪГҗВҫГҗВіГҗВҫ (ГҗВё ГҗВөГҗВҙГҗВёГҗВҪГ‘ВҒГ‘вҖҡГҗВІГҗВөГҗВҪГҗВҪГҗВҫГҗВіГҗВҫ) ГҗВјГҗВҫГҗВҙГҗВөГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГ‘вӮ¬ГҗВ° ГҗВҪГҗВ° Г‘ВҚГ‘вҖҡГҗВҫГҗВј Г‘вҖһГҗВҫГ‘вӮ¬Г‘Ж’ГҗВјГҗВө Гҗ¶ÑƒÑвҖҡГҗВәГҗ°ÑВҸ ГҗВ°ГҗВ»ГҗВ»ГҗВөГ‘вӮ¬ГҗВіГҗВёГ‘ВҸ ГҗВҪГҗВ° ГҗВ»Гҗ°ÑвҖҡГҗВёГҗВҪГ‘ВҒГҗВәГҗВёГҗВө ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ :) ГҗвҖҷГҗВҫГ‘вҖҡ ГҗВәГҗВ°ГҗВә ГҗВҝГ‘вӮ¬ГҗВёГҗВҙГ‘вҖҳГ‘вҖҡ ГҗВҫГҗВҪГҗВ° ГҗВҪГҗВ° Г‘вҖһГҗВҫГ‘вӮ¬Г‘Ж’ГҗВј, Г‘вҖҡГҗВ°ГҗВә Г‘ВҒГ‘вӮ¬ГҗВ°ГҗВ·Г‘Ж’ ГҗВ¶ГҗВө Г‘вҖҡГҗВөГҗВјГ‘Ж’ ГҗВё ГҗВ·ГҗВ°ГҗВәГ‘вӮ¬ГҗВҫГҗВөГ‘вҖҡ. ГҗЕёГҗВҫГҗВҪГҗВ°ГҗВұГҗȄЕҪГҗВҙГҗВ°ГҗВ№Г‘вҖҡГҗВө :) ГҗВЈГҗВ¶ГҗВө ГҗВ·ГҗВ°ГҗВәГ‘вӮ¬Г‘вҖ№ГҗВ»ГҗВ° ГҗВІГҗВөГ‘вӮ¬Г‘вҖҰГҗВҫГҗВІГҗВҪГҗ°ÑВҸ ГҗВјГҗВҫГҗВҙГҗВөГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГ‘вӮ¬Г‘ЛҶГҗВ° Г‘вҖҡГҗВөГҗВјГ‘Ж’. ГҗВҘГҗВ°-Г‘вҖҰГҗВ°-Г‘вҖҰГҗВ°! :))) ГҗВқГҗВө ГҗВҙГ‘Ж’ГҗВјГҗВ°ГҗВ»ГҗВ° Г‘ВҸ, Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВҪГҗВ° ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГ‘вҖ№ ГҗВјГҗВҫГҗВ¶ГҗВөГ‘вҖҡ ГҗВұГ‘вҖ№Г‘вҖҡГ‘Е’ ГҗВ°ГҗВ»ГҗВ»ГҗВөГ‘вӮ¬ГҗВіГҗВёГ‘ВҸ. ГҗвҖҷ Г‘вҖЎГ‘вҖҳГҗВј ГҗВҝГ‘вӮ¬ГҗВҫГ‘ВҸГҗВІГҗȄВҸГҗВөГ‘вҖҡГ‘ВҒГ‘ВҸ? ГҗвҖңГҗВҙГҗВө Г‘ВҒГҗВІГҗВөГ‘вӮ¬ГҗВұГҗВёГ‘вҖҡ? :) ГҗвҖңГҗВҙГҗВө ГҗВҝГҗВҫГҗВәГ‘вӮ¬Гҗ°ÑВҒГҗВҪГҗВөГҗВҪГҗВёГҗВө ГҗВәГҗВҫГҗВ¶ГҗВё? ГҗВҗ ГҗВіГҗВҙГҗВө ГҗВҝГҗВҫГ‘ВҒГҗВёГҗВҪГҗВөГҗВҪГҗВёГҗВө? |
 Natalia Makarova Natalia MakarovaSend message Joined: 22 Oct 17 Posts: 3091 Credit: 0 RAC: 0 |
ГҗЕҫГҗВҝГҗВ°! ГҗВҗ Г‘вҖЎГ‘вҖҡГҗВҫ ГҗВҪГҗ°ÑЛҶГҗВ»ГҗВ° ГҗВІ Г‘ВҒГҗВІГҗВҫГҗВөГҗВ№ Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ГҗВө, ГҗВҪГҗВ°ГҗВҝГҗВёГ‘ВҒГҗВ°ГҗВҪГҗВҪГҗВҫГҗВ№ ГҗВІ ГҗВјГҗ°ÑвӮ¬Г‘вҖҡГҗВө 2009 ГҗВі. ГҗвҖңГҗВ ГҗВЈГҗЕёГҗЕёГҗВ« MOLS 20-ГҗВіГҗВҫ ГҗВё 21-ГҗВіГҗВҫ ГҗЕёГҗЕҫГҗВ ГҗВҜГҗвҖқГҗЕЎГҗВҗ http://www.natalimak1.narod.ru/mols20_21.htm ГҗВҰГҗВёГ‘вҖҡГҗВёГ‘вӮ¬Г‘Ж’Г‘ЕҪ ГҗВўГҗВөГҗВҝГҗВөГ‘вӮ¬Г‘Е’ ГҗВҙГҗȄВҸ ГҗВҝГҗВҫГҗВ»ГҗВҪГҗВҫГ‘вҖҡГ‘вҖ№ ГҗВәГҗ°ÑвӮ¬Г‘вҖҡГҗВёГҗВҪГ‘вҖ№ ГҗВҝГҗВҫГҗВәГҗВ°Гҗ¶Ñƒ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ MOLS 20-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ° ГҗВёГҗВ· Г‘вҖҡГ‘вӮ¬Г‘вҖҳГ‘вҖҰ ГҗВ»Гҗ°ÑвҖҡГҗВёГҗВҪГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ, ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВҪГ‘Ж’Г‘ЕҪ ГҗВјГҗВөГ‘вҖҡГҗВҫГҗВҙГҗВҫГҗВј Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВ°ГҗВІГҗВҪГ‘вҖ№Г‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВҫГҗВІ (Г‘вӮ¬ГҗВёГ‘ВҒ. 13 ГўвӮ¬вҖң 15). ГҗЕёГҗВөГ‘вӮ¬ГҗВІГ‘вҖ№ГҗВө ГҗВҙГҗВІГҗВ° ГҗВ»Гҗ°ÑвҖҡГҗВёГҗВҪГ‘ВҒГҗВәГҗВёГ‘вҖҰ ГҗВәГҗВІГҗВ°ГҗВҙГ‘вӮ¬Гҗ°ÑвҖҡГҗВ° ГҗВІ Г‘ВҚГ‘вҖҡГҗВҫГҗВ№ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВө ГҗВҙГҗВёГҗВ°ГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№ГҗВө. ГҗЕҫГҗВәГҗВ°ГҗВ·Г‘вҖ№ГҗВІГҗВ°ГҗВөГ‘вҖҡГ‘ВҒГ‘ВҸ, ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ MOLS 20-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘ВҸГ‘вҖ°Г‘Ж’Г‘ЕҪ ГҗВёГҗВ· ГҗВҙГҗВІГ‘Ж’Г‘вҖҰ ГҗвҖқГҗвҖәГҗЕЎ ГҗВё ГҗВҫГҗВҙГҗВҪГҗВҫГҗВіГҗВҫ ГҗвҖәГҗЕЎ, Г‘ВҸ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВёГҗВ»ГҗВ° 12 ГҗВ»ГҗВөГ‘вҖҡ ГҗВҪГҗВ°ГҗВ·ГҗВ°ГҗВҙ. ГҗВЎГҗВјГҗВҫГ‘вҖҡГ‘вӮ¬ГҗВёГ‘вҖҡГҗВө Г‘ВҚГ‘вҖҡГ‘Ж’ ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘Ж’ MOLS ГҗВІ Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ГҗВө. ГҗВқГ‘Ж’, ГҗВіГҗВҫГҗВ»ГҗВҫГҗВІГҗВ° ГҗВҫГҗВҙГҗВёГҗВҪГҗВ°ГҗВәГҗВҫГҗВІГҗВҫ Г‘вҖҡГҗВҫГҗВіГҗВҙГҗВ° Г‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗВ°ГҗВ»ГҗВ° ГҗВё Г‘ВҒГҗВөГҗВ№Г‘вҖЎГҗ°ÑВҒ Г‘вӮ¬ГҗВ°ГҗВұГҗВҫГ‘вҖҡГҗВ°ГҗВөГ‘вҖҡ :) ГҗвҖҷ Г‘ВҒГ‘вҖҡГҗ°ÑвҖҡГ‘Е’ГҗВө Г‘вҖҡГҗВ°ГҗВәГҗВ¶ГҗВө ГҗВҫГҗВҝГҗВёГ‘ВҒГ‘вҖ№ГҗВІГҗВ°ГҗВөГ‘вҖҡГ‘ВҒГ‘ВҸ ГҗВҝГҗВҫГ‘ВҒГ‘вҖҡГ‘вӮ¬ГҗВҫГҗВөГҗВҪГҗВёГҗВө ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГ‘вҖ№ MOLS 20-ГҗВіГҗВҫ ГҗВҝГҗВҫГ‘вӮ¬Г‘ВҸГҗВҙГҗВәГҗВ°, Г‘ВҒГҗВҫГ‘ВҒГ‘вҖҡГҗВҫГ‘ВҸГ‘вҖ°ГҗВөГҗВ№ ГҗВёГҗВ· Г‘вҖЎГҗВөГ‘вҖҡГ‘вҖ№Г‘вӮ¬Г‘вҖҳГ‘вҖҰ ГҗВІГҗВ·ГҗВ°ГҗВёГҗВјГҗВҪГҗВҫ ГҗВҫГ‘вӮ¬Г‘вҖҡГҗВҫГҗВіГҗВҫГҗВҪГҗВ°Гҗ»ÑŒГҗВҪГ‘вҖ№Г‘вҖҰ ГҗвҖәГҗЕЎ ГҗВҝГҗВҫ ГҗВёГҗВ·ГҗВІГҗВөГ‘ВҒГ‘вҖҡГҗВҪГҗВҫГҗВ№ ГҗВәГҗВІГҗВ°ГҗВ·ГҗВё-Г‘вӮ¬ГҗВ°ГҗВ·ГҗВҪГҗВҫГ‘ВҒГ‘вҖҡГҗВҪГҗВҫГҗВ№ ГҗВјГҗ°ÑвҖҡГ‘вӮ¬ГҗВёГ‘вҖ ГҗВө. ГҗЛңГҗВҪГ‘вҖҡГҗВөГ‘вӮ¬ГҗВөГ‘ВҒГҗВҪГҗВҫ: Г‘ВҒГҗВҫГҗВІГҗВҝГҗВ°ГҗВҙГҗВ°ГҗВөГ‘вҖҡ ГҗВ»ГҗВё Г‘ВҚГ‘вҖҡГҗВ° ГҗВіГ‘вӮ¬Г‘Ж’ГҗВҝГҗВҝГҗВ° MOLS Г‘ВҒ Г‘вҖҡГҗВҫГҗВ№, ГҗВәГҗВҫГ‘вҖҡГҗВҫГ‘вӮ¬Г‘Ж’Г‘ЕҪ ГҗВІГ‘вҖ№ГҗВҙГҗ°ÑвҖҳГ‘вҖҡ ГҗВҝГ‘вӮ¬ГҗВҫГҗВіГ‘вӮ¬ГҗВ°ГҗВјГҗВјГҗВ° SageMath? |

©2026 ©2024 Progger & Stefano Tognon (ice00) & Reese
